Abstract
Radiation dosimetry is an essential input for epidemiological studies of radiotherapy patients aimed at quantifying the dose-response relationship of late-term morbidity and mortality. Individualized organ dose must be estimated for all tissues of interest located in-field, near-field, or out-of-field. Whereas conventional measurement approaches are limited to points in water or anthropomorphic phantoms, computational approaches using patient images or human phantoms offer greater flexibility and can provide more detailed 3-dimensional dose information. In the current study, we systematically compared four different dose calculation algorithms so that dosimetrists and epidemiologists can better understand the advantages and limitations of the various approaches at their disposal. The four dose calculations algorithms considered were: (1) Analytical Anisotropic Algorithm (AAA) and (2) Acuros XB algorithm (Acuros XB) as implemented in the Eclipse treatment planning system (TPS); (3) a Monte Carlo radiation transport code, EGSnrc; (4) an accelerated Monte Carlo code, XVMC. The four algorithms are compared in terms of their accuracy and appropriateness in the context of dose reconstruction for epidemiological investigations. Accuracy in peripheral dose was evaluated first by benchmarking the calculated dose profiles against measurements in a homogenous water phantom. Additional simulations in a heterogeneous cylinder phantom evaluated the performance of the algorithms in the presence of tissue heterogeneity. In general, we found that the algorithms contained within the commercial TPS (AAA and Acuros XB) were fast and accurate in-field or near-field, but not acceptable out-of-field. Therefore, the TPS is best suited for epidemiological studies involving large cohorts and where the organs of interest are located in-field or partially in-field. The EGSnrc and XVMC codes showed excellent agreement with measurement both in-field and out-of-field. The EGSnrc code was the most accurate dosimetry approach, but is too slow to be used for large-scale epidemiological cohorts. The XVMC code showed similar accuracy to EGSnrc, but was significantly faster so that application to epidemiological applications seem feasible, especially when the organs of interest reside far away from the field edge.
Keywords: radiation dosimetry, radiotherapy, epidemiology, phantom, DICOM, Monte Carlo
1. Introduction
Recent advances in cancer treatment and screening have resulted in substantial improvements in survival rates [1]. Radiotherapy has undoubtedly played an important role in this success such that currently about half of all cancer patients receive radiation at some point during the course of their treatment [2]. However, radiotherapy has also been implicated as a causal factor in the development of late-term toxicities such as second primary cancers [3–5] and cardiovascular disease [6,7]. There is a growing body of literature suggesting a dose-response relationship for these morbidities and mortality, with the elevated risk persisting decades after treatment [8,9]. As cancer survival rates improve, greater focus is being placed on reducing the risk of such late-term outcomes, particularly for pediatric patients owing to their increased susceptibility to radiation injury and their long remaining life expectancy [10]. Consequently, external radiotherapy techniques have trended towards methods which spare normal tissues to an increasingly greater extent (e.g. intensity modulated radiation therapy and image-guided radiation therapy). Although modern treatment techniques can spare nearby organs at risk from unnecessary high dose, these gains are sometimes achieved at the expense of increasing the volume of normal tissue receiving low dose [11,12]. Epidemiological research, in the form of cohort or case-control studies, are an important way to evaluate the health effects of this unintended peripheral dose.
Radiation dosimetry is essential for quantifying the dose-response relationship of radiotherapy-related health effects. Individualized organ dose must be estimated for all normal tissues of interest which can be located inside the radiotherapy field (“in-field”), adjacent to the field edge (“near-field”), or at a distance (“out-of-field”). The radiation dose decreases substantially with distance beyond the treatment field edge and is composed of: (1) scatter radiation within the patient; (2) scatter radiation from the head of the linear accelerator (LINAC); and (3) leakage radiation penetrating through the LINAC shielding [13]. Accurate dose assessment should account for each of these components. This poses a significant challenge because of the need to consider the detailed geometry and elemental composition of the LINAC and patient, as well as the radiotherapy plan (e.g. target location, prescribed dose, beam energy, field size, collimator angle, multi-leaf collimators, wedges, etc.). These difficulties become especially apparent in the context of epidemiological studies which typically involve a large number of patients who were treated many years in the past, for whom anatomical images may be inaccessible, and for whom only limited radiotherapy plan information may be known.
Previous epidemiological studies have reconstructed radiotherapy organ dose based on measurements performed in physical phantoms [14–16] or calculations performed using a commercial radiotherapy treatment planning system (TPS) [6,17]. Each of these methods has its limitations. Measurement approaches, such as those described by Stovall et al. [18] and Howell et al. [19], are labor-intensive and limited to water or anthropomorphic physical phantoms which may not capture the unique anatomy of each patient. Commercial TPSs are specifically commissioned for in-field dose calculation, and are known to have errors that increase with distance beyond the radiotherapy field edge [20]. One study by Joosten et al. [21] reported TPS errors in a water phantom as large as 179 % at points within 10 cm of the field edge in the inplane direction. As an alternative, some researchers [22,23] have demonstrated analytical methods for modeling LINAC peripheral dose in water phantoms. While an important research milestone, it is unresolved how this approach will be extended to account for tissue heterogeneities or patient-specific body scatter which can be important for out-of-field dose estimation. The electronification of medical records is expanding access to more detailed, patient-specific radiotherapy data than ever before. Therefore, future epidemiological studies will benefit from the development of dosimetry methods which can seamlessly incorporate such personalized data for improving the dosimetry estimates.
We previously introduced an image-based dosimetry approach for reconstructing radiotherapy organ dose [24]. A key feature of our method is that it interfaces directly with Digital Imaging and Communications in Medicine radiotherapy (DICOM-RT) files. The detailed anatomy (DICOM-CT) and available organ definitions (DICOM-RT STRUCTURE) along with the radiotherapy technique (DICOM-RTPLAN) can be used to reconstruct dose with unprecedented accuracy and flexibility. If patient computed tomography (CT) images are not available for members of a cohort, as is often the case for retrospective studies, a computational human phantom [25,26] matched to the patient based on data from medical records (e.g. age, gender, height, weight) can be used as a surrogate anatomy. If the DICOM-RTPLAN is also unavailable, then a phantom or patient CT is loaded into the TPS and an approximate plan can be created using information abstracted from the radiotherapy medical records. The advantage of this flexible approach is that it can incorporate all available information for more accurate dose estimation. Once the patient geometry and treatment techniques are modeled, organ doses can be estimated by using one of several possible dose calculation algorithms. However, the paper [24] did not evaluate the differences among available dose calculation algorithms for radiotherapy organ dose estimation. Therefore, a comparison of normal tissue dose calculation methods is needed so that dosimetrists and epidemiologists can better understand the advantages and limitations of the various approaches at their disposal.
In the current study, we systematically compare four different dose calculation algorithms in terms of their accuracy and appropriateness in the context of dose reconstruction for epidemiological investigations. The four dose calculations algorithms considered were: (1) Analytical Anisotropic Algorithm (AAA) and (2) Acuros XB algorithm (Acuros XB) as implemented in the Eclipse treatment planning system (TPS); (3) a Monte Carlo radiation transport code, EGSnrc; (4) an accelerated Monte Carlo code, XVMC.
2. Methods
2.1. Dose calculation algorithms
Our comparison considered four different dose calculation algorithms. The AAA and Acuros XB methods were selected because these are conveniently available on the Eclipse TPS (Version 13.6, Varian Medical Systems, Palo Alto, CA). The EGSnrc code was selected because it is a state-of-art Monte Carlo radiation transport code which is widely accepted as the de facto gold standard method for performing radiation dose calculations. The XVMC code was selected because it is an accelerated Monte Carlo code designed specifically for simulating radiotherapy treatments. A brief description of each algorithm is provided below.
The AAA dose calculation method is a 3-dimenisonal (3D) pencil beam convolution algorithm [27]. The algorithm uses a superposition of pre-calculated mono-energetic dose deposition functions and scattering kernels which are weighted according to the beam spectrum. Heterogeneities are accounted for by scaling the dose deposition functions and scattering kernels to account for the mean electron density in each CT voxel relative to water.
Acuros XB is a grid-based multi-group discrete ordinates method for solving the 3D photon-electron coupled linear Boltzmann radiation transport equation [28]. The uncollided fluence in each voxel of the patient CT is calculated using a ray-tracing algorithm which accounts for attenuation through the patient. The total uncollided fluence from all beams is then used as source term in a scattering calculation to deterministically solve for the energy-dependent electron fluence in every voxel. Acuros XB handles heterogeneities explicitly by using look-up tables to automatically assign materials to each voxel depending on the CT Hounsfield unit (HU). The user can also manually assign materials from a library. Dose is calculated as a post-processing step by multiplying the scalar flux with energy deposition cross-sections for the assigned material. The absorbed dose in each voxel can be reported as either dose-to-water or dose-to-medium.
The EGSnrc code is a general-purpose Monte Carlo radiation transport code [29]. The BEAMnrc module within EGSnrc allows for detailed modeling of a LINAC starting with electrons striking the tungsten target [30]. The output of BEAMnrc is a LINAC phase space file which is tallied on a user-selected exit plane. The resulting phase space file is then used as a source term for scoring dose in a voxelized patient anatomy using the DOSXYZnrc module. Heterogeneities are explicitly accounted for in EGSnrc by assigning every region of space with a material defined by its elemental composition and density.
The X-ray Voxel Monte Carlo (XVMC) code was developed by Fippel [31] for performing photon radiotherapy dose calculations and is an extension of the Voxel Monte Carlo (VMC) electron transport code develop by Kawrakow et al. [32]. A key feature of XVMC is its speed compared to general-purpose Monte Carlo codes such as EGSnrc. The acceleration is due to the use of a virtual source model for generating pseudo-particles, a simplified treatment for multiple elastic scattering of electrons, and several variance reduction techniques to speed up the particle transport [33]. The patient geometry in XVMC is represented by a 3D voxel grid of mass densities which is derived from a patient CT. The required photon cross-sections and electron stopping powers are estimated as a function of the mass density using analytical fits.
2.2. Phantoms for testing
The four dose calculation algorithms were compared using simplified geometric phantoms, rather than realistic patient anatomies, to better highlight the differences between the algorithms. Accuracy in peripheral dose was evaluated first by benchmarking the dose calculation algorithms against experimental measurements performed in a homogenous water phantom. Accuracy in the presence of heterogeneity was then evaluated through additional calculations involving a computational cylinder phantom representing a simplified patient thorax. The dose calculation algorithms were also compared in terms of computation time as this is an important practical consideration for large-scale epidemiological research.
The homogenous water phantom consisted of a 40 × 110 × 20 cm3 rectangular prism (Figure 1a). These dimensions were chosen so that longitudinal dose profiles could be compared out to ~30 cm beyond the field edge for a radiotherapy beam incident from the antero-posterior (AP) direction. The dose received at larger distances is not of much epidemiological interest as Diallo et al. [34] showed that most second primary cancers following radiotherapy occur within 30 cm from the irradiated volume. Voxels inside and outside the phantom were assigned HU values of 0 (water with density 1.0 g cm−3) and -1000 (air), respectively.
Figure 1.
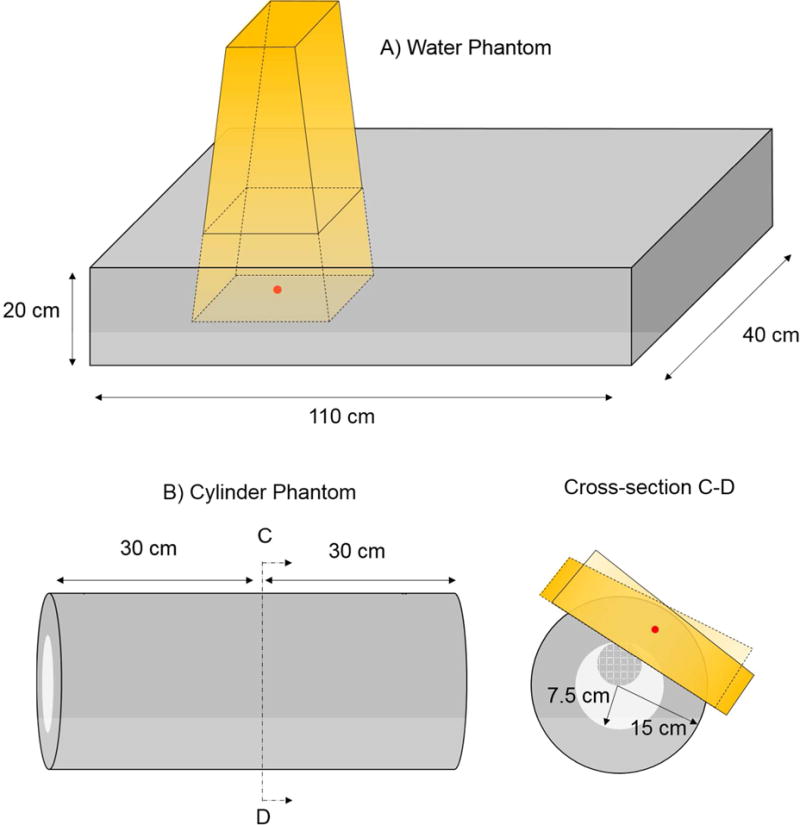
Drawings of the homogeneous water phantom (a) and hetereogeneous cylinder phantom (b). The lung region in the heterogeneous phantom is shown in light grey. The heart sphere is shown in dark grey with the checkered pattern. Drawings are not to scale. The isocenter for the respective treatment plans are shown in red. Schematics of the radiotherapy beams are show in yellow. For the hetergenous phantom, the field-in-field technique was used with two opposing primary fields and two sub-fields. For clarity, the overlapping sub-fields are not shown.
The geometry of the computational heterogeneous phantom was designed to loosely represent a patient’s thorax. The phantom consisted of two concentric right circular cylinders of length 60 cm. The outer cylinder had a diameter of 30 cm and was assigned an HU value of 0 (water with density 1.0 g cm−3). The inner cylinder had a diameter of 15 cm and was assigned an HU value of −750 to represent water at a fictitious density of 0.25 g cm−3 (approximating lung tissue). A sphere of diameter 7.5 cm and HU value 0 was inserted inside the inner cylinder to represent the heart and was located 3.75 cm away from the central axis of the cylinder. Voxels outside the phantom were assigned a HU value of −1000 (air). The MATLAB (The Mathworks Inc., Natick, MA) Image Processing Toolkit was used to generate images of the heterogeneous cylinder phantoms in DICOM CT format. The heterogeneous cylinder consisted of 211 axial images with slice thickness 3 mm (including 5 images of air padded to the beginning and end of the image stack). Each image slice had matrix size of 512 × 512 and square pixel spacing of 1 mm. A drawing of the computational heterogeneous cylinder is shown in Figure 1b.
2.3. Radiation beam planning
The phantom images were imported into an Eclipse TPS so that radiotherapy plans could be generated. The TPS was commissioned for a Varian Clinac 2100 series LINAC (Varian Medical Systems, Palo Atlo, CA) located at the University of Michigan.
The radiotherapy plan for the homogenous water phantom consisted of a single 6 MV photon beam entering the phantom in the AP direction with a source to surface distance of 100 cm. Four different square field sizes were considered: 6 × 6 cm2, 10 × 10 cm2, 20 × 20 cm2, and 30 × 30 cm2. In all cases, the collimator angle was 0 degrees so that the motion of the lower jaw was perpendicular to the long axis of the phantom and no tertiary multi-leaf collimator (MLC) was used.
The radiotherapy plan for the heterogeneous cylinder phantom was designed to mimic a simple breast treatment (Figure 1). The plan was developed using the field-in-field technique [35] and involved 2 pairs of opposing 6 MV tangential beams. A dose of 10 Gy was planned to the treatment isocenter, which was located at a radial distance of 11.1 cm from the phantom’s center axis. The field sizes were selected so that the beams would partially cover the heart and lung regions of the phantom, as can sometimes happen in breast treatments.
2.4. Dose calculations
The irradiation of the homogeneous water phantom and heterogeneous cylinder phantom were simulated using the four dose calculation algorithms to obtain 3D dose information.
As the beam plans were created in Eclipse TPS, the dose distributions were calculated with the AAA and Acuros XB algorithms contained in the software. The TPS dose calculation grids were chosen to coincide with the phantom CT and covered the entire phantom geometry. For the Acuros XB calculations, Eclipse assigned materials automatically based on the phantom HU values and reported dose to medium. By default, Acuros XB uses electron and photon cut-off energies of 500 keV and 10 keV, respectively.
The EGSnrc and XVMC simulations were setup using data extracted from the DICOM RTPLAN files exported from the TPS. In-house MATLAB scripts were developed to convert DICOM-RT objects into XVMC and EGSnrc input files [24]. The resulting Monte Carlo-calculated dose maps were then converted to the DICOM RTDOSE file format so that they could be imported back into Eclipse for comparison with the results from other algorithms. The Monte Carlo dose calculations throughout this study were performed on dual six core 2.93 GHz Intel XEON CPU processor with 12.0 GB RAM. Sufficient particle histories were run to ensure that the Monte Carlo statistical uncertainties were less than 0.5% for the voxel receiving largest dose. At points 30 cm away from the field edge in the in-plane direction the statistical uncertainties were ~8 % (EGSnrc) and ~12 % (XVMC).
The EGSnrc simulations used a Varian Clinac 2100 series LINAC head model which was previously developed according to geometry specifications provided by the manufacturer [36]. Phase space files for a 6 MV beam were generated from the BEAMnrc module for each of the various field sizes. For treatment plans with more than one beam, as in the case of the heterogeneous cylinder phantom, a separate DOSXYZnrc simulation was performed for each beam. The resulting dose maps were then normalized to the prescribed dose at the prescription point and then summed. The EGSnrc simulations were run using the default settings, including electron kinetic energy cut-off of 189 keV, photon cut-off energy of 10 keV, and maximum fractional energy loss per electron step size of 25%. For the heterogeneous cylinder phantom case, the PEGS4 program was used to produce photon cross section data for water at fictitious density of 0.25 g/cm3.
The XVMC code used in this work was commissioned for a Varian Clinac 2100 series LINAC so that the calculated in-field dose profiles agreed with ion chamber measurements to within 1% [37]. Iterative adjustments were made to the source model to achieve better agreement with measurements in the out-of-field region [38]. More specifically, the extra-focal scatter source distance and standard deviation parameters in the XVMC source model were adjusted to match experiment [33]. Because XVMC does not account for scatter off the lower jaws for fast calculation, we adopted two different virtual source models depending on the field size to maintain acceptable accuracy both in-field and out-of-field (i.e. small field sizes ≤ 15 × 15 cm2, large field sizes > 15 × 15 cm2). The same beam normalization procedure used for EGSnrc was also used for the XVMC simulations. By default the XVMC simulations used an electron energy cut-off of 250 keV, photon energy cut-off of 50 keV, and a maximum electron energy step-size of 12%. The photon cut-off energies for kerma approximation was set to 50 keV and 2 MeV for primary and secondary photons, respectively.
2.5. Experimental measurements
The dose calculations for the homogeneous water phantom were compared to ion chamber measurements performed for 6 MV photons beams from a Varian Clinac 2100 series LINAC. These measurements were taken as part of a previous study by Owrangi et al. [38]. Additional unpublished measurements were collected for the case of collimator angle at 0 degrees and no MLC. The individual ion chamber measurements have an estimated accuracy of ±1%.
In-field lateral dose profiles were measured at 5 cm and 10 cm depths in a liquid water phantom (Blue Phantom, Scanditronix Wellhofer, Germany). For the 6 × 6 cm2 and 10 × 10 cm2 field size the measurements were acquired at 0.6 mm increments. For the 20 × 20 cm2 and 30 × 30 cm2 field sizes an increment of 1.2 mm was used. This same liquid water phantom was also used to measure percent depth dose (PDD) curves from the phantom surface to a depth of 10 cm. Out-of-field lateral dose profile measurements were performed using a Solid Water phantom (Gammex RMI Inc., Milwauki, WI). The peripheral dose measurements were acquired with a Farmer-type ionization chamber (Exradin A12, Standard Imaging, Middleton, WI) at distances of 5, 10, 20, and 30 cm beyond the field edge and at depths of 5 and 10 cm.
3. Results
3.1. Dose comparison in homogeneous water phantom
The PDD and lateral dose profiles (in-plane) for each dose calculation algorithm were compared against the measurements. The PDD curves showed excellent agreement with measurement in all cases (differences typically < 1%) and for brevity are not shown. For comparison purposes, the lateral dose profiles in the homogenous water phantom were normalized to the central axis dose and are plotted together in Figures 2 through 5 for the field sizes of 6 × 6, 10 × 10, 20 × 20, and 30 × 30 cm2, respectively, at depths of 5 and 10 cm. The lateral dose profile data are also provided in Table 1.
Figure 2.
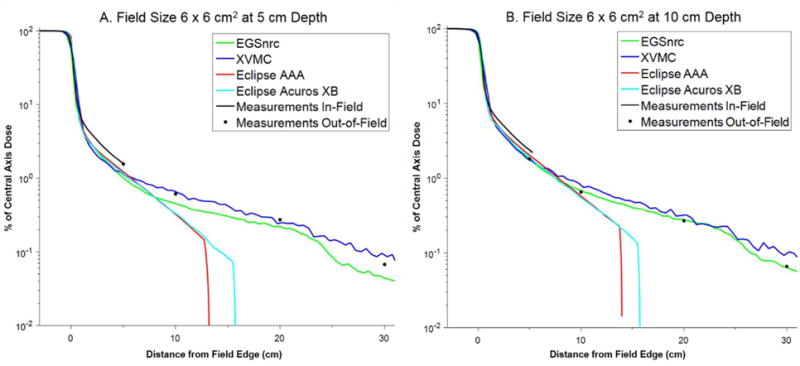
Comparison of in-plane dose profiles for field size 6 × 6 cm2 at (a) 5 cm and (b) 10 cm depth.
Figure 5.
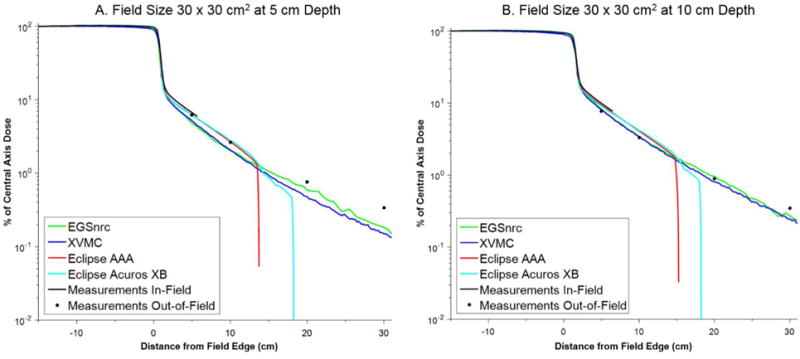
Comparison of in-plane dose profiles for field size 30 × 30 cm2 at (a) 5 cm and (b) 10 cm depth.
Table 1.
Comparison between the lateral dose profiles in the homogenous water phantom calculated using the four dose calculation algorithms and experimental measurement.
| Field Size (cm2) | Depth (cm) | Distance (cm) | Measurement | EGSnrc | XVMC | AAA | Acuros XB | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| From Central Axis | From Field Edge | Dose (% CAX) | Dose (% CAX) | % Diff | Dose (% CAX) | % Diff | Dose (% CAX) | % Diff | Dose (% CAX) | % Diff | ||
| 6 × 6 | 5 cm | 8 | 5 | 1.554 | 1.015 | 34.7 | 1.140 | 26.6 | 1.224 | 21.2 | 1.160 | 25.3 |
| 13 | 10 | 0.614 | 0.455 | 25.9 | 0.658 | 7.2 | 0.324 | 47.2 | 0.332 | 45.9 | ||
| 23 | 20 | 0.273 | 0.222 | 18.7 | 0.246 | 10.0 | 0.000 | — | 0.000 | — | ||
| 33 | 30 | 0.067 | 0.044 | 34.0 | 0.091 | 36.1 | 0.000 | — | 0.000 | — | ||
| 10 cm | 8 | 5 | 1.799 | 1.809 | 0.5 | 1.746 | 2.9 | 2.027 | 12.6 | 1.890 | 5.0 | |
| 13 | 10 | 0.651 | 0.682 | 4.7 | 0.804 | 23.5 | 0.576 | 11.5 | 0.548 | 15.9 | ||
| 23 | 20 | 0.270 | 0.277 | 2.5 | 0.318 | 17.6 | 0.000 | — | 0.000 | — | ||
| 33 | 30 | 0.065 | 0.064 | 2.1 | 0.098 | 51.2 | 0.000 | — | 0.000 | — | ||
| 10 × 10 | 5 cm | 10 | 5 | 2.951 | 2.763 | 6.4 | 2.338 | 20.8 | 2.430 | 17.7 | 2.410 | 18.3 |
| 15 | 10 | 1.123 | 1.165 | 3.8 | 1.366 | 21.6 | 0.756 | 32.7 | 0.794 | 29.3 | ||
| 25 | 20 | 0.376 | 0.406 | 7.9 | 0.548 | 45.8 | 0.000 | — | 0.000 | — | ||
| 35 | 30 | 0.156 | 0.214 | 36.8 | 0.161 | 2.8 | 0.000 | — | 0.000 | — | ||
| 10 cm | 10 | 5 | 4.546 | 4.366 | 4.0 | 3.478 | 23.5 | 3.801 | 16.4 | 3.698 | 18.7 | |
| 15 | 10 | 1.667 | 1.791 | 7.4 | 1.770 | 6.2 | 1.246 | 25.3 | 1.247 | 25.2 | ||
| 25 | 20 | 0.546 | 0.575 | 5.5 | 0.637 | 16.7 | 0.000 | — | 0.000 | — | ||
| 35 | 30 | 0.201 | 0.285 | 42.0 | 0.207 | 3.3 | 0.000 | — | 0.000 | — | ||
| 20 × 20 | 5 cm | 15 | 5 | 4.519 | 3.719 | 17.7 | 4.142 | 8.3 | 4.605 | 1.9 | 4.502 | 0.4 |
| 20 | 10 | 1.932 | 1.513 | 21.7 | 1.519 | 21.4 | 1.719 | 11.0 | 1.875 | 2.9 | ||
| 30 | 20 | 0.550 | 0.446 | 18.8 | 0.318 | 42.2 | 0.000 | — | 0.000 | — | ||
| 40 | 30 | 0.240 | 0.166 | 30.7 | 0.089 | 62.7 | 0.000 | — | 0.000 | — | ||
| 10 cm | 15 | 5 | 5.438 | 6.355 | 16.9 | 6.300 | 15.9 | 6.957 | 27.9 | 6.768 | 24.5 | |
| 20 | 10 | 2.160 | 2.513 | 16.3 | 2.445 | 13.2 | 2.707 | 25.3 | 2.866 | 32.7 | ||
| 30 | 20 | 0.595 | 0.696 | 17.0 | 0.547 | 8.1 | 0.000 | — | 0.000 | — | ||
| 40 | 30 | 0.253 | 0.222 | 12.1 | 0.157 | 37.8 | 0.000 | — | 0.000 | — | ||
| 30 × 30 | 5 cm | 20 | 5 | 6.182 | 4.782 | 22.6 | 5.182 | 16.2 | 6.198 | 0.3 | 6.208 | 0.4 |
| 25 | 10 | 2.618 | 2.024 | 22.7 | 2.070 | 20.9 | 2.688 | 2.7 | 2.764 | 5.6 | ||
| 35 | 20 | 0.756 | 0.585 | 22.6 | 0.475 | 37.3 | 0.000 | — | 0.000 | — | ||
| 45 | 30 | 0.337 | 0.182 | 45.9 | 0.151 | 55.3 | 0.000 | — | 0.000 | — | ||
| 10 cm | 20 | 5 | 7.723 | 8.264 | 7.0 | 8.067 | 4.5 | 9.320 | 20.7 | 9.117 | 18.0 | |
| 25 | 10 | 3.290 | 3.427 | 4.1 | 3.431 | 4.3 | 4.090 | 24.3 | 4.156 | 26.3 | ||
| 35 | 20 | 0.884 | 0.958 | 8.3 | 0.810 | 8.4 | 0.000 | — | 0.000 | — | ||
| 45 | 30 | 0.348 | 0.273 | 21.6 | 0.245 | 29.6 | 0.000 | — | 0.000 | — | ||
The lateral dose profiles for the EGSnrc simulations agree remarkably well with measurement out to 30 cm beyond the field edge, especially considering that the dose spans three orders of magnitude. At a depth of 10 cm, the average percent difference (with the standard deviation in the parenthesis) between EGSnrc and measurement at 5, 10, 20, and 30 cm from the field edge was 7.1 % (7.0 %), 8.2 % (5.6 %), 8.3 % (6.2 %), and 19.5 % (17.0 %), respectively. At a depth of 5 cm these values were 20.3 % (11.7 %), 18.5 % (10.0 %), 17.0 % (6.3 %), and 36.9 % (6.5 %), respectively. In most cases the errors were less than 16 % (10 cm depth) and 23 % (5 cm depth).
Very similar performance was observed for the XVMC dose calculation, although the XVMC calculations were significantly faster for the same computing conditions (hours versus days for XVMC and EGSnrc, respectively). At a depth of 10 cm, the average percent difference (with the standard deviation in the parenthesis) between XVMC and measurement at 5, 10, 20, and 30 cm from the field edge was 11.7 % (9.8 %), 11.8 % (8.7 %), 12.7 % (5.1 %), and 23.1 % (25.3 %), respectively. At a depth of 5 cm these values were 18.0 % (7.7 %), 17.8 % (7.1 %), 33.8 % (16.3 %), and 39.2 % (26.8 %), respectively. The errors with XVMC compared to measurement were generally smaller than 25%, except at distances greater than 20 cm where they approached 50 % in a few instances. Nonetheless, these errors are deemed acceptable because the absolute dose received by tissues at these distances will be quite small (< 1 % of the prescribed dose).
The treatment planning system (AAA and Acuros XB) generally provided accurate dosimetry out to ~5 to 8 cm beyond the field edge (percent difference compared to measurement less than 30%). The calculation time for these algorithms was 8 to 10 seconds, with Acuros XB calculations taking slightly longer than AAA. At larger distances, both of these algorithms tended to systematically underestimate the out-of-field dose. Better agreement with measurements was observed for the larger field sizes (e.g. 20 × 20 cm2 and 30 × 30 cm2). Notably, the dose profiles for the TPS falls off steeply at distance of about 12 to 15 cm (AAA) and 16 to 18 cm (Acuros XB). Beyond these distances we found that the algorithms reported a dose of zero, even though the dose calculation grid extended throughout the entire phantom.
3.2. Dose comparison in heterogeneous cylinder phantom
We used EGSnrc-based doses as the gold standard for the comparison for the heterogeneous cylinder phantom and compared it with other three algorithms: AAA, Acuros XB, and XVMC.
Isodose curve plots for the heterogeneous cylinder phantom are shown in Figure 6 for the four dose calculation algorithms. Qualitatively the isodose curves show good agreement between all the methods except for the AAA method which performs differently out-of-field. The 2 % (0.2 Gy) and 5 % (0.5 Gy) isodose curves for AAA are curvilinear, not straight lines as for the other algorithms. To better illustrate the differences, we compared dose profiles for line segments running perpendicular (Figure 7a) and parallel (Figure 7b) to the field edge. From these figures, it is clear that the AAA algorithm systematically overestimates dose in the mock lung region compared to the other methods suggesting that this method has difficultly accounting for tissue heterogeneities. This is consistent with a previous study by Wang and Ding [39] which found that AAA overestimates dose in low density media. By design the different regions of the cylinder phantom were defined as the material water with different density. Thus, the observed AAA errors in Figure 7b specifically represent a difficulty in correcting for lung density. Acuros XB demonstrated better accuracy compared to AAA. The Acuros XB correctly assigned a lung material to the mock lung region of the computational phantom.
Figure 6.
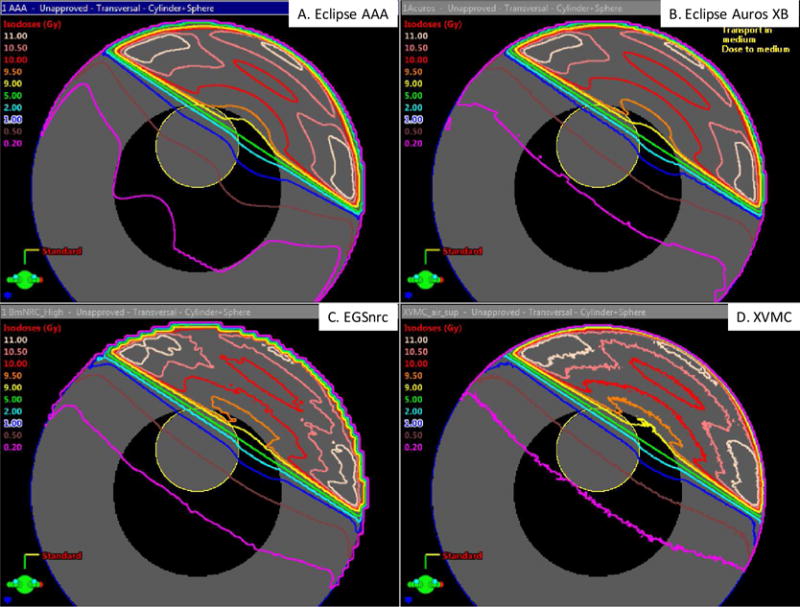
Isodose curves from (a) Eclipse AAA, (b) Eclipse Acuros XB, (c) EGSnrc, and (d) XVMC superimposed on cross-sectional image of the heterogeneous cylinder phantom.
Figure 7.
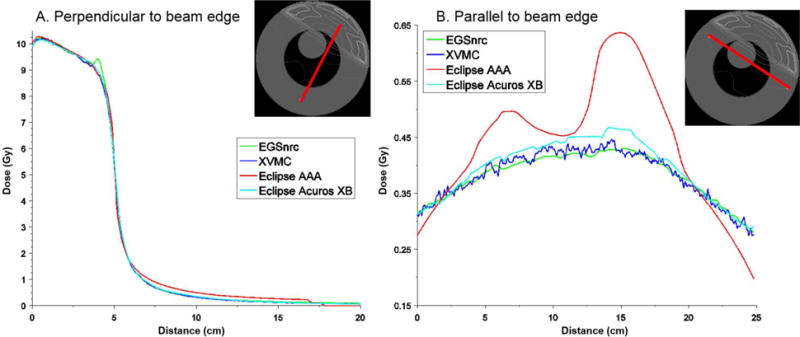
Dose profiles for line segments (marked red on the cross-section of the cylinder phantom) running (a) perpendicular and (b) parallel to the field edge
To quantitatively examine the differences between the dose calculation algorithms, several common organ dose statistics were recorded for the mock heart and lung regions, including the mean and maximum dose as well as the volume of each region receiving at least 0.5 Gy (V05 Gy) and 1 Gy (V1 Gy). As the prescribed dose for this case was 10 Gy, the V05 Gy and V1 Gy correspond to the volume of each region receiving 5 % and 10 % of the prescribed dose, respectively. Table 2 summarizes the results for each dose calculation algorithm and shows the percent difference relative to that calculated by EGSnrc (gold standard for comparison). The Acuros XB and XVMC algorithms showed the best agreement with EGSnrc, with XVMC tending to slightly outperform Acuros XB. The AAA method estimated the maximum mock heart and lung dose to within 2.3 %, but the mean heart and lung dose were overestimated by 6.4 % and 21.7 %, respectively. The AAA algorithm particularly struggled to estimate V0.5 Gy and V1 Gy, with the errors ranging from 16.9 % to 46.4 %.
Table 2.
Dose statistics for the mock heart and lung regions of the heterogeneous cylinder for each of the dose calculation algorithms. Percent difference is also shown relative to the dose calculated by EGSnrc (gold standard for comparison).
| Region | Metric | EGSnrc | AAA | Acuros XB | XVMC | |||
|---|---|---|---|---|---|---|---|---|
| Value | Value | % Diff | Value | % Diff | Value | % Diff | ||
| Mock Heart | Mean Dose (Gy) | 0.94 | 1.00 | 6.4% | 0.95 | 1.1% | 0.94 | 0.0% |
| Maximum Dose (Gy) | 9.78 | 9.44 | −1.2% | 9.72 | 1.8% | 9.55 | −2.4% | |
| V1 Gy (cm3) | 37.73 | 43.79 | 21.0% | 33.50 | −7.5% | 36.20 | −4.1% | |
| V0.5 Gy (cm3) | i 19.54 | 143.79 | 18.4% | 128.69 | 6.0% | 121.46 | 1.6% | |
| Mock Lung | Mean Dose (Gy) | 0.25 | 0.28 | 21.7% | 0.24 | 4.3% | 0.23 | −8.0% |
| Maximum Dose (Gy) | 9.66 | 9.34 | −2.3% | 9.72 | 1.7% | 9.56 | −1.0% | |
| V1 Gy (cm3) | 316.11 | 362.38 | 16.9% | 315.06 | 1.7% | 309.86 | −2.0% | |
| V0.5 Gy (cm3) | 627.13 | 897.82 | 46.4% | 659.14 | 7.4% | 613.46 | −2.2% | |
4. Discussion
Our previous paper [24] outlined the framework of our dosimetry approach for epidemiological studies of radiotherapy patients. The primary aim of this study was to explore several possible dose calculations algorithms and to identify appropriate investigative scenarios where they might be used. Our intent was not to advocate for one method over another because one should always choose the most appropriate dosimetry method for a given application. Such decision-making could be made on the basis of a variety of factors such as the size of the epidemiological cohort or the quality of the information available to reconstruct dose. For instance, for many retrospective studies no patient anatomy is available and sometimes only a few details of the radiotherapy plan are known (e.g. prescribe dose, beam energy, type of treatment). In such cases, missing radiotherapy parameters must be assigned nominal values and the uncertainties due to these unknown factors may outweigh the need to use a sophisticated Monte Carlo dosimetry approach.
The current study showed that out-of-field dosimetry using a commercial TPS can disagree significantly with that determined by measurement. Similar findings have been reported by others [20,39]. Our study, however, clarifies that commercial TPSs may still be useful dosimetry tool for epidemiologic research in the special case that the organs of interest are located in-field or partially in-field. Specifically, our study showed that TPSs have the advantage of being very fast (typical calculation time was several seconds) and can be accurate out to ~8 cm beyond the field edge. In particular, it is noteworthy that the mean dose to the heart in the heterogeneous phantom reported by TPS was similar to that calculated by EGSnrc, the gold standard dose calculation method (1.00 Gy vs. 0.94 Gy). This study also found that Acuros XB was more accurate than the AAA method in presence of heterogeneities. Furthermore, as the calculation times of Acuros XB and AAA were very similar, it would seem that Acuros XB would be preferred TPS dosimetry method—at least for the limited scenarios we examined. A study by Yan et al. [40] came to a similar conclusion. However, as the TPS dose calculator abruptly cuts off at some distance from the field edge, we recommend comparing TPS dosimetry to Monte Carlo results (e.g. EGSnrc) before adopting the TPS as the primary dosimetry method for a specific epidemiological application.
It is also important to note that commercial TPS-reported dose may serve as a valuable biomarker for optimizing treatments even if the dosimetry is not quantitatively accurate. The reported TPS dose could also be converted to true out-of-field dose through an appropriate calibration scheme. Of course, the TPS is not useful if it reports zero dose, as was observed in this study with the water phantom beyond ~13.5 cm (AAA) and ~20 cm (Acuros XB). The TPS used in this work could not be customized by the user to provide extended dosimetry capability. This is a key advantage of XVMC and EGSnrc as shown in this work.
It is not surprising that this study found EGSnrc to be the most accurate dose calculation algorithm. However, EGSnrc was also the slowest of all the computational methods we investigated. Two EGSnrc simulations are needed for each radiotherapy beam—a BEAMnrc simulation to generate the phase space data and a DOSXYZnrc simulation to calculate dose in the patient. For the heterogeneous cylinder phantom simulations described in this study, the total calculation time was approximately 86 hours (58 hours for BEAMnrc and 28 hours for DOSXYZnrc). Such calculation times are clearly not practical for epidemiological studies often consisting of thousands of patients. Based on our experience with preliminary works, for example, we define the upper limit of feasibility as being around 8 hours per patient simulation which for 5000 patients and spread across 30 CPUs can be completed in approximately 2 months. At the current time, we foresee EGSnrc being primarily used as a gold standard for validation and for small exploratory studies (less than 30 patients) involving high-quality patient and treatment information (i.e., all DICOM-RT files are available).
The XVMC dose calculation algorithm showed similar accuracy to EGSnrc but was significantly faster. The heterogeneous cylinder phantom simulations took approximately 1.5 hours to complete, which is only about 1.7% of the time taken for the EGSnrc calculations. While still slower than the TPS, such calculation times are more reasonable so that one could conceivably, with a large computing cluster, perform dosimetry on a cohort consisting of thousands of patients. However, such a computational effort would only make sense if the organs of interest are located sufficiently out-of-field so that the TPS would not be a reasonable alternative.
Lastly, the accuracy requirements of dosimetry for epidemiological research is worthy of discussion. There are no general answers to this because the required accuracy will, of course, depend on the size of the health effect being investigated and how the data are analyzed. For some studies, patients are assigned to dose-level categories, so that errors in the dosimetry are only consequential if they result in a misclassification. In other studies, dose may be treated as a continuous variable, in which case errors have the effect of widening confidence intervals or altering the slope of a dose-response line depending on whether they are random or systematic in nature. In practice, however, epidemiological studies must contend with a variety of confounding factors and methodological issues so that the accuracy of the dosimetry may not be always the foremost concern. The XVMC and EGSnrc dose calculation methods described in this study have similar or better accuracy compared to the dosimetry methods used for previous studies [41]. One of the primary advantages of the dose calculation approach is the ease with which the dosimetry can be revised over time as source models improve or for purposes of studying the uncertainty introduced by imputed parameters. The expense, in both time and resource, involved with measurement approaches [18,19] impedes the revision of dose estimates and precludes extensive sensitivity testing. For these reasons, we anticipate that the field of epidemiology will increasingly look towards computational approaches to perform the radiation dosimetry.
5. Conclusions
We systematically compared four dose calculation algorithms in terms of their accuracy and feasibility of application to epidemiological studies looking at the risk of late-effects following radiotherapy. As each dose calculation algorithm has its strengths and weaknesses, the best choice of calculation method will depend on the specifics of the application. In general, we find that the algorithms contained in the TPS (AAA and Acuros XB) are fast, but are inaccurate in out-of-field regions, so that they are best suited for studies involving large cohorts and where the organs of interest are located in-field or partially in-field. Monte Carlo simulation using the EGSnrc code is the most-accurate dosimetry approach, but is currently too slow for use in most epidemiological studies with very large cohorts. The XVMC method showed similar accuracy compared to EGSnrc, but was significantly faster, opening the possibility for application to epidemiological cohorts consisting of up to a few thousand patients. Ultimately, we plan to demonstrate the feasibility of such an approach using a large-scale computing cluster. If successful, this would represent the first time that Monte Carlo simulation was ever used in epidemiologic research, on a patient-specific basis, for the purposes of retrospective dose reconstruction.
Figure 3.
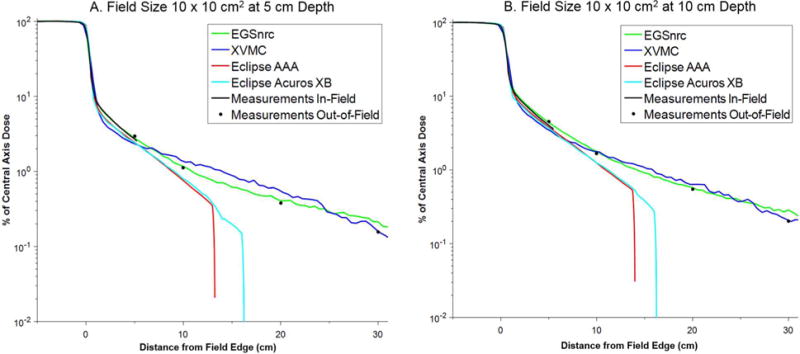
Comparison of in-plane dose profiles for field size 10 × 10 cm2 at (a) 5 cm and (b) 10 cm depth.
Figure 4.
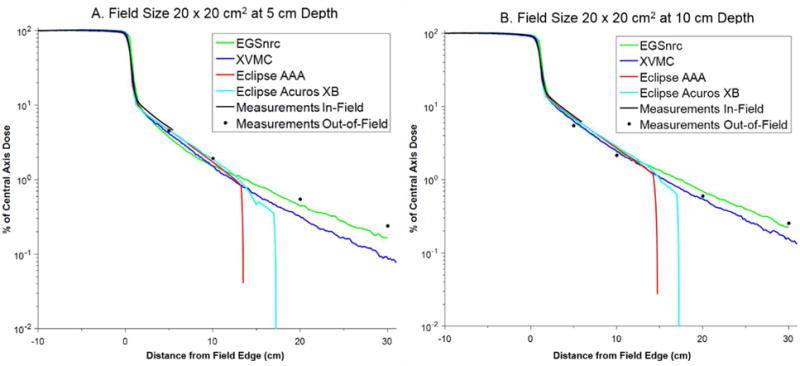
Comparison of in-plane dose profiles for field size 20 × 20 cm2 at (a) 5 cm and (b) 10 cm depth.
Acknowledgments
This work was funded by the intramural program of the National Institutes of Health, National Cancer Institute, Division of Cancer Epidemiology and Genetics. The contents are solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors would like to thank Dr. Jong Oh Kim of the University of Pittsburgh for his valuable comments on how to commission XVMC and EGSnrc for out-of-field dose calculations. Also, we would like to thank Rasha Makkia of East Carolina University for her contributions to the XVMC virtual source modeling and validation. Lastly, the authors thank Dr. Matthias Fippel who generously provided the XVMC source code for this research.
References
- 1.Jemal A, Ward EM, Johnson CJ, Cronin KA, Ma J, Ryerson AB, Mariotto A, Lake AJ, Wilson R, Sherman RL, Anderson RN, Henley SJ, Kohler BA, Penberthy L, Feuer EJ, Weir HK. Annual Report to the Nation on the Status of Cancer, 1975-2014, Featuring Survival. J Natl Cancer Inst. 2017;109 doi: 10.W93/jnci/djx030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Miller KD, Siegel RL, Lin CC, Mariotto AB, Kramer JL, Rowland JH, Stein KD, Alteri R, Jemal A. Cancer treatment and survivorship statistics, 2016. CA Cancer J Clin. 2016;66:271–89. doi: 10.3322/caac.21349. [DOI] [PubMed] [Google Scholar]
- 3.Berrington de Gonzalez A, Curtis RE, Gilbert E, Berg CD, Smith SA, Stovall M, Ron E. Second solid cancers after radiotherapy for breast cancer in SEER cancer registries. Br J Cancer. 2010;102:220–26. doi: 10.1038/sj.bjc.6605435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Berrington de Gonzalez A, Gilbert E, Curtis R, Inskip P, Kleinerman R, Morton L, Rajaraman P, Little MP. Second Solid Cancers After Radiation Therapy: A Systematic Review of the Epidemiologic Studies of the Radiation Dose-Response Relationship. Int J Radiat Oncol. 2013;86:224–33. doi: 10.1016/j.ijrobp.2012.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Taylor AJ, Little MP, Winter DL, Sugden E, Ellison DW, Stiller CA, Stovall M, Frobisher C, Lancashire ER, Reulen RC, Hawkins MM. Population-Based Risks of CNS Tumors in Survivors of Childhood Cancer: The British Childhood Cancer Survivor Study. J Clin Oncol. 2010;28:528793. doi: 10.1200/JCO.2009.27.0090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Darby SC, Ewertz M, McGale P, Bennet AM, Blom-Goldman U, Brennum D, Correa C, Cutter D, Gagliardi G, Gigante B, Jensen M-B, Nisbet A, Peto R, Rahimi K, Taylor C, Hall P. Risk of Ischemic Heart Disease in Women after Radiotherapy for Breast Cancer. N Engl J Med. 2013;368:987–98. doi: 10.1056/NEJMoa1209825. [DOI] [PubMed] [Google Scholar]
- 7.Galper SL, Yu JB, Mauch PM, Strasser JF, Silver B, LaCasce A, Marcus KJ, Stevenson MA, Chen MH, Ng AK. Clinically significant cardiac disease in patients with Hodgkin lymphoma treated with mediastinal irradiation. Blood. 2011;117:412–8. doi: 10.1182/blood-2010-06-291328. [DOI] [PubMed] [Google Scholar]
- 8.Turcotte LM, Liu Q, Yasui Y, Arnold MA, Hammond S, Howell RM, Smith SA, Weathers RE, Henderson TO, Gibson TM, Leisenring W, Armstrong GT, Robison LL, Neglia JP. Temporal Trends in Treatment and Subsequent Neoplasm Risk Among 5-Year Survivors of Childhood Cancer, 1970-2015. JAMA. 2017;317:814–24. doi: 10.1001/jama.2017.0693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Clarke M, Collins R, Darby S, Davies C, Elphinstone P, Evans V, Godwin J, Gray R, Hicks C, James S, MacKinnon E, McGale P, McHugh T, Peto R, Taylor C, Wang Y, Early Breast Cancer Trialists’ Collaborative Group (EBCTCG) Effects of radiotherapy and of differences in the extent of surgery for early breast cancer on local recurrence and 15-year survival: an overview of the randomised trials. Lancet Lond Engl. 2005;366:2087–106. doi: 10.1016/S0140-6736(05)67887-7. [DOI] [PubMed] [Google Scholar]
- 10.Robison LL, Armstrong GT, Boice JD, Chow EJ, Davies SM, Donaldson SS, Green DM, Hammond S, Meadows AT, Mertens AC, Mulvihill JJ, Nathan PC, Neglia JP, Packer RJ, Rajaraman P, Sklar CA, Stovall M, Strong LC, Yasui Y, Zeltzer LK. The Childhood Cancer Survivor Study: A National Cancer Institute–Supported Resource for Outcome and Intervention Research. J Clin Oncol. 2009;27:2308–18. doi: 10.1200/JCO.2009.22.3339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Purdy JA. Dose To Normal Tissues Outside The Radiation Therapy Patient’s Treated Volume: A Review Of Different Radiation Therapy Techniques. Health Phys. 2008;95:666–76. doi: 10.1097/01.HP.0000326342.47348.06. [DOI] [PubMed] [Google Scholar]
- 12.Halg RA, Besserer J, Schneider U. Systematic measurements of whole-body dose distributions for various treatment machines and delivery techniques in radiation therapy. Med Phys. 2012;39:7662–76. doi: 10.1118/1.4767773. [DOI] [PubMed] [Google Scholar]
- 13.Xu XG, Bednarz B, Paganetti H. A review of dosimetry studies on external-beam radiation treatment with respect to second cancer induction. Phys Med Biol. 2008;53:R193–241. doi: 10.1088/0031-9155/53/13/R01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Morton LM, Dores GcaM, Curtis RE, Lynch CF, Stovall M, Hall P, Gilbert ES, Hodgson DC, Storm HH, Johannesen TBrge. Stomach Cancer Risk After Treatment for Hodgkin Lymphoma. J Clin Oncol. 2013;31:3369–77. doi: 10.1200/JCO.2013.50.6832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bhatti P, Veiga LHS, Ronckers CM, Sigurdson AJ, Stovall M, Smith SA, Weathers R, Leisenring W, Mertens AC, Hammond S, Friedman DL, Neglia JP, Meadows AT, Donaldson SS, Sklar CA, Robison LL, Inskip PD. Risk of Second Primary Thyroid Cancer after Radiotherapy for a Childhood Cancer in a Large Cohort Study: An Update from the Childhood Cancer Survivor Study. Radiat Res. 2010;174:741–52. doi: 10.1667/RR2240.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Inskip PD, Robison LL, Stovall M, Smith SA, Hammond S, Mertens AC, Whitton JA, Diller L, Kenney L, Donaldson SS, Meadows AT, Neglia JP. Radiation Dose and Breast Cancer Risk in the Childhood Cancer Survivor Study. J Clin Oncol. 2009;27:3901–7. doi: 10.1200/JCO.2008.20.7738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Grantzau T, Thomsen MS, Væth M, Overgaard J. Risk of second primary lung cancer in women after radiotherapy for breast cancer. Radiother Oncol. 2014;111:366–73. doi: 10.1016/j.radonc.2014.05.004. [DOI] [PubMed] [Google Scholar]
- 18.Stovall M, Weathers R, Kasper C, Smith SA, Travis L, Ron E, Kleinerman R. Dose Reconstruction for Therapeutic and Diagnostic Radiation Exposures: Use in Epidemiological Studies. Radiat Res. 2006;166:141–57. doi: 10.1667/RR3525.1. [DOI] [PubMed] [Google Scholar]
- 19.Howell RM, Scarboro SB, Taddei PJ, Krishnan S, Kry SF, Newhauser WD. Methodology for determining doses to in-field, out-of-field and partially in-field organs for late effects studies in photon radiotherapy. Phys Med Biol. 2010;55:7009–23. doi: 10.1088/0031-9155/55/23/S04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Howell RM, Scarboro SB, Kry SF, Yaldo DZ. Accuracy of out-of-field dose calculations by a commercial treatment planning system. Phys Med Biol. 2010;55:6999–7008. doi: 10.1088/0031-9155/55/23/S03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Joosten A, Bochud F, Baechler S, Levi F, Mirimanoff RO, Moeckli R. Variability of a peripheral dose among various linac geometries for second cancer risk assessment. Phys Med Biol. 2011;56:5131–51. doi: 10.1088/0031-9155/56/16/004. [DOI] [PubMed] [Google Scholar]
- 22.Schneider CW, Newhauser WD, Wilson LJ, Schneider U, Kaderka R, Miljanić S, Knežević Ž, Stolarcyzk L, Durante M, Harrison RM. A descriptive and broadly applicable model of therapeutic and stray absorbed dose from 6 to 25 MV photon beams. Med Phys. 2017;44:3805–14. doi: 10.1002/mp.12286. [DOI] [PubMed] [Google Scholar]
- 23.Jagetic LJ, Newhauser WD. A simple and fast physics-based analytical method to calculate therapeutic and stray doses from external beam, megavoltage x-ray therapy. Phys Med Biol. 2015;60:4753–75. doi: 10.1088/0031-9155/60/12/4753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lee C, Jung JW, Pelletier C, Pyakuryal A, Lamart S, Kim JO, Lee C. Reconstruction of organ dose for external radiotherapy patients in retrospective epidemiologic studies. Phys Med Biol. 2015;60:230924. doi: 10.1088/0031-9155/60/6/2309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lee C, Lodwick D, Hurtado J, Pafundi D, Williams JL, Bolch WE. The UF family of reference hybrid phantoms for computational radiation dosimetry. Phys Med Biol. 2010;55:339–63. doi: 10.1088/0031-9155/55/2/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Geyer AM, O’Reilly S, Lee C, Long DJ, Bolch WE. The UF/NCI family of hybrid computational phantoms representing the current US population of male and female children, adolescents, and adults–application to CT dosimetry. Phys Med Biol. 2014;59:5225–42. doi: 10.1088/0031-9155/59/18/5225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sievinen J, Ulmer W, Kaissl W. AAA photon dose calculation model in Eclipse. Palo Alto, CA: Varian Medical Systems; 2005. Available Online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.468.1557&rep=rep1&type=pdf (last accessed 3/2/2018) [Google Scholar]
- 28.Failla G, Wareing T, Archambault Y, Thompson S. Accuros XB advanced dose calculation for eclipse treatment planning system. Palo Alto, CA: Varian Medical Systems; 2010. Available Online: https://www.varian.com/sites/default/files/resource_attachments/AcurosXBClinicalPerspectives_0.pdfref14 (last accessed 3/2/2018) [Google Scholar]
- 29.Kawrakow I, Rogers DWO. The EGSnrc code system: Monte Carlo simulation of electron and photon transport. Ottawa, Canada: National Research Council of Canada; 2003. (Technical Report PIRS-701). Available Online: https://nrc-cnrc.github.io/EGSnrc/doc/pirs701-egsnrc.pdf (last accessed 3/2/2018) [Google Scholar]
- 30.Rogers DWO, Faddegon BA, Ding GX, Ma CM, We J, Mackie TR. BEAM: A Monte Carlo code to simulate radiotherapy treatment units. Med Phys. 1995;22:503–24. doi: 10.1118/1.597552. [DOI] [PubMed] [Google Scholar]
- 31.Fippel M. Fast Monte Carlo dose calculation for photon beams based on the VMC electron algorithm. Med Phys. 1999;26:1466–75. doi: 10.1118/1.598676. [DOI] [PubMed] [Google Scholar]
- 32.Kawrakow I, Fippel M, Friedrich K. 3D electron dose calculation using a Voxel based Monte Carlo algorithm (VMC) Med Phys. 1996;23:445–57. doi: 10.1118/1.597673. [DOI] [PubMed] [Google Scholar]
- 33.Fippel M, Haryanto F, Dohm O, Nüsslin F, Kriesen S. A virtual photon energy fluence model for Monte Carlo dose calculation. Med Phys. 2003;30:301–11. doi: 10.1118/1.1543152. [DOI] [PubMed] [Google Scholar]
- 34.Diallo I, Haddy N, Adjadj E, Samand A, Quiniou E, Chavaudra J, Alziar I, Perret N, Guérin S, Lefkopoulos D, de Vathaire F. Frequency Distribution of Second Solid Cancer Locations in Relation to the Irradiated Volume Among 115 Patients Treated for Childhood Cancer. Int J Radiat Oncol Biol Phys. 2009;74:876–83. doi: 10.1016/j.ijrobp.2009.01.040. [DOI] [PubMed] [Google Scholar]
- 35.Fournier-Bidoz N, Kirova Y, Campana F, El Barouky J, Zefkili S, Dendale R, Bollet MA, Mazal A, Fourquet A. Technique alternatives for breast radiation oncology: Conventional radiation therapy to tomotherapy. J Med Phys Assoc Med Phys India. 2009;34:149–52. doi: 10.4103/0971-6203.54849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cho SH, Vassiliev ON, Lee S, Liu HH, Ibbott GS, Mohan R. Reference photon dosimetry data and reference phase space data for the 6MV photon beam from Varian Clinac 2100 series linear accelerators. Med Phys. 2005;32:137–48. doi: 10.1118/1.1829172. [DOI] [PubMed] [Google Scholar]
- 37.Yeo IJ, Jung JW, Yi BY, Kim JO. Feasibility study on inverse four-dimensional dose reconstruction using the continuous dose-image of EPID. Med Phys. 2013;40:051702. doi: 10.1118/1.4799941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Owrangi AM, Roberts DA, Covington EL, Hayman JA, Masi KM, Lee C, Moran JM, Prisciandaro JI. Revisiting fetal dose during radiation therapy: evaluating treatment techniques and a custom shield. J Appl Clin Med Phys Am Coll Med Phys. 2016;17:6135. doi: 10.1120/jacmp.v17i5.6135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wang L, Ding GX. The accuracy of the out-of-field dose calculations using a model based algorithm in a commercial treatment planning system. Phys Med Biol. 2014;59:N113–28. doi: 10.1088/0031-9155/59/13/N113. [DOI] [PubMed] [Google Scholar]
- 40.Yan C, Combine AG, Bednarz G, Lalonde RJ, Hu B, Dickens K, Wynn R, Pavord DC, Saiful Huq M. Clinical implementation and evaluation of the Acuros dose calculation algorithm. J Appl Clin Med Phys. 2017;18:195–209. doi: 10.1002/acm2.12149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Till JE, Beck HL, Grogan HA, Caffrey EA. A review of dosimetry used in epidemiological studies considered to evaluate the linear no-threshold (LNT) dose-response model for radiation protection. Int J Radiat Biol. 2017;93:1128–44. doi: 10.1080/09553002.2017.1337280. [DOI] [PubMed] [Google Scholar]


