A confidence building exercise in data and identifiability: Modeling cancer chemotherapy as a case study

Abstract

Mathematical modeling has a long history in the field of cancer therapeutics, and there is increasing recognition that it can help uncover the mechanisms that underlie tumor response to treatment. However, making quantitative predictions with such models often requires parameter estimation from data, raising questions of parameter identifiability and estimability. Even in the case of structural (theoretical) identifiability, imperfect data and the resulting practical unidentifiability of model parameters can make it difficult to infer the desired information, and in some cases, to yield biologically correct inferences and predictions.

Here, we examine parameter identifiability and estimability using a case study of two compartmental, ordinary differential equation models of cancer treatment with drugs that are cell cycle-specific (taxol) as well as non-specific (oxaliplatin). We proceed through model building, structural identifiability analysis, parameter estimation, practical identifiability analysis and its biological implications, as well as alternative data collection protocols and experimental designs that render the model identifiable. We use the differential algebra/input-output relationship approach for structural identifiability, and primarily the profile likelihood approach for practical identifiability. Despite the models being structurally identifiable, we show that without consideration of practical identifiability, incorrect cell cycle distributions can be inferred, that would result in suboptimal therapeutic choices. We illustrate the usefulness of estimating practically identifiable combinations (in addition to the more typically considered structurally identifiable combinations) in generating biologically meaningful insights. We also use simulated data to evaluate how the practical identifiability of the model would change under alternative experimental designs.

These results highlight the importance of understanding the underlying mechanisms rather than purely using parsimony or information criteria/goodness-of-fit to decide model selection questions. The overall roadmap for identifiability testing laid out here can be used to help provide mechanistic insight into complex biological phenomena, reduce experimental costs, and optimize model-driven experimentation.

1. Introduction

Identifiability addresses the question of whether (and with what degree of certainty) it is possible to uniquely estimate parameters for a given model and data set. Within the framework of identifiability, there are two categories that are commonly considered: structural identifiability (sometimes just referred to as identifiability) considers whether the parameters can be estimated uniquely, in the best-case scenario of noise-free, perfectly measured data. While this is unrealistic, it is a prerequisite to successful estimation from real-world data. Practical identifiability (also termed estimability (Jacquez and Greif, 1985; McLean and McAuley, 2012)) expands on this best case scenario to examine how noise, sampling frequency, and other real-world considerations may hinder our ability to uniquely estimate the parameters. Issues of parameter unidentifiability and uncertainty are highly common in mathematical biology—even for very simple models— and yet they are not often examined in practice. For example, simple cell population growth and treatment models are ubiquitous in cancer, however their identifiability properties are not often considered. Given that these models often form the backbone of many more complex, multiscale approaches (e.g. compartmental, network, partial differential equation, or hybrid models (Byrne, 2010), with the ODE model used for parameter estimation), under standing the identifiability properties of such simple models is all the more relevant.

When mechanistic models are fitted to experimental data without consideration of any underlying identifiability issues, it may be impossible to correctly infer important clinical or mechanistic parameters from a given model and data set, and hinder our ability to predict or infer specific variables (e.g. if using an unidentifiable model to infer the fraction of cells which are resistant to treatment). As dynamic models often have many parameters and must contend with relatively little data, issues of practical identifiability have the unfortunate combination of being relatively ubiquitous and also potentially highly problematic for estimating parameters from data. Indeed, given some of the common features of biological models, there are some identifiability issues that are likely to be frequently encountered (DiStefano and Landaw, 1984; Stroberg and Schnell, 2016).

For example, Hill, Michaelis–Menten, and sigmoid types of functions (e.g. the Michaelis–Menten function, y = V_max x/(K_m + x)) are frequently employed in systems biology models to represent the switch-like and saturating behavior so commonly seen in biological systems. Such models have common practical identifiability issues if the full range of the nonlinearity is not captured in the data—for example, the linear ((V_max/K_M) x) and saturated (V_max) forms seen in the Michaelis–Menten function at low and high dose ranges (x values) respectively. In each of these cases, if the model does not cover a wide enough range of values for x, it may become practically impossible to separately estimate the parameters V_max and K_m (i.e. they may become practically unidentifiable or inestimable) (Holmberg, 1982).

Similarly, it is common to measure sums of cell types which are resolved by the model, so that cells in different states or locations are combined to represent the experimental measurement. A model may distinguish between cells that are in different stages of the cell cycle, resistant to a particular treatment, or otherwise play different roles, yet experimental data used for quantifying a model often only gives the total cell count at a particular time. For example, tumor xenograft experiments typically only report total tumor volume over time. This opens up the potential for identifiability issues as the details of which cells account for the total at different points in the trajectory can be obscured.

The above discussion illustrates how questions of confidence and uncertainty in the parameters must be answered concurrently with biological or clinical considerations. In particular, what can experimental data really tell us about our parameters, and which experiments are most useful for quantifying the biology? These questions inform how to use models to optimize experimental resources, and how to ensure that the resulting models can make the clinical and mechanistic predictions we need. A wide range of identifiability and uncertainty methods have been developed in the literature to address such questions (e.g. Audoly et al., 2001; Jacquez and Greif, 1985; Raue et al., 2009, or see reviews (Chis et al., 2011; Miao et al., 2011; Raue et al., 2014)). These range from more analytical approaches focused on structural (theoretical) identifiability properties (Audoly et al., 2001; Meshkat et al., 2014; Villaverde et al., 2016), to numerical methods using the profile likelihood and Fisher information (Jacquez and Greif, 1985; Jacquez and Perry, 1990; Raue et al., 2009; 2011). Alone or in combination, such methods can be used to interrogate which parameters can be estimated, determine measurement scenarios to ensure identifiability (Anguelova et al., 2012; Cheung et al., 2013), improve predictions of different variables and dynamic patterns (Kreutz et al., 2012; Vanlier et al., 2012b), and evaluate the structure of dependencies between estimated parameters (Janzén et al., 2016; Raue et al., 2014). In the case of unidentifiability, such dependencies can often be used to reduce or reparameterize the model to ensure identifiability (Maiwald et al., 2016; Meshkat and Sullivant, 2014). Several studies have evaluated structural and/or practical identifiability for intracellular cancer regulatory network models (Bachmann et al., 2012; Raue et al., 2014), and the literature examining identifiability of compartmental models in pharmacokinetics and pharmacodynamics is quite extensive (e.g. Audoly et al., 2001; Cobelli and DiStefano, 1980; DiStefano and Landaw, 1984; Janzén et al., 2016 among others).

In this manuscript, we apply and build on these approaches to examine identifiability using compartmental models of cancer chemotherapy as a case study. Indeed, mathematical modeling has a long history in the field of cancer therapeutics, and continues to rapidly expand. It is increasingly being recognized that quantitative tools such as mathematical modeling can help elucidate the various mechanisms that underlie a growing tumor’s response to treatment. Such models can not only be used to check the validity of hypotheses that are postulated to explain experimental observations, but also improve experimental design by making testable predictions or revealing counter-intuitive physical principles (Altrock et al., 2015; Byrne, 2010). These models utilize various approaches such as ordinary or partial differential equations, cellular automata, branching processes and optimal control theory (Altrock et al., 2015; Byrne, 2010; Gatenby and Maini, 2003). Common to any of these approaches is the need to connect models with data in order to generate useful, quantitative predictions (sometimes even at the individual patient level) (Brouwer et al., 2016; Byrne, 2010; Hirata et al., 2012; Kuznetsov et al., 1994). This need to ‘develop mechanistic models that provide real insights into critical parameters’ has been highlighted by Gatenby and Maini (2003). We remark that structural identifiability questions have been examined more thoroughly for multi-stage clonal expansion models which are commonly used with population-level cancer data (Brouwer et al., 2016; Heidenreich et al., 1997; Luebeck and Moolgavkar, 2002). However, these models often do not consider more detailed mechanistic formulations at the cellular level.

Here we walk through the process of postulating a model that incorporates drug mechanisms of interest and estimate parameters from real data. We then highlight issues of unidentifiability even when the data might appear sufficient and demonstrate how neglecting consideration of these issues could lead to incorrect predictions. Finally, the analysis reveals novel experiments that would resolve the model identifiability and allow us to answer additional biological questions of interest. A detailed roadmap of the analysis process used in the manuscript is given in the Methods.

2. Materials and methods

We begin by outlining a roadmap of the analyses that follow in the next sections. While the specific methods and details needed for each situation may vary, these general steps are useful for a wide range of problems: 1) establishing the biological questions of interest and model development; 2) experimental data setup; 3) structural identifiability analysis; 4) parameter estimation; 5) practical identifiability analysis and examining how parameter uncertainty affects model predictions; 6) evaluating practically identifiable combinations; 7) determining alternative data collection strategies to resolve key parameters. As we will discuss later, in practice it may be more advantageous to use simulated data and perform this analysis prior to data collection. This would allow modelers and experimentalists to collaborate to generate tailor-made models and data to answer biological questions. Example code for model simulation, parameter estimation, and identifiability analysis is available at https://github.com/marisae/cancer-chemo-identifiability.

2.1. Mechanistic model development

The models proposed here are based on those developed in Jain et al. (2014) and Jain and Meyer-Hermann (2011). These models are relatively simple, but can be directly applied to examine treatment approaches, combination therapy, and drug targeting (Jain and Meyer-Hermann, 2011; Jain et al., 2014), making them an ideal case-study with which to evaluate unidentifiability issues. It should also be noted that these models can be improved or expanded upon (or other mechanisms proposed instead), and the same estimation and identifiability methods may be applied. The growth and response to chemotherapy of solid tumors is described in mathematical terms by a system of coupled nonlinear ordinary differential equations (ODEs) that govern the temporal dynamics of key model variables. These include: P (t), the number of cells in G2/M phase of the cell cycle; R (t), the number of cells in G1/S phase of the cell cycle; A_P (t), the number of cells arrested in G2/M due to drug action; and A_R (t), the number of cells arrested in G1/S due to drug action. We also designate by T, the administered dose of taxol, and by C, the administered dose of oxaliplatin, both of which are assumed to be constant for the duration of the experiments. The equations governing the dynamics of these species are explained below.

2.1.1. Control model equations

Cancer cells in the G2/M phase of the cell cycle are assumed to undergo cell division at a rate λ resulting in two new daughter cells in the G1/S phase. From G1/S, cells re-enter G2/M on completion of DNA synthesis. Our model takes into account limited availability of space for cells to occupy in the following manner. As the amount of free space decreases, cells are more likely to enter quiescence (Norton and Popel, 2014). However, for simplicity we do not include a separate compartment representing these cells; instead the rate at which cells re-enter G2/M from G1/S is assumed to be dependent on the available free space, and goes down as space becomes limited.

Combining these processes, we arrive at the following equations governing the growth of cancer cells in the absence of treatment.

$$\begin{gathered} \frac{dP}{dt}=-\lambda P+{\alpha }_{RP}R\frac{{V_F}^{\theta }}{V_0^{\theta }+{V_F}^{\theta }}, \\ \frac{dR}{dt}=2\lambda P-{\alpha }_{RP}R\frac{{V_F}^{\theta }}{V_0^{\theta }+{V_F}^{\theta }}, \end{gathered}$$ (1)

where, V_F (t) = V_T − P (t) − R (t) refers to the current free space in the experimental system, V_T is the total amount of free space, and θ determines how rapidly cells begin to detect crowding effects. We remark that in the above equations, the rate at which cells in G1/S progress to G2/M is maximized when V_F is maximumized.

2.1.2. Taxol treatment

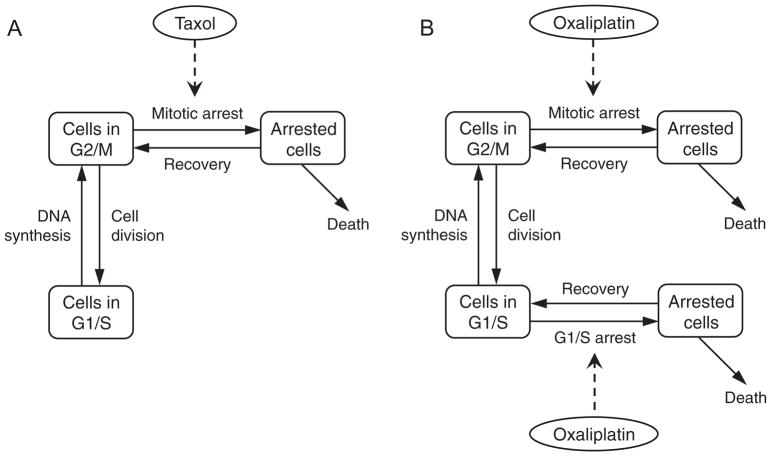
A schematic of taxol action is presented in Fig 1A. Taxol is an anti-mitotic compound that works by stabilizing microtubules in dividing cells. This results in mitotic arrest followed by either apoptosis or a return to the proliferating population via a process known as ‘slippage’ (Gascoigne and Taylor, 2008; Weaver, 2014). Because this is cell-cycle specific, we assume that it only affects cells in the G2/M phase. Therefore, a single arrested cell compartment is added, with cells in the G2/M phase undergoing cell-cycle arrest at a rate dependent on the amount of therapy administered. This rate is assumed to be an increasing and saturating function of drug concentration, with the maximum rate of arrest being α_P and the half-saturation constant k_α.

Fig. 1.

Model schematic. (A), Taxol treatment affects cells in G2/M phase of the cell cycle, leading to arrest and subsequent cell death or recovery to original state. (B), Oxaliplatin treatment affects cells in both G1/S and G2/M phases of the cell cycle, leading to arrest and subsequent cell death or recovery to original state.

From an arrested state, cells may undergo apoptosis or recover to the proliferating population. Cell cytotoxicity is assumed to be dependent on the amount of therapy administered, and is taken to be an increasing and saturating function of drug concentration, with δ₀ representing the maximum rate of death and k_δ the half-saturation constant. Finally, arrested cells may return to their original state as a result of slippage, at a rate ρ_0.

Combining these processes, we arrive at the following equations governing the response of cancer cells to treatment with taxol.

$$\begin{gathered} \frac{dP}{dt}=-\lambda P+{\alpha }_{RP}R\frac{{V_F}^{\theta }}{V_0^{\theta }+{V_F}^{\theta }}-{\alpha }_P\frac{T^a}{k_{\alpha }^a+T^a}P+{\rho }_0{A}_P, \\ \frac{dR}{dt}=2\lambda P-{\alpha }_{RP}R\frac{{V_F}^{\theta }}{V_0^{\theta }+{V_F}^{\theta }}, \\ \frac{d{A}_P}{dt}={\alpha }_P\frac{T^a}{k_{\alpha }^a+T^a}P-{\delta }_0\frac{T^b}{k_{\delta }^b+T^b}{A}_P-{\rho }_0{A}_P, \end{gathered}$$ (2)

where, as before, V_F (t) = V_T − P (t) − R (t) − A_P (t) refers to the current free space in the experimental system. The exponents a and b determine the steepness of the Hill functions for drug effects on the cells.

2.1.3. Oxaliplatin treatment

Oxaliplatin is a cell-cycle nonspecific (Baker, 2002) platinum-based compound that interacts with DNA to form DACH-Pt DNA adducts, resulting in DNA damage. This damage is recognized by a number of candidate proteins and eventually leads to cell-cycle arrest, followed by apoptosis or recovery to the proliferating population based on the extent, and hence reparability, of DNA damage (Alcindor and Beauger, 2011; Raymond et al., 2002).

To model the effects of oxaliplatin on cancer cells, two additional compartments representing arrested cells are added to the cell population, a schematic of which is presented in Fig 1B. Upon drug application, cells in both G2/M and G1/S phase undergo cell-cycle arrest at rates dependent on the amount of therapy administered. These rates are assumed to be increasing and saturating functions of drug concentration, with the maximum rate of arrest from G2/M being α_P and from G1/S being α_R. For simplicity, the half-saturation constant k_α is assumed to be the same in both instances.

From an arrested state, cells may undergo apoptosis or recover to the proliferating population. Cell cytotoxicity is assumed to be dependent on the extent of DNA damage. Further, cell cytotoxicity has been found to be linearly correlated with the amount of platinum bound to the DNA (Siddik, 2003). Consequently, the rate of cell death from either arrested compartment is assumed to be (the same) increasing and saturating function of drug concentration, with δ₀ representing the maximum rate of death and k_δ the half-saturation constant. Finally, arrested cells that have successfully repaired any DNA-damage may return to their original states upon recovery, at a rate ρ_0.

Combining these processes, we arrive at the following equations governing the response of cancer cells to treatment with oxaliplatin.

$$\begin{gathered} \frac{dP}{dt}=-\lambda P+{\alpha }_{RP}R\frac{{V_F}^{\theta }}{V_0^{\theta }+{V_F}^{\theta }}-{\alpha }_P\frac{C^a}{k_{\alpha }^a+C^a}P+{\rho }_0{A}_P, \\ \frac{dR}{dt}=2\lambda P-{\alpha }_{RP}R\frac{{V_F}^{\theta }}{V_0^{\theta }+{V_F}^{\theta }}-{\alpha }_R\frac{C^a}{k_{\alpha }^a+C^a}R+{\rho }_0{A}_R, \\ \frac{d{A}_P}{dt}={\alpha }_P\frac{C^a}{k_{\alpha }^a+C^a}P-{\delta }_0\frac{C^b}{k_{\delta }^b+C^b}{A}_P-{\rho }_0{A}_P, \\ \frac{d{A}_R}{dt}={\alpha }_R\frac{C^a}{k_{\alpha }^a+C^a}R-{\delta }_0\frac{C^b}{k_{\delta }^b+C^b}{A}_R-{\rho }_0{A}_R, \end{gathered}$$ (3)

where, V_F (t) = V_T − P (t) − R (t) − A_P (t) − A_R (t) refers to the current free space in the experimental system. The exponents a and b determine the steepness of the Hill functions for drug effects on the cells.

2.2. Experimental data

Parameters relating to the effect of taxol on cancer cells were estimated from in vitro tumor spheroid growth assays described in Terzis et al. (1997), while those relating to the effect of oxaliplatin on cancer cells were estimated from in vitro cell growth inhibition assays described in Jang et al. (2002). We describe these data sets in further detail below.

2.2.1. Taxol data

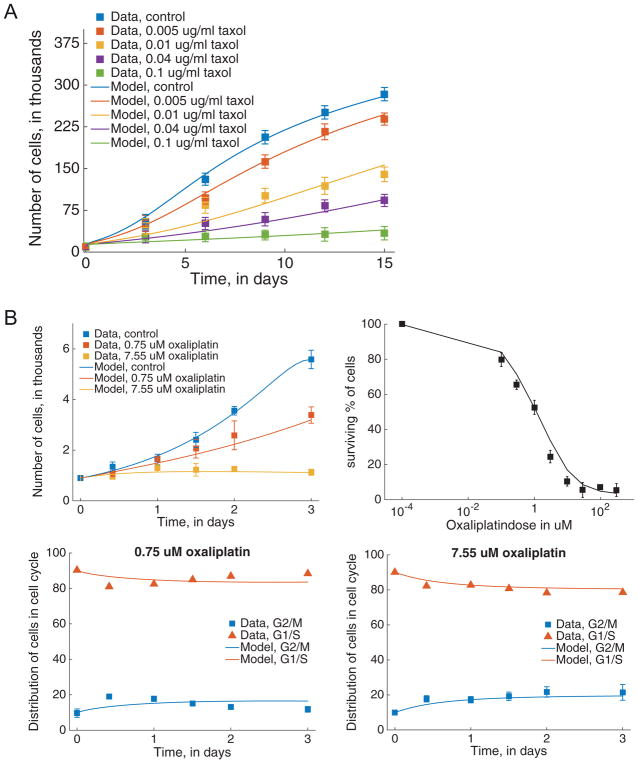
We consider five time course data sets of tumor spheroid growth (using human glioma cell line D-54Mg) under treatment and control conditions, from Terzis et al. (1997). Tumor spheroids were generated by seeding cells in the presence of culture medium in agar-coated tissue culture flasks for a period of 10 days. Spheroids with diameters between 200 and 250 μm were selected, and time course responses of spheroid growth inhibition in response to drug application were generated by continuously exposing the spheroids to four constant concentrations of taxol (0.005 μg/ml, 0.01 μg/ml, 0.04 μg/ml, 0.1 μg/ml) or no drug (control). The volume of the spheroids was recorded at five time points over a period of 15 days, with the data shown in Fig. 2A. Assuming that spheroid volume is proportional to the number of cells it contains, we can estimate total cell number (N(t) = P (t) + R (t) + A_P (t)) as a function of time for the different drug concentrations from this data.

Fig. 2.

Model fits to data. (A), taxol model fitted to control and treatment data on total cancer cells over time, with treatment doses ranging from 0.005 μg/ml to 0.1 μg/ml. (B), oxaliplatin model fitted to data for control and treatment cases. Clockwise from top left: model trajectory when estimated using control and treatment data on total cancer cells over time, dose response to oxaliplatin, model fit to fractional breakdown of cells in G1/S and G2/M for 7.55 μM (right) and 0.75 μM (left) doses.

2.2.2. Oxaliplatin data

The growth inhibitory effects of oxaliplatin on the human gastric cancer cell line SNU-1 were measured in a series of experiments described in Jang et al. (2002), with data shown in Fig. 2B. Three time series data sets of cell growth in response to drug application were generated by culturing cells in control medium for 24 h, followed by exposure to: 2 different constant concentrations of oxaliplatin (0.75 μM and 7.55 μM) or no drug (control) for 72 h. At five time points, the number of viable cells were counted (Fig. 2B, top left). The two treatment time courses were analyzed by flow cytometry to determine the cell cycle distribution at each time point (Fig. 2B, bottom panels). This data provides us with total cell number (N(t) = P (t) + R (t) + A_P (t) + A_R (t)) as well as the numbers of cells in G2/M (P (t) + A_P (t)) and in G1/S (R (t) + A_R (t)) as functions of time, for the different drug concentrations.

In the same set of experiments, dose response curves were generated by exposing cells to nine concentrations of oxaliplatin for 72 hours, and measuring viable cells (as a percentage of control) at the end of this period (Fig. 2B, top right panel). For each dose of oxaliplatin administered, the percentage of viable cells can be expressed as $100\times \frac{N(t=72)}{N_{\mathit{control}}(t=72)}$.

2.3. Parameter estimation

Parameter values for the model equations in each case (control + taxol and control + oxaliplatin) were chosen so that tumor cell counts best fit the experimental data described above in a weighted least squares sense (using weights equal to the average of each data set in order to avoid over-weighting any particular time course). This was implemented in Matlab using the curve-fitting tool ‘lsqcurvefit’ coupled with the built-in ordinary differential equation solver ‘ode23s’. We remark that the model exponents θ, a and b are all taken to be positive and, for parsimony, the lowest value of each exponent is chosen which yields an optimal fit to the data. The exponents are then held fixed for the remainder of the simulations (see Results for an explanation).

Control data relating to each set of experiments and simulated by equations (1) was used to estimate: λ, the tumor cell division rate; α_RP, the rate parameter controlling transition from G1/S to G2/M; V_T, total free volume available; and V_0, sensitivity of cells in G1/S to over-crowding. After initial estimation, for simplicity we assumed these parameters were fixed. While there may be issues of uncertainty in the control parameters as well, there is less room for examining alternative data collection strategies (as we cannot give alternative doses). Additionally, it is possible to directly experimentally measure the parameters for the control model (i.e. the duration of each cell cycle stage can be determined, as can the total volume of the experimental system). Thus, for the purposes of this study, these parameters are not varied.

Treatment data for taxol, simulated by equations (2), was used to estimate: α_P, the maximum rate of arrest of cells in G2/M; k_α, the sensitivity of proliferating cells to taxol; δ_0, the maximum rate of arrested cell death; k_δ, the arrested cell death rate half-saturation constant; and ρ_0, the rate of arrested cell recovery to the proliferating pool. As initial conditions for the taxol model, we note that the initial data value gives the initial condition for N, and the initial condition for P can be estimated from the slope of the first two data points by noting that d N/d t = λP. From these, we can get estimates of both P (0) and R (0), where A_P (0) is assumed to be zero at the beginning of the experiment.

Finally, treatment data for oxaliplatin, simulated by equations (3), was used to estimate: α_P and α_R, the maximum rates of arrest of cells in G2/M and G1/S respectively; k_α, the sensitivity of proliferating cells to oxaliplatin; δ_0, the maximum rate of arrested cell death; and k_δ, the arrested cell death rate half-saturation constant. The rate of recovery from either arrested compartment to the proliferating pool (ρ₀₎ was estimated to be 0.4005 per day from Zhen et al. (1992), and was held fixed in our numerical simulations. Since arrest begins only after the treatment starts, the initial data values of the numbers of cells in each stage give the initial conditions P (0) and R (0), with A_P (0) = A_R (0) = 0.

2.4. Structural identifiability

Structural identifiability analysis examines the identifiability properties inherent to the model structure given a particular form or type of data, without considering issues of data quantity or quality. Structural identifiability addresses whether model parameter estimates are unique for a given observation model (e.g., if you can only measure a subset or combination of state variables) assuming noise-free, perfectly measured data for all time points. As noted above, structural identifiability thus forms a best-case scenario in that it corresponds to the maximum possible parameter information for a given type or form of data.

A wide range of analytical methods have been developed for examining structural identifiability (Audoly et al., 2001; Chappell et al., 1990; Cobelli and DiStefano, 1980; Miao et al., 2011; Raue et al., 2009; Vajda et al., 1989). In this paper, we used the differential algebra approach (Audoly et al., 2001; Eisenberg et al., 2013; Margaria et al., 2001; Ollivier, 1989), as it gives global structural identifiability information and is applicable to the types of rational function differential equation models developed here. For a more complete review of the method, the reader is referred to Audoly et al. (2001) ; here we give a brief overview.

Consider a model of the form:

$$\begin{gathered} \frac{d\mathbf{x}}{dt}=f(\mathbf{x},\mathbf{u},t,\mathbf{p}) \\ \mathbf{y}=g(\mathbf{x},t,\mathbf{p}) \end{gathered}$$ (4)

where x is the vector of unobserved state variables, y the vector of observed output variables (i.e. variables which are measured), u the vector of known (observed) input functions to the system, and p the vector of unknown parameters to be estimated.

Because there may be specific degenerate parameter values or initial conditions for which an otherwise identifiable model is unidentifiable (e.g. if all initial conditions are zero), structural identifiability is often defined for almost all parameter values and initial conditions (Audoly et al., 2001; Eisenberg et al., 2013). A model is then said to be uniquely identifiable if p can be recovered uniquely from y and u, for almost all initial conditions and parameter values. This can be framed more formally as follows:

Definition 1

A parameter p_i in p (Eq. (4)) is globally or uniquely structurally identifiable if, for almost all values p* and almost all initial conditions, the equation y (x, t, p) = y (x, t, p*) implies $p_i=p_i^{\ast }$. In other words, the observation of an output trajectory uniquely determines the parameter value, so that only one value of p_i could have resulted in the observed output. Similarly, a parameter p_i is said to be locally or non-uniquely structurally identifiable if y (x, t, p) = y (x, t, p*) implies that p_i has a finite number of solutions (i.e. that only finitely many values of p_i could result in the observed output). We note that this implies that a globally identifiable parameter is also locally identifiable, however usually identifiability is only remarked upon as local if it is non-global.

Definition 2

A model is said to be globally (or uniquely) structurally identifiable if every parameter p_i is globally structurally identifiable. Similarly, a model is locally (or non-uniquely) structurally identifiable if every parameter is at least locally identifiable (i.e. they may be globally or locally identifiable).

Equivalently, a model is said to be uniquely structurally identifiable if the map from parameter values p to input and output trajectories (u (t, p), y (t, p)) is injective almost everywhere, locally structurally identifiable if this map is finite-to-one, and unidentifiable if the map is infinite-to-one (Meshkat and Sullivant, 2014). If a model contains any parameters which are not structurally identifiable, it is said to be structurally unidentifiable. In this case there typically exists a set of identifiable combinations of parameters that represent the dependencies between parameters.

The differential algebra approach was developed to determine structural identifiability and identifiable combinations for polynomial or rational function ODE models. In our case we also have some exponent parameters which are unknown; these can be dealt with separately as discussed in the Results section. The differential algebra approach can be briefly summarized as follows (for a more complete overview, see Audoly et al., 2001): given the model and measurement equations (Eq. (4)), construct the input-output equations for the model. These are monic differential polynomials in the input and output variables and their derivatives, with rational coefficients in the parameter vector p (i.e. with the state variables x and all of their derivatives eliminated from the equations). The input-output equations can be generated in many ways, such as via Ritt’s pseudodivision, Groebner bases, or other general solution methods (Audoly et al., 2001; Eisenberg et al., 2013; Meshkat et al., 2012), some of which are freely available in software packages for evaluating identifiability (Bellu et al., 2007 ; Meshkat et al., 2014). Once generated, the coefficients of these equations form a complete set of identifiable combinations for the model, and contain all structural identifiability information for that model and measurement setup. Structural identifiability of the parameters can then be inferred by testing injectivity of the map from the parameters to the coefficients. To illustrate, we use an even simpler form of the control model in which we assume no space limitations:

$$\begin{gathered} \frac{dP}{dt}=-\lambda P+{\alpha }_{RP}R, \\ \frac{dR}{dt}=2\lambda P-{\alpha }_{RP}R, \end{gathered}$$

assuming that we measure N(t) = P (t) + R (t). The equations can be rewritten to explicitly include the measured variable N :

$$\begin{gathered} \frac{dN}{dt}=\lambda P, \\ \frac{dP}{dt}=-\lambda P+{\alpha }_{RP}(N-P). \end{gathered}$$

Then, to determine the input output equation, we solve the dN/dt equation for P and substitute this in the dP/dt equation, yielding:

$$\left(\frac{\ddot{N}}{\lambda }\right)=-\lambda \left(\frac{\stackrel{.}{N}}{\lambda }\right)+{\alpha }_{RP}\left(N-\left(\frac{\stackrel{.}{N}}{\lambda }\right)\right).$$

Clearing denominators and collecting terms yields a monic differential polynomial only in terms of the measured variable N and unknown parameters—i.e. an input-output equation:

$$0=\ddot{N}+(\lambda +{\alpha }_{RP})\stackrel{.}{N}-{\alpha }_{RP}\lambda N.$$

Coefficients of input output equations are identifiable combinations (Audoly et al., 2001; Ollivier, 1989), which in this case tells us that both λ + α_RP and α_RP λ are structurally identifiable. Then if both of these combinations are known, we see that we can solve for λ and α_RP individually, so that we have a locally structurally identifiable model (with two possible solutions for λ and α_RP, as their values can be swapped).

2.5. Practical identifiability

While structural identifiability captures the maximum possible parameter information, additional analysis is needed to examine practical identifiability of a model using real, noisy data. A structurally identifiable model may still be practically unidentifiable for a variety of reasons—for example, if the model identifiability is sensitive to measurement error in the data or if measurements are taken too sparsely and miss key features of the system dynamics. In such cases, practically identifiable combinations can often be found (e.g. as seen in models of cholera (Eisenberg et al., 2013; Lee et al., 2016)). Because the degree of practical unidentifiability can range across a spectrum, customarily one defines a threshold for practical identifiability, e.g. requiring 95% confidence intervals less than a desired width, or a percent coefficient of variation (%CV) less than some threshold. There are many numerical approaches to examining identifiability (Cintrón-Arias et al., 2009; Jacquez and Greif, 1985; Jacquez and Perry, 1990; Raue et al., 2009); here we introduce two common methods, the Fisher information matrix and profile likelihood (Eisenberg and Hayashi, 2014). We also expand the use of profile likelihoods to consider practically identifiable combinations using a real-world data set.

2.5.1. Fisher information matrix

The Fisher Information Matrix (FIM) F (Edgeworth, 1908; Fisher, 1922) is a symmetric matrix that represents the amount of information contained in the data about the model parameters (Jacquez and Greif, 1985; Jacquez and Perry, 1990). Often, F is calculated using numerical approximations of the parameter sensitivities. The rank of the FIM gives the number of identifiable parameters or combinations in the model (Cintrón-Arias et al., 2009; Cobelli and DiStefano, 1980; Komorowski et al., 2011; Rothenberg, 1971).

Inverting the FIM results in the Cramér-Rao bound Covariance Matrix, C, whose diagonal entries correspond to asymptotic estimates of the parameter variances. If F is singular, the model is unidentifiable, in which case C does not properly exist; however it can usually be calculated numerically in spite of this (as the determinant of F is generally extremely small but numerically nonzero). Following Eisenberg and Hayashi (2014), we take the coefficient of variation (given by % CV = 100 · SD/p, where p is the value of the parameter) to be our parameter uncertainty measure, as this accounts for the size of the parameter value when evaluating parameter uncertainty. Similarly, we consider % CV > 100% to indicate practical unidentifiability (so that if the uncertainty is larger than the magnitude of the parameter it is considered practically unidentifiable), and > 10⁶ for structural unidentifiability.

2.5.2. Profile likelihood

One potential issue with FIM-based confidence intervals for practical identifiability results is that they are asymptotic and based on the local curvature of the likelihood; profile likelihood-based confidence intervals may be preferred if the quantity or quality of data is insufficient. The profile likelihood (Murphy and Van der Vaart, 2000; Venzon and Moolgavkar, 1988) approach ‘profiles’ a single parameter p_i by fixing p_i across a range of values, and estimating all remaining parameters for each fixed value of p_i. The maximum value of the likelihood function (or minimum sum of squares if least squares are used as equivalent to the negative log likelihood) for each parameter value constitutes the likelihood profile for the fixed parameter. The profile likelihood can generally reveal both structural and practical identifiability issues, although because the method is numerical rather than analytical, the structural identifiability information it generates is necessarily local rather than global. Structural unidentifiability manifests as a completely flat likelihood profile, while practical unidentifiability appears as a profile with a shallow and often one-sided minimum (i.e. forming an L-shaped rather than bowl-shaped curve, as will be seen for the δ₀ and k_δ profiles in the Results below).

The profile likelihood can be used to calculate confidence intervals based on a likelihood threshold—the parameter values at which the profile crosses the threshold (on either side of the optimal parameter value) define the confidence interval at a particular level of significance. Given a likelihood function L, the confidence interval for p_i at level of significance α is {p_i : log (L (p̂)) − log (L (p_i)) < Δ_α}, where Δ_α = χ² (α,df)/2 is given by a chi-squared distribution with df the number of model parameters (Raue et al., 2009).

A key advantage of the profile likelihood approach is that it can also reveal the form of identifiable combinations between parameters (Raue et al., 2009), which can provide mechanistic insight into why they are unidentifiable and what biological information can be extracted from the data. In general, the shape traced by the estimated parameters as one changes the fixed (profiled) parameter can be used to reveal the form of identifiable combinations between the profiled parameter and other parameters. (Raue et al., 2009). This can be problematic if more than two parameters are involved in a given combination (Eisenberg and Hayashi, 2014), in which case it may be advantageous to generate profiles using only particular subsets of the parameters at a time, to better elucidate the combination structure (see Eisenberg and Hayashi, 2014 for details). The idea of identifiable combinations is most commonly applied in the case of structural unidentifiability, but practical unidentifiability can result in parameter combinations/dependencies as well (Eisenberg and Hayashi, 2014; Eisenberg et al., 2013). However, as we will explore below, in the case of practical identifiability, many of the parameter relationships are less clear, and in particular it can be more difficult to disentangle combinations formed from more than two parameters at a time (since, e.g. the FIM often gives inconsistent results and ranks when faced with practical unidentifiability).

3. Results and discussion

3.1. Structural identifiability

We begin by examining the structural identifiability of the model in the control case (Eq. (1), i.e. with only P and R as variables). We assume that all parameters are positive and real.

Proposition 1

The control model (Eq. (1)) is structurally identifiable from data on total cancer cells, N = P + R.

Proof

The control form for the model (Eq. (1) can be rewritten in terms of P and N as:

$$\begin{gathered} \stackrel{.}{P}=-\stackrel{.}{N}+{\alpha }_{RP}R\frac{{(V_T-N)}^{\theta }}{V_0^{\theta }+{(V_T-N)}^{\theta }}, \\ \stackrel{.}{N}=\lambda P. \end{gathered}$$ (5)

To make the parameter θ a coefficient rather than an exponent, we can define an additional variable $X={(V_T-N)}^{\theta }/V_0^{\theta }$, and write a differential equation for X :

$$\begin{gathered} \stackrel{.}{P}=-\stackrel{.}{N}+{\alpha }_{RP}(N-P)\frac{X}{1+X}, \\ \stackrel{.}{X}=-\theta \frac{\lambda XP}{V_T-N}, \\ \stackrel{.}{N}=\lambda P. \end{gathered}$$ (6)

From here, the standard differential algebra approach (similar to the example given in the Methods) yields the input-output equation:

$$\begin{gathered} 0={\lambda }^2(-V_T){\stackrel{.}{N}}^2+(\theta +1){\lambda }^{2}N{\stackrel{.}{N}}^2-\frac{\theta \lambda ({\alpha }_{RP}+\lambda ){\stackrel{.}{N}}^3}{{\alpha }_{RP}} \\ +{\lambda }^2{V}_{T}N\ddot{N}-{\lambda }^2{N}^2\ddot{N}+\lambda (-V_T)\stackrel{.}{N}\ddot{N} \\ +(\theta +1)\lambda N\stackrel{.}{N}\ddot{N}-\frac{\theta ({\alpha }_{RP}+2\lambda ){\stackrel{.}{N}}^2\ddot{N}}{{\alpha }_{RP}}+V_T{\ddot{N}}^2 \\ -N{\ddot{N}}^2-\frac{\theta \stackrel{.}{N}{\ddot{N}}^2}{{\alpha }_{RP}}+\lambda V_{T}N\stackrel{⃛}{N} \\ -\lambda N^2\stackrel{⃛}{N}-V_T\stackrel{.}{N}\stackrel{⃛}{N}+N\stackrel{.}{N}\stackrel{⃛}{N}. \end{gathered}$$ (7)

Solving from the coefficients yields unique solutions for all four parameters, so that λ, V_T, θ, and α_RP are uniquely structurally identifiable. To establish the identifiability of V_0, we use Eq. (5), plugging in P = Ṅ/λ into the P equation to yield:

$$\frac{\ddot{N}}{\lambda }=-\stackrel{.}{N}+{\alpha }_{RP}(N-\frac{\stackrel{.}{N}}{\lambda })\frac{{(V_T-N)}^{\theta }}{V_0^{\theta }+{(V_T-N)}^{\theta }}.$$

As all parameters except V₀ are identifiable, and N is known, we can solve for V₀ to show it is also identifiable, yielding identifiability for the model.

We next examine the model in the two experimental cases of taxol and oxaliplatin. Because the control data will allow for identification of α_RP, λ, V_0, V_T, and θ, we assume these parameter values are known. We also note that while the drug inputs used in the experimental data are constant, time course data was taken for multiple drug concentrations, which we assume are sufficient to capture the range of low to high dose effects.

Proposition 2

Assume the control-case parameters from Proposition 1 are known. Then the taxol model (Eq. (2)) is structurally identifiable from time-course cancer cell count (measuring N(t) = P (t) + R (t) + A_P (t)) data sets in response to multiple (≥2) constant drug concentration inputs.

The proof proceeds entirely analogously to that of Proposition 3, given below.

Proposition 3

Assume the control-case parameters from Proposition 1 are known. Then the oxaliplatin model (Eq. (3)) is structurally identifiable from time-course cancer cell count (measuring N(t) = P (t) + R (t) + A_P (t) + A_R (t)) data sets in response to multiple (≥2) constant drug concentration inputs.

Proof

First, we rewrite the model equations (Eq. (3)) similarly to the proof of Proposition 1 :

$$\begin{gathered} \frac{dN}{dt}=\lambda P-{\delta }_0\frac{C^b}{k_s^b+C^b}(A_P+A_R), \\ \frac{dP}{dt}=-\lambda P+{\alpha }_{RP}\frac{{V_F}^{\theta }}{V_0^{\theta }+{V_F}^{\theta }}R-{\alpha }_P\frac{C^a}{k_{\alpha }^a+C^a}P+{\rho }_0{A}_P, \\ \frac{d{A}_P}{dt}={\alpha }_P\frac{C^a}{k_{\alpha }^a+C^a}P-{\delta }_0\frac{C^b}{k_{\delta }^b+C^b}{A}_P-{\rho }_0{A}_P, \\ \frac{d{A}_R}{dt}={\alpha }_R\frac{C^a}{k_{\alpha }^a+C^a}R-{\delta }_0\frac{C^b}{k_{\delta }^b+C^b}{A}_R-{\rho }_0{A}_R, \end{gathered}$$ (8)

As the control parameters for the model are assumed to be known, and N is measured (assumed to be known for all times), the values of the term ${\alpha }_{RP}\frac{{(V_T-N)}^{\theta }}{V_0^{\theta }+{(V_T-N)}^{\theta }}$ are thus completely known at all times as well. Then, to simplify our analysis, we denote this function by u (t), which we assume to be a known input to the system.

Next, note that for any particular single dose, the oxaliplatin (C) concentration is constant, so that we can combine terms to let:

$$\begin{gathered} {\stackrel{\sim }{\alpha }}_P:={\alpha }_P\frac{C^a}{k_{\alpha }^a+C^a} \\ {\stackrel{\sim }{\alpha }}_R:={\alpha }_R\frac{C^a}{k_{\alpha }^a+C^a} \\ {\stackrel{\sim }{\delta }}_0:={\delta }_0\frac{C^b}{k_{\delta }^b+C^b} \end{gathered}$$ (9)

Let us consider the identifiability of the model in this form (with unknown parameters ρ_0, α̃_P, α̃_R, and δ̃₀₎ from a single dose response time course data set (i.e. N (t) measured in response to a single constant drug concentration C). By simply following the standard differential algebra approach, we generate an inputoutput equation in terms of only the known/measured variables, their derivatives, and the parameters. The resulting input-output equation contains 50 monomial terms, and testing the coefficients reveals that the parameters ρ_0, α̃_P, α̃_R, and δ̃ ₀₎ are indeed identifiable from any single dose response time course data set.

Next, we note that Hill functions of the form $y=\frac{A{x}^n}{B^n+x^n}$ are structurally identifiable from multiple (x, y) pairs (although for practical identifiability, such points should span the linear-to-saturated ranges of the function). Then from the multiple drug dose data sets, we can identify multiple values for each of α̃_P, α̃_R, and δ̃_0, from which the individual parameters α_P, α_R, k_α, δ_0, k_δ, a, and b are identifiable, making the entire model structurally identifiable.

3.2. Practical identifiability

Parameter Estimation

Model fits for both the taxol and oxaliplatin models (control and experimental) are shown in Fig. 2, with parameter estimates given in Table 1. For parsimony, we chose the lowest values of the exponents a and b in 0.5 increments (i.e. so that each exponent is in {0. 5, 1, 1. 5, 2, . . .}) that yielded an optimal fit to the data, as the exponents were relatively insensitive once we were in a broad range.

Table 1.

Estimated parameter values.

Taxol			Oxaliplatin
Parameter	Value	Units	Parameter	Value	Units
λ	9.57	per day	λ	5.96	per day
αRP	20	per day	αRP	0.99	per day
VT	1.05 ×103	thousands of cells	VT	5.48	thousands of cells
V0	1.46 ×103	thousands of cells	V0	0.55	thousands of cells
θ	10	dimensionless	θ	1	dimensionless
αP	8.32	per day	αP	8.69	per day
kα	8.10	ng/ml	αR	3.00	per day
ρ0	0.06	per day	kα	21.67	μM
δ0	1.33	per day	δ0	0.96	per day
kδ	119.14	ng/ml	kδ	9.22	μM
a	3	dimensionless	a	0.5	dimensionless
b	4	dimensionless	b	1	dimensionless

Grey shading indicates control model parameters. Details of parameter estimation are described in the Methods.

3.2.1. Taxol model results

Fisher Information

Calculation of the FIM from the best fit parameter estimates resulted in a full rank matrix (rank 5), confirming the structural identifiability of the model. The parameter percent coefficient of variations (%CVs, given in Table 2) were mostly < 100%, which would indicate practical identifiability, although two were either greater than 100% or very nearly so.

Table 2.

FIM-based %CVs for the Taxol and oxaliplatin models.

Taxol			Oxaliplatin
Parameter	Estimate	%CV	Parameter	Estimate	%CV
αP	8.3170	37.08	αP	8.6899	71.65
kα	8.0959	17.62	αR	3.0046	81.91
ρ0	0.0582	123.84	kα	21.6653	171.13
δ0	1.3307	94.51	δ0	0.9568	62.83
kδ	119.1363	38.55	kδ	9.2240	87.84

Profile Likelihoods

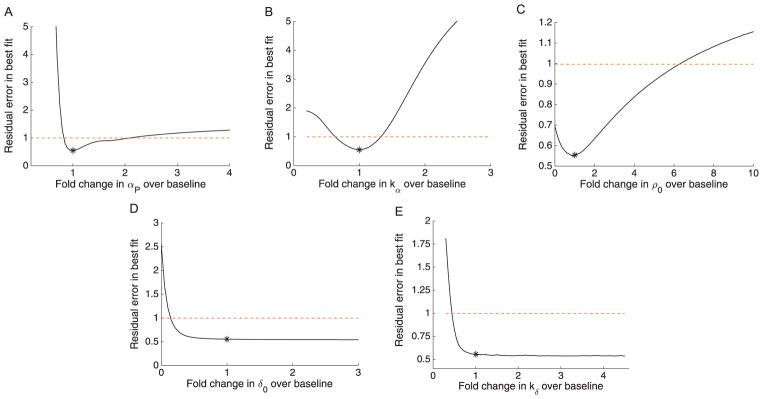
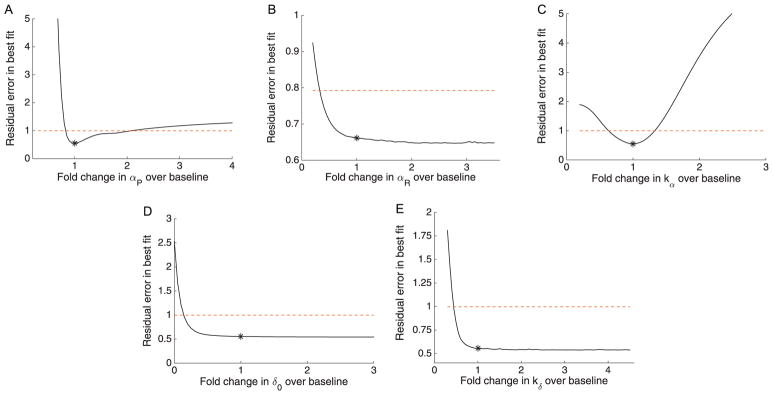
The profile likelihoods for the taxol model are given in Fig. 3 and parameter relationships in Supporting Information Fig S1. The profiles show practical unidentifiability for δ₀ and k_δ, with the lower side of the profile crossing the threshold for the 95% confidence bounds, but the opposing side appears quite flat. The remaining parameters (α_P, k_α, and ρ₀₎ show finite confidence bounds indicating practical identifiability, although we note that the confidence bounds are fairly wide for α_P and ρ_0, indicating high uncertainty that might be improved by further data or experimental measurement of one of the parameters.

Fig. 3.

Profile likelihoods for the taxol model. Profile likelihoods (solid lines) for: (A), α_P ; (B), k_α; (C), ρ₀ ; (D), δ₀ ; (E), k_δ. Thresholds for 95% confidence intervals shown as dashed red lines, and the parameter estimates given in Table 1 are shown as asterisks (*). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Practically Identifiable Combinations

Given that the only two fully practically unidentifiable parameters in Fig. 3 are δ₀ and k_δ, we focused on these two in examining potential practically identifiable combinations (Fig. 4). Fig. 4 shows the parameter relationship between k_δ and δ₀ that results when profiling either of these two parameters, which indicates that there is a consistently strong correlation between them. The mathematical form of this identifiable combination can be determined by plotting on a log-log scale (shown in Supporting Information Fig S3). The plot shows a wide linear region beginning just to the right of the estimated value for k_δ (around k_δ ≈140), with a best-fit slope of 4.

Fig. 4.

Parameter relationships and subset profiles for the taxol model. (A) and (B): Parameter relationships between α_P and ρ₀ (A) and between k_δ and δ₀ (B). Parameter estimates from the profile likelihoods are shown as blue squares, and the black squares indicate the overall optimal parameter estimates from Table 1. The 95% confidence intervals from Fig. 3 are shown as shaded grey regions. In (B), the low-dose approximation to the Hill function (red line) matches quite well for δ₀ and $k_{\delta }^4$, as these two parameters were fully practically unidentifiable. For (A), the parameter relationship for lower values of α_P appears to follow an approximate exponential relationship with ρ₀ (red line), but then switches to a near-linear relationship approximately for higher values. This lack of consistent combination structure is likely due to the fact that α_P and ρ₀ were practically identifiable but had fairly large confidence intervals. The estimated local practically identifiable combinations are shown as solid red lines. (C)–(E): Profile likelihoods where only the parameter set α_P, k_α, and k_δ are considered, assuming that ρ₀ and δ₀ are known via experimental data. The profiles now show practical identifiability with narrow confidence bounds for all three parameters. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

This combination is consistent with the model equations—even though the Hill function for cell death may not be in the low-dose linear range (as can be determined by fitting the linearized, reduced model to data, which results in significantly worse model fit (not shown), the two Hill function parameters may still approximately compensate for one another, resulting in their practical unidentifiability. The log-log linear slope of 4 is precisely consistent with the combination we would expect from the low-dose linear approximation to the Hill function, ${\delta }_0/k_{\delta }^4$. This suggests that while the compensation between δ₀ and k_δ is nonlinear at the estimated value, once k_δ increases above the estimated value (119.14), it becomes large enough compared to the maximum drug dose given (100 ng/mL), that the linear form of the Hill function becomes a close approximation, resulting in the apparent trade-off to the right of the estimated value.

Fig. 4 shows the fit of this combination, given by ${\delta }_0/k_{\delta }^4=\mathit{exp}(-19.2)$, to the profiled parameter relationship. This is close— but does not exactly match—the linear form of the Hill function at the estimated parameters, which would yield ${\delta }_0/k_{\delta }^4=\mathit{exp}(-18.8)$. The apparent discrepancy is due to the fact that the Hill function does not match up to the linear range until slightly above the estimated value of k_δ.

Proposed Experimental Data to Resolve Identifiability

A useful consequence of knowing which parameters are involved in identifiable combinations is that we can evaluate experimental data collection strategies to resolve the model undentifiability. Here, experimental measurements of either δ₀ or k_δ (e.g. using live/dead staining with taxol treatment at different levels) would in result in finite confidence bounds for all parameters. Often modelers may simply fix one of the parameters to its estimated value— however, this must be done with the understanding that the resulting estimate of the non-fixed parameter is really estimating the conserved quantity approximately equal to the combination (in this case ${\delta }_0/k_{\delta }^4$). Indeed, fixing δ₀ to its estimate yields finite confidence bounds (i.e. practical identifiability) for all parameters, as shown in Fig. 4 and Supporting Information Fig S2.

We remark that, while fixing δ₀ does generate finite confidence bounds for all parameters, it does not improve the width of the confidence bounds for α_P or ρ_0. Thus, we also considered how the uncertainty of the parameters could potentially be improved by additionally fixing either of these two parameters. As noted in the Parameter Estimation section for oxaliplatin, it is possible to experimentally measure ρ_0, the recovery rate for cells (Jang et al., 2002). We therefore tested an additional scenario in which we fixed both ρ₀ and δ₀ to their estimated values (e.g. supposing both were experimentally measured to be those values). This yielded quite narrow confidence bounds for the remaining three parameters, as shown in Fig. 4.

3.2.2. Oxaliplatin model results

Fisher Information

Calculation of the FIM from the best fit parameter estimates resulted in a full rank matrix (rank 5), confirming structural identifiability of the model. For all but one parameter, the percent coefficient of variations (%CVs, given in Table 2) were < 100%, which would indicate practical identifiability, although all parameter CV’s were also above 50%.

Profile Likelihoods

The overall profile likelihoods for the oxaliplatin model are shown in Fig. 5. In spite of the structural identifiability of the model and mid-range %CV values given by the FIM, the broader exploration of the parameter space using the profile likelihood reveals a lack of practical identifiability. Four of the five parameters cross the threshold for the 95% confidence interval only on the left side, while the fifth parameter remains below threshold for the entire 6-fold change region examined. All profiles have large relatively flat regions, often with a lower boundary due to poor fits when the parameter values approach zero.

Fig. 5.

Profile likelihoods for the oxaliplatin model. Profile likelihoods (solid lines) for A: α_P, B: α_R, C: k_α, D: δ_0, E: k_δ. Thresholds for 95% confidence intervals shown as dashed red lines, and the parameter estimates given in Table 1 are shown as asterisks (*). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Interestingly, the k_δ profile appears to actually decrease slightly to the left of the estimated parameter value, seemingly in contrast with the FIM results (although there is a small, very local minimum not visible in the profile plot). This result suggests that it might be possible to improve the practical identifiability issues by fixing k_δ = 0. However, the profiles after setting k_δ = 0 (Supplementary Information Fig S4) reveal worsening of the unidentifiability for α_R, with the profile below threshold on both sides. This potential simplification also yields unrealistically high estimates for the maximum arrest rate from G2/M (α_P approximately 15 per day), making this simplification biologically unfeasible.

Implications for Predicting Unobserved Variable Trajectories

Even if models have been derived mechanistically, and we have confidence in the model structure, parameter unidenifiability can lead to erroneous conclusions in the model inferences, predictions, and parameter estimates. The difference between the FIM-based and profile-based confidence bounds raises the possibility that if only FIM-based confidence bounds are considered (as is often used in practice), one might draw false confidence in the ability of the data to inform the biological or mechanistic predictions of the model. In particular, predicting or inferring the trajectories of clinically important variables that are not separately measured in the data can be quite fraught in the presence of unidentifiability.

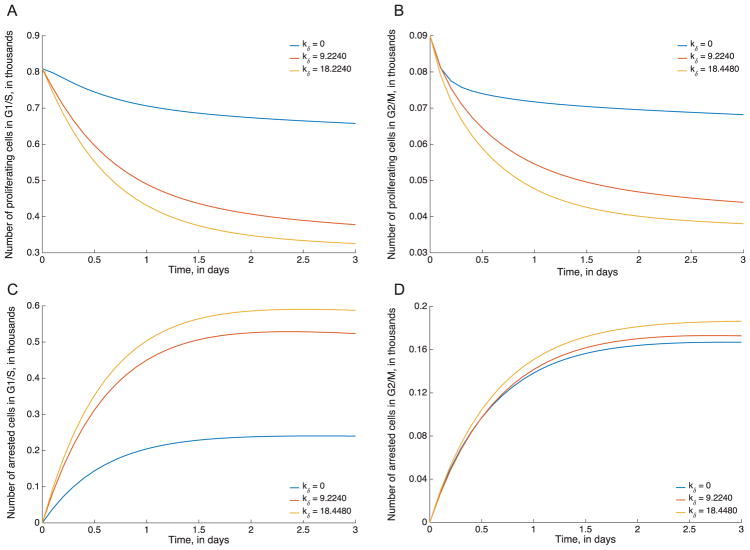
To illustrate this, we plotted the individual trajectories of arrested vs. non-arrested and G1/M vs. G2/S (that is, four variables, P, R, A_P and A_R), using different values of the parameters drawn from the k_δ profile (Fig. 5E). All three profiled parameter sets tested had essentially the same fit the data, but yield sharply different predictions of the fractions of cells in different states, as shown in Fig. 6. While some trajectories are relatively conserved across the three parameter sets tested (for instance, G2/M arrested cells), the other cell type trajectories are markedly different. In the current setting (cancer chemotherapy), this is of especial concern since platinum-based drugs are frequently combined with taxanes in treating solid tumors (Bunn and K, 1998; Pavlidis and Pentheroudakis, 2012; Utsunomiya et al., 2006). Taxanes are cell-cycle specific and it is therefore important to know the cell cycle distributions resulting from exposure to one or the other drug accurately in order to successfully predict optimal combination dosing strategies.

Fig. 6.

Model predictions by cell type for the oxaliplatin model. Model simulations for proliferating G1/S (A) and G2/M (B) cells, and arrested G1/S (C) and G2/M (D) cells. In each case, trajectories are shown for three different profiled parameter sets with different values of k_δ, all of which yield very similar fits the data but different predictions for cell dynamics.

Practically Identifiable Combinations

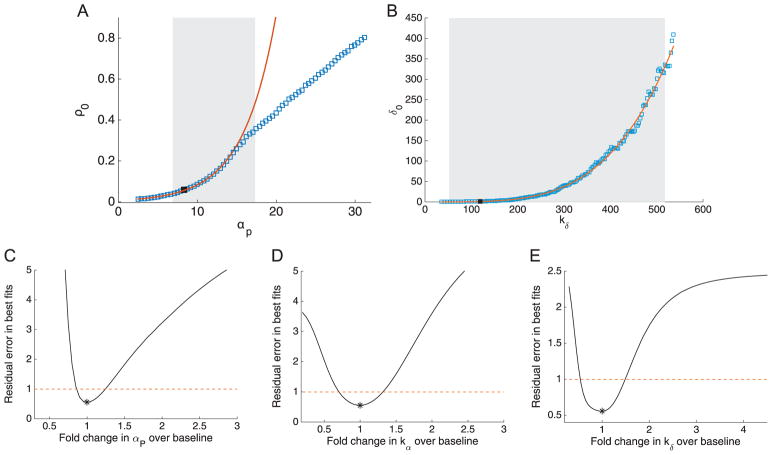
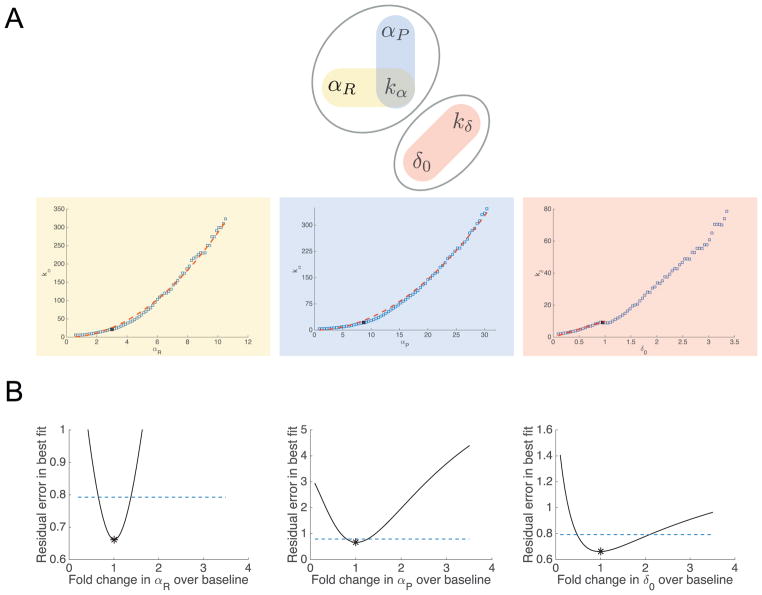
Returning to the full five-parameter model, all parameter relationship plots appear to be strongly correlated with one another, making determination of specific combinations within the larger set of five somewhat difficult (a subset is shown in Fig. 7 and the full set in Supplementary Information Fig S5). This illustrates some of the difficulties in characterizing identifiable combinations in the case of practical unidentifiability, as there are many compensating parameter relationships, and the shape or structure of parameter relationships can change across the profiled parameter space.

Fig. 7.

Parameter relationships and subset profiles for the oxaliplatin model. (A) Identifiable combination structure for oxaliplatin model. Top: parameter graph for the practically identifiable combinations in the oxaliplatin model. We consider two sets of combinations, {α_P, α_R, k_α}, and {δ_0, k_δ}. Within these sets, the combinations proposed are highlighted in red, blue, and yellow ovals. The corresponding combinations are plotted as blue squares, with potential combination forms plotted as red dashes. For the {α_P, α_R, k_α} set (yellow and blue), the combinations approximately fit the forms $\frac{{\alpha }_P}{k_{\alpha }^a}=1.7$ and $\frac{{\alpha }_R}{k_{\alpha }^a}=0.6$. For δ₀ and k_δ (red), the combination appears nonlinear, but the combination structure given by the linear-range approximation of the Hill function, δ_0/k_δ, approximately matches the profiled relationship for low values of δ_0. (B) Profile likelihoods for the oxaliplatin model, using only a subset of the parameters. Profile likelihoods (solid lines) for the parameter subset α_P, α_R, and δ_0, assuming k_α and k_δ are fixed (i.e. known, e.g. from experimental data). Thresholds for 95% confidence intervals are shown as dashed lines, and the parameter estimates given in Table 1 are shown as asterisks (*). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

However, similar to the taxol model, we note the positive combination relationships between α_P, α_R and k_α (see Fig. 7A, lower panel). These suggest that it may be possible to (for example) compensate for an increase in α_P by also increasing k_α and α_R (so that the overall values of both Hill function terms are approximately preserved). Thus, while the dose response functions show that the Hill functions are not fully in the linear range, there may still be some compensation between the Hill function parameters, yielding two practically identifiable combinations between α_P − k_α and α_R − k_α. Additionally, we see a positive relationship between δ₀ and k_δ. This overall combination structure is illustrated as a parameter graph (Eisenberg and Hayashi, 2014) in Fig. 7A.

Because these combinations are practical rather than structural, it is not a binary, yes-or-no question whether two parameters are in a combination—rather, all parameters may be correlated to varying degrees. The identifiability properties that emerge with real data may be more graduated, but nonetheless, by examining the parameter relationships further, we may be able to discern useful and biologically meaningful combinations. Verily, in examining the profiled parameter relationships in Supporting Information Fig S5, it is notable that many correlations between pairs of parameters take different forms depending on which parameter is profiled (e.g. if δ₀ is profiled the relationship with α_R looks quite different than if α_R is profiled with the resulting δ₀ values plotted). This is not necessarily surprising—since all parameters appear to have correlations with one another, there is no particular reason the same compensation must occur in each case. However, the parameters in the Hill-function-based subsets described above ({α_P, α_R, k_α}, and {δ_0, k_δ}) give (at least qualitatively) consistent results regardless of which parameter in a given pair is profiled (shown in the highlighted pairs in Supplementary Information Fig S5). This suggests that the correlation/identifiable combination structure for these parameters may be more consistent or strong for these parameters.

If we examine the form of the combinations traced between the Hill-function parameters in Fig. 7A, we see that the α_P − k_α and α_R − k_α combinations are reasonably well approximated by the combination structures $\frac{{\alpha }_P}{k_{\alpha }^a}=1.7$ and $\frac{{\alpha }_R}{k_{\alpha }^a}=0.6$. These take the same form as the linear approximation of the Hill function, although as in the taxol model, the values of the combination are slightly different from the values generated if we simply use the parameter estimates (1.87 and 0.65 respectively). The analogous linear combination for δ₀ and k_δ would be $\frac{{\delta }_0}{k_{\delta }}=0.1$, i.e. k_δ = 10δ_0, which fits well for the lower values of δ₀ profiled (Fig. 7A), but the combination then becomes nonlinear at higher values of δ_0. These deviations from the exact linear form of the combination may illustrate the fact that they are practical rather than structural—there need not be a single exact polynomial or rational function form for a practical combination, as there would for a structural combination with this type of model.

Typically, when faced with structural unidentifiability and structurally identifiable combinations, one would attempt to reparameterize the model in terms of the combinations (Evans and Chappell, 2000; Meshkat and Sullivant, 2014). In the case of practical unidentifiability, this may not always be possible, as the combination structures need not follow consistent relationships across parameter space. Another common approach involves fixing parameters to reduce the degrees of freedom to one parameter per combination (Chis et al., 2011; Eisenberg and Hayashi, 2014), although it is important to note that this does not truly resolve the underlying unidentifiability if the fixed parameter values are not experimentally measured. The combination structures here suggest that one way to resolve the practical unidentifiability would be to fix one parameter from each subset, i.e. one from {α_P, α_R, k_α} and one from {δ_0, k_δ}. We chose to fix k_α as it appears in both of the proposed combinations (one could rearrange to write the combinations in terms of any two pairs, but the Hill function-based form shown here is most natural). For {δ_0, k_δ}, either would suffice to ensure identifiability; we chose k_δ here. The resulting profiles do indeed yield practical identifiability with finite confidence bounds on both sides, shown in Fig. 7B. We also note that fixing only one of the parameters does not resolve the identifiability issues, as shown in the Supporting Information Fig S6. This also illustrates that even when the FIM may not be informative enough to use the full methods proposed in Eisenberg and Hayashi (2014), we can often explore the identifiability structure of the system by profiling specific subsets of parameters and examining which parameter confidence bounds become finite. In this case, fixing one of {δ_0, k_δ} does not change the confidence bounds for the {α_P, α_R, k_α} set, and vice versa, confirming the distinct subsets of dependent parameters shown in Fig. 7A. Similarly, fixing k_α resolves the identifiability for both α_P and α_R, confirming that these three parameters have the proposed structure in Fig. 7A.

Biological Insights From the Identifiable Combinations

Although our analyses demonstrate that additional data is necessary to resolve the model parameters and predict cell cycle distributions, nonetheless some biologically relevant conclusions can still be drawn. We noted previously that while oxaliplatin affects all cell cycle stages, there may be important differences in sensitivity which could help to explain any observed synergy or antagonism between the two drugs. If we examine the estimates in Table 1, it would appear that oxaliplatin predominantly arrests glioma cells from the proliferating state (since α_P is nearly three times α_R). It would appear that no real conclusions can be drawn since both parameters are practically unidentifiable. However, evaluating the form of the identifiable combinations showed that both parameters have the same form of combination with k_α (i.e. ${\alpha }_P/k_{\alpha }^a$ and ${\alpha }_P/k_{\alpha }^a$), which implies that the difference in magnitudes of the two arrest rates is meaningful. The three-fold difference in estimates of α_P and α_R suggests that the combination of oxaliplatin with drugs that arrest cells in G1/S may be sub-optimal (i.e. less than additive). This could help to save valuable experimental and clinical resources in developing combination therapies.

Parameter estimates often have biological or clinical implications, and without identifiability analysis one might draw spurious conclusions from point estimates of unidentifiable parameters. On the other hand, a useful facet of identifiability analysis is that the identifiable combination structure can sometimes ‘rescue’ meaningful parameter information from unidentifiable parameters, as was the case here. If one only examined the uncertainty of the parameters and not the practically identifiable combinations, this would be obscured, and the parameter estimates would appear less informative than they are.

Alternative Data Collection Strategies

It is notable that the taxol model fits, which had fewer types of data but more doses, showed better initial identifiability than did the oxaliplatin model (finite confidence intervals for three of the five parameters as opposed to unidentifiability for all five parameters). One could resolve the unidentifiability here by experimentally measuring two parameters (as explored above and in the Taxol Results section), but these two data sets also raise the possibility of conducting alternative time course experiments. We simulated several data collection strategies measuring different model variables, using the best fit parameter estimates from Table 1. In each case we generated data by running model simulations and sampling at the same frequency as the original data (that is, at 12, 24, 36, 48, and 72 h). While we consider only a few specific alternatives here, this highlights the use of identifiability and uncertainty analysis in testing possible experiment designs. For more detailed examination of the ways that identifiability can inform experiment design and data collection strategies, the reader is referred to Kreutz et al. (2012), Skanda and Lebiedz (2010), Anguelova et al. (2012), Cheung et al. (2013), Chu and Hahn (2008), Apgar et al. (2010), Banga and Balsa-Canto (2008), Vanlier et al. (2012a) and Liepe et al. (2013) (which include FIM, Bayesian, and information theoretic methods).

Apoptotic Cell Data

In this simulated data set, we used the existing two oxaliplatin doses and added simulated time course data for apoptotic cells (that is, the cumulative total cells that have died following arrest). This simulated data is motivated by the identifiable combination of cell death parameters δ₀ and k_δ, with the idea that adding data about the cell death process might resolve this unidentifiability. Such data could be obtained experimentally via live/dead staining or other apoptosis assays such as a cell death ELISA or caspase 3 activity assay. The resulting profiles are shown in Supplementary Information Fig S7, and confirm that adding apoptotic cell data yields identifiability for δ₀ and k_δ. However, adding this data does not improve identifiability issues with the parameters relating to cell arrest from the G1/S or G2/M phases of the cell cycle.

Arrested Cell Data

To resolve the unidentifiability of the cell arrest parameters, we considered an alternative data collection strategy in which we replace collection of data on cell cycle distribution with data on cell arrest. DNA damage induced by Oxaliplatin leads to the phosphorylation and activation of the checkpoint kinases CHK1/2 (Bartek and Lukas, 2003; Pires et al., 2010) resulting in cell arrest. Activation of these kinases could be measured in vitro (e.g. via immunofluorescence imaging), allowing experiments to evaluate the fraction of cells which are arrested. Measuring the overall fraction of cells arrested allows us to still split the total cell population, but by arrest status rather than cell cycle status. We initially tested this using the same two treatment arms as in the original oxaliplatin data, however we found this did not significantly alter the uncertainty on the parameters, so we added two additional treatment arms at doses bisecting the existing doses (to yield the same total number of treatment arms as for the taxol model; see Supplementary Information Fig S8. This resulted in identifiability (finite confidence bounds) for all parameters (though the confidence interval for k_α was fairly wide).

Arrested and Apoptotic Cell Data

As a third potential approach, we considered an oxaliplatin data set where we replaced both the cell cycle distribution and the dose response curve with the arrested and apoptotic cell data described in the previous two data sets. For simplicity, we supposed that in this case we add three additional treatment arms (i.e. for five treatment and one control). In each arm, we simulated measurement of the corresponding numbers of apoptotic and arrested cells. This also yielded full identifiability of the model parameters (shown in Supplementary Information Fig S9, but reduced the number of doses needed (for the dose response curve). This highlights how alternative data collection strategies may be able to provide the same amount of information about the parameters, but one experimental strategy may be simpler, less costly, or more efficient.

These simple exploratory studies highlight how identifiability and uncertainty analysis can be used to help design experiments and optimize the use of resources to best estimate clinically relevant parameters. While in this case we are simulating potential data collection strategies post hoc, this type of approach could be used to design initial experiments or to inform follow-up experiments that build upon the data used here. We found that even though the model is resolved at the level of both cell cycle and cell arrest, the cell cycle distribution data adds relatively little to the parameter estimation, while data on apoptosis or arrest is much more informative. Increasingly, we have seen tighter linkage between model and experimentation, with models often driving experimental measurements and vice versa. These types of explorations using simple simulated data can be run in a systematic way and on a larger scale to help decide optimal experiment design to maximize parameter identifiability. This will help to ensure that key clinical or treatment related parameters needed from the models can be measured effectively.

4. Conclusions

Dynamical models are increasingly being recognized as a valuable tool with which to uncover mechanistic details that drive complex biological phenomena such as cancer growth and response to treatment. However, imperfect data and the resulting practical unidentifiability of model parameters can make it impossible to infer important mechanistic information. Additionally, it is always possible to postulate mechanistic models that are in excellent agreement with experimental data, but which give misleading conclusions since parameter unidentifiability issues haven’t been addressed (Cortez and Weitz, 2013; DiStefano, 1982; Eisenberg et al., 2015; Hines et al., 2013; Hopkins and Leipold, 1996; Kitching et al., 2006; May, 2004). In this study, we discussed a general framework to address these issues using a range of identifiability methods (Audoly et al., 2001; Jacquez and Greif, 1985; Raue et al., 2009; 2011), starting from model building, parameter estimation, identifiability analysis and its biological implications, as well as alternative data generation strategies that render the model identifiable. We illustrate how practically identifiable combinations can be more difficult to characterize compared to structural combinations, and propose some general strategies for examining combinations in the practical unidentifiability case.

To illustrate the overall approach, we used two compartmental models of cancer chemotherapy and fit them to time course treatment data sets using oxaliplatin and taxol as the drugs of choice. We found that while both models were structurally identifiable from the proposed data, practical identifiability remained a roadblock to successful parameter estimation. In particular, both models illustrated the limitations of asymptotic confidence bounds based on the FIM (Raue et al., 2009)—these provide a lower bound for parameter uncertainty, but the profile likelihood analysis revealed much wider uncertainty in both the parameters and model predictions. By examining the practically identifiable combination structure of the profile likelihoods, it was possible to determine what parameter combinations can be successfully estimated, and what new data would need to be collected to resolve the estimation of individual parameters. We also highlighted the potential pitfalls of not fully analyzing the identifiability of a model, such as incorrect biological predictions.

Effort s to optimize the number and timing of measurements have long been studied in optimal experiment design (Emery and Nenarokomov, 1998; Forssell and Ljung, 2000; Pukelsheim, 1993), and are often linked to resolving unidentifiability and uncertainty issues (Cheung et al., 2013; Skanda and Lebiedz, 2010). Here we evaluated the experimental design post hoc, proposing alternative data collection strategies using an existing data set. However, as more joint data collection occurs by both modelers and experimentalists, these analyses would be best applied in concert with experiment design, so that data generation can be optimized to answer the questions of interest. The analyses shown here illustrate how different types of data (e.g. apoptotic vs. arrested cells) improve the uncertainty of particular parameter sets.

Our results highlight the importance of understanding the underlying mechanisms rather than purely using parsimony or information criteria/goodness-of-fit to decide model selection questions. Many mechanistic models will be practically unidentifiable, particularly given that the pressures of evolution push cells towards more robust behaviors, which intrinsically means less identifiability (i.e. the ability to reproduce the same behavior for many parameter values). Thus, lower dimensional models may outcompete more detailed mechanistic ones in model selection, however this can result in parameter values that are outside of realistic biological ranges. For example, the practical unidentifiability of the oxaliplatin model could seemingly be resolved by fixing k_δ = 0, however, this resulted in biologically unrealistic estimates for the remaining parameters. In general, one must take care to understand what mechanistic parameters or features are being collapsed when a more identifiable, lower dimensional model is used in place of a more mechanistic one—it can be difficult to discern when model simplification indicates mechanism versus when it indicates insufficiently informative data.

A common pattern in the parameter uncertainty of these models was a one-sided profile that was quite flat for larger values but increased for smaller values to generate a tighter lower bound (often indicating that the parameters yield poor fits near zero), shown in Figs. 3 and 5 (this type of profile is often observed in practical unidentifiability (Raue et al., 2009; 2011)). This curvature resulted in smaller FIM-based asymptotic confidence bounds (as these are symmetric and based on the local curvature of the likelihood), which may be misleading for the relatively small amounts of data often used in fitting models in mathematical biology. This profile shape is in part due to the Hill function structure of the models, wherein the functions are nearly in the saturated or linear range, but not quite. Given the ubiquity of Hill-like functions in biological applications, this type of practical unidentifiability is likely to be a frequently encountered issue.

The oxaliplatin model also illustrated how evaluating the underlying practically identifiable combination structure can be a challenge—the profiled parameter relationships showed strong correlations between all parameters, and the FIMs are not useful in determining the appropriate subsets (e.g. using the approach developed in Eisenberg and Hayashi, 2014). In this work, we found that qualitative consistency of the parameter relationships regardless of which parameter was profiled (e.g. the same relationship between k_δ and δ₀ regardless of which parameter was profiled vs. estimated) was a useful initial indicator of combination structure. However, future studies are needed to evaluate the generalizability of this finding, and to convert what was presented here as a somewhat ad hoc approach into a more procedural algorithm. More broadly, the gradiated nature of practical unidentifiability (a model may have finite confidence bounds for one significance level but infinite for another) means that there are choices that must be made for what level of uncertainty is acceptable (i.e. where the line is drawn between identifiable vs. not). Most approaches to identifiable combinations focus on structural identifiability, as this has a clearer formulation; however practically identifiable combinations present an important but incompletely addressed challenge. Knowledge of the practically identifiable combinations can generate biological insights, such as allowing us to evaluate arrest rate differences across the cell cycle even if the individual parameters for the Hill function are unidentifiable. These two models also illustrated one of the tensions between structural and practical identifiability: nonlinearity in the model structure lends itself towards structural identifiability (DiStefano, 1982), but if that nonlinearity is not fully observed or utilized in the data, then it does not help (or can even hamper) the practical identifiability of the model.

While we began to examine the potential for alternative data collection strategies and therapeutic implications, we did not explore synergy and antagonism between taxol and oxaliplatin. This is both because the cell types and experimental conditions used in the example data sets are different, and the model unidentifiability precluded determining the cell cycle distributions. We plan to address these questions in future work. The methods for rigorous, practical identifiability illustrated in this case study can also be used more broadly to help provide mechanistic insight into complex biological phenomena, reduce experimental costs, and speed up translation of treatment strategies from bench to bedside in clinical settings.