Abstract
Integrated information theory (IIT) has established itself as one of the leading theories for the study of consciousness. IIT essentially proposes that quantitative consciousness is identical to maximally integrated conceptual information, quantified by a measure called Φmax, and that phenomenological experience corresponds to the associated set of maximally irreducible cause–effect repertoires of a physical system being in a certain state. With the current work, we provide a general formulation of the framework, which comprehensively and parsimoniously expresses Φmax in the language of probabilistic models. Here, the stochastic process describing a system under scrutiny corresponds to a first-order time-invariant Markov process, and all necessary mathematical operations for the definition of Φmax are fully specified by a system’s joint probability distribution over two adjacent points in discrete time. We present a detailed constructive rule for the decomposition of a system into two disjoint subsystems based on flexible marginalization and factorization of this joint distribution. Furthermore, we show that for a given joint distribution, virtualization is identical to a flexible factorization enforcing independence between variable subsets. We then validate our formulation in a previously established discrete example system, in which we also illustrate the previously unexplored theoretical issue of quale underdetermination due to non-unique maximally irreducible cause–effect repertoires. Moreover, we show that the current definition of Φ entails its sensitivity to the shape of the conceptual structure in qualia space, thus tying together IIT’s measures of quantitative and qualitative consciousness, which we suggest be better disentangled. We propose several modifications of the framework in order to address some of these issues.
Keywords: consciousness, theories and models, computational modelling, integrated information, qualia
Introduction
Integrated information theory (IIT; Tononi 2004, 2005, 2008, 2012, 2015; Oizumi et al. 2014; Tononi et al. 2016) has established itself as one of the most prominent theories in the study of the physical substrates of consciousness. IIT essentially proposes that quantitative consciousness, i.e. the degree to which a physical system is conscious, is identical to its state-dependent level of maximally integrated conceptual information, which can be quantified by a measure called ‘Φmax’. Integration here means that the information generated by the system as a whole is in some measurable sense more than the information generated by its parts and intuitively corresponds to finding an index of a system state’s causal irreducibility. Intriguingly, IIT also equates the set of maximally integrated cause–effect repertoires associated with a system state to qualitative consciousness, i.e. the actual phenomenological experience or ‘what-it-is-like-ness’ (Nagel 1974) of a physical system being in a certain state, and thus aims at nothing less than a formal description of a quale. While this approach is not undisputed (e.g. Aaronson 2014; Cerullo 2015), IIT has both explanatory and predictive power, and thus the idea of measuring integrated information has by now gained widespread popularity in the cognitive neuroscience literature and beyond (e.g. Balduzzi and Tononi 2008, 2009; Deco et al. 2015; Koch et al. 2016; Tegmark 2016).
With the current work, we provide a general probabilistic formulation of the framework, starting from the most recent instantiation of the theory called ‘III 3.0’ (Oizumi et al. 2014), which features several important theoretical advances over previous versions of IIT. Henceforth, we thus use the abbreviation ‘IIT’ to refer exclusively to IIT 3.0 as developed by Oizumi et al. (2014). In the methods section, we first present a comprehensive formulation of IIT with respect to the general language of probabilistic models, by which we simply mean joint probability distributions over random entities (e.g. Barber 2012; Murphy 2012; Gelman et al. 2014; Efron and Hastie 2016). We derive a constructive rule for the decomposition of a system into two disjoint subsets, central to the definition of information integration. Moreover, we show that for a given joint distribution, virtualization is identical to distribution factorization. All mathematical operations presented herein are sufficiently specified by a system’s joint probability distribution over two adjacent points in discrete time by flexible marginalization and factorization. We then validate our general formulation in the ‘Results’ section by evaluating Φmax in a previously established discrete state example system. Here, we also illustrate the previously unexplored theoretical issue of ‘quale underdetermination’, and we show that the current definition of Φ combines IIT’s measures of quantitative and qualitative consciousness, which we suggest be better disentangled. Finally, we discuss some open theoretical questions regarding further development of IIT and propose constructive modifications of the framework to overcome some of these issues.
Notation, terminology, and implementation
A few remarks on our notation of probabilistic concepts are in order. To denote random variables/vectors and their probability distributions, we use an applied notation throughout. This means that we eschew a discussion of a random entity’s underlying measure-theoretic probability space model (e.g. Billingsley 2008), and focus on the random entity’s outcome space and probability distribution. For a random variable/vector X, we denote its distribution by p(X), implicitly assuming that this may be represented either by a probability mass or a probability density function. To denote different distributions of the same random variable/vector, we employ subscripts. For example, pa(X) is to indicate a probability distribution of X that is different from another probability distribution pb(X). In the development of integrated information, stochastic conditional dependencies between random variables are central. To this end, we use the common notation that the statement p(X|Y) = p(X) is meant to indicate the stochastic independence of X from Y and the statement is meant to indicate the (stochastic) conditional independence of X on Y given Z (Dawid 1979; Geiger et al. 1990). Since the notion of a system subset being in a particular state is crucial for the definition of Φ, we refer to a given subset of the D-dimensional system by the superscript S (i.e. ) and the realization of a state with an elevated asterisk.
Since IIT comes with its own terminology, it may be helpful to highlight some expressions used throughout the manuscript. In the following, by ‘system’ we mean a network of physical elements described by a corresponding set of random entities (the joint probability distribution over which is assumed to adequately capture the system’s causal structure see below. A ‘purview’ refers to the notion of considering a particular subset of random entities in describing the system. For any subset being in a particular state at a specific time, the ‘cause repertoire’ of that state refers to a conditional probability distribution over past states, and the ‘effect repertoire’ describes the conditional distribution over future states. A ‘partition’ means rendering the system into two independent parts. The terms ‘concept’ and ‘conceptual structure’ refer to maximally integrated cause and effect repertoires and are explained in the context of our formulation in the section ‘On composition and exclusion’. The reader wishing to retrace our formulation of IIT will find all Matlab code (The MathWorks, Inc., Natick, MA, USA) developed for the implementation of the below and the generation of the technical figures herein from the Open Science Framework (https://osf.io/nqqzg/).
Methods: Defining Φ
System model
IIT models the temporal evolution of a system by a discrete time multivariate stochastic process (Cox and Miller 1977)
| (1) |
In the probabilistic model (1), denotes a finite set of D-dimensional random vectors. Each random vector Xt comprises random variables with that may take on values in one-dimensional outcome spaces , such that
| (2) |
may take on values in the D-dimensional outcome space . We assume throughout.
IIT further assumes that the stochastic process fulfills the Markov property, i.e. that the probabilistic model (1) factorizes according to
| (3) |
and that the ensuing Markov process is time-invariant, i.e. that all conditional probability distributions on the right-hand side of Equation (3) are identical (Fig. 1A). We will refer to as the system’s ‘transition probability distribution’ in the following. Finally, IIT assumes that the random variables constituting Xt are conditionally independent given Xt–1, i.e. that the conditional distribution factorizes according to
| (4) |
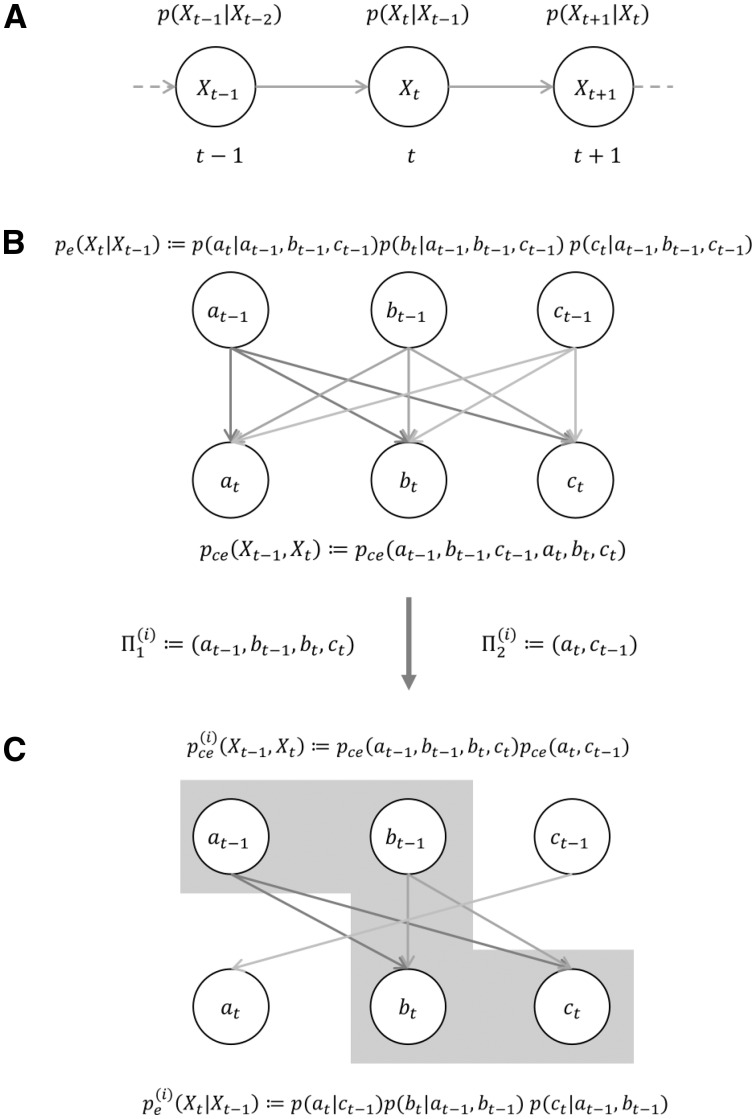
Figure 1.
System model and system decomposition for integrated cause–effect information. IIT models the system of interest by a time-invariant first-order Markov process, depicted as a graphical model in panel A (e.g. Bishop 2006). Nodes denote random vectors and directed links denote the stochastic dependence of the child node on the parent node. Panels B and C display the exemplary decomposition of a three-dimensional system with state vector as a graphical model. Here, nodes denote the constituent random variables of the random vectors Xt–1 and Xt. Panel B depicts the unpartitioned system, in which all potential stochastic dependencies of the elements are visualized. The constituent random variables of Xt are conditionally independent given Xt–1 (cf. Equation (4)), and the joint distribution is invoked by the assumption of a maximally uncertain marginal distribution for each . Panel C shows an exemplary decomposition of the system, which is based on the bipartition of into the subsets (gray inset) and . In the factorized joint distribution , the directed links across the partition boundary are removed, while the links within each partition remain.
On causal structure and interventional calculus
In IIT, a system of elements in a state is required to exert cause–effect power upon itself to meet the postulate of (intrinsic) existence (Tononi 2015). Furthermore, the system is required to be ‘physical’ in the sense that it can be intervened on. In Oizumi et al. (2014), assessing the causal structure of the system under scrutiny therefore rests on interventional calculus as introduced in Pearl (2009). Specifically, IIT makes use of the ‘do’ operator, which corresponds to perturbing a system into all possible states and observing the system transitions as a means of assessing the ensuing probability distributions. This has the advantage of being able to define a non-sparse transition probability distribution even if it is not a priori possible to observe every possible system state. In the following, we assume that the causal structure of the system under question (i.e. the distributions in Equation (4)) is known (cf. discussion section). The perturbational approach also entails the notion of virtualization to enforce independence between variable subsets, which, as we will detail in the following sections ‘Virtualization is factorization’, corresponds to a flexible factorization given the system’s joint distribution as defined below.
Characterization of a system by its joint probability distribution
The stochastic process’ forward transition probability distribution is defined as the conditional distribution of Xt given Xt–1
| (5) |
Next, we define a joint distribution pce over Xt–1 and Xt by multiplication of the Markov transition probability distribution with a marginal distribution , i.e.
| (6) |
Here, the marginal distribution is meant to represent a maximum of uncertainty about Xt–1, and for the case of a finite outcome space amounts to the uniform distribution over all states. This corresponds to the maximum entropy perturbational distribution used for perturbing the system into all possible states with equal probability in Oizumi et al. (2014) (see also Tegmark (2016)). Based on the joint distribution of Equation (6), the backward transition probability distribution is then defined as the conditional distribution of Xt–1 given Xt:
| (7) |
Definition of integrated cause–effect information
Based on the assumptions of Equations (1), (3), and (4), IIT defines the integrated cause–effect information of a set of system elements in a state as follows:
| (8) |
where and are defined as
| (9) |
and
| (10) |
respectively. Note that this applies generally, regardless of whether we consider the whole system XD or a subset of system elements . In Equations (10) and (9),
and are referred to as ‘integrated effect information’ and ‘integrated cause information’ of the state ,
and are conditional probability distributions that are constructed from the joint probability distribution of the stochastic process as detailed below and are referred to as the ‘effect repertoire’ and ‘cause repertoire’ of state , respectively,
and are ‘decomposed variants’ of the effect and cause repertoires, that result from the removal of potential stochastic dependencies in the system’s transition probability distribution as detailed below,
I is an index set, the elements of which index the decomposed variants of the effect and cause repertoires, and
denotes a divergence measure between (conditional) probability distributions over the same random entity, with P indicating the set of all possible distributions of this entity. While a variety of distance measures can be used for this assessment in principle (see also Tegmark (2016)), we will in practice follow Oizumi et al. (2014) in defining D as the earth mover’s distance for discrete state systems (Mallows 1972; Levina and Bickel 2001) due to its increased sensitivity to state differences when compared with the Kullback–Leibler Divergence (Kullback and Leibler 1951).
We next discuss the intuitive and technical underpinnings of the constituents of the definition of by Equations (8)–(10) in further detail.
System decomposition
To evaluate integrated cause–effect information , IIT first considers all possible ways to decompose a system into two subsets that do not influence each other. The aim is then to identify the system decomposition which, for a given set of system elements in a particular state, is most similar to the actual system in terms of the divergence between the system state’s effect and cause repertoires (cf. Equations (9) and (10)). The particular decomposition which fulfills this criterion is labelled the minimum information partition (MIP). In technical terms, the system to be decomposed corresponds to the collection of random variables and their conditional dependencies that define the discrete time multivariate stochastic process (cf. Equation (1)). Because of the process’ time-invariant Markov property (cf. Equation (3)), the relevant random variables are the constituents of two time-adjacent random vectors Xt–1 and Xt. As seen above, based on an uncertain marginal distribution over Xt–1, one may define a joint distribution of these vectors for each . Note that the joint distribution can equivalently be regarded as a joint distribution over the set of all constituent random variables of the random vectors Xt–1 and Xt,
| (11) |
IIT then uses the intuitive appeal of graphical models (Lauritzen 1996; Jordan 1998) to introduce the idea of ‘cutting a system’ into two independent parts (therefore a bipartition). Technically, cutting the graphical model of corresponds to (i) partitioning the set of random variables in Equation (11) into two disjoint subsets and (ii) removing all stochastic dependencies across the boundary between the resulting random variable subsets while retaining conditional dependencies within each subset as detailed below (cf. also Fig. 1B, C). Notably, there are unique ways to bipartition a set of cardinality n (see the Appendix in the online Supplementary Material for proof). This corresponds to k ways of cutting the corresponding graphical model and thus induces a set of k differently factorized joint distributions , which form the basis for the decomposed effect and cause repertoires and in the definition of (cf. Equations (9) and (10)).
We next formalize the construction of for . To this end, first recall that a partition of a set S is a family of sets P with the properties
| (12) |
Let denote a bipartition of a subset of random variables under scrutiny, i.e.
| (13) |
where
| (14) |
Let further
| (15) |
denote the marginal distributions of (cf. Equation (6)) of the random variables contained in and , respectively. Then the elements of the set of factorized variants of the joint distribution are given by
| (16) |
When partitioning a system into two independent parts, IIT evokes the notion of virtual elements to enforce conditional independence across the border of this partition. In the supplementary section of Oizumi et al. (2014), however, the exemplary calculations do not necessitate the actual introduction of virtual elements once the system’s transition probability distribution has been determined via perturbation. Therefore, we now aim to show that, given the system’s joint probability distribution, virtualization is in fact always identical to factorization, and we then provide general formulas for the evaluation of cause and effect repertoires in both the unpartitioned and the partitioned case.
Virtualization is factorization
The intuition behind virtualization is to account for correlation effects over the subset of variables in question due to common input from outside this considered subset. In order to decorrelate this common input, virtual elements are introduced with independent output to the elements inside of the considered subset, and a maximum entropy distribution is defined over the input states of these virtual elements. If, for instance, a system element provides input to two elements and , then the state of will indeed lead to correlations between and because the input (i.e. the state of ) will automatically affect both and due to the connectivity of the system. If we are to assess the effect that the state of has on and independently, however, we must remove this correlation. In this case, IIT defines two virtual elements and that can be perturbed independently, thereby effectively removing the stochastic dependence of these variables (or ‘noising the connections’). Formally, the idea behind virtualization is thus to enforce conditional independence on the variables within a subset in question from elements outside this subset. In the following, we aim to show that given the transition probability distribution in Equation (5) factorization is identical to virtualization because (i) ‘inputs’ from one element to another have an implicit temporal direction (input always refers to the previous temporal state), (ii) virtual elements and real past elements share the same state space, and a maximum entropy marginal distribution is placed over virtual elements just as over past states (cf. Equation (6)), and (iii) in calculating the actual probability distributions, we always marginalize over virtual elements, thus leading to the same output distributions.
Figure 2 shows the system decomposition in IIT 3.0 for the cause repertoire along with the virtualization, which we will denote in the following by the superscript V. For explicit reference (cf. Supplementary Text S2 in Oizumi et al. (2014)), we refer to the numerator by (the inputs) and to the denominator by which are partitioned into and , respectively, depending on partition i. The cause repertoire is factorized according to
| (17) |
Figure 2.
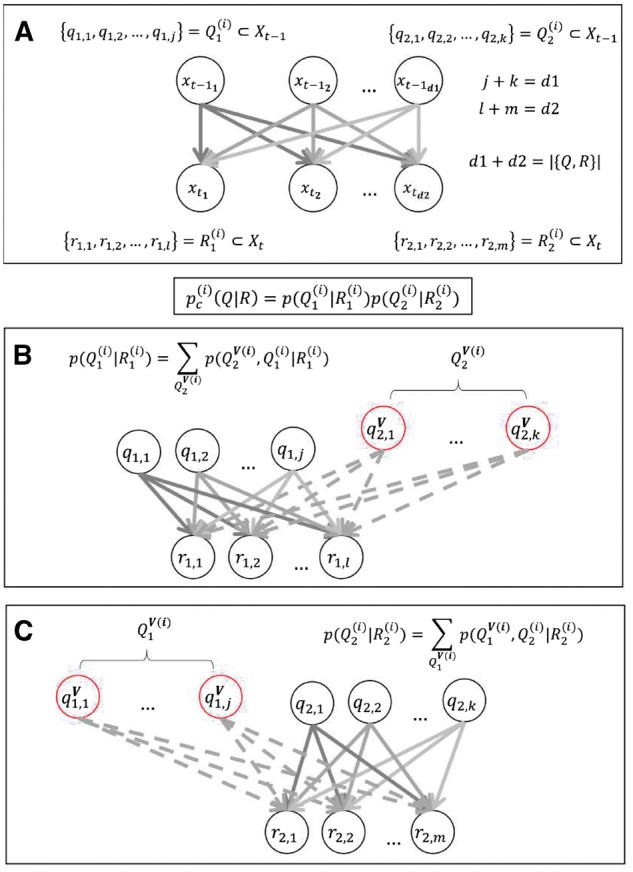
General system decomposition and virtualization in IIT 3.0 (Oizumi et al. 2014). Panel A visualizes the system decomposition in a general manner for the cause repertoire. The cause repertoire is decomposed as a factorization of two conditional distributions for every partition i (see equation inset below panel A). For unique reference to Oizumi et al. (2014) (Supplementary Text S2), we denote the elements in the partition of a subset of Xt–1 with cardinality d1 by , where . Likewise, the elements in the partition of a subset of Xt with cardinality d2 are denoted by , where . Panel B shows the first conditional distribution, and Panel C the second conditional distribution of the factorization. Virtualization is indicated by the superscript V. Every element in comprises l virtual elements with independent connections to each element in , and likewise for , yielding a total of virtual elements in the former and in the latter virtual set. Every red circle in panels B and C thus summarizes a set of independent virtual elements connected to the respective elements in the partition of R. As we show in the main text, virtualization is identical to a factorization of the system’s joint distribution.
For a system subset under consideration (purview) with , and (see Fig. 2),
| (18) |
Similarly,
| (19) |
For each of the two subsets, virtual elements are introduced over the complement of the respective partition of with regard to (i.e. over the ‘inputs’ outside of the subset in question), i.e.
| (20) |
Note, however, that for every element in , there are in fact individual virtual elements because perturbation requires a single independent input element from to , and in analogy for the connections from to . In Fig. 2, we summarize this as a single red circle for every set of independent virtual elements for visual coherence (see also Appendix B in the online Supplementary Material). For every input element in , IIT places a maximally uncertain perturbational distribution over its states, and likewise for (cf. maximum entropy distribution over past states in Equation (6)). We now form the joint distribution for the two factorized conditional distributions in Equation (17) (cf. Fig. 2, panels B and C) as
| (21) |
and equivalently for . Note that we sum over all virtual elements to obtain this subjoint distribution, and that with Equations (12)–(16) we have
| (22) |
With the above and by forming the joint distribution in Equation (17), we state that
| (23) |
where the last equation is the expression stated Equation (16). The equality for the effect repertoire follows in analogy, with the difference that we now condition on , with which Equation (21) becomes
| (24) |
and equivalently for . Note that the above subjoint distribution is identical to Equation (21), and thus the equivalence in Equation (23) follows in analogy.
Factorization and distribution normalization
Apart from partitioning, the application of virtualization in IIT also concerns the calculation of cause and effect repertoires over a subset , where the maximum cardinality of S is D (i.e. the whole system of interest). Similarly, (but note that we do not necessarily refer to the same variables in the subset and , e.g. if we want to find ).
The ensuing subjoint distribution is found from the original joint distribution by marginalizing over the complement of the subset with regard to the whole system, i.e. and . The aim of virtualization is again to enforce the independence of system elements at time t given their respective inputs. For the case of the effect repertoire, this corresponds to the independence of given . For every element in , virtual elements are introduced over the complement of with regard to X. Similar to the above, however, the necessary independence is equally enforced by marginalization and multiplication of the ensuing subjoint distributions
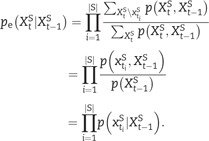 |
(25) |
The above essentially corresponds to the assumption of conditional independence inherent to the system model in Equation (4). Note also that in the absence of any constraint from the past system state, the expression in Equation (25) reduces to
| (26) |
which represents the definition of a maximum entropy distribution in the forward temporal direction (‘unconstrained future repertoire’ in IIT).
For the cause repertoire, we again enforce independence of the elements in based on their respective inputs in . However, we now condition the subjoint on (intuitively, enforcing ‘backward’ conditional independence), which again corresponds to the factorization of the joint distribution into the corresponding subjoint distributions and forming their product
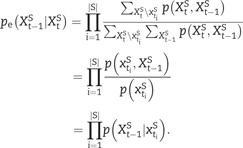 |
(27) |
Based on Equation (25) and Equation (27), there are a couple of interesting aspects to mention. First, note that in the second line of both equations, the subjoint distribution in the numerator is the same and all necessary distributions are easily obtained from the whole system’s joint distribution. Second, we can state a general rule of when repertoire normalization is necessary in IIT. This will be the case for the cause repertoire if
| (28) |
i.e. depending on whether it makes a difference to the cause repertoire if the marginal over factorizes or not. If it does, the cause repertoire must be normalized by the sum over all previous states for every current state to ensure unity, i.e. , which, computationally, corresponds to column-wise matrix normalization and is equivalent to the formulations in Tononi (2015) and Marshall et al. (2016). Note that the effect repertoire in Equation (25) is always conditioned on the marginal , and thus never needs to be normalized. Third, if the cardinality of is 1, i.e. we assess the cause repertoire over a single variable , then the inequality in Equation (28) is never true, which means that these repertoires do not require normalization and which is also the reason why virtualization (i.e. factorization) is necessary for ‘higher order mechanisms’ in IIT (see cause repertoire in Text S2 (Oizumi et al. 2014)). Finally, note that based on the system decomposition related above, we factorize the system’s joint distribution into two subjoint distributions and in order to induce independence between the corresponding two subsets of variables. In evaluating the cause and effect repertoires of the partitioned system, we then factorize (cf. Equation (16)) again, according to Equation (25) and Equation (27). To this end, let
| (29) |
and equally
| (30) |
Let z1 and z2 denote the cardinality of and , respectively. Note that if , then , and vice versa, and always . Intuitively, z1 and z2 thus describe the number of output elements in the respective subsets and due to partition i. Similarly, let and . We now apply the general formulas in Equations (25) and (27) to by defining
| (31) |
Intuitively, we thus factorize the subjoints and into as many factors as they contain variables in , where the case distinction above accounts for the marginal cases in which one of the subsets is empty due to a particular partition i (see the Results section ‘On non-unique maximally irreducible cause and effect repertoires’ for how this relates to the ‘empty conditionals’ sometimes occurring in IIT). With Equation (31), we now have a general rule to factorize the systemiz joint distribution. In order to state a general rule to calculate the cause and effect repertoires, however, we still need to condition the thus factorized joint distribution on the corresponding marginal distribution. For the effect repertoire, this marginal is given by
| (32) |
For the cause repertoire, the marginal always factorizes (cf. Equation (27)) and is thus
| (33) |
We thus generally state that for every partition i, the cause repertoire is given by
| (34) |
and the effect repertoire by
| (35) |
Finally, for the sake of completeness, note that the above fully and generally applies to the system model as detailed above, accounting for all potential dependencies in the graphical model between nodes at t – 1 and nodes at t. Of course, not all potential dependencies are necessarily present in a given network because they depend on the network’s connectivity. In these cases, the subjoints in Equations (31) and (32) may be further factorized to express independencies that are always present, i.e. simply that if a and b are independent variables (Barber 2012), in which cases the decomposed repertoires in Equations (34) and (35) also simplify (see example in the online Supplementary Materials). In formal terms of graphical models, this is the case if
| (36) |
for any , or intuitively, if not every output element in the respective subset is the child of all past nodes on their side of partition i (where pa denotes parents).
Example
For a brief illustration of the decomposition, we consider the exemplary system of Fig. 1. Here, the concatenated state vector over two adjacent time-points is given by (cf. Equation (11))
| (37) |
One of the bipartitions of Equation (37) (which we label here as ) is given by
| (38) |
Note that this corresponds to the partition depicted in panel B of Fig. 1. Hence, with Equation (15)
| (39) |
We have , and . Thus, , which yields (Equation (31)) the fully factorized joint distribution
| (40) |
and based on Equations (32) and (33) the marginal distributions
| (41) |
The decomposed cause repertoire is then given by Equation (34) as
| (42) |
requiring normalization by the sum over , and the decomposed effect repertoire (Equation (35)) evaluates to
| (43) |
For further illustration of this constructive process and a concrete example of the equivalence of factorization and virtualization given the joint distribution, please see the Supplementary Material.
On composition and exclusion
One of the main theoretical advances of IIT 3.0 over previous formulations is the extension of the general framework to exclude superposition of multiple causes and effects (exclusion principle) and to reflect the composition of the system in the definition of integrated information on a system level (composition principle). To this end, the evaluation of and as specified above is carried out in two distinct ways over the powerset of the system elements.
Exclusion principle
The intuition behind the exclusion principle is that just as any conscious experience excludes all others, in physical systems sustaining consciousness, causes and effects must not be ‘multiplied beyond necessity’ and only maximally integrated cause and effect repertoires of a set of elements can contribute to consciousness, thereby excluding all other possible causes and effects (Oizumi et al. 2014). Mathematically, for a given subset , the evaluation of and is therefore carried out over all possible cause and effect repertoires, which are specified by the powerset of the system elements. Excluding the empty set, the system’s powerset is generally given by
| (44) |
with cardinality . For notational clarity, let every subset in the powerset be denoted by . For a given subset , we thus compute a total of C cause and C effect repertoires. The set of cause repertoires for is thus given by
| (45) |
and the set of effect repertoires by
| (46) |
with . For illustration, consider the thus defined set of cause repertoires for the case . We thus compute , or, explicitly, the distributions .
Through system decomposition, we obtain a total of C different and values, one for every decomposition of the jth cause and effect repertoires. Of all those and values obtained over the powerset, the exclusion postulate in IIT 3.0 now requires that only the maximally integrated cause (and respectively effect) information be considered.
| (47) |
The cause repertoire whose decomposition yields is called the maximally integrated cause repertoire of (recall that this is always evaluated for being in a particular state), and equivalently for the maximally integrated effect repertoire. Here, refers to the corresponding subset of the powerset (note that does not have to be the same for and ). The minimum of maximally integrated cause and maximally integrated effect information then defines maximally integrated cause–effect information,
| (48) |
If a subset of being in a particular state specifies , it forms a maximally irreducible cause–effect repertoire (a ‘concept’ in Oizumi et al. (2014)). Notably, in the IIT framework, this concept is identical to a quale in the strict sense of the word. Intriguingly, the particular repertoire yielding (and equivalently for ) is not necessarily unique. While this may seem like a mathematical detail at this point, it has important implications both for the quantification of capital Φ (see below) and the interpretation of a concept as a point in qualia space (see discussion).
Composition principle
The composition principle is a natural extension of the above. By iterating over all possible cause and effect repertoires for a subset of being in a particular state, we define for that subset in its state. In order to take system composition into account, we now compute not only for a specific subset but rather over all possible subsets of the system , i.e. again over the powerset. For every element j in the powerset, we thus compute the set of cause repertoires as
| (49) |
and the set of effect repertoires as
| (50) |
for . We thus obtain a total of C values for . Together, all those subsets that specify a maximally integrated cause–effect repertoire are considered a ‘conceptual structure’ in IIT, i.e. a set of concepts. In the following, let the number of concepts be denoted by .
Integrated conceptual information Φ
We are now in a position to define the integrated information capital Φ of the conceptual structure of a system being in a particular state . The idea behind Φ is to quantify how much a constellation of concepts specified by a system state is irreducible to its individual parts. Formally, this corresponds to quantifying how much the information inherent in a system state’s conceptual structure can be reduced. Thus, we first need to define the conceptual information CI that is specified by the constellation of concepts. IIT defines this as the sum of the distances between a maximally integrated cause and effect repertoire to the respective maximum entropy distribution in the past or future (cf. Equation (6) and Equation (26)), weighted by their values, for all concepts that a system X in state specifies:
| (51) |
However, due to the aspect of non-unique maximally integrated cause and effect repertoires (which we will illustrate in a discrete state example system below), we instead define the conceptual information of a constellation of concepts simply as the sum of all values of those concepts
| (52) |
As we will exemplify in the applications section, this has the advantage of being unaffected by the underdetermination due to non-unique maximally integrated cause and effect repertoires while still depending on whether or not a particular system subset in a state specifies a concept.
Unidirectional partitions
At this point, we have to partition the system again to define Φ. This kind of partition differs somewhat from the system decomposition presented above in that it is a unidirectional partition. The aim behind unidirectional partitioning is to evaluate whether a subset has both selective causes and selective effects on its complement . Intuitively, this corresponds to noising the connections from XS to and — in an independent calculation — the connections from to XS (‘unidirectional’ partition). Again, this is readily done by factorization of the system’s original joint distribution . To this end, for a subset XS, we compute two subjoint distributions, , where we noise the input to XS (making its current state independent by factorization), and where we noise the input from XS (making its past state independent by factorization):
| (53) |
and
| (54) |
Here, we implicitly take advantage of the fact that the original joint distribution encompasses two adjacent points in time and that, therefore, every variable in has its counterpart in . For the two newly defined joint distributions, we repeat the above calculations for the same system state to see whether and how many of the original concepts (maximally integrated cause and effect repertoires) we can recover and if their values change. For all possible cuts, we then define the unidirectional partition that makes the least difference to the original constellation of concepts as the minimum (conceptual) information partition (MIP). IIT then essentially defines the integrated conceptual information Φ as the amount of conceptual information that is lost due to the partition over the MIP. Similarly, but again avoiding the underdetermination due to non-unique maximally integrated cause and effect repertoires, we define Φ of a system being in a state based on Equation (52) as
| (55) |
Maximally integrated conceptual information Φmax
Defining the maximally integrated conceptual information Φmax of a system being in a specific state corresponds to the reiteration of the above evaluation over all possible subsystems. First, there is an important conceptual distinction to make. Until this point, we have always considered a subset describing a set of D physical elements. A subsystem YB with B < D now refers to the notion of treating YB as a new system while regarding the elements as external background conditions. Formally, this corresponds to keeping the state of the outside elements fixed in the marginal conditional distributions in Equation (4). We thus essentially define a new forward TPM over the subsystem YB and therefore a new joint distributions based on Equation (6). We then determine Φ as in Equation (55) over the subsystem. This process is repeated for all possible subsystems, with the constraint that B ≥ 2 because one-element subsystems cannot be partitioned and therefore cannot be integrated by definition. The maximum value of Φ over all subsystems is then defined as maximally integrated conceptual information Φmax (and the corresponding subsystem is called a ‘complex’ in IIT). Notably, IIT claims that Φmax is identical to the degree to which a physical system is conscious.
In summary, the measure of integrated information Φ rests on a standard probabilistic model approach to dynamical systems—a multivariate stochastic process that fulfills the Markov property (cf. Equations (1), (3), and (4)). Against this background, the integrated information of a system state is defined by the irreducibility of its conceptual structure as assessed by partitioning the system, which corresponds to the removal of stochastic dependencies between the random entities describing the system. The system’s joint probability distribution over two adjacent points in time is uniquely defined by the system’s transition probability distribution and is sufficient for all necessary mathematical operations in the evaluation of Φ. In the following sections, we show how this general definition of Φ can be applied in the context of a specific example system.
Results: Computing Φ
In the current section, we consider a concrete application of the general formulation above in a system with discrete state space which is defined non-parametrically by the explicit definition of the transition probability distribution factors as logical operations. This system corresponds to the exemplary system discussed in Oizumi et al. (2014) and serves the validation of our formulation and the illustration of quale underdetermination.
Characterization of the system by its joint distribution
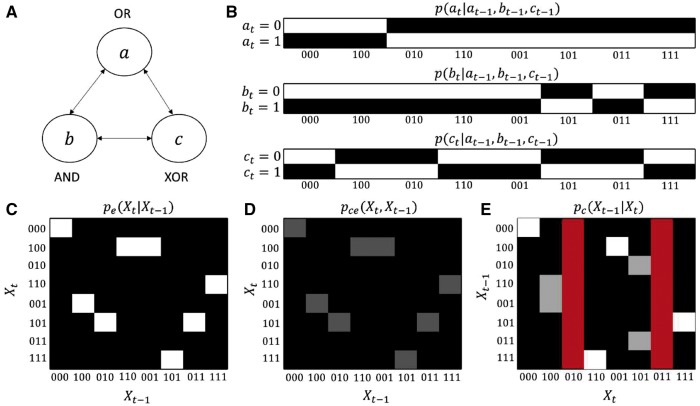
In discrete state systems, the random variables that model the system’s elements take on a finite number of states with a certain probability mass. As an exemplary discrete state system, we consider a system presented in Oizumi et al. (2014). This system is three-dimensional, and, in concordance with Oizumi et al. (2014), we denote its state vector by (Fig. 3A). The system is defined in terms of the marginal conditional distributions of its component variables (cf. Equation (4)). Specifically, the variables at, bt, and ct may take on values in {0, 1}, such that the outcome space is defined as , and implement logical operations on the state of their predecessors and . As shown in Fig. 3B, at implements a logical OR, bt implements a logical AND, and ct implements a logical XOR operation (constituting the causal structure of the system). Note that in this case, the relevant distributions of Equation (3) correspond to probability mass functions, which can be represented on the implementational level by high-dimensional numerical arrays.
Figure 3.
Characterization of the exemplary discrete state system. The system is identical to that presented in Oizumi et al. (2014) (e.g. Figs. 1 and 4 therein). Panel A shows the system comprising three random variables that implement the logical operations OR, AND, and XOR. Panel B visualizes the corresponding marginal conditional probability distributions, with black tiles indicating a probability mass of 0 and white tiles indicating a probability mass of 1. The product of these marginal conditional probability distributions yields the conditional distribution depicted in panel C, i.e. the state transition probability matrix. By multiplication with a maximally uncertain distribution over past states, i.e. , the joint distribution of panel D is obtained. Here, dark gray tiles indicate a probability mass of 0.125. For the current example, corresponds to the uniform distribution over past system states. Based on the formulation presented herein, the joint distribution in panel D sufficiently characterizes the system for the derivation of Φ. Moreover, conditioning on Xt yields the backward TPM shown in panel E. Here, white tiles indicate a probability mass of 1, gray tiles a probability mass of 0.5, and red tiles represent undefined entries. These entries correspond to states of Xt that cannot have been caused by any of the states of Xt–1 due to the logical structure of the network.
As discussed above, the forward transition probability matrix of the system corresponds to the product of the marginal conditional distributions (cf. Equation (4)). This distribution is shown in Fig. 3C. The joint distribution is derived by multiplication of the transition probability distribution with a maximally uncertain distribution over past states (cf. Equation (6)). In this example, the maximally uncertain distribution is given by the uniform distribution over past states, i.e. for all (cf. Fig. 3D). From the ensuing joint distribution , the backward TPM can be evaluated by conditioning on Xt. The resulting distribution is shown in Fig. 3E. Note that there are some undefined entries (displayed in red). These undefined entries correspond to system states that cannot have been caused by any previous state due to the constraints placed by the logical operations of the system variables. In the following, we illustrate the application of the theoretical formulation above in the evaluation of Φ for the system state .
Exclusion principle and computation of
First, we illustrate the computation of maximally integrated cause–effect information (i.e. the implementation of the exclusion principle) in the discrete state system. To this end, we focus on the example of the system subset and evaluate the maximally integrated effect information for this subset being in the state bt = 0. Recall that this corresponds to computing the values for all possible conditional distributions over the system’s powerset (Equation (46)), which in the example system is given by
| (56) |
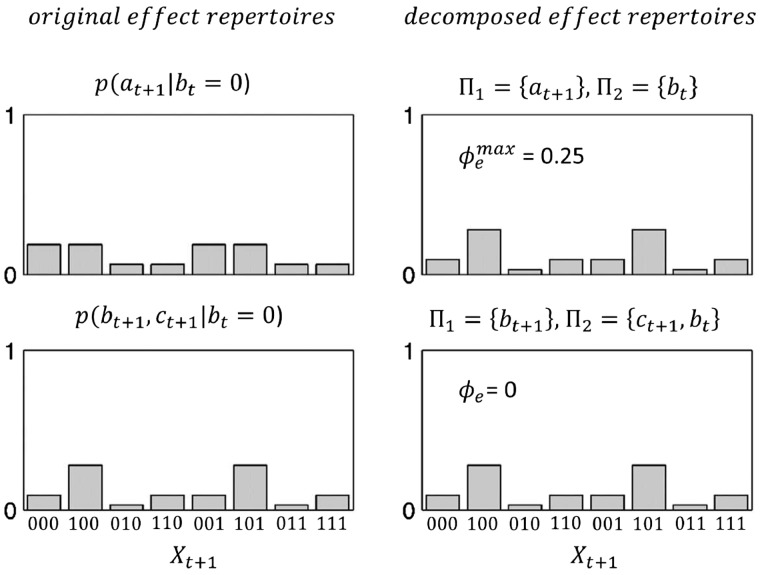
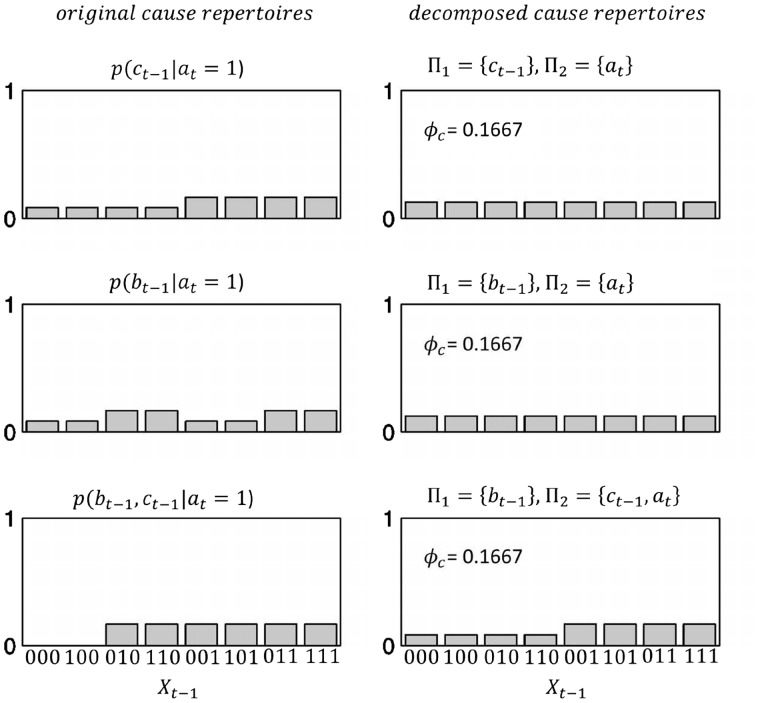
according to Equation (44). Note that the powerset is of cardinality (cf. Equation (44)). We thus compute the seven conditionals for to find the one whose decomposition yields the maximum value compared with all the others. Explicitly, we thus compute and their respective decomposed variants according to the system decomposition rule (cf. Equation (35)) and calculate the corresponding values based on Equation (9) (for a detailed illustration of how a single value is computed, the reader is kindly referred to Appendix C in the Supplementary Material). Figure 4 shows two out of the seven conditionals together with their decomposed variants. Note that the respective conditional distributions are always expanded to the states over the whole system (here, ) in order to compare conditional distributions of differing dimensionality (see figure caption). The distribution yields over its MIP . The conditional distribution on the other hand is identically recovered over its MIP, and thus . This is also true for all other five conditional distributions, so that , and the corresponding maximally irreducible effect repertoire is . We proceed in analogy with the set of seven cause repertoires for bt = 0 to define . The minimum of and then defines maximally integrated cause–effect information (cf. Equation (48)).
Figure 4.
Exclusion principle. Illustration of the computations necessary for the evaluation of maximally integrated effect information for the system subset in the state bt = 0. The maximally irreducible effect repertoire corresponds to the conditional distribution with , while all other conditional distributions of the system’s powerset are identically recovered by their respective minimum information partitions (MIPs). The lower panels depict one of these conditionals, . Note that the corresponding distributions are expanded to the whole system’s states in order to compare conditional distributions of differing dimensionality. This is done by multiplication of the particular conditional with the marginal distribution over the respective complement with respect to , i.e. for the upper panels and for the lower panels. For the cause repertoires, this is done in analogy for Xt–1.
Composition principle and conceptual information
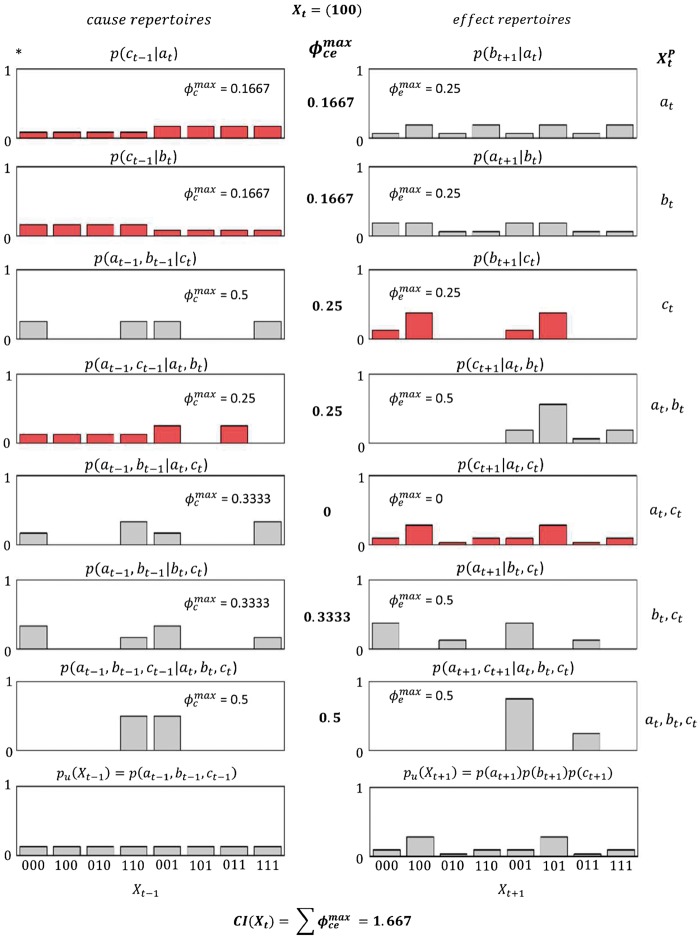
To implement the composition principle, we now apply the process illustrated above not only to the subset but to all possible subsets, i.e. again over the system’s powerset in Equation (56) according to Equations (49) and (50). Figure 5 visualizes the results of these calculations (similar to figs 10 and 11 in Oizumi et al. (2014)). Based on the powerset, we thus obtain seven values, one for every element in the powerset. All those elements of the powerset that yield a form a maximally irreducible cause–effect repertoire, called a ‘concept’ in Oizumi et al. (2014). We see that this is the case for all except for because the effect repertoires over this variable subset are not maximally integrated, i.e. all possible effect repertoires for yield . The example system being in the state thus specifies a total of six concepts with their corresponding values, which, importantly, are identical to the ones reported in Oizumi et al. (2014). Note, however, that not all of the depicted distributions are the same as in IIT 3.0. This is because all those distributions highlighted in red correspond to cases in which the maximally integrated cause or effect repertoire is not unique, i.e. there are several conditional distributions for the particular subset which yield the same maximal value. Note first that in the case of the effect repertoires over , this is a logical necessity. If any of the possible conditional distributions were to specify a , then that distribution would automatically become the maximally integrated effect repertoire, or, more generally, if or , then the corresponding set of repertoires is never unique. As we can see in Fig. 5, however, there are also cases in which or and the corresponding repertoire is not unique. These cases have several important implications for IIT, which we consider to some detail in the example below.
Figure 5.
The set of maximally irreducible cause and effect repertoires for the system state . The figure visualizes the implementation of the composition principle, i.e. the computation of the maximally integrated cause and effect repertoires for every subset in the powerset of the system elements. All those subsets for which form a ‘concept’, a maximally integrated cause–effect repertoire. As we discuss in the main text, however, the distributions highlighted in red are not unique. These distributions differ from the ones reported in Oizumi et al. (2014) as we enforce lower distribution dimensionality in underdetermined cases. The definition of conceptual information CI as the sum over all applied here is unaffected by non-unique repertoires. The bottom panels show the maximum entropy distributions in the respective temporal direction past () and future ().
On non-unique maximally irreducible cause and effect repertoires
In the following, we will briefly focus on the reason why non-unique maximally irreducible cause and effect repertoires are of interest to the IIT framework. First, note that the original definition of conceptual information CI (Equation (51) and Oizumi et al. (2014)) and integrated conceptual information Φ rests on the distance between the respective maximally integrated repertoire and the maximum entropy distribution in the respective direction past or future. These distributions are depicted in the bottom panels in Fig. 5. Due to the definitions in Oizumi et al. (2014), the values of CI and Φ are thus not only dependent on the maximally integrated cause–effect information but also on the actual distributions yielding these values (cf. Equation (51)). In the case of the highlighted distributions in Fig. 5, however, there are multiple of these maximally irreducible distributions so it is underdetermined which one to choose. As an example, consider the cause repertoire over the system subset (top left panel indicated by an asterisk in Fig. 5). In this case, there are in fact three distributions whose decomposition leads to the maximal value of , which we visualize together with their respective decompositions in Fig. 6. The distribution in the top panel corresponds to the one depicted in Fig. 5, and the bottom panel relating the distribution is identical to the one reported in Oizumi et al. (2014). As a brief side note, first consider the decomposition of , which is given by the MIP . In IIT 3.0, this is denoted as a factorization of conditionals over the empty set, i.e. . With our decomposition rule in Equation (31), we have and , and thus the decomposed cause repertoire is given by . The case distinction in the methods section is thus mathematically identical to IIT’s implicit definition that and . In any case, we can see from Fig. 6 that the respective partitions all yield the same value. In contrast, the Earth Mover’s Distance to the maximum entropy distribution in the past (i.e. the uniform distribution , see Fig. 5) may of course differ, depending on which distribution we choose. For and , this evaluates to D = 0.1667, while for , D = 0.3333. Since this distance measure directly contributes to the definition of conceptual information in Oizumi et al. (2014), CI and Φ can change depending on which distribution we label the maximally integrated cause repertoire. Note that the definitions of CI and Φ we propose in Equation (52) and Equation (55) are not sensitive to the actual distributions but only depend on the value of and thus we report them here.
Figure 6.
Non-unique maximally integrated cause repertoires over at = 1. All three conditional distributions depicted here lead to the same maximal value of integrated cause information over their respective MIPs. The top panel corresponds to the distribution shown in Fig. 5, while the bottom panel corresponds to the distribution reported by Oizumi et al. (2014). In these cases, it is underdetermined which distribution to choose. However, the exclusion principle demands that causes should not be multiplied beyond necessity. We thus argue that exclusion favors the lower-dimensional distributions in these cases, i.e. the ones over fewer causes (cf. discussion).
A second but related aspect is that IIT interprets the maximally irreducible cause–effect repertoire as a ‘point’ in qualia space. If this repertoire is underdetermined, however, then so is the quale. It may thus be desirable to find a sensible criterion for which repertoire to choose in these cases. To this end, consider again the distributions in Fig. 5. Here, the distribution that is reported in IIT 3.0 is of dimensionality 3, while the one reported here only features two dimensions. In fact, this is true for all the non-unique distributions in Fig. 5. This is due to the fact that the computational implementation of IIT always chooses the distribution over the higher-dimensional set (the ‘bigger purview’) because it ‘specifies information about more system elements’ (see Supplementary Fig. S1 in Oizumi et al. (2014)). In contrast to this, however, we suggest that a strict interpretation of the exclusion principle should in fact favor the lower-dimensional distributions. Recall that the exclusion principle postulates that causes and effects should not be multiplied beyond necessity. As such, choosing the distribution in Fig. 6 (over ‘two causes’) thus seems less parsimonious than choosing one of the lower-dimensional distributions over fewer causes. Throughout the manuscript, we thus always enforce the lower dimensionality in the cases of underdetermination, and return to this issue in the discussion.
Integrated conceptual information Φ
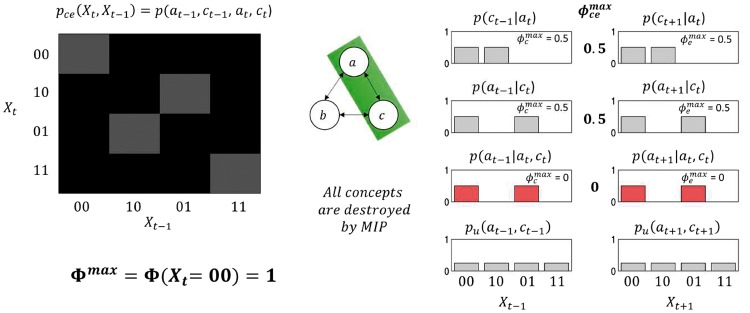
We can now illustrate the computation of integrated conceptual information Φ as defined by Equation (55). Recall that the definition of Φ requires unidirectional system partitions according to Equation (53) and Equation (54) in order to find the (system state’s) MIP. For the given example state, this evaluates to the factorization depicted in Fig. 7. The unidirectional MIP is given here by factoring out , which corresponds to noising the connections from a and b to c. Note the difference between the thus factorized joint distribution and the original joint distribution in Fig. 3. Based on this joint distribution, we thus reiterate the presented formulation and find that two out of the six original concepts are identically recovered while the other four vanish to . The conceptual information over the unidirectionally partitioned system is thus CI = 0.3333 according to Equation (52). Based on Equation (55), we thus obtain .
Figure 7.
Integrated conceptual information Φ for the discrete example system in state . The joint distribution on the left corresponds to the (system state’s) MIP. Here, the MIP is given by factoring ct out of the original joint distribution in Fig. 3, i.e. ‘noising the connections’ from a, b to c (see network depiction in the center). Gray tiles refer to a probability mass of 0.0625. The thus factorized joint distribution recovers two of the original six concepts in Fig. 5, while for the remaining four reverts to zero. For the current system state, we thus find that , based on Equation (55).
Maximally integrated conceptual information Φmax
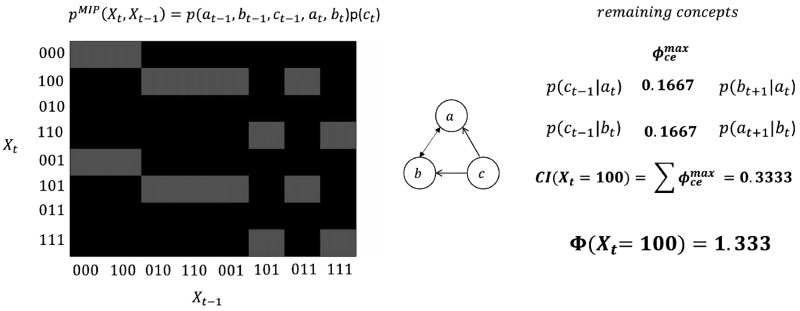
Finally, we briefly consider the evaluation of maximally integrated conceptual information Φmax. To this end, we evaluate Φ as illustrated above for every subsystem of a set of D elements. Recall from the methods section that only subsystems with at least two elements are considered (because one-element sets cannot be partitioned and are therefore not integrated by definition) and that the states of all elements outside of the subsystem are fixed. This corresponds to defining a new transition probability distribution according to Equation (4) and thus a new joint distribution based on Equation (6). For the example system, the possible subsystems are given by , and {a, b, c}. For a system state of interest, we thus obtain four Φ values, the maximum of which yields Φmax. In the current example of system state is found over {a, b, c} and thus corresponds to the value depicted in Fig. 7. To illustrate the above, we choose a different system state, , and compute Φ for each of the four subsystems. For this state, the whole system {a, b, c} specifies four maximally irreducible cause–effect repertoires and . The maximum Φ value for this system state, however, is found over the subsystem {a, c}, depicted in Fig. 8. Note that for this subsystem, the state of element b is fixed at b = 0, regardless of time. On a computational level, this is conveniently implemented by discarding all those states in which b = 1 from the marginal conditional distributions in Fig. 3. With these new marginal conditional distributions, we then form the new forward TPM according to Equation (4) and find the joint distribution with a maximum entropy distribution over past states based on Equation (6). The thus specified system yields two maximally irreducible cause–effect repertoires (concepts) which vanish to over the MIP. Hence, we find that .
Figure 8.
Maximally integrated conceptual information Φmax for the discrete example system in state . The maximum value of Φ over all possible subsystems is found in the subsystem {a, c}, highlighted in green in the network graph. Defining the subsystem corresponds to computing the new joint distribution on the left, which is found by keeping the state of b = 0 fixed in the marginal conditional distributions (Fig. 3 and Equation (4)). Here, gray tiles indicate a probability mass of 0.25. Again, the subsystem is fully characterized by this joint distribution. For the state , the subsystem specifies two concepts (the distributions in red are not unique because and ). Both these concepts vanish over the MIP, yielding .
Discussion
In the present work, we have developed a comprehensive general formulation of IIT in the language of probabilistic models, starting from its most recent instantiation as IIT 3.0 (Oizumi et al. 2014). Specifically, we show that all necessary mathematical operations in the derivation of Φ are parsimoniously specified by a system’s joint probability distribution over two adjacent points in discrete time. We present a constructive rule for the decomposition of the system into two disjoint subsets, which corresponds to a flexible marginalization and factorization of this joint distribution, and we show that, for a given joint distribution, virtualization is identical to factorization. On the implementational level, our formulation is readily applied to non-parametric discrete state systems, as validated in the exemplary system from IIT 3.0. Here, we also illustrate a previously unexplored theoretical issue, which regards the underdetermination of Φ due to the occurrence of non-unique maximally integrated cause and effect repertoires. We propose that a strict interpretation of the exclusion postulate should favor lower-dimensionality probability distributions in these cases, and we elaborate on this issue below. Related to this aspect is the sensitivity of Φ to qualia shape, which we account for by defining Φ merely as a function of maximum integration, regardless of which distribution is maximally integrated.
In the following, we focus on three major theoretical issues for further refinement of IIT. This regards (i) the estimation of a system’s causal structure, (ii) the definition of the MIP on the system level, and (iii) quale underdetermination.
Causal structure and probabilistic inference
We first focus on the issue of causality. IIT argues that a system element (or a subset of elements) can only contribute to consciousness if it exerts cause–effect power on the system (i.e. it only then exists intrinsically). Thus, in order to apply the IIT framework, the causal structure of a system under scrutiny must be known. As we have pointed out above, herein the causal structure of the system was assumed to be sufficiently determined. This amounts to a definition of the marginal conditional probability distributions in Equation (4), which can be regarded as a probabilistic translation of the logical operations the system elements carry out and which in turn define the system’s transition probability matrix (cf. panels B and C in Fig. 3). In Oizumi et al. (2014), the causal structure of the system is determined by system perturbations (Pearl 2009). In this regard, note that the natural evolution in a deterministic system will lead to a sparse transition probability matrix, unless all possible system states are observed. In the example system, for instance, none of the possible initial states allows for an observation of all possible system states. While the perturbational approach thus elegantly determines the system’s causal structure in deterministic discrete state systems, it may pose serious theoretical issues for ultimately transferring the integrated information framework to the realm of continuous variables because there are infinitely many possible states that the system would have to be perturbed into. Generally speaking, the evaluation of a theoretically derived measure from empirical data can be achieved by estimating a parameterized probabilistic model from the data, and applying the measure to the thus estimated system model (e.g. Ostwald et al. 2010, 2014). Hence, our formulation of integrated information could at least in principle facilitate progress toward evaluating Φ in empirical data, based on a system’s estimated joint probability distribution. However, this approach will only be theoretically equivalent to the current framework if the estimated distribution adequately captures the causal structure of the system. Essentially, the question is then if and under which conditions it is possible to identify causal effects within a system from observational data, a highly active area of research in contemporary statistics, philosophy, and artificial intelligence research (e.g. Spirtes et al. 2000; Maathuis and Colombo 2015; Schaffer 2016; Mahmoudi and Wit 2016; Malinsky and Spirtes 2016). The causal structure of a system is commonly represented by a directed acyclic graph (DAG), and the system perturbations by means of the ‘do’ operator can be regarded as a manipulation on these graphical models (Pearl 2009). For a known DAG, several criteria have been developed to infer causal effects from observational data, such as back-door and front-door adjustment (Pearl 2009; Maathuis and Colombo 2015). If the underlying DAG is unknown, it can be defined in terms of its Markov equivalence class, and recent developments show that it may be possible to estimate causal effects even in these cases while also allowing for unmeasured variables, i.e. without the assumption of causal sufficiency (Maathuis and Colombo 2015; Malinsky and Spirtes 2016) and without the assumption of Gaussianity (Mahmoudi and Wit 2016). While these approaches are part of ongoing research on the estimation of intervention effects, they may provide useful guidance for the eventual transferral of the integrated information framework to the realm of continuous variables.
System partitions and boundedness
As detailed in the methods section, partitioning a system is a key aspect of the IIT formalism. First, it is useful to highlight again a subtle but important distinction. The system decomposition corresponds to bipartitioning the set of random variables in order to compute a particular value of integrated cause–effect information , while the ‘unidirectional’ system partitions yield the integrated conceptual information Φ (over many individual evaluations of ). As we have shown above, a flexible factorization of the system’s joint distribution parsimoniously yields both types of partitions. The decompositions for the evaluation of mainly suffer from the computational issues of combinatorial explosion (see the Supplementary Material for a derivation of the number of partitions k), discussed in Oizumi et al. (2016); Tegmark (2016); Toker and Sommer (2016); and Arsiwalla and Verschure (2016). In the following, we focus on the unidirectional system partitions and some ensuing conceptual issues, which are linked to the lower bounds of integrated information. In this regard, first note that as presented herein is bounded by zero because the EMD cannot be negative (Levina and Bickel 2001; Cover and Thomas 2012). Φ as given in Equation (55) would be generally expected to lie in the interval between zero (if there is a unidirectional partition that identically recovers the concepts) and the conceptual information of the unpartitioned system (if all concepts are destroyed by the MIP) and could become negative if and only if the conceptual information of the partitioned system is in fact greater than that of the unpartitioned system. This is counter-intuitive, of course, because it would mean that we somehow generate information by cutting the system. On a subtle note, however, the PyPhi repository (Mayner et al. 2016) states that in rare cases this can actually occur, referred to as ‘magic cuts’. Formally, this corresponds to the emergence of maximally integrated cause–effect repertoires induced by a system partition. While this is not the case in the results presented herein, it raises general concerns regarding the current definition of the system partitions. Recall that with unidirectional partitioning, we are looking for the minimum information partition (MIP), i.e. the one that makes the least difference to the original system. The emergence of previously absent concepts due to a particular partition should therefore strongly argue against that partition being regarded as the MIP because it obviously makes a profound difference to the unpartitioned system. Note that magic cuts also violate the very basic intuition behind the theory, namely that the whole is causally more than the sum of its parts, because in some cases the sum of its parts can in principle be more than the whole. In this regard, the PyPhi repository gives two useful examples. In the first example, the MIP destroys one concept but also creates a new one, while the amount of maximally integrated conceptual information as given in Equation (55) decreases. In the second example, however, the MIP results in the same number of concepts over the same system subsets, while one particular subset specifies an increased value of , resulting in an increased total amount of maximally integrated cause–effect information. In summary, the above essentially amounts to the general question of whether the MIP on the system level should be defined based on state space (i.e. the difference it makes to the set of maximally integrated cause–effect repertoires) or integration (i.e. the difference it makes to the conceptual information) or perhaps a combination of both. The latter corresponds to the idea that the original system should be an upper bound on the partitioned system over the MIP in both a qualitative and a quantitative sense. The emergence of new concepts due to a system partition can violate either, however, and therefore requires a closer examination in the future.
Quale underdetermination
Finally, we return to the issue of non-unique concepts. Note that this issue has direct consequences on IIT's application to consciousness. If the maximally integrated cause–effect repertoires are underdetermined, then based on the distance measures in Equation (51), so are the conceptual information CI, the integrated conceptual information Φ, and the maximally integrated conceptual information Φmax, which IIT postulates to be identical to the quantitative consciousness of a system in a certain state. Moreover, IIT interprets a maximally irreducible cause–effect repertoire as a ‘quale sensu stricto’ (Oizumi et al. 2014) and the particular set of concepts associated with Φmax as a description of the actual phenomenological experience (a constellation in qualia space), which in turn is also underdetermined in these cases (quale underdetermination). With the formal definitions in Oizumi et al. (2014), IIT thus combines the measure of quantitative consciousness, Φmax, with the measure of qualitative consciousness, the associated structure of concepts in qualia space, because the value of the former depends on the actual arguments of the latter. As the authors note themselves, however, the content of phenomenological experience is not necessarily a prerequisite for the degree of consciousness (e.g. in certain meditative practices reaching high-level awareness with low phenomenological content (Oizumi et al. 2014)). In other terms, Φmax should be sensitive to whether or not there is a conscious experience and not to the content of that experience. Formally, a quantitative measure of consciousness based on information integration should thus be a priori independent of ‘what’ the system in a state integrates and only rely on ‘how much’ the system in a state is integrated, similar to our definition in Equation (55).
In any case, we argue that the underdetermination is an aspect of the theory that requires further study. As we have demonstrated in the discrete state example system, the computational implementation in IIT currently chooses the higher-dimensional repertoire in these cases. Due to the exclusion postulate that causes and effects should not be multiplied beyond necessity, however, we argue that the more parsimonious choice would in fact be the repertoire with the lowest dimensionality, i.e. over the fewest possible number of causes or, respectively, effects that are still maximally integrated. As the reader can see in the example in Fig. 6, this criterion would discard the distribution reported in Oizumi et al. (2014) but still leaves two distributions with minimum dimensionality. In order to find a sensible criterion of which distribution to label the maximally integrated cause repertoire in this case, one approach would be to choose the distribution over those system elements that contribute most to the constellation of concepts as a whole (the ones that most ‘shape’ the conceptual structure in the unique cases). Formally, this could for instance be evaluated by the number of unique concepts to which a particular subset contributes in the respective backward or forward temporal direction. In the case of Fig. 6, contributes more to the unique cause repertoires than over all system subsets in the past. We would therefore choose the distribution as the maximally irreducible cause repertoire that most shapes the conceptual structure. While, in the given example, this criterion uniquely identifies the distribution we ought to choose, it is of course not guaranteed that this will always be the case, and surely further clarification of this issue in terms of a comprehensive formal criterion is required. On a phenomenological level, however, choosing the element which most shapes the whole conceptual structure could perhaps make intuitive sense. Conscious experience features a set of distinct, yet unified phenomenological aspects, where some — such as a blaring sound or a blazing color — can seem to be in the foreground because they shape the unified experience more than other aspects which are also consciously experienced.
Conclusion
IIT is one of the leading theories in the study of consciousness, not least because it is arguably the first rigorous attempt at a formal description of what is necessary for a physical system to have phenomenological experience. With the presented formulation of integrated information in the language of probabilistic models, we hope to make a constructive contribution to the traceability, parsimony, and improvement of IIT.
Data Availability
Custom-written Matlab code (The MathWorks, Inc., Natick, MA, USA) was used to implement the formulation of integrated information presented herein. The corresponding files are available from the Open Science Framework (https://osf.io/nqqzg/).
Supplementary Material
Acknowledgments
We would like to thank Larissa Albantakis for providing insight into the framework of IIT 3.0. Furthermore, we extend our gratitude to Francisco J. Esteban and colleagues at the universities of Jaén and Seville for engaged and fruitful discussions regarding the current work. Finally, we wish to thank two anonymous reviewers for their highly detailed and constructive criticism of our manuscript.
Supplementary Data
Supplementary data are available at NCONSC Journal online.
Conflict of interest statement. None declared.
References
- Aaronson S. Why I Am Not an Integrated Information Theorist (or, the Unconscious Expander), 2014. http://www.scottaaronson.com/blog/?p=1799(2 May 2017, date last accessed).
- Arsiwalla XD, Verschure PF.. The global dynamical complexity of the human brain network. Appl Netw Sci 2016;1:16.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balduzzi D, Tononi G.. Integrated information in discrete dynamical systems: motivation and theoretical framework. PLoS Comput Biol 2008;4:e1000091.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balduzzi D, Tononi G.. Qualia: the geometry of integrated information. PLoS Comput Biol 2009;5:e1000462.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barber D. Bayesian Reasoning and Machine Learning. Cambridge: Cambridge University Press, 2012. [Google Scholar]
- Billingsley P. Probability and Measure. New York: John Wiley & Sons, 2008. [Google Scholar]
- Bishop CM. Pattern Recognition and Machine Learning (Information Science and Statistics). Secaucus, NJ: Springer-Verlag, 2006. [Google Scholar]
- Cerullo MA. The problem with phi: a critique of integrated information theory. PLoS Comput Biol 2015;11:e1004286.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cover TM, Thomas JA.. Elements of Information Theory. Hoboken, NJ: John Wiley & Sons, 2012. [Google Scholar]
- Cox DR, Miller HD.. The Theory of Stochastic Processes, Vol. 134. Boca Raton, FL: CRC Press, 1977. [Google Scholar]
- Dawid AP. Conditional independence in statistical theory. J R Stat Soc Ser B Methodol 1979;41:1–31. [Google Scholar]
- Deco G, Tononi G, Boly M. et al. Rethinking segregation and integration: contributions of whole-brain modelling. Nat Rev Neurosci 2015;16:430–9. [DOI] [PubMed] [Google Scholar]
- Efron B, Hastie T.. Computer Age Statistical Inference, Vol. 5 Cambridge: Cambridge University Press, 2016. [Google Scholar]
- Geiger D, Verma T, Pearl J.. Identifying independence in Bayesian networks. Networks 1990;20:507–34. [Google Scholar]
- Gelman A, Carlin JB, Stern HS. et al. Bayesian Data Analysis, Vol. 2 Boca Raton, FL: Chapman & Hall/CRC, 2014. [Google Scholar]
- Jordan MI. Learning in Graphical Models, Vol. 89.Berlin/Heidelberg: Springer Science & Business Media, 1998. [Google Scholar]
- Koch C, Massimini M, Boly M. et al. Neural correlates of consciousness: progress and problems. Nat Rev Neurosci 2016;17:307–21. [DOI] [PubMed] [Google Scholar]
- Kullback S, Leibler RA.. On information and sufficiency. Ann Math Statist 1951;22:79–86. [Google Scholar]
- Lauritzen SL. Graphical Models, Vol. 17 Oxford: Clarendon Press, 1996. [Google Scholar]
- Levina E, Bickel P.. The Earth mover’s distance is the mallows distance: some insights from statistics. In: Proceedings of the Eighth IEEE International Conference on Computer Vision ICCV 2001, Vol. 2, p. 251–6. IEEE, 2001. [Google Scholar]
- Maathuis MH, Colombo D.. A generalized back-door criterion. Ann Statist 2015;43:1060–88. [Google Scholar]
- Mahmoudi SM, Wit E.. Estimating Causal Effects from Nonparanormal Observational Data arXiv preprint arXiv:1611.08145, 2016. [DOI] [PubMed]
- Malinsky D, Spirtes P.. Estimating causal effects with ancestral graph Markov models. In: Antonucci A, Corani G, Campos CP (eds.), Proceedings of the Eighth International Conference on Probabilistic Graphical Models: Proceedings of Machine Learning Research, Vol. 52, p. 299–309. Lugano, Switzerland: PMLR, 2016. [PMC free article] [PubMed] [Google Scholar]
- Mallows C. A note on asymptotic joint normality. Ann Math Statist 1972;43:508–15. [Google Scholar]
- Marshall W, Gomez-Ramirez J, Tononi G.. Integrated information and state differentiation. Front Psychol 2016;7:926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayner WG, Marshall W, Marchman B. pyphi: 0.8.1, 2016. doi:10.5281/zenodo.55692.
- Murphy KP. Machine Learning: A Probabilistic Perspective. Cambridge, MA: MIT Press, 2012. [Google Scholar]
- Nagel T. What is it like to be a bat? Philos Rev 1974;83:435–50. [Google Scholar]
- Oizumi M, Albantakis L, Tononi G.. From the phenomenology to the mechanisms of consciousness: integrated information theory 3.0. PLoS Comput Biol 2014;10:e1003588.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oizumi M, Amari S, Yanagawa T. et al. Measuring integrated information from the decoding perspective. PLoS Comput Biol 2016;12:e1004654.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostwald D, Kirilina E, Starke L. et al. A tutorial on variational Bayes for latent linear stochastic time-series models. J Math Psychol 2014;60:1–19. [Google Scholar]
- Ostwald D, Porcaro C, Bagshaw AP.. An information theoretic approach to EEG–fMRI integration of visually evoked responses. NeuroImage 2010;49:498–516. [DOI] [PubMed] [Google Scholar]
- Pearl J. Causality. New York: Cambridge University Press, 2009. [Google Scholar]
- Schaffer J. The metaphysics of causation In: Zalta EN. (ed.), The Stanford Encyclopedia of Philosophy, Fall 2016 edition. Metaphysics Research Lab, Stanford University, 2016. https://plato.stanford.edu/archives/fall2016/entries/causation-metaphysics/ (2 May 2017, date last accessed). [Google Scholar]
- Spirtes P, Glymour CN, Scheines R.. Causation, Prediction, and Search. Cambridge, MA: MIT Press, 2000. [Google Scholar]
- Tegmark M. Improved measures of integrated information. PLoS Comput Biol 2016;12:e1005123.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toker D, Sommer F.. Moving Past the Minimum Information Partition: How to Quickly and Accurately Calculate Integrated Information arXiv preprint arXiv:1605.01096, 2016.
- Tononi G. An information integration theory of consciousness. BMC Neurosci 2004;5:42.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tononi G. Consciousness, information integration, and the brain. Prog Brain Res 2005;150:109–26. [DOI] [PubMed] [Google Scholar]
- Tononi G. Consciousness as integrated information: a provisional manifesto. Biol Bull 2008;215:216–42. [DOI] [PubMed] [Google Scholar]
- Tononi G. Integrated information theory of consciousness: an updated account. Arch Ital Biol 2012;150:293–329. [PubMed] [Google Scholar]
- Tononi G. Integrated information theory. Scholarpedia 2015;10:4164. [Google Scholar]
- Tononi G, Boly M, Massimini M. et al. Integrated information theory: from consciousness to its physical substrate. Nat Rev Neurosci 2016;17:450–61. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Custom-written Matlab code (The MathWorks, Inc., Natick, MA, USA) was used to implement the formulation of integrated information presented herein. The corresponding files are available from the Open Science Framework (https://osf.io/nqqzg/).