Methane emissions partially offset “blue carbon” burial in mangroves

Water and sediment methane emissions have the potential to offset “blue carbon” burial in mangrove coastal ecosystems.

Abstract

Organic matter burial in mangrove forests results in the removal and long-term storage of atmospheric CO₂, so-called “blue carbon.” However, some of this organic matter is metabolized and returned to the atmosphere as CH₄. Because CH₄ has a higher global warming potential than the CO₂ fixed in the organic matter, it can offset the CO₂ removed via carbon burial. We provide the first estimate of the global magnitude of this offset. Our results show that high CH₄ evasion rates have the potential to partially offset blue carbon burial rates in mangrove sediments on average by 20% (sensitivity analysis offset range, 18 to 22%) using the 20-year global warming potential. Hence, mangrove sediment and water CH₄ emissions should be accounted for in future blue carbon assessments.

INTRODUCTION

Climate change, driven primarily by increased atmospheric CO₂ concentrations, is one of the most significant global environmental issues facing the planet (1). Mitigation strategies include emission reduction and preserving and enhancing natural carbon stores. Most conservation programs have focused on the restoration of terrestrial ecosystems such as tropical rainforests and enhancing carbon reserves in agricultural farmland (2–4). More recently, the disproportionally large role of coastal vegetated ecosystems as efficient natural carbon sinks has been highlighted (5, 6). The term “blue carbon” was coined to describe carbon burial in vegetated coastal ecosystems such as mangrove forests, seagrass beds, and salt marshes (7–9). Although vegetated coastal habitats cover a relatively small area (<2%) of the coastal ocean, they have burial rates 40 times higher than tropical rainforests and account for more than half of the carbon burial in marine sediments (8).

Mangrove forests are highly productive ecosystems and one of the most carbon-rich ecosystems in the world (10, 11). The total net primary production (NPP) of mangroves is approximately 200 Tg C year⁻¹ (12, 13), but most of this carbon is lost or recycled via CO₂ flux to the atmosphere (34.1 Tg C year⁻¹, ~20%) or exported as particulate organic carbon (POC), dissolved organic carbon (DOC), and dissolved inorganic carbon (DIC) to the ocean (117.9 Tg C year⁻¹; ~60%) (13, 14). Of the remaining carbon, burial accounts for between 18.4 and 34.4 Tg C year⁻¹ (5, 11, 12, 15), and this blue carbon is considered a significant long-term storage of atmospheric CO₂ (Fig. 1). Mangrove ecosystems have been promoted as efficient natural carbon sinks (5, 7). However, on a global scale, annual mangrove blue carbon burial represents only about 0.2 to 0.3% of global anthropogenic CO₂ emission [mainly fossil fuel and deforestation, ~10 Pg C year⁻¹ (1)]. Furthermore, during the process of carbon burial, methanogenic archaea produce CH₄ in anoxic sediments (16, 17). Because CH₄ has a global warming potential (GWP) that is 34 to 86 times more powerful than CO₂ (1), CH₄ emissions have the potential to offset a part of the CO₂ initially removed from the atmosphere and buried as blue carbon. However, there is no estimate of the global magnitude of this potential offset.

Fig. 1. Mangrove NPP versus mangrove carbon loss.

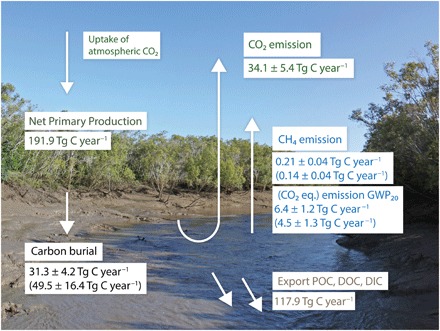
The mangrove NPP of 191.9 Tg C year⁻¹ and tidal exports of POC (25.6 Tg C year⁻¹), DOC (13.7 Tg C year⁻¹), and DIC (78.6 Tg C year⁻¹) are derived from Alongi and Mukhopadhyay (13) and scaled to the total global mangrove area estimate of Giri et al. (25). Global mangrove CO₂ emissions of 34.1 ± 5.4 Tg C year⁻¹ are from Rosentreter et al. (14). Global mangrove CH₄ emissions are further presented as CO₂ equivalent emissions using the GWP₂₀ (Table 2). The values presented in brackets are the latitudinal scaled total CH₄ emission and burial rates (Table 3). Photo used with permission from A. McMahon.

Mangrove forests are intertidal ecosystems, and although they are net autotrophic on a whole ecosystem scale, sediments and creek waters are generally sources of CO₂ (and CH₄) to the atmosphere. Along the tidal elevation gradient (creek to forest basin), the mangrove type, microbial processes, and sediment structure can change markedly. The intersite variability of mangrove ecosystems is primarily related to geophysical energies as well as climatic and geomorphological conditions such as the relative influence of rainfall, tidal amplitude, exposure to strong water movement, bed rock composition, and the local vegetation and fauna (18). Emissions of CH₄ from mangrove sediments are highly variable but are generally larger than emissions from creek waters and can be enhanced in the presence of plant roots and pneumatophores (19–21). The few published water-to-atmosphere CH₄ flux rates from India, Tanzania, Thailand, and Australia range from 6.3 to 828 μmol m⁻² day⁻¹, also suggesting high variability of CH₄ emissions from mangrove waters [for example, see the studies of Barnes et al. (22), Call et al. (23), and Linto et al. (24)].

Here, we use new data on seasonal (wet and dry) CH₄ emissions from three mangrove creeks in tropical Australia and previously published water-atmosphere and sediment-atmosphere flux rates to revise estimates of global mangrove CH₄ emissions. We then compare updated CH₄ emissions to revised estimates of global carbon burial rates using published data to calculate the degree to which blue carbon storage in mangrove forests may be offset by CH₄ emissions.

RESULTS

Tidal dynamics and physicochemical parameters

The tidal amplitude was highest in the Fitzroy River (FR) mangrove creek (2.9 to 4.4 m), followed by the Johnstone River (JR) (1.5 to 1.9 m) and the Burdekin River (BR) mangrove creek (1.2 to 1.7 m). Similarly, tidal currents were highest in the FR mangrove creek (pronounced in the wet season) with current velocity ranging from 2.2 to 90.1 cm s⁻¹. In the BR and JR, current velocities were similar, with values between 0.1 and 35.5 cm s⁻¹ (table S1). We measured high salinities in the BR (from 27.8 to 36.4). Salinities at the FR and JR mangrove study sites were lower, ranging from 5.5 to 35.7 and 0.4 to 23.4, respectively (table S1). Water temperature ranged between 19° and 29°C during the wet and dry seasons. Wind speed (u) was up to 7.9 m s⁻¹ in the FR, 7.7 m s⁻¹ in the BR, and generally lower in the JR (0 to 5.9 m s⁻¹; table S1).

CH₄ concentrations and flux rates in the BR, FR, and JR mangrove creeks

We found high temporal and intersite variability of CH₄ concentrations overall, ranging from 6 to 1069 nM in the BR, FR, and JR (Fig. 2). Concentrations of CH₄ followed a clear tidal pattern, with highest concentrations at low tide and lowest concentrations at high tide. An exception was in the JR in the wet season, where CH₄ concentrations peaked during the first high tide. No general pattern was found between surface water CH₄ concentration and salinity (Fig. 3). In the BR mangrove creek, CH₄ concentrations increased toward higher salinities. In the JR mangrove creek, CH₄ concentrations decreased toward higher salinities, and in the FR, surface water CH₄ and salinity displayed a hysteresis pattern.

Fig. 2. CH₄ concentrations over two tidal cycles.

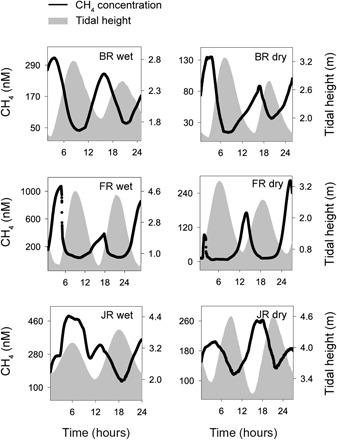
CH₄ concentration (nM) at the mangrove sites in the BR, FR, and JR estuaries in the wet and dry season.

Fig. 3. CH₄ concentrations versus salinity.

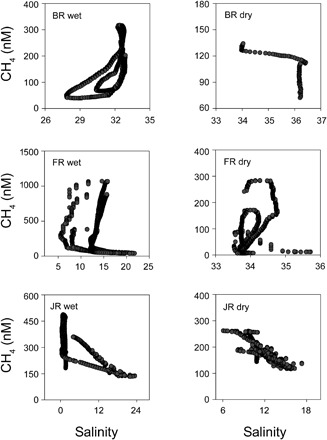
CH₄ concentration (nM) over the salinity range during the 24-hour time series in the wet and dry season in the BR, FR, and JR mangrove creeks. The salinity in the BR dry season is only available for the first 3 hours of the time series. Note the different scale of salinity in each system.

Water-to-atmosphere fluxes of CH₄ were tidally influenced with highest flux rates generally at mid to low tide when currents were strongest and gas concentrations in the water were highest. Table 1 shows the variability of the water-atmosphere CH₄ flux rates depending on the different k models used (see Materials and Methods). The CH₄ flux rates calculated based on the empirical models of H16 and RC01 were generally lower than those based on the R17 models. In contrast, CH₄ flux rates based on the B04 parameterization were always higher compared to the flux rates based on the R17 parameterizations. Because the empirical models of R17 were constructed for CH₄ gas transfer (k₆₀₀-CH₄) at the water-atmosphere interface and were also site-specific for the mangrove creeks in this study, the average of the three parameterizations was used to estimate CH₄ flux rates in the BR, FR, and JR. In the JR in the wet season, no current velocity or water depth data were available, and the RC01 k model likely underestimated the actual flux rate in our mangrove creeks (Table 1). For this reason, the difference between RC01 and the average R17 flux rate was applied to estimate the CH₄ flux in the JR in the wet season. Overall, water-atmosphere CH₄ flux rates in the three studied mangrove creeks ranged from 96.5 to 1049.8 μmol m⁻² day⁻¹ and were 64, 91, and 40% higher in the wet season compared to the dry season in the BR, FR, and JR, respectively.

Table 1. Average (± confidence interval) water-atmosphere CH₄ flux rates and gas transfer velocities using different empirical k models.

na, not available.

k model	Variables*	BR wet		BR dry		FR wet		FR dry		JR wet		JR dry
		flux (μmol m−2 day−1)	k600 (cm hour−1)	flux (μmol m−2 day−1)	k600 (cm hour−1)	flux (μmol m−2 day−1)	k600 (cm hour−1)	flux (μmol m−2 day−1)	k600 (cm hour−1)	flux (μmol m−2 day−1)	k600 (cm hour−1)	flux (μmol m−2 day−1)	k600 (cm hour−1)
R17 (27)	v	236.5 ± 7.4	5.7	103.7 ± 3.6	7.3	1059.0 ± 48.9	15.0	95.3 ± 6.4	8.3	na	na	484.4 ± 9.4	9.8
R17 (27)	v, u	283.7 ± 8.3	6.8	104.6 ± 4.3	6.9	1110.7 ± 49.5	16.4	99.2 ± 6.8	8.9	na	na	460.4 ± 9.6	9.3
R17 (27)	v, u, h	324.7 ± 8.8	7.9	115.7 ± 4.3	7.7	979.8 ± 40.7	15.5	94.8 ± 6.3	9.0	na	na	535.3 ± 8.7	10.9
Average flux (R17)		301.0 ± 8.7	6.8	108.0 ± 4.0	7.3	1049.8 ± 46.3	15.6	96.5 ± 6.5	8.7	826.2†	10.2†	493.3 ± 9.1	10.0
H16 (26)	v, u, h	275.0 ± 9.8	6.5	69.1 ± 3.6	3.8	601.4 ± 28.3	8.1	69.6 ± 4.9	6.0	na	na	167.0 ± 4.5	3.4
RC01 (54)	u	385.0 ± 13.8	9.2	93.5 ± 4.9	5.0	474.7 ± 17.1	8.1	74.8 ± 5.1	7.1	375.2 ± 8.7	4.7	224.0 ± 5.8	4.6
B04 (55)	v, u, h	623.2 ± 18.0	14.7	187.4 ± 7.8	10.9	1542.7 ± 75.7	19.3	191 ± 13.2	15.6	na	na	494.7 ± 10.1	10.2

*Current velocity (v) in cm s⁻¹, water depth (h) in m, and wind speed (u) in m s⁻¹.

†Calculated based on the % difference of RC01 and average R17 in the JR dry season.

Upscaled mangrove CH₄ emissions

Sediment-atmosphere flux rates from previously published studies were on average ~30% higher compared to water-atmosphere fluxes from this study and previously published studies (Table 2). Accounting for intertidal mangrove systems being inundated 50% of the time (water-atmosphere flux) and exposed 50% of the time (sediment-atmosphere flux), average mangrove CH₄ emissions were 339.6 ± 106.2 μmol m⁻² day⁻¹. Global total CH₄ emissions scaled to the most recent mangrove forest area of 137,760 km² (25) were 0.273 ± 0.053 Tg CH₄ year⁻¹. Using the conversion factor of the GWP for the 20- and 100-year time horizons, the “CO₂ equivalent” CH₄ emissions correspond to 6.41 ± 1.24 Tg C year⁻¹ (GWP₂₀) and 2.53 ± 0.49 Tg C year⁻¹ (GWP₁₀₀). With respect to latitude, we found the largest mangrove CH₄ flux at midlatitudes (20° to 25°; Fig. 4A). This was the case for both sediment-atmosphere fluxes and water-atmosphere fluxes (table S4 and fig. S1). Latitudinal scaled total CH₄ emissions were 0.191 ± 0.057 Tg CH₄ year⁻¹, and latitudinal scaled total CO₂ equivalent CH₄ emissions were 4.47 ± 1.34 Tg C year⁻¹ and 1.77 ± 0.53 Tg C year⁻¹ for the GWP₂₀ and GWP₁₀₀, respectively (Table 3).

Table 2. Global CH₄ emissions, carbon burial rates, and offsets in mangroves.

Global emission and carbon burial rates are upscaled to the global mangrove forest area of 137,760 km² (25). n refers to the number of study site locations (see tables S2, S3, and S5).

	CH4 flux rate (μmol m−2 day−1)	Global CH4 emission (Tg CH4 year−1)	Global CH4 emission (Tg C year−1)	CH4 (CO2 eq.) emission, GWP20 (Tg C year−1)	CH4 (CO2 eq.) emission, GWP100 (Tg C year−1)	Sequestration rate (g C m−2 year−1)	Global carbon burial (Tg C year−1)	Offset (%)*	Sensitivity analysis offset range (%)†
Water-air CH4 flux	(n = 9)	(n = 9)	(n = 9)	(n = 9)	(n = 9)	(n = 27)	(n = 27)
Min	35.10	0.028	0.021	0.66	0.26	56.60	7.80
Max	659.8	0.531	0.398	12.45	4.92	651.0	89.68
Average ± SE	288.0 ± 73.2	0.232 ± 0.059	0.174 ± 0.044	5.43 ± 1.38	2.15 ± 0.55	227.2 ± 30.67	31.30 ± 4.22	17.3	(15.7–18.5)
Sediment-air CH4 flux	(n = 14)	(n = 14)	(n = 14)	(n = 14)	(n = 14)	(n = 27)	(n = 27)
Min	0	0	0	0	0	56.60	7.80
Max	2,127.2	1.71	1.28	40.14	15.87	651.0	89.68
Average ± SE	391.2 ± 153.4	0.315 ± 0.123	0.236 ± 0.093	7.38 ± 2.90	2.92 ± 1.14	227.2 ± 30.67	31.30 ± 4.22	23.6	(22.0–25.8)
Global total	(n = 23)	(n = 23)	(n = 23)	(n = 23)	(n = 23)	(n = 27)	(n = 27)
Average ± scaled error	339.6 ± 106.2‡	0.273 ± 0.053‡	0.205 ± 0.040‡	6.41 ± 1.24‡	2.53 ± 0.49‡	227.2 ± 30.67	31.30 ± 4.22	20.5	(19.8–21.0)

*Offset is calculated from carbon burial (Tg C year⁻¹) and the CH₄ flux using the GWP₂₀ (Tg C year⁻¹).

†Carbon burial (Tg C year⁻¹) and CH₄ emissions (GWP₂₀; Tg C year⁻¹) are adjusted up and down by their errors.

‡Accounting for mangrove ecosystems being inundated 50% of the time (water-atmosphere flux) and exposed 50% of the time (sediment-atmosphere flux).

Fig. 4. Latitudinal average mangrove CH₄ flux rates and carbon burial rates.

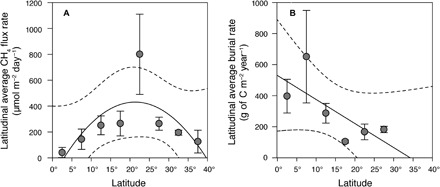
(A) Combined average sediment-atmosphere and water-atmosphere CH₄ flux rate (±SE) of the latitudinal regions 0° to 40° (in 5° steps), including this study and previously published studies. Note that in latitudinal regions where no water-atmosphere or sediment-atmosphere CH₄ flux data were available, we used the next closest latitudinal region or the average of the next higher and lower latitudinal region (see Materials and Methods and table S4). The black line indicates the quadratic regression line (r² = 0.49, n = 8, P < 0.5). (B) Average carbon burial rate (±SE) of the latitudinal regions 0° to 30° (in 5° steps) of previously published studies. The black line indicates the linear regression line (r² = 0.69, n = 6, P < 0.05). The dashed lines indicate the 95% confidence interval.

Table 3. Latitudinal CH₄ emissions, carbon burial, and offsets in mangroves.

Mangrove latitudinal areas are based on Giri et al. (25). Error (±) is scaled error (see text) unless marked with “^a” (in these cases, the SE is used).

Latitude	Mangrove area (km2)	Average CH4 flux rate (μmol m−2 day−1)*	Latitudinal CH4 emission (Tg CH4 year−1)	Latitudinal CH4 emission (Tg C year−1)	Latitudinal CH4 (CO2 eq.) emission, GWP20 (Tg C year−1)	Latitudinal CH4 (CO2 eq.) emission, GWP100 (Tg C year−1)	Average burial rate (g C m−2 year−1)	Latitudinal carbon burial (Tg C year−1)	Offset (%)†	Sensitivity analysis offset range (%)‡
0–5°	44,000	40.26 (± 40.3)a	0.010 (± 0.005)	0.008 (± 0.004)	0.24 (± 0.12)	0.10 (± 0.05)	396.6 (± 108.5)a	17.45 (± 4.78)	1.4	(1.0–1.6)
5–10°	30,000	143.8 (± 78.3)a	0.025 (± 0.013)	0.019 (± 0.009)	0.59 (± 0.29)	0.23 (± 0.12)	651.0 (± 298.0)a	19.53 (± 8.94)	3.0	(2.8–3.1)
10–15°	23,500	251.0 (± 72.8)a	0.034 (± 0.006)	0.026 (± 0.004)	0.81 (± 0.14)	0.32 (± 0.05)	286.8 (± 63.3)a	6.74 (± 1.49)	12.0	(11.5–12.7)
15–20°	16,500	265.1 (± 95.5)a	0.026 (± 0.001)	0.019 (± 0.001)	0.60 (± 0.03)	0.24 (± 0.01)	104.4 (± 10.4)a	1.72 (± 0.17)	34.8	(33.4–36.5)
20–25°	18,800	800.5 (± 310.4)a	0.088 (± 0.032)	0.066 (± 0.024)	2.06 (± 0.75)	0.81 (± 0.30)	166.6 (± 50.7)a	3.13 (± 0.95)	65.8	(63.2–67.2)
25–30°	4,300	264.1 (± 50.3)a	0.007 (± 0.003)	0.005 (± 0.002)	0.16 (± 0.06)	0.06 (± 0.02)	182.8 (± 19.7)a	0.79 (± 0.08)	19.8	(13.5–24.8)
30–35°	310	194.9 (± 18.9)a	0.0004 (± 0.0001)	0.0003 (± 0.0001)	0.008 (± 0.003)	0.003 (± 0.001)	182.8 (± 19.7)a	0.057 (± 0.006)	14.6	(10.0–18.3)
35–40°	350	125.7 (± 88.1)a	0.0003 (± 0.0001)	0.0002 (± 0.0001)	0.006 (± 0.002)	0.002 (± 0.001)	182.8 (± 19.7)a	0.064 (± 0.007)	9.4	(6.4–11.8)
	Total	Average	Total	Total	Total	Total	Average	Total	Average	Range
Latitudinal total	137,760	260.6 (± 94.3)a	0.191 (± 0.057)	0.143 (± 0.043)	4.47 (± 1.34)	1.77 (± 0.53)	269.2 (± 73.7)a	49.48 (± 16.4)	20.1	(17.7–22.0)

*Combined sediment-atmosphere and water-atmosphere flux accounting for mangrove ecosystems being inundated 50% of the time (water-atmosphere flux) and exposed 50% of the time (sediment-atmosphere flux; see table S4).

†Offset is calculated from carbon burial (Tg C year⁻¹) and the CH₄ flux using the GWP₂₀ (Tg C year⁻¹).

‡Carbon burial rates (Tg C year⁻¹) and CH₄ emissions (GWP₂₀, Tg C year⁻¹) are adjusted up and down by their scaled errors.

Upscaled mangrove burial rates

Published average burial rates ranged from 56.60 to 651.0 g C m⁻² year⁻¹ based on 27 study sites (Table 2 and table S5). Global total burial rates scaled to the total mangrove area of 137,760 km² were, on average, 31.30 Tg C year⁻¹ (range, 7.80 to 89.68 Tg C year⁻¹). Latitudinal scaled total burial rates were higher than total global burial rates, with an average of 49.48 ± 16.4 Tg C year⁻¹ (Table 3). Figure 4B shows the average burial rates over the latitudinal regions 0° to 40° in 5° steps. Burial rates showed a weak increase toward the lower latitudes.

Carbon burial offsets by CH₄ emissions

Global total carbon burial offsets by CH₄ emissions (based on the GWP₂₀) were 20.5%, and the sensitivity analysis offsets ranged from 19.8 to 21.0% (Table 2). Global CH₄ emission offsets scaled over the latitudes 0° to 40° were similar, with an average of 20.1% and a sensitivity analysis offset range of 17.7 to 22.0% (Table 3). We found the highest average offset (~65%) at the midlatitudinal region 20° to 25°. The largest unknowns are the average offsets calculated for the latitudinal regions 30° to 40° and 0° to 5° due to the lack of measured CH₄ emission rates (and carbon burial between 30° and 40°). The regions 30° to 35° and 35° to 40° have very small areas of mangroves and therefore have little impact on overall global offsets; however, the 0° to 5° latitudinal region has a large area of mangroves and will influence the overall global offsets.

DISCUSSION

Variability of CH₄ emissions from mangrove ecosystems

We calculated water to atmosphere CH₄ flux rates for the FR, BR, and JR mangrove creeks in two field campaigns in the wet and dry season. The evasion rates (96.5 to 1049.8 μmol m⁻² day⁻¹) are at the high end or higher than previously published CH₄ flux rates for mangrove ecosystems (table S2) (22, 23). This is most likely because CH₄ flux rates vary greatly depending on k in the flux computation. In shallow tidal mangrove ecosystems, k is mainly controlled by current generated turbulence, and reliable water-to-atmosphere fluxes should therefore be based on site-specific k parameterizations that include current velocity (26, 27). In addition, our study measured in situ CH₄ concentrations continuously (<1 s), and water-atmosphere flux rates were calculated at high resolution (per minute). Most previous studies calculated CH₄ emissions based on discrete sampling that can miss some of the tidally influenced temporal variability that is evident in our data (20, 22, 24).

Water CH₄ evasion rates were significantly higher (40 to 91%) in the wet season compared to the dry season (Table 1). Higher flux rates in the wet season (>17%) were also found in the mangrove waters of the Andaman Islands (24) and may be driven by freshwater riverine inputs that increase nutrient loading, increase the supply of labile organic matter, and reduce the supply of sulfate (and therefore inhibit sulfate reduction), all of which can enhance CH₄ production rates (19, 28).

In the three studied mangrove creeks, surface water salinity was always lower in the rainy season. No clear pattern was observed between surface water CH₄ concentration and salinity (Fig. 3). Surface water salinity covaried with other drivers of CH₄ emissions such as tidal height and pore water flushing. The inverse relationship of surface water CH₄ concentrations and tidal height is indicative of tidal pumping—the exchange of CH₄-enriched (and CO₂-, DIC-, and alkalinity-enriched) groundwater or sediment pore water with surface water (29–31), which has been found in previous studies driving high surface water CH₄ (Fig. 2) (22–24). However, in the JR in the wet season, the enhanced CH₄ concentrations during the first high tide were likely driven by freshwater flushing to the mangrove creek (salinity during the first high tide ranged from 0.5 to 1.6; table S1). With regard to this offset exercise, we assumed that sediment-atmosphere and water-atmosphere emissions as well as carbon burial are autochthonous, but further research in this area is needed.

The literature review showed that CH₄ fluxes from exposed mangrove sediments are highly variable (0 to 2127.2 μmol m⁻² day⁻¹) but generally larger than emissions from the mangrove creek waters (Table 2). This is consistent with the findings of a study in two Tanzanian mangrove forests, where the highest CH₄ emissions occurred at low tide (exposed sediments) and the lowest CH₄ emissions occurred at high tide (inundated) (20). During the high tide, increased hydrostatic pressure can inhibit CH₄ emissions (32). Furthermore, CH₄, that is, fluxes at the sediment-water interface, can be oxidized by methane-oxidizing bacteria before it reaches the atmosphere (33). At low tide, the flux through pneumatophores, plant roots, and crab burrows can further enhance total CH₄ emissions from sediments (20, 21); however, the emitted CH₄ originates from methanogenesis of the surrounding sediments and not from the plant roots or crabs themselves. Ebullition is a major flux component in shallow freshwater ecosystems with high organic matter supply (34, 35) and may also contribute to total CH₄ emissions from mangrove sediments. In the three studied mangrove creeks, there was no ebullition from sediments, and results from 209 floating chamber deployments measuring water-atmosphere CH₄ fluxes did not show any evidence of ebullition (27). To our knowledge, only one published study measured CH₄ concentration in sediment gas bubbles (21), but we actively stirred the gas bubbles from the Pichavaram mangrove sediments and therefore do not consider them naturally occurring ebullition. Ebullition from sediments and other tree-mediated (stems and leaves) CH₄ emissions is not sufficiently available for mangrove ecosystems and hence we could not incorporate it in our mangrove CH₄ emission estimate. Our global CH₄ emission and corresponding carbon burial offsets may therefore be underestimated and should be seen as a lower-bound estimate.

Latitudinal mangrove carbon burial rates increased toward lower latitudes (Fig. 4B), which is consistent with an early review of carbon burial in mangrove sediments over four latitudinal zones (18). The average carbon sequestration rate proposed by Twilley et al. (18) is, however, much lower (100 g C m⁻² year⁻¹) than the latitudinal average estimate in this study (269.2 ± 73.7 g C m⁻² year⁻¹). There is also a similar latitudinal trend for mangrove aboveground and belowground biomass (18, 36), mangrove litter fall (37), and soil carbon stocks (18, 36). Mangrove production (NPP) is also higher at the tropical west Pacific region between the Sunda Sea and Philippine Sea (approximately 0° to 10°) compared to higher latitudinal regions such as the west Indian coast of Africa or the northeast Pacific region between Mexico and Panama (13). Average CH₄ emissions were highest in mangroves at midlatitudes. However, there is a lack of CH₄ emission data from sediments and the water column at low latitudes (<10°; Fig. 5 and fig. S1). Generally higher temperatures and precipitation in tropical/monsoonal climate zones suggest that mangroves of the wet tropics may be more productive and have higher carbon burial rates and CH₄ emissions than mangroves of the dry tropics (13). Ouyang et al. (38) also found that the impact of geographic (latitude), climatic, and biotic (ecosystem type) drivers influences mangrove root decomposition rates. In particular, mangrove type (for example, riverine, fringe, and overwash) and mangrove species have a strong influence on the rates of mangrove root decomposition and root decay rates (38). There was no obvious pattern between mangrove species, mangrove type, and CH₄ emissions. Certainly, more data on CH₄ emissions and carbon burial rates from different geographic and climatic regions, different mangrove ecosystem types, and levels of disturbance would help to better explore these relationships.

Fig. 5. Map of CH₄ emission studies and carbon burial studies in mangroves.

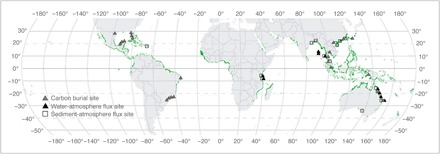
Gray triangles are mangrove carbon burial study sites (table S5). Black triangles are mangrove water-atmosphere CH₄ flux study sites (table S2). Open squares are mangrove sediment-atmosphere CH₄ flux study sites (table S3). Mangrove forest distribution is in green. Map based on the global mangrove forest distribution of Giri et al. (25).

Latitudinal scaled total CH₄ emissions were 30% lower than CH₄ emissions that were upscaled to the total mangrove forest area (Tables 2 and 3). Latitudinal scaled burial rates were 37% higher than global scaled burial rates. The discrepancy may be explained by the few data that are available for latitudes 0° to 10° and >30°. We estimated the missing CH₄ emissions and burial rates of these latitudinal regions from the next closest latitudinal region or are the average of the next two closest regions (Fig. 4 and table S4). Hence, the accuracy of the CH₄ emission and carbon burial estimates for these regions is unknown. Because we also used the low water CH₄ flux for 5° to 10° for the latitudinal region 0° to 5° and did not observe any sediment CH₄ emissions for 0° to 5° latitudes (table S4), we applied a low average CH₄ flux rate (40.3 μmol m⁻² day⁻¹) to 54% of the total mangrove area, resulting in lower latitudinal scaled CH₄ emissions compared to global total scaled emissions (Fig. 4A and Tables 2 and 3). Similarly, we applied the very high carbon burial rates for the latitudinal region 5° to 10° to 22% of the total mangrove area, resulting in higher latitudinal scaled total carbon burial compared to global total scaled burial (Fig. 4B and Tables 2 and 3). Nevertheless, latitudinal scaled total estimates and the comparison of mangrove emissions and burial over different climatic and latitudinal regions give important insights into global trends and help to reveal hot spots of mangrove CH₄ emissions, carbon burial rates, and hence burial offsets by CH₄ emissions, and highlight areas where further work is required.

The global total and the latitudinal scaled total CH₄ emissions from mangrove ecosystems in this study (0.2 to 0.3 Tg CH₄ year⁻¹) are lower than previous estimates (11, 22). The global estimate of 2.2 Tg CH₄ year⁻¹ proposed by Barnes et al. (22) is based on only one study of relatively high CH₄ flux rates in a pristine mangrove creek on the Andaman Islands (552 to 828 μmol m⁻² day⁻¹) and upscaled to a mangrove area of 360,000 km². A more recent global estimate is even higher (5 Tg C year⁻¹) (11). This estimate used the same mangrove area estimate that we used in this study (25), but it was unclear what data were included in their estimate and how they were calculated. Although there are still relatively high uncertainties in the upscaled mangrove CH₄ emissions presented in this study, our global estimates include previously published sediment and water CH₄ emissions, newly measured seasonal data of CH₄ fluxes from three mangrove ecosystems, and upscaling by latitudinal region, which is an important control of CH₄ emissions.

Mangrove CH₄ emissions partially offset mangrove carbon burial

Global total and latitudinal scaled carbon burial offsets by CH₄ emissions are similar and estimated to be ~20% (Tables 2 and 3). The global total mangrove carbon burial estimate in this study (31.3 ± 5.2 Tg C year⁻¹) is in agreement with previous mangrove carbon burial estimates (18.4 to 34.4 Tg C year⁻¹) (5, 11, 12, 15) and accounts for approximately 16% of mangrove NPP (Fig. 1). We expected this because all the previous estimates were also based on upscaling average carbon burial rates to the global total mangrove forest area. In contrast, our latitudinal scaled total burial estimate is higher because it emphasizes denser mangrove forests (biomass) and concomitant higher burial rates at low latitudes [for example, Tamandaré, Brazil, 8.7°S, 651 g C m⁻² year⁻¹ (39)]. The lack of carbon burial rates at the latitudinal regions 30° to 35° and 35° to 40° likely underestimates the potential offsets in these regions, but because of the small area of mangroves in these regions, they have little impact on the overall global offset estimates (Table 3). The adjusted offsets are highest at the latitudes 20° to 25°, driven by lower burial rates and high CH₄ emissions. Mangrove biomass and carbon burial decrease toward higher latitudes (25, 38), but emissions of CH₄ may still be high relative to burial rates due to, for example, groundwater inputs and tidal pumping, which can enhance surface water CH₄ (40, 41) but may have a less pronounced effect on burial rates. Carbon burial offsets by CH₄ emissions should therefore be highest at midlatitudes, where burial rates were ~200 g C m⁻² year⁻¹ and CH₄ emissions were ~800 μmol m⁻² day⁻¹ (Table 3).

Measurements of carbon burial rates, sediment, and water CH₄ emissions are available for the same mangrove system in southern Moreton Bay (Australia) (23, 42). Local offsets of carbon burial by CH₄ emissions in southern Moreton Bay were on average 24.1% (range, 19.5 to 28.7%). This is similar to our average global estimates, giving some confidence in the upscaled mangrove CH₄ emissions and carbon burial rates. Although our estimates presented here have relatively large uncertainties (Tables 2 and 3), mangrove CH₄ emissions and offsets should be accounted for in future mangrove blue carbon assessments and global CH₄ budgets.

Uncertainties of global emissions and future research

The sensitivity analysis and the comparison of offsets over different latitudinal regions (Table 3) show that although there could be a large range in the possible mangrove carbon burial offset by CH₄ emissions, the overall conclusion that there is some offset remains the same. However, there are also several other factors that contribute to the uncertainties in our global CH₄ emission and carbon burial estimates (Tables 2 and 3) that are not accounted for in our error and sensitivity analysis, some of which also influence our partial offsets of carbon burial rates. First, few or no CH₄ flux rates are available for the latitudes 0° to 10° and 30° to 40° (Fig. 5). However, the world’s largest mangrove areas are in low latitudinal regions, such as Indonesia (22.6% of global total), Australia (7.1%), or Brazil (7.0%) (25). The world’s best developed mangrove forests can be found in the Sundarbans, the Mekong Delta, the Amazon, Madagascar, and Southeast Asia (25). Further, Indonesia has the highest mangrove species diversity [48 species (42)] and exceptionally high carbon stocks in mangrove sediments (43). Given the high variability and uncertainties in global mangrove CH₄ emissions, more studies are needed, especially in extensive mangrove forest regions such as the Niger Delta, the West Africa mangrove coast (Rivières du Sud), Indonesia, northern Brazil, and southern Papua.

Second, global mangrove CH₄ emission and carbon burial estimates depend on accurate global mangrove area estimates. Although the global mangrove area proposed by Giri et al. (25) seems to be the most precise estimate to date (44), the Global Land Survey (GLS) data, based on high-resolution 30-m Landsat satellite imagery from U.S. Geological Survey (USGS), cover a period from 1997 to 2000 and do not account for small patches (<2700 m²), which can make a substantial difference to the total area (25). Moreover, the loss of mangrove forest due to natural and anthropogenic impacts is occurring globally (43, 45, 46). Loss rates vary greatly between countries, ranging from 1 to 20% of the total mangrove forest area, which makes it difficult to predict global mangrove forest changes in the future (47). Duke et al. (48) predict a mangrove loss rate of 1 to 3% per year. The decline of mangroves is largely attributed to anthropogenic perturbations and disturbance such as mechanical destruction (mariculture/aquaculture ponds), urbanization, land use change, chemical spill, and climate change impacts (25, 46, 48, 49). Climate change—particularly sea level rise—may be the biggest threat to mangroves in future decades (46, 50). An update of global and latitudinal mangrove area estimates would help to better constrain global mangrove CH₄ emissions and their implication on global CH₄ budgets. Although the area estimates influence the amount of carbon buried and the amount of CH₄ emitted by mangroves globally, they do not affect the offset estimates because both terms use the same area.

Data collection and sampling strategy may also be responsible for some variation of global CH₄ flux estimates. Most of the previous published CH₄ flux rates are based on discrete sampling. To account for tidal variability, high-resolution (1 min) continuous sampling of CH₄ concentrations and ancillary data in mangrove waters allows more accurate estimates of CH₄ emissions. For annual estimates, seasonal measurements will be required. Furthermore, our CH₄ emission estimate does not account for potential ebullition from sediments or tree-mediated (stems and leaves) fluxes. More studies are needed not only on different CH₄ emission pathways in mangrove ecosystems but also on mangrove NPP production rates (for example, belowground wood production).

Finally, we want to emphasize that we attribute uncertainties and the variability of CH₄ flux rates, to a certain extent, to the uncertainty of the gas transfer velocity in the flux computation. k₆₀₀-CH₄ in our three mangrove creeks was on average 9.7 ± 0.9 cm hour⁻¹ (range, 5.7 to 16.4 cm hour⁻¹; Table 1), hence slightly higher than the average k₆₀₀-CO₂ that we estimated for the same mangrove sites (7.5 ± 1.1 cm hour⁻¹) in a previous study (14). In tidal mangrove ecosystems, CH₄ flux rates may be most accurate when based on kCH₄ parameterizations that include current velocity, water depth, and wind speed (26, 27) and account for a nondiffusive microbubble flux component in addition to the diffusive flux of CH₄ across the water-atmosphere interface [for example, see the studies of Rosentreter et al. (27), McGinnis et al. (51), and Prairie and del Giorgio (52)]. However, there is still a need to further explore the behavior and the drivers of gas transfer velocities of greenhouse gases (CO₂, CH₄, and N₂O) at the aqueous boundary layer, particularly in tidally influenced systems such as mangrove ecosystems.

CONCLUSION

The preservation and enhancement of natural carbon stores are part of global climate change mitigation strategies. Despite offering valuable ecosystem services to the coastal zone and its inhabitants, coastal vegetated ecosystems also stand out as large natural carbon stores. The term “blue carbon” was coined to describe the carbon captured in coastal habitats such as mangrove forests, seagrass beds, and salt marshes. Mangrove forests, in particular, are highly productive ecosystems with global carbon sequestration rates that are disproportionate to their area. However, here, we show that CH₄ emissions from mangrove waters have the potential to offset blue carbon burial rates in sediments on average by 20% (sensitivity analysis offset range, 18 to 22%). Hence, CH₄ emissions from mangroves need to be accounted for when assessing their importance in climate change mitigation.

MATERIALS AND METHODS

Study locations

This study compares three mangrove creek sites in different estuaries in the wet and dry seasons, located in the tropical convergence zone along the north-eastern coast of Queensland, Australia. The mangrove-dominated FR estuary (23°31′22.8″S, 150°52′30.0″E), the BR estuary (19°41′13.2″S, 147°36′39.6″E), and the JR estuary (17°30′32.4″S, 146°3′47.6″E) all discharge into the Great Barrier Reef lagoon. In general, the estuaries are dominated by episodic, short-lived, large freshwater inputs during the wet season and low or no discharge and high evaporation rates during the dry season. The river catchments are characterized by different degrees of anthropogenic impacts. Disturbance is higher (mainly land use change) in the JR catchment compared to the FR and BR catchments. Mangroves, predominantly Avicennia, Rhizophora, and Ceriops, cover a large area of the coast and fringe of the estuaries with an overall area of 178 km².

Experimental design

Time series of 24 hours were conducted in February/March 2014 (wet season) and September/October 2014 (dry season) in small mangrove creeks in the FR, BR, and JR estuaries. CH₄ concentrations were measured using a cavity ring-down spectroscopy analyzer (G2201-i; Picarro). Briefly, water was pumped from a depth of ~30 cm by a submersible pump to a shower-head exchanger, where water was sprayed into a chamber, creating fine droplets that maximize gas equilibration. From the equilibrator, a continuous air loop was linked to the Picarro analyzer, where CH₄ was measured (±60 parts per billion) in the dried gas stream (Drierite desiccant, water vapor maintained at <0.1%) before returning back to the equilibrator. Creek water was pumped into a flow-through chamber on board, where ancillary data (salinity, temperature) were measured every 5 min using a calibrated HydroLab logger (DS5X Sonde, AquaLab). Water current velocity, depth, and direction were detected every 10 min using an acoustic Doppler current profiler (Argonaut-XR-Flowmeter, SonTek), which was deployed at the water bottom a minimum of 5 m away from the boat to ensure no interference with boat movements. A weather station (150 WX, Airmar) was attached on top of the boat to measure wind speed and wind direction every minute over the 24-hour time series.

Flux computation

Water to atmosphere CH₄ fluxes were calculated using the equation

$$\mathit{F}=\mathit{k} {\mathit{K}}_0({\mathit{C}}_{\mathrm{w}}-{\mathit{C}}_{\mathrm{a}})$$ (1)

where F is the flux of CH₄ across the water-atmosphere interface, k is the gas transfer velocity (m day⁻¹), K₀ is the solubility coefficient depending on temperature and salinity, C_w is the partial pressure of CH₄ in the water, and C_a is the partial pressure of CH₄ in the atmosphere. For the flux computation, we used a range of k values derived from different empirical models. First, a recent study determined k models for the same mangrove systems (BR, FR, and JR) using an improved design of the floating chamber method (R17) (27). The first parametrization accounts solely for current velocity (v)

$${\mathit{k}}_{600}-{\text{CH}}_4=2.03+0.43\mathit{v}$$ (2)

where k₆₀₀ (cm hour⁻¹) is the gas transfer velocity normalized to the Schmidt number of 600 as a function of temperature and salinity (53). The second parameterization accounts for v and wind speed calculated to the height of 10 m over water surface (u)

$${\mathit{k}}_{600}-{\text{CH}}_4=-0.77+0.45\mathit{v}+0.92\mathit{u}$$ (3)

The third parameterization accounts for v, u, and water depth (h)

$${\mathit{k}}_{600}-{\text{CH}}_4=-1.07+0.36\mathit{v}+0.99\mathit{u}+0.87\mathit{h}$$ (4)

CH₄ flux rates were further compared to the k₆₀₀ parameterization suggested by Ho et al. (26) (H16), which was determined from a dual tracer (³He/SF₆) release experiment in a mangrove estuary in the Everglades National Park in Florida, also accounting for current velocity, wind speed, and water depth. The wind speed parameterization of Raymond and Cole (54) (RC01) was suitable for CH₄ flux calculation in the JR wet season, where only wind speed data were available. Finally, CH₄ flux rates were calculated using the parameterization of Borges et al. (55) (B04), which was constructed for estuarine environments.

Global mangrove area estimates

Mangrove area estimates before 2007 ranged from 110,000 to 240,000 km² (Food and Agriculture Organization, 2003). The area range has decreased to 152,361 and 137,760 km² due to recent availability of high-resolution imagery (25, 49). The mangrove area estimate of 137,760 km² by Giri et al. (25) was generated from GLS data from 1997 to 2000 by Landsat 30-m-resolution satellite imagery provided by the USGS (25) and is currently the most precise mangrove forest area estimate (44).

Global mangrove CH₄ emissions

The percent inundated and exposed area in the BR, FR, and JR mangrove creeks was estimated based on digital elevation model data (1-m grid interval; precision, ±0.15 m) derived from airborne laser scanning surveys (LiDAR, Department of Natural Resources and Mines, State of Queensland, 2013). The BR mangrove sediments were exposed 52% of the time over the two tidal cycles. The FR mangrove sediments were exposed 42%, and the JR mangrove sediments were exposed 88% of the time. Average CH₄ emissions from this study and previously published studies were calculated, accounting for tidal mangrove systems being inundated 50% of the time (water-atmosphere flux) and exposed 50% of the time (sediment-atmosphere flux). Water-atmosphere CH₄ flux rates (μmol m⁻² day⁻²) are based on different empirical k models in our study and previously published studies. Only studies that were conducted in tidal mangrove creeks were included in global flux estimates. Studies from outer estuaries and open lagoons adjacent to mangroves were excluded because they may be more indicative of marine than mangrove environments. Sediment-atmosphere fluxes that were included were measured using static chamber studies over (low tide) bare sediments and also include plant-mediated flux (pneumatophores and roots), crab burrows, and different tidal zones. Only Scopus-listed publications were included, because some studies published in non–Scopus-listed journals that meet the above criteria did not adequately describe their methodology and calculations or present their data, and therefore, it was uncertain whether the data were reliable.

Two different approaches were used to upscale CH₄ flux rates to global mangrove CH₄ emissions. First, the average CH₄ flux rate is scaled to the total global mangrove forest area of 137,760 km² (the “global total”) (25). Second, we estimate latitudinal average CH₄ flux rates over the latitudes 0° to 40° in 5° steps. At latitudinal regions where no CH₄ flux data (water-atmosphere or sediment-atmosphere) were available, the next closest latitudinal region or the average of the next higher and lower latitudinal region was used (table S4). The average CH₄ flux rate of each latitudinal region was then scaled to the mangrove forest area estimate at each latitudinal region (25) and summed up to a global total estimate (the “latitudinal total”). Global total and latitudinal scaled total mangrove CH₄ emissions are presented in Tg CH₄ year⁻¹ and Tg C year⁻¹.

CH₄ “equivalent CO₂” emissions

We account for CH₄ emissions as CO₂ equivalent emissions using the GWP. The most recent GWPs of CH₄ are 86 and 34 for the time horizons 20 and 100 years, respectively, including climate-carbon feedbacks (1). The choice of time horizon has a strong effect on the GWP values and hence the calculated CO₂ equivalent emissions. In the case of CH₄, the GWP decreases by approximately a factor of 3 for a changing time horizon from 20 to 100. The time horizon usually used for GWPs is 100 years; however, the 20-year GWP prioritizes gases with shorter lifetimes such as CH₄ [lifetime, 9.1 ± 0.9 years (56)]. Nevertheless, for the best comparison, we present CO₂ equivalent emissions of CH₄ for the GWP₂₀ and GWP₁₀₀ time horizons

$${\text{CH}}_4({\text{CO}}_2\text{eq}.) \text{emission} ={\text{CH}}_{4\text{emission}}\times \text{GWP}\times \mathit{f}$$ (5)

where CH_4emission is the mangrove CH₄ emission expressed in Tg CH₄ year⁻¹; GWP is 86 and 34 for the time horizons 20 and 100, respectively; and f is the conversion factor to Tg C year⁻¹ (multiplied by 12/44).

Global carbon burial estimate

The global total and latitudinal total mangrove carbon burial rates were estimated using the same two approaches that were used to estimate global total and latitudinal total mangrove CH₄ emissions. The global total carbon burial is based on published (Scopus-listed) burial sequestration rates in mangrove sediments and upscaled to the total mangrove forest area (25). The latitudinal scaled total carbon burial rate is estimated using the average burial rate of each latitudinal region 0° to 40° in 5° steps. Missing burial rates at the latitudinal region 30° to 40° were estimated from the latitudinal region 25° to 30°, upscaled to the mangrove forest area of each latitudinal region (25), and summed to a global total estimate.

Global offset calculations

Although the measured CH₄ emissions and carbon burial rates operate over very different timescales, we assumed that CH₄ production has been in steady state over the longer time frame of carbon burial. The global total CH₄ emission offset to global total carbon burial was calculated using the global total CH₄ emission rate (GWP₂₀) and global total carbon burial rate. The latitudinal CH₄ emission offset to latitudinal carbon burial was calculated using the latitudinal CH₄ emission rate (GWP₂₀) 0° to 40° in 5° steps and the corresponding latitudinal carbon burial rate 0° to 40° in 5° steps and averaged over the latitudes 0° to 40°.

Error and sensitivity analysis

Errors for the upscaled estimates were propagated for each carbon burial and CH₄ flux term (F_R)

$$\text{Scaled error} ={\mathit{F}}_{\mathrm{R}}{\mathit{F}}_{\%}/100$$ (6)

The % error of each term (F_%) was determined [modified from Eyre (57)] as

$${\mathit{F}}_{\%}={({({\mathit{E}}_{\mathrm{R}})}^2+{({\mathit{E}}_{\mathrm{M}})}^2+({\mathit{E}}_{\mathrm{R}}\times {\mathit{E}}_{\mathrm{M}}))}^{0.5}$$ (7)

where E_R is the SE of the carbon burial or CH₄ flux rate. The error associated with mangrove area (E_M) was estimated to be ±5% (57).

A sensitivity analysis was done, where each of the terms in the global total and latitudinal total offsets were adjusted up and down by their estimated errors to determine if the overall conclusions derived from the upscaling changed [modified from Eyre et al. (58)]. The CH₄ emissions adjusted down were compared to the carbon burial rates adjusted down, and the CH₄ emissions adjusted up were compared to the carbon burial rates adjusted up. This is because it would be unlikely to get maximum burial rates with minimum CH₄ emissions or minimum burial rates with maximum CH₄ emissions.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/6/eaao4985/DC1

table S1. Wet and dry season physicochemical parameters and CH₄ concentration in the three studied mangrove creeks.

table S2. Mangrove water-atmosphere CH₄ fluxes from this study and published studies.

table S3. Published mangrove sediment-atmosphere CH₄ fluxes.

table S4. Combined mangrove sediment-atmosphere and water-atmosphere CH₄ fluxes for each latitude region (5° steps).

table S5. Published mangrove carbon burial rates.

fig. S1. Average mangrove CH₄ flux rates over latitudes (5° steps).

References (59–91)