Abstract
We show that theoretical microscopic titration curves (THEMATICS) can be used to identify active-site residues in proteins of known structure. Results are featured for three enzymes: triosephosphate isomerase (TIM), aldose reductase (AR), and phosphomannose isomerase (PMI). We note that TIM and AR have similar structures but catalyze different kinds of reactions, whereas TIM and PMI have different structures but catalyze similar reactions. Analysis of the theoretical microscopic titration curves for all of the ionizable residues of these proteins shows that a small fraction (3–7%) of the curves possess a flat region where the residue is partially protonated over a wide pH range. The preponderance of residues with such perturbed curves occur in the active site. Additional results are given in summary form to show the success of the method for proteins with a variety of different chemistries and structures.
There is a need to develop methods to predict protein function from structure; this need becomes particularly acute as novel protein folds are discovered for which there are no proteins of similar structure with known function. We show that theoretical microscopic titration curves (THEMATICS) can be used to identify active-site residues in enzymes of known structure. This information will prove to be important in the current challenging quest to predict protein function from sequence and structure.
Knowledge of protein sequences and structures has burgeoned very recently as a result of genome sequencing (1) and structural genomics efforts. To translate such information into tangible benefits to humankind, the next step is to develop methods that enable one to predict and to establish function from structure. Techniques used to predict function from sequence or function from structure are in their infancy and rely either on analogies to related proteins of known function (2–8) or on computational searches for binding sites by docking (9) of selected sets of small molecules onto the structure. For instance, recent work has searched the Protein Data Bank (PDB; ref. 10; http://www.rcsb.org/pdb/) for previously unrecognized cation-binding sites (11).
However, there is as yet no reliable method to identify active sites of enzymes or other interaction sites of proteins in the absence of biochemical data, even when the structure is known. There is a wealth of biochemical data that demonstrates that active-site residues involved in specific kinds of chemistry possess predictable chemical properties that enable one to identify them as active-site residues. The most important of these properties is a perturbed pKa that can be determined experimentally by pH titrations of the activity of the enzyme. Herein we demonstrate that theoretical titration functions can identify active-site residues that are involved in Brønsted acid–base chemistry for a variety of proteins, thereby identifying the active site from the location of the residues.
In an experimental titration curve, one typically plots pH as a function of the volume of standardized solution added. In a theoretical titration curve for a residue in a protein, one generally plots the net charge on the residue (for an ensemble of protein molecules) as a function of pH. Thus, we regard pH as the control variable and the charge on the group as the dependent variable. The calculated charge on a residue in a protein can sometimes be verified by spectroscopic measurements. Also, the pKa values of the catalytic residues can be determined indirectly by the measured reaction rate as a function of pH. This measured pKa can then be compared with the computed pKa's of the residues of the protein to identify the active site. We now show that the shapes of the theoretical titration functions carry information about active-site location, even in the absence of experimental kinetic data.
The titration curves of most of the ionizable residues in a protein have a typical shape: as pH is increased, there is a sudden, sharp decline in the predicted net charge. This decline occurs, as expected, in a narrow pH range around the pKa. This behavior is well known as the source of the buffer capacity of the ionizable groups of amino acids. Thus, most ionizable residues go from their protonated to unprotonated forms within a relatively narrow pH range, as predicted by the Henderson–Hasselbalch equation, written as
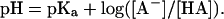 |
1 |
A small fraction of the ionizable residues have curves with perturbed shapes that do not fit Eq. 1.
Methods
A number of methods are available for the prediction of pKa values of ionizable groups in proteins based on a finite difference Poisson–Boltzmann method (12–15). This requires calculation of the electrostatic potentials, for which we employ the UHBD (16) program. We use the program HYBRID (15, 17) to calculate the mean net charge as a function of pH (18–21) for each ionizable group (all Lys, Arg, Asp, Glu, His, Tyr, Cys, N terminus, and C terminus) of each protein. For each residue type in a given enzyme, a plot is drawn of predicted mean net charge as a function of pH—THEMATICS. Thus, for each residue type, we have a plot with a family of curves: one plot with a curve for each Lys residue, another plot with a curve for each Arg residue, etc. We compare the curves for residues of the same type; curves with unusual shape are noted by visual inspection.
In this brief report we feature the results for three representative enzymes: triosephosphate isomerase (TIM), aldose reductase (AR), and phosphomannose isomerase (PMI). We also give results in summary form for eight other proteins. For all three of the featured enzymes and for many others as well, we observe theoretical titration functions with perturbed shapes for some of the ionizable active-site residues. Other ionizable residues that are not in the active site almost always have titration functions that are more typical in that they fit the Henderson–Hasselbalch equation. From the theoretical titration functions alone, one is therefore able to identify the physical location of the active site in a variety of different protein structures. We shall also discuss the probable catalytic advantage afforded by the observed perturbations in the titration functions.
Results
We have obtained theoretical titration functions for all ionizable residues of enzymes of several different types and have noticed a high correlation between a particular type of perturbed shape and the location of the residue in the active site. Our results correlate strongly with biochemical results of kinetic titrations that implicate specific residues in acid–base chemistry of a catalyzed reaction. We note that two of the three featured enzymes, TIM and AR, have similar folds, the α/β-barrel (or “TIM barrel”) structure, although they catalyze different chemical reactions. We note further that TIM and PMI catalyze the same kind of chemical reaction but have very different structures. These three proteins have no significant sequence identity; alignment scores obtained with the program CLUSTALW (ref. 22; http://www.ebi.ac.uk/clustalw) for the three possible pairings of the three sequences used herein were 9%, 6%, and 11% for TIM-AR, AR-PMI, and TIM-PMI, respectively. These values are considered unacceptable for identification of structure from sequence similarity.
TIM.
TIM (23–28) catalyzes the isomerization of d-glyceraldehyde 3-phosphate to dihydroxyacetone phosphate, a key reaction in the glycolytic pathway. Calculations on TIM from Gallus gallus (chicken) were performed by using the 1.80-Å resolution structure 1TPH (10, 23) of the TIM-phosphoglycolohydroxamate complex. Theoretical titration functions were obtained for the biologically active dimer from which the coordinates for the inhibitor were removed.
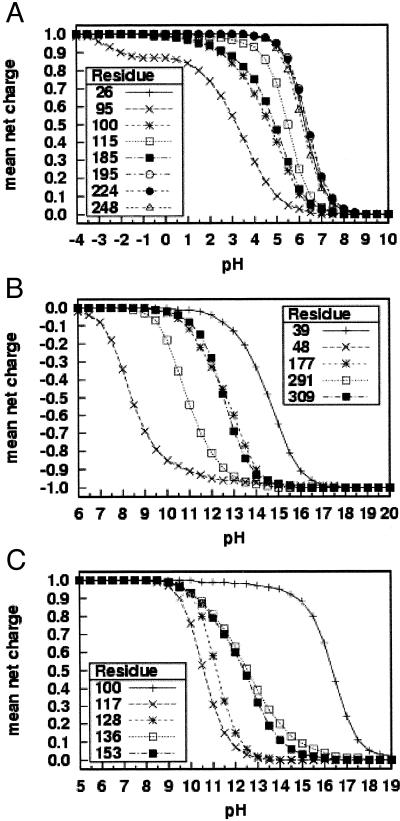
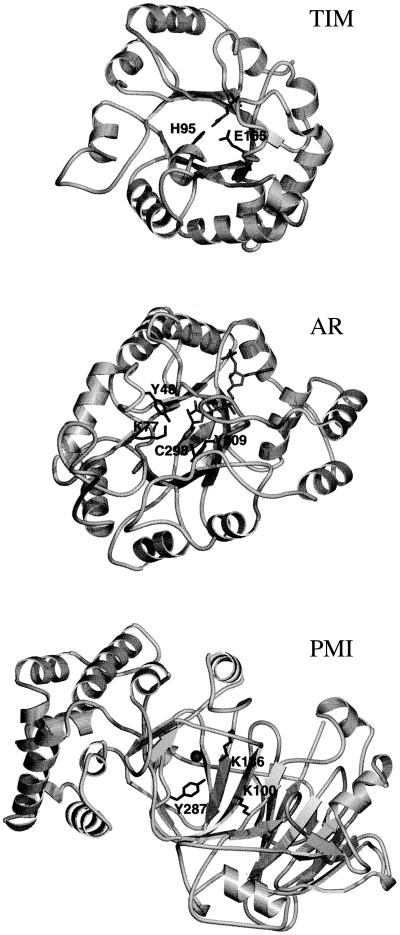
Our observations of the theoretical titration functions for all of the ionizable residues of TIM find that four residues have curves with highly perturbed shapes: His-95, Glu-165, Lys-112, and Tyr-164. Fig. 1A shows the predicted mean net charge as a function of pH for the eight histidine residues in the A chain. Predicted titration functions for the B chain (not shown) are similar to the A chain. Fig. 2a shows the location of His-95 and Glu-165 in the active site of TIM.
Figure 1.
Sample theoretical titration curves. Predicted mean net charge as a function of pH. (A) All of the histidine residues in the A chain of TIM: His-26 (+), His-95 (×), His-100 (✠), His-115 (□), His-185 (■), His-195 (○), His-224 (●), and His-248 (▵). (B) Selected tyrosine residues of AR: Tyr-39 (+), Tyr-48 (×), Tyr-177 (✠), Tyr-291 (□), and Tyr-309 (■). (C) Selected lysine residues of PMI: Lys-100 (+), Lys-117 (×), Lys-128 (✠), Lys-136 (□), and Lys-153 (■).
Figure 2.
Ribbon diagrams of the three protein structures. Backbone is shown in light gray; active-site residues with perturbed titration curves are shown in black and labeled. TIM, looking down the α/β barrel at the active site. Substrate analog is shown in medium gray. AR, looking down the α/β barrel at the active site. NADPH cofactor is shown in medium gray. PMI, looking down at the presumptive active site. Zinc ion is shown as a medium gray ball.
First, one notes that the theoretical titration functions for most of the histidine residues depicted in Fig. 1A have the typical shape. However we observe that His-95 has a strikingly different predicted titration function. Not only is the pKa of the conjugate acid downshifted to 3.2, but also the shape of the curve is perturbed; in particular, the curve for His-95 has a flat region where the mean net charge stays nearly constant over a few pH units (about pH −2.0 to +1.5).¶ Thus, His-95 is predicted to stay partially protonated over a wide pH range. This change in shape of the titration curve is the most significant difference between His-95 and the other His residues. The predicted mean net charge for His-95 is 0.10, 0.03, and 0.00 for pH 5.0, 6.0, and 7.0, respectively, consistent with experimental data, as discussed below. Similarly, the predicted titration curve for Glu-165 is different from the curves for the other glutamates. Again there is an unusual, nearly flat region in the curve (at about pH 1.0 to 4.0), and the residue is predicted to be partially protonated over an uncommonly wide pH range, with a downshifted pKa of −0.5.¶ A third residue, Lys-112, is found to have a flat region of partial protonation in the pH range 11–14, with an upshifted pKa of about 16.5¶ for its conjugate acid. A fourth residue, Tyr-164, is found to have a nearly flat region of partial ionization in the theoretical titration curve (at about pH 13.0–16.0). It is predicted to remain uncharged up to pH 13 with predicted charges of −0.01, −0.03, and −0.10 at pH 13.0, 15.0, and 17.0, respectively, and a calculated pKa of 18.2.¶ Thus, it is predicted to have an unusually high pKa. Furthermore, the shape of the predicted titration curve is noticeably different from the curves of the other tyrosine residues.
Three of the four residues with perturbed titration curves are in close spatial proximity: His-95, Glu-165, and Tyr-164. This region of physical space correlates with biochemical evidence for the location of the active site. Structural evidence suggests (23) that the two residues that are active in acid–base catalysis are Glu-165 and His-95. Earlier affinity-labeling experiments established the side chain of Glu-165 as the catalytic base (24–26). Spectroscopic evidence suggested that an electrophilic residue was involved in the catalysis (27) and the x-ray crystal structure revealed His-95 as the likely electrophile (23). 15N NMR spectra show that the imidazole ring of His-95 is substantially uncharged over the pH range 4.9–9.9, implying that the pKa is less than 4.5 (28). Our predicted mean net charges and calculated pKa of 3.2 for His-95 are consistent with the 15N NMR data. Tyr-164 is located right next to the active site. The x-ray crystal structure indicates that the side chain of Tyr-164 is pointing away from the precise location where the substrate is believed to bind (23), although this does not necessarily preclude involvement in catalysis. Lys-112 is physically well removed from the active site and is considered to be a “false positive.”
AR.
AR (29–31) is an NADPH-dependent enzyme that catalyzes the reduction of the aldehyde group in an aldose to the corresponding alcohol. Calculations were performed on the biologically active monomer. We used the 1.76-Å resolution x-ray crystal structure 2ACS (29) of human aldose reductase from the PDB (10). The structure 2ACS contains the nicotinamide cofactor and a citrate ion; the calculation was performed on the protein alone without the cofactor or ion. Fig. 2 a and b shows the relationship between the structures of TIM and AR.
The theoretical titration functions for AR reveal seven residues with unusual curves: Tyr-48, Cys-298, Glu-185, Lys-21, Lys-77, Tyr-107, and Tyr-209. Fig. 1B shows the predicted mean net charge as a function of pH for five selected tyrosine residues. (Tyrosine residues were selected to show typical curves that do not obscure the curve for Tyr-48.) Tyr-48 is predicted to have an extended region of partial protonation (i.e., noninteger mean net charge) in the pH range 12.5–17.5¶. The curve for Tyr-48 is nearly flat from about pH 12.0 to 15.0, with a long tail on the higher pH end that crosses over curves of residues with higher pKa. The pKa of Tyr-48 is calculated to be 8.4, a few pH units lower than the other tyrosine residues shown. The low pKa and the flat region at the higher pH side of the curve make Tyr-48 partially protonated over the remarkably wide pH range of 5.0 through 17.5. It is also observed that Cys-298 has a wider range of partial protonation than the other cysteine residues and a flat region in the pH range 14–16. Its calculated pKa of 10.2 is similar to that of most of the other cysteine residues in this protein, although a little higher than typically observed for a thiol group free in solution. The calculated titration curve for Glu-185 exhibits a nearly flat region in the pH range 0–3; the calculated pKa of −1.7¶ is significantly downshifted from the other glutamates. Calculated mean net charges for Glu-185 are −0.94, −0.97, −0.98, and −0.99 for pH 0.0, 1.0, 2.0, and 3.0, respectively. The titration curve for Lys-21 has a flat region of noninteger net charge in the pH range 8–11, with a predicted pKa of 13.4¶ for its conjugate acid. Lys-77 has an extended flat region of partial protonation in the pH range 9–17, with a heavily upshifted predicted pKa of 19.6¶ for the conjugate acid. The predicted curve for Tyr-107 exhibits a flat region in the pH range 11–15 with noninteger mean net charge; the pKa is predicted to be upshifted to 17.0¶. Finally, Tyr-209 was found to have an extended flat region of partial protonation in the pH range 9.5–15.5, with a very upshifted predicted pKa of 17.9¶. An eighth residue, His-110, has an extended region of partial protonation but we are not counting it for present purposes because the differences in its titration curve are not as apparent as they are for the seven residues discussed above.
Again, the majority of the residues with positive results are close in space and the active-site location indicated by the theoretical titration functions is consistent with biochemical data. The 1992 x-ray crystal structure at 1.65-Å resolution suggested that Tyr-48, His-110, and Cys-298 are the active-site residues (30). Site-directed mutagenesis experiments showed that the Y48F mutant has no activity and the H110Q and H110A mutants lose activity by 1 × 103- to 2 × 104-fold (31); thus, it was concluded that Tyr-48 is the proton donor and His-110 is involved in the catalysis. Ref. 31 also reports pH profiles of kinetic data and from them infers that the pKa of Tyr-48 in the wild-type enzyme is 8.4, with which our calculated value is in good agreement. Four of the seven residues with positive results, Tyr-48, Cys-298, Lys-77, and Tyr-209, were all identified as active-site residues from structural and biochemical data (30). Two more of the seven, Glu-185 and Lys-21, are located right next to active-site residues: Lys-21 is just behind active-site residue Trp-20 and also next to the cofactor; Glu-185 is located just behind active-site residues Tyr-209 and Cys-298. Tyr-107 is located behind active-site residue Lys-77, but is far enough away from the catalytic site that we consider it to be a “false positive.”
PMI.
PMI (32–35) catalyzes the reversible interconversion of mannose 6-phosphate and fructose 6-phosphate. PMI is a metal-dependent enzyme containing one atom of zinc per protein molecule. The 1.70-Å resolution x-ray crystal structure of 1PMI (32), the enzyme from Candida albicans, was used in the calculations here. The zinc ion was included in the calculation.
On examination of the theoretical titration functions for PMI, we find four residues with perturbed curves that possess a flat or nearly flat region: His-135, Lys-100, Lys-136, and Tyr-287. The titration curve for another residue, Glu-294, has an obviously perturbed curve in that its slope is considerably less steep than that of the other glutamates. It is predicted to be partially protonated over the very wide range of about pH −2.0 through 7.0 with a pKa of 2.5.¶ Specifically, it lacks a flat region of partial protonation but instead has an unusually shallow, nearly constant, slope over a wide pH range. For present purposes, we are interpreting the curves in conservative fashion and are excluding Glu-294 from the “positive” list.
Fig. 1C shows the predicted mean net charge as a function of pH for five selected‖ lysine residues in PMI. Lys-100 exhibits a flat region of noninteger mean net charge at about pH 11–14; its conjugate acid is predicted to have a high pKa of 16.4. Lys-136 has a more typical pKa (of 12.5 for the conjugate acid) but it has a tail on the high pH end of its titration curve, with a flat region at about pH 16.0–17.5.¶ Also, His-135 has a flat region of partial protonation in the pH range 1–4; its predicted pKa of 5.8 is a typical value for the conjugate acid of a histidine residue. Tyr-287 has a flat region of noninteger mean net charge in the pH range 14.5–17.0 and has a very unusually high pKa (>19).¶
The precise mechanism of action of PMI is not yet known. However, because it is a metalloenzyme and the metal ion is essential for activity (33), the active site is presumed to be located in an observed cleft near the zinc ion. The structural data of ref. 32, together with labeling studies (34), identify six ionizable active-site residues that are not involved in coordination of the zinc ion: Arg-304, Glu-48, Glu-294, Lys-100, Lys-136, and Tyr-287. Fig. 2c shows the structure and some of the presumed active-site residues for PMI. Experimental evidence supports a proton transfer mechanism by means of a cis ene–diol intermediate (35), rather than by a hydride shift as for xylose isomerase (36, 37).
Therefore, of the four residues with a positive result, all are in close proximity and three residues, Lys-100, Lys-136, and Tyr-287, are in the presumed active site. His-135 is located just behind the presumed active-site residue Lys-136.
Additional Examples.
The method has been used on a number of different enzymes to illustrate its breadth and utility. Table 1 shows some of these additional examples. The proteins in Table 1 represent a variety of different structure types. They act on different kinds of substrates with differing mechanisms. The PDB (10) ID, the protein name, and the chemistry type are given, followed by the list of residues for which a positive result is obtained. Residues in close proximity are listed together inside square brackets. The residues located in the known active site are shown in boldface. Second-shell residues are shown in italics.
Table 1.
Positive results for some additional examples
| PDB ID | Name | Chemistry | Residues with positive results |
|---|---|---|---|
| 1AMQ | Aspartate aminotransferase* | Transamination | [H189, Y225, K258, R266, C191, C192], [Y256], [Y295], [H301] |
| 1CSE | Subtilisin Carlsberg | Peptide hydrolysis (serine protease) | [D32, H64] |
| 1EA5 | Acetylcholinesterase | Ester hydrolysis | [Y130, E199, E327, H440, D392], [Y148], [H398], [H425] |
| 1HKA | 6–Hydroxymethyl–7,8–dihydropterin pyrophosphate kinase* | Kinase | [D97, H115] |
| 1OPY | 3-Keto-Δ5-steroid isomerase | Isomerase | [Y16, Y32, Y57], [C81] |
| 1PIP | Papain | Peptide hydrolysis (Cys protease) | [C25, H159], [K17, K174, Y186], [R59], [R96] |
| 1PSO | Pepsin | Peptide hydrolysis (acid protease) | [D32, D215, D303], [D11] |
| 1WBA | Winged bean albumin | Storage–no known chemistry | No positive results |
Positive results that form a cluster in coordinate space are shown in brackets. Active-site residues are shown in boldface. Second-shell residues are shown in italics.
Both 1AMQ and 1HKA are known to undergo conformational changes when the substrate binds. Calculations for both were run on the open (unbound) form. We note that the method still identifies the active site. K258 of 1AMQ is the residue that binds the cofactor. The calculation was run in the absence of cofactor.
We note first that 1WBA, winged bean albumin, a storage protein with no known catalytic function, yielded no positive results. This protein was used as a control to see whether a protein that is not known to have any catalytic function would yield any positive results. Indeed, no positive results were obtained. For six of the seven remaining proteins, the only cluster of two or more residues is the active site cluster. Thus, for six of the seven enzymes given in Table 1, the THEMATICS method identifies the location of the known active site from the cluster of positive results in coordinate space. Three of the enzymes listed (1CSE, 1PIP, and 1PSO) are peptide hydrolases and represent three different structure types and three different mechanisms. Papain, 1PIP, is unusual in that we find two clusters. The C25–H159 cluster is the known active site. There is another larger cluster of positive results, K17–K174–Y186; we are not aware of any particular function for this region of the enzyme. In this case, the THEMATICS method has narrowed down the active site location to one of two possibilities.
Summary and Discussion
A computational method that identifies the active site of a protein in the absence of biochemical data, derived only from a three-dimensional structure, is described. This method relies on the calculation of the theoretical microscopic titration curves. Traditionally, the experimental determination of the macroscopic pH dependence of kinetic data is used to obtain the pKa of candidate residues involved in the catalyzed reaction. Theoretical calculations of the type used in this work have been used extensively to predict the pKa values of residues and to explain experimentally observed perturbations in pKa. In a few cases, a small fraction of the theoretical titration curves have been reported to have perturbed shapes (18–21). We now establish that these shapes can be used as a diagnostic tool to determine the location of the active site.
For a given protein molecule, most of the positive results form a cluster in physical space around the site where enzymatic catalysis occurs. For each of the three featured protein molecules presented here, the THEMATICS method gives positive results for at least two active-site residues and most of the positive results are for active-site residues. Less often, positive results are obtained for a residue just outside the active site, which we have termed second-shell residues. Occasionally, we find an apparent false positive, a residue with a perturbed theoretical titration function that is not located near a known active site. However, the majority of positive results do cluster and do occur in the active site, such that its location can be identified with confidence. These trends hold true for a number of types of enzymes, including six of the seven additional examples of enzymes shown in Table 1.
For present purposes, we have defined a positive result as a theoretical titration function with a visibly perturbed shape that possesses a flat or nearly flat region of noninteger predicted charge. For TIM, our method yields four positive results. Two of the four (His-95 and Glu-165) are active-site residues known to be involved in catalysis. The residue yielding the third positive result, Tyr-164, is located right next to the active site, in what might be thought of as the second shell surrounding the reacting substrate. A fourth residue, Lys-112, is a false positive. We find seven positive results for AR: Tyr-48 is an active-site residue and is known to be involved in catalysis; Cys-298, Lys-77, and Tyr-209 are known active-site residues; and Glu-185 and Lys-21 are located just outside the active site, again in the second shell; Tyr-107 we consider to be a false positive. For PMI, we find four positive results: three residues (Lys-100, Lys-136, and Tyr-287) are located in the presumed active site; one (His-135) is in the second shell of the presumed active site. We note that the total number of ionizable residues equals 77 per chain for TIM, 103 for AR, and 134 for PMI. For these proteins, therefore, about 3–7% of the ionizable residues yield a positive result under the present definition.
Our calculated pKa value for His-95 of TIM is consistent with 15N NMR data (28). Our calculated pKa of 8.4 for Tyr-48 of AR is identical to the value reported in ref. 31. This excellent agreement may be fortuitous. All of the calculations reported here have been performed in the absence of cofactors and substrate mimics, to simulate conditions where a structure is built from genomic data and knowledge of the location or identity of such species in the protein structure may not be available. The presence of the NADPH cofactor in AR will cause some shifting of the pKa values of adjacent residues. It is also important to note that the presence of a substrate or substrate mimic can cause substantial shift in the calculated pKa of an adjacent residue; this type of behavior was reported recently for alanine racemase (38).
In addition to the perturbed curves that fit the present criteria for a positive result, we do sometimes see other types of perturbed curves, although the vast majority of residues have typical Henderson–Hasselbalch type curves. Other types of perturbed residues include curves that have no flat region with noninteger net charge but do possess either an inflection point or a slope that is significantly less steep than for other residues of the same type. Also, some active-site residues are predicted to have a strongly shifted pKa.
Our working hypothesis is that the pH-dependent electrical potential caused by ionizable residues (both near and further away) perturbs the substrate and the catalytically active residues, so that efficient and favorable proton transfer is enabled between them over the desired pH range. For an active-site residue involved in Brønsted acid–base chemistry, there is likely to be significant catalytic advantage afforded by the perturbed titration curves. For a simple, uncoupled acid dissociation reaction in the absence of any perturbing field, the species is expected to be protonated when the pH is less than the pKa and deprotonated when the pH is greater than the pKa; appreciable concentration of both the protonated and deprotonated forms occurs in a relatively narrow pH range. However, for a residue to be effective as a catalytic acid or base, it must be a strong enough acid or base and at the same time it must be in the proper protonation state. For instance, a Lys residue with a pKa of 12 and a typical titration curve will not be very useful as a base at pH 7 because it is expected to be fully protonated at that pH and, thus, unavailable to act as a base. The perturbed titration curves, in which a residue remains partially protonated over a wide pH range, can affect exactly the right combination of chemical properties needed. To put it another way, a facile acid–base reaction requires a match between the pKa values of the donor and acceptor. For more typical titration curves, this is difficult to achieve because of the very steep slope in the region of the pKa. For perturbed titration curves where noninteger net charge persists over a wide pH range, a less precise match is needed and, thus, it is easier to achieve this desired match. Furthermore, catalytic acids and bases in enzyme systems often must be amphoteric because they transfer the proton from one atom to another on the substrate molecule. (This is probably true, for instance, in the isomerization reactions catalyzed by TIM and PMI.) The perturbed titration curves in which partial protonation persists over a wide pH range enable amphoteric behavior over a wider pH range. We suggest that these are the reasons why the catalytically active residues exhibit perturbed titration functions where noninteger net charge is preserved over a wide pH range.
We have obtained a few positive results for residues that are presumed to be just outside the active site, in what we have called the second shell. These residues are Tyr-164 in TIM, Glu-185 and Lys-21 in AR, and His-135 in PMI. We are uncertain at this time whether these residues have perturbed titration functions because they actually participate in catalysis, or because they are simply physically very close to the area where catalysis occurs. In the latter case, they would presumably be subject to the same pH-dependent potentials as the species that are engaged in catalysis. We note that three of four of these residues are conserved. For each of the three proteins, a search was performed to find proteins of similar sequence by using the program WU-BLAST2 (ref. 39 and http://blast.wustl.edu). Tyr-164 in TIM and His-135 in PMI are conserved across a range of species.** Glu-185 in human AR is conserved over a number of human enzymes with some sequence identity.‡‡ This observed conservation lends some support to the notion that these residues do play functional roles, either in catalytic efficiency or in the stabilization of the protein fold.
The question why there are sometimes apparent false positive results is intriguing. One possible explanation is that proteins simply have strong electric fields and that occasionally these pH-dependent fields, arising either from long-range forces or from a strongly coupled neighbor, will just happen to cause perturbations in the titration functions that resemble those of catalytic residues. Another possible explanation is that these residues actually do have some chemical function that has not yet been established. A third possibility is that these residues are a part of a vestigial (or incipient) active site that had (or will have) a function for some past (or future) species. A fourth possibility is that they are artifacts related to the quality of the input atomic coordinates. Namely, the interpretation of the electron density maps in a region of some disorder may position residues inaccurately.
Parts of these theoretical titration functions are hypothetical, in the sense that the protein structure often is not preserved at extreme values of pH. However, it is useful to look at the wide pH range as we have done here because we are using the curves as a diagnostic tool to observe where the unusual pH dependence might occur. Indeed, one advantage of a computational approach is that one can study pH-dependent effects that could not be realized experimentally. For instance, the absence of cofactors and substrates can cause titration curves to shift such that the pKa of a residue might be in an accessible pH range when cofactors and/or substrate is/are present, but shifted to an extreme value for the free enzyme. Hence, it is useful to examine theoretical titration functions over a wide pH range.
One of the advantages of the present method is its simplicity. It is computationally fast, is not database-dependent, and is amenable to automation for high-volume computational screening. This method requires only the structure of the subject protein and, thus, complements the database-dependent approaches. With the number of protein structures of unknown function beginning to emerge from genome sequence data, our method effects the first step in the determination of function, in that it identifies the active site. Theoretical titration functions thus supply valuable information in the exciting quest to understand protein function and to translate genomic information into useful form.
Acknowledgments
M.J.O. is grateful to Prof. G. A. Petsko and the Rosenstiel Basic Medical Sciences Research Center for hosting her sabbatical leave. This work was supported by National Science Foundation Grants MCB-0074574 and CHE-9974642 (to M.J.O.), a grant from Children's Hospital (to J.G.C.), and in part by a grant from the Lucille P. Markey Charitable Trust.
Abbreviations
- THEMATICS
theoretical microscopic titration curves
- TIM
triosephosphate isomerase
- AR
aldose reductase
- PMI
phosphomannose isomerase
- PDB
Protein Data Bank
Footnotes
Theoretical titration functions are reported over a wide pH range, one that exceeds the range of stability of most protein structures. These functions are a diagnostic tool; we do not mean to imply that these extremes of pH could actually be achieved.
Residues were selected to show some with typical curves (Lys-117 and Lys-128), one with a slightly perturbed slope (Lys-153), and the two curves with unusual shapes (Lys-100 and Lys-136).
A clustalw (20) alignment was run for TIM sequences from chicken, human, mouse, Drosophila melanogaster, Zea mays (maize), and Emericella nidulans (a mold). His-95, Tyr-164, and Glu-165 are conserved in TIM from all of these species. A clustalw (20) alignment was run for PMI sequences from Candida albicans, human, Saccharomyces cerevisiae, E. nidulans, and Salmonella typhimurium. Lys-100, His-135, Lys-136, and Tyr-287 are conserved across all of these species.
A clustalw (20) alignment was run for sequences of the human enzymes AR, bile acid binding protein, chlordecone reductase, 3-oxo-5β-steroid reductase, and aldehyde reductase. Tyr-48, Glu-185, Lys-77, and Tyr-107 are conserved across these enzymes. Cys-298 and Lys-21 are not conserved. Tyr-209 is conserved across all of the proteins except chlordecone reductase, where it is replaced by a His.
References
- 1.Birney E, Bateman A, Clamp M E, Hubbard T J. Nature (London) 2001;409:827–828. doi: 10.1038/35057004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wallace A C, Birkakoti N, Thornton J M. Protein Sci. 1997;6:2308–2323. doi: 10.1002/pro.5560061104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fetrow J S, Skolnick J. J Mol Biol. 1998;281:949–968. doi: 10.1006/jmbi.1998.1993. [DOI] [PubMed] [Google Scholar]
- 4.Babbitt, P. C. & Klein, T. E. (1998) in Encyclopedia of Computational Chemistry, ed. Schleyer, P. v. R. (Wiley, Chichester, U.K.), pp. 2859–2870.
- 5.Fetrow J S, Siew N, Skolnick J. FASEB J. 1999;13:1866–1874. doi: 10.1096/fasebj.13.13.1866. [DOI] [PubMed] [Google Scholar]
- 6.Hegyi H, Gerstein M. J Mol Biol. 1999;288:147–164. doi: 10.1006/jmbi.1999.2661. [DOI] [PubMed] [Google Scholar]
- 7.Skolnick J, Fetrow J S. Trends Biotechnol. 2000;18:34–39. doi: 10.1016/s0167-7799(99)01398-0. [DOI] [PubMed] [Google Scholar]
- 8.Fetrow J S, Siew N, DiGennaro J A, Martinez-Yamout M, Dyson H J, Skolnick J. Protein Sci. 2001;10:1005–1014. doi: 10.1110/ps.49201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Oshiro C M, Kuntz I D, Knegtel R M A. In: Encyclopedia of Computational Chemistry. Schleyer P, editor. 1998. v. R. (Wiley, Chichester, U.K.), pp. 1606–1613. [Google Scholar]
- 10.Berman H M, Westbrook J, Feng Z, Gilliland G, Bhat T N, Weissig H, Shindyalov I N, Bourne P E. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Waugh A, Williams G A, Wei L, Altman R B. Pac Symp Biocomput. 2001;1:360–371. doi: 10.1142/9789814447362_0035. [DOI] [PubMed] [Google Scholar]
- 12.Yang A-S, Gunner M R, Sampogna R, Sharp K, Honig B. Proteins Struct Funct Genet. 1993;15:252–265. doi: 10.1002/prot.340150304. [DOI] [PubMed] [Google Scholar]
- 13.Bashford D, Karplus M. J Phys Chem. 1991;95:9556–9561. [Google Scholar]
- 14.Warwicker J, Watson H C. J. Mol. Biol. 1982. 157671–157679. [DOI] [PubMed] [Google Scholar]
- 15.Antosiewicz J, Briggs J M, Elcock A H, Gilson M K, McCammon J A. J Comp Chem. 1996;17:1633–1644. [Google Scholar]
- 16.Madura J D, Briggs J M, Wade R C, Davis M E, Luty B A, Ilin A, Antosiewicz J, Gilson M K, Bagheri B, Scott L R, McCammon J A. Comput Phys Commun. 1995;91:57–95. [Google Scholar]
- 17.Gilson M K. Proteins Struct Funct Genet. 1993;15:266–282. doi: 10.1002/prot.340150305. [DOI] [PubMed] [Google Scholar]
- 18.Bashford D, Gerwert K. J Mol Biol. 1992;224:473–486. doi: 10.1016/0022-2836(92)91009-e. [DOI] [PubMed] [Google Scholar]
- 19.Sampogna R V, Honig B. Biophys J. 1994;66:1341–1352. doi: 10.1016/S0006-3495(94)80925-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Beroza P, Fredkin D R, Okamura M Y, Feher G. Biophys J. 1995;68:2233–2250. doi: 10.1016/S0006-3495(95)80406-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Carlson H A, Briggs J M, McCammon J A. J Med Chem. 1999;42:109–117. doi: 10.1021/jm980351c. [DOI] [PubMed] [Google Scholar]
- 22.Thompson J D, Higgins D G, Gibson T J. Nucleic Acids Res. 1997;22:4673–4680. doi: 10.1093/nar/22.22.4673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhang Z, Sugio S, Komives E A, Liu K D, Knowles J R, Petsko G A, Ringe D. Biochemistry. 1994;33:2830–2837. doi: 10.1021/bi00176a012. [DOI] [PubMed] [Google Scholar]
- 24.Coulson A F W, Knowles J R, Priddle J D, Offord R E. Nature (London) 1970;227:180–181. doi: 10.1038/227180a0. [DOI] [PubMed] [Google Scholar]
- 25.Waley S G, Miller J C, Rose I A, O'Connell E L. Nature (London) 1970;227:181. doi: 10.1038/227181a0. [DOI] [PubMed] [Google Scholar]
- 26.Hartman F C. Biochem Biophys Res Commun. 1970;39:384–388. doi: 10.1016/0006-291x(70)90588-7. [DOI] [PubMed] [Google Scholar]
- 27.Komives E A, Chang L C, Lolis E, Tilton R F, Petsko G A, Knowles J R. Biochemistry. 1991;30:3011–3019. doi: 10.1021/bi00226a005. [DOI] [PubMed] [Google Scholar]
- 28.Lodi P J, Knowles J R. Biochemistry. 1991;30:6948–6956. doi: 10.1021/bi00242a020. [DOI] [PubMed] [Google Scholar]
- 29.Harrison D H, Bohren K M, Ringe D, Petsko G A, Gabbay K H. Biochemistry. 1994;33:2011–2020. doi: 10.1021/bi00174a006. [DOI] [PubMed] [Google Scholar]
- 30.Wilson D K, Bohren K M, Gabbay K H, Quiocho F A. Science. 1992;257:81–84. doi: 10.1126/science.1621098. [DOI] [PubMed] [Google Scholar]
- 31.Bohren K M, Grimshaw C E, Lai C-J, Harrison D H, Ringe D, Petsko G A, Gabbay K H. Biochemistry. 1994;33:2021–2032. doi: 10.1021/bi00174a007. [DOI] [PubMed] [Google Scholar]
- 32.Cleasby A, Wonacott A, Skarzynski T, Hubbard R E, Davies G J, Proudfoot A E I, Bernard A R, Payton M A, Wells T N C. Nat Struct Biol. 1996;3:470–479. doi: 10.1038/nsb0596-470. [DOI] [PubMed] [Google Scholar]
- 33.Gracy R W, Noltmann E A. J Biol Chem. 1968;243:3161–3168. [PubMed] [Google Scholar]
- 34.Wells T N C, Scully P, Magnenat E. Biochemistry. 1994;33:5777–5782. doi: 10.1021/bi00185a015. [DOI] [PubMed] [Google Scholar]
- 35.Malaisse-Lagae F, Liemans V, Yaylali B, Sener A, Malaisse W J. Biochim Biophys Acta. 1989;998:118–125. doi: 10.1016/0167-4838(89)90262-8. [DOI] [PubMed] [Google Scholar]
- 36.Lavie A, Allen K N, Petsko G A, Ringe D. Biochemistry. 1994;33:5469–5480. doi: 10.1021/bi00184a016. [DOI] [PubMed] [Google Scholar]
- 37.Carrell H L, Hoier H, Glusker J P. Acta Crystallogr D. 1994;50:5469–5480. doi: 10.1107/S0907444993009345. [DOI] [PubMed] [Google Scholar]
- 38.Ondrechen M J, Briggs J M, McCammon J A. J Am Chem Soc. 2001;123:2830–2834. doi: 10.1021/ja0029679. [DOI] [PubMed] [Google Scholar]
- 39.Gish W, States D J. Nat Genet. 1993;3:266–272. doi: 10.1038/ng0393-266. [DOI] [PubMed] [Google Scholar]