Abstract
We report the observation and analysis of the gain curve of amplified Kα x-ray emission from solutions of Mn(II) and Mn(VII) complexes using an x-ray free electron laser to create the 1s core-hole population inversion. We find spectra at amplification levels extending over 4 orders of magnitude until saturation. We observe bandwidths below the Mn 1s core-hole lifetime broadening in the onset of the stimulated emission. In the exponential amplification regime the resolution corrected spectral width of ~1.7 eV FWHM is constant over 3 orders of magnitude, pointing to the buildup of transform limited pulses of ~1 fs duration. Driving the amplification into saturation leads to broadening and a shift of the line. Importantly, the chemical sensitivity of the stimulated x-ray emission to the Mn oxidation state is preserved at power densities of ~1020 W/cm2 for the incoming x-ray pulses. Differences in signal sensitivity and spectral information compared to conventional (spontaneous) x-ray emission spectroscopy are discussed. Our findings build a baseline for nonlinear x-ray spectroscopy for a wide range of transition metal complexes in inorganic chemistry, catalysis, and materials science.
X-ray free-electron (XFEL) sources [1,2] provide x-ray pulses of femtosecond and potentially attosecond duration [3] of unprecedented high intensities [4] and could become game changers for x-ray spectroscopy applications. Current experiments are using primarily the linear interaction of matter with the x-ray pulses taking advantage of their ultrashort duration [5,6]. However, given the ultrahigh intensities that can be obtained when focusing these pulses, nonlinear x-ray matter interaction can also occur [7–11]. An exciting future perspective is the transfer of nonlinear spectroscopy from the optical to the x-ray spectral region [12–15]. Here, one can envision tuning two or more x-ray pulses to inner-shell ionization edges or resonances of particular atomic constituents in the sample, creating an element sensitive, local probe. Phase matching geometries in such setups could result in directed, background free emission of a nonlinear signal, encoding a particular component of the nonlinear polarization of the system under study. Moreover, nonlinear spectroscopy may provide a way to differentiate between inhomogeneous and homogeneous line broadening [16], and metal centers could be sensitively probed by such techniques in a coherent manner to unravel long-range charge and energy transfer processes [17,18]. In particular 3d transition metals play a critical role in many of these processes and are also at the heart of many catalytic reaction centers. While these experimental techniques are currently still out of reach, our work presented here is a first step towards the spectroscopic use of nonlinear x-ray methods for the chemical analysis of 3d transition metal systems.
As a conventional (linear) x-ray probe of 3d transition metals, core-to-core x-ray emission spectroscopy (XES) after 1s ionization, such as 2p → 1s (Kα) and 3p → 1s (Kβ), encode the effective oxidation and spin state [19,20], resulting in characteristic shifts (“chemical shifts”) of the emission spectra. XES has been successfully applied to characterize the electronic and geometric structure of 3d transition metal complexes [21,22] and expanding XES into the nonlinear regime will further enhance our understanding of these systems. Two of the basic phenomena of nonlinear x-ray spectroscopy are amplified spontaneous emission and impulsive stimulated x-ray scattering. Both have been demonstrated in atomic gases resulting in a directed emission of the x-ray signal in a laserlike beam and coherent amplification factors of up to 108 [23,24]. The onset of amplified spontaneous emission was recently observed in the condensed phase in the VUV regime [25] (amplification factors of 2) and hard x-ray regime [13] (amplification factors of 10). These proof-of-principle experiments aimed for first demonstration of these stimulated x-ray emission effects, but did not focus on spectroscopy aspects. Here, we present the observation of amplified spontaneous Kα emission of Mn compounds in aqueous solution and the quantitative study of its gain curve and spectroscopic features. Throughout the Letter we refer to this phenomenon simply as stimulated x-ray emission or stimulated emission.
Stimulated x-ray emission requires very bright x-ray pump pulses, which at present are based on self-amplified spontaneous emission (SASE) XFEL sources [1,2]. The stochastic SASE process produces a sequence of spikes of highly fluctuating intensity, both in the spectral and temporal domain. This results in pulses of limited temporal coherence, thus impeding the experimental control and analysis. To measure stimulated emission driven by a stochastic source, high gain and optically dense samples are necessary [26,27]. In order to become a valuable spectroscopic technique, the spectral evolution at these high gain conditions have to be understood and examined. One of the central question is if valuable chemical information remains preserved at these extreme x-ray pump intensities. This has motivated our study of stimulated Kα x-ray emission from two chemically distinct Mn compounds in aqueous solutions, Mn(II)Cl2 and NaMn(VII)O4.
Experiments were performed at the Coherent X-ray Imaging (CXI) instrument [28] at the Linac Coherent Light Source (LCLS) at the SLAC National Accelerator Laboratory [1]. The experimental setup is sketched in Fig. 1(a). The 10–30 fs long incoming x-ray pulses were tuned to a photon energy of 6.6 keV. They were focused onto a liquid jet with a thickness of 200 μm at the beam interaction with an estimated spot size of ~150 nm diameter [29]. The stimulated x-ray emission spectra were analyzed using Bragg reflections from flat Si crystals and a position sensitive 2d detector [30]. Spontaneous XES spectra of the 5M MnCl2 and 4M NaMnO4 solution samples were recorded at the Stanford Synchrotron Radiation Lightsource (SSRL) at beam line 6-2 [31]. Theoretical spontaneous XES spectra were obtained using charge transfer multiplet calculations [32–35]. Details are given in the Supplemental Material [36].
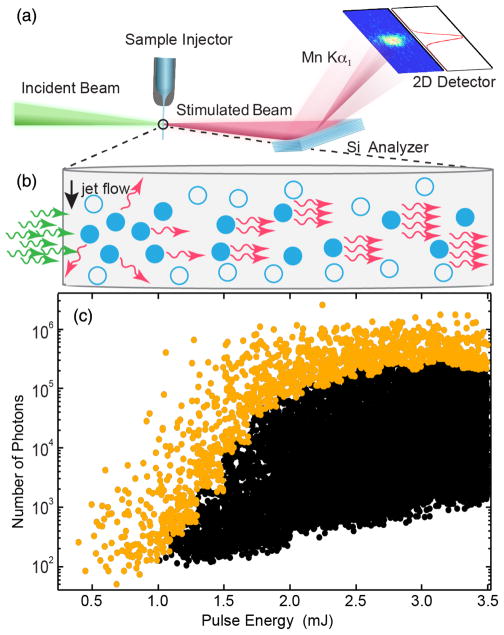
FIG. 1.
(a) Experimental setup. The incoming XFEL pulses are focused onto the liquid jet. The simulated x-ray emission is detected using a flat analyzer crystal and a position sensitive 2d detector. (b) Sketch of stimulated x-ray emission. The arrows represent incoming (green) and emitted (red) photons, while the circles indicate the excited (filled) and nonexcited (open) Mn ions respectively. (c) Detected number of photons in the Mn Kα1 region (5 eV integration window) as a function of the nominal incoming XFEL pulse energy for the 5M MnCl2 solution. The actual pulse energy on target is ~20% of the nominal pulse energy shown in the figure. The 50 strongest shots in each 0.1 mJ interval are shown in orange, all other shots in black.
We create stimulated x-ray emission by photoionization of inner-shell electrons [37] in a quasi gain-swept geometry [38–40]. Specifically, the x-ray beam generates a short-lived core-excited state 1s12p63dn (n=5 for MnCl2, n = 0 for NaMnO4) leading to a population inversion inside a volume created by the incident XFEL pulse [filled circles in Fig. 1(b)]. Part of these excited ions decay spontaneously to a 1s22p53dn final state configuration, isotropically emitting Kα fluorescence. Spontaneously emitted photons propagating in the forward direction along with the XFEL pulse can stimulate emission along the inverted medium. This results in exponential amplification of the initial fluorescence photons and generates an intense self-seeded stimulated emission pulse in the forward direction, as sketched out in Fig. 1(b) [41]. This is shown in Fig. 1(c), where we plot the measured stimulated Kα emission yield per shot versus the incident pulse energy on a logarithmic scale, after filtering the signal with the Si analyzer. An exponential increase of the maximum intensity is observed until ~2 mJ, after which the signal saturates with a maximal number of 106 measured photons in a single shot, corresponding to 4 × 107 generated photons according to the 2.5% efficiency of our analyzer. The gain curve shows strong variations in the stimulated emission strength extending over several orders of magnitude for a given XFEL pulse energy (see discussion below). To illustrate the gain curve limit, the top 50 strongest shots in each 0.1 mJ interval are shown in orange.
We find an onset of saturation of the experimental gain curve (bending of the curve) at 2 × 105 detected photons. Taking into account the 2.5% analyzer efficiency, an estimated source diameter of 150 nm and a stimulated emission pulse duration of ~1 fs, this measured photon output at saturation corresponds to a saturation intensity of ~4 × 1016 W/cm2. This experimental value of the saturation intensity can be compared to a simple gain model of transient x-ray lasers [42], for which the saturation intensity is determined by equating the stimulated emission rate with the decay rate (Auger and fluorescence rate) of the core-excited state. In our case, the decay width of the core hole excited state is 1.16 eV and the Kα width of 1.48 eV [43]. Using these values to calculate the stimulated emission cross section we find a saturation intensity of ~1017 W/cm2. Given the simplicity of the model this is value is reasonably close to our experimentally observed value of ~4 × 1016 W/cm2. The strongest recorded shot was measured at an XFEL pulse energy of 2.4 mJ, for which 2 × 106 photons were detected. Correcting for the ~2.5% analyzer efficiency, this translates to ~8 × 107 photons emitted by stimulated emission. To estimate the amplification factor over spontaneous emission we attenuated the incoming beam to 8% to avoid stimulated emission and measured the spontaneous emission for 30 min. We observed a signal rate of 0.08 photons/pulse for the Kα1 spectrum, which, correcting for this attenuation, corresponds to ~1 photon per pulse. Comparing this number to the strongest measured stimulated emission shot corresponds to an amplification factor of ~2 × 106 (as both measurements used the same ~2.5% efficient analyzer). Our amplification gain findings go well beyond previous data [13], which showed the onset of stimulated emission in Cu foils with a gain of approximately 1 order of magnitude.
There are several contributions that cause the strong variations observed in the stimulated emission intensity [Fig. 1(c)]. One of them comes from the stochastic nature of the stimulated emission process. Additional contributions are caused by the inherent shot-to-shot SASE fluctuations and the pointing instability of the XFEL onto the beam transport and focusing optics. There might also be some fluctuations of the sample thickness caused by incomplete reformation of the jet after being disrupted in the previous pulse. Furthermore, each SASE XFEL pulse consists of a temporal series of coherent spikes of random intensity with essentially 100% fluctuation [44]. This stochastic temporal intensity profile of the pulse creates different gain conditions in the sample, even when the overall peak power of the pulse does not change.
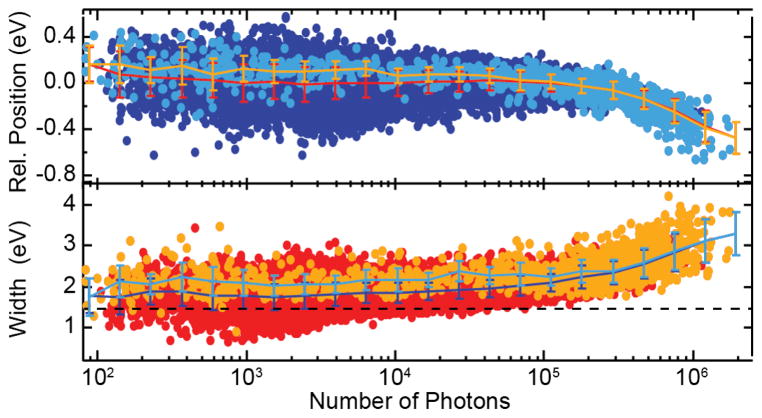
The relative peak position and width (FWHM) of the emission line as a function of the emitted number of photons for the individual shots are shown in Fig. 2. The gain and the emission width depend on the exact SASE pulse property of the pump field for a fixed gain-length product, i.e., the exponential amplification factor. Consequently, similar to the observed scatter of intensities shown in Fig. 1(c), the width of the stimulated emission spectrum for a particular number of output photons shows a strong pulse-to-pulse fluctuation.
FIG. 2.
Relative position (top) and width (bottom) of the stimulated XES peak as a function of the number of detected photons in the emission line. The bright colors represent the selected shots given in yellow in Fig. 1(c). Both position and width are constant within error bars up to a peak intensity of ~2 × 105 detected emission photons per shot, before they get broader and shift towards lower emission energies. The dashed line represents the natural lifetime broadening of 1.48 eV.
The mean value of the peak width as a function of photon number shows an essentially constant line width of 1.9 ± 0.25 eV FWHM extending over the exponential region covering 3 orders of magnitude up to 2 × 105 detected photons (Fig. 2, bottom). Note that this observed Kα1 line width is much narrower than that of spontaneous emission. To understand this difference, we first describe the contributions to the spontaneous XES spectrum of MnCl2 shown in Fig. 3(b). The calculation shows that it consists of multiple final states that contribute to its width of 3.5 eV FWHM. In contrast, in the exponential region of stimulated emission, the strongest emission channel, i.e., the transition to a particular final state with the highest oscillator strength in the spontaneous spectrum, is most likely to be amplified first. This results in an inherent narrowing of the XES spectrum in the exponential regime.
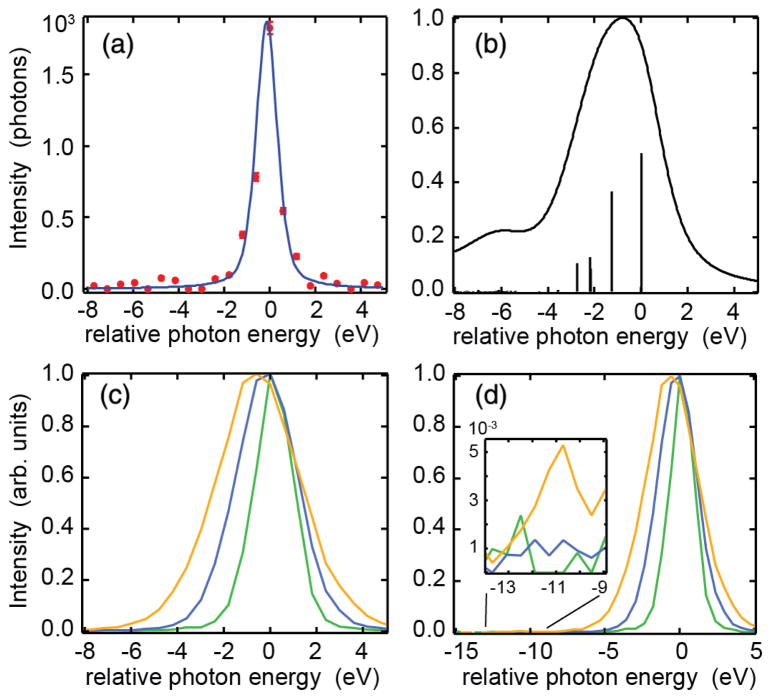
FIG. 3.
Line shapes of MnCl2 solution. (a) Single shot spectrum together with a pseudo-Voigt fit with FWHM = 0.8 eV (Gaussian) and 0.5 eV (Lorentzian). (b) Multiplet simulation of the MnCl2 Kα1 line, the vertical sticks represent the intensities at the corresponding final state energies. (c) Single shot spectra normalized to maximum with increasing intensity and increasing peak width FWHM = 2.0 (green), 3.1 (blue), and 4.2 eV (yellow), respectively. (d) The same as (c), but for a wider energy range that also includes the Kα2 region. The inset shows an enlargement to the Kα2 region with only the widest line carrying intensity.
Transient amplification schemes, i.e., amplifiers with a rapid gain decay are known to manifest the buildup of transform limited pulses, which has been shown in the quantum treatment of an ideal gain-swept laser by Hopf and Meystre [45]. In a semiclassical treatment of stimulated x-ray emission for a simple two level atomic system [46], it has been numerically demonstrated that the amplification starts with gain narrowing both in the temporal and spectral domain in the first 1–2 gain lengths. After that, transform limited pulses are created that amplify with almost constant pulse profile, until saturation sets in. Therefore, our observation of a constant emission line width over 3 orders of magnitude of amplification (Fig. 2, bottom) points to the buildup of transform limited pulses. The line width of 1.9 eV FWHM includes 0.8 eV instrumental resolution (FWHM). For a Gaussian line profile the real width is therefore ~1.7 eV FWHM, translating into a pulse duration of ~1 fs FWHM. Importantly, we also observe spectral widths below the 1.48 eV natural Kα lifetime broadening [43] at low peak intensities (Fig. 2, bottom), pointing to initial strong gain narrowing at the onset of the exponential region [46]. The narrowest spectrum of stimulated Kα1 XES with a bandwidth of 0.95 eV FWHM is shown in Fig. 3(a), where we fit the data with a pseudo-Voigt with FWHM = 0.8 (Gaussian) and 0.5 eV (Lorentzian) for the experimental resolution and the lifetime broadening, respectively. Note that previously line widths below the natural lifetime at the onset of the exponential region were only observed by using a second color to seed the amplification [13].
Broadening beyond 1.9 eV and a shift towards lower emission energies can be seen for > 2 × 105 detected photons (Fig. 2), corresponding to the saturated gain region in Fig. 1(c). Here, amplification of additional final state intensities occurs leading to a broadening and shift towards lower emission energies, because all the weaker multiplet transitions occur at lower energies [Figs. 3(b), 3(c)]. An analogous effect of enhancement of the strongest final-state component and a shift and broadening of the strongest emission line has been predicted previously for vibrational modes [47] in small organic molecules. This interpretation of our observed broadening and shift due to the turning on of additional final states is also supported when comparing Kα1 and Kα2 emission strengths: In spontaneous emission, the integrated Kα2 intensity is approximately half of that of Kα1, while it is several orders of magnitude weaker in the exponential region of stimulated emission [see Figs. 4 and 3(d)]. It gains strength only after saturation of Kα1 has been reached [Fig. 3(d)]. A similar observation has been found previously [13]. Our observed initial spectral sharpening, the buildup of bandwidth limited pulses in the exponential gain region, as well as the sequential onset of additional transitions after saturation of the strongest lines (broadening and shift) are unique features of stimulated XES. Note that in the saturation regime, strong-field effects also become increasingly prominent. These can include power broadening and the buildup of spectral side bands due to Rabi flopping [45,46]. We provide a simple 3-level (1 s−1 and states) atomic model for Mn in the supporting information, extending previous work [46]. These calculations give a qualitative explanation of the key features of our experimental findings.
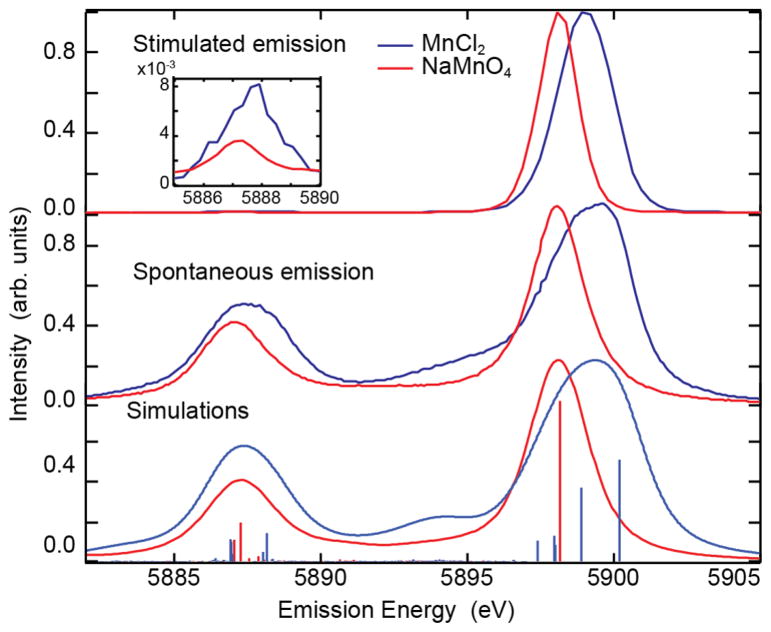
FIG. 4.
Comparison of the averaged stimulated emission spectra of 5M MnCl2 (3773 spectra) and 4M NaMnO4 (3569 spectra) in the lower exponential region (top), and the spontaneous XES spectra taken at SSRL (middle). Note that the presence of a very weak Kα2, as shown in the inset, is indicative of weak stimulated XES for these emission channels, far from the saturation regime. Simulations of the spontaneous emission spectra including transitions lines shown as vertical sticks are given in the bottom figure.
To apply stimulated XES for electronic structure analysis, it is critical that its chemical sensitivity is preserved. To address this question, we compare spectra from two systems as shown in Fig. 4. In the top panel, stimulated XES spectra in the exponential region of formally 3d5 high spin MnCl2 and 3d0 NaMnO4 are shown. The spectra were obtained by averaging a number of single shot spectra in the lower exponential region. Comparing the stimulated emission spectra with those from spontaneous emission (middle panel), shows that the stimulated emission spectra are narrower due to gain narrowing and a selection of a subset of transition lines. In addition, a shift in energy of approximately 1.0 eV between NaMnO4 and MnCl2 is observed. This trend agrees with shifts of Mn(VII) and Mn(II) compounds reported in literature [48], as well as with the spontaneous XES data taken at the synchrotron [see Fig. 4 (middle)] and theoretical simulations (bottom).
The figure also shows a lack of Kα2 intensity in the stimulated XES spectra, as discussed above. However, since the spectra shown in Fig. 4 were recorded in the lower exponential region, a weak Kα2 signal is still present (see inset). The observed Kα2 energy shift between NaMnO4 and MnCl2 is smaller than that of the Kα1 emission (0.6 vs 1.0 eV, respectively), which is similar to spontaneous XES. This result is a further indication that the sensitivity to the electronic structure is preserved in stimulated XES despite the very high XFEL pump intensities used.
Yet, it should be noted that the Kα1 energy shifts between NaMnO4 and MnCl2 for the stimulated and spontaneous XES spectra are slightly different (see Fig. 4). One possible reason for this difference lies in the fact, that for MnCl2 several multiplet lines (see Figs. 3 and 4) fall within the natural line width of the common upper lasing state. This couples their oscillator strengths and can lead to a shift compared to their natural resonances (see theoretical discussion in the Supplementary Material [36]). Another possible reason is the ill-defined spatial beam profile in focus. While emission signals along the highest intensity parts of the spatial profile are saturated, showing the strong shift to lower energy, other contributions of lower pump intensity are not saturated. A total average over the focus profile could thus lead to a shift. For a quantitative prediction of this shift, an extended theoretical study is necessary. This is beyond the simple one dimensional gain propagation model presented in the Supplementary Material [36] and would include treatment of polarization, angular momentum projection of the involved multiplet lines and more accurate calculations of the transition dipoles. Other possible explanations include phenomena such as Auger, ionization, and other strong field effects that could, in principle, lead to a shift mainly for MnCl2 due to its 3d5 electronic configuration. A similar hypothesis for the shift in emission in the Cu experiment upon ionization of 3d electrons was provided previously [13].
To enhance the chemical sensitivity of stimulated XES one can envision using a narrow-band second color beam that co-propagates with the excitation pulse [49] to out compete the stimulated emission from the strongest channel and selectively amplify weaker multiplet regions that are more chemically sensitive. This, as well as better beam diagnostics and a better theoretical understanding of nonlinear and saturation effects, will help to further disentangle the different spectral contributions and thereby strengthen this new approach.
Acknowledgments
Use of the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program (T. K.) is supported by the DOE Office of Biological and Environmental Research, and by the National Institutes of Health, National Institute of General Medical Sciences (including P41GM103393). The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official views of NIGMS or NIH. A part of this work was supported by the Director, Office of Science, Office of Basic Energy Sciences (OBES), Division of Chemical Sciences, Geosciences, and Biosciences (CSGB) of the Department of Energy (DOE) (Contract No. DE-AC02-05CH11231, J. Y. and V. K. Y.), National Institutes of Health (NIH) Grants No. GM055302 (V. K. Y.), No. GM110501 (J. Y.), the Ruth L. Kirschstein National Research Service Award (F32GM116423, F. D. F.), and the Human Frontiers Science Project Award No. RGP0063/2013 310 (T. F., J. Y., U. B.) and the Department of Energy, Laboratory Directed Research and Development program at SLAC National Accelerator Laboratory, under Contract No. DE-AC02-76SF00515 (U. B., Y. Z.). We would like to thank Matt Hayes and the CXI technical staff for experimental support and Gregory Stewart for visual art.
References
- 1.Emma P, et al. Nat Photonics. 2010;4:641. [Google Scholar]
- 2.Ishikawa T, et al. Nat Photonics. 2012;6:540. [Google Scholar]
- 3.Huang S, Ding Y, Huang Z, Marcus G. Phys Rev Accel Beams. 2016;19:080702. [Google Scholar]
- 4.Guetg MW, Lutman AA, Ding TJ, Maxwell Y, Decker FJ, Bergmann U, Huang Z. Phys Rev Lett. 2018;120:014801. doi: 10.1103/PhysRevLett.120.014801. [DOI] [PubMed] [Google Scholar]
- 5.Zhang W, et al. Nature (London) 2014;509:345. doi: 10.1038/nature13252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bergmann U, Yachandra VK, Yano J, editors. X-ray Free Electron Lasers—Applications to Materials, Chemistry and Biology. Royal Society of Chemistry; 2017. [Google Scholar]
- 7.Rohringer N, Santra R. Phys Rev A. 2007;76:033416. [Google Scholar]
- 8.Young L, et al. Nature (London) 2010;466:56. [Google Scholar]
- 9.Kanter EP, et al. Phys Rev Lett. 2011;107:233001. doi: 10.1103/PhysRevLett.107.233001. [DOI] [PubMed] [Google Scholar]
- 10.Doumy G, et al. Phys Rev Lett. 2011;106:083002. [Google Scholar]
- 11.Rudek B, et al. Nat Photonics. 2012;6:858. [Google Scholar]
- 12.Tanaka S, Mukamel S. Phys Rev Lett. 2002;89:043001. doi: 10.1103/PhysRevLett.89.043001. [DOI] [PubMed] [Google Scholar]
- 13.Yoneda H, Inubushi Y, Nagamine K, Michine Y, Ohashi H, Yumoto H, Yamauchi K, Mimura H, Kitamura H, Katayama T, Ishikawa T, Yabashi M. Nature (London) 2015;524:446. doi: 10.1038/nature14894. [DOI] [PubMed] [Google Scholar]
- 14.Mukamel S, Healion DM, Zhang Y, Biggs JD. Annu Rev Phys Chem. 2013;64:101. doi: 10.1146/annurev-physchem-040412-110021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bennett K, Zhang Y, Kowalewski M, Hua W, Mukamel S. Phys Scr. 2016;T169:014002. [Google Scholar]
- 16.Mukhamel S. Principles of Nonlinear Optical Spectroscopy. Oxford University Press; New York: 1995. [Google Scholar]
- 17.Dorfman KE, Zhang Y, Mukamel S. Proc Natl Acad Sci USA. 2016;113:10001. doi: 10.1073/pnas.1610729113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang Y, Biggs JD, Govind N, Mukamel S. J Phys Chem Lett. 2014;5:3656. doi: 10.1021/jz501966h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Vanko G, Rueff JP, Mattila A, Nemeth Z, Shukla A. Phys Rev B. 2006;73:024424. [Google Scholar]
- 20.Glatzel P, Bergmann U. Coord Chem Rev. 2005;249:65. [Google Scholar]
- 21.van Bokhoven JA, Lamberti C. X-Ray Absorption and X-Ray Emission Spectroscopy: Theory and Applications. Wiley; New York: 2016. [Google Scholar]
- 22.DeBeer S, Bergmann U. In: X-Ray Emission Spectroscopic Techniques in Bioinorganic Applications in Encyclopedia of Inorganic and Bioinorganic Chemistry. Scott RA, editor. John Wiley; Chichester: 2016. [Google Scholar]
- 23.Rohringer N, Ryan D, London RA, Purvis M, Albert F, Dunn J, Bozek JD, Bostedt C, Graf A, Hill R, Hau-Riege SP, Rocca JJ. Nature (London) 2012;481:488. doi: 10.1038/nature10721. [DOI] [PubMed] [Google Scholar]
- 24.Weninger C, Purvis M, Ryan D, London RA, Bozek JD, Bostedt C, Graf A, Brown G, Rocca JJ, Rohringer N. Phys Rev Lett. 2013;111:233902. doi: 10.1103/PhysRevLett.111.233902. [DOI] [PubMed] [Google Scholar]
- 25.Beye M, Schreck S, Sorgenfrei F, Trabant C, Pontius N, Schüßler-Langeheine C, Wurth W, Föhlisch A. Nature (London) 2013;501:191. doi: 10.1038/nature12449. [DOI] [PubMed] [Google Scholar]
- 26.Kimberg V, Rohringer N. Struct Dyn. 2016;3:034101. doi: 10.1063/1.4940916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kimberg V, Sanchez-Gonzalez A, Mercadier L, Weninger C, Lutman A, Ratner D, Coffee R, Bucher M, Mucke M, Agaker M, Sathe C, Bostedt C, Nordgren J, RJE, Rohringer N. Faraday Discuss. 2016;194:305. doi: 10.1039/c6fd00103c. [DOI] [PubMed] [Google Scholar]
- 28.Liang M, Williams GJ, Messerschmidt M, Seibert MM, Montanez PA, Hayes M, Milathianaki D, Aquila A, Hunter MS, Koglin JE, Schafer DW, Guillet S, Busse A, Bergan R, Olson W, Fox K, Stewart N, Curtis R, Miahnahri AA, Boutet S. J Synchrotron Radiat. 2015;22:514. doi: 10.1107/S160057751500449X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nagler B, Aquila A, Boutet S, Galtier EC, Hashim A, Hunter MS, Liang M, Sakdinawat AE, Schroer CG, Schropp A, Seaberg MH, Seiboth F, van Driel T, Xing Z, Liu Y, Lee HJ. Sci Rep. 2017;7:13698. doi: 10.1038/s41598-017-13710-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Herrmann S, Boutet S, Duda B, Fritz D, Haller G, Hart P, Herbst R, Kenney C, Lemke H, Messerschmidt M, Pines J, Robert A, Sikorski M, Williams G. Nucl Instrum Methods Phys Res, Sect A. 2013;718:550. [Google Scholar]
- 31.Sokaras D, Weng TC, Nordlund D, Alonso-Mori R, Velikov P, Wenger D, Garachtchenko A, George M, Borzenets V, Johnson B, Rabedeau T, Bergmann U. Rev Sci Instrum. 2013;84:053102. doi: 10.1063/1.4803669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cowan RD. The Theory of Atomic Structure and Spectra. University of California Press; Berkeley: 1981. [Google Scholar]
- 33.Butler PH. Point Group Symmetry: Applications, Methods and Tables. Plenum Press; New York: 1981. [Google Scholar]
- 34.Thole BT, van der Laan G, Fuggle J, Sawatzky GA, Karnatak RC, Esteva JM. Phys Rev B. 1985;32:5107. doi: 10.1103/physrevb.32.5107. [DOI] [PubMed] [Google Scholar]
- 35.de Groot FMF, Kotani A. Core Level Spectroscopy of Solids. CRC Press; Boca Raton: 2008. [Google Scholar]
- 36.See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevLett.120.133203 for details of the experimental methods and materials as well as theoretical results. The material includes samples and sample delivery, x-ray beam parameters, x-ray optics and detectors, calculation of spontaneous x-ray emission spectra, simulations of amplified spontaneous emission of a simple atomic manganese model system to explain the major experimentally observed trends.
- 37.Duguay MA, Rentzepis GP. Appl Phys Lett. 1967;10:350. [Google Scholar]
- 38.Louisell WH, Scully MO, McKnight WB. Phys Rev A. 1975;11:989. [Google Scholar]
- 39.Hopf FA, Meystre P. Phys Rev A. 1975;12:2534. [Google Scholar]
- 40.Hopf FA. Opt Lett. 1982;7:605. doi: 10.1364/ol.7.000605. [DOI] [PubMed] [Google Scholar]
- 41.Self-seeded stimulated emission is also sometimes referred to as “amplified spontaneous emission” (ASE). Throughout the Letter we refer to it simply as “stimulated emission.”
- 42.Rohringer N, London R. Phys Rev A. 2009;80:013809. [Google Scholar]
- 43.Krause MO, Oliver JH. J Phys Chem Ref Data. 1979;8:329. [Google Scholar]
- 44.Krinsky S, Gluckstern RL. Phys Rev ST Accel Beams. 2003;6:050701. [Google Scholar]
- 45.Hopf FA, Meystre P. Phys Rev A. 1975;12:2534. [Google Scholar]
- 46.Weninger C, Rohringer N. Phys Rev A. 2014;90:063828. [Google Scholar]
- 47.Kimberg V, Rohringer N. Phys Rev Lett. 2013;110:043901. doi: 10.1103/PhysRevLett.110.043901. [DOI] [PubMed] [Google Scholar]
- 48.Bergmann U, Glatzel P. Photosynth Res. 2009;102:255. doi: 10.1007/s11120-009-9483-6. [DOI] [PubMed] [Google Scholar]
- 49.Lutman AA, Coffee R, Ding Y, Huang Z, Krzywinski J, Maxwell T, Messerschmidt M, Nuhn HD. Phys Rev Lett. 2013;110:134801. doi: 10.1103/PhysRevLett.110.134801. [DOI] [PubMed] [Google Scholar]