Abstract
The multibreath nitrogen washout (MBNW) test, as it is currently practiced, provides parameters of potential physiological significance that are derived from the relationship between the volume-normalized Phase III slope of the exhaled nitrogen fraction () vs. the cumulative change in lung volume (V). Reliable evaluation of these parameters requires, however, that the subject breathe deeply and evenly, so that Phase III can be clearly identified in every breath. This places a burden on the test subject that may prove troublesome for young children and those with lung disease. Furthermore, the determination of the slope of Phase III requires that a decision be made as to when Phase II ends and Phase III begins. In an attempt to get around these methodological limitations, we develop here an alternative method of analysis based on a multicompartment model of the lung that accounts for the entire exhaled nitrogen profile, including Phases I, II, and III. Fitting this model to and V measured during a MBNW provides an estimate of the coefficient of variation of specific ventilation, as well as functional residual capacity, dead space volume, and a parameter that reflects structural asymmetry at the acinar level in the lung. In the present study, we demonstrate the potential utility of this modeling approach to the analysis of MBNW data.
NEW & NOTEWORTHY The multibreath nitrogen washout test potentially provides important physiological information about regional ventilation heterogeneity throughout the lung, but the conventional analysis requires the subject to breathe deeply and regularly, which is not always practical. We have developed a model-based analysis method that avoids this limitation and that also provides measures of functional residual capacity and dead space volume, thereby expanding the applicability and scope of the method.
Keywords: acinar asymmetry, dead space volume, functional residual capacity, Phase III, ventilation heterogeneity
INTRODUCTION
The multibreath nitrogen washout (MBNW) test has recently regained popularity as a means of assessing the heterogeneous nature of the lung (6, 16, 17, 19), prompted, in part, by the current availability of relatively affordable techniques for acquiring the necessary data (4, 5). This resurgence of interest has also been driven by the finding that the relationship between the volume-normalized Phase III slope of exhaled nitrogen fraction vs. the cumulative lung volume since the beginning of the test allows the determination of two parameters of potential physiological significance (18). One of these parameters, Sacin, is the intercept of the line fitted to the slope-turnover relationship, while the other, Scond, is the slope of the relationship. Sacin is thought to reflect structural asymmetry in the very distal airways of the lung, while Scond is thought to reflect the degree of ventilation heterogeneity in the lung arising from time-constant differences caused by regional differences in conducting airway resistance (17).
The MBNW test, as it is currently practiced, requires that the subject breathe in a regular manner, such that the volume of oxygen inhaled with each breath is as constant as possible (18, 19). It also requires that the inhaled volume be significantly greater than the dead space volume so that Phase III can be readily identified. These requirements place a burden on the test subject that, while not particularly difficult for normal adults to satisfy, may prove troublesome for young children and those with lung disease. Furthermore, the determination of the slope of Phase III requires that a decision be made as to when Phase II ends and Phase III begins. While objective means of making this decision have been proposed (15), it, nevertheless, remains somewhat arbitrary and may be confounded by the presence of cardiogenic oscillations.
In an attempt to get around these methodological limitations of the MBNW test, here, we have developed an alternative method of analysis based on a multicompartment model of the lung that accounts for the entire exhaled nitrogen profile, including Phases I, II, and III. Fitting this model to MBNW data provides an index of lung heterogeneity in addition to estimates of functional residual capacity (FRC), dead space volume, and Sacin.
METHODS
Model development.
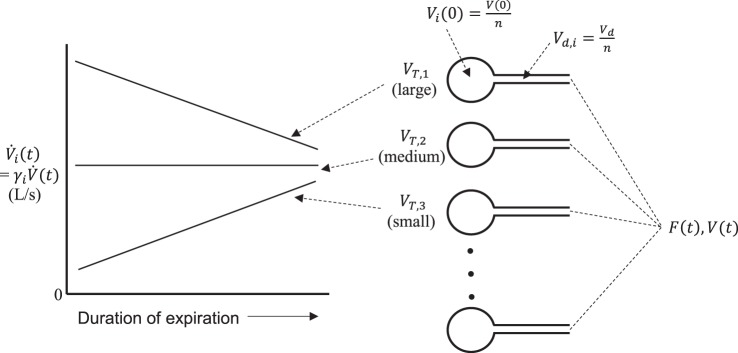
The lung is modeled as a collection of parallel alveolar units served by individual airways that intersect at the airway opening (Fig. 1). The volume of an airway comprises the anatomic dead space of the unit it serves. The unit dead space volumes are all identical and are, thus, each equal to VD/n, where VD is the total anatomic dead space of the model. The FRCs of the units are also identical and, thus, are given by the total FRC of the model divided by . The model performs a MBNW maneuver by having its total volume, V(t), cycle over a number of consecutive breaths. Pure oxygen enters the airway opening during each inspiration of the maneuver, while the mole fraction of nitrogen, , leaving the airway opening is calculated during each expiration. The mole fractions of nitrogen in each unit at the start of the MBNW maneuver (i.e., at t = 0 when the first inspiration of O2 begins) are identical. This initial mole fraction is denoted F0.
Fig. 1.
Schematic of the key elements of the computational model used for simulating multibreath nitrogen washout (MBNW) data. A parallel collection of lungs with identical functional residual capacities, Vi(0), and dead space volumes, Vd,i, connect at the airway opening where a flow-weighted sum of the contributions from each unit add to produce the mole fraction of nitrogen, F(t), measured at the mouth. The fractional contribution to expired flow from each unit, γi, determines the individual unit flows, , according to the individual unit tidal volumes, VT,i, such that units with high tidal volumes contribute fractional flows that decrease linearly as V(t) decreases throughout expiration, while units with low tidal volumes contribute fractional flows that increase linearly. This ensures the slope of Phase III is positive and that this slope increases as regional differences in increase.
The following model development is based on the ideal situation in which a MBNW maneuver is performed with perfectly regular breathing, meaning that the excursions in V(t) during a breath (i.e., tidal volume, VT) are identical for each breath in the maneuver. We also assume that the volume of gas in the lungs at the start of the maneuver, V(0) = V0, equals FRC, so that the initial volumes of each unit are identical and equal to V0/n. The only functional attribute that distinguishes one unit from another is then its tidal volume, VT,i, where i = 1,2, …, n. This causes the specific ventilations, , of the units to vary according to
| (1) |
The slope of Phase III is invariably positive, and this slope tends to increase with increasing ventilation heterogeneity (18). This implies that the relative contributions of units with high (those with large VT,i via Eq. 1) must decrease progressively as expiration proceeds compared with units with low specific ventilation (those with small VT,i). Accordingly, we let the units with lower than average VT,i make fractional contributions, γi(t), to the total flow, , that increase as expiration proceeds, and conversely for units with greater than average VT,i. For simplicity, we make these variations in γi(t) depend linearly on V(t). Furthermore, if a unit has a γi(t) that decreases throughout expiration, its tidal volume, and, thus, its mean value of γi(t), is higher than that of a unit whose γi(t) increases throughout expiration, as illustrated in Fig. 1.
It is convenient to express γi(t) relative to the value of V(t) at the midpoint, of its range throughout expiration, so that
| (2) |
where ai and bi are dimensionless constants and
| (3) |
Equation 2 shows that γi(t) is antisymmetric relative to V(t) about , which means that the contribution to VT,i from the term in bi in Eq. 2 averages to zero over expiration. Consequently, ai alone determines VT,i, and is, therefore, equal to VT,i as a fraction of VT. The mean value of ai is then 1/n.
We impose heterogeneity of ventilation in the model by choosing the bi from a zero-mean Gaussian distribution having standard deviation σb (to generate smooth curves, the actual values used in the model were spaced at precisely equal increments of cumulative probability spanning two standard deviations either side of zero). This gives equal and symmetric weight to units with increasing and decreasing contributions to flow as expiration proceeds. We further suppose that the way that a unit’s contribution to flow varies throughout expiration is exactly coupled to its specific ventilation. This is achieved by having the ai in Eq. 2 vary about their mean value of 1/n by an amount proportional to their respective value of bi, with the constant of proportionality A. That is,
| (4) |
which gives
| (5) |
Equation 5 means, however, that γi will achieve physically meaningless negative values in units with specific ventilations that are high enough to allow their flow contributions to decrease to zero before expiration has ended. To avoid this, we impose the condition that if γi(t) ever reaches zero during expiration, it remains at zero until V(t) returns to the point where γi(t) becomes positive again during the subsequent inspiration. Nevertheless, the flow contributions from all of the units must always sum to provide the total flow. Accordingly, whenever γi(t) becomes zero for any of the units, the remaining γi(t) are scaled to maintain their sum at unity. The definition of γi(t), thus, becomes
| (6) |
where the function α(t) is chosen, such that, at each value of t,
| (7) |
Therefore, α(t) = 1 whenever none of the γi(t) are zero, but α(t) > 1 otherwise.
The model is driven by V(t) or (one being determined from the other by numerical differentiation or integration, respectively, with respect to t). The flow into each unit is then
| (8) |
using γi(t) from Eq. 6 and is numerically integrated to give the unit volume, Vi(t). The mole fraction of nitrogen, , in each unit is the ratio of the volume of nitrogen in the unit divided by Vi(t). During the early part of each inspiration, the volume of nitrogen in each unit increases due to the inhalation of the nitrogen-containing gas present in its airway dead space from the previous expiration, and which has the same nitrogen fraction as the unit itself had at the end of the previous expiration. Once the dead space gas has passed back into a unit, however, the volume of nitrogen it contains stays constant for the remainder of inspiration because only pure oxygen is inhaled thereafter. Therefore, decreases during the later stages of expiration as the fixed volume of nitrogen it contains becomes progressively diluted by inspired oxygen. During expiration, remains constant but the volume of nitrogen in each unit decreases at a rate given by the product of and . These various situations are expressed mathematically as
| (9) |
During inspiration, the nitrogen mole fraction, , at the common entrance to the unit airways (i.e., the equivalent of the mouth) is zero. During expiration, is the flow-weighted sum of the nitrogen mole fractions, , in each unit dead space (i.e., in the flows exiting the individual unit airways). That is,
| (10) |
Early in expiration, because each dead space is filled with pure oxygen from the previous inspiration. Once a unit has emptied itself of oxygen, however, its dead space is completely full of gas from the unit itself, and this gas then exits the dead space at the mouth as expiration proceeds, in which case .
So far, we have been assuming that is constant during expiration. This is not strictly true for several reasons, but by far, the most important is the diffusive-convective interaction within the structurally asymmetric acinus (11) that has been described as a form of “diffusive pendelluft” (4), and which is responsible for the finite value of the parameter Sacin. We represent this phenomenon empirically in the model by replacing the constant expiratory value of with a quantity that increases linearly with V(t) about a mean value of . That is,
| (11) |
The constant of proportionality, μ, is assumed to be the same for all units. Since Sacin is, by definition, the slope of vs. normalized to , we have that
| (12) |
Strictly speaking, should replace in the last line of Eq. 9 and should replace in Eq. 10, but this would involve the significant computational overhead of determining how the nitrogen mole fraction in each unit’s dead space changes throughout expiration due to a mole fraction input from the unit that varies with time. We elected not to do this in the interests of simplicity on the grounds that the antisymmetry of about (Eq. 11) means that the total volume of nitrogen exhaled from a unit into its dead space throughout an entire expiration is the same as if .
Model fitting.
The above model has only five free parameters—V0, VD, σb, A, and μ—all of which would seem to have clear physiological interpretations. V0 represents FRC, VD represents the volume of the physiologic dead space, σb reflects the heterogeneity of lung emptying as a function of lung volume, A reflects the heterogeneity of regional tidal volume, and μ reflects structural asymmetry at the level of the acinus. The values of these parameters can be estimated by fitting the model to a set of MBNW data consisting of measurements of and V(t) (the latter referenced to the initial volume of the lungs rather than absolute lung volume as in the model development above). However, inspection of Eq. 6 reveals that σb and A have the capacity to compensate for each other because the effects on γi(t) of an increase in one of these parameters are offset to some degree by a decrease in the other. Also, γi(t) is the primary reflection of ventilation heterogeneity in the model; σb and A merely serve to formulate how this heterogeneity occurs. This suggests that some combination of these two parameters might be a more robust and meaningful quantity with which to characterize ventilation heterogeneity than either alone. Indeed, they can be combined to provide the coefficient of variation of regional specific ventilation throughout the lungs, , as follows. From Eqs. 1 and 4, we have that
| (13) |
is the standard deviation of normalized to its mean, the latter being simply the specific ventilation of the entire lung, namely VT/V0. This gives, from Eq. 13,
| (14) |
Therefore, we replace A with as one of the model’s five free parameters.
For this model to be applicable to the description of experimental MBNW data, however, it cannot be limited to perfectly regular breathing, as per the above development, because even well-trained subjects exhibit breath-to-breath variations in end-expiratory lung volume and tidal volume. To make the model applicable to real data, we use the midpoint of the measured V(t) signal for in Eq. 1, and the mean tidal volume for VT. With these substitutions, we can use the remaining model equations to predict a measured signal from its corresponding V(t) signal, for a specified set of initial conditions.
The initial conditions include the initial fraction of nitrogen, F0, which is the same for all units. In principle, one could equate F0 to the expiratory nitrogen fraction seen before switching the subject to breathing pure oxygen. However, this requires a sufficiently long expiration from the subject to get a good sample of alveolar gas, and we wish to avoid placing constraints on the subject’s breathing pattern. Also, the device we used to collect MBNW data in human subjects (see below) incorporated an inspiratory demand valve for inspiratory oxygen that likely bled small amounts of oxygen into the breathing circuit toward the very end of expiration when flow was low. This could have diluted the nitrogen in the dead space and, thus, the amount of subsequently inspired oxygen by a small but unknown amount, which would have affected the model fits so as to alter the effective value of F0. Indeed, we found that the fits were improved by making F0 an additional parameter of the model, giving the model six free parameters—V0, VD, F0, σb, μ, and . These six parameters were evaluated by fitting the model to pairs of experimentally measured V(t) and signals using a grid-search method (see appendix).
Parameter sensitivity analysis.
Once the model had been fit to a MBNW data set, a parameter sensitivity analysis was performed by varying each parameter in turn by ±5% either side of its best-fit value and determining the mean of the two resultant increases in the root mean squared residual (RMSR) between the measured and predicted signals, expressed as a fraction of the minimum RMSR. The mean of such fractional increase for parameter p is denoted ΔRp. The empirical uncertainty, Δp, in each parameter about its value of best fit, pbest, is then expressed as the change in that parameter causing a 5% increase in RMSR above its minimum value, approximated as
| (15) |
Data collection.
To demonstrate that the model described above can be satisfactorily fit to MBNW data, we obtained and V(t) signals from six adult human subjects aged 43 ± 7 yr. The subjects were obese (BMI: 44.4 ± 5.1 kg/m2) but otherwise healthy. The study protocol was approved by the University of Vermont Institutional Review Board, and the subjects gave written informed consent. The subjects were instructed to breathe regularly and deeply on a mouthpiece connected to the measurement apparatus. While on the mouthpiece, and during a chosen expiration, the inspired gas source was switched from room air to pure oxygen. The subjects then continued to inspire pure oxygen from that point on until peak expired had decreased to close to zero, after which the subjects came off the mouthpiece and continued to breathe normally.
Data were collected with the EasyOne Pro Laboratory system (ndd Medizintechnik AG, Zurich) that uses ultrasound to measure both flow of gas at the mouth (i.e., and the molar mass, M(t), of the gas. The system also measures the mole fraction of carbon dioxide, , in the gas. We determined , according to the manufacturer’s instructions (9), from the recorded signals of M(t) and on the basis that M is the fraction-weighted sum of the molar masses of nitrogen, oxygen, carbon dioxide, water vapor, and argon, which have molar masses of 28, 32, 44, 18, and 40, respectively. That is,
| (16) |
where , , and FAr are the mole fractions of oxygen, water vapor, and argon, respectively. Assuming that the mole fractions of all five gases in Eq. 16 sum to unity, and that FAr(t) is always because nitrogen and argon bear a fixed relationship to each other in the atmosphere, Eq. 16 can be recast as
| (17) |
Because of the way in which gas is processed by the measurement system (9), is the ambient mole fraction of water vapor, which we did not measure. However, we were able to estimate it as the value that caused in Eq. 17 to be zero during inspiration of pure oxygen.
Three of the six subjects studied performed duplicate MBNW maneuvers, while the remaining three subjects performed the maneuver in triplicate.
Comparison of model parameters to conventional parameters.
We performed a conventional analysis of the data by first identifying Phase III as the portion of each expired profile remaining after discarding the first Vdiscard of the expirate. Vdiscard was chosen for each subject to be from 300 to 400 ml, such that no remnants of Phase II remained in the alveolar plateaus retained for analysis, as best as we could tell by visual inspection. We then fit straight lines to Phase III vs. cumulative V(t) and normalized the slope of each line by the mean value of throughout Phase III.
The normalized Phase III slopes were plotted against cumulative V(t) at the midpoint of each Phase III, and a straight line fit to this relationship. The slope of this line was taken as Scond, while its intercept at V(0) was taken as conventional Sacin. Using standard regression theory (1), we determined 95% confidence intervals about Sacin and Scond, assuming normally distributed residuals. This is essentially equivalent to the procedure described by Verbanck et al. (18), except that, here, we fit the line to the entire relationship of Phase III slope vs. V(t) rather than only when lung turnover is greater than 1.5, which likely makes little difference since the entire relationship appears well approximated by a straight line. Also, Sacin and Scond are conventionally determined from the relationship between Phase III slope vs. lung turnover rather than vs. cumulative lung volume as we have done here. This does not affect the intercept of the relationship (Sacin), but it does affect the slope (Scond); converting our values of Scond to those relative to lung turnover is achieved via multiplication by FRC (i.e., V0).
RESULTS
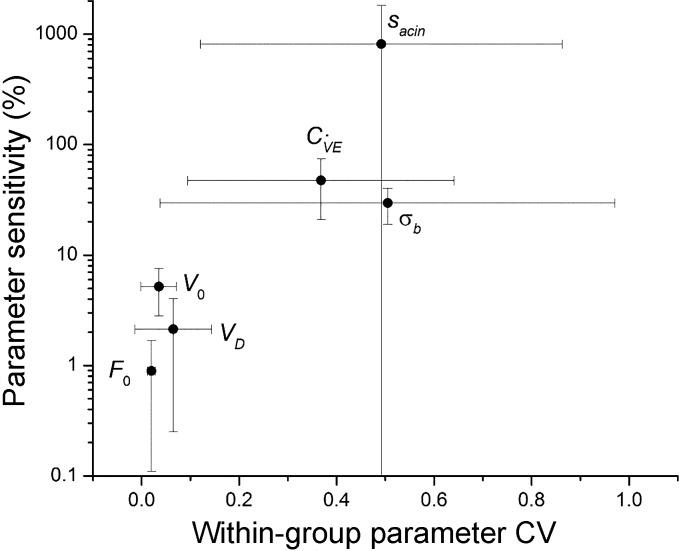
Figure 2 shows from a subject that was able to breathe regularly and deeply enough for the Phase III plateaus to be clearly identifiable. The best-fit provided by the model, also plotted in Fig. 2, matches the measured data closely in its important details. The best-fit values of the model parameters are listed in Table 1 together with their uncertainties (Eq. 15) expressed as percentages of the parameter values. The six parameters break out into two groups. The first group, which comprises V(0), VD, and , governs how the mean values of expiratory descend from breath to breath. This is a larger component of the overall signal compared with the more subtle information contained in the changes in Phase III slope from breath to breath that are governed by the values of σb, μ, and . Accordingly, the first group of parameters is more strongly determined by the data than the second group, which explains the large differences in their respective uncertainties shown in Table 1. This difference in uncertainty was found for all six subjects studied. The mean (SD) values of percent uncertainty for V(0), VD, and for all six subjects were 2.1 (1.9), 5.2 (2.4), and 0.9 (0.8), respectively. The corresponding values for σb, μ, and were 30 (11), 47 (26), and 813 (1006), respectively.
Fig. 2.
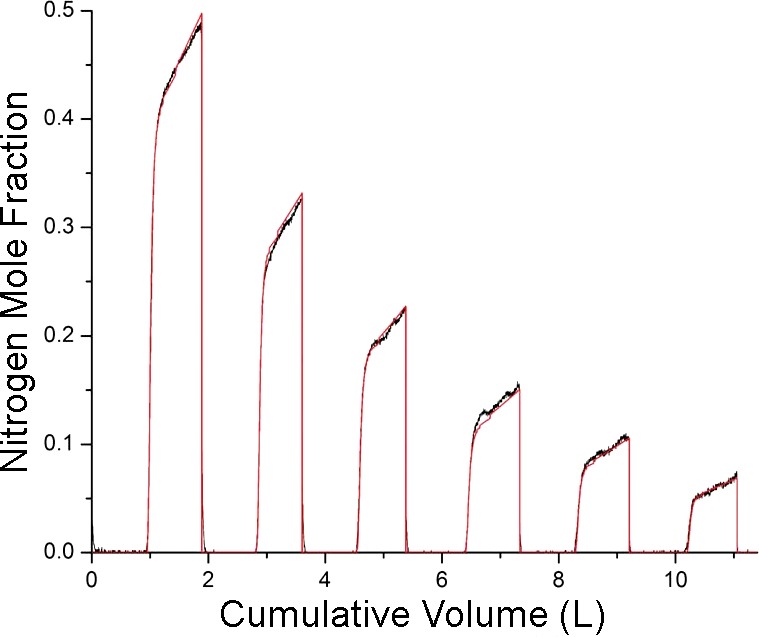
F(t) measured in a subject performing a MBNW maneuver (black) together with F(t) predicted by the model (red). These data show deep even breathing from the subject.
Table 1.
Model parameter values for the fitted curves shown in Figs. 2 and 5
| Figure 2 |
Figure 5 |
|||
|---|---|---|---|---|
| Parameter | Best-Fit Value | Uncertainty, % | Best-Fit Value | Uncertainty, % |
| V0 | 2.270 | 0.9 | 2.540 | 4.4 |
| VD | 0.130 | 2.8 | 0.112 | 2.7 |
| F0 | 0.675 | 0.4 | 0.628 | 1.5 |
| σb | 0.015 | 27.5 | 0.033 | 24.5 |
| 0.222 | 43.5 | 0.292 | 28.5 | |
| Sacin | 0.220 | 114.5 | 0.813 | 364.0 |
The parameter sensitivities were mirrored by the repeatability of each parameter between repeat MBNW maneuvers in each subject. Figure 3 shows that larger mean values of % uncertainty for a parameter correspond to larger within-subject coefficients of variation. The relationship is linear in a semilogarithmic plot of FRC, however, demonstrating that parameter uncertainty, as we have defined it above, increases exponentially with the variation in that parameter between multiple runs in a given subject.
Fig. 3.
Sensitivity (%) for each model parameter determined as described in the text (means ± SD) vs. the corresponding coefficient of variation (SD) determined from multiple runs within each subject (means ± SD).
Figure 4 shows the conventional analysis applied to the data in Fig. 2. Phase III was considered to begin after the initial 300 ml of gas had been expired from each breath, leaving the remainder of each expiration with a nicely linear relationship between and V(t) (Fig. 4A). A linear fit to the normalized Phase III slopes vs. cumulative V(t) (Fig. 4B) provides values for Sacin and Scond of 0.183 liter−1 and 0.23, respectively. However, the 95% confidence intervals about these values are wide, being 0.110–0.256 and 0.013– 0.034, respectively.
Fig. 4.
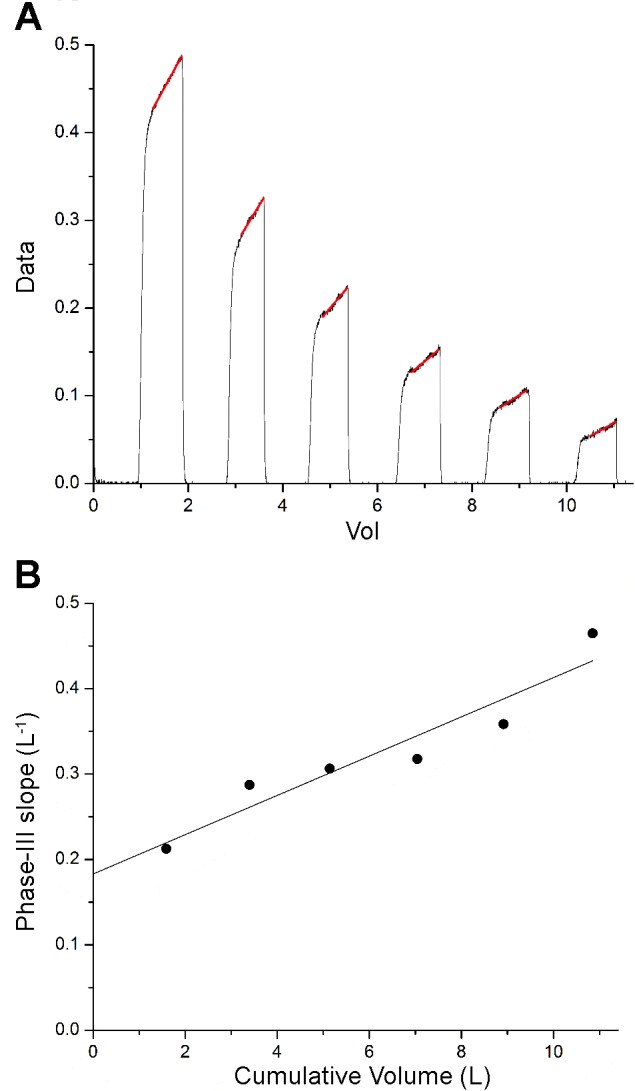
The conventional analysis of the data shown in Fig. 2A) The data (black) are shown together with the straight-line fits to Phase III in each breath (red). B: normalized slopes of the lines fit to Phase III vs. the cumulative volume change of the lungs at the midpoint of each expiration (●) together with the line fit through the points (line). The slope of the line is Scond, while the intercept is Sactin.
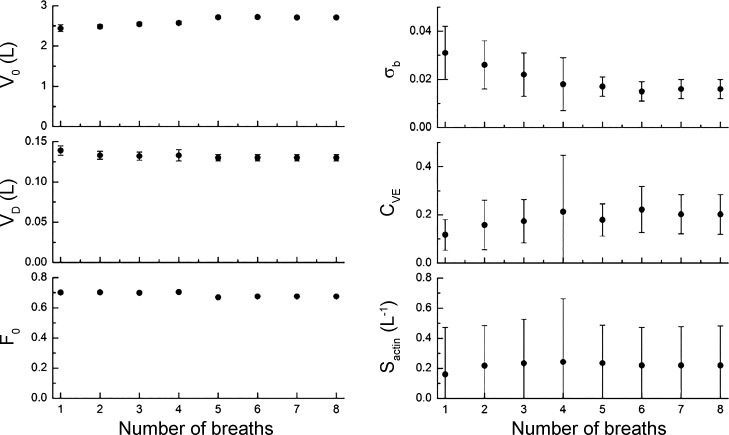
Figure 5 shows how the best-fit model parameters depend on the number of breaths included in the MBNW data set. The model is able to return values for the six adjustable parameters even when fit to only the first expiration. With the successive inclusion of the second through the eighth breaths, the parameters and their uncertainty ranges appear to converge toward stable values. Again, the uncertainty ranges are much larger for σb, μ, and than for V(0), VD, and .
Fig. 5.
The best-fit model parameters obtained from the data shown in Fig. 2 vs. the number of breaths that were fit, beginning with the first breath.
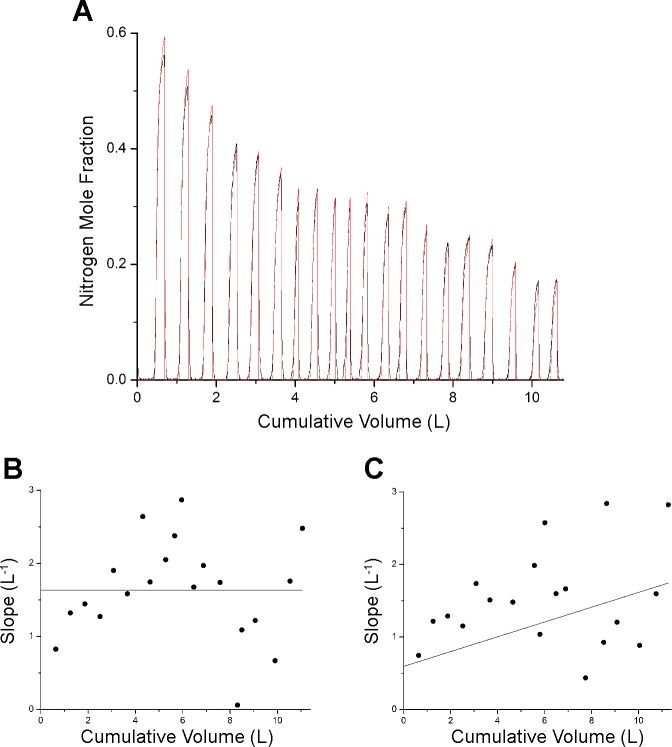
Figure 6A shows the model fit to from a subject who breathed with a tidal volume that is too small for Phase III to manifest fully before expiration ends. Nevertheless, the model captures the main features in the data and yields the parameter estimates listed in Table 1. The conventional analysis, however, fails with these data. For example, if Phase III is defined as beginning after the first 0.15 liter of gas has been expired in each breath, the plot of normalized Phase III slopes vs. cumulative volume is extremely noisy (Fig. 6B), and a straight-line fit through the points yields very large 95% confidence limits for Sacin (0.913–2.354) and Scond (0–0.109). If, on the other hand, Phase III is defined as beginning after 0.16 liter has been expired (only 10 ml more than before), the result is quite different (Fig. 6C) with even larger 95% confidence intervals for Sacin (0–2.153) and Scond (0–0.334). Again, the confidence range for Sactin encompasses its value determined by model fitting (Table 1).
Fig. 6.
A: F(t) measured in a subject performing a MBNW maneuver (black) together with F(t) predicted by the model (red). These data show shallow breathing from the subject. B: conventional slope analysis in which Phase III was defined as beginning after the first 150 ml had been expired. C: conventional slope analysis in which Phase III was defined as beginning after the first 160 ml had been expired.
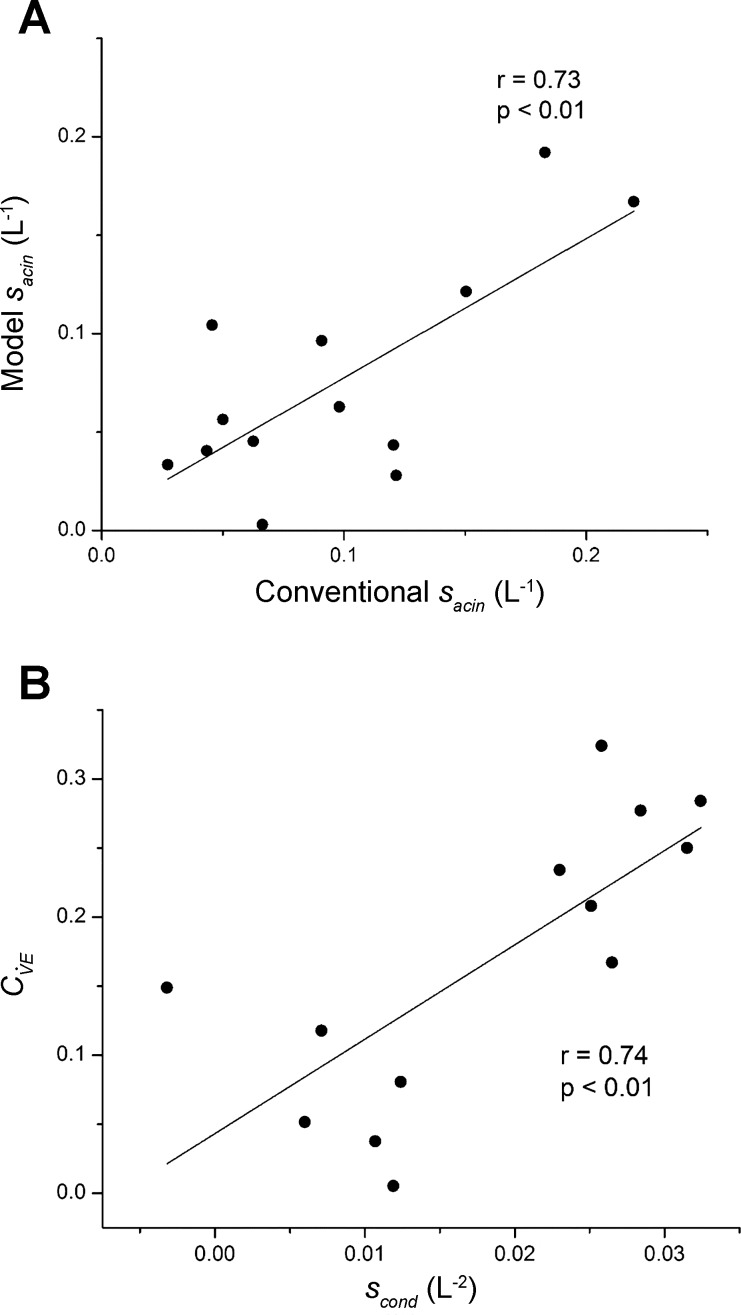
Figure 7 compares corresponding parameters evaluated by the model-fitting approach vs. the conventional approach. Figure 7A shows Sacin for the two methods, which have a significant correlation and lie approximately along the line of identity, as would be expected if these two estimates are, indeed, measures of the same quantity. Figure 7B compares Scond from the conventional analysis to obtained from the model. While Scond and do not represent exactly the same thing, they are both determined by regional ventilation heterogeneity at the level of the conducting airways, so their significant correlation in Fig. 7B is again as expected.
Fig. 7.
A: Sacin determined by fitting the model (Eq. 12) vs. its value determined in the conventional manner from the normalized slopes of Phase III in each breath (symbols), along with their linear regression (line) with intercept = 0.0066 liter−1 and slope = 0.7074. B: coefficient of variation of regional specific ventilation in the model (Eq. 14) vs. Scond determined in the conventional manner from the normalized slopes of Phase III in each breath (symbols), along with their linear regression (line) with intercept = 0.0432 and slope = 6.834 liter−2. The r values shown are Pearson correlation coefficients. Note that the conventional quantities were determined by plotting the normalized Phase III slopes against the cumulative change in lung volume rather than against lung turnover as is usually done. This does not affect the value of Sacin, but it does affect Scond. Conversion of Scond from the former to the latter representation is achieved merely by dividing the former by FRC (i.e., the parameter V0).
DISCUSSION
Nitrogen washout of the lungs, produced by breathing pure oxygen, has been employed for decades in various forms as a means of assessing the nature of pulmonary ventilation (2). In its simplest manifestation, it can be used to determine FRC from the gas dilution inherent in the sequential decay of alveolar nitrogen plateaus from breath to breath; when breathing is perfectly regular and the lungs are uniformly ventilated, this decay is exponential with a rate constant directly relatable to FRC. If there are multiple compartments that wash out their nitrogen at different rates, then the decay is multiexponential (8). Information about regional ventilation in the lung is also provided, however, by the shape of a single alveolar nitrogen plateau, although here the situation is more complicated (11). The slope of the nitrogen Phase III is invariably positive for reasons that have intrigued researchers for many years. The most obvious potential explanation for this positive slope is variations in the contributions of different lung regions to flow at different points in time, with those relatively underventilated regions (i.e., with higher nitrogen mole fractions) contributing relatively more later in expiration. Such differences in regional ventilation were originally ascribed largely to gravity, since the upper lung regions support the lower regions and are, therefore, more distended at FRC with less room to further expand during inspiration. Studies of nitrogen washout in microgravity, however, have shown that although the slope of Phase III is markedly diminished in weightlessness, a significant positive slope remains (7, 13). Thus, gravity is not the sole culprit behind the slope of Phase III. Classic studies by Paiva and Engel (3, 12) showed that interactions between diffusive and convective gas transport in the lung periphery can give rise to a positive Phase III slope purely on the basis of asymmetries in parallel acinar structures, and this is now accepted as the principle reason for the nongravity-dependent slope of Phase III.
Interest in the use of nitrogen washout to study ventilation heterogeneity in the lung has been rekindled in recent years by the work of Verbanck and Paiva (16–19), who combined the information inherent in single-breath and multibreath nitrogen washout maneuvers. They analyzed not only the slope of Phase III, but also how this slope changes from breath to breath as nitrogen is washed from the lungs. Their analysis provides parameters Scond and Sacin, the former purportedly reflecting time-constant differences of parallel lung regions fed by the conducting airways, and the latter reflecting structural asymmetry at the level of the acinus. The availability of rapid, accurate, and relatively cheap gas analyzers is now making this a viable clinical test (9, 14), and recent studies are beginning to demonstrate its diagnostic potential (15, 17, 19). Nevertheless, the clinical usefulness of the procedure is limited by the challenges associated with identifying Phase III in each breath of a MBNW maneuver because there is often no sharp demarcation between the end of Phase II and the beginning of Phase III. This means that the expired volumes in a MBNW washout maneuver must be larger than in normal resting breathing to ensure that the gas observed at the end of expiration is all alveolar in origin. This can make the maneuver challenging for some subjects to perform. Even with large expiratory volumes, however, it is somewhat arbitrary as to when one decides that Phase III has truly begun, particularly in pathological situations in which variations in regional emptying can be large.
The present model-based approach to analyzing MBNW data was motivated by the desire to avoid the practical issues just mentioned. Accordingly, we developed a computational model of the lung of sufficient complexity to simulate expiratory nitrogen profiles having a realistic appearance and that includes the entirety of phases I, II, and III, so that no single phase needs to be identified in isolation. At the same time, the number of free parameters governing the model behavior must be small enough that they can be robustly estimated from a typical MBNW data set. These two goals are somewhat conflicting, but we believe we have met them in a model having only six free parameters (see appendix). Nevertheless, the necessary simplicity of the model represents numerous assumptions that collectively embody the limitations of our approach. Perhaps most important of these is the representation of the lung as a series of parallel compartments each having its own independent anatomic dead space. This ignores the fact that the conducting airways are actually a tree structure and that time-constant differences between different parallel lung regions are not entirely independent of each other. In addition, we assume that the dead space volume is the same for all units. This has the advantage of parsimony by producing a sigmoidal Phase II purely as a result of the different expiration profiles of the various units, but in so doing, it makes a deterministic link between the shape of Phase III and the slope of Phase III, something that is more convenient than evidence based. We also represent the complex phenomena involved in diffusive-convective gas transport interactions in the lung periphery as a fixed proportional contribution to the Phase III slope that is common to all regions of the lung regardless of their other differences, which belies the complexities of this phenomenon (10–12).
Despite these simplifying assumptions, however, the model mimics during nitrogen washout quite accurately (Figs. 2 and 6A) in situations where the conventional analysis of normalized Phase III slopes is both successful (Fig. 4) and unsuccessful (Fig. 6, B and C). This suggests that the model-based approach may be more applicable than the conventional approach when the subject either has difficulty in following instructions to breathe deeply and regularly (e.g., young children) or when they are simply unable to do so (e.g., patients with severe restrictive lung disease). The modeling approach also provides similar physiological information to that embodied in the two parameters Sacin and Scond. In fact, the modeling approach estimates Sacin directly and gives values comparable to those of the conventional slope analysis (Table 1, Fig. 7A). However, there is large uncertainty in the estimates of Sacin from both methods (Fig. 3) due to the subtle effect that this parameter has on the expiratory profile. The modeling approach does not estimate Scond directly, but instead provides the related parameter . Like Scond, reflects the way in which the shape of the expiratory profile changes from breath to breath as a result of regional ventilation heterogeneity. The precise mathematical relationship between these two parameters is not readily specified, but they are clearly correlated (Fig. 7B), and is arguably more intuitively relatable to the regional heterogeneity of ventilation. Even so, the uncertainly in is large (Table 1, Fig. 3), as it is for Sacin, because the slope of Phase III does not account for as much of the variation in the profile as does the breath-to-breath decrements in mean nitrogen fraction. It must be remembered, however, that these parameter uncertainties are functions of the number of breaths to which the model is fit (Fig. 5). Accordingly, noise can be reduced by including all available breaths until the expiratory changes in are too small to be discernable, by averaging parameter values determined from multiple repeat runs of the MBNW maneuver, and by ensuring that breathing is as regular as possible.
As well as providing parameters that correspond to those of the conventional Phase III slope analysis, the modeling approach provides four additional parameters. One of these, σb, is also a determinant of the slope of Phase III and, like both Sacin and , has a large range of uncertainty (Table 1) and for the same reason. The physiological interpretation of σb relates to the way that the contribution to respiration from different lung regions varies throughout the breath, although it remains to be seen how well this effect is recapitulated in a real lung. Of the remaining three parameters, F0 is likely a function of the ventilation history of the subject before the start of the MBNW maneuver and may also be affected by the technical details of the instrumentation used to collect the data. As such, its use in the model is purely practical. The parameters V0 and VD, however, estimate the subject’s FRC and dead space volume, respectively, and are, thus, of major physiological significance. They are also robust in the sense of being strongly determined by the data (i.e., have small uncertainty ranges as shown in Table 1), and, thus, are likely to be useful for physiological or clinical studies.
In summary, we have developed a model-based method of interpreting MBNW data that potentially avoids the need to identify Phase III. This approach may be useful in situations where the regularity and depth of breathing are less than satisfactory for the conventional approach based on the analysis of normalized Phase III slopes. The model-based method provides a number of parameters that have clear physiological interpretations, and, thus, may provide a novel means for obtaining useful information about lung function.
GRANTS
This work was supported by NIH grant R01 HL-130847.
DISCLOSURES
The author is a member of the advisory board and a minor share-holder in Oscillavent, LLC, a start-up company currently of zero value.
AUTHOR CONTRIBUTIONS
J.H.B. conceived and designed research; J.H.B. and U.P. performed experiments; J.H.B. analyzed data; J.H.B. and U.P. interpreted results of experiments; J.H.B. prepared figures; J.H.B. drafted manuscript; J.H.B. and U.P. edited and revised manuscript; J.H.B. and U.P. approved final version of manuscript.
ACKNOWLEDGMENTS
The author thanks Dr. Anne Dixon for help with obtaining the experimental data used in this study.
APPENDIX
The model has six free parameters—V0, VD, F0, σb, μ and —which break into two groups in terms of the way they account for . The parameters V0, VD and F0 govern the rate at which expiratory decreases from breath to breath during nitrogen washout. The parameters σb, μ, and govern the slope of Phase III within each breath. This allowed the two groups of parameters to be evaluated in alternating blocks using the following grid-search scheme. First, μ and were both set to zero, and F0 was given the nominal value of 0.75. The root mean squared residual R between the measured and model-predicted was minimized over a 5 × 5 × 5 grid of values of V0, VD, and F0 encompassing their likely respective ranges. Next, the grid was refined by centering it on the best-fit parameter values and reducing the previous grid spacings by a factor of 1.7. Searching the refined grid produced updated best-fit parameter values. Next, V0, VD, and F0 were kept at their current best-fit values while an identical grid-search procedure was performed for σb, μ, and . If grid refinement ever led to the new grid, including physically meaningless negative values for a parameter, the lower range of the grid was replaced with 1% of the previous best-fit value, and the grid spacing was redefined accordingly.
The above two-phase grid search was repeated, first for V0, VD, F0, and then for σb, μ, and , beginning with the best-fit parameters values from the previous search cycle but with grid spacings that were twice the last spacings used in the previous cycle (because this widened the search area to reduce the chances that the global RMSR minimum had been eliminated from the range of the previous search). The entire process was continued 12 times on ever finer grids, which almost always resulted in the grid spacing for each parameter becoming less than 1% of its respective best-fit parameter value.
REFERENCES
- 1.Bates JHT. Lung Mechanics: An Inverse Modeling Approach. Cambridge, UK: Cambridge University Press, 2009, chapt. 3. doi: 10.1017/CBO9780511627156. [DOI] [Google Scholar]
- 2.Bouhuys A, Lichtneckert S, Lundgren C, Lundin G. Voluntary changes in breathing pattern and N2 clearance from lungs. J Appl Physiol 16: 1039–1042, 1961. doi: 10.1152/jappl.1961.16.6.1039. [DOI] [PubMed] [Google Scholar]
- 3.Crawford AB, Makowska M, Paiva M, Engel LA. Convection- and diffusion-dependent ventilation maldistribution in normal subjects. J Appl Physiol (1985) 59: 838–846, 1985. doi: 10.1152/jappl.1985.59.3.838. [DOI] [PubMed] [Google Scholar]
- 4.Engel LA. Gas mixing within the acinus of the lung. J Appl Physiol Respir Environ Exerc Physiol 54: 609–618, 1983. doi: 10.1152/jappl.1983.54.3.609. [DOI] [PubMed] [Google Scholar]
- 5.Fuchs SI, Buess C, Lum S, Kozlowska W, Stocks J, Gappa M. Multiple breath washout with a sidestream ultrasonic flow sensor and mass spectrometry: a comparative study. Pediatr Pulmonol 41: 1218–1225, 2006. doi: 10.1002/ppul.20524. [DOI] [PubMed] [Google Scholar]
- 6.Gonem S, Scadding A, Soares M, Singapuri A, Gustafsson P, Ohri C, Range S, Brightling CE, Pavord I, Horsley A, Siddiqui S. Lung clearance index in adults with non-cystic fibrosis bronchiectasis. Respir Res 15: 59, 2014. doi: 10.1186/1465-9921-15-59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lauzon AM, Prisk GK, Elliott AR, Verbanck S, Paiva M, West JB. Paradoxical helium and sulfur hexafluoride single-breath washouts in short-term vs. sustained microgravity. J Appl Physiol (1985) 82: 859–865, 1997. doi: 10.1152/jappl.1997.82.3.859. [DOI] [PubMed] [Google Scholar]
- 8.Lewis SM. Emptying patterns of the lung studied by multiple-breath N2 washout. J Appl Physiol Respir Environ Exerc Physiol 44: 424–430, 1978. [DOI] [PubMed] [Google Scholar]
- 9.Medizintechnik EasyOne Pro LAB. Measurement Technology Background. AppNote EOPLAB-TechBackground, V11R. Zurich, Switzerland: ndd Medizintechnik AG, 2016. [Google Scholar]
- 10.Paiva M. Gas transport in the human lung. J Appl Physiol 35: 401–410, 1973. doi: 10.1152/jappl.1973.35.3.401. [DOI] [PubMed] [Google Scholar]
- 11.Paiva M, Engel LA. The anatomical basis for the sloping N2 plateau. Respir Physiol 44: 325–337, 1981. doi: 10.1016/0034-5687(81)90027-X. [DOI] [PubMed] [Google Scholar]
- 12.Paiva M, Engel LA. Pulmonary interdependence of gas transport. J Appl Physiol Respir Environ Exerc Physiol 47: 296–305, 1979. [DOI] [PubMed] [Google Scholar]
- 13.Prisk GK, Guy HJ, Elliott AR, Paiva M, West JB. Ventilatory inhomogeneity determined from multiple-breath washouts during sustained microgravity on Spacelab SLS-1. J Appl Physiol (1985) 78: 597–607, 1995. doi: 10.1152/jappl.1995.78.2.597. [DOI] [PubMed] [Google Scholar]
- 14.Singer F, Houltz B, Latzin P, Robinson P, Gustafsson P. A realistic validation study of a new nitrogen multiple-breath washout system. PLoS One 7: e36083, 2012. doi: 10.1371/journal.pone.0036083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stuart-Andrews CR, Kelly VJ, Sands SA, Lewis AJ, Ellis MJ, Thompson BR. Automated detection of the phase III slope during inert gas washout testing. J Appl Physiol (1985) 112: 1073–1081, 2012. doi: 10.1152/japplphysiol.00372.2011. [DOI] [PubMed] [Google Scholar]
- 16.Verbanck S, Paiva M, Schuermans D, Hanon S, Vincken W, Van Muylem A. Relationships between the lung clearance index and conductive and acinar ventilation heterogeneity. J Appl Physiol (1985) 112: 782–790, 2012. doi: 10.1152/japplphysiol.01221.2011. [DOI] [PubMed] [Google Scholar]
- 17.Verbanck S, Paiva M, Schuermans D, Malfroot A, Vincken W, Vanderhelst E. Acinar and conductive ventilation heterogeneity in severe CF lung disease: back to the model. Respir Physiol Neurobiol 188: 124–132, 2013. doi: 10.1016/j.resp.2013.05.011. [DOI] [PubMed] [Google Scholar]
- 18.Verbanck S, Schuermans D, Van Muylem A, Paiva M, Noppen M, Vincken W. Ventilation distribution during histamine provocation. J Appl Physiol (1985) 83: 1907–1916, 1997. doi: 10.1152/jappl.1997.83.6.1907. [DOI] [PubMed] [Google Scholar]
- 19.Verbanck S, Thompson BR, Schuermans D, Kalsi H, Biddiscombe M, Stuart-Andrews C, Hanon S, Van Muylem A, Paiva M, Vincken W, Usmani O. Ventilation heterogeneity in the acinar and conductive zones of the normal ageing lung. Thorax 67: 789–795, 2012. doi: 10.1136/thoraxjnl-2011-201484. [DOI] [PubMed] [Google Scholar]