Learned rather than online relative weighting of visual-proprioceptive sensory cues

Abstract

When reaching to an object, information about the target location as well as the initial hand position is required to program the motor plan for the arm. The initial hand position can be determined by proprioceptive information as well as visual information, if available. Bayes-optimal integration posits that we utilize all information available, with greater weighting on the sense that is more reliable, thus generally weighting visual information more than the usually less reliable proprioceptive information. The criterion by which information is weighted has not been explicitly investigated; it has been assumed that the weights are based on task- and effector-dependent sensory reliability requiring an explicit neuronal representation of variability. However, the weights could also be determined implicitly through learned modality-specific integration weights and not on effector-dependent reliability. While the former hypothesis predicts different proprioceptive weights for left and right hands, e.g., due to different reliabilities of dominant vs. nondominant hand proprioception, we would expect the same integration weights if the latter hypothesis was true. We found that the proprioceptive weights for the left and right hands were extremely consistent regardless of differences in sensory variability for the two hands as measured in two separate complementary tasks. Thus we propose that proprioceptive weights during reaching are learned across both hands, with high interindividual range but independent of each hand’s specific proprioceptive variability.

NEW & NOTEWORTHY How visual and proprioceptive information about the hand are integrated to plan a reaching movement is still debated. The goal of this study was to clarify how the weights assigned to vision and proprioception during multisensory integration are determined. We found evidence that the integration weights are modality specific rather than based on the sensory reliabilities of the effectors.

INTRODUCTION

The nervous system integrates information from different sensory modalities to form a coherent multimodal percept of the world (Ernst and Bülthoff 2004), a process called multisensory integration. For example, to plan a reach, information about both the target and the hand location is necessary to form a desired movement vector. While the target position can be derived from visual information alone, hand position is typically determined by two sensory modalities: vision and proprioception. Proprioception is the sense of body position that allows us to know where the different parts of the body are located relative to each other. It has been demonstrated that the brain integrates visual and proprioceptive signals to form a unified estimate of the hand location (Rossetti et al. 1995; van Beers et al. 2002). However, it remains unclear what determines the criterion by which these signals are combined.

According to the Bayesian cue combination theory, during multisensory integration the sensory modalities are weighted proportional to their reliabilities; the higher the reliability, the more weight is given to that sense (Deneve and Pouget 2004; Ernst and Bülthoff 2004; Jacobs 2002; Lalanne and Lorenceau 2004; O’Reilly et al. 2012). This has been shown to be true for perception across many different modalities (Alais and Burr 2004; Battaglia et al. 2003; Braem et al. 2014; Butler et al. 2010; Ernst and Banks 2002) as well as for action, specifically to determine hand position (Burns and Blohm 2010; McGuire and Sabes 2009; Sober and Sabes 2003, 2005; van Beers et al. 1999). To date, it has been assumed that multisensory weights are based on task-dependent (e.g., Sober and Sabes 2005) and effector-dependent (e.g., Ren et al. 2007) sensory reliability requiring an explicit real-time neuronal representation of variability (Fetsch et al. 2012; Knill and Pouget 2004; Vilares et al. 2012). Instead, sensory reliabilities could be learned through experience, which would predict a default weighting of different sensory modalities. The latter would predict that individual sensory reliabilities in specific unimodal experimental conditions should be poor predictors for multisensory weightings, a prediction that is consistent with what has been observed in some visual-vestibular heading estimation experiments (Butler et al. 2010; Zaidel et al. 2011). On a similar note, within the perception domain, it has been demonstrated that the weights of multiple visual cues may not be entirely dependent on their variances (van Beers et al. 2011).

Here we tested which of the two above hypotheses (reliability-based integration vs. learned weights) best described visual-proprioceptive integration during reaching. To do so, we asked participants to carry out a reaching task in which we introduced a visual-proprioceptive conflict with shifting prisms (similar to Rossetti et al. 1995) to measure multisensory weights. The prisms shift the perceived visual location of initial hand position (IHP) before the reach, thus introducing a conflict between the visual (shifted) and proprioceptive (veridical) information about the hand position. This allowed us to estimate the weights attributed to the proprioceptive vs. visual information about the hand. We did so separately for the left and right hands, as it has been shown that left and right arms have different sensory variabilities (Goble and Brown 2008; Wong et al. 2014), predicting different multisensory weighting for reaching if reliability-based integration is used and predicting the same multisensory weights if modality-specific learned weights are used. Hand position estimation requires the integration of both visual and proprioceptive information. The proprioceptive variabilities are dependent on the hands, whereas the visual variability is not (it should not change when using either hand). That is why proprioceptive variabilities should be assessed separately for left and right hands when estimating their respective position. To estimate unisensory reliabilities of vision and proprioception, we used two different tasks: a passive localization task without movements (perceptual) and an active localization task (motor). We collected both passive and active sensory reliability measures since it has previously been shown that multisensory integration can be different between perception and action (Knill 2005). We found evidence supporting modality-specific learned weights rather than reliability-based estimation of hand position for reaching, i.e., we found the same proprioceptive weights for left and right hands despite large differences in proprioceptive reliabilities between the hands as measured in both the perceptual and motor contexts.

METHODS

Participants

Sixteen participants between the ages of 22 and 55 yr (3 men, 13 women; mean age = 32.8 ± 7.6 yr) took part in this study. All but three were naive to the purposes of the study. All participants were neurologically healthy, and all had normal or corrected-to-normal vision. They provided written informed consent to participate in the experiment, which conformed to the Declaration of Helsinki for experiments on human subjects. All experimental procedures were approved by the health research ethics committees in France (CPP Nord-Ouest I, Lyon, 2017-A02562-51) and at the University of Montreal.

Apparatus and Task Design

Participants were seated on a height-adjustable chair, in front of a 30°-slanted table over which they performed reaching movements (Fig. 1A). Their forehead rested on a head support to minimize head movements and so that head position was the same for all participants. Eye movements were recorded through an electrooculogram (EOG) by means of three electrodes placed on the left cheekbone, above the right eyebrow, and on the first thoracic vertebra. The room was completely dark so that there was no visual information about hand position unless the IHP light was illuminated. Each participant completed two sessions separated by a maximum of 1 wk.

Fig. 1.

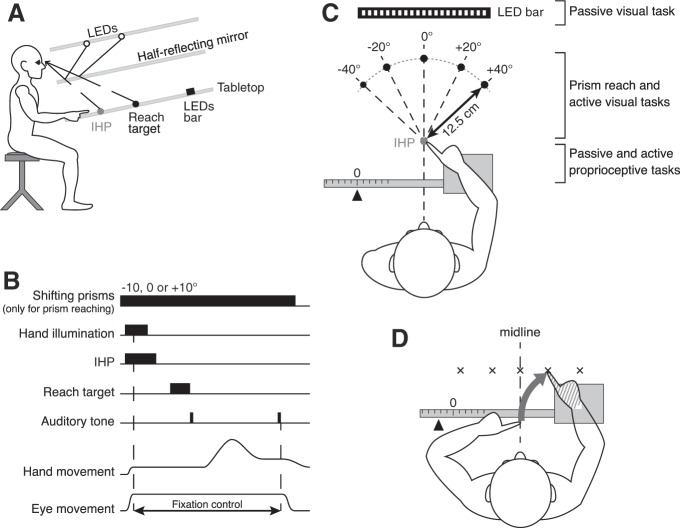
A: apparatus, side view. The participant executed pointing movements on the tabletop reflected from the top of the setup with a half-reflecting mirror. Gray dot represents the initial hand position (IHP) and black dot the reach target. Black rectangle represents the LED bar. B: sequence of the prism reaching and the active visual localization. Hand movements were captured by the Optotrak motion-analysis system. Eye fixation on the IHP was controlled by EOG. The trial did not begin until the participant’s eyes were on the IHP and the EOG calibration was completed. During the active visual localization task, only the 0° prism was presented throughout the block. C: apparatus, bird’s eye view. Five reach targets (black dots) were presented: 1 at the center (0°), 2 on the left side (−20° and −40°), and 2 on the right side (20° and 40°) compared with the cyclopean eye position. The distance from the participants’ eyes to the LED bar was ~63.5 cm. The hand tested during the session (right hand here) was maintained on a sled that moved laterally. The 0 position on the ruler was set so that participants’ index fingertip was aligned with the IHP. Where all tasks were performed within the workspace area is indicated on right. D: active proprioceptive localization. The target hand (hatched) was passively moved to 1 of the 5 target locations. Participants had their eyes closed and had to indicate where they thought their target index fingertip was by reaching with their opposite hand. Reaching errors relative to the target index fingertip were used to determine the variability associated with the target hand localization.

For the prism reach task as well as the active visual localization, red light-emitting diodes (LEDs) were projected onto the tabletop through a half-reflecting mirror (Fig. 1A). The half-reflecting mirror allowed participants to see their hand at the beginning of each trial (when the IHP light was illuminated) but not during the trial itself.

The reliability (variability) of visual and proprioceptive information was assessed in both a passive, perceptual (without reaching movements) and an active, motor localization task (see specific task descriptions below). Thereafter, participants performed a reaching task with shifting prisms to quantify the relative sensory weights given to vision and proprioception during motor planning.

Prism reach experiment: measuring multisensory weights.

This task was used to assess the relative weights given to vision and proprioception during the planning of reaching movements. One of the three prisms (0, −10°, or +10°) was pseudorandomly selected at the beginning of each trial and remained in place for the rest of the trial (sequence of trial depicted in Fig. 1B). We used pseudorandom prism presentation to avoid adaptation to systematic prism-induced displacements of the visual field. After prism selection, hand lighting was switched on so that participants could align their index fingertip with the IHP, which was located 50 cm away from the participants’ eyes. Once the index finger remained still for 500 ms, hand lighting was extinguished. A 300-ms EOG calibration was performed while participants were looking at the IHP; they had to maintain fixation at this position until the end of the trial. The IHP was then switched off, and after a 500-ms gap one of the five reach targets appeared for 700 ms before being extinguished; targets were located on a radius 12.5 cm away from the IHP, at −40°, −20°, 0, 20°, and 40° (Fig. 1C). A first auditory tone serving as a “go” signal was then heard. Participants were asked to make smooth, rapid movements to the remembered position of the target. After the movement ended (detected online), a second tone signaled to the participants to return to the IHP (remembered, not visible). Participants were asked to remain with eyes fixating on the remembered location of the IHP throughout the trial, so all the reaching movements were made in peripheral vision. Eye position was monitored online, and if eye fixation was broken the trial was aborted and replayed later. The prism reaching task was performed in the middle workspace, between the IHP and the five visual reach target locations.

We used shifting prisms that displaced vision and created a conflict between visual and proprioceptive feedback of the hand (Fig. 2, A–C). The horizontal pointing errors resulting from the visual displacement allowed us to compute the sensory weights of vision and proprioception. Three shifting prisms were used (Fig. 2D): one that did not displace vision (0° prism), one inducing a rightward visual shift of 10° (+10° prism), and another inducing a leftward visual shift (−10° prism). With respect to the orthogonal distance between the participants’ eyes and the tabletop on which targets were projected, a 10° prism shift displaced the visual positions of the hand and the central target by 70.5 mm. Because of their eccentricities, each of the four remaining targets had a slightly different displacement. Participants completed 12 trials for each of the five reach targets and the three prismatic conditions, totaling 180 trials per hand and participant. Trials were split into two 90-trial blocks. Participants performed two blocks in the first session with the right hand pointing and two blocks in the second session with the left hand pointing.

Fig. 2.

A: filled and open figures represent hands’ and targets’ real positions and positions viewed through a rightward shifting prism, respectively. Dashed arrows correspond to programmed movements; solid arrows depict resulting movements, starting from the felt (i.e., real) hand position. Errors equal the target horizontal displacement minus the origin of the planning vector. When the reach is planned based on visual information only, the movement vector is encoded from the seen hand position. Since eccentricities are different for the hand and the target, they are subject to slightly different deviations and small errors are observed after the resulting movement. B: when using proprioceptive information only, the programmed and the resulting movements are the same because they both start from the felt/real hand position coded by proprioception. Pointing errors are equal to the prismatic shift for the corresponding target. C: when vision and proprioception are integrated, the programmed movement is encoded from an integrated position of the hand, located between the felt and the seen hand locations. Thus, based on the horizontal pointing errors, it is possible to compute the weights that a given participant assigns to vision and proprioception. D: prisms used in our study induced a visual shift of 10° to the left (−10° prism, dashed-outline targets) or to the right (+10° prism, solid-outline targets). E: sensory weight estimation. Individual mean X-errors were plotted as a function of the prismatic shift applied to each target. The slope of the linear regression was calculated. Participants with a slope close to 0.02 (horizontal dashed line) rely more on vision (light gray area). In contrast, the closer the slope to 1 (solid line), the more participants rely on proprioception (dark gray area).

Passive, perceptual visual localization task.

This task was designed to measure the reliability (variability) of the visual information through psychophysics without any reaching movements. We used 25 small red LEDs on the tabletop, aligned horizontally on a bar (Fig. 1C). LEDs were spaced at 1° intervals and covered a visual field from −12° to +12° (negative angles indicate leftward relative to straight-ahead from the participant’s point of view). The task of the participant was to respond (2-alternative forced choice) whether a presented LED was on the left or right of the midline (straight-ahead direction, 0°). Each trial consisted of a presentation of a randomly selected LED that remained visible until the end of the trial (i.e., until the participant verbally gave his/her answer to the experimenter). There was no constraint of time for the response. Each block was composed of 78 trials, with central targets having more repetitions than peripheral ones (in order to construct psychometric functions). Each participant completed one block of trials during the first experimental session. The passive visual localization task was performed in the far workspace; the LED bar was located ~63.5 cm away from participants’ eyes.

Passive, perceptual proprioceptive localization task.

For the passive, perceptual proprioceptive localization task, the arm was held on a sled that could move from left to right (parallel to the torso) along a horizontal graduated ruler (Fig. 1C). Participants had to respond whether their index fingertip was located to the left or right of midline (2-alternative forced choice). The setup was built in such a way that a displacement of 1 cm indicated by the ruler was almost equivalent to a 1° displacement of the hand (12 cm = 11.89°). The distance of the hand from the body corresponded with the IHP used for the reaching experiment (see Prism reach experiment: measuring multisensory weights). Thirteen proprioceptive targets from −12° to +12° relative to midline and spaced in 2° intervals were randomly presented to the participant. The most eccentric proprioceptive targets (i.e., −12° and +12°) were tested twice, and the more central targets were tested more often (up to 10 times for the 0° target). The experimenter passively moved the sled to align the fingertip to each of the different randomly selected locations. To prevent participants from estimating the position of their hand based on the duration and/or the magnitude of the movement, the experimenter switched from one position to another by moving the sled back and forth a number of times before arriving at the target position. Thereafter, the participants were asked to report whether their index fingertip was on the left or on the right relative to their midline (straight-ahead direction, 0°). They kept their eyes closed during the entire block of 78 trials. Participants performed one block with the right hand placed on the sled during the first experimental session and another block with the left hand during the second session. This task was performed in the near workspace, in the area surrounding the IHP.

Active, motor visual localization task.

This task was designed to assess visual reliabilities through visually guided reaching movements to one of the five randomly presented targets (Fig. 1C). The trial sequence was the same as the prism reach task, except that the prism that did not displace vision (0° prism) was the only one that was presented at the beginning of the trial. Participants completed 10 trials for each of the five targets, totaling 50 trials per hand. They performed one block using each of the left and right hands during the first and second experimental sessions, respectively. As for the prism reach, the active visual localization task was performed in the middle workspace.

Active, motor proprioceptive localization task.

This task was designed to assess proprioceptive reliabilities during active movements. We asked participants to match the location of a target hand (specifically index fingertip), which was moved passively on the sled, by reaching to it with the opposite hand (Fig. 1D). Five target hand positions were chosen: one at the center (0°), two on the left (−5° and −11°), and two on the right (+5° and +11°) with respect to the participants’ midline and on the same horizontal plane as the IHP in the prism reach experiment described above. Positions were randomly determined; participants had their eyes closed and were asked to indicate where their target hand (index fingertip) was by reaching with their opposite hand slightly above the target hand’s index fingertip from a central IHP. In this task, proprioceptive reliability for the left hand was assessed in the condition where the left hand was the target and the right hand was pointing. In the same way, right hand proprioceptive reliability was assessed when participants localized their right target hand by reaching with the left hand. As in the passive localization task, to prevent participants from estimating the position of their target hand based on the duration and/or the magnitude of the movement, the experimenter switched from one position to another by moving the sled back and forth a number of times before arriving at the target position. Participants completed 10 trials for each of the five targets, totaling 50 trials per hand and participant. They performed one block in the first session with the right hand in the sled and the left hand pointing and vice versa for the second session. Just like the passive proprioceptive localization task, the active proprioceptive localization task was performed in the near workspace.

Data Analysis

In the prism experiments, we were interested in horizontal errors (x-axis), since the prisms shift vision horizontally. First, the X-errors expected when using only vision or proprioception were computed for each target and prism. These errors were obtained by subtracting the origin of the planned movement vector from the horizontal target displacement induced by prisms. As shown in Fig. 2B, when using proprioception only, errors are equal to the prismatic deviation corresponding to the target presented. When relying only on vision (Fig. 2A), small errors are expected when applying prisms because eccentricities, and thus prismatic deviations, are not the same for hand position and targets. Then, X-errors were plotted as a function of the prismatic deviations (for all targets) and linear regressions were performed (Fig. 2E). A slope of 1 was found when using proprioception only (α_p = 1), while the slope when using vision only was equal to 0.02 (α_v = 0.02). To evaluate the proprioceptive weights for every participant, the slope (α) of the linear regression between the individual mean X-errors for each target and the corresponding prismatic deviations was first computed. The slope of the linear regression corresponds to the relative weights of vision and proprioception. Therefore, participants showing a slope close to 0.02 give more weight to vision, whereas those with a slope closer to 1 rely more on proprioception (Fig. 2E). Then, each participant’s proprioceptive weight (W_p) was calculated as follows:

$${\text{W}}_{\mathrm{p}}=\frac{\text{α}-{\text{α}}_v}{{\text{α}}_{\mathrm{p}}-{\text{α}}_v}$$ (1)

This allowed correction for α_v, which was different from 0. When W_p equals 0 the participant relies completely on vision, whereas W_p is equal to 1 if he/she relies entirely on proprioception.

For the passive, perceptual localization tasks, the proportion of rightward choices was plotted as a function of target position. For each participant, three separate psychometric curves were calculated, one for vision and one for right hand and left hand proprioception respectively. The data were fitted with cumulative Gaussians using the psignifit toolbox (Wichmann and Hill 2001a, 2001b) for MATLAB (MathWorks, Natick, MA). The psychometric model we used included a lapse rate that was set to 10%. The psychometric function for a representative participant is depicted in Fig. 3. The just-noticeable difference (JND) was computed as the inverse slope of the psychometric curve between 30% and 70% of rightward responses. We used the JND as a measure of variability; the steeper the psychometric curve’s slope, the smaller the variability.

Fig. 3.

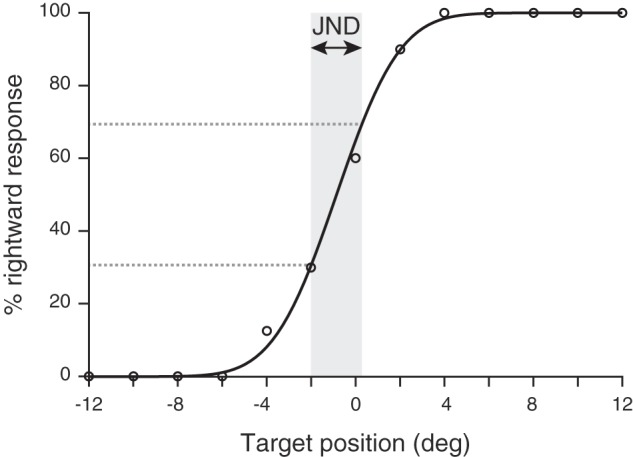
Psychometric curve from 1 representative participant for the passive proprioceptive localization task. The percentage of rightward response is represented as a function of the target hand position). The participant’s response data (open circles) are fitted with a psychometric function. JND corresponds to the measure of the proprioceptive variability.

During active, motor localization tasks, positions and movements of both index fingers were recorded with the Optotrak motion-analysis system (NDI, Waterloo, ON, Canada). Data were sampled at 1,000 Hz, and finger movements were measured in three-dimensional space (in mm) relative to the IHP. Hand movements were detected with a velocity criterion (80 mm/s). End positions of the index fingertip were recorded for each trial, and pointing errors were computed with MATLAB, by subtracting the end position of the finger from the target position. Errors in the horizontal x-axis (X-errors) were thus calculated for each pointing movement and expressed in millimeters, such that a negative error would correspond to an end point to the left of the target. The visual variability (${\text{σ}}_{\text{V}}^2$) of each participant was defined as the standard deviation of the mean reach X-errors relative to the visual targets, whereas left and right hand proprioceptive variabilities (${\text{σ}}_{\text{P}}^2{}_{\text{l}}$ and ${\text{σ}}_{\text{P}}^2{}_r$) corresponded to the standard deviation of the mean X-errors when reaching to the left and right target hands, respectively.

On the basis of the measured estimates of unisensory variabilities, we predicted the multisensory proprioceptive weights (W) through simple Bayesian cue integration (Gaussian assumption) and calculated them for both the passive and active localization tasks as follows:

$${\text{W}}_i=\frac{{\text{σ}}_{\text{V}}^2{}_i}{{\text{σ}}_{\text{V}}^2{}_i+{\text{σ}}_{\text{P}}^2{}_i}$$ (2)

with i corresponding to the hand that was tested (left or right). This was the same for the passive localization task, but since vision was tested without movements only one visual variability was available. The two sets (active and passive) of predicted multisensory weights were then evaluated against the measured multisensory weights from the prism experiment.

For both left and right hands, normal distributions of the proprioceptive weights as well as the variabilities and the biases of vision and proprioception were assessed with Shapiro-Wilk tests. Given that some variables were not normally distributed, nonparametric tests were used for subsequent analyses. Correlations between parameters for the left and right hands were calculated, and the strength of these relationships was assessed by Spearman’s rank correlation coefficients and Wilcoxon signed-rank tests. When a Wilcoxon test was found to be nonsignificant, equivalence testing was additionally performed to determine whether both correlated variables were similar. In traditional significance tests, the absence of an effect can be rejected but not statistically supported. Equivalence tests aim to provide support for the null hypothesis (Lakens 2016). We used the two one-sided test procedure (Schuirmann 1987), where equivalence is established at the α level if the (1 − 2α) × 100% confidence interval for the difference in means falls within the equivalence interval [−Δ; Δ]. In the two one-sided test approach, two t-tests are used and equivalence is declared only when both tests are statistically rejected. The equivalence bounds were based on the smallest effect size our study had sufficient power to detect (d_z = 0.75), such that Δ = d_z × SD_diff, where SD_diff is the standard deviation of the difference in means. Moreover, for each individual participant, we calculated whether the difference between the left and right hand parameters was significantly different from 0. To do that, the difference D between left and right hand parameters was first computed individually such that D = left − right. Then, the total standard deviation Σ_D was calculated for each participant as follows: ${\text{Σ}}_D=\sqrt{{\text{Σ}}_{\text{L}}^2+{\text{Σ}}_{\text{R}}^2}$. D was considered significantly different from 0 when

$$D\pm {\text{Σ}}_D>0\hspace{0.17em}\text{if}\hspace{0.17em}D>0\text{\hspace{0.17em}or\hspace{0.17em}}D\pm {\text{Σ}}_{\text{D}}<0\hspace{0.17em}\text{if}\hspace{0.17em}D<0$$ (3)

For all analyses, the statistical threshold was set at P < 0.05 (2-tailed tests) and α = 0.05.

RESULTS

The hand location during movement planning is determined through the integration of both visual and proprioceptive information. The visual variability should be the same regardless of the hand that is tested; therefore, the multisensory integration process requires the estimation of proprioceptive reliabilities for the left and right hands independently. Visual-proprioceptive integration predicts that the visual and proprioceptive signals are combined and weighted according to their respective reliabilities. This is what is generally assumed to be true; however, to our knowledge this has never been verified. To test this prediction explicitly, we first computed the relative contributions of vision and proprioception to reaching for both the left and right hands. We then independently evaluated the visual reliability as well as the left and right hand proprioceptive reliabilities in a passive and an active localization task. Finally, we used these independent measures to test whether multisensory integration weights could be predicted by the sensory reliabilities. The following sections describe the results of these three steps in detail.

Proprioceptive-Visual Weights

The relative contributions of vision and proprioception to reaching planning were assessed by pointing toward visual targets while shifting prisms were applied. Sensory weights were estimated for the left and right hands separately. As depicted for a typical participant in Fig. 4A, reach end points while using the right hand are deviated toward the direction of the shifting prisms that have been applied (e.g., end points on the left side of the target when the −10° prism is presented). As can be seen, this participant tended to undershoot the targets in depth (Y-direction), but this occurred across all targets and prism shifts. We presumed this was an overall bias and analyzed only the horizontal reach error. To evaluate the proprioceptive weight, we performed a linear regression between observed mean reach errors (deviations in X-direction) for each target and the corresponding prismatic deviations (Fig. 4B). In Fig. 4B, the X-errors from Fig. 4A are shown as a function of the prismatic shift. Since the hand and the target had different eccentricities relative to midline, the horizontal displacements induced by prisms were not the same for both. Therefore, if only visual information was used one would predict small reach errors across all three prism conditions (Fig. 2A). In contrast, if vision was ignored a reach end-point displacement equivalent to the prism shift would be expected (Fig. 2B). Here, using Eq. 1, we calculated the proprioceptive weight for this participant for the right hand as 0.37. This weight can be interpreted as meaning that the participant relied on vision (1 − 0.37 = 0.63) more than on proprioception.

Fig. 4.

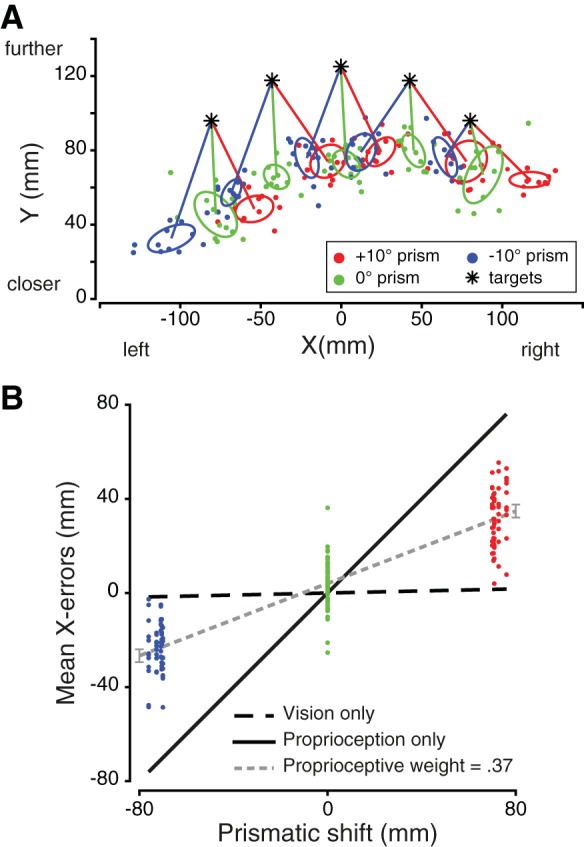
A: reach end points of 1 participant using his right hand, in the 3 prismatic conditions: 10° rightward, neutral (0°), and 10° leftward shifting prisms. The 1-standard deviation ellipses were computed for each target and each prism. The center of the ellipses corresponds to the mean error in each condition. B: estimation of the participant’s sensory weights when using the right hand. Data points for the −10° (blue) and +10° (red) prisms are more scattered because each of the 5 targets is displaced slightly differently depending on its eccentricity. The slope of the linear regression is 0.38. Thus, according to Eq. 1, the proprioceptive weight equals 0.37, whereas the visual weight is 0.63.

We calculated the proprioceptive weights in this manner for both hands separately for each of the 16 participants. We then averaged the individual proprioceptive weights across all participants for each hand. The mean proprioceptive weights for left and right hands were equal to 0.55 (±0.17) and 0.54 (±0.16), respectively. A one-sample Wilcoxon signed-rank test showed that, for both hands, the average proprioceptive weights were significantly different from 0 and 1 (all P < 0.001). These results show that participants used a combination of visual and proprioceptive information, rather than just one or the other, when planning a reaching movement. Importantly, we directly compared individual proprioceptive weights for the left and right hands (Fig. 5). Left and right proprioceptive weights were highly correlated (r = 0.94, P < 0.001; R² = 0.75, P < 0.001), suggesting that the sensory reliabilities determining these weights were very similar across both hands within each participant. Moreover, the 95% confidence interval for the linear regression between left and right proprioceptive weights was [0.63; 1.25]. Additionally, we tested whether there were overall differences in weights between left and right hands across all participants. A Wilcoxon test comparing the left and right hand weights showed no significant difference (Z = 0.98, P = 0.33), so an equivalence test was then performed. The equivalence region was set at Δ = d_z × SD_diff = 0.75 × 0.084 = 0.06. The 90% confidence interval for the difference in the means was [−0.02; 0.05] and was significantly within the equivalence bounds [t(15) = −2.95, P = 0.01]. These results indicate that, across the population, the weights for the left and right hands were equivalent. In other words, the range of proprioceptive (and visual) weights were similar for the left and right hands across participants (ranging from 0.37 to 0.94 for the left hand and from 0.37 to 0.91 for the right hand). Finally, the difference between the left and right proprioceptive weights was computed for each individual participant and compared to 0. As depicted in Fig. 5, 4 participants showed a significant difference while the 12 remaining participants showed no significant difference between the left and right proprioceptive weights.

Fig. 5.

Correlation between left and right hand proprioceptive weights. Error bars illustrate the 95% confidence intervals for the regression coefficients calculated individually for left and right hands (vertical and horizontal bars, respectively). Dashed gray line represents the line of best fit for the significant correlation for the 16 participants (r = 0.94, P < 0.001; R² = 0.75, P < 0.001), which is very close to the perfect positive correlation. Solid line corresponds to the line of unity, open circles represent participants who do not show left/right difference, and filled circles represent participants showing a significant left/right difference.

We also investigated whether fast and slow movements had different weights. To do that, a median split was performed on the movement durations for each participant and each hand and the proprioceptive weights were then computed and compared. The proprioceptive weights for slow and fast movements were significantly different for both the left [slow = 0.59, fast = 0.46; t(15) = 3.5, P = 0.004] and the right [slow = 0.61, fast = 0.42; t(15) = 6.0, P < 0.001] hands. However, the left and right hand proprioceptive weights were not significantly different from each other for either slow [t(15) = −0.7, P = 0.48] or fast [t(15) = 1.5, P = 0.15] movements. Thus, although there were differences in visual-proprioceptive integration for fast and slow movements, the left and right hand multisensory integration weights were not different from one another for either slow or fast movements.

Sensory Reliabilities of Left and Right Hands and Vision

To obtain an independent evaluation of visual and proprioceptive variability, we next compared the sensory reliabilities of the left and right hands during the passive and active localization tasks. If proprioceptive weights were based on actual sensory reliabilities, we should observe similar strong positive correlations between the sensory variabilities of the left and right hands. Each sensory reliability was assessed by the variability. We tested for significant correlations between left and right hand parameters to determine whether the same proprioceptive weights across both hands could be explained by similar sensory reliabilities between left and right hands.

Passive localization tasks.

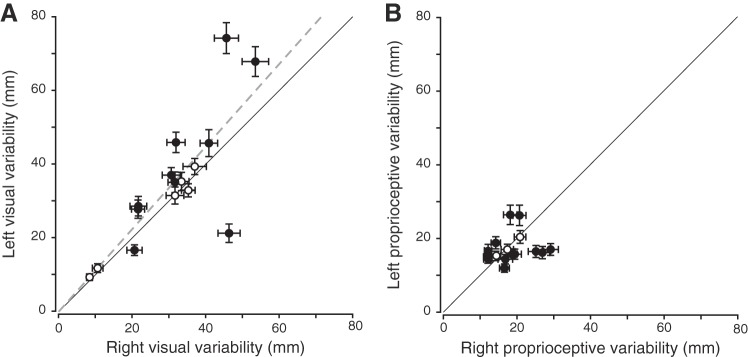
The participants were presented with visual or proprioceptive targets at different locations and were asked to respond whether they were on the left or the right relative to the body midline. Because sensory modalities were tested without movements in this particular context, we only measured variability for visual targets once, whereas we measured this twice for proprioceptive targets: once for each hand. Therefore, correlations between left and right hands were not possible for vision in the passive localization task. For proprioception, the correlation between left and right proprioceptive variabilities was nonsignificant (P > 0.05), as depicted in Fig. 6. This result indicates that, unlike the weights, each participants’ variabilities were not the same across the two hands. Pairwise comparisons showed that the range of proprioceptive variabilities (Z = −1.29, P = 0.20, left hand range = [0.05; 1.28], right hand range = [0.14; 1.08]) did not differ between left and right hands across the population. At the individual level, half of the participants showed a significant difference between the left and right proprioceptive variabilities (Fig. 6).

Fig. 6.

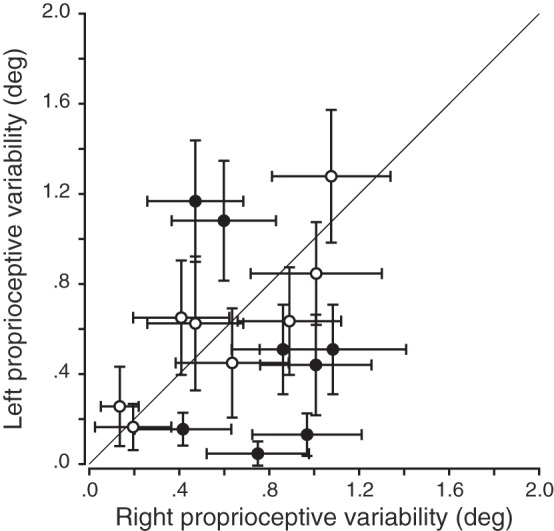
Correlation between left and right proprioceptive variabilities in the passive localization task. Error bars are the 95% confidence intervals for the JNDs. No significant correlation between left and right hands was observed for the proprioceptive variabilities (P > 0.05). Solid black line corresponds to the line of unity, open circles represent participants who do not show left/right difference, and filled circles represent participants showing a significant left/right difference.

Active localization tasks.

The participants were asked to point toward either visual or proprioceptive targets, with their left and right hands separately. This task was designed to measure the sensory reliabilities in a movement context similar to that used in the reaching task (but without shifting prisms). The performance of a typical participant is depicted in Fig. 7 while using the right hand to reach toward visual (Fig. 7A) or proprioceptive (Fig. 7B) targets. For reaches to visual targets, there was a positive correlation between reach variability when using left and right hands (Fig. 8A; r = 0.72, P = 0.002; R² = 0.62, P < 0.001). However, across the population, the left hand visual variability was greater overall than the right hand visual variability (left hand range = [9.38; 74.34], right hand range = [8.42; 53.53]; Z = 2.02, P = 0.04). In addition, 10 of 16 participants showed different hand visual variabilities between the left and right hands (Fig. 8A).

Fig. 7.

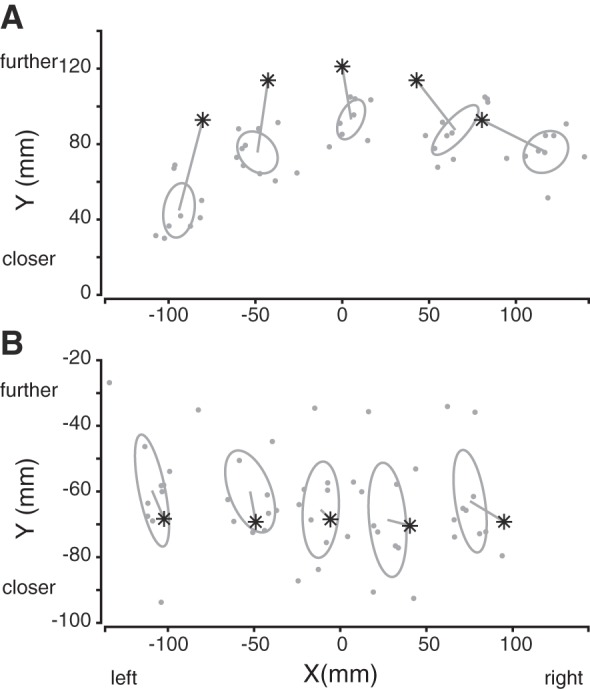
Right hand reach end points of 1 participant when pointing toward visual (A) and proprioceptive (B) targets. Our workspace area is centered around the initial hand position, whose coordinates are thus (0,0). Asterisks represent the targets, and the 1-standard deviation ellipses were computed for each target. The center of the ellipses corresponds to the mean end-point error.

Fig. 8.

Correlations between left and right hand variabilities for vision (A) and proprioception (B) in the active localization task. Error bars are the bootstrapped standard deviations. Dashed gray line illustrates the line of best fit for the significant correlation. Solid black line corresponds to the line of unity, open circles represent participants who do not show left/right difference, and filled circles represent participants showing a significant left/right difference. A: there was a significant correlation between left and right visual variabilities (r = 0.72, P = 0.002; R² = 0.62, P < 0.001). B: no significant correlation was observed between left and right proprioceptive variabilities (P > 0.05).

Regarding reaches to proprioceptive targets (Fig. 8B), no significant correlation was found between left and right hand variabilities (P > 0.05). Thus we also found differences in the proprioceptive variabilities between the left and right hands within each individual for this task. Note that proprioceptive variability of the right hand was evaluated in the condition in which participants had to localize their right target hand when reaching with their opposite, left hand. Similarly, left hand proprioceptive variability was obtained when the left hand was the target hand. This is because we wanted to measure the precision of proprioceptive spatial position for each hand. Pairwise comparisons did not show differences in the overall proprioceptive variabilities between the two hands (Fig. 8B; Z = −0.52, P = 0.61; left hand range = [11.95; 26.42], right hand range = [12.03; 29.14]). At the individual level, 13 of 16 participants showed a significant difference between the left and right hand proprioceptive variabilities (Fig. 8B). Taken together, these findings suggest an influence of the visual reach target information on reach variability rather than an influence of the hand used.

In summary, we found no correlation between the left and right hand proprioceptive variabilities for each participant in both the active and passive localization tasks. These findings demonstrate differences in left and right hand proprioceptive variability at the individual participant level that should—if combined in a statistically optimal fashion with vision—result in different proprioceptive weights for left and right hands. This is explicitly evaluated in Testing for Statistical Optimality and contrasted against the proprioceptive weights found in the multisensory integration task (with prism shifts).

Testing for Statistical Optimality

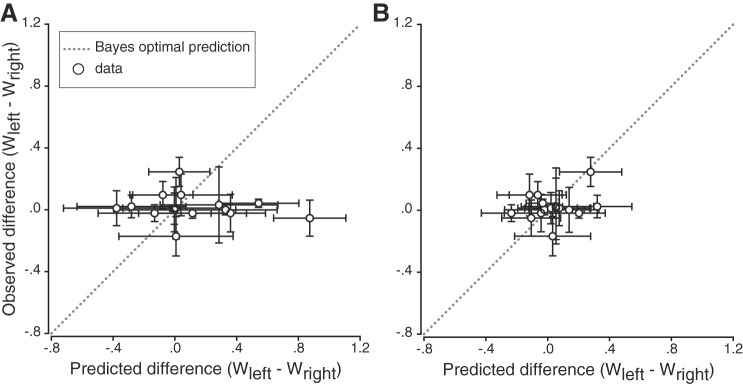
If sensory variability is indeed used to determine multisensory integration weights, individual participant differences between left and right proprioceptive reliabilities should result in different proprioceptive weights between the hands. To determine whether the attribution of sensory weights was in line with the Bayes-optimal cue combination hypothesis, the proprioceptive weights observed during the reaching task (computed through linear regression; see Figs. 2 and 4 and methods) using shifting prisms were compared to those predicted from the sensory variabilities measured in the passive and active localization tasks (Eq. 2). The differences in proprioceptive weights between left and right hands were then calculated (W_left − W_right) for each participant. A difference equal to 0 means that the sensory weights are the same for left and right hands. Figure 9 depicts the individual participants’ observed differences in proprioceptive weights (prism shift task) plotted as a function of the differences predicted by the Bayesian cue combination model (separately for active and passive tasks, Fig. 9, A and B, respectively). In both the passive and the active localization tasks, most participants showed intermanual differences in predicted proprioceptive weights. However, these differences did not correlate with measured differences in proprioceptive multisensory integration weights (all P > 0.05), contradicting reliability-based proprioceptive weight computations. Moreover, simple linear regressions were performed to determine whether there were significant relationships between observed and predicted differences in proprioceptive weights. The results showed that there was no linear relationship between the two variables, either for the passive (R² = 0.02, P = 0.57) or the active (R² = 0.08, P = 0.30) localization task.

Fig. 9.

Observed differences plotted as a function of predicted differences in proprioceptive weights (W_left − W_right) computed with the sensory variabilities measured in the passive (A) and active (B) hand localization tasks. Vertical error bars are the 95% confidence intervals for the regression coefficients, and horizontal error bars are the standard deviations obtained by bootstrapping. Gray dotted line illustrates the Bayesian optimal prediction (i.e., observed and predicted sensory weights are the same). Most participants’ differences in proprioceptive weights were around 0 for both localization tasks.

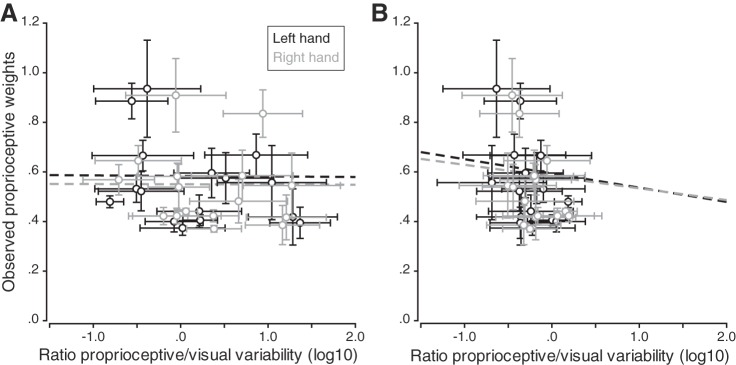
An alternative way to evaluate whether visual and proprioceptive variability was accounted for is to look at the ratio of proprioceptive variance over visual variance. If for a given participant the ratio is high (i.e., if proprioceptive variability is greater than visual variability), the proprioceptive weight should be low for that participant. Thus, when plotting observed proprioceptive weights against these ratios, we should observe negative correlations for both left and right hands. Correlations were computed separately for left and right hands, in both active and passive localization tasks (Fig. 10, A and B, respectively). None of the four correlations reached significance (all P > 0.05), and the four simple linear regressions showed that the ratio of sensory variances did not predict the proprioceptive weights that we observed (all P > 0.05). These results suggest that the individual sensory variabilities we measured were not taken into account to determine the sensory weights used for multisensory integration.

Fig. 10.

Observed proprioceptive weights as a function of the log10 of the ratio of proprioceptive and visual variabilities measured in the passive (A) and active (B) hand localization tasks. Vertical error bars are the 95% confidence intervals for the regression coefficients, and horizontal error bars are the bootstrapped standard deviations. Dashed lines correspond to the correlations between the observed proprioceptive weights and the ratio of sensory variabilities; none of them was significant (all P > 0.05).

DISCUSSION

Multisensory integration is conceived as an optimal combination of information from several sensory modalities to gain a more accurate representation of the environment and our body (Deneve and Pouget 2004). Bayesian theory postulates that the weight given to each sensory modality is proportional to the reliability (i.e., the inverse variance) of each signal (Deneve and Pouget 2004; Ernst and Banks 2002; Ernst and Bülthoff 2004; Jacobs 2002; Lalanne and Lorenceau 2004; O’Reilly et al. 2012). While overall data seem to be consistent with this prediction (e.g., Ernst and Banks 2002; Körding and Wolpert 2004; Sober and Sabes 2005; van Beers et al. 1999), it has to our knowledge never been critically tested. Here we devised such a test and show that differences in proprioceptive reliabilities of the left and right hands are not predictive of differences in multisensory weights for reaching.

Limitations

There are several important limitations to our study. One possible limitation is that the prism shift has introduced a sensory conflict between vision and proprioception. In that case, following the causal inference framework (Kayser and Shams 2015; Körding et al. 2007; Shams and Beierholm 2010), one would expect either that vision was not used at all (total breakdown of causality), which was not observed, or that it would be weighted less (partial breakdown of causality) than predicted. The result of a partial breakdown of causality would be a reduced visual weighting that should result in a slope <1 (but >0) in Fig. 9. However, we did not find any relationship between predicted and observed weights, although on average both vision and proprioception were weighted about equally (no total breakdown of causality). Thus we do not think that the introduction of prism shifts can explain our findings.

We were interested in how visual and proprioceptive information about the hand are weighted during the planning of reaching movements, that is to say at the IHP before movement initiation. One may argue that since our tasks measuring visual and proprioceptive variabilities were performed in different areas of the workspace (as indicated in Fig. 1C), they might therefore differ from those performed at the IHP. Both passive and active proprioceptive localization tasks were performed in the near workspace, close to the IHP area, whereas passive and active visual localizations tasks were performed in the further and the middle workspace, respectively. It has been shown that hand localization is more precise for positions closer to the shoulder than further away (van Beers et al. 1998) and also that target distance did not significantly affect visual localization precision. The visual targets they used were roughly arranged between 35 and 55 cm from the cyclopean eye. Our workspace area did not exceed 63.5 cm (position of the LED bar), so distance should have no (or very little) influence on the visual reliabilities we measured. In addition, the passive visual task using the LED bar in the far workspace was a left-right discrimination, and vision has been shown to be more precise in azimuth (horizontal plane) than in depth (van Beers et al. 1998). These insights suggest that our measures of visual and proprioceptive variabilities are appropriate to investigate visual-proprioceptive integration about the hand when planning a reaching movement. More importantly, however, where possible we compared left and right hand variabilities as well as weights within the same task and not across tasks.

We assume that our perceptual and motor tasks are appropriate to measure proprioceptive variability of the hands. We chose these tasks because one could argue in two different ways regarding the brain’s evaluation of sensory reliability: 1) The brain uses the actual sensory reliability that is inherent to performing a certain task—captured by our motor task. Therefore we measured visual and proprioceptive variabilities using a reaching task similar to the prism task. 2) The brain uses the perceived reliabilities in a default fashion—captured by our perceptual task. This follows a prominent thesis by which perception can guide our actions (Binsted and Elliott 1999; Both et al. 2003; Brenner and Smeets 1996; Elliott et al. 2009; Jackson and Shaw 2000; McCarley et al. 2003; Sheliga and Miles 2003; Taghizadeh and Gail 2014; van Donkelaar 1999; Westwood et al. 2001). However, neither reliability measure could explain our multisensory integration data during action. This was less surprising for the perceptual context, since previous research suggested that multisensory integration was different for perception and action (Blangero et al. 2007; Dijkerman and de Haan 2007; Knill 2005), in line with visual information processing within the ventral and the dorsal streams (Goodale and Milner 1992). Moreover, a recent study showed that spatial priors learned in a sensorimotor task do not generalize to a computationally equivalent perceptual task, thus suggesting that priors differ between perception and action (Chambers et al. 2017). It was much more surprising that our motor task did not predict multisensory weightings. As discussed below, we think that this might point toward a learned, default weighting rather than an individual trial and effector reliability-based weighting of multisensory information for reaching.

Several previous studies have reported effects of nonuniform priors on perception and action (Fernandes et al. 2014; Jacobs 1999; Körding and Wolpert 2004; Verstynen and Sabes 2011). Unlike uniform priors where all prior probabilities are equal, nonuniform priors favor some particular values over others and can bias the cue combination results. It is possible that such priors also play a role in visual-proprioceptive integration tasks. For example, the sensory variability measured in the active proprioceptive localization task includes both the effector and target variabilities. This target variability can be described as a nonuniform prior because it cannot be isolated and excluded, thus leading to an overestimation of the variance and therefore a potential bias in the multisensory weights. In that case, the prior would act like another cue in the multisensory integration. The result of that would be a reduction of the sensory weights because the denominator of the Bayesian weight term would have an additional, prior variance term (assuming Gaussian distributions), or in other words the sum of all weights (visual, proprioceptive, prior) still has to be 1, thus reducing the visual and proprioceptive weights when introducing a prior. As a result, this would predict a reduced slope when comparing observed to predicted weights in Fig. 9. However, the fact that we did not find any relationship whatsoever between observed and predicted weights indicates that the potential influence of priors cannot explain our results.

Interpretation of Main Findings

We found a strong correlation between the sensory weights of left and right hands (Fig. 5), but no such correlation was present between left and right proprioceptive reliabilities, in either the passive or the active localization task (Figs. 6 and 8). Indeed, individual sensory weights were very similar between both hands despite individual differences in left and right hand proprioceptive reliabilities measured in the perceptual and motor contexts. Jones et al. (2010) also assessed the precision of proprioception in two different contexts, using passive and active localization tasks similar to ours: judgment of proprioceptive hand location relative to visual or proprioceptive reference for the former and reaching with a seen hand to the proprioceptive hand location (unseen other hand) for the latter. The authors reported that the precision of proprioceptive localization did not differ significantly between left and right hands across the population; however, they did not investigate whether there was a significant difference between left and right hands of each individual participant.

Moreover, in the present study, the relative variability of vision and proprioception, i.e., the ratio measured for each hand in the motor context, also failed to predict the sensory weights. It was not possible to know whether a similar relationship measured in the passive localization task would predict the relative sensory weights of the two hands because the visual variability was measured by a unique verbal judgment and thus cannot be compared between hands. These findings are not in agreement with the predictions made by the Bayesian model of multisensory integration. Thus it seems that the sensory weights that are used for multisensory integration during reach planning are independent of left and right hand sensory reliabilities.

Our results rather suggest that the sensory weighting of hand location for reaching is task dependent and learned. Task dependence has previously been suggested in a different context, although interpreted as an attentional effect (Sober and Sabes 2005). The similar sensory weights we found across hands suggest that they might be determined through learning the contingencies of the task rather than being specific to each effector. Our findings are in line with previous research showing that in certain cases the brain does not seem to compute a maximum-likelihood estimate of hand position (Jones et al. 2012). Likewise, when performing a bimanual task, proprioceptive signals from left and right arms are not assigned integration weights that are related to their respective proprioceptive reliabilities (Wong et al. 2014). This latter study showed that unimanual proprioceptive variabilities were different between the two limbs and that the bimanual estimate of hand position did not result from an optimal combination of proprioceptive signals from left and right limbs. Instead, the nervous system seemed to ignore information from the arm with the lower reliability and to use only signals from the limb that has the best proprioceptive acuity for the bimanual task. Generalized motor programs (GMPs) have been introduced by Schmidt (1975) and are thought to specify generic, but not specific, instructions to execute movements. This allows for motor equivalence, which is the capacity to achieve the same movement output irrespective of the effector used. The GMP comprises invariant features describing the overall movement pattern as well as parameters that are context dependent and adjusted according to the goal of the action. Invariant components of the GMP might specify a common proprioceptive weight to both left and right hands, whereas parameters induce small variations between the effectors, as observed in the present study. Invariant features of the GMP are likely to be learned early in development, since children typically refine their reaching movements during the first years (Hadders-Algra 2013). In contrast, parameters are task dependent and might involve learning on a shorter timescale, maybe on a trial-by-trial basis, allowing for adjustments to specific situations.

One implication of Bayes-optimal integration is that the brain should have a good representation of sensorimotor variabilities. However, some studies have demonstrated that the motor system does not always exactly estimate motor variability. It seems that, under some circumstances, human observers underestimate their own motor uncertainty (Mamassian 2008) and do not show an accurate estimate of their motor error distributions (Zhang et al. 2013). In this last study, the authors concluded that reach planning in their specific task was based on an inaccurate internal model of motor uncertainty. Similarly, it has been found that humans have limited knowledge of their retinal sensitivity map, resulting in an inaccurate model of their own visual uncertainty during visual search (Zhang et al. 2010). In the case of multisensory integration and in the absence of the ability to robustly and accurately estimate sensorimotor variability, it might be advantageous for the brain to use integration weights that are learned and thus are more stable rather than based on highly inaccurate sensory reliabilities. Thus our study supports the notion that multisensory weights might be learned, which could represent an advantageous alternative for the sensorimotor system when sensory variability is difficult to reliably estimate.

Conclusions

In the present study, we investigated how visual and proprioceptive signals about hand position are weighted during multisensory integration for the planning of pointing movements. We found very similar proprioceptive weights for left and right hands despite differences in proprioceptive reliabilities between the two effectors, as measured in active perceptual and motor contexts. These results are in accordance with the hypothesis of modality-specific integration weights that are learned across both hands, rather than weights that are based on task- and hand-dependent sensory reliabilities.

GRANTS

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. G. Blohm and A. Z. Khan were supported by the Natural Sciences and Engineering Research Council of Canada. A. Z. Khan was additionally supported by the Canada Research Chair program. L. Pisella was supported by Centre National de la Recherche Scientifique and the Labex/Idex ANR-11-LABX-0042 (France).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

L.M., V.G., L.P., A.Z.K., and G.B. conceived and designed research; L.M. and V.G. performed experiments; L.M., A.Z.K., and G.B. analyzed data; L.M., L.P., A.Z.K., and G.B. interpreted results of experiments; L.M. and A.Z.K. prepared figures; L.M. drafted manuscript; L.M., L.P., A.Z.K., and G.B. edited and revised manuscript; L.M., V.G., L.P., A.Z.K., and G.B. approved final version of manuscript.