Tuning ESIPT fluorophores into dual emitters

Using first-principle approaches, we show how ESIPT can be controlled by fine-tuning of substituents, hence leading to new dual emitters.

Abstract

Dyes undergoing excited-state intramolecular proton transfer (ESIPT) are known to present large Stokes shifts as a result of the important geometrical reorganisation following photon absorption. When the ESIPT process is not quantitative, one can obtain dual emitters characterised by two distinct fluorescence bands, observed due to emissions from both the canonical and ESIPT isomers. However, dual emission generally requires to maintain a very specific balance, as the relative excited-state free energies of the two tautomers have to be within a narrow window to observe the phenomenon. Consequently, simple chemical intuition is insufficient to optimise dual emission. In the present contribution, we investigate, with the help of quantum-mechanical tools and more precisely, time-dependent density functional theory (TD-DFT) and algebraic diagrammatic construction (ADC), a wide panel of possible ESIPT/dual emitters with various substituents. The selected protocol is first shown to be very robust on a series of structures with known experimental behaviour, and next is applied to novel derivatives with various substituents located at different positions. This work encompasses the largest chemical library of potential ESIPT compounds studied to date. We pinpoint the most promising combinations for building dual emitters, highlight unexpected combination effects and rationalise the impact of the different auxochromes.

1. Introduction

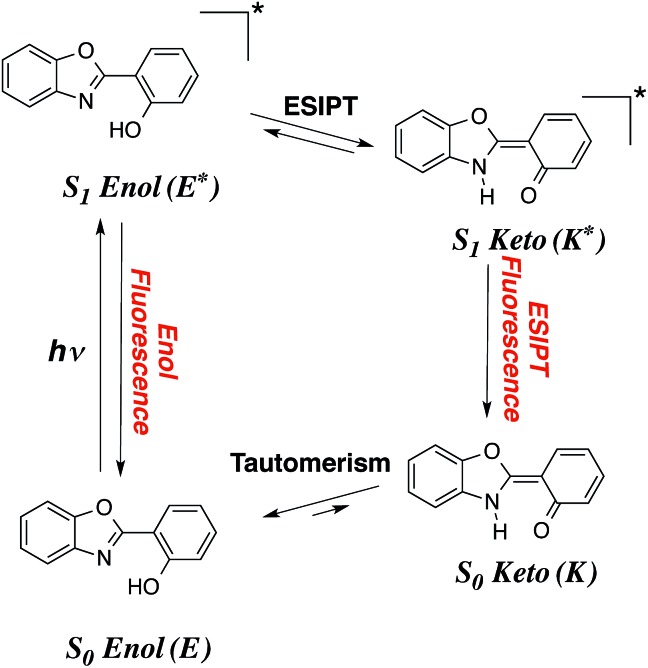
Despite more than a century of history, dye chemistry remains a very active field of research. During the latest decades, the main developments in the field have been related to emission, and more specifically to fluorescence. Indeed fluorophores are extremely versatile and can be used in several devices, e.g., they can be employed to probe several analytes in various biological environments. To limit the possibility of absorption of the emitted photon by other dyes or by molecules present in the medium, it is highly desirable to obtain both redshifted emission and large Stokes shifts. In that framework, molecules undergoing an excited-state intramolecular proton transfer (ESIPT) are particularly attractive. In these compounds (see Fig. 1), the absorption takes place from the S₀-stable enol (E) form while the emission occurs from the S₁-favored keto (K*) isomer, implying large structural changes at the ES, and, consequently enhanced Stokes shifts.1–8 ESIPT can be viewed as a very fast phototautomerisation process taking place along a strong intramolecular hydrogen bond between two atoms presenting acidities/basicities that are significantly tuned by an electronic excitation. ESIPT dyes have found applications in many fields,9–14 and present the extra advantage to be very effective in solid-state, contrary to most fluorophores that are limited by fluorescence quenching in both films and crystals. If the ESIPT process is not quantitative, it is possible to obtain dual emission with fluorescence from both S₁-enol (E*) and S₁-keto (K*). Such phenomenon paves the way to the development of white organic light-emitting diodes, if the positions and relative intensities of the two emissions can be adequately selected in the coulourimetric space.

Fig. 1. Representation of a typical ESIPT process in a typical dye.

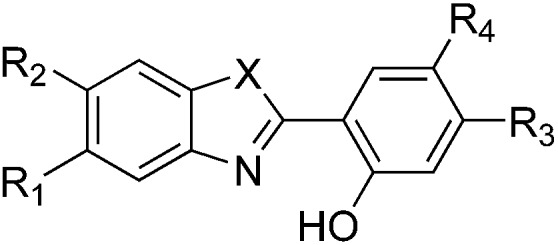
Several series of compounds undergo ESIPT and they have been investigated with both experimental and theoretical approaches. Since the discovery of the phenomenon in methylsalicylate by Weller in 1956,15 and the realistic interpretation by Otterstedt16 and Kasha,17 many investigations have been reported. A non exhaustive list of studies includes works focussed on salicylic acid,18–22 methyl salicylate,23–28 salicylideneaniline,29–32 hydroxy-acetophenones,26,28,33 hydroxy-indanone,20–22,26 hydroxy flavones,17,34–41 (pyridyl)-pyrroles, -pyrazoles and -indoles,42–49 fluorescent protein chromogens,50,51 hydroxy-benzofluorenone,52 phenyl-phenol,53 hydroxyphenyl-oxazole (HO),28 hydroxyphenyl-benzoxazoles (HBO),54–69 hydroxybenzofuran-benzoxazoles (HBBO),70 hydroxyphenyl-benzothiazole (HBT)54,61,62,71–80 and hydroxyphenyl-benzimidazoles (HBI).56,60–62,77,81–88 The typical HBO and HBI structures, two of the most popular ESIPT cores, are displayed in Fig. 2.

Fig. 2. ESIPT compounds studied herein. The X = O, X = NH and X = CH₂ structures are respectively named hydroxyphenyl-benzoxazole (HBO), -benzimidazole (HBI) and [3H]-indole (HI), respectively. R_1,2,3,4 indicate the substitution positions used in this work.

ESIPT, as many excited-state processes, is difficult to rationalise using intuitive organic chemistry concepts. Indeed, the excited-state acidities and basicities governing ESIPT are related to pK*a/b values that cannot be easily inferred but for trivial cases. In that framework, the use of quantum theories able to treat electronically excited-states often allows to take the inner track to efficient analysis and predictions of ESIPT. Without surprise, numerous theoretical works have appeared to deal with ESIPT compounds. For tiny model molecules, advanced excited-state post-Hartree-Fock methods, e.g., equation-of-motion coupled cluster, configuration interaction and multiconfigurational self-consistent field theories, can be used,20,21,53,89–92 but for “real-life” cases, density functional theory (DFT) and its time-dependent version (TD-DFT), are generally selected,20,21,30,52,65,70,89,93–97 a choice justified by several benchmark studies demonstrating the adequacy of TD-DFT for ESIPT.20,21,89 The second-order Algebraic Diagrammatic Construction [ADC(2)] method was also shown to provide a valuable compromise for medium-sized molecules.53,68,90,98 Recently, we have used a TD-DFT protocol accounting for solvent effects to tackle two HBO69 and seven HBBO dyes,70 in order to rationalise why dual emission was observed only in certain compounds. For the former, we could explain the appearance of dual fluorescence upon substitution with two dialkylamino groups and estimate the relative quantum yields of E* and K* through calculations of the vibronic couplings.69 For the HBBO series, the relative free energies of the E* and K* computed with TD-DFT correlated almost perfectly with the emission ratio obtained experimentally.70 In two other cases, this same level of theory allowed us to prove beyond reasonable doubts that ESIPT was not taking place, in contrast with former experimental analysis.97,99

Whilst there exists, as discussed above, a very large panel of experimental and theoretical studies for a vast variety of ESIPT systems, much less investigations tackled the impact of chemical substitutions on the ESIPT properties, and these works mainly focused on HBO, HBT, HBI and HBBO derivatives.59–62,66,70,75 For HBO, the data are summarised in Table 1 (see Section 4) and two main conclusions emerge: (i) adding a strong donor, e.g., NAlk₂, on the phenol side favours emission from E*; (ii) adding strong acceptors on the benzoxazole side also yields more intense emissions from E*. However, it should be noted that all these experimental studies typically considered only a few (ca. 1–3) derivatives, generally differing by several groups. Clearly a systematic investigation on a very large set of compounds would be welcome to obtain accurate design rules. The present contribution aims to fill this gap by using theoretical tools, shown to be effective for existing molecules, to provide a throughout investigation of substituent effects on ESIPT dyes.

Table 1. Available experimental values compared to theoretical simulations for HBO-ESIPT dyes. All emission wavelengths are expressed in nm, whereas the relative Gibbs energies are given in eV (see Fig. 3), a negative value indicating a more stable K*. We summarise the experimental observations, giving the approximated relative E* and K* intensities in the emission spectra, w and vw standing for weak and very weak contributions from the minority tautomer. CH, CHL, DCM, DIOX, HEP and 3 MP stand for cyclohexane, chloroform, dichloromethane, 1,4-dioxane, n-heptane and 3-methylpentane, respectively116.

Structures						Experiment				Theory
	R1	R2	R3	R4	Solv.	Observations	λ E* fl	λ K* fl	Ref.	λ E* fl	λ K* fl	ΔGES	ΔGES#
1	H	H	H	H	3 MP	Keto	—	ca. 480	55	—	492	–0.315	–0.146 a
2	H	H	H	H	CH	Keto	—	ca. 490	117	—	491	–0.314	–0.144
3	H	H	H	H	CHL	Keto	—	ca. 489	59	—	482	–0.303	–0.119
4	H	H	H	NH2	DCM	Keto (4/5) + enol (1/5)	442	565	62	460	593	–0.078	–0.079
						Keto	—	551	118
5	H	H	H	CHO	CHL	Keto + vw enol	ca. 405	474	119	352	455	–0.280	–0.072
6	H	H	H	CHO	DIOX	Keto	—	483	119	—	463	–0.292	–0.091
7	H	H	NEt2	H	CHL	Enol	382	—	59	377	—	0.087	0.176
						Enol	451	—	66
8	H	H	NEt2	H	DIOX	Enol	471	—	66	373	—	0.023	0.159
9	H	H	NH2	H	DCM	Keto (7/8) + enol (1/8)	376	467	62	359	458	–0.055	0.072
						Keto (3/5) + enol (2/5)	390	460	120
10	H	H	NH2	H	CHL	Keto (3/4) + enol (1/4)	390	460	120	357	464	–0.086	0.054
11	H	H	NH2	H	DIOX	Keto (3/4) + enol (1/4)	415	487	121	354	478	–0.150	0.019
12	H	H	OMe	H	CHL	Keto + vw enol	ca. 375	ca. 467	59	351	488	–0.241	–0.019
13	H	H	Me	H	3 MP	Keto	—	ca. 480	55	—	505	–0.297	–0.125
14	H	C C(CN)2	H	H	CH	Keto + w enol	ca. 425	ca. 550	122	408	586	0.083	0.074
15	H	C C(CN)2	H	H	CHL	Keto + enol	ca. 450	ca. 625	122	425	642	–0.032	0.173
16	H	CHO	H	H	CHL	Keto	—	ca. 517	59	—	500	–0.202	–0.082
17	H	COOEt	H	H	CHL	Keto	—	ca. 495	59	—	497	–0.254	–0.100
18	H	NH2	H	H	HEP	Keto + vw enol	390	500	123	376	481	–0.065	0.012
19	H	NH2	H	H	DCM	Keto (9/10) + enol (1/10)	420	485	123	399	468	0.037	0.085
20	H	COOEt	NEt2	H	CHL	Enol	421	—	59	401	—	0.188	0.245
21	H	COOEt	OMe	H	CHL	Keto + vw enol	ca. 375	ca. 482	59	365	505	–0.202	0.012
22	H	NH2	NEt2	H	DIOX	Enol	460	—	66	389	—	0.146	0.201
23	H	NO2	NEt2	H	DIOX	Keto + enol	476	656	66	434	550	0.327	0.353
24	NH2	H	NEt2	H	DIOX	Enol	440	—	66	389	—	0.129	0.216
25	NO2	H	NEt2	H	DIOX	Enol	440	—	66	435	—	0.356	0.297
26	NH2	H	H	H	HEP	Keto (9/10) + enol (1/10)	400	500	124	406	488	0.054	0.182
27	NH2	H	H	H	DCM	Enol + vw keto	450	ca. 480	124	432	474	0.076	0.197

^aA negative barrier indicates a barrierless process on the free energy surface. The transition states can nevertheless be found on the energy surface.

This paper is organised as follows: in the two following Sections we briefly describe our original computational procedure combining TD-DFT and ADC(2), and detail the results for a test case for which the reaction paths were investigated. In Section 4, we provide extensive comparisons with experiments for HBO dyes before investigating numerous mono- and di-substituted compounds in Section 5. In Section 6, HBI and HI compounds are investigated before concluding.

2. Methods

Here, the structures and vibrational frequencies have been obtained with TD-DFT, the total and transition energies with ADC(2) and the solvent effects with the Polarisable Continuum Model (PCM).100 The different properties (P, e.g., the fluorescence energies and the free energies) were obtained as,

P = P(Gas, ADC) + P(PCM, TD) – P(Gas, TD). 1

For all TD-DFT calculations, we have used the latest revision of the Gaussian09 program,101 applying default thresholds and algorithms, except when noted below. These calculations relied on the M06-2X hybrid exchange-correlation functional,102 a choice justified by previous benchmarks demonstrating the accuracy of this functional for determining both vertical and adiabatic transition energies as well as for predicting band shapes and proton transfer in HBO compounds.69,102–108 Here, we have applied a recently proposed approach for ESIPT69 which is to determine the geometrical and vibrational parameters with the 6-31G(d) atomic basis set, whereas the total and transition energies are corrected with a much more extended atomic basis set, namely 6-311+G(2d,p). This combination leads nearly basis set converged values at the TD-DFT level. To achieve numerically-stable and accurate values, we have tightened self-consistent field (10^–10 a.u.) and geometry optimisation (10^–5 a.u.) convergence thresholds, as well as used a (99 590) pruned integration grid (so-called ultrafine grid). For each molecule, both the enol and keto excited-state geometries have been fully optimised using TD-DFT analytical gradients. We have also determined the corresponding transition states on the excited-state potential energy surface for all experimentally available compounds and a selection of new compounds (see below). TD-DFT Hessian calculations were performed to confirm the nature of all excited-state structures and to determine the free energies (G).

Environmental effects (here cyclohexane, except when noted) have been accounted for using the well-known PCM,100 as implemented in Gaussian09.101 While TD-DFT geometry optimisations, Hessian calculations, enthalpies and entropies (and hence G) have been determined with the popular linear-response PCM approach, the transition energies have been evaluated using the more accurate corrected linear-response scheme.109 This latter scheme allows to correct the cavity polarisation in the ES by accounting for the change of electron density upon electronic transition. Therefore, it allows to more accurately estimate the emission wavelengths, while remaining computationally affordable. Of course, while we applied the equilibrium PCM limit for optimisation and vibrational TD-DFT calculations (slow phenomena), fluorescence wavelengths are corrected for non-equilibrium effects (fast phenomena).

The gas phase ADC(2) total and transition energies determined on the TD-DFT structures have been obtained with the Turbomole code.110 These ADC(2) calculations relied on the so-called ADC(2)-s formalism111 and used the resolution of identity technique.112,113 Wavefunction approaches being more sensitive to basis set effects than TD-DFT, the very extended aug-cc-pVTZ atomic basis set was used for all ADC(2) calculations.

3. Shape of the potential energy surfaces

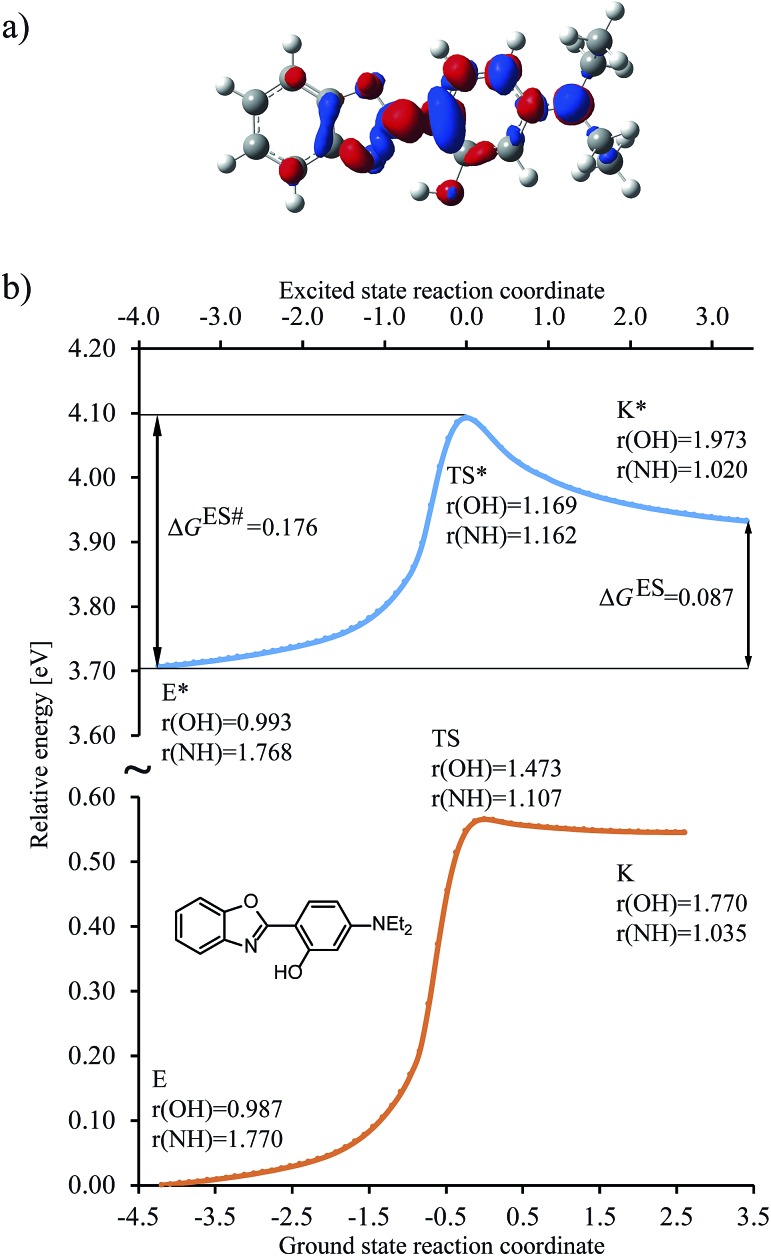
To set the scope of this study, a typical shape of the energy change along the reaction coordinate is depicted in Fig. 3 (see also Fig. S1 in the ESI†) for the R₃ = NEt₂ (R_1,2,4 = H) HBO dye (7 in Table 1).

Fig. 3. Results obtained for the HBO dye 7. (a) Density difference plot (isovalue = 0.0018 a.u.). The red/blue zones indicate an increase/decrease of the electronic density upon absorption of light. (b) Energy profile for proton transfer along the ground- and excited-states IRC. Energy scale is relative to the ground-state enol form and is calculated at the M06-2X/6-31G(d) level.114 Bond lengths are in Å, reaction coordinates are defined in mass weighted coordinates (Bohr ).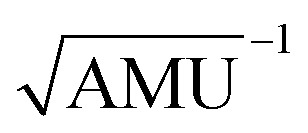

We determined the intrinsic reaction coordinate (IRC) connecting the enol and keto forms through transition state in both ground and excited states using the local quadratic approximation (LQA) technique.115 In the ground-state the activation energy to go from E to K is too high and the back-reaction is nearly barrierless, both factors confirming the presence of the enol form only, before photon absorption, a completely usual outcome for HBO structures. After excitation the molecule reaches the ES (S₁) surface, where the barrier for proton transfer is significantly smaller and K* is now a stable isomer. However, both the difference of free energy between the K* and E* isomers (ΔG^ES, see Fig. 3b) and the height of the free energy barrier for ESIPT (ΔG^ES#, see Fig. 3b) are positive and relatively large which favours emission from E* as was also experimentally observed (see next Section). The change of electron density upon excitation can be seen on Fig. 3a. The most important features are, one the one hand, the gain of density of the nitrogen atom (in red), which is connected with the stabilisation of K* form and, on the other hand, the relatively small (blue) lobe on the OH group, indicating a small change of density and, consequently, a limited increase of the acidity of the hydroxyl in the excited state. For some compounds in which K* is more stable than E*, e.g., for the non-substituted structure, the density loss in the OH area can be much larger (see Fig. S4 in the ESI†). In Fig. 3, the activation energies for both states are in accordance with Hammond postulate, i.e., GS proton transfer from K to E goes through an early TS (NH distance in TS is only 0.05 Å longer than in the optimal K geometry) which indicates very small activation energy. In contrast the geometry of TS for ESIPT supports comparable activation energies for both direct and backward reactions at the selected level of theory. We underline that the geometries of the GS and ES transition states are different. As a consequence computing only single point energies on the top of ground-state IRC leads to large errors in estimating the reaction parameters (see Fig. S2 in the ESI†) and should be discouraged. On the other hand, 6-311+G(2d,p) ES single-point calculations obtained on the ES 6-31G(d) IRC nicely follows the path of the smaller basis set, which supports our protocol (see Fig. S3 in the ESI†).

4. Comparisons with experiments

In Table 1, we compare the theoretical and measured results for a series of HBO compounds, some in different media, for a total of twenty-seven cases. First, we underline that all the theoretical values reported in that table are obtained through eqn (1), that is, include an ADC(2) correction to the TD-DFT energies. The uncorrected TD-DFT values can be found in the ESI (Table S2†). It turns out that: (i) TD-DFT tends to provide too small emission wavelengths, an effect that we relate to the selection of the M06-2X functional that yields consistent but too large transition energies;104 (ii) both the TD-DFT's ΔG^ES and ΔG^ES# are larger than their ADC(2) counterparts, indicating that TD-M06-2X tends to overestimate the stability of the E* isomer in most cases – 26 being a notable exception to this general trend. As a consequence, TD-DFT provides inaccurate predictions for a series of cases, e.g., 9, 18 and 27, for which eqn (1) gives reliable estimates. Consequently, we do not further discuss the “raw” TD-DFT estimate in the following.

Let us now turn towards the emission wavelengths (λ_fl in Table 1). First, one notes that there are serious discrepancies between experimental values obtained by different research groups. For instance, for 9, the emission of E* in dichloromethane was reported to occur at 376 nm (ref. 62) and 390 nm,120 a sizeable difference (0.12 eV). The two values reported for 7 in chloroform, 382 nm (ref. 59) and 451 nm,66 are also in so strong disagreement (0.50 eV) that invoking apparatus differences or the presence of small fraction of impurities is not satisfying. The emission wavelength reported for the K* of 23, 656 nm, was also extracted from an oversaturated spectrum,66 and should be considered cautiously as well. If one removes from the set the data measured in the puzzling ref. 66, we note that the theoretical emission wavelengths are in reasonable match with experiment, a statement holding for both tautomers. Indeed, for E* the absolute errors range from 0.04 to 0.51 eV, with an average of 0.19 eV, whereas for K* the deviations are slightly smaller (from 0.01 to 0.16 eV with an average of 0.08 eV). These deviations are in the expected range at this level of theory.111,125 We note that we obtain a theory-experiment linear correlation coefficient of 0.96 for the emission energies, further justifying the selected level of theory.

For the ΔG^ES and ΔG^ES# (see Fig. 3), there are of course, no available experimental values allowing direct comparisons. However, one can see from the data listed in Table 1 that the computed free energies can nicely explain the experimental outcomes. Indeed, when a positive ΔG^ES is calculated, indicating that ESIPT is not a thermodynamically favoured process, only E* emission is experimentally observed. By contrast, significantly negative ΔG^ES (in the –0.20 to –0.30 eV range), corresponding to a strong driving force for the proton transfer, are computed for cases in which only the K* emission was obtained experimentally. The intermediate situations (–0.20 eV < ΔG^ES < 0.00 eV) are related either to dual emission or to E* emission. In these intermediate cases, it could be expected that relatively small ESIPT barriers, ΔG^ES#, would favour K* emission whereas large ΔG^ES# would indicate a dominating E* emission. However, the number of experimental data available is too limited to provide reliable boundaries for ΔG^ES#. Despite these interesting trends, we note some disagreements: (i) for 23 theory foresees a strongly favoured E*, whereas experiment finds both E* and K* emission bands,66 though the latter is questionable (see above); (ii) for 19, a dominating K* band is observed in dichloromethane123 although the computed ΔG^ES is positive – for the same compound in the less polar solvent (18) the trend is however correctly given by theory; (iii) for both 14 and 26 a strong K* band is observed122,124 which is not reproduced by the calculations, though theory again provides the correct results in other media (15 and 27). At this stage, we can logically attribute the latter problems to the limitations of the PCM solvation approach, rather than to the inadequacy of the electronic structure description. To further improve the accuracy of the ΔG^ES, one would probably need to explicitly model solvent molecules, a task beyond our scope here. We also recall that we have selected only non-protic solvents to be within the range of applicability of the PCM model. In addition, there is an overall high degree of correlation between the estimated theoretical free energies and the experimental observations, but for a few exceptions (ca. 15% of the cases). Consistently with one of our previous work devoted to HBBO,70 we note that dual emission can only be obtained in a narrow energetic window, as the E* and K* energies should only differ by ca. 0.00 to –0.20 eV for HBO dyes. This hints that only subtle and well-thought chemical substitutions should be used when dual emission is looked for.

In short, this investigation demonstrated the robustness of the proposed protocol: the theoretical emission wavelengths present the expected accuracy at the selected level of theory, whereas the computed relative excited-state free energies allow predicting the experimental outcome (enol, keto or dual emission) in the vast majority (85%) of cases.

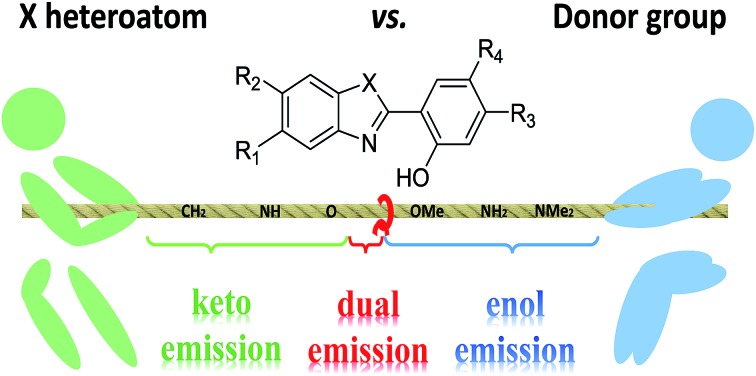
5. Substitution effects

In this Section, we investigate the impact of 6 auxochromic groups, CN, CF₃, F, OMe, NH₂ and NMe₂ [a set that was selected to contain both electron-donating groups (EDG) and electron-withdrawing groups (EWG) of different strengths and natures] considering various substitution positions (R₁, R₂, R₃ and/or R₄, see Fig. 2). First, a systematic investigation of singly-substituted HBO derivatives is performed to unravel the impact of each substituent. Next, we assess combination effects by tackling doubly-substituted HBO with substituents at both R₁ and R₃ positions. To have a clearer view of the substituent effects, we report in the body of the text the relative free energies contribution [Δ(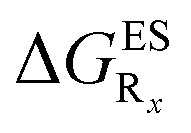), x = 1, 2, 3 and/or 4] with respect to the non-substituted case,

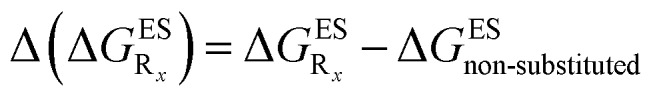2

The interested reader can find the 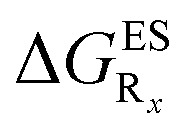in the ESI (Table S2†).

5.1. Singly-substituted

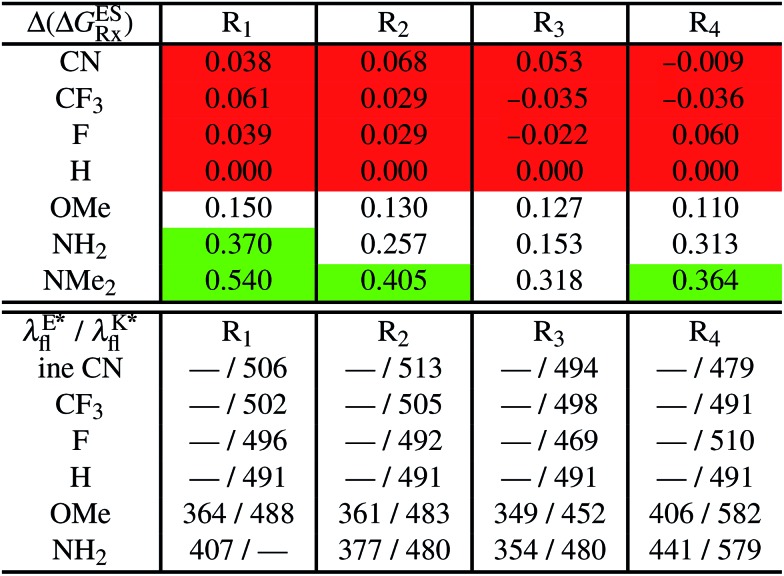
In Table 2, we list the energetic contributions to the relative stability of both forms and the computed emission wavelengths for the emissive species. A negative (positive) value indicates that the K* form is relatively stabilised (unstabilised) by the substitution compared to the non-substituted HBO dye. Let us first discuss the impact of EWG. When located on the benzoxazole side, acceptor groups systematically decrease the stability of the keto isomer. Indeed, such substitution decreases the electronic density on the nitrogen atom, and hence its basicity (see Fig. S4† and associated comments in the ESI†). At the R₂para position, the largest effect is obtained with the mesomeric cyano substitutent, whereas at the R₁meta position, the strongest impact is obtained with the inductive trifluoromethyl group. In contrast, adding a EWG on the phenol side can favour both the E* and K* tautomers. At the para position (R₄), both CF₃ and CN stabilises the K* form, whereas the fluoro substitution surprisingly yields the reverse trend. At the meta position (R₃), the mesomeric CN group stabilises E*, whereas adding an inductive EWG yields the opposite effect. Whilst some EWG reduce the energetic difference between the two isomers, their effect is too limited to change the trend obtained for the unsubstituted HBO compound, and only K* emission is predicted in all cases (red background in Table 2).

Table 2. Theoretical results for HBO dyes in cyclohexane. Top: relative Gibbs energy differences with respect to the non-substituted HBO, 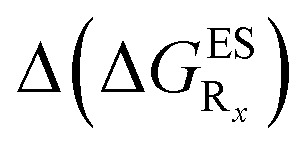in eV, a negative value indicating that substitution relatively favours the K* form (see Table S2 in the ESI for 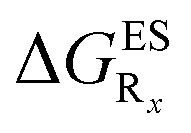that can be obtained by adding –0.314 eV to the value reported here). Bottom: E*/K* emission wavelengths (λE*fl/λK*fl in nm) for the tautomers that is (are) predicted to be present. The background colour indicates the predicted emission based on the 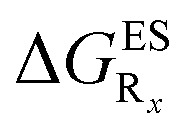: red/green/white background corresponding to sole K*/sole E*/dual fluorescence.

Let us now turn to EDG. One first notes that, irrespective of their position, donor groups systematically stabilise the E* form, and consequently, tend to yield dual or sole E* emission. The magnitude of this stabilisation is (much) larger than for the EWG and follows the logical OMe < NH₂ < NMe₂ ranking. Of course, for substitutions on the phenol side, these results were expected, i.e., adding EDG increases the electron density on the hydroxyl in the excited-state and consequently reduces its acidity, the effect being larger for the para than meta positions (see the ESI†). More surprising is the fact that EDG yield a similar effect when substituting the benzoxazole moiety, the magnitude of the E* stabilisation being even larger. Indeed, chemical intuition would have led to foresee that EDG would increase the basicity of the nitrogen centre and hence strengthen the ESIPT process. In Fig. S4 in the ESI,† the density difference plots allow to explain this unexpected outcome: EDG at R₁ and R₂ actually decrease the acidity of the phenol (in the excited-state) by localising the excited-state on the benzoxazole side, the change of density on the hydroxyl after absorption becoming too small to favour ESIPT. One also notices that this impact is slightly larger at R₁ than R₂ positions, consistently with the values of Table 2. With EDG, two different emission patterns can be obtained: (i) pure E* emission for the strongest stabilisation (e.g., NMe₂ group at R₁, R₂, and R₄ position); (ii) dual emission with groups that present an intermediate contribution to the E* stabilisation, enabling to obtain a ΔG^ES in the energetic window determined in Section 4 (–0.20 to 0.00 eV). For these latter cases, we systematically computed the energetic barrier separating the E* to K*, ΔG^ES#. The values are listed in the ESI (Table S2†) and do not exceed 0.129 eV, indicating that proton transfer can most probably take place. Indeed, this value is smaller than the barrier obtained in Section 4 for compound 15 (ΔG^ES# = 0.173 eV) that experimentally displays dual emission.

As discussed in Section 1, another attractive feature of ESIPT dyes is the possibility to redshift the emission due to the strong geometrical reorganisation following absorption. Of course, designing such compounds first requires that emission from the K* form is actually possible. For example, while the most red-shifted emission predicted by theory was obtained with the NMe₂ EDG at R₄, this dye is inadequate as only the E* tautomer emits, as explained above. Amongst the derivatives displaying an emissive keto isomer, the most red-shifted bands (ca. 580 nm, a rather long wavelength for compact compounds) are obtained for HBO presenting a OMe or NH₂ group at R₄.

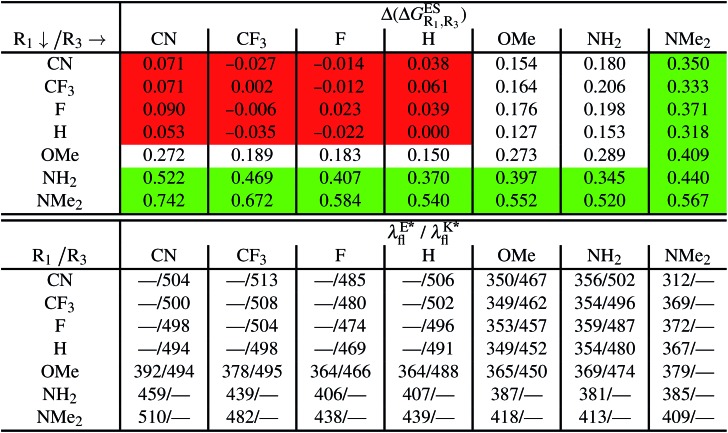
5.2. Doubly-substituted

We investigate in this Section, the combination of substitutions at both R₁ and R₃ positions, these two position being selected as they yield diverse outcomes (see Table 2). Our data are reported in Table 3. To facilitate the discussion, we have also reported in the ESI (Table S3†) the additive contributions, 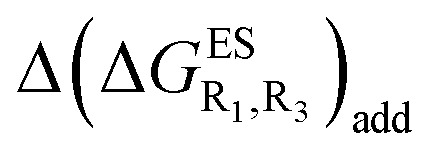, that have been obtained by summing the single contributions, 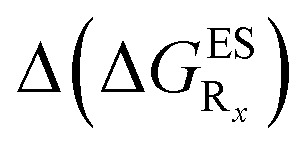reported in Table 2.

Table 3. Theoretical results for doubly-substituted HBO dyes in cyclohexane. See caption of Table 2 for more details.

When comparing the results in Tables 3 and S3,† one first observes a similar prediction in the emission profile, i.e., the same background colour patterns are found, hinting a qualitatively additive trend. Other conclusions emerge: (i) combining two EWG only slightly tunes the relative energies, and only K* emission is obtained; (ii) inserting EDG that strongly stabilise E* (NH₂ at R₁ and NMe₂ at both R₁ or R₃) yields a sole E* emission, irrespective of the second substituent, that is unable to counterbalance the effect; (iii) for the remaining cases, e.g., R₃ = OMe or NH₂ with EWG at R₁, dual emission is likely to occur. For these latter compounds, the ESIPT barrier, ΔG^ES#, was computed and the results are listed in Table S4 in the ESI.† As in the singly-substituted group, all barriers are relatively small (<0.14 eV).

Despite the qualitative parallelism between the results of Tables 2 and 3, a quantitatively additive pattern is clearly not obtained. Indeed, the absolute differences between the computed and additive energetic contributions, show both a large spread (from 0.002 to 0.291 eV) and a non-negligible average (0.067 eV). We found that substantial discrepancies are obtained for the series presenting a NH₂ or a NMe₂ group at R₁, with deviations from additivity ranging from 0.059 to 0.291 eV; the largest difference being obtained for dye bearing two NMe₂ groups. For the other compounds, the maximal discrepancy only attains 0.074 eV (with an average of 0.026 eV) but changes of sign between the computed and additive contributions are obtained for dyes presenting a calculated negative 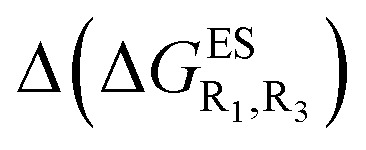– the additive approach systematically providing positive values for this parameter. For instance, the R₁ = CF₃, R₃ = F dye presents a 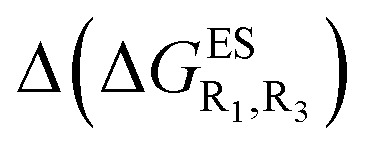of –0.012 eV whereas simple addition of substituent effects foresees a free energy difference of 0.039 eV compared to the unsubstituted HBO.

Regarding the emission wavelengths, one notes that the most redshifted values are obtained for the HBO derivatives presenting a strong EWG (CN or CF₃) at R₁ combined to another active group at R₃. The redshift is nevertheless smaller than in the HBO dye substituted by a single OMe or NH₂ group at R₄ (see previous section). This result is related to the fact that HBO dyes developing a strong push–pull character, known to yield bathochromic shifts, are not subject to ESIPT and do not show K* emission.

6. Impact of the heteroatom

In this Section, we investigate the impact of the core on both the relative stabilities and spectra of the enol and keto forms by replacing the heteroatom (X = O atom in Fig. 2) by X = NH or X = CH₂. The same two-step methodology as in Section 5 is applied: (i) we first compare the theoretical and measured results for experimentally available data; (ii) we perform a systematic study of the impact of single-substitution using the same auxochromes in the same solvent as above.

6.1. Benzimidazoles

As in Section 4, let us first compare the available experimental data to ADC(2)-corrected theoretical results for a series of HBI compounds (see Table 4). The TD-DFT values can be found in the ESI (Table S1†) and as for HBO series, it turns out that TD-DFT overestimates both the transition energies (too small emission wavelengths) and the stability of the E* isomer (ΔG^ES and ΔG^ES# being too large compared to the ADC(2) values). The theoretical emission wavelengths are in good agreement with experiments except for 37 for which the error attains 0.72 eV. However, one can wonder if the attribution of the emission band to E*, suggested in ref. 62, is valid. Indeed, while the theoretical λE*fl (at 354 nm) clearly does not match the observed band peaking at 445 nm, the calculated emission wavelength for the K* isomer at 440 nm perfectly fits the measurement. Except for this case, the absolute errors for the E* form (from 0.02 to 0.47 eV) and the K* tautomer (from 0.03 to 0.14 eV) are rather similar to those obtained for HBO derivatives. The average error for emission energies for the data reported in Table 2 is 0.10 eV.

Table 4. Available experimental values compared to theoretical simulations for HBI-ESIPT dyes. See caption of Table 1 for more details.

Structures						Experiment				Theory
	R1	R2	R3	R4	Solv.	Observations	λ E* fl	λ K* fl	Ref.	λ E* fl	λ K* fl	ΔGES	ΔGES#
28	H	H	H	H	CH	Keto	—	470	117	—	479	–0.388	–0.127
						Keto	—	ca. 470	77
29	H	H	H	H	DIOX	Keto + vw enol	350	468	81	345	473	–0.393	–0.125
30	H	H	H	NH2	DCM	Keto	—	539	118	—	571	–0.213	–0.144
						Keto + vw enol	414	544	62
31	H	H	H	NH2	DIOX	Keto + enol	414	568	81	428	564	–0.158	–0.125
32	H	H	H	OMe	DIOX	Keto + vw enol	368	530	81	395	560	–0.345	–0.123
33	H	H	H	OH	DIOX	Keto + vw enol	358	525	81	388	537	–0.319	–0.170
34	H	H	H	Me	DIOX	Keto + vw enol	352	489	81	354	501	–0.353	–0.114
35	H	H	H	Cl	DIOX	Keto	—	474	81	—	489	–0.379	–0.129
36	H	H	H	F	DIOX	Keto + vw enol	350	486	81	361	497	–0.362	–0.166
37	H	H	NH2	H	DCM	Enol a	445	—	62	354	440	–0.170	–0.083
38	H	H	NEt2	H	CH	Keto + w enol	ca. 370	ca. 453	82	368	460	–0.072	0.067
39	H	H	NEt2	H	DIOX	Enol	386	—	84	368	—	–0.079	0.131
40	H	NH2	NEt2	H	DIOX	Enol	431	—	84	382	—	0.054	0.115
41	H	NO2	NEt2	H	DIOX	Keto + vw enol	—	531	84	—	489	–0.214	–0.244

^aWe report the form that is probably emitting according to ref. 62.

Comparing the experimental emission profiles with the computed relative stabilities of the tautomers, we found the same energetic criteria as for the HBO structure: (i) an unique K* emission band is observed when the Gibbs energy difference in the ES is strongly negative (in the –0.20 to –0.40 eV); (ii) a positive ΔG^ES indicates that the enol isomer is the only emissive species; (iii) an intermediate situation, –0.20 eV < ΔG^ES < 0.00 eV, is observed for both 31 and 38 that actually display dual emission. However, one notes a disagreement for 39 in 1,4-dioxane, that also presents an intermediate ΔG^ES though only emission from E* is observed. As in Section 4, we highlight that the correct trend is obtained for the same compound in cyclohexane, so that this discrepancy can probably be attributed to the limitation of the environmental model. Overall, theoretical results are consistent with the experimental outcomes for 12 out of 13 cases (>90% of the cases) which confirms here again the robustness of the computational protocol.

We now compare the experimental observations for similar HBO (see Table 1) and HBI (see Table 4) derivatives considered in the same solvent, i.e., 2/28, 7/39 and 4/30. The two former display the same emission profile but for the latter couple, a substantial dual emission (4/5 K* + 1/5 E*) is obtained with X = O whereas the spectrum of the compound with X = NH displays a negligible E* band. Consequently, replacing the benzoxazole with a benzimidazole core tends to stabilise K* and hence to favour the ESIPT process, a fact that is confirmed theoretically. Indeed, for the three couples cited above, but also for all the singly-substituted derivatives, the ΔG^ES values are systematically more negative for the HBI structures than for their HBO counterparts (see Table S2 in the ESI†). For instance, for the non-substituted compounds, we computed a ΔG^ES of –0.314 eV and –0.388 eV for HBO and HBI, respectively.

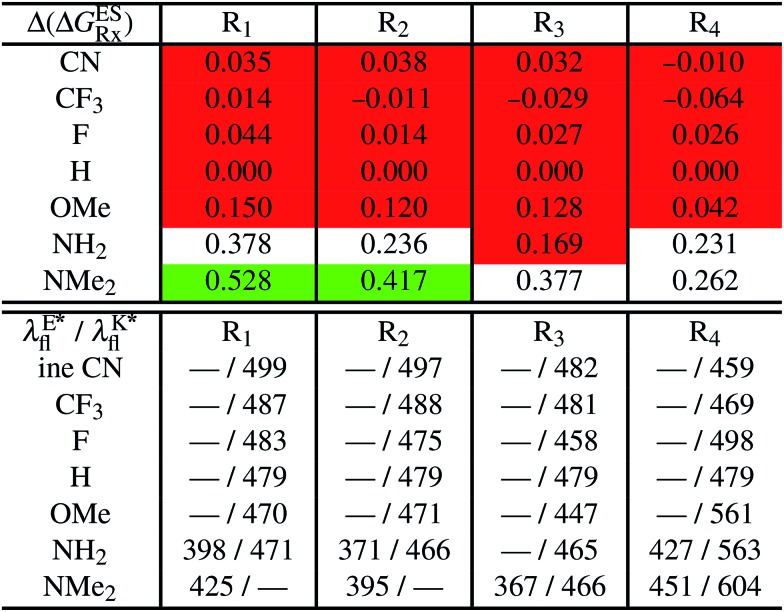
In Table 5, the counterpart of Table 2, we report the emission wavelengths of the emissive species and the relative contributions of each substituent for HBI dyes. The 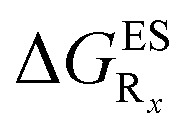values are reported in the ESI (Table S2†). Let us first discuss acceptor groups. When located on the benzimidazole side, EWG slightly decrease the relative stability of the keto isomer (similarly to the benzoxazoles), except for R₂ = CF₃ that yields a reverse trend, that is, a negative contribution corresponding to a K* stabilisation. With respect to HBO, the impact of the CF₃ group at R₁ is reduced in HBI whereas those of the CN and F groups are similar. At the R₂para position to the nitrogen atom involved in the ESIPT process, the impact of all EWG is smaller than in the corresponding HBO structure, though the largest effect is still obtained with the strong mesomeric cyano group. For the phenol substitution, a stabilisation of the keto isomer is obtained for both the mesomeric CN group at the R₄para position and the strong inductive CF₃ group at both R₃ and R₄, the latter auxochrome having a large quantitative impact. The other substitution patterns tend to decrease the stabilisation of the keto isomer. However, like in the HBO series, the impacts of EWG remain too limited to significantly tune the tautomeric equilibrium and the same emission profile as for the non-substituted compound is systematically predicted.

Table 5. Theoretical results for a series of HBI dyes in cyclohexane: substituent effects. See caption of Table 2 for more details. The ΔG^ES of the unsubstituted HBI is –0.388 eV, and this value should be added to the 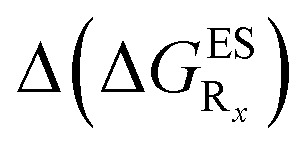reported at the top to obtain the 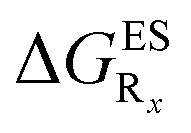(see also Table S2 in the ESI).

Similarly to the HBO series, EDG decrease the stability of the K* isomer with a magnitude in line with their donating strength, that is, OMe < NH₂ < NMe₂, the effect being stronger when substituting the benzimidazole side. Dual emission is likely to occur for intermediate auxochromic contributions (in the 0.188–0.388 eV range), i.e. for NH₂ at R₁, R₂ and R₄ positions and for NMe₂ on both positions of the phenol ring. As the K* form is more stabilised in the unsubstituted HBI than HBO derivative, it is well-understandable that donor groups with a stronger impact have to be selected to reach dual emission with the former core.

In Table 5, the most red-shifted fluorescence wavelength (604 nm) is obtained for the K* fluorescence of the R₄ = NMe₂ derivative. This substitution, that likely yields dual emission, indeed provides the most red-shifted emission of all HBO and HBI compounds investigated and therefore stands as a valuable candidate for synthesis.

6.2. 3H-Indoles

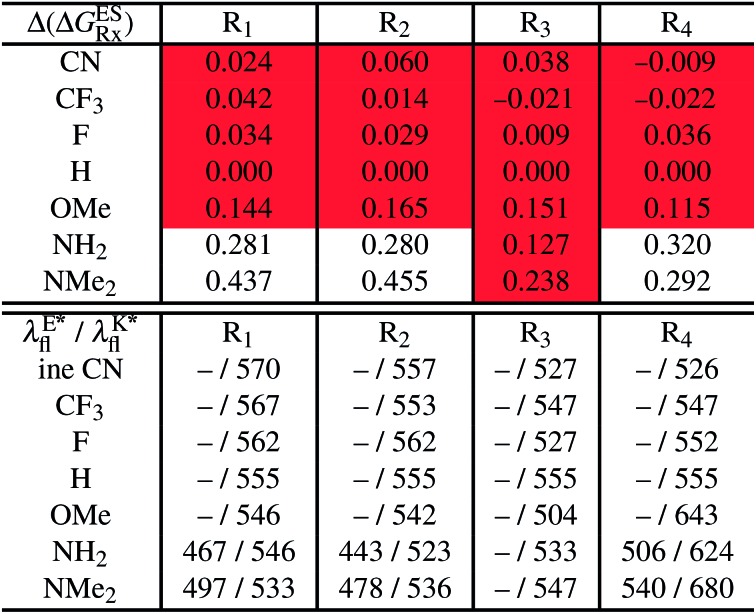
We finally describe the impact of substitution on HI and compare the results to the two preceding series. To the best of our knowledge, they are no experimentally available data for HI (X = CH₂ in Fig. 2) derivatives. In Table 6, we report the computed emission wavelengths and the relative free energies contributions for these compounds. One notices that the values in that Table are systematically more negative for HI than for both HBO and HBI compounds. This effect is far from negligible, e.g., the free energy difference of the non-substituted HI is –0.463 eV whereas the computed ΔG^ES are –0.314 eV and –0.388 eV for HBO and HBI, respectively. Therefore the use of 3H-indole tends to strongly favour ESIPT and hence the emission from the K* isomer.

Table 6. Theoretical results for a series of HI dyes in cyclohexane. To determine the nature of the emission, we used the same energetic windows as for both HBO and HBI. See caption of Table 2 for more details. The ΔG^ES of the unsubstituted HBI is –0.463 eV, and this value should be added to the reported at the top to obtain the (see also Table S2 in the ESI).

We note that the impact of EWG on HI dyes is slightly smaller than in HBO and of the same order of magnitude as in HBI. Like above, EWG on the 3H-indole side favours the enol, whereas substitution on phenol moiety can induce E* or K* stabilisation. For all EWG-substituted HI, theory predicts a sole emission from the K* tautomer, which is consistent with the relatively weak effect of EWG. Adding EDG provides larger changes, with a magnitude that can be smaller (e.g., at R₁) or larger (e.g., at R₄) than in HBI derivatives. To reach dual emission, it is mandatory to add strong amino donor groups, that yield a significant stabilisation of E*. However, in contrast with HBI, a R₃ = NMe₂ substitution is not sufficient to significantly counter the ESIPT trend. Interestingly, all HI compounds display significantly redshifted emission compared to the other series. The fluorescence wavelengths determined for the OMe, NH₂ and NMe₂ groups at R₄ now attain 643, 624 and 680 nm, respectively. Therefore, starting from a dye core strongly favouring ESIPT, but frustrating the proton transfer through the addition of very strong donor groups, allows reaching both dual emission and strong bathochromic shifts in the same molecule. To our knowledge, such strategy was not extensively considered previously.

7. Conclusions and outlook

We have investigated a large number (>110) of potential ESIPT dyes belonging to the HBO, HBI and HI families with a focus on the impact of chemical substitutions. To reach reliable ab initio predictions, we used an advanced computational protocol in which the structures and vibrational parameters are determined with TD-DFT, the total and transition energies with ADC(2) and the environmental effects with PCM. First, by comparing experimental and theoretical values for more than 40 cases for which fluorescence spectra have been measured, we found that theory was able to deliver reasonably accurate fluorescence wavelengths, and more importantly, to predict the experimental spectroscopic outcome (enol, keto or dual emission) with a very good consistency. Indeed, the relative free energies of the two tautomers in the excited-state provides the correct prediction in more than 85% of the cases, the remaining discrepancies being most probably related to the limitations of continuum solvation approaches. Second, we defined an energetic window corresponding to dual emission and found it to be quite narrow for this family of compounds (K* more stable than E*, by 0.00 to –0.20 eV), indicating that subtle substitutions patterns need to be found. Third, we showed that going from HBO to HBI and next HI core induces systematic stabilisation of K* tautomer compared to E* form, and does not significantly perturb the effect of the substituents. Fourth, it turns out that adding acceptor groups yields relatively limited variations, and a stabilisation of the K* or the E* isomer can be obtained depending on the substitution side. In contrast, adding donor groups systematically favours the E* form, and hence limits ESIPT, irrespective of the substitution side. This unexpected result was explained by examining the localisation of the excited-state given by density difference plots. Fifth, we have also shown that combining two substituents does not give simple additive effects. Notably when a strong pushing group is present, adding a second donor has a rather limited impact on the tautomeric equilibrium.

Going across Tables 2, 3, 5 and 6, we found 32 relatively simple compounds (single or double substitutions) that are predicted to display a dual emission behaviour. In Table 2, one notices that the methoxy substituent is predicted to yield dual emission in HBO irrespective of its position, and we can relate this finding to the fact that HBBO derivatives, that can be viewed as extended HBO with an additional oxygen atom, are known to show dual emission.70 At this stage, we can therefore recommend these compounds for synthesis, experimental spectroscopic characterisations and feedback. One also finds a few (4) compounds with predicted emission wavelengths up to 600 nm, a remarkably high value for relatively compact molecules. For instance, for the R₄ = NMe₂ X = CH₂ derivative, dual emissions are predicted at 540 and 680 nm, and this compound seems therefore promising for designing a ratiometric probe in a biological environment.

Finally, let us comment on environmental effects. First, the extreme sensitivity of several dyes to the used solvent (see the results of Table 1) makes these compounds particularly appealing for applications as probes, but also extremely challenging for theoretical modelling. It is rather clear that more advanced solvation model, including the consideration of dynamical effects and the explicit characterisation of hydrogen bonds, will have to be used in the future to obtain accurate theoretical insights regarding the specific solvatochromic effects. Secondly, one further theoretical challenge to be tackled is the estimation of possible (dual-)emission in the solid-state.14 While there are experimental examples of efficient solid-state ESIPT-based dual emitters,70 the modelling of the crystal-packing effects on the emission of these derivatives remains to be performed. We note that first simulations, devoted to absorption, already appeared,30 but more would certainly be necessary in the framework of optimising actual devices.