Episodic creep events on the San Andreas Fault caused by pore-pressure variations

Abstract

Recent seismic and geodetic observations indicate that interseismic creep rate varies in both time and space. The spatial extent of creep pinpoints locked asperities, while its temporary accelerations, known as slow-slip events, may trigger earthquakes. Although the conditions promoting fault creep are well-studied, the mechanisms for initiating episodic slow-slip events are enigmatic. Here we investigate surface deformation measured by radar interferometry along the central San Andreas Fault between 2003 and 2010 to constrain the temporal evolution of creep. We show that slow-slip events are ensembles of localized creep bursts that aseismically rupture isolated fault compartments. Using a rate and state friction model, we show that effective normal stress is temporally variable on the fault, and support this using seismic observations. We propose that, compaction-driven elevated pore fluid pressure in hydraulically isolated fault zone and subsequent frictional dilation cause the observed slow slip episodes. We further suggest that the 2004 M_w6 Parkfield earthquake might have been triggered by a slow-slip event, which increased the Coulomb failure stress by up to 0.45 bar per year. This implies that while creeping segments are suggested to act as seismic rupture barriers, slow-slip events on these zones might promote seismicity on adjacent locked segments.

Fault creep, which accounts for the release of up to half of the seismic moment budget, is a pivotal component of the earthquake cycle¹. The spatial extent of creep and its rate determine the degree to which a fault is locked and frequency of earthquakes^2,3. Creeping behavior is mainly attributed to geometrical complexity⁴ and frictional strength of the fault zone material, with the latter in turn depending on lithology^5–7, temperature⁸, and pore fluid pressure^9,10. On the other hand, temporary episodes of creep acceleration, known as slow slip events (SSEs), have been interpreted as earthquake precursors and as possible triggering factor for major earthquakes^11–15. Ambient stress perturbations due to nearby earthquakes^16–18 and transient pore fluid pressure changes⁹ are among the major causes of these creep events. However, recent observations indicate that SSEs can occur semi-periodically in different tectonic settings^13,19,20, which places additional constraints on the underlying mechanism. In this paper, we provide evidence for episodic SSEs on a creeping transform boundary fault, its interaction with seismicity on surrounding locked segments, and suggest a physically plausible mechanism explaining the occurrence of these events.

Slow-slip event on the central San Andreas fault

The 130 km central segment of the San Andreas Fault (CSAF) in California is characterized by a fast creep of rate ~3 cm/year, and is surrounded by two major locked segments that were the sources of the M_w7.9 earthquakes of 1857 and 1906. The continuous creep on the CSAF is attributed to the frictional weakness, suggested by the lack of elevated heat flow²¹ and nearly fault-normal orientation of maximum horizontal stress²². The frictional weakness, likely caused by intrinsic low friction of fault zone material^5–7 and abnormally elevated pore pressure within the fault core^9,23, suggests that the CSAF is incapable of storing enough strain to generate large earthquakes. Yet, episodic unsteady slip with limited speed in the form of SSEs are observed over entire seismogenic depth of CSAF at semi-regular intervals^19,20, which might modulate the time of seismic events on nearby locked zones. Although the maximum rate of these SSEs does not exceed several times the plate boundary shear strain rate, they share all other characteristics of the well-known SSEs on the subduction zones^19,20. Stress transfer from nearby seismic events^16–18, transient inflow of fluid from depth into seismogenic zone⁹, and shallow frictional heterogeneity²⁴ are suggested to trigger SSEs on the CSAF and nearby creeping segments. Availability of dense geodetic and seismic measurements and observations of CSAF fault properties at San Andreas Fault Observatory at Depth (SAFOD)^5,6 provide the opportunity to investigate the mechanism that drives SSEs and controls their velocity, duration and repeat time.

We used the time series of line-of-sight (LOS) surface deformation obtained from interferometric processing of synthetic aperture radar (SAR) data set, collected between 26 March 2003 and 7 July 2010 with average temporal sampling interval of ~2 months, to measure surface fault creep (Fig. 1 and Supplementary Video 1). The data set is obtained^20,25 by applying an advanced multitemporal InSAR processing algorithm²⁶ on 16 and 30 images acquired by ERS and Envisat C-band satellites, respectively. These LOS observations are thoroughly validated by Khoshmanesh et al.²⁰ and Turner et al.²⁵ using independent geodetic observations (see also Supplementary Fig. 1). Here we calculate the near-field LOS creep time series²⁷ using a moving window of 0.5 km × 2.7 km (from 0.3 km to 3 km fault-normal distance) and along-strike step size of 0.3 km (inset in Fig. 1). The observations of near-field LOS creep reflect the slip behavior of the shallow few kilometer portion of the fault, which might have a similar pattern to that of deeper seismogenic depths^20,28. The spatiotemporal distribution of the difference between short- and long-term LOS creep rate along the CSAF depicts the local variations of creep rate in both space and time (Fig. 2). To increase the signal to noise ratio, we average the rate differences in the spatial domain (magenta curve in Fig. 3a and Supplementary Fig. 2), which reveals the semi-periodic SSEs. To focus on the interseismic slip and disregarding the co- and post-seismic deformations due to the 2004 Parkfield earthquake in our analysis, we exclude the affected observations (inside the black dashed rectangle in Fig. 2). Then, the roughness of LOS creep distribution along the fault is estimated through self-affinity analysis²⁹ implemented on the fault-parallel profiles of rate difference at each time step (see Methods). The roughness amplitude also exhibits time-dependent behavior (black curve in Fig. 3b), which has an 87±3% correlation with creep rate difference. This means that surface LOS creep is rougher during the SSEs, likely due to more heterogeneous creep distribution on the fault. In other words, each observed SSE results from an ensemble of localized creep bursts, namely clusters of accelerated creep exceeding the long-term rate²⁷. These bursts aseismically rupture isolated fault segments, separated by stable creeping patches, instead of a single burst rupturing the entire extent of the fault.

Fig. 1. Creeping segment of the San Andreas Fault with long-term InSAR LOS velocity^20,25.

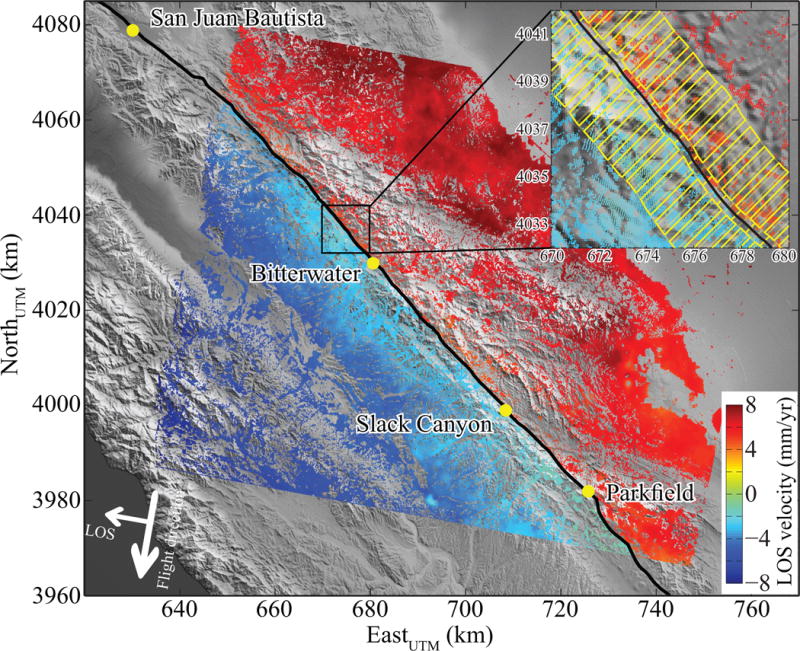
The trace of the SAF is shown with the black line. Warm and cold colors correspond, respectively, to the movement toward and away from the descending satellite. The inset depicts the moving window used for estimation of near-field creep rate, with every other step shown with a lower opacity for visualization purposes. Shaded relief topography is digital train model from Shuttle Radar Topography Mission.

Fig. 2. Spatiotemporal distribution of rate difference and seismicity.

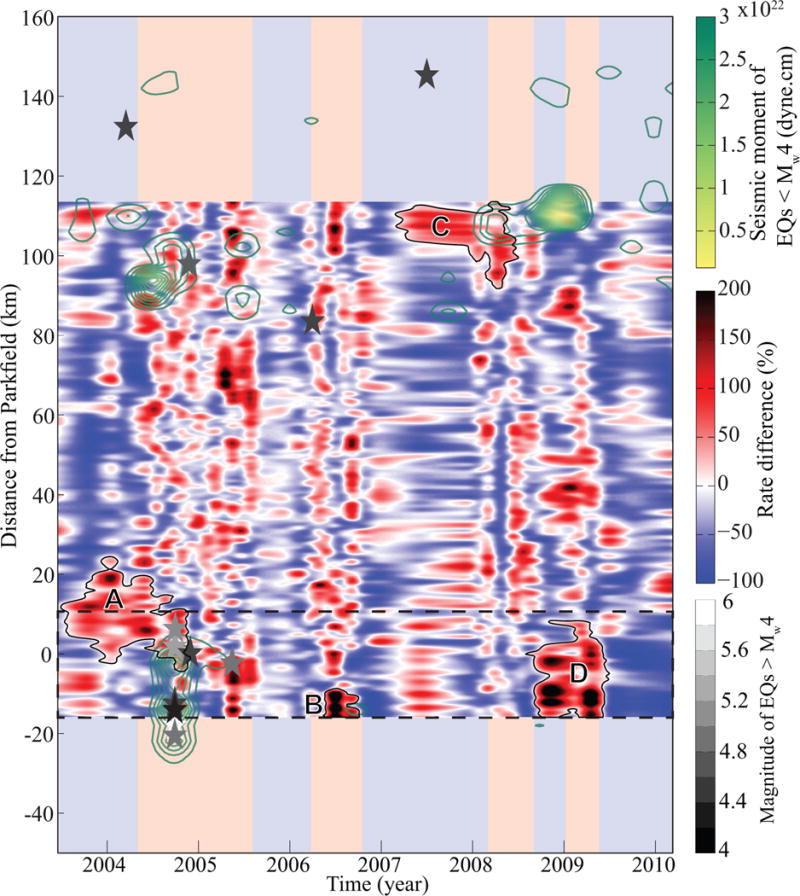
The difference between short-term (between consecutive time steps) and long-term LOS creep rate (slope of the cumulative time series) along with moment released for earthquakes <M_w4 (green contours). Grayscale stars show the location and time of the earthquakes >M_w4. The light red and blue bands on the neighboring segments highlight the time intervals of SSEs and the decelerated creeping, respectively. The dashed rectangle shows the approximate location of the Parkfield transition zone which is excluded from our analysis. The areas indicated by capital letters show the extent of the significant local bursts that are discussed in the main text.

Fig. 3. Temporal evolution of creep rate, effective normal stressing rate, roughness, and b-value.

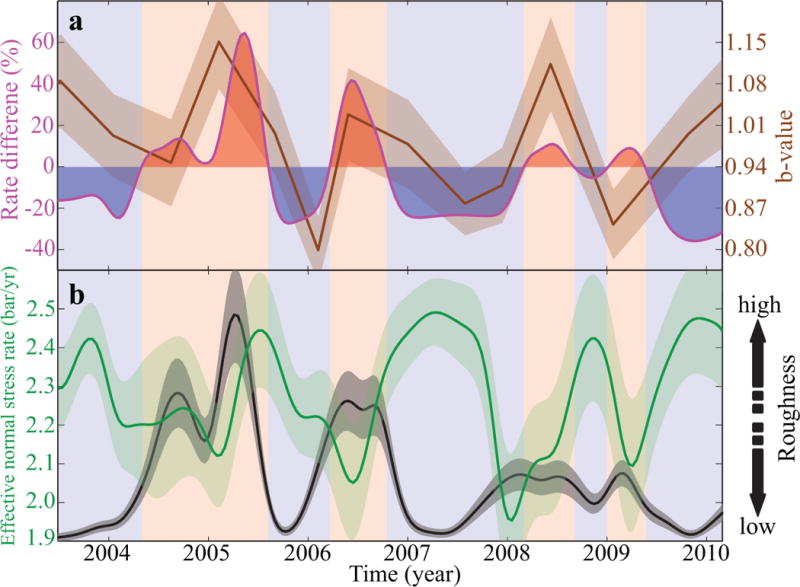
a, Time series of spatially averaged LOS creep rate difference in percentage (magenta), and b-value (brown) alongside its one-sigma uncertainty (shaded brown). Background red and blue bands highlight the time interval of SSEs and decelerated creeping, respectively. b, Temporal evolution of spatially averaged effective normal stress rate (green) and its standard deviation (shaded green), and roughness amplitude of LOS creep rate difference along the fault (black) and its one-sigma uncertainty (shaded gray). All the curves in this figure, beside the b-value are smoothed using a Gaussian smoothing filter with a window size of 6 months.

Possible mechanisms of slow-slip events

In order to nucleate SSEs several mechanisms are suggested, including velocity-weakening frictional properties of certain materials at very low velocities^30,31, and frictional strength reduction with steady slip, i.e., slip weakening³². Stress perturbations due to nearby earthquakes or pore pressure variations are also suggested to generate transient SSEs on the unstable-stable transition zone with velocity-neutral properties³³. Switching to velocity-strengthening properties at higher (sub-seismic) creep rates^30,31, and frictional dilation leading to a reduction of pore pressure³⁴, on the other hand, are proposed as mechanisms for arresting the premature slip in SSEs, preventing these events from turning into an earthquake. The combination of these nucleation and arrest mechanisms are used to simulate SSEs on the downdip end of the seismogenic zone in subduction faults³³, where creep velocity reaches up to 10²-10³ times the tectonic shearing rate^11,35. However, much slower semi-periodic accelerated creep events that are shown to occur on the entire seismogenic depth of the CSAF^19,20 which exhibits a velocity-strengthening properties^5,6, likely belong to a new class of SSEs. These require a new explanation perhaps based on localized perturbation of shear strength on the fault³⁶.

The common aspect of aforementioned mechanisms for initiation of SSEs is the requirement of constant or transient near-lithostatic pore pressure. In subduction zones, elevated pore pressure is speculated to be caused by dehydration of hydrous minerals in a down-going plate¹⁰. But, the mechanism for pore pressure fluctuations on crustal transform faults is less clear. The inflow of mantle driven fluid^9,23 into the highly permeable active fault zone of CSAF, as an existing hypothesis, implies a time lag between SSEs at different depths, which is not supported by slip models²⁰. Thermal pressurization due to shear heating³⁷ is an alternative explanation for the elevation of pore pressure, which results in seismic rupture nucleation. However, this mechanism is significant only when creep rate reaches to orders of magnitude higher than the maximum rate of SSEs on the CSAF³⁷. Compaction of intergranular pore spaces within the hydraulically isolated fault core^38–40, on the other hand, can serve as a viable mechanism for cyclic elevation of pore pressure on CSAF. Elevated pore pressure in this mechanism is self-generating⁴⁰, and does not require an external fluid source.

Rate-and-state friction modelling

To investigate the role of pore pressure variation in generating SSEs, we quantify the time series of effective normal stress rate on the fault using a rate and state friction model under a steady-state condition (see Methods). The effective normal stress (σ_e=σ_n-p) is related to steady-state shear stress (τ_ss, Supplementary Fig. 3) through ${\tau }_{\mathit{ss}}={\sigma }_e(f_0+(\mathit{\text{a-b}})\text{log}\frac{V_{\text{ss}}}{V_0})$, where σ_n is the tectonic normal stress and p is the pore pressure, f₀ is nominal coefficient of friction, a-b is the frictional rate parameter, V_ss is the steady-state rate and V₀ is the reference creep rate⁴¹. The estimated effective normal stress rate (Supplementary Fig. 4) depicts the spatiotemporal variation of pore pressure along the CSAF, given that there is no evidence for variable tectonic normal stressing rate during our study period. Averaging along the fault and comparing the temporal evolution of effective normal stress rate (green curve in Fig. 3b) with that of surficial creep rate difference, we find that an increase (decrease) in average LOS creep rate corresponds with reduction (increases) in the effective normal stressing rate that we attribute to pore pressure elevation (reduction).

Insights from seismicity

Microseismicity, a distinguishing attribute of creeping faults⁴², can also provide insight into the temporal evolution of fault strength and shed light on the possible mechanism for transient events. The temporal evolution of estimated Gutenberg-Richter b-value⁴³ (Supplementary Figs. 5-7, brown curve in Fig. 3a, see Methods), exhibits a 60±8% correlation with the variation of LOS creep rate difference, showing clear increase in b-value during the dominant SSEs on the CSAF. However, the reason for poor correlation starting in 2009 and before mid-2004 is unclear. Moreover, time series of the total seismic moment of microearthquakes exhibits a negative correlation with b-value and surface creep rate (Supplementary Fig. 7). This suggests that larger microearthquakes (lower b-value) occur when the fault is creeping with a relatively slower rate⁴³, due to pore pressure drop leading to restrengthening of the fault. A similar conclusion can also be reached by comparing earthquake counts and the creep rate difference (Supplementary Fig. 8), which suggest that microseismic activity maximizes when the frictional strength is increased. This is followed by a decline in microseismicity when the pore pressure is elevated while CSAF is experiencing an episode of SSE. Spatiotemporal distribution of seismic moment along the CSAF and adjacent locked segments is also overlain on the distribution of LOS creep rate difference (Supplementary Fig. 9). Comparisons confirm that segments with elevated seismic moment release are predominantly creeping slower than the long-term rate (indicated by the colder colors).

Preferred mechanism driving creep events on San Andreas Fault

Our observations and analyses suggest that elevated pore pressure possibly driven by compaction^38–40 and subsequent frictional dilation³⁴ are responsible for initiating and arresting the episodic SSEs along the CSAF. Within a dilated fault zone with an average pore pressure below lithostatic, intergranular pore spaces undergo compaction due to ductile creep³⁹. Under an undrained condition, namely being hydraulically isolated from the surrounding country rock through a permanent impermeable seal layer⁴⁴, compaction results in increased pore pressure to lithostatic level^38,39, which correlates with incipient creep acceleration⁴⁵. Considering a compressibility of 10⁻¹⁰ to 10⁻⁹ Pa⁻¹, a porosity reduction of 1-6% at depth of 8 km results in elevation of pore pressure from hydrostatic to lithostatic level. Due to the heterogeneous fault zone material and geometrical irregularity of the fault surface, however, rate of porosity reduction due to compaction is not the same for the entire fault, leading to heterogeneous distribution of overpressurized fluid on the fault^46,47. Moreover, extremely low permeability of fault gouge on CSAF (10⁻²³ to 10⁻²¹ m²)⁴⁸ reduces the specific discharge rate from zones of high pressure to low. This divides the fault into natural compartments with different fluid pressures, resulting in a heterogeneous distribution of pore pressure across the seismogenic zone^40,49. The isolated creep bursts, therefore, pinpoint the location of these overpressurized compartments along the CSAF. An ensemble of these localized creep burst, observed as heterogeneous creep rates on the surface, which is quantified using increased roughness estimates makes up the episodic SSEs.

Frictional dilation³⁴ due to accelerated creep, on the other hand, restores the porosity and restrengthen the overpressurized compartments, which is correlated with the incipient creep deceleration⁴⁵. Frictional dilation also increases the permeability of fault gouge, which leads to redistribution of fluid within the fault zone, and therefore homogenous distribution of pore pressure along the fault^38,39. This coincides with decelerated creep rate with a spatially uniform pattern throughout the fault, observed as a smoother surface creep rate distribution (Supplementary Fig. 10), which also marks the initiation of the next compaction cycle. The increased effective normal stress during creep deceleration, causing negative Coulomb stress changes, may additionally trigger slip transients, which are characterized by significantly smaller amplitude, and temporal delays proportional to the size of stress perturbations³⁶. Nonetheless, modulation of these dilation-induced slip transients onto the compaction-induced SSEs might be responsible for some of the irregularity that we observe in amplitude and timing of the SSEs on the CSAF.

In this mechanism, therefore, creep rate variation is not instantaneous, and instead, creep evolves in consecutive intervals of acceleration and deceleration, which correlate with similar variations in pore pressure. This is consistent with the results of laboratory experiments, documenting the role of elevated pore pressure and decreased permeability in generating the transient events⁴⁵. The observed concurrence of the decreased b-value and increased number of microseismic events and their released moment during the decelerated creep, when the frictional strength is elevated, is also aligned with our proposed mechanism for SSEs on the CSAF^38,40,49. Our suggested mechanism does not require an external fluid source^38–40, which makes it a favorable explanation for the observed variation of creep rate on other velocity-strengthening crustal faults²⁸ and possibly subduction zones.

Slow-slip events impact on seismic hazard

SSEs are suggested as a mechanism for triggering major earthquakes on subduction zones^11–13 and as also being triggered due to adjacent earthquakes on crustal faults^16–18. Distribution of the seismicity⁵⁰ along the CSAF and the transition segment to the south (From −50 to 115 km in Fig. 2) reveal that earthquakes larger than M_w4, including the 2004 M_w6 Parkfield earthquake, occurred during SSEs on the CSAF. The timing of the earthquakes in the northern locked segment (From 115 to 160 km in Fig. 2), however, is not correlated with the timing of SSEs on the CSAF, perhaps due to more complex fault structure in this segment. Our observations show that initiation of the accelerated creep phase on the creeping segment precedes the 2004 earthquake, suggesting that this seismic event could have been triggered due to stress transfer from this SSE. We estimate that the rate of Coulomb stress change at the hypocenter (see Methods) increased up to 0.45 bar/yr during the SSE. Additionally, the study of deep tremors suggested an SSE, possibly ~16 km below the hypocenter, preceded the Parkfield earthquake¹⁴. However, our geodetic observation does not provide adequate resolution to resolve the signal associated with this deep SSE.

The ruptured asperity of the 2004 event, on the other hand, slowly re-ruptured in the form of a localized burst during the following episodes of SSE on the CSAF (bursts B and D in Fig. 2). This calls for an additional explanation for the complex response of the Parkfield transition zone to the SSE on the CSAF, and most importantly the underlying triggering mechanism of the 2004 event. A closer examination of the creep rate difference distribution suggests that a combination of a significant localized burst (burst A in Fig. 2) initiated about one year prior to this event, persistent until the time of nucleation, and the SSE on the CSAF might have triggered this earthquake. Coseismic slip distribution of this earthquake⁵¹ also suggests that the area experiencing the maximum coseismic slip has an overlap with the burst A. This is likely due to thermal pressurization of fluids³⁷ in addition to the pre-existing compaction-induced elevated pore pressure. This observation is also supported by a distinguishable increase in the microseismicity, following another significant local burst that occurred between 2007 to 2009 at the northern end of our study area (burst C in Fig. 2), having similar scale and amplitude to that of burst A. These findings highlight the role of observation and analyses of the surface creep rate to detect the SSEs and significant local bursts to improve the time-dependent estimates of seismic hazard associated with transform faults²⁷. Moreover, considering the periodicity of these SSEs as opposed to the conventional assumption of a constant loading rate, time-dependent probabilistic earthquake forecast models can be greatly improved.

Methods

Rate and state friction model

The effective normal stress σ_e=σ_n-p, where σ_n is tectonic normal stress and p is the pore pressure, is related to steady-state shear stress (τ_ss) through ${\tau }_{\mathit{\text{ss}}}={\sigma }_e(f_0+(\mathit{\text{a-b}})\text{log}\frac{V_{\text{ss}}}{V_0})$. In this equation, f₀ is nominal coefficient of friction, a-b is the frictional rate parameter, V_ss is the steady-state rate and V₀ is the reference creep rate⁴¹. The shear stress change on fault patch i between time steps t₁ and t₂= t₁+dt is estimated⁵² through $\tau (\mathit{\text{i,dt)}}={\dot{\tau }}_0\mathit{\text{dt}}+\mathit{\text{dτ}}(\mathit{\text{i,dt}})$, in which the first term on the right side is the stress due to tectonic plate loading⁵³ with ${\dot{\tau }}_0$=0.25 bar/yr. The second term accounts for the imparted stress due to slip on the adjacent fault patches, provided by $d\mathit{\text{τ(i,dt)}}={\displaystyle \sum }_{\mathit{j}=1}^{n}G(\mathit{\text{i,j}})d(\mathit{\text{j,dt}})$, where slip (d) on the fault, discretized into n dislocation patches, is obtained from the time-dependent model of creep along the CSAF from Khoshmanesh et al.²⁰. The elastic kernel, G(i,j) represents the shear stress change at the patch i due to a unit rake-directed slip on patch j. This kernel is defined by the analytical solution of a rectangular dislocation buried in an elastic half-space⁵⁴, with Poisson ratio and shear modulus of 0.25 and 30GPa, respectively. Supplementary Figs. 3b and 3c demonstrate the temporal average and standard deviation of the shear stress rate on the CSAF. Without loss of generality, we choose V₀ = V_lt(i) where V_lt(i) is the long-term creep rate estimated for each fault patch along CSAF²⁰. Time series of V_ss, which is considered as the rate of creep between consecutive time steps, is also obtained from the time-dependent model of creep from Khoshmanesh et al.²⁰. Moreover, based on the laboratory experiments on SAFOD samples⁵, frictional parameter (a-b) and coefficient of friction (f₀) are chosen to be 0.01 and 0.1 for entire fault, respectively. Given that $\tau (\mathit{\text{i,dt}})$ and, therefore estimated ${\sigma }_e$ are a function of interval between consecutive time steps, our estimates could be affected by irregular temporal sampling of creep model. Therefore, temporally-normalized effective normal stress with respect to period between consecutive time steps is presented and discussed throughout the paper. Spatial distribution of average rate of σ_e and its standard deviations are depicted in Supplementary Fig. 4.

Fault creep self-affinity analysis

A self-affine 2-D profile in xy plane has constant statistical properties under an affine transformation of the form δx→ λδx, δy→ λ^Hδy, where λ is the scale factor and H is the Hurst exponent²⁹. To investigate the self-affinity of a given profile, the method of Fourier analysis is widely used⁵⁵. Through this method, Fourier power spectrum (P) as a function of wave number (k) follows a linear trend in log-log space, which is related to the Hurst exponent through P(k)=Ck^−1−2H, where C is the pre-factor. Thus, fitting a line to the log-log plot of P(k) versus wave number k using a robust regression method, enables estimating the Hurst exponent and pre-factor, as well as their standard deviations. The Hurst exponent, ranging between 0 and 1, describes how the profile roughness changes with scale, with a smoother and more persistent trend in larger scales, for higher values. The pre-factor, C, on the other hand, gives information about the amplitude of roughness and is used for comparing the relative roughness of multiple profiles⁵⁶. The black curve in Fig. 3b shows the temporal evolution of pre-factor estimated for the time series of fault-parallel profiles of the creep rate difference.

Gutenberg-Richter b-value

Gutenberg-Richter law relates the frequency of occurrence to the magnitude of earthquakes through log₁₀N=a-bM, where N is the cumulative number of events larger than magnitude M, and a and b are constants⁵⁷. To obtain the parameter b (so-called b-value), we implemented the maximum likelihood estimation (MLE) method^58,59. Using this method, b_MLE=log₁₀(e)/[M_m-(M_c-dM/2)], where M_m is the mean magnitude, M_c is the magnitude of completeness, e is the Euler’s number, and the magnitudes are rounded to dM=0.01. The associated standard deviation can also be calculated⁶⁰ using ${\sigma }_b=2\text{.30×}{\left(b_{\mathit{\text{MLE}}}\right)}^2\sqrt{{\displaystyle \sum }_{\mathit{\text{i=1}}}^n{\left(M_i-M_m\right)}^2/n\left(\mathit{\text{n-1}}\right)}$, where n is the size of observation window, containing n earthquakes with magnitudes M_i. To avoid underestimation of b-value, one needs to carefully consider the completeness magnitude (M_c) for a given seismic catalogue⁶¹. Following previous estimations of completeness magnitude for the seismic catalogue near CSAF and Parkfield segment^43,62,63, we used M_c=1.3. To account for the distribution of events near the fault surface, we assigned a distance-dependent weight to all the earthquakes in the vicinity of the fault⁶⁴. We used an exponential weighting function⁶⁴, w(d)=λe^−λd, in which d is the closest distance between earthquake hypocenter and the fault surface, and λ=0.7 after Tormann et al.⁶⁴. We have tested various values of λ ranging from 0.3 to 1 and all yield comparable results. Given its relatively homogeneous and fast rate of creep, we consider the central zone (20 to 90 km) for b-value calculation. The magnitude distribution of all the earthquakes considered for this analysis is shown in Supplementary Fig. 5.

Sorting the earthquakes based on the occurrence time, we used n number of events, as the size of the moving window, without any overlap between consecutive windows, and estimated the time-dependent b-value⁴³. The optimum size of this moving window is estimated through a Monte Carlo search algorithm⁶⁴. To this end, we simulated 1000 synthetic earthquake catalogues with true b-value of b₀=1, using M=(M_c-dM/2)-log(r)/β, in which β=log(10)b₀, and r is a set of random numbers between 0 and 1, produced using Matlab’s rand function⁶⁴. The number of events in each synthetic catalogue and their weight as a function of distance from the fault are the same as that of the CSAF observed seismic catalogue. To identify the acceptable range of window size, we test a range of n from 50 to 300 with steps of 2. As a result, we obtain a time series of b-value as a function of n, per synthetic catalogue. Next, for each window size n, considering the estimated values for different time steps across all 1000 simulations, we calculate the time series of mean b-value and associated standard deviation. For each window size, the highest standard deviation and the maximum difference between mean b-value time series and the true value of b₀=1, are considered as the representative precision and accuracy of the time series (Supplementary Fig. 6). The criterion for acceptable window sizes is the associated accuracy and precision being less than 5% and 10% of the true b-value. We find that the accuracy of the estimated mean b-value time series is acceptable for the window sizes of larger than ~60 events (Supplementary Fig. 6). However, considering the precision criterion, our Monte Carlo search algorithm results in an optimum window size of larger than 160 events (Supplementary Fig. 6). Our preferred b-value time series (Fig. 3) is estimated using window size of 170 events, which yields a sampling rate of roughly half a year (Supplementary Fig. 7).

Coulomb failure stress

Time series of Coulomb failure stress change ΔCFS is estimated using the time dependent model of creep on the CSAF from Khoshmanesh et al.²⁰. The total shear (Δτ) and normal stress (Δσ) imposed at the earthquake hypocenter in each time step is estimated as superposition of the stress imparted by creep at all patches across the CSAF⁵⁴. The Coulomb failure stress change ΔCFS=Δτ-μΔσ is then estimated assuming a friction coefficient of μ=0.6 on a fault with the mean strike (313°) and dip (86°) of the CSAF.

Code availability

Computer code that supports the findings of this study is available from the corresponding author upon request.

Data availability

The InSAR time series was obtained from Khoshmanesh et al.²⁰ and Turner et al.²⁵. The seismic catalogue is obtained from Waldhauser & Schaff⁵⁰. The creepmeter data at Slacks Canyon was obtained from United States Geological Survey. The data and observational results that support the findings of this study are available from the corresponding author upon request.