¹H Dynamic Nuclear Polarization Based on an Endogenous Radical

Abstract

We demonstrate a 15-fold enhancement of solid-state NMR signals via dynamic nuclear polarization (DNP) based on a stable, naturally occurring radical in a protein: the flavin mononucleotide (FMN) semiquinone of flavodoxin. The linewidth of flavodoxin’s EPR signal suggests that the dominant DNP mechanism is the solid effect, consistent with the field-dependent DNP enhancement profile. The magnitude of the enhancement as well as the bulk-polarization build-up time constant (τ_B) with which it develops are dependent on the isotopic composition of the protein. Deuteration of the protein to 85 % increased the nuclear longitudinal relaxation time T_1n and τ_B by factors of five and seven, respectively. Slowed dissipation of polarization can explain the two-fold higher maximal enhancement than that obtained in proteated protein, based on the endogenous semiquinone. In contrast, the long τ_B of TOTAPOL-based DNP in non-glassy samples was not accompanied by a similarly important long T_1n, and in this case the enhancement was greatly reduced. The low concentrations of radicals occurring naturally in biological systems limit the magnitude of DNP enhancement that is attainable by this means. However, our enhancement factors of up to 15 can nonetheless make an important difference to the feasibility of applying solid-state NMR to biochemical systems. We speculate that DNP based on endogenous radicals may facilitate MAS NMR characterization of biochemical complexes and even organelles, and could also serve as a source of additional structural and physiological information.

TOC image

Introduction

Dynamic nuclear polarization (DNP) is a powerful method for enhancing signal intensities in liquid and solid-state NMR experiments, and enhancement factors of up to 200 for ¹H nuclei have been observed for model systems and biomolecules^1–5. In a DNP experiment, the large Boltzmann electron polarization of a paramagnetic polarizing agent is transferred to nuclei in close proximity by irradiating the sample with microwave radiation near the electron paramagnetic resonance (EPR) transition frequency. Depending on the sizes of the inhomogeneous (Δ) and homogeneous (δ) breadths of the EPR signal relative to the nuclear Lamor nuclear frequency (ω_0n) the DNP process at high magnetic fields (> 5 T) can either occur through the solid effect (SE, ω_0n > Δ, δ) or through the cross-effect (CE, Δ> ω_0n > δ)^6–9. Currently the largest signal enhancements are observed in DNP-enhanced solid-state NMR experiments that exploit the CE using exogeneous biradicals such as TOTAPOL as polarizing agents^10,11. In this approach the solvent, usually a glassy matrix such as glycerol/H₂O, is polarized and ¹H-¹H spin diffusion distributes the polarization uniformly throughout the sample. In a second step the enhanced ¹H polarizaton is transferred to ¹³C, ¹⁵N or other nuclei in solutes of interest. However for optimum DNP performance a large amount of the exogenous polarizing agent has to be added to the sample; this is generally assumed to be distributed randomly throughout the matrix and to not affect the integrity of the molecules of interest^12,13.

In addition to exogenous polarizing agents biology offers several endogenous radicals whose use does not perturb the system and moreover offers control over the location of the radical, and coupling of its occurrence to a particular state of the sample. Biological systems are typically more complex and more dilute than model systems, so the enhancements possible by DNP would be particularly valuable. With a view to enabling DNP-enhanced NMR to address intact biological systems, we propose the use of endogeneous radicals that occur naturally in many proteins as sources of polarization.

Some 10 % of biological macromolecules possess a paramagnetic center such as a paramagnetic metal ion (eg. Cu²⁺, Fe³⁺, Mn²⁺), metal cluster (eg. Fe_xS_y) or transient or stable organic radical (quinone, flavin, tyrosine, etc.). Based on a recent (January 2012) search of the Protein Data Bank (www.rcsb.org), the number of protein structures whose annotation included the name of a metal ion that readily adopts a paramagnetic oxidation state accounted for 9 % of all protein structures, and the number of structures whose annotation included either ‘FMN’, ‘FAD’, ‘quinone’ or ‘radical’ accounted for 3 %. When protein structures that posses diamagnetic cations Zn²⁺, Mg²⁺ and Ca²⁺ were also included, the total percentage of structures containing a metal ion came to 40%, in qualitative agreement with more formal determinations¹⁴. Diamagnetic cations can often be replaced by paramagnetic metal ions to produce a paramagnetic site, for example for studies by EPR^15–18. These cofactors are essential to the activity of many redox-active enzymes and electron transport proteins that participate in the respiratory or photosynthetic electron transport chains. Many of the above cofactors alternate among different oxidation and spin states depending on the physiological state of the system, leading to the possibility that DNP enhancement could be used as a probe of physiological status.

Our proposed use of a naturally-occurring endogenous radical for DNP-enhanced NMR spectroscopy is supported by numerous successes with related techniques. A popular implementation of chemically-induced DNP (CIDNP) has exploited photoexcited flavins that can react with Trp, His and Tyr side chains to produce a radical pair. When the recombination efficiency is greater in the presence of one nuclear spin state than the other, for example based on electron-nuclear hyperfine facilitated intersystem crossing, then the resulting diamagnetic ground state retains net nuclear polarization^19,20. In the case of dye-supported photo-CIDNP, flavins free in solution serve as the dye and can produce enhanced NMR resonances from exposed aromatic amino acid side chains^19,21. Photogenerated endogenous radicals in bacterial reaction centers have also been used to obtain thousand-fold enhancements of ¹³C and ¹⁵N solid-state NMR signals of the pigments that participate in photosynthetic electron transfer, and several different mechanisms have been proposed^22–24. In this case, effects are restricted to nuclei in hyperfine contact with the endogenous radicals so the method yields primarily local information. Moreover its reliance on a pair of highly divergent electron recombination rates for the two participating spin states, and large electron-hyperfine coupling, limits the general applicability of the method. This combination of spin properties has been proposed to be an evolved characteristic of photosynthetic reaction centers²³, but the effect has recently been demonstrated in a photoactive flavoprotein as well²⁵. Stable naturally-occurring radicals have also been used to measure important distances in biochemical systems^26–28. A recent example of double electron-electron resonance (DEER) exploits the naturally occurring flavin radical of the electron transfer flavoprotein (ETF) that is generated specifically upon turnover of a coupled enzyme²⁹. Thus, the resulting signal is not only a probe of structure, but also a signature of physiological state. In contrast, the diverse opportunities natural radicals offer to DNP-enhanced NMR spectroscopy have barely been explored.

In this first example of using an endogenous stable radical for DNP-enhanced NMR spectroscopy we exploit the flavin mononucleotide (FMN) radical semiquinone (SQ) of flavodoxin (FD). FDs are small well-behaved electron transport proteins containing a single non-covalently bound FMN. FDs accept a single electron at low potential (for example from photosystem I) and then serve as electron donors to a variety of enzymes and processes in microbial metabolism (for example nitrogen fixation). Thus, FD’s bound FMN cycles between a diamagnetic oxidized state and a stable neutral SQ radical formed upon acquisition of an electron and a proton. The FD from Desulfovibrio vulgaris has been extensively characterized electrochemically³⁰ and by various forms of optical spectroscopy³¹. Many mutants have been characterized^32–34, the crystal structures of all three oxidation states have been solved^35,36 and NMR resonance assignments have been published for both the diamagnetic states^37–39. The structure of flavodoxin is depicted in Figure 1 and is unaffected by the flavin oxidation state, with the exception of residues 59-62 and 95-102 immediately adjacent to the flavin^36,38–40. Thus, FD provides a robust and familiar system in which to explore the practicality of using a stable endogenous radical that participates in biological function, as a source of DNP.

Figure 1.

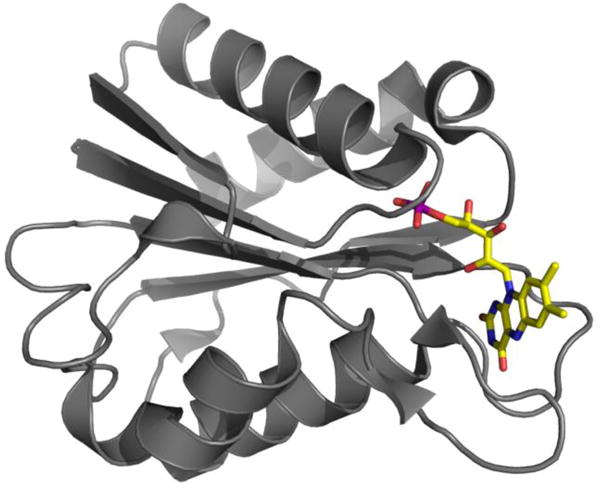
Ribbon structure of FD depicting elements of secondary structure with ribbon segments and intervening stretches of backbone with cord. Amino acid side chains are omitted for simplicity however the flavin is shown in atomic detail with N atoms in blue, O atoms in red and the P atom in purple. H atoms are not shown and C is in yellow consistent with FMN’s intense yellow color. Figure generated using Pymol⁴¹.

In this paper we report a 15-fold DNP enhancement of ¹H magic-angle spinning solid-state NMR (MAS NMR) spectra despite the ten-fold lower concentration of our FD SQ as compared to typical concentrations used of exogenous polarization agents for DNP-enhanced NMR spectroscopy. In addition we show that the enhancement is responsive to the isotopic composition of the FD protein and that the increased enhancement upon deuteration can be attributed to a longer T_1n. The enhancement we observe conforms to other expectations for SE DNP, as anticipated based on the breadth of the SQ EPR signal. Thus we show that an endogenous radical can support DNP just as exogenous radicals do, albeit with smaller enhancements most likely as a result of its lower concentration.

Materials and Methods

Overexpression and Purification of Flavodoxin (FD)

The gene encoding the FD of Desulfovibrio vulgaris was cloned into the pET23d vector, which provides a C-terminal Leu-Glu-His₆ tag. The base substitution required to produce an NcoI site also produced a Pro -> Ala amino acid substitution at position 2. These changes had no apparent effect on FD’s optical properties or EPR signal. The resulting FD-pET23d plasmid was transformed into Escherichia coli BL21 (DE3) competent cells.

Unlabelled FD

Unlabelled FD was expressed in Luria-Bertani (LB) medium containing 50 μg/mL ampicillin, upon addition of IPTG to 1 mM when the optical density at 600 nm (OD₆₀₀) reached approximately 0.6. The temperature was lowered from 37 °C to 32 ˚C and after an additional 4 hours of shaking, cells were harvested by centrifugation. The cell pellet was resuspended in lysis buffer (50 mM potassium phosphate, pH = 7.30, containing 300 mM KCl, 10 mM imidazole) with 0.5 mg/mL 4-(2-aminoethyl) benzenesulfonyl fluoride hydrochloride (AEBSF) and 0.1 mM FMN, and lysed by passage through a French press twice at 12,000-15,000 psi. The suspension was centrifuged at 4 °C, 15000 × g for 45 min. to remove cell debris. Supernatant from about 10 g of cells, wet weight, was applied to a 20 mL Ni-NTA (nitrilotriacetate) agarose column equilibrated with 200 mL of lysis buffer. The flow-through was collected and reloaded three more times. The column was washed with wash buffer (50 mM potassium phosphate, pH = 7.30, containing 300 mM KCl, 20 mM imidazole) to remove non-specifically bound protein until the OD₂₈₀ of the eluant was constant and lower than 0.02. His-tagged FD was eluted using high imidazole elution buffer (50 mM potassium phosphate, pH = 7.30, containing 300 mM KCl, 250 mM imidazole). Fractions were collected and their OD₂₈₀ was monitored to identify those containing protein. The eluted protein’s identity was determined on the basis of molecular weight by sodium dodecyl sulfate polyacrylamide gel electrophoresis (SDS-PAGE) and yellow color. Fractions containing pure His-tagged FD were combined and dialyzed against dialysis buffer (200 mM potassium phosphate, pH = 7.50). The protein was concentrated using an Amicon Ultra-15 centrifugal filter device (10 kDa nominal molecular weight limit). The concentration of FD was determined based on measured values of OD₂₇₃ and OD₄₅₈ using a HP8452B diode array spectrophotometer. (ε₂₇₃ = 46,300 M⁻¹cm⁻¹, ε₄₅₈ = 10,700 M⁻¹cm^{−1 30}). Resulting FD had an A₄₅₈/A₂₇₃ ratio of 0.196 or higher, and was electrophoretically pure.

[¹³C, ¹H] labeled FD

[¹³C, ¹H] labeled FD was expressed in 1 L M9 medium including only 3 g ¹³C D-glucose (vs. the standard 10 g) prepared as a separate filter-sterilized stock solution. Cells were produced by growing 1 L of LB culture at 37 °C to an OD₆₀₀ of 0.5, harvesting by centrifugation, washing the pellet with 20 ml of the ¹³C-glucose-free M9 medium and then suspending the cells in 1 L ¹³C-glucose-complete M9 supplemented with 10 μM FeCl₂, 4 mM MgSO₄, 100 μM CaCl₂, 50 μg/mL carbenicillin, 0.5 mM IPTG and 1 mL of micronutrient solution. The culture was incubated at 32 °C with shaking for 12 hours before harvesting. FD was purified as above.

[¹³C, ²H] labeled FD

[¹³C, ²H] labeled FD was expressed as above but using 1 L of M9 medium made up in ²H₂O and filter-sterilized. Stock solutions of Fe, Mg, Ca, micronutrients, carbenicillin and IPTG were made up in ¹H₂O. FD was purified as above. The protein was estimated to be 85% deuterated in aliphatic positions based on the intensity of aliphatic ¹H NMR signals vs. ¹H backbone amide signals, which had acquired ¹H from ¹H₂O.

Sample preparation for DNP

Purified FD was concentrated to > 2 mM and exchanged into a solution that was 70 % by volume ²H-glycerol and 30 % by volume perdeuterated-buffer (200 mM potassium phosphate pH 7.5, 0.02 % NaN₃ in ²H₂O) by repeated dilution and re-concentration. The samples were rendered anaerobic and then reduced to the SQ state using a calibrated anaerobic solution of dithionite also in 70 % ²H-glycerol: 30 % perdeuterated buffer (v:v). Calibration was achieved by titrating a known amount of FMN with the dithionite solution and using optical spectrophotometry to determine when the sample had been fully reduced (oxidized FMN’s ε₄₄₅ of 12.5 mM⁻¹cm^{−1 42} and the known volume were used to determine the amount of FMN in use). The dithionite was used within 2 hours of calibration, during which time it was kept anaerobic and on ice. Sample reductions were performed in septum-sealed anaerobic reactivials (Pierce) and each NMR sample’s color was monitored until the transition from yellow (oxidized) to purple (neutral SQ radical) was complete (~15 min.). Working in a glove bag, the material was then loaded into degassed NMR rotors, sealed, frozen and stored in Ar-filled sealed vials. Such samples remained in the SQ state for months at − 80 °C.

For samples prepared with the exogenous biradical polarizing agent TOTAPOL¹¹, the FD was used in its diamagnetic oxidized state and TOTAPOL was added to a final concentration of 10 mM (20 mM unpaired e⁻).

Data shown here were all obtained using samples made up in fully deuterated buffer and glycerol. This is important because the paramagnetic flavin of FD is exposed at the surface of the protein (Figure 1), so that bleeding of the ¹H polarization into the solvent matrix can readily occur.

DNP experiments

DNP experiments were performed using a custom-built DNP MAS NMR spectrometer operating at a nuclear Larmor frequency of 212 MHz for ¹H (140 GHz for electrons) corresponding to a magnetic field strength of 5 T. Experiments were performed in a custom-designed 4 mm triple-resonance (e⁻, ¹H, ¹³C) low-temperature MAS NMR probe, or a similar 2.5 mm triple resonance probe using a commercial stator (Revolution NMR Inc.). Microwave radiation was generated by a gyrotron operating at a frequency of 139.662 GHz^43,44. The data presented here were obtained using a microwave power of approximately 2.5 W (estimated at the position of the sample). The sample was contained in a 4.0 mm or a 2.5 mm sapphire rotor (Insaco, Quakertown, PA USA).

DNP-enhanced ¹H MAS NMR spectra were obtained at approximately 90 K using direct ¹H detection at 212 MHz. While MAS NMR experiments using the naturally-occurring SQ radical where performed using either a 4 mm sapphire rotor typically spinning at ω_r/2π ≈ 3 kHz or a 2.5 mm sapphire rotor, all experiments using TOTAPOL as the polarizing agent were performed using a 2.5 mm rotor at a spinning frequency of ω_r/2π ≈ 5 kHz. For all experiments a ¹H pre-saturation sequence was applied (saturation train of 16 120º pulses interspersed with 2 ms delays) followed by polarization for a time period t_mw and then a single 90° detection pulse (83 kHz field strength). During the polarization period the sample was either irradiated with microwave radiation (“on-signal”) or not (“off-signal”). The free induction decay (FID) was typically digitized for 2048 μs before the sequence was repeated. No additional recycle delay was necessary. To record the DNP enhancement profile the applied magnetic field was varied using a superconducting sweep coil (± 75 mT). At each point in the profile, the actual field strength was measured using a field/frequency lock system accessory built into the spectrometer⁴⁵. DNP enhancement profiles were recorded using a t_mw of 5 s.

For DNP buildup curves, the static field (B₀) was adjusted to 4987.8 mT so that the microwave irradiation frequency coincided with ω_0e + ω_0n, and t_mw was varied. In each case two series of ¹H MAS NMR spectra were obtained, one with application of microwave irradiation to the sample and one without microwave radiation. The first such series yields the polarization build-up time τ_B as described below and the second yields the corresponding T_1n via the same analysis.

¹H detection suffers from technical artifacts, such as incompletely resolved rotational sidebands, or receiver ring-down, which can interfere with other measurements. However since such artifacts are not related to the DNP mechanism, they remain constant throughout the enhancement profiles and series of ¹H spectra were used to construct build-up curves and field profiles.

For ¹³C-labeled samples containing TOTAPOL as the polarizing agent the ¹H polarization was transferred to ¹³C with a 0.7 ms cross-polarization (CP) step using a 50 kHz field strength on the ¹H and ¹³C channels⁴⁶. This enabled us to observe only polarization that diffused into the protein because only the protein was uniformly ¹³C labelled whereas glycerol in the buffer was ¹²C-glycerol.

NMR Data Processing and Analysis

Processing of ¹H detected FIDs included left-shifting of the data set by two points (to eliminate a large contribution of receiver ring-down) and zero-filling to twice the number of experimental data points followed by magnitude-mode Fourier transformation. The MAS NMR signal intensity was calculated as the peak-to-trough height of the center-band in order to minimize contributions from broad background signals. Build-up of bulk-polarization was characterized by fitting observed ¹H MAS NMR signal intensity S to a mono-exponential function of the microwave polarization time t_mw

$$\mathrm{S}={\mathrm{M}}_{\mathrm{\infty }}(1-{\mathrm{e}}^{{\mathrm{t}}_{\text{mw}}/{\tau }_{\mathrm{B}}})$$ Eq. 1

where M_∞ is the (maximal) steady-state signal amplitude, and τ_B is the bulk-polarization build-up time. All fits were performed in Matlab (Mathworks) using home-written routines. The DNP enhancement of the ¹H MAS NMR signal (ε_H) was calculated based on the t_mw → ∞ steady-state asymptotes of the buildup curves, M_∞, as the ratio of the value obtained with microwave irradiation (‘on-signal’) divided by the value obtained without (‘off-signal’). We estimate errors on the order of 5-10 % based on reproducibility of the results obtained from different data sets and different samples.

EPR experiments

EPR experiments were performed on a custom-designed high-field EPR spectrometer operating at a microwave frequency of 139.504 GHz^47,48. The sample, with a volume of approximately 250 nL, was transferred to a Suprasil quartz tube (o.d. 0.55 mm) and frozen to 40 K, the temperature at which data were collected. EPR spectra were recorded using a two-pulse echo sequence (π/2–τ–π–τ–echo) using a 80 ns π/2 pulse length and a τ of 200 ns. The data were recorded at a 1 kHz repetition rate and 10 points per field position were averaged. To obtain an EPR spectrum the integrated echo intensity was plotted as a function of the magnetic field over a range of 4976 ± 10 mT. The spectrometer was equipped with a field/frequency lock system⁴⁵ to ensure accurate field measurements at each point. Pseudo-modulated spectra were calculated from the absorption-mode spectra using a modulation amplitude of 0.3 mT as per Hyde et al.⁴⁹.

X-band EPR data were recorded using a Bruker EMX spectrometer in continuous wave mode using a microwave power of 0.2 mW and a modulation amplitude of 0.5 G with the sample (250 μl, 4 mm quartz tube) immersed in liquid N₂ (at 77 K).

Results and Discussion

Optical Titration of Flavodoxin and Production of the Semiquinone

To maximize the efficiency of DNP, FD was quantitatively reduced to the neutral (blue) flavin SQ state via one-electron reduction with dithionite under anaerobic conditions³⁰ (see Scheme 1). Anaerobic formation of the SQ state of FD was monitored optically between small additions of a calibrated solution of dithionite. The isosbestic at 515 nm shared by the spectra ranging from black through red in Figure 2 confirms simple conversion of the yellow oxidized state (λ_max = 462 nm) to the violet SQ (λ_max = 581 nm), prior to onset of the second reductive phase (violet to grey traces, not detailed) in which the SQ is converted to the faintly colored hydroquinone³⁰. Our absorption maxima are very close to the literature values of 458 nm and 580 nm, respectively. The use of a calibrated solution of dithionite permitted virtually quantitative production of FD SQ at the high, optically opaque concentrations required for MAS NMR spectroscopy (central region of lower inset).

Scheme 1.

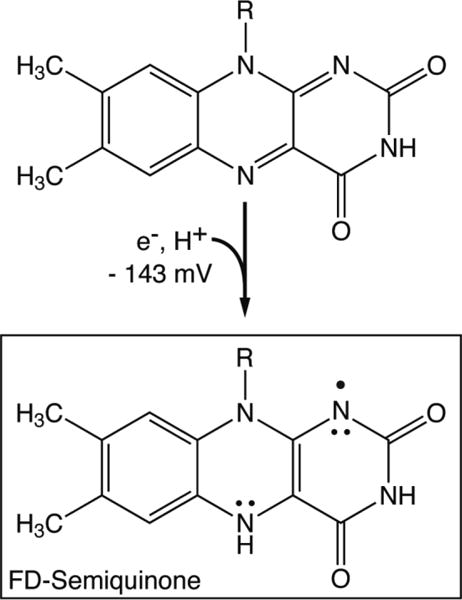
Reduction of FMN cofactor by one electron. The reduction potential indicated is that of D. vulgaris FD (vs. N.H.E)³⁰ and R = ribose phosphate. Only one of several resonance structures is shown for the SQ.

Figure 2.

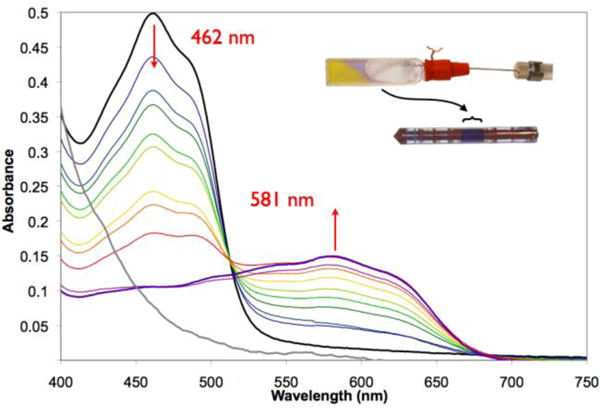
Optical profile of conversion of diamagnetic oxidized FD (black trace and yellow material in the inset cuvette) to the neutral SQ radical form (purple trace and violet material in the inset cuvette and MAS NMR rotor). Experimental conditions are described in the Methods section. The MAS NMR rotor (lower inset) is magnified relative to the optical cuvette (upper inset), to improve visibility of the purple-coloured FD SQ in the region indicated by the brace symbol.

High-field EPR Spectroscopy and DNP Enhancement Profile

To verify the paramagnetic state of the FD SQ sample we performed 9 GHz and 140 GHz EPR spectroscopy prior to DNP experiments. The 140 GHz high-field EPR absorption spectrum of the FD SQ radical together with its pseudo-modulated spectrum⁴⁹ are shown in Figure 3 (supplemental Figure S1 shows the X-band signal). The spectrum is very similar to high-field EPR spectra of the FMN SQ radical of photolyase^40,50. Schnegg et al. have explained the features of the photolyase signal in terms of g-anisotropy and large hyperfine interactions between the electron spin and a hydrogen plus two nitrogen nuclei.^40,51. A simulation of the 140 GHz EPR spectrum of the FD SQ radical using parameters obtained by Schnegg et al. is given in Figure S2 of the supplemental material.

Figure 3.

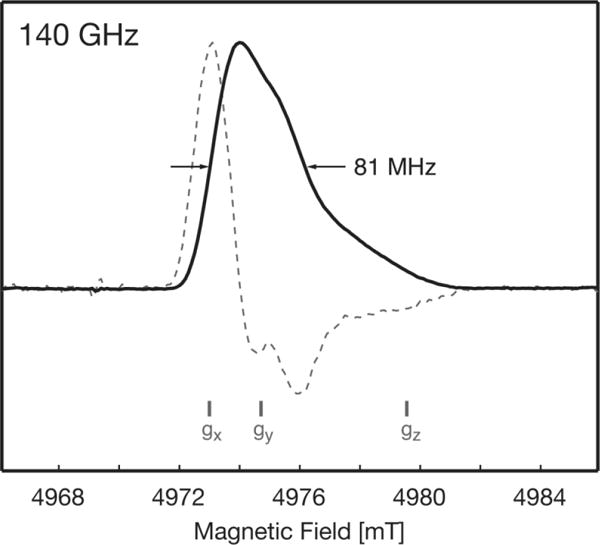
140 GHz pulsed EPR spectrum of FD SQ in ²H₈-glycerol/²H2O buffer (60:40 v:v) at 40 K (solid line). The pseudo-modulated spectrum was calculated using a modulation amplitude of 0.3 mT (dashed line).

At a magnetic field strength of 5 T, an inhomogeneous breadth of Δ = 81 MHz was observed (full width at half height), which is smaller than the ¹H Larmor frequency ω_0n = 212 MHz at the same magnetic field strength. Therefore, ¹H-DNP from this SQ is expected to occur through the SE mechanism¹.

The SE can be understood via a two-spin system composed of an electron (S = ½) and a nucleus (I = ½). In this system the energy levels can be described by a four-level system including two allowed NMR transitions of resonant frequency ω_0n and two allowed EPR transitions of resonant frequency ω_0e. In the presence of an anisotropic hyperfine interaction electron-nuclear state-mixing occurs, and the formally-forbidden zero- and double-quantum transitions (ZQ, DQ) become partially allowed. Excitation of these forbidden transitions, which occur at frequencies of ω_0e ± ω_0n (matching conditions), mediates DNP through the SE^7,52,53. Since the SE relies on excitation of forbidden transitions reflecting admixture of Zeemann states, the efficiency of SE decreases at high magnetic fields in proportion to B₀⁻², and the observed enhancements are typically smaller than those observed via the CE⁵⁴. Fortunately, FD’s EPR linewidth is sufficiently narrow that no differential SE is expected, which would otherwise result in overlap and cancellation of negative and positive enhancements, effectively decreasing the observed overall DNP enhancement^52,55.

For DNP via the SE maximal enhancement of the NMR signal intensity is expected when the microwave frequency satisfies a matching condition, and the sign of the signal is expected to depend on which matching condition is being met. Because our gyrotron oscillator operates at a fixed frequency of 139.662 GHz, we measured the MAS NMR signal intensity as a function of the static field B₀ (effectively varying ω_0n = γ_nB₀ and ω_0e = g_eβ_eB₀/ħ) to record the field-dependent ¹H-DNP enhancement profile shown in Figure 4 (where β_e is the Bohr magneton, g_e is the electron g-value and γ_n is the nuclear gyromagnetic ratio).

Figure 4.

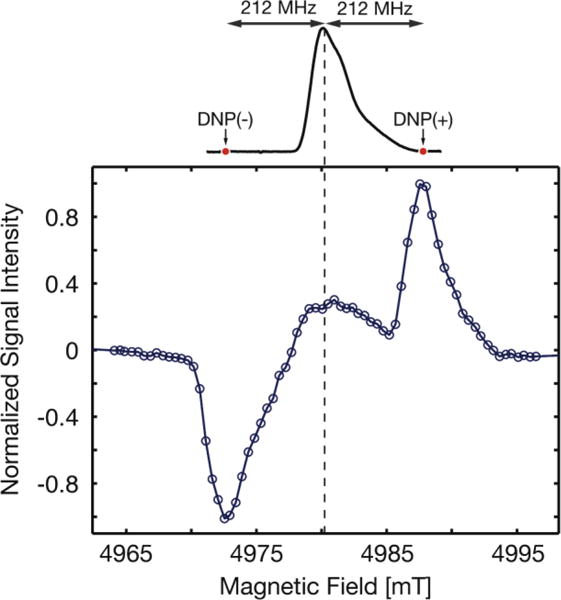
Field dependence of the DNP enhancement and EPR spectrum of the FD SQ radical. Bottom: ¹H-MAS NMR detected DNP enhancement as a function of magnetic field for DNP based on the FD SQ radical; ω_r/2π = 3.0 kHz. Top: 140 GHz echo-detected EPR spectrum of FD in ²H₈-glycerol/²H2O (60:40), T = 40 K.

The ¹H-DNP enhancement profile for the FD SQ radical shows a maximum at a magnetic field of 4987.8 mT (DNP(+)) and a minimum at 4972.6 mT (DNP(-)) (Figure 4). These features are separated by exactly twice the ¹H Larmor frequency (2^*212 MHz ≡ 15.2 mT at 5 T) as expected for well-resolved SE⁵². The overall shape of the DNP enhancement profile also reflects the strong asymmetry of FD’s EPR signal, as expected^11,52,56.

Maximum enhancement

At a temperature of 90 K, we obtained a steady-state ¹H enhancement of ε_H = 7 for ¹H-FD. While this number is low, it can be understood in terms of the DNP mechanism in effect, the concentration of the polarization source and the isotopic composition of the system. Comparable enhancements of 10 and 15 were obtained via SE DNP based on added polarizing agents BDPA or trityl radical at concentrations of 50 and 40 mM, respectively^48,57. This is in contrast to enhancements obtained via DNP based on the CE. Depending on the CE polarizing agent used (e.g. TEMPO or TOTAPOL) enhancement factors of 120 and up to 200 have been reported for nanocrystals of the polypeptide GNNQQNY or model samples, respectively^10,13,58. Thus, the lower enhancement produced by FD’s SQ is attributable in part to the relatively low efficiency of the SE mechanism compared to the CE, especially as optimized by biradicals.

Our enhancements also reflect the relatively low 2 mM concentration of the SQ. Published DNP enhancement factors have also been found to depend on the concentration of the polarization agent. For the example of TEMPO radical the observed enhancements increased with increasing TEMPO concentration up to approximately 40 mM, beyond which accelerated paramagnetic relaxation eroded the MAS NMR signal strength^59,60. Qualitatively similar behaviour is observed for biradicals except that the optimal concentration is lower at approximately 10 mM, consistent with the two-fold higher stoichiometry of unpaired electrons per molecule and more efficient polarization¹¹. However in the case of endogenous radicals, the ratio of unpaired electrons to nuclei is fixed by the choice of protein, and 40 mM concentrations of radical are only possible for protein crystals or other highly condensed phases. Thus, two disadvantages of using endogenous radicals are that we is limited by the CE vs. SE nature of the naturally occurring radical as well as by achievable concentrations, which may not be ideal for spectroscopy. The MAS NMR signal intensities will be smaller than those possible with exogenous radicals, although we show here that they are still much larger than MAS NMR in the absence of DNP.

On the other hand the isotopic composition of the biochemical system can easily be manipulated by overexpression in deuterated medium. By using FD that was 85% deuterated (²H-FD) we were able to double the enhancement to ε_H = 15 (see Figure 5). This is consistent with published reports that deuteration can slow down nuclear spin-lattice relaxation and yield larger enhancements for DNP based on exogenous radicals^61,62, as well as our own experience with FD, wherein enhancements were only half as large when the buffer used was made up with ¹H₂O (see also Rosay⁶⁰). Similarly, Abkey et al. demonstrated a four-fold larger TOTAPOL-based enhancement upon perdeuteraton of the protein under study, and also reported that the enhancement obtained depends strongly on the ¹H content (at exchangeable sites). Thus, although deuteration decreases the concentration ¹H available for detection or cross polarization, it also confers important advantages, which moreover can be deployed strategically via selective deutration, as appropriate.

Figure 5.

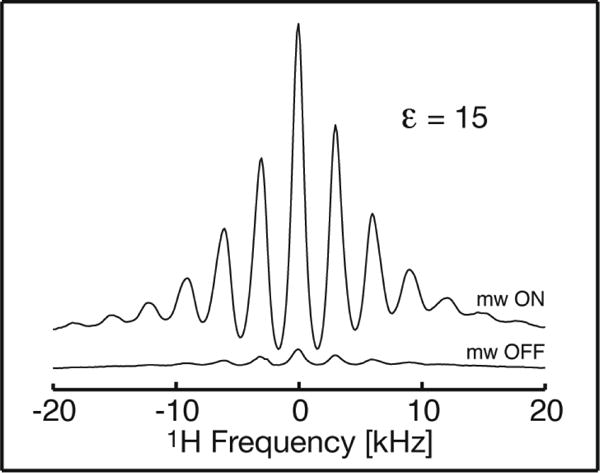
DNP-enhanced ¹H MAS NMR spectrum of ²H-FD based on the endogenous SQ radical as the source of polarization. The signal collected with microwave pre-irradition of 500 s (upper trace) is compared to the signal obtained with a simple 500 s delay (lower trace) for the same sample. Spectra were collected at 90 K at a field position corresponding to DNP(+) in Figure 4, spinning at ω_r/2π = 3 kHz, as described in the Methods section.

For both ¹H-FD and ²H-FD samples, the ¹H enhancement was observed to increase with increased microwave power to the maximum power obtainable with our apparatus (supplementary Figure S3). Indeed, since SE DNP occurs via forbidden electron-nuclear transitions with small transition moments at high magnetic fields, we do not expect that the DNP effect can be saturated with our gyrotron. However larger SE enhancements could in principle be obtained if larger microwave field strengths could be achieved at the position of the sample. Upon extrapolation of the microwave power dependence (supplementary Figure 3S) we obtain a DNP enhancement of 25 for ¹H-FD at infinite microwave power.

The steady-state ¹H enhancement expected for the well-resolved SE can be approximated by

$${\epsilon }_H=1+3\times {10}^{-21}\frac{N_e{B}_{1e}^2{\tau }_B}{\mathrm{\Delta }}$$ Eq. 2

where N_e is the number of unpaired electron spins per m⁻³, B_1e is the amplitude of the microwave field in mT, τ_B is the proton bulk-polarization build-up time and Δ is the inhomogeneous breadth of the EPR signal⁵⁵. Using our values for the enhancement and the bulk-polarization build-up times given in Table 1 we can estimate an average microwave field strength of B_1e of 0.35 MHz (0.013 mT) at the position of the sample, which is similar to values reported for analogous instrumentation⁵⁵. In our experiments, the microwave radiation is delivered to the sample using a rectangular fundamental waveguide. However, since no microwave resonator is employed, the coupling efficiency of the TE₀₁₁ mode of the rectangular waveguide to the sample is very poor. More recent probe designs employ a circular corrugated waveguide and irradiate the sample using a Gaussian-like mode. This approach yields larger B_1e field strengths at the position of the sample and values of 0.84 MHz (0.031 mT) have been reported for such systems⁶³. Using this value for B_1e we would estimate that steady-state enhancement factors of 23 and 147 would be achievable for DNP experiments based on the SQ radical in proteated and 85% deuterated FD, respectively, consistent with our extrapolation result for ¹H-FD (above). Thus, ongoing advances in DNP MAS NMR probe design, which can yield large microwave fields at the position of the sample, are producing exciting improvements for DNP enhancements, especially for SE DNP (Personnal communication, B. Corzilius, A. Smith). Regardless, even our observed enhancement of 15 can make hitherto-impractical experiments viable for biological systems.

Table 1.

Bulk polarization build-up times τ_B and T_1n relaxation times for ¹H-FD and ²H-FD, along with DNP enhancement factors ε_H.

			1H-FD			2H-FD
	[e-] (mM)	τB (s)	T1n (s)	εH	τB (s)	T1n (s)	εH
SQ	2	21	18	7	140	100	15
TOTAPOL	20	4	4	25	5	4	30

Bulk-Polarization Build-Up Times and their Dependence on Isotopic Composition of the Protein

The propagation of ¹H polarization through the sample during the DNP process can be characterized by recording the amplitude of the ¹H MAS NMR signal as a function of the duration of microwave irradiation t_mw to obtain the bulk-polarization build-up curve. Repetition of the same experiment but with no microwave irradiation (off-signal) yields analogous longitudinal magnetization recovery curves from which T_1n can be determined. In Figure 6 the build-up curves of ¹H-FD and ²H-FD for SE DNP based on the flavin SQ (‘SQ’) and CE DNP based on 10 mM TOTAPOL (‘T’) are shown.

Figure 6.

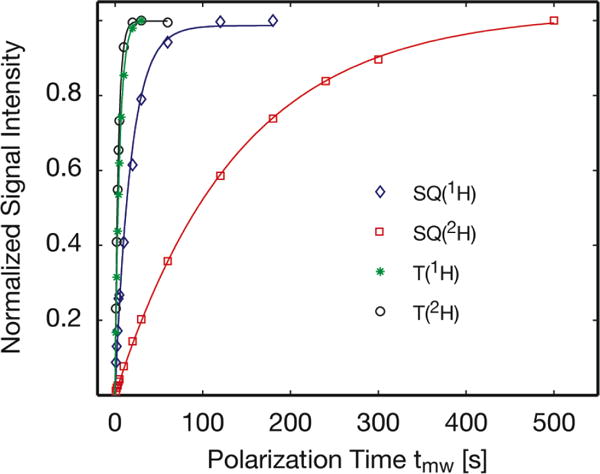
¹H bulk-polarization build-up curves for SE DNP based on the endogenous SQ radical (SQ) or CE DNP based on TOTAPOL (T). The kinetics of ¹H polarization were compared for ¹H-FD and 85% deuterated ²H-FD, for the SE and the CE DNP mechanisms. Measurements were performed at a field position corresponding to DNP(+) in Figure 4. Data points were fit using a mono-exponential recovery curve (Eq. 1, methods section) to obtain build-up time constants, τ_B. All traces are normalized to a maximum signal intensity of one.

For SE DNP based on the SQ, 85 % deuteration caused the build-up time constant to increase seven-fold from τ_B = 21 s for ¹H-FD to 140 s for ²H-FD (Table 1). Similarly, the T_1n increased by a factor of five upon 85 % deuteration. The changes in both τ_B and T_1n can be explained by slowed spin-diffusion when ¹H atoms are diluted to greater distances from another.

The buildup curves describe the propagation of nuclear polarization to the more distant nuclei whose resonances are observed at unperturbed chemical shifts (bulk nuclei), by spin diffusion^64–66. Based on the 18.2 nm³ volume of FD³⁵ and FD’s 969 H atoms, we calculate a ¹H concentration of 88 M for ¹H-FD and 13 M for ²H-FD (see supporting information). Both are high compared to the ¹H concentration of 0.8 M of the medium that makes up the rest of our samples (see supporting information). Thus we anticipate that for both ¹H-FD and ²H-FD, polarization will spread much more efficiently within the protein than in the medium, and that the buildup curve of DNP based on the SQ will reflect primarily polarization of the Hs within the same protein as the SQ polarization source.

A lower concentration of ¹Hs will tend to attenuate the spin-diffusion process due to the greater average distance between ¹H nuclei and thus the lower strength of homonuclear dipolar coupling. In the case of inhomogenously broadened lines, the spin diffusion constant D is given by:

$$D\propto \langle r^2\rangle \mathrm{\Delta }{v}_{1/2}$$ Eq. 3

where 〈r²〉 is the average squared distance between nuclei participating in the spin-diffusion process and Δv_1/2 is the full line width at half intensity^67,68. The average ¹H-¹H distance within ¹H-FD is 2.9 Å and that in ²H-FD is 5.5 Å, based on the proton concentration inside each protein (see supporting information). Thus, we estimate that the diffusion constant in the proteated protein is some 4-fold larger than that in the 85% deuterated protein, using equation 3. This is in reasonable agreement with the factor of 5 increase in the ¹H T_1n relaxation time (see Table 1).

When 10 mM TOTAPOL was used as the polarization source, the τ_B and T_1n were drastically shorter, moreover neither τ_B nor T_1n changed much upon deuteration of the protein. Most likely T_1n relaxation of ¹H inside the protein is not limited by spin-diffusion⁶⁹ as in the case of the SQ-containing samples, but is foreshortened, or quenched, by the high concentration of the paramagnetic polarization agent. Indeed, paramagnetic impurities or dopants are known to sharply decrease the relaxation times of surrounding nuclei in an effect called paramagnetic relaxation enhancement (PRE)^70,71.

The much shorter T_1n values observed in the presence of TOTAPOL can be understood as consequences of the higher concentration of unpaired electrons overall, as well as a different distribution of distances from ¹H to the closest unpaired electron in FD. Our 10 mM concentration of the bi-radical TOTAPOL creates an unpaired electron concentration ten times that present in the FD SQ samples. This will increase the importance of PRE by shortening the average distance between an H atom and an unpaired electron. In addition, the spatial distribution of the flavin SQ and the TOTAPOL are very different and create contrasting distance distributions from a FD ¹H atom to the nearest unpaired electron. Because PRE depends on the inverse sixth power of the electron-nuclear separation, PRE drops off very fast with increasing separation and is dominated by the contribution of the free radical’s closest approach to a given ¹H atom. For the case of PRE due to flavin SQ, ¹H atoms in the protein have fixed distances to the flavin, the distribution of which is shown in Figure 7. For the case of TOTAPOL in solution, no information is available as to possible discrete binding sides for TOTAPOL on the FD protein. Therefore, we calculated the closest possible distance of approach of TOTAPOL to each H in FD via the proxy of calculating the distance to the closest solvent water, for each H in FD, using the positions of crystallographic waters in the structure of D. vulgaris FD (4FX2.pdb). Thus we assume that TOTAPOL will not penetrate the FD protein or get closer than a surface water molecule could. While individual distances from the surface to specific ¹H atoms are expected to be only approximate, the set of the closest approach distances should to reproduce the shape of the distribution of closest-approach distances of TOTAPOL. This distribution of closest approaches to the surface is compared with the distribution of distances between an H and the centre of the flavin central ring in Figure 7.

Figure 7.

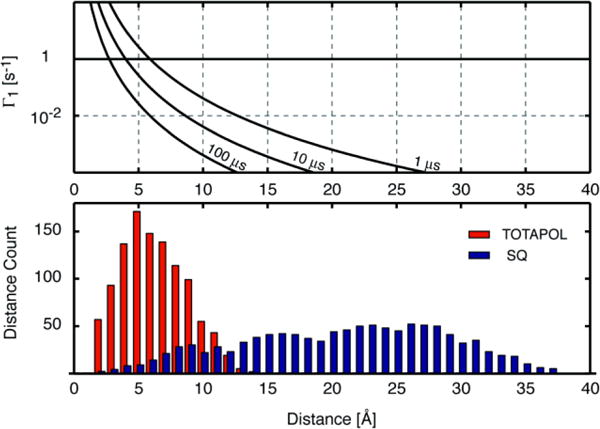
Top: Paramagnetic relaxation enhancement (Γ₁ = 1/T_1,p) for ¹H vs. distance from an electron with T_1e = 1, 10 or 100 μs (a logarithmic scale is used for Γ₁). Bottom: Numbers of ¹H atoms at different distances from the closest high-occupancy water (red) and at different distances from the centre of the flavin (blue). The average distance to the closest high-occupancy water is 6.3 Å. The average distance to the centre of the flavin’s central ring is 21 Å. (Further details are given in the supporting information and Figure S4).

In FD containing SQ radical, the majority of the H atoms are more than 10 Å away from the flavin ring with an average separation of 21 Å. This is in strong contrast to the scenario in the presence of added TOTAPOL, in which case the distance of closest calculated approach between a TOTAPOL molecule and a FD H atom is usually less than 10 Å, with an average of approximately 6 Å. Thus TOTAPOL’s ability to approach from all sides exposes more of FD’s Hs to PRE. The effect was modelled based on the distance dependence of PRE (see Bertini et al. equation 3.19⁷²) for a range of electron spin-lattice relaxation times T_1e since precise electron spin relaxation rates are not known for these samples under the conditions used (see Figure 7). Even for a very short T_1e of 1 μs, only ¹H nuclei at a distance of less than 6 Å would be significantly influenced by the paramagnetic center (Γ₁ ≥ 1). Thus only in the samples containing TOTAPOL do we expect that a significant fraction of the ¹Hs of FD will be affected by PRE. In addition the SQ is expected to have a much longer T_1e than TOTAPOL, further decreasing the importance of PRE effects in case of DNP experiments based on the endogenous SQ radical⁷³. We can therefore explain the shorter T_1n relaxation times in the TOTAPOL samples on the basis of PRE from both more and closer unpaired electrons. This will also affect τ_B since it has been found to correspond closely to the T_1n relaxation time on numerous occasions⁵⁹.

We also note that the DNP enhancements obtained based on TOTAPOL are considerably lower than have been reported previously^10,13. This may be because the values in Table 1 were obtained from direct detection of total ¹H polarization. Bulk ¹H polarization is typically not a good measure of DNP enhancement due to large probe ring-down effects in conjunction with the very broad signals of ¹H ⁷⁴. When ¹H polarization was transferred to ¹³C nuclei for detection using cross-polarization ⁴⁶ we measured a greater-than 100-fold enhancement of ¹H polarization based on TOTAPOL, consistent with other work ^10,11 (supplementary Figure S5). In addition, buildup times measured via ¹³C detection agreed well with values obtained via direct ¹H detection (supplementary Figure S6). However we used ¹H detection for comparative studies and time courses because the lower SQ concentration and enhancements attainable made ¹³C detection of FD more difficult than for model samples. Thus the enhancements reported here are likely under-estimates of the ¹³C enhancement that may be possible based on endogenous SQ in 2mM FD.

Importance of a good glass for DNP experiments

The samples described above were all prepared in mixtures of glycerol and water that form a glass at low temperatures, ensuring homogenous distribution of exogenous polarizing agents while also providing cryoprotection for the protein. Moreover studies have shown that non-glass-forming solvent matrices typically yield smaller DNP enhancements⁷⁴. We studied this effect by preparing samples with lower glycerol content that formed fragile glasses, or did not form a glass at cryogenic temperature (Supplementary Figure S7). We found that non-glassy samples had bi-exponential bulk-polarization build-up curves with a very slow buildup rate (long τ_B) characterizing a large fraction of the population (Figure 8 and Table 2). We speculate that this reflects slow polarization transfer across microscopic domain boundaries in the frozen sample, whereas the faster buildup rate would reflect polarization of ¹H nuclei in the same domain as a TOTAPOL molecule because the faster buildup occurs on a timescale similar to that observed in homogenous (glassy) samples. However even in samples that did not form a glass, T_1n displayed only a small contribution from a slow phase and the T_1n value characterizing most of the signal was similar to the values obtained for glassy samples (Table 2).

Figure 8.

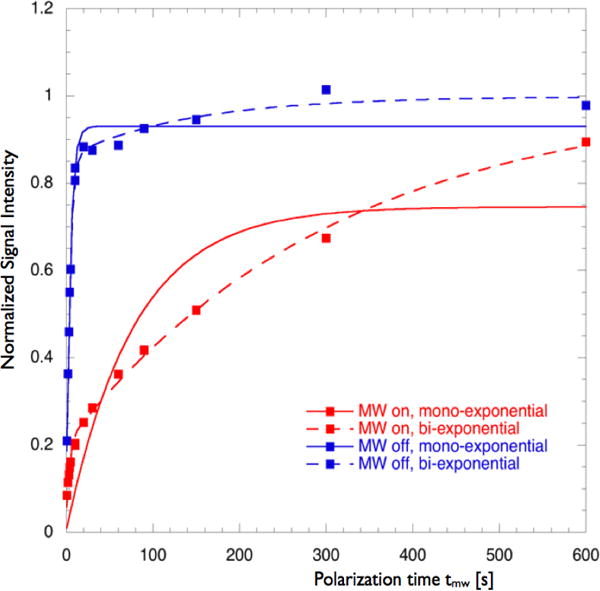
¹H-DNP bulk-polarization build-up (shown in red) and saturation recovery traces (shown in blue) for a non-glass sample (12% ²H₆-glycerol vol%). Signal intensities are scaled by the steady-state polarization M_∞ (t_mw → ∞). Original data were fit to eq. 1 (mono-exponential buildup) or $M(t)=M_{\mathrm{\infty }}(1-f_1{e}^{-t/{\tau }_{B1}}-(1-f_1)e^{-t/{\tau }_{B2}})$ (bi-exponential buildup) where f₁ is the fraction of the population with the buildup time τ_B1 and τ_B2 is the buildup time that describes the balance of the population.

Table 2.

Bulk-Polarization build-up times τ_B, T_1n recovery times and DNP enhancements ε_H for DNP in glassy and non-glass samples.^a

Glycerol [vol%]	Σtate upon freezing	τB [s]	T1 [s]	εH
70	glass	4.9 ± 0.1	4.0 ± 0.1	30
50	fragile glass	3.0 ± 0.1	3.8 ± 0.1	24
12	no glass	310 ± 40 (80 %) 3.2 ± .5 (20 %)	3.9 ± 0.2 (86 %) 140 ± 70 (14 %)	14

^aDNP was based on 10 mM TOTAPOL. Data were fit with the equation $M(t)=M_{\mathrm{\infty }}(1-e^{-t/{\tau }_B})$ when possible (mono-exponential buildup) or $M(t)=M_{\mathrm{\infty }}(1-f_1{e}^{-t/{\tau }_{B1}}-(1-f_1)e^{-t/{\tau }_{B2}})$ (bi-exponential buildup) when it was necessary to include two time constants.

MAS NMR studies of polymer blends have employed spin-diffusion measurements to determine the the sizes of domains⁶⁸. Further experiments are planned to assess the applicability of such models for FD in glassy and non-glassy matrices.

Non-glass samples dominated by a large τ_B but a normal T_1n achieved enhancements of only 14 compared to 30 for samples whose τ_B and T_1n were comparable. Thus we confirm that the enhancement is related inversely to τ_B.⁶¹ Since τ_B was increased in SQ-based DNP of ²H-FD, and this alone should have caused a decrease in enhancement, we can conclude that the net increase in enhancement obtained upon deuterating FD reflects additional direct dependence of ε_H on T_1n.

Kagawa et al. have already shown that the propagation of polarization and the spin lattice relaxation need not have identical mechanisms or kinetics⁶¹. They found that the magnitude of steady-state enhancement increases in proportion with the inverse of τ_B but that it also increases with T_1n. Thus, reduced spin lattice relaxation rates (longer T_1n) are expected to increase the enhancement. This is consistent with the two-fold larger enhancement produced by our 85% deuterated FD with its 5-times longer T₁ than ¹H-FD, although the effect is tempered by a larger τ_B as well.

Potential Applications of DNP based on Endogenous Radicals

For maximum DNP enhancement the best choice of polarization agent is currently a biradical such as TOTAPOL that supports efficient DNP via the CE^11,74,75. However, for many of the naturally-occurring radicals the less effective SE will be the active DNP mechanism. Nonetheless there are compensating advantages. Unique features of the use of an endogenous radical are that the built-in radical occupies a defined location in the protein under study, it is genuinely non-perturbative and its oxidation state may be related to the physiological state of the system. The positional invariance of the built-in radical suggests the possibility of using the magnitude and build-up rate of DNP enhancement as sources of insight as to whether a species being observed (based on selective isotopic labeling) is closely associated with the protein containing the radical. Thus a ¹³C-labelled protein might gain stronger enhancement when complexed with a protein containing a radical than when the two are independent. Similarly, cofactors that adopt a radical state only under certain physiological conditions should produce DNP enhancements that depend on the system’s physiological state. Even though the enhancement is modest due to the low concentrations expected for biological radicals, the ≈15-fold enhancements we report here could make MAS NMR observation possible in complex biochemical preparations and perhaps even some organelles and photosynthetic membranes, allowing MAS NMR observation of minimally perturbed functional biological systems. This could enable exciting new applications of MAS NMR. Thus, the enhancement from endogenous radicals could provide more and different sorts of information than are accessible now via conventional MAS NMR.

A few examples of systems in which a flavin semiquinone occurs naturally include nitric oxide synthase^76,77 the cytochrome P450 reductases⁷⁸, electron transfer flavoprotein⁷⁹ and photolyase⁸⁰. Moreover our method is applicable to other types of radicals as well. The larger enhancements and more favorable B₀ dependence of the CE could also be exploited in conjunction with the use of an endogenous radical by addition of a second, exogenous radical whose resonant frequency is offset from that of the endogenous radical by the NMR frequency⁵⁷. Similarly, recent work demonstrating DNP from a Mn²⁺ complex raises the possibility of DNP from endogenous metal sites with favourable properties⁸¹.

Conclusions

To our knowledge, this is the first demonstration of the use of a stable, endogenous biological paramagnetic cofactor as a basis for high-field DNP. We have demonstrated ¹H-MAS NMR enhancement by a factor of 15, consistent with the low concentration of the radical that is expected of biological systems. DNP based on the endogenous radical conforms to the theoretical and experimental expectations for SE DNP. We found that deuteration of the protein yields a larger enhancement reflecting the longer T_1n, likely because methyl rotors that can act as polarization sinks are eliminated and the ¹H-¹H dipolar interaction is attenuated. The observed enhancements are significant and could be used to increase MAS NMR signal intensities in ¹³C/¹⁵N-CPMAS spectra of biologically interesting samples. We hope that the enhancements provided by DNP in combination with the resolution provided by MAS NMR and selective isotopic labeling may make new experiments practical in minimally perturbed biochemical systems.