Abstract
Cognition and behavior depend on synchronized intrinsic brain activity that is organized into functional networks across the brain. Research has investigated how anatomical connectivity both shapes and is shaped by these networks, but not how anatomical connectivity interacts with intra-areal molecular properties to drive functional connectivity. Here, we present a novel linear model to explain functional connectivity by integrating systematically obtained measurements of axonal connectivity, gene expression, and resting-state functional connectivity MRI in the mouse brain. The model suggests that functional connectivity arises from both anatomical links and inter-areal similarities in gene expression. By estimating these effects, we identify anatomical modules in which correlated gene expression and anatomical connectivity support functional connectivity. Along with providing evidence that not all genes equally contribute to functional connectivity, this research establishes new insights regarding the biological underpinnings of coordinated brain activity measured by BOLD fMRI.
SIGNIFICANCE STATEMENT Efforts at characterizing the functional connectome with fMRI have risen exponentially over the last decade. Yet despite this rise, the biological underpinnings of these functional measurements are still primarily unknown. The current report begins to fill this void by investigating the molecular underpinnings of the functional connectome through an integration of systematically obtained structural information and gene expression data throughout the rodent brain. We find that both white matter connectivity and similarity in regional gene expression relate to resting-state functional connectivity. The current report furthers our understanding of the biological underpinnings of the functional connectome and provides a linear model that can be used to streamline preclinical animal studies of disease.
Keywords: anatomical connectivity, connectomics, gene expression, resting state functional connectivity MRI
Introduction
The brain is organized into a network of synchronized activity that has a complex and reproducible topological structure (Bullmore and Sporns, 2009; Miranda-Dominguez et al., 2014a, 2017; Wang et al., 2015). Resting-state functional connectivity (FC) MRI, a technique that measures inter-areal correlations in spontaneous brain activity, has been particularly useful for studying functional network organization in both health and disease (Mills et al., 2017; Rudolph et al., 2017). Local and global features of this functional network are carefully calibrated to support healthy cognition (Petersen and Sporns, 2015), and network dysfunction is seen in numerous neurodevelopmental (Vértes and Bullmore, 2015; Cary et al., 2017; Grayson and Fair, 2017) and neurodegenerative diseases (Seeley et al., 2009; Fornito et al., 2015). Therefore, identifying the substrates that shape functional network organization is critical in linking molecular (e.g., gene transcription) and behavioral (e.g., psychometric) markers of disease to brain function.
Despite an abundance of prior work examining the correspondence of large-scale functional and anatomical connectivity, the precise substrates that shape functional network organization remain unknown. Modeling approaches to predict FC networks based on macro- or meso-scale anatomical connectivity networks commonly simulate mass neuronal activity by optimizing parameters that describe local population dynamics as well as the contribution of inter-areal connectivity (Honey et al., 2009; Messé et al., 2014; Sanz-Leon et al., 2015). These approaches allow for detailed theoretical exploration regarding the relative contributions of local dynamics versus global coupling, but they are limited by a lack of empirical data regarding true areal differences in function. Furthermore, analytic measures of anatomical communication appear to predict FC at comparable values (Abdelnour et al., 2014; Goñi et al., 2014; Miranda-Dominguez et al., 2014b), suggesting an upper limit to the predictive validity of models based on anatomical connectivity alone.
The integration of diverse data from different scales of investigation in such models may enhance our understanding of how functional networks are shaped. Although the idea is intuitive to most that FC may be guided by a combination of factors above and beyond anatomical wiring, studies investigating how the molecular properties of a given tissue influence these functional dynamics have historically been difficult to study and remain incompletely understood. There is work emerging suggesting that gene expression and areal chemoarchitecture influence spontaneous functional brain activity. For instance, associations have been found between areal densities of excitatory receptors and strength of functional connections (Turk et al., 2016; van den Heuvel et al., 2016). Others have found that correlated gene expression, a measure of transcriptional similarity between regions, is greater within than between functional networks and that the genes driving these relationships are involved in ion channel activity and synaptic function (Richiardi et al., 2015). With that said, questions remain regarding the degree to which these relationships can be explained and might interact. Previous studies in this realm have been limited in their sparsity of regions and networks investigated, and a detailed understanding of the brain's complex network structure requires that gene expression data be comprehensively mapped onto corresponding whole-brain parcellations of structural and functional data. Furthermore, it remains unknown whether transcriptional similarity and anatomical connectivity modulate FC in a distinct or an interactive manner and whether these relationships change depending on connection.
Here we present a model of inter-regional FC in the mouse brain by integrating comprehensively and systematically obtained measurements of axonal connectivity (Oh et al., 2014) and gene expression data (Lein et al., 2007) from the Allen Institute for Brain Science (Seattle, WA). We investigated whether anatomical communication capacity and correlated gene expression (CGE) contribute uniquely or cooperatively to functional network architecture. We also examined whether these relationships are homogeneously expressed across the brain or whether these dependencies change according to cortical or subcortical subdivisions. Finally, to examine the molecular bases of the FC signal, we examined whether specific clusters of genes disproportionately support these FC patterns.
Materials and Methods
Subjects
In total, 23 C57BL/6J adult male mice ranging from 18 to 22 g in body weight were used in the experiments. Mice were maintained on a 12 h light/dark cycle (lights on at 6:00 A.M.) at a room temperature of 21 ± 1°C and allowed food and water ad libitum. All experiments were performed during the animal's light cycle. Protocols were approved by Institutional Animal Use and Care Committees of the Oregon Health & Science University and the VA Portland Health Care System and conducted in accordance with the National Institutes of Health Principles of Laboratory Animal Care.
Animal preparation
Imaging in rodents generally requires the use of anesthesia to limit movement of the animals in the scanner. Here, anesthesia was induced by 3–4% isoflurane and maintained with 1–1.5% isoflurane. The selection of anesthesia may influence FC (Grandjean et al., 2014). Of various anesthetic regimens, we selected low-dose isoflurane for the present study based on the following previous findings. (1) Functional connectivity after 1% isoflurane is preserved and comparable with that of awake mice and rats (Wang et al., 2011; Shah et al., 2013; Jonckers et al., 2014; Stafford et al., 2014; B. D. Mills et al., 2016). (2) c-Fos activation (an immediate early gene) can be observed in isoflurane-anesthetized mice and rats (Kufahl et al., 2009, 2015; Smith et al., 2016). That being said, acclimated awake animals or other anesthesia regimens, such as a combination of dexmedetomidine and lower-dose isoflurane (0.5–0.75%; Ash et al., 2016; Brynildsen et al., 2017), may be an alternative.
During scanning, the head set stationary in a custom-built head holder designed to fit in the radiofrequency (RF) coil, as well as restrict any motion during the scan. Respiration (80–100 bpm) and animal temperature (maintained at 37°C) were monitored and controlled by a small animal monitoring system (Model 1030 Monitoring and Gating System; SA Instruments).
Imaging acquisition
The imaging protocol is as described in our previous publication with slight modifications (Stafford et al., 2014). Imaging was performed during a single session for each animal on an 11.75T Bruker BioSpec scanner equipped with a Resonance Research high-bandwidth shim power supply. A 20 mm inner diameter RF quadrature volume coil (M2M) was used for all studies. All scans were performed with Paravision 5. Using MAPSHIM, a 3D field-map phase image was acquired; TR, 20 ms; TE1, 2 ms; interecho time, 4.003 ms; FA, 20°; FOV, 40 × 18 × 25 mm; matrix, 80 × 90 × 125 (voxel size, 0.5 × 0.2 × 0.2 mm3; matching the EPI voxel size). This was followed by a T2-weighted structural image (RARE; TR, 4590 ms; effective TE, 32 ms; RARE factor, 8; 30 contiguous slices (0.5 mm thick) with interleaved acquisition; FOV, 18 × 18 mm; matrix, 150 × 150; voxel size, 0.12 × 0.12 × 0.5 mm3; two repetitions). Global (volume) and local (brain voxel) shimming with MAPSHIM were performed to calculate first- and second-order shims before the functional MRI (fMRI) scan. The resting-state fMRI consisted of a single-shot gradient echoplanar imaging (EPI) sequence with the following parameters: 360 repetitions (total scan time, 15 min); TR, 2500 ms; TE, 10 ms; FA, 60°; 30 contiguous slices (0.5 mm thick) with interleaved acquisition; FOV, 25.6 × 16 mm; matrix, 128 × 80; voxel size, 0.2 × 0.2 × 0.5 mm3. An identical EPI sequence with 20 repetitions was acquired in the reverse phase encoding direction for top-up distortion correction.
General fMRI BOLD preprocessing
Functional images were preprocessed to reduce artifact. These steps include the removal of a central spike caused by MR signal offset by discarding the first 10 EPI frames, slice-timing correction using FSL's slicetimer tool, and correction of field inhomogeneities by applying top-up field-map correction. This required that data were collected with reversed phase-encode blips, resulting in pairs of images with distortions going in opposite directions. From these pairs, the susceptibility-induced off-resonance field was estimated using a method similar to that described by Andersson et al. (2003) as implemented in FSL (Smith et al., 2004), and the two images were combined into a single corrected one, and within run intensity normalization to a whole-brain mode value of 1000. Via the T2 scan, each scan's functional data were transformed to an anatomical rodent atlas supplied by the caret software (map 015 atlas; Van Essen et al., 2001; Van Essen, 2012). We chose to map data to the caret atlas because it is MRI based, free of the distortion from histological preparation, and allows for 3D surface-based visualization (Caret, map_015; available at http://sumsdb.wustl.edu/). Each run then was resampled in atlas space on an isotropic 0.2 mm grid combining atlas transformation in one interpolation (Lancaster et al., 1995).
Resting state functional connectivity (FC) preprocessing
FC preprocessing was performed as described previously with the exception of small modifications (Stafford et al., 2014). Several additional preprocessing steps were used to reduce spurious variance unlikely to reflect neuronal activity (e.g., heart rate and respiration). These steps included the regression of the whole-brain signal and the first-order derivative of the whole-brain signal, followed by a temporal lowpass filter (f < 0.1 Hz).
Regions of interest
One hundred sixty cortical predefined areas based on the connectional and architectonic subdivisions in the mouse were used. These areas were obtained from the atlas as provided by the Allen Mouse Brain Connectivity Atlas (AMBCA) at the Allen Institute for Brain Science (Oh et al., 2014). Regions are freely available online (Allen Brain Atlas Data Portal; connectivity.brain-map.org). To directly compare the Allen data with the functional MRI data, the Allen regions of interest (ROIs) were registered to the caret, map_015 atlas using a six-parameter rigid-body transformation. ROIs within the cerebrum were used, which comprise both cerebral cortical areas and cerebral nuclei. Areas defined as brainstem and cerebellum by the Allen Institute for Brain Science and olfactory bulb regions were not included in these analyses because of potential differences in EPI data quality. All regions included in these analyses and their anatomical module assignments (Oh et al., 2014) can be seen in Fig. 3-1. Their anatomical projections can be visualized via the Allen Mouse Brain Connectivity Atlas at the Allen Brain Atlas Data Portal.
Extraction and computation of regionwise resting-state correlations
For each animal, 15 min of resting-state BOLD time series data were collected. For each ROI, a resting time series was extracted after processing, and Pearson's correlations were calculated for every region pair for each animal. Finally, ROI–ROI correlation, Fisher z-transformed r values, were averaged across all subjects and used for analysis.
Allen anatomical projection acquisition methods
Structural data were obtained from the Allen Institute for Brain Science (Oh et al., 2014). Briefly, structural data on 400 adult male C57Bl/6J mice were obtained by performing stereotaxic tracer injection (recombinant adeno-associated virus expressing EGFP anterograde tracer mapping of axonal projections), image acquisition of tracer migration (serial two-photon tomography), and data processing to make structural connection matrices. Mutual connections among 426 regions (213 ipsilateral and 213 contralateral regions) were calculated, and of these 426 regions, 160 cortical regions were used for comparison with the functional data (80 ipsilateral/right-hemisphere regions and 80 contralateral/left-hemisphere regions). The best-fit model for connections resulted from a bounded optimization followed by a linear regression to determine connection coefficients, which assigned statistical confidence (p value) to each connection in the matrix. Structural connectivity matrices were obtained by first calculating the ratio of connection density to connection strength for each ROI–ROI pair and then normalizing the ratio by the volume of the target region (ROI). For more details, see the study by Oh et al. (2014).
Unlike the functional data that were undirected, the structural data contain directionality (e.g., efferent vs afferent pathways between two nodes/ROIs). We found that this directed matrix required a very lenient threshold (p < 0.75) in order for the matrix to maintain connectedness (the ability to traverse from one node to any other node via one or more network links; a key property for making inferences regarding functional connectivity of each ROI pair). To minimize the possibility of including spurious connections, an undirected matrix was obtained, allowing us to reduce the threshold to p < 0.05. This threshold was applied first on the directional matrix (i.e., each directional edge was thresholded based on its p value). Then, symmetry was imposed by taking the average of the directed matrix and its transpose. Using this same procedure for generating undirected matrices, higher thresholds were also tested (p < 0.25) and did not alter any variance estimates by >1%.
Relationships between FC and anatomical connectivity were assessed using both monosynaptic connectivity strength and using a metric called communicability (G), which describes the ease of communication between regions via monosynaptic and polysynaptic connections. For instance, communicability between two nodes will be stronger if there are multiple or strong alternate paths connecting the two regions. For communicability (Crofts and Higham, 2009) in a weighted matrix W, we begin by normalizing each connection weight and defining a new matrix W′, such that Wij′ = , where Si and Sj are the strengths of node i and j. Communicability between i and j is defined as follows:
 |
G is based on the notion of total communication capacity via parallel pathways and is computed by assigning exponentially decaying coefficients to the weight of pathways as the walk length increases. Our previous work in macaques suggested that these coefficients may be roughly optimal for predicting FC, resulting in superior results relative to other communication-based models including structural connectivity weight or path length (Grayson et al., 2016). Therefore, we also chose to examine the matching index (Hilgetag et al., 2000), which captures a conceptually different way in which functional connectivity could arise. Rather than relying predominantly on the strength of communication paths, the matching index captures the similarity of the connectivity patterns between two nodes. This accounts for third-party contributors that may simultaneously influence activity patterns of both nodes through emergent network effects but may not necessarily mediate communication (Adachi et al., 2012).
For weighted undirected networks, the matching index quantifies the similarity of connections between two nodes excluding their mutual connection, as follows where Θ(Wik) = 1 if Wik > 0 and 0 otherwise.
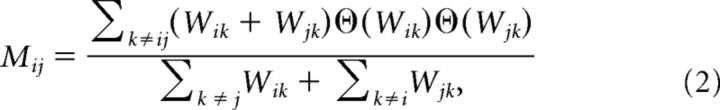 |
Allen gene expression data
Gene expression data measured using in situ hybridization (ISH) from the adult C57BL/6J male mouse at age P56 were obtained from the Allen Mouse Brain Atlas (Lein et al., 2007). Expression levels were quantified using “expression energy” (fraction of stained volume * average intensity of stain), as described previously (Lein et al., 2007). Because ISH data were only available for one hemisphere, we retrieved expression energies for the same set of 80 functional ROIs used in our analyses. Because of potential differences in data quality between coronal and sagittal methods of ISH data collection (Fulcher and Fornito, 2016), we used only the higher-quality coronal data. To obtain this list, we queried the Allen API (http://help.brain-map.org/display/mousebrain/API) to obtain gene expression energy for each region in the coronal plane called using the following API query: api.brain-map.org/api/v2/data/query.json?criteria=model::StructureUnionize,rma::criteria, section_data_set[id$eqXXX],structure[id$eqYYY]. This resulted in 3318 genes; of these, a final set of 3079 genes had expression energy data available for each of the 80 ROIs, which was the set used for the analyses. Gene expression energies were then normalized (z-scored) across brain regions, and Pearson's correlations were computed between brain regions to assess transcriptional similarity between ROIs.
Statistical methods
Visualization of functional networks.
Modular partitions of the network were obtained using the “Louvain” community detection algorithm (Blondel et al., 2008) adapted for full, unthresholded networks with positive and negative weights (Rubinov and Sporns, 2011). This algorithm identifies groups of nodes (communities, or modules) through optimization of the modularity index, or the fraction of edge weights within module partitions.
We found that the resulting partitions were stable for the current dataset at the default resolution parameter (γ = 1). Across 1000 iterations of the algorithm with the default settings, 96.0% returned exactly three modules and only 4.0% returned two modules, and the variation of information (Meila, 2007; Rubinov and Sporns, 2011) from one iteration to the next was, on average, only 0.049 (SD, 0.055). Therefore, we selected the result of one iteration at random, which was representative nonetheless.
The Q score for this partitioning was 0.36. Across different iterations of the Louvain algorithm, the mean was 0.36 (SD, 0.0014). This was significantly greater than comparable null models that were rewired to preserve weight and strength distributions (Rubinov and Sporns, 2011; p < 0.001, 1000 null permutations), which had a mean Q score of 0.244 (SD, 0.21). Across the 1000 null networks, 64.3% resulted in two modules, 34.3% had three modules, and 1.4% had four modules.
We also tested the agreement between the Louvain decomposition and another conceptually very different partitioning approach known as Infomap (Rosvall and Bergstrom, 2008; Gates et al., 2016). Infomap is another widely used algorithm for functional connectivity data, which requires thresholding (setting weights below a certain value to 0). We used a previously described approach for generating a consensus partition across thresholds (Power et al., 2011; Eggebrecht et al., 2017) and applied it here on network sparsities of 10–50%. We again obtained a three-network partition that was qualitatively not discernibly different from the Louvain results. Likewise, we found extremely low variation of information between the Infomap partition and the Louvain results (mean variation of information, 0.057). These data suggest that the modules ultimately displayed (see Fig. 3) are quite robust with well vetted approaches such as Louvain and Infomap.
Figure 3.
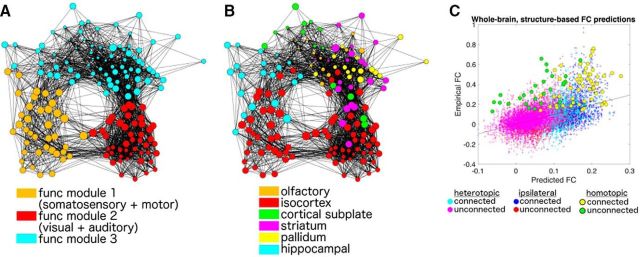
Clustering of the mouse functional connectome. Each brain region (node) shares an FC value (edge) with other nodes. Regions with strong FC are pulled more closely together, and region pairs with weak FC are moved further apart. A, B, Nodes are colored by functional modularity assignment (A) and anatomical assignment (B). Nodes are sized by their connectivity strength (i.e., the sum of all connectivity weights to that region). C, Empirical FC values across all region pairs, illustrated as a function of anatomical connectivity network-based (i.e., structure-based) predictions of FC. Each dot represents a unique region pair, colored according to whether it is heterotopic, ipsilateral, or homotopic and whether the region pair possesses a direct anatomical link or not. Homotopic region pairs exhibit markedly higher FC than what is predicted by structure. Regions and their corresponding networks can be seen in Figure 3-1.
The network was visualized using a force-directed graph layout where connections serve as attractive forces between nodes such that well connected groups of nodes are pulled closer together (Fruchterman and Reingold, 1991). Although no thresholding of the FC matrix was used in generating modular partitions, these types of spring-embedded diagrams require that some threshold is used to illustrate graphically the strongest links in the network. When this threshold is set too low, it is difficult to stably embed the low-degree nodes as they disconnect from the rest of the graph. When it is too high, nodes become “latticized” and the edges are so densely populated that they become imperceptible. Again, this threshold affects none of the quantitative analyses or number of modules identified and is purely for visualization purposes. We chose a threshold corresponding to a 20% network density (the top 20% of network edges are illustrated), as it provided a very reasonable trade-off, although reasonable results could be obtained within a range of densities from 10 to 30%.
Modeling structure–function across both hemispheres
For making FC predictions across both hemispheres, only the structural network was used since gene expression data is only available as an average of both hemispheres. We used a general linear model of FC using communicability and the matching index as the two sole predictors. FC was then plotted as a function of the predicted values from the dual-variable model. ROI pairs were plotted as separate colors depending on whether it was an ipsilateral, heterotopic, or homotopic connection and monosynaptic connection.
Modeling the transcriptional and anatomical contributions to the FC signal
Because the ABI gene expression data were only available as an average across hemispheres, the following analyses were conducted after averaging the FC networks across hemispheres as well. A series of linear regression models were assessed to examine the relationship between FC and transcriptional similarity, metrics derived from anatomical connectivity, and anatomical distance (computed as the log-transformed Euclidean distance between the center of each ROI). See Figure 1 for the full equation for each linear model.
Figure 1.
Models used to assess the relationships between FC and measures of anatomical structure, communicability, matching index, correlated gene expression, Euclidean distance between region pairs, and spatial adjacency, a binary measure of whether two regions are touching. Models A–J correspond to models used in scatter plots in Figure 4 and models described in Tables 1 and 2.
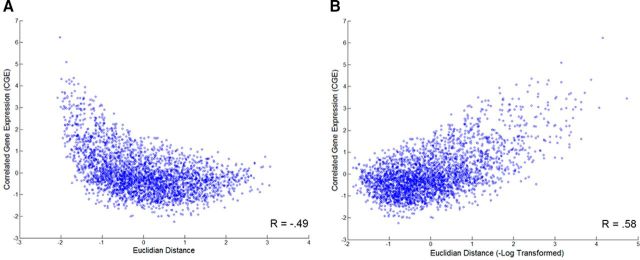
As identified by previous work (Fulcher and Fornito, 2016), as well as our own (Fig. 2), Euclidean distance follows not only a distance-dependent relationship but a logarithmic relationship with CGE. That is, connectivity is better explained by the exponential than linear fit of distance on functional connectivity (Fulcher and Fornito, 2016). Spatial adjacency, a binary measure indicating whether two regions are touching, was also included in distance-dependent models. Together, log-transformed Euclidean distance and spatial adjacency are referred to as spatial topography.
Figure 2.
The relationship between Euclidean distance and CGE is exponential; therefore, Euclidean distance was −log-transformed before applied to all models throughout this manuscript. A, CGE by Euclidean distance (without transforming the distance matrix) shows an exponential relationship. B, The −log of Euclidean distance better fits the relationship between distance and CGE.
For the sake of brevity, we also refer to “structure” as a predictor signifying the weighted combination of the two metrics derived from anatomical connectivity (i.e., G and M).
Anatomical, CGE, and FC matrices were converted to z-scores before being fit in each linear model. For these analyses, all matrices (distance, anatomy, CGE, and FC) were unthresholded. Variance in FC explained was assessed after the inclusion of each term, as well as after the inclusion of the anatomy by CGE interaction (see all models in Fig. 1). All linear models were calculated using the “fitlm” function in Matlab (version 2014a). Models were compared to determine which were best-fitting using the log-likelihood ratio test (Wilks, 1938). Model fits were measured via the akaike information criterion (AIC), and models were compared using a χ2 test (Neyman and Pearson, 1933; K. L. Mills et al., 2016; Muschinski et al., 2016), via the χ2 cumulative distribution function “chi2cdf” in Matlab. The model with the lowest AIC that was also most significant than less complex models was selected. A Bonferroni's adjusted p value was then calculated to account for multiple comparisons (based on five model comparisons described next). Models were compared with assess independent effects (Did structure and CGE explain more variance than spatial topology?), additive effects (Did the combination of CGE and structure explain more variance than either factor alone?), and interactive effects (Did the interaction between CGE and structure explain more variance then their additive effects?).
Shared connection patterns with FC
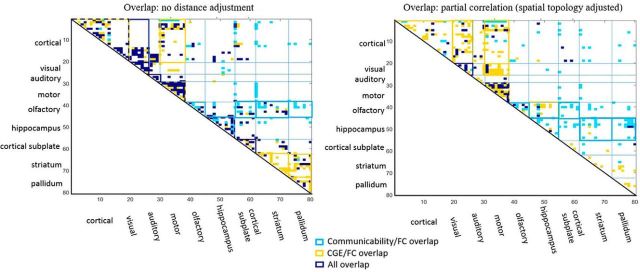
To assess the overlap between each connection type, the following analyses were conducted. First, the FC, G, and CGE matrices (z-scored matrices) were thresholded and binarized in 1% increments from 10 to 30% connection densities. Next, connections that survived a given threshold for all three matrices were given a value of 1. Similarly, connections that survived a threshold for FC and CGE and for FC and G were given a value of 1. For each category, (1) overlap between all three matrices, (2) overlap between FC and G, and (3) overlap between FC and CGE binary matrices were averaged across each connection density. Resulting matrices for each category were then binarized if their average value was greater than 0.5, indicating an overlap for that category across at least 50% of connection densities. Finally, to assess the significance of these overlapping patterns, we took a network-level approach to see whether particular anatomical clusters (defined anatomically by the ABI) were over-represented for each category. This was implemented with a χ2 approach. Briefly, the χ2 test compares the observed number of binary connections within a network pair with what would be expected if the overall number of connections were evenly distributed across all network pairs. The resulting statistic is large when there are more connections than expected by chance. An empirical p value is calculated by a permutation test, which is nonparametric and does not make assumptions about the population distribution (Backes et al., 2014; Eggebrecht et al., 2017). Here, 10,000 permutations were performed, each time randomly shuffling the binary values for each overlapping category (see above), and the reported p values for each network reflect the observed χ2 statistic compared with the permuted χ2 statistics obtained from the given network–network pair. Significant networks for each category (p < 0.05, false discovery rate (FDR) corrected) are highlighted in Figure 5. To examine whether overlapping effects were driven by spatial topology, an identical analysis was performed on residual matrices after each variable (FC, CGE, and G) was adjusted for spatial topology.
Figure 5.
Regional distribution overlap between FC, G, and CGE. The overlap between the strongest FC, CGE, and anatomical communicability (G) matrices was compared. Connections with shared overlap shared between FC and G (aqua), between FC and CGE (yellow), or between all three metrics (purple) are shown. Anatomical modules that show significant over-representation of one category are outlined (based on an FDR-corrected χ2 test). Overlap between matrices was calculated as the consensus across 10–30% connection densities. Spatial topology adjustment indicates that metrics (FC, G, and CGE) were adjusted for distance and spatial adjacency.
Peak analyses
To examine which genes were most critical for supporting the relationship between FC and CGE, the following analyses were performed. First, we computed the FC–CGE relationship (i.e., with the inclusion of the full set of 3079 genes in the CGE matrix). We then incrementally removed one gene before calculating the CGE matrix and recomputed the FC–CGE relationship. Then, we subtracted the FC–CGE relationship from the FC–CGE relationship with one gene removed. Next, we rank ordered each gene according to how much the relationship dropped after the removal of the gene. Finally, after rank ordering each gene we incrementally reintroduced each gene (in rank order) into the CGE matrix and refit of the statistical models testing the relationship between FC and each predictor. We then identified the number of genes included in the CGE matrix that resulted in the highest amount of variance explained. Two analyses were performed, including one that assessed the FC–CGE relationship in a linear model correcting for distance. An identical analysis was performed without correcting for Euclidean distance between region pairs.
Over-representation analysis
ErmineJ software (version 3.0.2; Gillis et al., 2010) was used for over-representation analyses (ORA) comparing our target gene set corresponding to genes most related to FC (peaks with and without covarying Euclidean distance in the gene rank list) with the background list of all coronal genes (3079 genes). Gene annotations (Ashburner et al., 2000) were assigned gene ontology (GO) terms (Ashburner et al., 2000) using an annotation file from GEMMA (Zoubarev et al., 2012): Generic_mouse_ncbiIds_noParents.an was downloaded from http://www.chibi.ubc.ca/microannots/ on December 6, 2016. From the 3079 genes in our set, the annotations matched 3076 genes, the final list of genes included in our ORA analyses. Over-represented biological processes, molecular processes, and cellular components were tested. We used a maximum and minimum gene set size of 100 and 20 genes, respectively. We used the best scoring replicate, and for scoring, we weighted each gene within the peak as 1 and the remaining background genes as −1.
Results
Resting-state functional connectivity of the mouse connectome
C57BL/6J mice (n = 23) were maintained under light anesthesia (1–1.5% isoflurane) and scanned in an 11.75T MRI. We computed FC (z-transformed correlations) between 160 bilateral ROIs defined by AMBCA (Oh et al., 2014) and detailed in previous work (Stafford et al., 2014). ROIs excluding regions labeled as brainstem and cerebellum by the AMBCA were chosen (see Materials and Methods and Fig. 3-1 for a complete list of regions). Figure 3 shows qualitative clustering of the mouse functional connectome, where brain regions (nodes) are pulled together if they share strong functional connections (edges) and weak functional connections are further apart in graphical distance. Regions are colored by functional module (Fig. 3A) as well as anatomical assignment based on the ABI region set (Fig. 3B). The mouse functional connectome appears to cluster by both functional as well anatomical subdivisions; the degree to which anatomical and transcriptional similarly between regions guides this organization is a major goal of this work.
80 bilateral regions of interest were used to assess the relationship between FC, CGE, and G. Full names, acronyms, and anatomical divisions were defined by Oh et al., 2014 and the Allen Mouse Brain Connectivity atlas. Download Figure 3-1, TIF file (199.7KB, tif)
Relationships between structural and functional connectivity
Measurements of anatomical connectivity, as assessed by viral tracing, were derived from the from the AMBCA (Oh et al., 2014). Anatomical communication capacity between the 160 ROIs used in the functional analyses was then computed on the weighted structural connectivity measurements. This communication capacity metric is termed “communicability” (denoted G) and is a weighted measure that describes the ease of communication between two regions (Estrada and Hatano, 2008; Crofts and Higham, 2009). It takes into account all possible routes between nodes (both monosynaptic and polysynaptic), but it weights shorter pathways (those with fewer steps) exponentially higher. We chose this measurement of structural connectivity because of our recent work that highlights its improved capacity to model functional connectivity over simple monosynaptic connectivity (Grayson et al., 2016). We also use the matching index (denoted M; Hilgetag et al., 2000), an index that quantifies the similarity of connections between two nodes excluding their mutual connection. Matching index captures additional small contributions to FC driven by inter-regional similarities in connectivity patterns, as demonstrated previously (Adachi et al., 2012).
Assessing the relationship between FC (unthresholded FC matrix using the bilateral 160 × 160 ROI set), the linear combination of G and M explained 22.1% of the variance in FC (Fig. 3C) and was driven mostly by G (β = 0.504 vs β = 0.154 for M). Ipsilateral and heterotopic region pairs conformed closely to the overall regression line. However, homotopic region pairs showed consistently higher FC than expected by the overall regression line. This suggests an effect of functional areal similarity that is not explainable by network effects of anatomical connectivity alone.
Inter-regional CGE, anatomical communication capacity, and spatial topology explain functional connectivity
To explain additional factors that contribute to the mouse functional connectome, we investigated the contribution of inter-regional CGE on resting-state FC. For CGE, we obtained measurements from the ABI mouse brain ISH data (Lein et al., 2007), which offers finely sampled whole-genome expression data within each of the Allen ROIs. Because of potential differences in data quality between coronally and saggitally collected ISH data (Fulcher and Fornito, 2016), we used coronally obtained genes to ensure the highest data quality and to avoid mixing measures from both data sets. Genetic expression of all 3188 coronally obtained ISH probes were obtained for each ROI and for each gene. Expression intensities for all genes were z-scored within each ROI, and Fisher's z-transformed Pearson's correlations were computed between each anatomical region pair across genes, yielding an 80 × 80 matrix of inter-regional CGE. The ABI gene expression data are provided as an average of both hemispheres, thus for all subsequent measurements, G and FC were averaged across left and right hemispheres yielding comparable 80 × 80 matrices.
Among ipsilateral region pairs connected via monosynaptic projections, we found FC to be significantly correlated with the weighted measure of monosynaptic anatomical connectivity (r = 0.33, p = 10−6), but more so with communicability among monosynaptically connected ROI pairs (G; r = 0.40, p = 10−6), in accordance with previous work (Grayson et al., 2016). FC and G were also correlated among region pairs with no monosynaptic connectivity (r = 0.35, p = 10−6), which is also in line with our previous work (Grayson et al., 2016). FC and G were most strongly related when considering all connections (G; r = 0.48, p = 10−6).
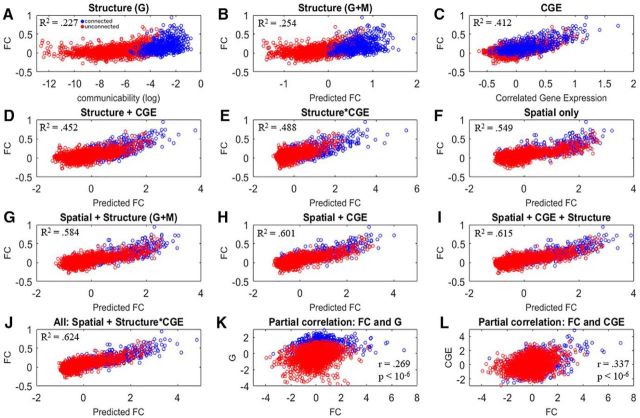
Scatter plots shown in Figure 4 correspond to models and their corresponding those detailed in Figure 1. We found a strong relationship between G and FC among all region pairs (FC is unthresholded in all models; Fig. 4A; R2 = 0.227, β = 0.479). CGE was also strongly correlated with FC (Fig. 4C; R2 = 0.412, β = 0.642). Models including the linear combination of both CGE and communicability (Fig. 4D; R2 = 0.452) and the addition of the interaction between CGE and G increased the variance in FC explained (Fig. 4E; R2 = 0.488, all individual terms except for M, are significant at p < 10−6).
Figure 4.
Relationships between FC, anatomical connectivity measures communicability (G) and matching index (M), and correlated gene expression (CGE). Blue points indicate region pairs that share a direct monosynaptic anatomical connection, and red points are region pairs that are anatomically unconnected. A, B, FC is illustrated as a function of anatomical structure defined by only G (A) and anatomical structure defined by the linear regression of FC on G and M (B). C, The relationship between FC and CGE. D, E, FC predicted by a linear combination of structure (G+M) and CGE (D) and the FC relationship is shown relationship after the inclusion the interaction between G and CGE (E). G–J, Next, we started with a null model predicting FC as a function of spatial topography (Euclidean distance plus spatial adjacency) and show that each variable adds to the variance explained above and beyond spatial topography (G–I), ending with a final omnibus model including all variables and the interaction between structure and CGE, which explains the most variance in FC (J). Full equations for models depicted in A–J can be found in Figure 1, and β weights and significance for each parameter are shown in Table 1. K, L, Partial correlations analyses. Relationships between G and FC and between CGE and F were computed after adjusting each metric (FC, G, and CGE) for distance and spatial adjacency (i.e., correlation between residuals after spatial topology adjustment).
Importantly, FC, CGE, and G all are distance dependent in real and biological meaningful ways. For instance, gene expression is more similar between similar structures that are also closer in proximity, white matter connectivity is stronger between regions that are closer from their source area, and FC is stronger between similar regions which are closer in proximity. That being said, Euclidean distance may also be partially driven by artifact, for instance, from virus spreading to nearby areas in anatomical viral tracing studies, and in FC where various artifacts can induce higher correlations between neighboring voxels. This has led to some controversy regarding the nature the overlap between CGE and FC (Pantazatos et al., 2015; Richiardi et al., 2017). For these reasons, all analyses were analyzed, including both Euclidean distance and spatial adjacency, a binary measure of whether two connections are touching, included as regressors in each linear model.
As expected, spatial topology explains a large amount of variance in the FC signal (Fig. 4F; R2 = 0.549). Critically, the addition of each variable explains more variance than spatial topology alone, with the addition of G and M (Fig. 4G; R2 = 0.584), CGE (Fig. 4H; R2 = 0.601), their linear combination (Fig. 4I; R2 = 0.601), and their interaction (Fig. 4J; R2 = 0.624) explaining a total amount of variance of 62.4% of the FC matrix.
We also computed distance-adjusted relationships between FC and G and between FC and CGE. Here, residuals for each matrix (FC, G, and CGE) were computed after the effects of spatial topology (spatial adjacency plus Euclidean distance) were accounted for in a linear model. Residuals were then correlated. Scatter plots for FC and G (Fig. 4K; r = 0.269, p < 10−6) and FC and CGE (Fig. 4L; r = 0.337, p < 10−6) can be seen in Figure 4.
Model comparisons
Importantly, direct comparisons of model fits based on their AIC and resulting χ2 distributions confirmed the independent, additive, and interactive effects (Table 2). Independent effects were demonstrated by model comparisons showing that structure [i.e., G and M; χ2(2) = 379.96, p = 7.27−54] and CGE [χ2(1) = 247.93, p = 6.33−84] explain more variance than spatial topology alone. The linear effects combination of CGE, structure, and spatial topology explained more variance than structure and spatial topology [χ2(1) = 240.66, p = 1.41−53] or CGE and spatial topology [χ2(2) = 108.63, p = 1.29−23]. Finally, the interactive effect of CGE and structure explained more variance the linear combination of structure and CGE alone [all models including spatial topology; χ2(1) = 80.19, p = 9.76−25]. Overall, we show that transcriptional similarity and network effects of axonal connectivity interact, but also uniquely support FC beyond what can be explained by Euclidean distance and spatial adjacency between regions pairs.
Table 2.
Comparison of functional connectivity models
| Model comparisons | |
|---|---|
| Full model | Null model |
| 1. Independent effects | F) Spatial topography only |
| G) Spatial topography + structure | χ2(2) = 379.96, p = 7.27−54 |
| H) Spatial topography + CGE | χ2(1) = 247.93, p = 6.33−84 |
| 2. Additive effects | G) Spatial topography + structure |
| I) Spatial topography + CGE + structure | χ2(1) = 240.66, p = 1.41−53 |
| I) Spatial topography + CGE + structure | H) Spatial topography + CGE |
| χ2(2) = 108.63, p = 1.29−23 | |
| 3. Interactive effects | I) Spatial topography + CGE + structure |
| J) Full model: Spatial topography + structure * CGE | χ2(1) = 80.19, p = 9.76−25 |
Highlighted are the significant independent effects of structure and CGE above spatial topology, the additive effect of CGE and structure above each of their independent effects, and the interactive effect of CGE and structure above their linear combination. The null models to which these effects are compared are shown in the second column (e.g. model F, spatial topology only). The p values for each model comparison are based on a χ2 statistic based on the difference in model AICs and are Bonferroni's corrected for multiple comparisons.
Table 1.
Multivariate models of functional connectivity
| Model | Models of functional connectivity |
||||
|---|---|---|---|---|---|
| Metric | Beta | AIC | R2 | p value | |
| Without spatial topology | |||||
| A) Structure (G) | G | 0.4799 | 8143.188 | 0.227 | <10−6 |
| B) Structure (G + M) | G | 0.5432 | 8040.427 | 0.254 | <10−6 |
| M | 0.1705 | <10−6 | |||
| C) CGE | CGE | 0.6421 | 7290.793 | 0.412 | <10−6 |
| D) Structure + CGE | G | 0.2439 | 7076.004 | 0.452 | <10−6 |
| M | 0.0441 | 0.002 | |||
| CGE | 0.5231 | <10−6 | |||
| E) Structure + CGE + Structure*G | G | 0.2666 | 6862.353 | 0.488 | <10−6 |
| M | 0.0334 | n.s. | |||
| CGE | 0.4247 | <10−6 | |||
| G*CGE | 0.2111 | <10−6 | |||
| With Spatial topology | |||||
| F) Spatial topography only | Distance | 0.5035 | 6455.007 | 0.549 | <10−6 |
| SA | 0.3187 | <10−6 | |||
| G) Spatial topography + structure | Distance | 0.4527 | 6207.076 | 0.584 | <10−6 |
| SA | 0.2622 | <10−6 | |||
| G | 0.2219 | <10−6 | |||
| M | 0.0462 | <10−4 | |||
| H) Spatial topography + CGE | Distance | 0.3834 | 6075.042 | 0.604 | <10−6 |
| SA | 0.2350 | <10−6 | |||
| CGE | 0.2914 | <10−6 | |||
| I) Spatial topography + CGE + Structure | Distance | 0.3750 | 5966.409 | 0.615 | <10−6 |
| SA | 0.2095 | <10−6 | |||
| CGE | 0.2408 | <10−6 | |||
| G | 0.1426 | <10−6 | |||
| M | 0.0099 | n.s. | |||
| J) Full Model: spatial topography + structure*CGE | G | 0.1616 | 5886.251 | 0.624 | <10−6 |
| CGE | 0.2048 | <10−6 | |||
| M | 0.0043 | n.s. | |||
| G*CGE | 0.1144 | <10−6 | |||
| Distance | 0.3654 | <10−6 | |||
| SA | 0.1816 | <10−6 | |||
Statistical models of functional connectivity include combinations of anatomical structure, correlated gene expression, and spatial topology (A–E, corresponding to equations in Figure 1). Structure indicates a both communicability (G) and match index (M), two polysynaptic anatomical connectivity metrics. CGE measures similarity in gene expression between regions, and G*CGE denotes the interaction term. Spatial topology is the combination of Euclidean distance between ROI centroids and spatial adjacency (SA), a dichotomous variable indicating whether or not two regions share a border. Models are assembled without and with the inclusion of spatial topology. Betas represent standardized coefficients, and the variance explained for each model is represented by the R2. AIC values denote each model's goodness of fit, with lower values indicating better model fit.
Distinct anatomical modules are responsible for the contribution of correlated gene expression and anatomical communicability on functional connectivity
We found that both CGE and G, independent of spatial topology, help shape/explain functional connectivity networks. As such, we then explored whether this relationship is heterogeneous or homogenous across the brain. That is, are there anatomical subdivisions in which there are distinct or overlapping relationships between FC, anatomy, and gene expression? Specifically, we examined which functional connections may be supported uniquely by CGE, by G, or by a combination of CGE and G. First, to explore these patterns, we binarized each matrix in 1% increments from the top 10–30% connection densities. For each matrix (FC, CGE, and G) connections were considered if they survived at over half of these connection densities. To examine overlapping profiles, a matrix was derived indicating whether there was overlap between FC and CGE, FC, and G or between all three matrices. We then calculated the statistical significance of this overlap by computing an FDR-corrected χ2 statistic for each anatomical module, which tests whether each overlap metric was more prevalent within an anatomical module than expected by chance; see Materials and Methods for more details on the χ2 approach.
Overlap between FC, G, and CGE was non-uniform across the brain and depended on partial correlation adjustment based on distance. As can be seen in Figure 5, we found that overlap between the strongest FC and CGE within and between cortical, motor, cortical-to-motor, striatal, and pallidal networks. After adjustment for spatial topology (adjusting metrics to correct for distance and spatial adjacency), cortical and sensory networks increase in overlap between FC and CGE, where subcortical overlap is partially dependent on distance. In regard to overlap between FC and G, with and without distance adjustment we found that overlap within hippocampal and olfactory areas. However, distance adjustment influenced the degree to with FC and G overlapped between hippocampal and olfactory-to-subcortical networks. With and without spatial topology adjustment, overlap between all three metrics was most robust within motor and visual networks. Distance adjustment decreased the amount of overlap between all three metrics. This was unsurprising as we know that distance dependence is real and a prominent driver of all three metrics. Although these patterns are observed at the level of gross anatomical modules, a more granular view may also be informative. For instance, G, rather than CGE, may drive a subset of longer-range cortical to subcortical connections. Overall, this analysis suggests that FC may be shaped by independent and interactive effects between G and CGE and that this relationship is non-uniform across the brain but depends on the anatomical module.
A subset of genes supports the relationship between correlated gene expression and functional connectivity
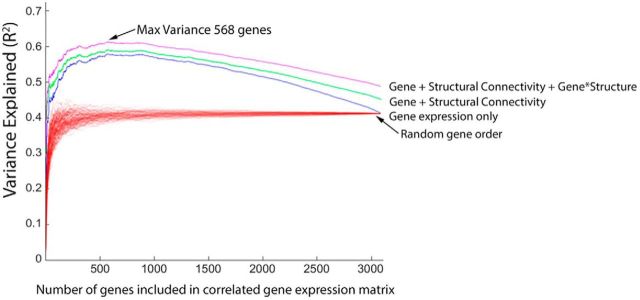
It is likely that not all genes contribute equally to the variations in the FC signal. Next, we asked whether all genes equally contribute to the relationship between CGE and FC and how many genes drive this relationship. To examine this, we computed the FC–CGE relationship (with and without covarying distance). Next, we removed one gene and recalculated a new CGE matrix. Then, we subtracted the variance explained in the model with all genes included in the CGE matrix from the model, which was calculated on the leave-one-out CGE matrix, and rank ordered each gene according to the magnitude of the difference in variance explained between the full and leave-one-out CGE matrix. Next, after rank ordering each gene by most to least related to FC, we incrementally re-introduced each gene into the CGE matrix (i.e., each time adding back one gene before computing the CGE matrix) and refit each model. Figure 6 shows the variance in FC explained with each model, as a function of how many genes were reintroduced into the CGE matrix. The maximum amount of variance emerged after 568 genes were included in the CGE matrix (model peak without distance R2 = 0.613, with distance in model R2 = 0.726). Similar results were found when rank ordering genes without considering distance, with a maximum variance at 445 genes (model peak without distance, R2 = 0.671 and with distance in model, R2 = 0.702; see Fig. 6-1). Note the marked decline in explanatory power of the CGE after the inclusion of additional genes beyond the peak, suggesting that a subset of genes contribute disproportionately to the observed CGE–FC relationship.
Figure 6.
A subset of genes support the relationship between CGE and functional connectivity. Genes were rank ordered (x-axis) based on their contribution to the CGE–FC correlation (correcting for distance). Then, each model predicting FC was refit after incrementally adding each gene to the CGE matrix. The maximum variance was observed after the inclusion of 568 of the most explanatory genes to the CGE matrix (R2 = 0.6131). Each red line indicates a different permutation for gene expression only, where gene rankings were randomized on each permutation. One hundred random permutations are shown. A similar peak was observed without correcting for distance and can be seen in Figure 6-1.
Genes that support CGE and FC, without distance correction. Incremental inclusion of genes into CGE matrix without distance correction during rank ordering of gene importance. A subset of genes support the relationship between CGE and functional connectivity. Genes were rank ordered (x-axis) based on their contribution to the CGE-FC correlation (after covarying Euclidian distance). Then, each model predicting FC was refit after incrementally adding each gene to the CGE matrix. The max variance was observed after the inclusion of 445 of the most explanatory genes to the CGE matrix, r2 = .702). Each red line indicates a different permutation for gene expression only, where gene rankings were randomized on each permutation. 1000 permutations are shown. Download Figure 6-1, XLSX file (12.6KB, xlsx)
These results suggest that a limited number of genes contributed to the relationship between FC and CGE. To examine the functions of genes that most strongly contributed to the FC signal, we performed an ORA using the software ErmineJ. Top-ranked genes within the maximum variance peak in Figure 6 (maximum variance, 568 genes) were selected and compared with the background set of genes (3079 genes). This procedure identifies clusters of genes that are over-represented within this peak, their biological and molecular processes, and their cellular components. Interestingly, as opposed to some previous work in humans (Richiardi et al., 2015; Fulcher and Fornito, 2016), no clusters passed statistical significance after FDR correction, potentially suggesting that these strongest-related genes are equally related to several molecular and biological processes (see Discussion). With that said, Table 3 shows the uncorrected results of all significant gene clusters (p < 0.05; peaks identified with and without covarying for Euclidean distance), which show interesting trends that lay fodder for future study and empirical manipulation. Most notably with these findings was the over-representation of molecular processes related to voltage-gated cation channel activity, a gene cluster that was consistently over-represented regardless of distance correction.
Table 3.
Functions of genes that support the relationship between CGE and FC
| Functional classification | Gene ontology | Multifunctionality | p value |
|---|---|---|---|
| Molecular process | |||
| Distance correction | |||
| Voltage-gated cation channel activity | GO:0022843 | 0.168 | 0.047 |
| No distance correction | |||
| Voltage-gated potassium channel activity | GO:0005249 | 0.007 | 0.048 |
| Voltage-gated cation channel activity | GO:0022843 | 0.168 | 0.030 |
| Cation channel activity | GO:0005261 | 0.742 | 0.034 |
| Cellular component | |||
| Distance correction | |||
| Presynaptic membrane | GO:0042734 | 0.624 | 8.94E-03 |
| Synaptic membrane | GO:0097060 | 0.724 | 0.011 |
| presynapse | GO:0098793 | 0.846 | 8.02E-03 |
| No distance correction | |||
| N.S. | |||
| Biological Process | |||
| Distance correction | |||
| Glutamate receptor signaling pathway | GO:0007215 | 0.684 | 0.049 |
| Multicellular organismal homeostasis | GO:0048871 | 0.897 | 0.046 |
| Pallium development | GO:0021543 | 0.902 | 0.049 |
| Positive regulation of sequence-specific DNA binding transcription factor activity | GO:0051091 | 0.905 | 0.031 |
| Regulation of leukocyte migration | GO:0002685 | 0.909 | 0.029 |
| No distance correction | |||
| DNA repair | GO:0006281 | 0.598 | 0.023 |
| Regulation of fat cell differentiation | GO:0045598 | 0.806 | 0.048 |
| Response to light stimulus | GO:0009416 | 0.883 | 0.027 |
| Response to radiation | GO:0009314 | 0.897 | 0.039 |
| Multicellular organismal homeostasis | GO:0048871 | 0.897 | 0.046 |
| Chemical synaptic transmission | GO:0007268 | 0.898 | 0.050 |
| Anterograde trans-synaptic signaling | GO:0098916 | 0.898 | 0.050 |
| Synaptic signaling | GO:0099536 | 0.898 | 0.050 |
| Trans-synaptic signaling | GO:0099537 | 0.898 | 0.050 |
| Regulation of intracellular transport | GO:0032386 | 0.913 | 0.048 |
| Positive regulation of ERK1 and ERK2 cascade | GO:0070374 | 0.928 | 4.52E-03 |
| Regulation of ERK1 and ERK2 cascade | GO:0070372 | 0.929 | 7.35E-03 |
Genes that most strongly supported the CGE–FC relationship (top genes identified in figure 6) were compared with the background set of all genes used to construct the full CGE matrix. Results are shown for gene rankings produced with and without correction for Euclidean distance between region pairs. Results are ordered by multifunctionality and were produced using the over-representation analyses in the ErmineJ software package.
Discussion
Modeling correlated gene expression and anatomical communicability across the functional connectome
This report investigates the white matter anatomy and regional similarity in gene expression related to synchronous large-scale brain activity. We found that functional connectivity is related to distinct aspects of structural communication (measured via communicability) and interareal similarities in gene expression. Our model accounts for a significant amount of variance in the resting-state FC signal (R2 = 0.624) at its peak without considering improvement related to spatial proximity. The present report extends key findings by Richiardi et al. (2015), who showed in humans that CGE is enriched within key functional brain networks relative to between these networks. Here we show that these principles hold in rodents and that CGE predicts FC across the brain. Interestingly, CGE explains more variance in the FC signal than anatomical communication capacity (G), suggesting that transcriptional similarity, and presumably similarities in protein expression, may be a crucial foundation of the FC signal in addition to anatomical wiring. We also found a significant interaction between CGE and G, suggesting that a region's transcriptional profile and anatomical wiring may work in coordination to modulate functional synchrony with other regions. The addition of CGE to models of FC is significant given the abundance of literature that has been aimed at identifying the substrates that support functional connectivity via structural network analysis (Stafford et al., 2014; Miranda-Dominguez et al., 2014b; Grayson et al., 2016; for review, see Bassett and Sporns, 2017). The present findings suggest that a more accurate modeling strategy requires the integration of structural connectivity with empirical measurements of areal molecular properties.
Relationships between physical proximity, functional and structural connectivity, and correlated gene expression
One area of caution, and interest, is the role of spatial proximity to the relationships across the three modalities. Areas that are close in spatial proximity are more likely to share more similar gene transcription profiles, have stronger anatomical connections, and share stronger functional connections. These distance relationships represent biologically meaningful information; however, there is nonetheless a concern that the spatial smoothness of the fMRI signal might artifactually inflate estimates of structure–function correspondences. All fMRI data were processed without any spatial blurring to mitigate this possibility. Furthermore, given the relationship between CGE and Euclidean distance, with exponentially higher CGE between region pairs close in spatial proximity (Pantazatos et al., 2015), it is important that these type of studies also take into account how these variables relate above and beyond spatial proximity. Here, we show that although highly related to distance, as expected, relationships between FC, G, and CGE are independent of Euclidean distance and spatial adjacency. When examining relationships between FC and CGE, others have similarly corrected for Euclidean distance (but not the additional parameter of spatial adjacency; Fulcher and Fornito, 2016) or have taken alternative approaches to examine these FC–CGE relationships between spatially distributed functional networks (Richiardi et al., 2015). Given that covariation between distance and FC, G, and CGE is partly biological, we suggest that, when possible, the results should be compared with and without these types of corrections.
The distribution of overlap between these three metrics was also of interest, as relationships with FC may be driven more prominently between some networks than others. Interestingly, we found that cortical, striatal, and sensory regions had a large degree of overlap between CGE and FC, where hippocampal and long-range FC were more likely to be driven by overlap between G and FC. However, distance correction partially influenced some of these results (hippocampal) but not others (cortical and sensory). More work will need to be done to understand exactly how and between which connections CGE and G selectively relate to FC. Just as importantly, in our view, will be future experiments with a more thorough characterization of these relationships through experimental manipulation of either anatomical wiring or gene expression profiles.
Correlated expression of a subset of genes disproportionately relate to functional connectivity
Given that transcriptional similarity between regions had a large effect on FC, our next aim was to understand the contributions of specific gene clusters. That is, is the regional similarity across the entire transcriptome predictive, or do some genes disproportionately affect this relationship? By ranking each gene's contribution to the CGE–FC relationship, we found that a subset of genes (568 of 3079) disproportionally drive this relationship, suggesting that covariance in particular subsets of processes may be more influential in supporting the FC signal. In this report, we used gene ontology ORA to identify the processes associated with these genes. In this section, we discuss these analyses, some potential gene clusters, which may support FC, common themes, and considerations.
Although it is clear that a subset of genes disproportionately drive the relationship between CGE and FC, in contrast to previous results (Richiardi et al., 2015; Fulcher and Fornito, 2016), ORA on genes that are most likely to contribute to FC did not yield robust results, and as noted above, no gene cluster reached FDR-corrected statistical significance. Such discrepancies here, relative to prior reports, may be attributable to methodological differences or differences in gene selection used for ORA. Alternatively, this finding could suggest that across the brain, a complex mixture of genes support FC and that the contribution of the genes spreads across multiple functions (at least enough such that no clusters passed correction). This finding could also mean that different gene clusters are critical between different anatomical connections and that a unifying genetic function cannot describe the FC-to-CGE relationship across the brain. Both of these considerations deserve further investigation.
That being said, when analyzing patterns at a relaxed threshold (p < 0.05, uncorrected), several interesting patterns emerged yielding somewhat convergent evidence to similar reports (Richiardi et al., 2015; Fulcher and Fornito, 2016). For instance, genes that were most related to FC were more likely to be involved in molecular processes, which were specific to voltage-gated ion channel and potassium channel activity. This finding is in good accordance with the work of Richiardi et al. (2015), who also found preferential enrichment for these processes within functional networks. This correspondence would suggest that similar mechanisms might underlie the FC signal across species. In our report, we also identified several biological processes, including glutamate receptor signaling, a putative candidate for neural bases for the functional signal (Raichle, 2001; Attwell and Iadecola, 2002), as well as cellular components related to synaptic membrane proteins and synaptic signaling.
When examining these results, it is also important to note that some gene clusters may have multiple functions that are not perfectly circumscribed to a particular process. Some genes may have many more functions than others (Gillis et al., 2011), and this can be qualified by a multifunctionality score. Genes can have many diverse biological roles, and highly multifunctional genes are not necessarily incorrectly assigned to a particular role but should be interpreted with more caution (Gillis and Pavlidis, 2012). In our analyses, ion channels represent a gene cluster that supports FC with relatively low multifunctionality. However, we also identify additional over-represented biological clusters with high multifunctionality scores including genes coding for homeostatic and developmental processes. These processes might be interpreted with caution as these genes also supply a rich diversity of alternative functions that, in turn, might also be related to the FC signal.
There is a complex set of neuronal, vascular, and cellular influences on the FC signal. Any given region's activity may be modulated by neurotransmitter signaling (Attwell and Iadecola, 2002; Magistretti and Allaman, 2015), the excitatory-to-inhibitory ratio (Turk et al., 2016; van den Heuvel et al., 2016), local energy demands (Tomasi et al., 2013; Lu and Stein, 2014; Magistretti and Allaman, 2015), and/or cytoarchitectural features such as synaptic density (Attwell and Iadecola, 2002; Magistretti and Allaman, 2015). Each of these contributions may be reflected in inter-regional variability in both gene expression and spontaneous activity. Along the same lines, molecular influences on regional activity might vary across different brain subdivisions. For example, we show that the distribution of high-CGE, high-FC links are non-uniform and occurs to a greater extent in particular types of connections (i.e., striato-pallidal). Future work should address whether the gene clusters that most contribute to the functional signal vary by connection. Overall, the specific relationships between gene transcription and FC is far from resolved and will require experimental manipulation.
Applications and conclusions
Models that explain functional brain organization are particularly useful in preclinical animal models, where genetic and pharmacological manipulation allow the exploration of both etiology and therapy in various neurological disorders. With this consideration in mind, one of the most straightforward applications of the current statistical model would be to determine the theoretical impact of experimental perturbation to specific regions, systems, or even gene clusters within specific systems. There is evidence from work in monkeys that simulated lesions can accurately predict many widespread neurophysiological changes in response to focal empirical inactivation (Grayson et al., 2016). Extending this approach to rodents, in combination with improved modeling techniques that account for transcriptional similarity, might be exceptionally useful given the time and cost associated with pharmacological screening and gene therapy testing. Recent rodent work highlights the usefulness of simulated lesions for predicting memory impairments (Vetere et al., 2017), but it has yet to account for the influence of areal gene expression in the modeling framework. Our results here suggest that identifying both candidate brain systems and candidate genes via simulated perturbation might be feasible for interrogating other cognitive deficits as well. Finally, experimental manipulation of activity and/or gene expression combined with simultaneous in vivo functional measurement might be used to assess what gene clusters (and what modeling framework) are best predictive of variation in typical or atypical brain function.
Footnotes
We thank Benjamin Jarrett, Martin Pike, and Alina Goncharova for their work on MRI acquisition, pipeline development, and data processing. This work was supported by the National Institutes of Health (grants R01 MH096773 and K99/R00 MH091238 to D.A.F.), R01 MH105538 to D.A.F.), the Oregon Clinical and Translational Research Institute (D.A.F.), the Gates Foundation (D.A.F.), the Destafano Innovation Fund (D.A.F.), a OHSU Fellowship for Diversity and Inclusion in Research Program (O.M.-D.), and a National Library of Medicine Postdoctoral Fellowship (E.F.).
The authors declare no competing financial interests.
References
- Abdelnour F, Voss HU, Raj A (2014) Network diffusion accurately models the relationship between structural and functional brain connectivity networks. Neuroimage 90:335–347. 10.1016/j.neuroimage.2013.12.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adachi Y, Osada T, Sporns O, Watanabe T, Matsui T, Miyamoto K, Miyashita Y (2012) Functional connectivity between anatomically unconnected areas is shaped by collective network-level effects in the macaque cortex. Cereb Cortex 22:1586–1592. 10.1093/cercor/bhr234 [DOI] [PubMed] [Google Scholar]
- Andersson JLR, Skare S, Ashburner J (2003) How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 20:870–888. 10.1016/S1053-8119(03)00336-7 [DOI] [PubMed] [Google Scholar]
- Ash JA, Lu H, Taxier LR, Long JM, Yang Y, Stein EA, Rapp PR (2016) Functional connectivity with the retrosplenial cortex predicts cognitive aging in rats. Proc Natl Acad Sci U S A 113:12286–12291. 10.1073/pnas.1525309113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, Harris MA, Hill DP, Issel-Tarver L, Kasarskis A, Lewis S, Matese JC, Richardson JE, Ringwald M, Rubin GM, Sherlock G, et al. (2000) Gene Ontology: tool for the unification of biology. Nat Genet 25:25–29. 10.1038/75556 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attwell D, Iadecola C (2002) The neural basis of functional brain imaging signals. Trends Neurosci 25:621–625. 10.1016/S0166-2236(02)02264-6 [DOI] [PubMed] [Google Scholar]
- Backes C, Rühle F, Stoll M, Haas J, Frese K, Franke A, Lieb W, Wichmann HE, Weis T, Kloos W, Lenhof HP, Meese E, Katus H, Meder B, Keller A (2014) Systematic permutation testing in GWAS pathway analyses: identification of genetic networks in dilated cardiomyopathy and ulcerative colitis. BMC Genomics 15:622. 10.1186/1471-2164-15-622 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Sporns O (2017) Network neuroscience. Nat Neurosci 20:353–364. 10.1038/nn.4502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blondel VD, Guillaume JL, Lambiotte R, Lefebvre E (2008) Fast unfolding of communities in large networks. J Stat Mech 2008:P10008 10.1088/1742-5468/2008/10/P10008 [DOI] [Google Scholar]
- Brynildsen JK, Hsu L-M, Ross TJ, Stein EA, Yang Y, Lu H (2017) Physiological characterization of a robust survival rodent fMRI method. Magn Reson Imaging 35:54–60. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O (2009) Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10:186–198. [DOI] [PubMed] [Google Scholar]
- Cary RP, Ray S, Grayson DS, Painter J, Carpenter S, Maron L, Sporns O, Stevens AA, Nigg JT, Fair DA (2017) Network structure among brain systems in adult ADHD is uniquely modified by stimulant administration. Cereb Cortex 27:3970–3979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crofts JJ, Higham DJ (2009) A weighted communicability measure applied to complex brain networks. J R Soc Interface 6:411–414. 10.1098/rsif.2008.0484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eggebrecht AT, Elison JT, Feczko E, Todorov A, Wolff JJ, Kandala S, Adams CM, Snyder AZ, Lewis JD, Estes AM, Zwaigenbaum L, Botteron KN, McKinstry RC, Constantino JN, Evans A, Hazlett HC, Dager S, Paterson SJ, Schultz RT, Styner MA, et al. (2017) Joint attention and brain functional connectivity in infants and toddlers. Cereb Cortex 27:1709–1720. 10.1093/cercor/bhw403 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estrada E, Hatano N (2008) Communicability in complex networks. Phys Rev E 77:36111 10.1103/PhysRevE.77.036111 [DOI] [PubMed] [Google Scholar]
- Fornito A, Zalesky A, Breakspear M (2015) The connectomics of brain disorders. Nat Rev Neurosci 16:159–172. 10.1038/nrn3901 [DOI] [PubMed] [Google Scholar]
- Fruchterman TMJ, Reingold EM (1991) Graph drawing by force-directed placement. Softw Pract Exp 21:1129–1164. 10.1002/spe.4380211102 [DOI] [Google Scholar]
- Fulcher BD, Fornito A (2016) A transcriptional signature of hub connectivity in the mouse connectome. Proc Natl Acad Sci U S A 113:1435–1440. 10.1073/pnas.1513302113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gates KM, Henry T, Steinley D, Fair DA (2016) A Monte Carlo evaluation of weighted community detection algorithms. Front Neuroinform 10:45. 10.3389/fninf.2016.00045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillis J, Mistry M, Pavlidis P (2010) Gene function analysis in complex data sets using ErmineJ. Nat Protoc 5:1148–1159. 10.1038/nprot.2010.78 [DOI] [PubMed] [Google Scholar]
- Gillis J, Pavlidis P, Chan C, Richard N, Laird M, Allen N, Tanzi R, Khoury M, Ioannidis J, Bertram L (2011) The impact of multifunctional genes on “guilt by association” PLoS One 6:e17258 10.1371/journal.pone.0017258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillis J, Pavlidis P (2012) “Guilt by association” is the exception rather than the rule in gene networks. PLoS Comput Biol 8:e1002444. 10.1371/journal.pcbi.1002444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goñi J, van den Heuvel MP, Avena-Koenigsberger A, Velez de Mendizabal N, Betzel RF, Griffa A, Hagmann P, Corominas-Murtra B, Thiran J-P, Sporns O (2014) Resting-brain functional connectivity predicted by analytic measures of network communication. Proc Natl Acad Sci U S A 111:833–838. 10.1073/pnas.1315529111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grandjean J, Schroeter A, Batata I, Rudin M (2014) Optimization of anesthesia protocol for resting-state fMRI in mice based on differential effects of anesthetics on functional connectivity patterns. Neuroimage 102:838–847. 10.1016/j.neuroimage.2014.08.043 [DOI] [PubMed] [Google Scholar]
- Grayson DS, Fair DA (2017) Development of large-scale functional networks from birth to adulthood: A guide to the neuroimaging literature. Neuroimage 160:15–31. 10.1016/j.neuroimage.2017.01.079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grayson DS, Bliss-Moreau E, Machado CJ, Bennett J, Shen K, Grant KA, Fair DA, Amaral DG (2016) The rhesus monkey connectome predicts disrupted functional networks resulting from pharmacogenetic inactivation of the amygdala. Neuron 91:453–466. 10.1016/j.neuron.2016.06.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilgetag CC, Burns GA, O'Neill MA, Scannell JW, Young MP (2000) Anatomical connectivity defines the organization of clusters of cortical areas in the macaque monkey and the cat. Philos Trans R Soc Lond B Biol Sci 355:91–110. 10.1098/rstb.2000.0551 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meuli R, Hagmann P (2009) Predicting human resting-state functional connectivity from structural connectivity. Proc Natl Acad Sci U S A 106:2035–2040. 10.1073/pnas.0811168106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonckers E, Delgado y Palacios R, Shah D, Guglielmetti C, Verhoye M, Van der Linden A (2014) Different anesthesia regimes modulate the functional connectivity outcome in mice. Magn Reson Med 72:1103–1112. 10.1002/mrm.24990 [DOI] [PubMed] [Google Scholar]
- Kufahl PR, Pentkowski NS, Heintzelman K, Neisewander JL (2009) Cocaine-induced Fos expression is detectable in the frontal cortex and striatum of rats under isoflurane but not α-chloralose anesthesia: Implications for FMRI. J Neurosci Methods 181:241–248. 10.1016/j.jneumeth.2009.05.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kufahl PR, Peartree NA, Heintzelman KL, Chung M, Neisewander JL (2015) Region-specific effects of isoflurane anesthesia on Fos immunoreactivity in response to intravenous cocaine challenge in rats with a history of repeated cocaine administration. Brain Res 1594:256–266. 10.1016/j.brainres.2014.10.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lancaster JL, Glass TG, Lankipalli BR, Downs H, Mayberg H, Fox PT (1995) A modality-independent approach to spatial normalization of tomographic images of the human brain. Hum Brain Mapp 3:209–223. 10.1002/hbm.460030305 [DOI] [Google Scholar]
- Lein ES, Hawrylycz MJ, Ao N, Ayres M, Bensinger A, Bernard A, Boe AF, Boguski MS, Brockway KS, Byrnes EJ, Chen L, Chen L, Chen TM, Chin MC, Chong J, Crook BE, Czaplinska A, Dang CN, Datta S, Dee NR, et al. (2007) Genome-wide atlas of gene expression in the adult mouse brain. Nature 445:168–176. 10.1038/nature05453 [DOI] [PubMed] [Google Scholar]
- Lu H, Stein EA (2014) Resting state functional connectivity: its physiological basis and application in neuropharmacology. Neuropharmacology 84:79–89. 10.1016/j.neuropharm.2013.08.023 [DOI] [PubMed] [Google Scholar]
- Magistretti PJ, Allaman I (2015) A cellular perspective on brain energy metabolism and functional imaging. Neuron 86:883–901. 10.1016/j.neuron.2015.03.035 [DOI] [PubMed] [Google Scholar]
- MATLAB and Statistics Toolbox Release (2014a) The MathWorks, Inc. Natick, MA. [Google Scholar]
- Meila M. (2007) Comparing clusterings - an information based distance. J Multivar Anal 98:873–895. 10.1016/j.jmva.2006.11.013 [DOI] [Google Scholar]
- Messé A, Rudrauf D, Benali H, Marrelec G (2014) Relating structure and function in the human brain: relative contributions of anatomy, stationary dynamics, and non-stationarities. PLoS Comput Biol 10:e1003530. 10.1371/journal.pcbi.1003530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mills BD, Pearce HL, Khan O, Jarrett BR, Fair DA, Lahvis GP (2016) Prenatal domoic acid exposure disrupts mouse pro-social behavior and functional connectivity MRI. Behav Brain Res 308:14–23. 10.1016/j.bbr.2016.03.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mills BD, Miranda-Dominguez O, Mills K, Earl E, Cordova M, Painter J, Karalunas SL, Nigg JT, Fair DA (2017) ADHD and attentional control: impaired segregation of task positive and task negative brain networks. Netw Neurosci 1–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mills KL, Goddings AL, Herting MM, Meuwese R, Blakemore S-J, Crone EA, Dahl RE, Güroğlu B, Raznahan A, Sowell ER, Tamnes CK (2016) Structural brain development between childhood and adulthood: convergence across four longitudinal samples. Neuroimage 141:273–281. 10.1016/j.neuroimage.2016.07.044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miranda-Dominguez O, Mills BD, Carpenter SD, Grant KA, Kroenke CD, Nigg JT, Fair DA (2014a) Connectotyping: model based fingerprinting of the functional connectome. PLoS One 9:e111048. 10.1371/journal.pone.0111048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miranda-Dominguez O, Mills BD, Grayson D, Woodall A, Grant KA, Kroenke CD, Fair DA (2014b) Bridging the gap between the human and macaque connectome: a quantitative comparison of global interspecies structure-function relationships and network topology. J Neurosci 34:5552–5563. 10.1523/JNEUROSCI.4229-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miranda-Dominguez O, Feczko E, Grayson DSDS, Wallum H, Nigg JT, Fair DADA (2017) Heritability of the human connectome: a connectotyping study. Netw Neurosci 1–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muschinski J, Feczko E, Brooks JM, Collantes M, Heitz TR, Parr LA (2016) The development of visual preferences for direct versus averted gaze faces in infant macaques (Macaca mulatta). Dev Psychobiol 58:926–936. 10.1002/dev.21421 [DOI] [PubMed] [Google Scholar]
- Neyman J, Pearson ES (1933) On the problem of the most efficient tests of statistical hypotheses. Philos Trans R Soc A Math Phys Eng Sci 231:289–337. 10.1098/rsta.1933.0009 [DOI] [Google Scholar]
- Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM, Mortrud MT, Ouellette B, Nguyen TN, Sorensen SA, Slaughterbeck CR, Wakeman W, Li Y, Feng D, Ho A, Nicholas E, et al. (2014) A mesoscale connectome of the mouse brain. Nature 508:207–214. 10.1038/nature13186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pantazatos SP, Altmann A, Milazzo AC, Chang C, Chakravarty MM, Banaschewski T, Barker GJ, Bokde AL, Bromberg U, Büchel C, Conrod P, Fauth-Bühler M, Flor H, Frouin V, Gallinat J, Garavan H, Gowland P, Heinz A, Lemaître H, Mann KF, (2015) Commentary: brain networks. Correlated gene expression supports synchronous activity in brain networks. Science 348:1241–1244. 26068849 [Google Scholar]
- Petersen SE, Sporns O (2015) Brain networks and cognitive architectures. Neuron 88:207–219. 10.1016/j.neuron.2015.09.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power J, Cohen A, Nelson S, Wig G, Barnes K, Church J, Vogel A, Laumann T, Miezin F, Schlaggar B, Petersen S (2011) Functional network organization of the human brain. Neuron 72:665–678. 10.1016/j.neuron.2011.09.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raichle ME. (2001) Cognitive neuroscience. Bold insights. Nature 412:128–130. 10.1038/35084300 [DOI] [PubMed] [Google Scholar]
- Richiardi J, Altmann A, Milazzo AC, Chang C, Chakravarty MM, Banaschewski T, Barker GJ, Bokde AL, Bromberg U, Büchel C, Conrod P, Fauth-Bühler M, Flor H, Frouin V, Gallinat J, Garavan H, Gowland P, Heinz A, Lemaître H, Mann KF, et al. (2015) Brain networks. Correlated gene expression supports synchronous activity in brain networks. Science 348:1241–1244. 10.1126/science.1255905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richiardi J, Altmann A, Greicius M (2017) Distance is not everything in imaging genomics of functional networks: reply to a commentary on “Correlated gene expression supports synchronous activity in brain networks. [Google Scholar]
- Rosvall M, Bergstrom CT (2008) Maps of random walks on complex networks reveal community structure. Proc Natl Acad Sci U S A 105:1118–1123. 10.1073/pnas.0706851105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O (2011) Weight-conserving characterization of complex functional brain networks. Neuroimage 56:2068–2079. 10.1016/j.neuroimage.2011.03.069 [DOI] [PubMed] [Google Scholar]
- Rudolph MD, Miranda-Domínguez O, Cohen AO, Breiner K, Steinberg L, Bonnie RJ, Scott ES, Taylor-Thompson K, Chein J, Fettich KC, Richeson JA, Dellarco DV, Galván A, Casey BJ, Fair DA (2017) At risk of being risky: the relationship between “brain age” under emotional states and risk preference. Dev Cogn Neurosci 24:93–106. 10.1016/j.dcn.2017.01.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanz-Leon P, Knock SA, Spiegler A, Jirsa VK (2015) Mathematical framework for large-scale brain network modeling in the virtual brain. Neuroimage 111:385–430. 10.1016/j.neuroimage.2015.01.002 [DOI] [PubMed] [Google Scholar]
- Seeley WW, Crawford RK, Zhou J, Miller BL, Greicius MD (2009) Neurodegenerative diseases target large-scale human brain networks. Neuron 62:42–52. 10.1016/j.neuron.2009.03.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah D, Jonckers E, Praet J, Vanhoutte G, Delgado Y Palacios R, Bigot C, D'Souza DV, Verhoye M, Van der Linden A (2013) Resting state fMRI reveals diminished functional connectivity in a mouse model of amyloidosis. PLoS One 8:e84241. 10.1371/journal.pone.0084241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith M, Li J, Cote D, Ryabinin A (2016) Effects of isoflurane and ethanol administration on c-Fos immunoreactivity in mice. Neuroscience 316:337–343. 10.1016/j.neuroscience.2015.12.047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM (2004) Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 23 [Suppl. 1]:S208–S219. [DOI] [PubMed] [Google Scholar]
- Stafford JM, Jarrett BR, Miranda-Dominguez O, Mills BD, Cain N, Mihalas S, Lahvis GP, Lattal KM, Mitchell SH, David SV, Fryer JD, Nigg JT, Fair DA (2014) Large-scale topology and the default mode network in the mouse connectome. Proc Natl Acad Sci U S A 111:18745–18750. 10.1073/pnas.1404346111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomasi D, Wang GJ, Volkow ND (2013) Energetic cost of brain functional connectivity. Proc Natl Acad Sci U S A 110:13642–13647. 10.1073/pnas.1303346110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turk E, Scholtens LH, van den Heuvel MP (2016) Cortical chemoarchitecture shapes macroscale effective functional connectivity patterns in macaque cerebral cortex. Hum Brain Mapp 37:1856–1865. 10.1002/hbm.23141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel MP, Scholtens LH, Turk E, Mantini D, Vanduffel W, Feldman Barrett L (2016) Multimodal analysis of cortical chemoarchitecture and macroscale fMRI resting-state functional connectivity. Hum Brain Mapp 37:3103–3113. 10.1002/hbm.23229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC. (2012) Cortical cartography and Caret software. Neuroimage 62:757–764. 10.1016/j.neuroimage.2011.10.077 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Dickson J, Harwell J, Hanlon D, Anderson CH, Drury HA (2001) An integrated software suite for surface-based analyses of cerebral cortex. J Am Med Inf Assoc 41:1359–1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vértes PE, Bullmore ET (2015) Annual research review: growth connectomics–the organization and reorganization of brain networks during normal and abnormal development. J Child Psychol Psychiatry 56:299–320. 10.1111/jcpp.12365 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vetere G, Kenney JW, Tran LM, Xia F, Steadman PE, Parkinson J, Josselyn SA, Frankland PW (2017) Chemogenetic interrogation of a brain-wide fear memory network in mice. Neuron 94:363–374.e4. 10.1016/j.neuron.2017.03.037 [DOI] [PubMed] [Google Scholar]
- Wang D, Buckner RL, Fox MD, Holt DJ, Holmes AJ, Stoecklein S, Langs G, Pan R, Qian T, Li K, Baker JT, Stufflebeam SM, Wang K, Wang X, Hong B, Liu H (2015) Parcellating cortical functional networks in individuals. Nat Neurosci 18:1853–1860. 10.1038/nn.4164 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K, van Meer MP, van der Marel K, van der Toorn A, Xu L, Liu Y, Viergever MA, Jiang T, Dijkhuizen RM (2011) Temporal scaling properties and spatial synchronization of spontaneous blood oxygenation level-dependent (BOLD) signal fluctuations in rat sensorimotor network at different levels of isoflurane anesthesia. NMR Biomed 24:61–67. 10.1002/nbm.1556 [DOI] [PubMed] [Google Scholar]
- Wilks SS. (1938) The large-sample distribution of the likelihood ratio for testing composite hypotheses. The Ann Math Statist 9:60–62. 10.1214/aoms/1177732360 [DOI] [Google Scholar]
- Zoubarev A, Hamer KM, Keshav KD, McCarthy EL, Santos JR, Van Rossum T, McDonald C, Hall A, Wan X, Lim R, Gillis J, Pavlidis P (2012) Gemma: a resource for the reuse, sharing and meta-analysis of expression profiling data. Bioinformatics 28:2272–2273. 10.1093/bioinformatics/bts430 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
80 bilateral regions of interest were used to assess the relationship between FC, CGE, and G. Full names, acronyms, and anatomical divisions were defined by Oh et al., 2014 and the Allen Mouse Brain Connectivity atlas. Download Figure 3-1, TIF file (199.7KB, tif)
Genes that support CGE and FC, without distance correction. Incremental inclusion of genes into CGE matrix without distance correction during rank ordering of gene importance. A subset of genes support the relationship between CGE and functional connectivity. Genes were rank ordered (x-axis) based on their contribution to the CGE-FC correlation (after covarying Euclidian distance). Then, each model predicting FC was refit after incrementally adding each gene to the CGE matrix. The max variance was observed after the inclusion of 445 of the most explanatory genes to the CGE matrix, r2 = .702). Each red line indicates a different permutation for gene expression only, where gene rankings were randomized on each permutation. 1000 permutations are shown. Download Figure 6-1, XLSX file (12.6KB, xlsx)