Hydrogen Bonding Regulates the Rigidity of Liposome‐Encapsulated Chlorin Photosensitizers

Abstract

Liposomal formulations facilitate the administration of hydrophobic drugs, avoiding precipitation and aggregation phenomena when injected in polar solvents. The integration of the photosensitizer into the liposome may alter the fluidity of the system and, thus, modify the delivery process of the drug. Such a change has been observed for the liposomal formulation of Temoporfin, which is one of the most potent chlorin photosensitizers employed in photodynamic therapy. Here, all‐atom molecular dynamics simulations have been performed to identify the nature of the intermolecular interactions that might be responsible of the different lipids freedom of motion when the drug is introduced in the bilayer. It is found that Temoporfin participates as a hydrogen donor in strong hydrogen‐bonding interactions with the polar groups of the phospholipids. The theoretical analysis suggests that the rigidity of drug/liposome complexes can be modulated by considering the different hydrogen‐bond ability of the photosensitizer and the carrier material.

1. Introduction

Photodynamic therapy is a treatment that exploits the interaction of light with a photosensitive drug in the presence of molecular oxygen.1, 2, 3 Such an interaction produces cytotoxic reactive oxygen species that may induce the death of the targeted tumor cells.4, 5 The advantage of photodynamic therapy lies in its potential to achieve high selectivity towards the diseased tissues through the following therapeutic mechanism: the drug is administered to the patient and, after a specific interval, in which the drug accumulates in the tumor tissues, the interested region is irradiated with a source of light with appropriate wavelength.2, 3, 5 Chlorin derivatives are second‐generation photosensitizers widely employed in approved clinical treatments and also in clinical trials.1, 6, 7 These compounds are porphyrin‐based species,8 in which one of the double bonds has been reduced to enhance the light absorption at lower energies,9 in the so‐called therapeutic window.4 The best performance of second‐generation photosensitizers over first‐generation photosensitizers is well illustrated when comparing Temoporfin (mTHPC) to Photofrin®, with the former being 100 times more photoactive than the latter.10, 11

However, porphyrin derivatives present several disadvantages, especially at the time of administration into patients. In polar media, like water or blood, porphyrins tend to form aggregates,11, 12 which are less photoactive13 and considerably diminish the efficacy of the treatment.14 This is the case for mTHPC (see Figure 1 a), currently employed in photodynamic therapy to treat certain types of cancer and precancerous conditions.11, 15, 16 This drug is nowadays administrated as Foscan® (biolitec pharma Ltd.) within an ethanol/propylene glycol mixture and it has shown aggregation and precipitation phenomena at the moment of injection, when the photosensitizer enters the blood stream. Liposomes have been identified as valuable nanocarriers of hydrophobic drugs, favoring the accumulation of the photosensitizer in the tumor tissues and solving the solubility issue in the administration phase of the treatment.17 As shown in Figure 1 b, liposomes consist of an assembly with a hydrophilic inner cavity formed by the phosphate groups of the lipids, which contains water inside, a hydrophobic inner part of the double layer formed by the alkyl chains, and an outer polar spherical surface also formed by the phosphate groups.

Figure 1.

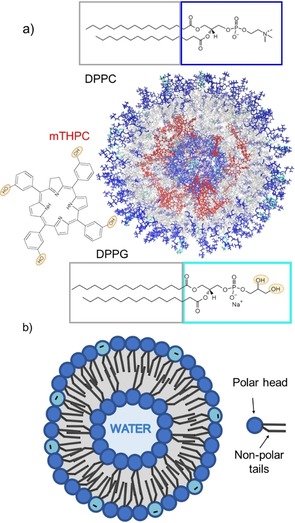
a) Structure of the simulated liposome; the mTHPC molecules are represented in red, the phosphate groups of the DPPC and DPPG molecules are represented in blue and cyan, respectively, whereas the alkyl chains are pictured in grey. The structure has been clipped to show also the inner layer of the double layer. The structural formula of the two phospholipids 1,2‐dipalmitoyl‐sn‐glycero‐3‐phosphocholine (DPPC) and 1,2‐dipalmitoyl‐sn‐glycero‐3‐phosphorylglycerol sodium salt (DPPG) and the Temoporfin (mTHPC) photosensitizer are shown. b) Schematic representation of the structure of a liposome and of a phospholipid, highlighting the polar head and the hydrophobic tails.

The efficacy of liposomal formulations of chlorin derivatives has been demonstrated for mTHPC, in which the drug has been embedded in the non‐polar region of the liposome, as it is the case of the Foslip® formulation. First, these formulations solve the solubility problem, providing an easier administration of the drug to the patient, as the final product can be dispersed in water and administrated orally, intravenously, or through skin permeation.18, 19 Second, Foslip® and other liposome formulations show a higher efficiency with respect to Foscan®, presenting a larger selectivity for tumor tissues with respect to healthy ones and provoking faster dissociation of the tumor cells, which results in more effective growth inhibition.17, 20, 21, 22, 23 More importantly, liposomal formulations of Temoporfin do not manifest any dark toxicity.21, 24 Finally, the liposomal formulation ensures the presence of the drug in its monomeric form, which is the most photoactive species.25, 26

The factors that most influence the success of a liposomal formulation are the loading capacity of the carrier and the release of the drug to the targeted cells, that is, the actual delivery process. Both factors are regulated by the interactions between the vehicle material and the drug. To provide an optimal formulation, such interactions should be of medium strength so that the drug is safely hosted in the carrier, but its release is not hindered. Intermolecular interactions, therefore, play a very important role in the transport and delivery of the drug,27 and the elucidation of the nature of such interactions is relevant to design nanocarriers with optimal properties.

Different molecular compositions for possible mTHPC liposomal formulations have been investigated by differential scanning calorimetry and electron spin resonance spectroscopy.28 The latter has shown that the photosensitizer is located in the hydrophobic part of the double layer and that its presence hinders the motion of the phospholipids, giving more rigid vesicles.28 Thus, the drug–lipid interactions lower the molecular motion of the phospholipids. However, the nature of these interactions, responsible for the high loading capacity of the carrier and its different fluidity is unknown.

Coarse‐grained methods are typically used to investigate the structural behaviour of loaded and pure liposomes.29, 30 However, these methods are not able to provide atomistic details, such as interatomic interactions responsible for the final structural properties of the system. Therefore, in this work, we have performed all‐atom classical molecular dynamics simulations to unveil the nature of the lipid–drug interactions that might be relevant in the liposomal formulation Foslip® as a model for chlorin‐based photosensitizers. We show that hydrogen bonding between the photosensitizer and the phosphate heads of the lipids is the main interaction responsible for the large loading capacity of the carrier and the different mobility shown by the phospholipids in calorimetric experiments and electron spin resonance measurements.28, 31

2. Results and Discussion

2.1. Convergence to a Steady State

The first step in any molecular dynamics simulation of a large system is to obtain an equilibrated structure. However, this is very hard to achieve in liposomes of small size, which are metastable systems that converge very slowly to a steady state.32 Liposomes with diameters smaller than 20 nm have a very high propensity to fuse with other liposomes, forming larger vesicles such that the stress imposed by the high curvature of small spherical shapes, which constrains the lipids to be very tightly packed, is released.33 Therefore, the relatively small‐sized liposome modelled in this work (diameter of 12.6 nm; see Figure 2 a) undergoes very strong curvature effects, which influence the packing of the phospholipids and make equilibration very difficult.

Figure 2.

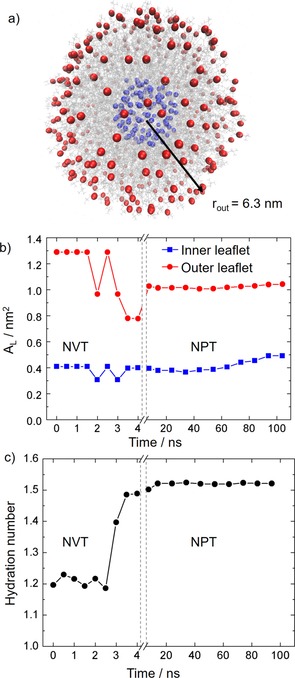
a) Representation of all the phosphate atoms located in the inner shell (blue) and outer shell (red) used to calculate the surface areas in the model liposome. The outer radius of the model liposome is reported in nanometers. b) Time evolution of the area per lipid (A _L) for the inner and outer leaflets of the bilayer along the simulations. c) Time evolution of the hydration number of the lipid polar heads forming the bilayer.

Commonly, coarse‐grained methods are employed to study lipid vesicles, allowing larger sizes (20–34 nm of diameter) and longer simulation times,32, 34 at the price of losing atomistic insight. Even in such cases, the definition of a true steady state is extremely difficult and requires simulation times that can reach hundreds of microseconds.34 Achieving a true equilibrated structure, in fact, would require the simulation of phenomena like the flip‐flop of phospholipids between the inner and outer shell of the double layer as well as water exchange between the inner cavity of the liposome and the surrounding solvent.32

In this work, we have monitored two parameters to analyze the structural quasi‐equilibration of the system: the area per lipid A _L of the two layers of the membrane and the hydration number of the polar heads of the phospholipids. These two properties converge very slowly to a steady value in flat lipid membranes and are, therefore, employed as criteria to define the equilibrium of the system.35 The area per lipid A _L has been calculated considering the two spherical surfaces formed by the phosphorus atoms of the polar heads of the lipid chains, as shown in Figure 2 a. The radius of such spheres was calculated at intervals of 0.5 ns along the heating simulation in the canonical ensemble (constant number of atoms, volume and temperature [NVT]) and at intervals of 10 ns along the simulation in the isothermal‐isobaric ensemble (constant number of atoms, pressure and temperature [NPT]). The average radius (r) obtained for the inner and outer leaflets was employed to calculate the area of the two surfaces defined by the phosphate groups of the lipids (Figure 2 a). Then, the area per lipid is given by the area of the surface divided by the number of lipid molecules of the leaflet (N _L) [Eq. (1)]:

$${\displaystyle A{}_{\mathrm{L}}=\left(4\pi ⟨r{}_{(\mathrm{in}/\mathrm{out})}⟩{}^2\right)/N{}_{\mathrm{L}(\mathrm{in}/\mathrm{out})}}$$ (1)

As seen in Figure 2 b, A _L presents strong oscillations along the NVT heating step, especially for the outer shell of lipid molecules. Instead, in the simulation at constant pressure (NPT), A _L reaches a constant value almost immediately. The area per lipid of the inner leaflet oscillates around 0.4 nm² with a small deviation in the last 20 ns of the simulation, where it slightly increases up to 0.49 nm². This shows that a full equilibrated structure is hard to achieve for relatively small liposomes, as explained above. The A _L value for the outer shell molecule is 1.02 nm² and remains stable throughout the whole NPT simulation. The observed inner‐leaflet structural fluctuations is a consequence of the curvature of the double layer, which influence the stability of the membrane inner leaflet to a larger extent.32

The experimental A _L for flat phospholipids double layers is found in a range of 0.55–0.72 nm².35 However, such values are only valid for very large vesicles where the surface locally approximate a flat bilayer. The small size of our theoretical model induces a high curvature that constrains the inner shell lipids to be very tightly packed, whereas the ones in the outer layer are more loosely arranged. As there is no free lunch, such geometrical alterations introduce an error in the simulated A _L. Previous molecular dynamics simulations,29, 30 employing a coarse‐grained model to describe a liposome, reported A _L values for the inner and outer shells of 0.5 and 0.8 nm², respectively, that is, in better agreement with the experimental estimation, but still affected by the spherical shape of the bilayer.

As intermolecular interactions are relevant for the structural properties of the bilayer,36 we have selected the hydration number as the second parameter to monitor the equilibration process, which directly correlates with A _L. The hydration number represents the total number of water molecules per polar lipid head present in the first solvation shell of the liposome. This has been calculated by integrating the first peak of the radial distribution function of the water molecules and the negatively charged phosphate oxygen atom of the DPPC lipids.35 As seen in Figure 2 c, the hydration number shows important oscillations during the heating simulation, but it converges to a value of 1.52 water molecules after 20 ns in the NPT simulation. We conclude, therefore, that the drug/liposome assembly is relatively well equilibrated after 20 ns of dynamics in the NPT ensemble, attending to the time evolution of the area per lipid and the hydration number, which were recommended convergence criteria.35 Accordingly, the following analyses are performed using frames from the dynamics between 20 and 100 ns.

2.2. Diffusion Coefficients

As shown by electron spin resonance spectroscopy experiments,28 the integration of mTHPC into the liposome induces a lowering in the molecular freedom of motion of the lipids. This change in the mobility is a consequence of the different chemical environment experienced by the lipid chains when they are in the presence of the drug versus when they are located in the pure liposome. The appearance of new intermolecular interactions might induce an increase or decrease of the lipid motion, depending on the strength of the drug–lipid interactions. The lowering of the motion, experimentally observed,28 indicates that the interactions in the loaded liposome are stronger than in the pure one.

To theoretically investigate the effect of the drug on the mobility of the lipids, we have calculated the root‐mean‐square displacement (RMSD) of the lipids along the 100 ns of the simulation in the NPT ensemble by considering different regions of the liposome, defined by the separation between the lipids and a drug molecule (see Figure 3 a). We expect that the lipids in the immediate surroundings of the drug present less fluidity because of possible strong drug–lipid intermolecular interactions. First, the RMSD of the mTHPC molecules (without lipids) has been computed. Then, we have extended the analysis to the surrounding lipid molecules, gradually increasing the distance from the drug molecules between 2 and 10 Å, as sketched in Figure 3 a. The RMSD of the lipids located in the different regions, plotted in Figure 3 b, clearly evidences that the lipid molecules in the immediate surroundings of the drug molecules show less freedom of motion. In other words, the farther the residues are from the drug, the larger is their freedom of motion and, therefore, their displacement along the simulation. This behavior indicates that the lipid molecules interact stronger with the drug than with other lipid molecules, and that their motion is reduced with respect to the situation where they are surrounded by only other lipid molecules. A more quantitative analysis can be performed by calculating the diffusion coefficient D from the mean‐square displacement (MSD), along the simulation time t, using the so‐called Einstein relation [Eq. (2)]:37, 38

$${\displaystyle \mathrm{MSD}=6Dt}$$ (2)

Figure 3.

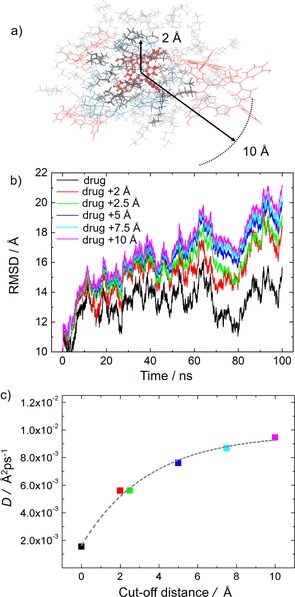
a) Schematic representation of the drug Temoporfin and the surrounding residues used in the RMSD analysis. The molecules represented with bolder lines are found in a sphere of 2 Å radius centered at the drug. Thinner lines represent instead residues inside a sphere of 10 Å radius. b) RMSD of the residues contained in the different size spheres surrounding the drug residues during the NPT simulation. c) Diffusion coefficient reported against the separation from the drug molecules. The color scheme is the same as in (b).

The MSD of the last 80 ns of the simulation is linearly fitted and the slope provides the diffusion constant D of the lipid residues located at different distances from the drug. Figure 3 c shows that the variation of the diffusion coefficient with the separation r from the drug residues can be interpolated by the increasing exponential function D(r)=Ae ^B(r) +D ₀, where A, B, and D ₀ are fitting parameters with values of −0.008 Ų ps⁻¹, −0.289 Å⁻¹, and 0.01 Ų ps⁻¹. This indicates that the diffusion coefficient of the lipid chains increases with the separation between the lipids and the drug, and it reaches the value of 0.01 Ų ps⁻¹ at larger distances, where drug–lipid interactions are less significant or absent and are replaced by lipid–lipid interactions. In addition, the fast increase of D with the distance r from the drug residues (D reaches half of its maximum value already at a drug–lipid separation of only 2.5 Å) confirms that the interactions controlling the system are of short‐range character.

After confirming that the liposome presents larger rigidity due to the intermolecular interactions between the drug and the phospholipids, the next step was to identify the nature of such interactions. To this aim, first, we investigated which fragments of the lipid chains, namely heads or tails, play a more significant role in the interactions with the drug molecules. Thus, the RMSD in the NPT ensemble is computed for the polar heads and the nonpolar tails of the phospholipids. In addition, this analysis (Figure 4) is performed by considering two different regions of the carrier material: 1) lipid chains located in the proximity of a drug molecule within a sphere of 2 Å, and 2) less influenced lipid chains located in a region of 10 Å from a drug molecule (see Figure 3 a). In the case of the residues in the immediate surroundings of the drug molecules (cutoff of 2 Å, Figure 4 a), the RMSD of the drug and the polar heads almost overlap and oscillates around a RMSD of 13 Å. The nonpolar tails, instead, show a larger mobility with an average RMSD value of 20 Å throughout the simulation. The smaller mobility of the polar heads in comparison with the nonpolar tails clearly points to an existing interaction between the polar heads and mTHPC. Considering now the RMSD of the residues at farther distances from the drug (cutoff of 10 Å, Figure 4 b), the coupling between the polar heads and drug molecules is lost, and the tail and head residues show approximately the same freedom of motion. Clearly, the drug–head interactions, which are evident at short distances, vanish at larger separations, where the motion of the lipids is less perturbed by the presence of the drug.

Figure 4.

Comparison of the RMSD of the polar heads and the hydrophobic tails of the lipid molecules in a region of a) 2 Å and b) 10 Å radius around the drug residues. The RMSD of the drug is also reported as reference.

The large number of hydrogen donor and acceptor atoms present in both the drug and polar heads of the phospholipids (Figure 1 a) and the short‐range character of the drug/head interactions, as indicated by the rapid change of the diffusion coefficient of the lipids with the distance from the drug (Figure 3 c), suggest that hydrogen bonding is responsible for the rigidity in the proximity of the Temoporfin molecules.

2.3. Hydrogen‐Bond Analysis

The presence of a network of hydrogen bonds between mTHPC molecules and the polar heads of the lipids would explain the rigidity of the phospholipids in the direct proximity of the drug molecules. Hydrogen bonds are, in fact, interactions that are particularly relevant in a hydrophobic environment, where water molecules cannot easily interfere. Hydrogen bonds are also somewhat directional interactions and can form rather ordered structures. Finally, the presence of hydrogen bonds between the photosensitizer and the carrier material would assure a good loading capacity of the vesicle.27

The polar heads of the DPPC lipids are hydrogen acceptors, whereas the polar heads of the DPPG lipids and the drug molecules can act as both hydrogen donors and acceptors in the formation of hydrogen bonds. Therefore, we can classify the hydrogen bonds as drug–drug, head–drug, and head–head hydrogen bond pairs, see Scheme 1.

Scheme 1.

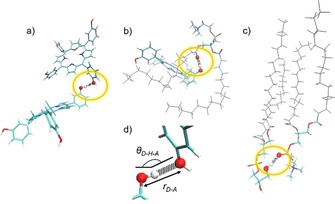
Schematic representation of the three categories considered for the hydrogen‐bond analysis: drug–drug pair forming a hydrogen bond (a), drug–head pair involved in a hydrogen bond (b), and two phospholipids connected through a hydrogen bond between the polar head residues (c). The tails of the phospholipids are pictured in gray, whereas, for the residues involved in the bonds, the color scheme is red for oxygen atoms, blue for nitrogen, tan for phosphate, cyan for carbons, and white for hydrogens. d) A zoom on the atoms involved in the hydrogen bond (encircled in yellow in the previous panels), with the geometrical parameters shown.

According to the coupling of the polar head and the drug motion found in the analysis of the RMSD reported in Figure 4 a, the drug–head hydrogen bonds are strong enough to lower the freedom of motion of the phospholipids.

The strength of a hydrogen bond is intimately related with the geometrical parameters of the atoms involved in the interaction, specifically, with the hydrogen donor–hydrogen acceptor distance r _D‐A and with the angle θ _D‐H‐A formed by hydrogen donor, hydrogen atom, and hydrogen acceptor shown in Scheme 1 d. Table 1 shows the total number of hydrogen bonds found along the full simulation, the number of hydrogen bonds that last for more than half of the simulation time, the total number of fragment pairs that can potentially form hydrogen bonds, and the average values of the geometrical parameters for the different categories of hydrogen bonds. We consider a hydrogen bond formed when r _D‐A is smaller than 3 Å and θ _D‐H‐A is larger than 135°. As reported in Table 1, the number of long‐lived head–drug hydrogen bonds (27) is larger than the number of long‐lived head–head hydrogen bonds (12), despite the number of head–drug pairs (113050) being smaller than the number of head–head pairs (116886). Although the number of hydrogen bonds depends on the number of species considered in the box, the present numbers clearly indicate that the lipid chains are more prone to participate in hydrogen bonding with the drug than with other lipid chains. In addition, the head–drug hydrogen bonds are not only more abundant but also stronger, as indicated by the smallest r _D‐A value (2.67 Å) and the largest θ _D‐H‐A value (162°).

Table 1.

Number of hydrogen bonds (HBs) identified along the dynamics, HBs that last for more than half of the simulation time (long‐lived HBs), total number of interacting pairs, average value of the D–A distance r _D‐A and average value of the d–H–A angle θ _D‐H‐A for the three hydrogen bond categories. The geometrical parameters are shown in Scheme 1 d.

HB pair [a]	Total HBs	Long‐lived HBs	Number of pairs	r D‐A [Å]	θ D‐H‐A [°]
H–H	424	12	116 886	2.70	160
H–D	249	27	113 050	2.67	162
d–D	76	7	780	2.85	157

[a] H–H stands for a head–head pair, H–D for a head–drug pair, and D–D for a drug–drug pair.

A more quantitative picture is obtained by considering the distribution of the hydrogen‐bond lifetimes and geometrical parameters obtained by the analysis of all hydrogen bonds formed along the simulation. Figure 5 a shows the number of drug–drug, head–drug, and head–head hydrogen bonds, grouped according to their lifetimes as a percentage of the total simulation time. Head–head hydrogen bonding dominates at short lifetimes (less than 10 % of simulation time), whereas they are surpassed by the drug–head hydrogen bonds at longer lifetimes, especially at lifetimes over 70 % of the simulation time. The drug–head distribution in Figure 5 a presents a minimum at a life time of 50 %; such a feature is just a result of the way the distribution was built and has no physical meaning.

Figure 5.

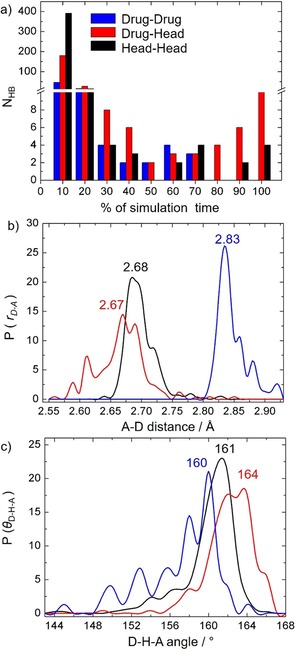
a) Number of drug–drug, drug–head, and head–head hydrogen bond pairs grouped according to their persistency in percentage during the simulation time. b) Probability distribution of donor‐acceptor distances r _D‐A. c) Probability distribution of donor‐hydrogen‐acceptor angles θ _D‐H‐A.

To compare the strength of the interactions between the three different pairs of residues, the probability distribution of r _D‐A and θ _D‐H‐A is depicted in Figures 5 b and 5 c, respectively. The r _D‐A distribution peaks at a shorter distance for the drug–head interaction (2.67 Å) than those for the head–head (2.69 Å) and the drug–drug (2.83 Å), whereas the θ _D‐H‐A distribution peaks occur at larger angles for the drug–head interaction (162° and 164°) than for head–head (161°) and the drug–drug (160°) ones. Therefore, both the hydrogen‐bond lifetimes and the probability distribution of the geometrical parameters indicate that the hydrogen‐bond strengths follow the order drug–head > head–head > drug–drug. The stronger hydrogen bonds found between Temoporfin and the polar heads explain why the mobility of the phospholipids is smaller in close proximity to the drug. In addition, the hydrogen‐bond behavior also explains the good loading capacity of the liposomes and the loss of mobility of several liposomal formulations of mTHPC.28

Finally, we discuss the reasons behind the stronger interactions between the photosensitizer and the lipid heads than between different lipid heads. A closer inspection of the atoms involved in hydrogen bonding reveals that, in the drug–head interaction, mTHPC plays the role of hydrogen donor from its phenol moieties virtually all the time, whereas, in the head–head interaction, the hydrogen donor atoms are the O atoms of the ethylene glycol moiety of the DPPG lipids (see Figure 1 a). Owing to the electron‐withdrawing effect of the aromatic ring of the phenolic substituent, mTHPC is a better hydrogen donor than the glycol moiety of the DPPG. In general, aromatic alcohols are better hydrogen donors than aliphatic ones. This is the reason why phenol acts as a hydrogen donor and methanol as a hydrogen acceptor in the phenol–methanol dimer.39 Based on our analysis, one can conclude that the rigidity of the liposomal formulation of mTHPC, closely related with the loading and release capacity of the liposome, can be modulated considering the strength of the hydrogen bonds that the phenol moieties of the drug could form with phospholipids suitable for liposomal formulations.

This consideration can be extended to different photosensitizers baring H‐bonding groups in their substituents. In case of phenol moieties, further functionalization of the photosensitizer can be pursued. If the functionalization enhances the electron‐withdrawing ability of the aromatic ring, the drug would be a better hydrogen donor and the drug/liposome assembly would be more stable. Contrarily, if the aromatic ring loses its electron‐withdrawing ability upon functionalization, the drug is a less effective hydrogen donor and the drug/liposome assembly would be less stable. However, it is important to note that such a functionalization should not modify other properties of the drug, for example, its hydrophobicity or the energy of the electronically excited states and, thus, the photosensitization efficiency and mechanism of the drug should not be altered.

3. Conclusions

In this work, we have performed all‐atom molecular dynamics simulations to unravel the reasons behind the smaller membrane fluidity experimentally found for several liposome formulations of the photosensitizer Temoporfin,28 a prototypical chlorin photosensitizer. The analysis of the motion of the different residues composing the liposome and the calculation of diffusion coefficients of the lipid chains in the immediate surroundings of the photosensitizer have shown that the interactions that confer rigidity to the drug/liposome assembly are of short‐range character. These interactions are identified as relatively strong hydrogen bonds between the photosensitizer and the polar heads of the phospholipids. Owing to electron withdrawing effects, the drug is a powerful hydrogen donor and, thus, the rigidity of the liposome induced by the drug into the phospholipids in its immediate surroundings derives from the tenacity of such interactions. Our theoretical analyses suggest that the stability of Temoporfin liposomal formulation could be also ascribed to the strength of the hydrogen bond formed by the drug and the carrier material. Such considerations on the hydrogen‐bonding capability of the drug and the phospholipids can be extended to other chlorin photosensitizers and, thus, can be relevant to design new drug formulations, as intermolecular interactions between the drug and the nanocarrier affect the loading capacity of the carrier, the drug release process, and the pharmacokinetic properties of the drug.40

Computational Details

The liposome initial structure was built with the Packmol software package,41 with a composition of DPPC/DPPG phospholipids with a ratio of 9:1 (w/w) and with a molar ratio of lipid/mTHPC of 12:1. The inner leaflet of the liposome bilayer is formed by 118 phospholipid molecules confining 472 molecules of water in the inner cavity. The number of water molecules placed in the inner cavity was calculated so that the density of the solvent in the inner cavity equals the one that surrounds the liposome. The second leaflet of the vesicle is assembled from 366 lipid molecules, resulting in a liposome with a diameter of about 126 Å. The liposome also contains 40 molecules of Temoporfin, placed in the hydrophobic region of the double layer, based on previous electron spin resonance spectroscopy measurements.28 The resulting drug/liposome complex was solvated with 109 387 water molecules confined in a cubic box of 83 Å side. Na⁺ counter ions were added to neutralize the DPPG negative charges and NaCl was added to reach a salt concentration of 0.15 M.

The energy of the system was first minimized in seven steps. In the first step, only 200 residues of the liposome were minimized, whereas the other residues were spatially constrained by employing a harmonic force constant of 50 kcal mol⁻¹ Å⁻². In each of the next five steps, 200 more residues were allowed to move during minimization together with the ones already optimized in the previous steps. In the final minimization step, the whole liposome was minimized without any constrains. Each minimization calculation consists of 10 000 steps, where the first 5000 were performed by employing the steepest descent algorithm while the last 5000 were performed by employing the conjugated gradient algorithm. The system was then slowly heated in the canonical ensemble (NVT ensemble) from 0 to 300 K in four different simulations of 1 ns each. In the first three heating simulations, the temperature was increased by 100 K intervals from 0 to 300 K. During the three heating steps, the motion of the residues forming the liposome was constrained with decreasing harmonic force constants of 10, 5 and 1 kcal mol⁻¹ Å⁻². The last heating simulation was performed at a fixed temperature of 300 K and with no constraints applied on the motion of the drug/liposome assembly. Afterwards, the system was run in the isothermal‐isobaric ensemble (NPT ensemble) to equilibrate the density of the system and the structure of the liposome for 100 ns, and the snapshots were printed every 20 ps for analysis. As discussed above, after 20 ns, the system reached a metastable state and, therefore, the last 80 ns of the simulation were employed in the analyses.

For all of the simulations, periodic boundary conditions were applied and a time step of 2 fs was employed. The SHAKE algorithm42 was used to freeze bonds involving H atoms. The Langevin thermostat was used with a collision frequency gamma of 1.0 ps⁻¹ while the pressure was kept fixed at 1 atm with the Berendsen barostat and isotropic position scaling. For the non‐bonded interactions calculation, a cutoff of 10.0 Å was employed together with the particle‐mesh Ewald method to calculate the coulombic interactions.43 The phospholipids were described by the Lipid1744 force field, available in the AmberTools17.45 The intramolecular and Lennard–Jones parameters of the drug were taken from the general Amber force field.46 The restrained electrostatic potential (RESP) charges were computed by density functional theory, employing the B3LYP47 functional and the 6‐31G* basis set48 using the Gaussian0949 software package. We employed the TIP3P model50 for the water molecules and appropriate Amber parameters to describe the NaCl ions.51 All the simulations were performed with the GPU‐based module PMEMD implemented in AMBER16.45

The visualization of the simulation trajectories and the RMSD calculations were performed with the visual molecular dynamics (VMD) program,52 the hydrogen‐bond analysis was performed with the CPPTRJ software53 by employing a cutoff of 3 Å for the D–A distance and 135° for the d–H–A angle. By using the Einstein relation, Equation (2), the RMSD curves were linearly fitted to calculate the diffusion coefficient of the drug and lipid molecules.

Conflict of interest

The authors declare no conflict of interest.

M. D. Vetta, L. González, J. J. Nogueira, ChemistryOpen 2018, 7, 475.