Finding optimal mentor-mentee matches: A case study in applied two-sided matching

Abstract

Two-Sided Matching is a well-established approach to find allocations and matchings based on the participants' preferences. While its most prominent applications are College Admissions and School Choice problems, this paper applies the concept to the matching of mentors to mentees in a higher education context. Both mentors and mentees have preferences with whom they ideally want to be matched, as well as who they want to avoid. As the general formulation for these types of preferences is NP-hard, several existing approximation algorithms and heuristics are compared with respect to their ability to find a matching with desirable properties. The results show that a combination of evolutionary heuristics and local search approaches works best in finding high-quality solutions, allowing us to find mentor-mentee pairs which are close to the respective ideal match.

1. Introduction

Two-Sided Matching approaches are a well-established process to coordinate markets and resource allocations based on participants' preferences. For example, they are commonly applied in School Choice (see [1]), College Admission scenarios (see [2]), and in innovative scenarios such as (dynamic) resource allocation in wireless networks [3], [4]. In these settings, one side provides resources (e.g., schools and colleges offer places) and the other side is interested in obtaining these resources (e.g., being admitted to the respective school or college). At the same time, both sides have preferences for their most preferred choices, expressed by an ordinal ranking where a higher rank indicates that a match would be preferred.

The matching of mentors and mentees in a professional and/or higher education lends itself as an application of Two-Sided Matching. A good relationship between mentors and their mentees can have fundamental effects/benefits for mentees' careers, hence finding a good mentor is crucial. In settings where there is a pool of potential mentors as well as interested mentees, calculating an allocation (match) which satisfies both sides and has favorable properties can be of substantial complexity. Manual calculation of the matching in this case is challenging, both in terms of required work as well as the achievable quality of the solution. Hence, we make use of computational methodologies to find a good solution for mentors and mentees.

This paper has two main goals. First, we want to apply Two-Sided Matching procedures to find a high-quality solution which is beneficial for as many participants as possible. For this, we have to define which criteria we want to use for evaluation. Common criteria are stability of the solution, the closeness to the most preferred choice, and the number of mentor/mentee pairs that can be successfully matched. Hence, the goal is to find a mentor-mentee matching that matches as many pairs as possible, while achieving desirable solution qualities and matching the participants close to the respective most preferred option. Second, for the given real data, we want to analyze which algorithm performs best for the given set of criteria. For this, we consider several approximation algorithms and heuristics that have been developed for this setting, offering solutions with different quality trade-offs. We apply them to a set of preferences obtained by a mentor-mentee matching at a university program, thus representing realistic preferences as they occur in similar settings. Our analysis shows that heuristics, which can simultaneously optimize multiple objectives, offer the best solution quality for the given setting. In particular, high-quality solutions can be found that, on average, match the participants close to their most preferred options.

The contribution of this paper is twofold. First, we show that Two-Sided Matching is a useful approach for problems such as matching mentors and mentees at a workplace, and we provide a recommendation for the type of algorithm that should be used in this case. Second, we extend the current literature on Two-Sided Matching by evaluating a real data set, collected based on real preferences from a mentor-mentee matching at our university.

The paper is structured as follows. After introducing Two-Sided Matching fundamentals in Section 2, we describe the algorithms and preferences used in this study in Section 3. The evaluation of solution quality differences of the various approaches and their implications are discussed in Section 4. Section 5 provides an overview on related work, and Section 6 concludes with an outlook on further work.

2. Theory

We consider the matching of a set of mentors, X, and mentees, Y, in a university advising program that encourages women to pursue a career in computing. The task at hand is to find a match of mentors with potential mentees, $\langle X,Y\rangle$ consisting of pairs of individuals $\langle x,y\rangle$ where $x\in X$ and $y\in Y$, while aiming to ensure that both sides are as happy with the matching as possible. As the number of mentors and mentees does not have to be equal, a match does not guarantee that each mentor or mentee will be matched. However, as in our setting the number of mentors is higher than the number of mentees, our goal is to find a mentor for each mentee.

Both mentors and mentees have preferences $P_i=(P_{i,j_1},\dots ,P_{i,j_n})$, $j\in Y$ and $i\in X$, or $i\in Y$ and $j\in X$ with whom they want to be matched. The preferences are represented by ordinal ranks, where $P_{i,j}$ denotes the preference rank that user i has towards user j. The most preferred option (match) has rank 1, the second-most preferred match rank 2, and so on. The preferences represent transitive priority structures ≿ , where each user of the opposite side is ranked according to its priority. The asymmetric part ${\succ }_i$ indicates a strict priority, whereas the symmetric part indicates an indifference. For example, $j_1\succ j_2$ means $j_1$ is preferred over $j_2$, whereas $j_1\sim j_2$ means the user is indifferent between $j_1$ and $j_2$. The preference towards being unmatched is defined as $P_{i,\varnothing }$. A preference profile is said to be complete if $j\succ \varnothing$ for all users j, meaning that the user is willing to be matched with any user of the other side. If $\varnothing \succ j$ for some user j, the preference profile is said to be incomplete. This indicates that user i wants to remain unmatched rather than being matched to user j. A preference profile is strict if $\forall j\in X$ $(j\in Y)$, ${\succsim }_j$ is asymmetric. If $j\sim k$ for some users j and k, then the preference profile is said to have indifferences, or ties.

In our case, we allow for preferences that are both incomplete and include ties. Mentors are allowed to place restrictions on the specific mentees that they are willing to supervise (e.g., some mentors only want to be matched with undergrad students). Similarly, in our setting mentees provide the names of up to 5 mentors that they would prefer. While this restriction seems arbitrary, we decided to limit the number of mentors that each mentee has to rank to reduce the time (and complexity) for the mentees to form a ranking out of a large pool of mentors. Due to these restrictions, preferences on both sides are incomplete. Furthermore, mentees are allowed to be indifferent between their listed options. For example, they might state that some mentors are equally preferred, while the remaining mentors are less preferred. Mentors do not provide a further preference ranking, i.e., are by default indifferent between all allowed options (i.e., allowed mentees after the previous restrictions).

Based on these stated preferences, Two-Sided Matching calculates a match $\langle X,Y\rangle$ where mentors are matched with mentees (or not matched at all). To evaluate the quality of a matching between mentors and mentees, we use following standard criteria to consider the solution quality: stability, the number of matched pairs, and the average welfare.

Stability is the core requirement of practically all approaches for Two-Sided Matching. In a stable solution, no participant can be better off (be matched with a more preferred mentor/mentee) by switching their allocated partner with another mentor/mentee pair. Proposed mentor-mentee matches may fail in the sense of become undone after having been proposed, because some participants see better opportunities. Specifically, a match $\langle X,Y\rangle$ containing at least one pair of matched individuals $\langle x_1,y_1\rangle$ and $\langle x_2,y_2\rangle$, $x_1,x_2\in X$ and $y_1,y_2\in Y$, where $x_1$ prefers $y_2$ to $y_1$ as a partner and $y_2$ prefers $x_1$ to $x_2$ as a partner is said to be unstable. If the unhappy participants, here $x_1$ and $y_2$, are aware of this, they would break their proposed mentor relationships and form a new pair. Stability is important as otherwise even one unstable pair can lead to chaotic unraveling [5]. Note that stability is not further described as solution property as all algorithms considered in this paper yield stable solutions, thus removing the requirement to compare the stability of the different approaches.

The second criterion is the number of matched pairs, i.e., the number of pairs $\langle x,y\rangle$ where x is a mentor and y is a mentee. This might seem obvious, yet finding a solution with the maximum number of matched pairs is itself an NP-hard problem [6]. In our context, we aim to provide a mentor-mentee match for as many mentees as possible as it is not guaranteed that a stable solution exists where all mentees are matched.

As a third criterion, Welfare describes the average preference rank that each participant is matched with. That is, for each matched participant we sum up the preference rank $P_{ij}$ of their respective match and calculate the mean matched preference rank. For example, given that the highest (most preferred) rank is 1, a welfare score of 2 would mean that participants are, on average, matched with their second most preferred choice. While welfare is an important criterion for the solution, it is not commonly considered by many approximation algorithms or heuristics in the general case of incomplete preferences with ties, due to the NP-hardness of the problem. However, it can be easily included in evolutionary algorithms as additional objective (see e.g., [7]).

Finally, Equality considers if both sides of participants are treated equally. For each matched pair of mentor and mentee, the rank of the respective matched partner is calculated. The equality score for a pair is defined as the difference of these two ranks. A solution is considered to be more equal if both mentor and mentee are close in the respective other preference ranking. A solution that is completely equal would have score of 0 in this case.

Given these solutions quality criteria, we aim to find a stable solution that matches as many mentees as possible, while at the same time matching each participant as close to their most preferred choice as possible. Several algorithms have been suggested for this case, and they are described in the next section.

3. Methodology

Given the preferences and solution evaluation criteria introduced in the previous chapter, we compare a set of different algorithms in their ability to find a good solution for this NP-hard problem. As a baseline, we use the first and most famous approach in Two-Sided Matching: The Deferred Acceptance (DA) algorithm [8]. Having been developed to find a stable solution in case of complete preferences without ties, it does not guarantee that the maximum number of mentor/mentee pairs are found in case of incomplete preferences with ties. However, by breaking the ties (even in an arbitrary fashion), the DA can calculate a stable solution based on this tie breaking, which produces a stable solution under the original preferences (see, e.g., [6]). We use this approach of arbitrary tie breaking as a baseline for our evaluation. In addition to the DA, we compare two general sets of approaches that aim to find a solution with as many matched pairs as possible: Approximation algorithms and heuristics.

3.1. Approximation algorithms

Approximation algorithms provide a guaranteed performance with respect to the number of matched pairs. In other words, given the actual optimal solution (the one with the highest number of matched pairs), the calculated solutions are within a certain boundary to this optimal solution. We consider following approaches that have been proposed in the previous years:

• •Shift: [9] describe an approximation algorithm for this case, in the following abbreviated as Shift. For certain preference structures, this algorithm provides non-trivial quality bounds for finding the stable match of maximum size. Shift operates through breaking indifferences in a systematic manner and applying the DA on the resulting set of strict preferences. In particular, if indifferences occur on both sides of the market, Shift guarantees non-trivial quality bounds if the length of indifferences is at most 2.
• •Király: [10] presents an algorithm with a 5/3 approximation ratio in the general stable matching case, and a 3/2 approximation ratio when ties are only allowed on one side.
• •McDermid: [11] presents an algorithm that improves upon the algorithm by [10] by providing a 3/2 approximation ratio, which is the best known approximation ratio for the general case without restrictions on tie lengths.
• •GSModified: [12] presents another algorithm with the same 3/2 approximation ratio as the algorithm by [11], yet with an additional improvement in runtime.

3.2. Heuristics

In contrast to approximation algorithms, heuristics do not provide a guaranteed solution quality. However, it is less clear how the algorithms perform on average. Hence, we consider following heuristics:

• •LocalSearchSMTI: [13] present local search heuristics to solve the generalized stable matching. They start with solving the relaxed version of the problem (assuming complete preferences), thereby potentially introducing instability, and then deleting unstable pairs through an iterative process until stable solutions are found.
• •Genetic Algorithm in combination with Threshold Acceptance: [7], [14] suggest the use of Genetic Algorithms (GA) for the general problem with incomplete preferences and ties. The GA is initialized with a set of 50 different (but stable) starting solutions, which are calculated by arbitrary tie breaking and using the DA to calculate a stable solution. These starting solutions are then evolved by using mutation and crossover operators. Crossover operators take two existing stable solutions, exchange certain (randomly selected) parts of the respective solution, and uses the resulting new solutions in the next evolution step. Mutation operators randomly switch participants in two matched pairs, resulting in local changes to the solution. The GA typically uses the best solution of the population after 100 evolution rounds. After this initial GA, a Threshold Accepting (TA) algorithm is used to further improve the solution quality. The TA evaluates small adjustments to the solution (similar to the Mutation in GA) in every round until no improvement can be found. TAs are efficient in finding local improvements, as shown in [14], and well suited to complement the GA.

  We use two variants of the heuristic for the evaluation, depending on the set of starting solutions: GATA uses Deferred Acceptance to calculate starting solutions, evolves them, and uses a subsequent TA approach to optimize the best GA solution. GATA-Mixed is similar, yet uses a mix of DA, Király, McDermid, GSModified, and LocalSearchSMTI solutions.

3.3. Algorithm complexity and runtime

Due to the NP hardness of the underlying problem, it is necessary to consider the runtime and complexity of the various algorithms used to calculate the solutions. While the runtime is of less concern for the comparably small dataset at hand, it is a relevant aspect when scaling the approach to hundreds or even thousands of participants.

Table 1 provides an overview of each algorithm's complexity. In general, algorithms that explicitly check whether or not a match is stable include the complexity factor L, the sum of the lengths of the preferences. This stems from the requirement to check for the stability of the solution, and no algorithm is known to run in less than $O(L)$ for this. For example, the DA algorithm as well as Shift and GATA all check for stability in (some of their) calculation steps. Shift additionally depends on the factor ${\tau }^2$, where τ represents the length of ties (indifferences) in the preferences. Similarly, the GATA heuristic additionally depends on the population size factor p, although this can be arguably neglected for complexity considerations as it usually is a fixed factor of 50. The runtime of the Király, McDermid, and GSModified algorithms also depend on L (as well as the number of participants n for McDermid). Finally, the LocalSearchSMTI algorithm promises an $O(n⁎log(n))$ runtime growth, although the heuristic needs to calculate one stable solution first (which again could require $O(L)$ depending on the algorithm used).

Table 1.

Computational complexity of considered two-sided matching algorithms.

Type	Authors	Abbreviation	Complexity
No Guarantee	[8]	DA	$O\left(L\right)$
Approximation	[9]	Shift	$O\left({\tau }^{2}L\right)$
Approximation	[10]	Kiraly	$O\left(L\right)$
Approximation	[11]	McDermid	$O\left(n^{3/2}L\right)$
Approximation	[12]	GSModified	$O\left(L\right)$
Heuristic	[13]	LocalSearchSMTI	$O(n\log (n))$
Heuristic	[7]	GATA / GATA-Mixed	$O\left(pL\right)$

Considering the runtime of the algorithms, due to the small problem size all algorithms were able to compute the solutions for the given preferences in less than 5 seconds. Individual runtimes varied slightly due to the different setup of the algorithms, yet can be considered negligible for the given problem.

3.4. Preferences

For the preferences, we used a set of real preferences coming from a mentor-mentee matching at our university. For the given setting, our set of participants consists of 29 mentees and 31 mentors who wanted to participate in a college-wide program. After an initial meeting, mentees provided a preference ranking for mentors based on common (research) interests and other considerations. As described above, the mentees were allowed to list up to 5 mentors, and were allowed to include ties between two or more mentors. Roughly half of the mentees listed only strict preferences (no ties), while only 8 listed less than 5 mentors. On the mentor side, 7 mentors indicated that they are willing to be matched with more than one mentee. In this case, the preferences were duplicated into a new ‘dummy’ mentor with the same preference structure as the ‘real’ mentor, effectively duplicating the preference structures for these mentors.

3.5. Simulation

To evaluate the different algorithms, we use a simulation approach with 100 independent repetitions and calculate the solution quality for each algorithm. This is necessary as all algorithms utilize certain random procedures in their calculations, resulting in a potentially different solution per run. In each run, we compute the resulting match for each algorithm, and calculate the solution quality criteria for the matches. In the end, the results for the number of matched pairs as well as the average welfare and equality of the solution is calculated and saved.

4. Results

In this section, we compare the performance of the different solution approaches with respect to the three previously described metrics: Number of matched pairs, average welfare of the match as well as the average equality. It is noteworthy that the approximation algorithms in the previous section are developed to only focus on the first criterion, the number of matched pairs. Indeed, for the general matching problem with indifferences and incompleteness, [9] showed that creating algorithms with guaranteed quality boundaries is an NP hard problem in itself, which explains the lack of approximation algorithms that consider welfare and equality in addition to the number of matched pairs. One of the main advantages of using heuristics such as GATA is that they are able to include these additional criteria, even though they cannot provide performance guarantees. The main reason why we compare the algorithms with the additional two criteria is that they have strong influence on the participants' perception of the solution, i.e., how satisfied they will be.

4.1. Number of matched pairs

The maximum number of matched pairs in our case is 29, as stable solutions have been found where all 29 mentees were matched. Hence, we can compare the average performance of the algorithms against their ability to find solutions with 29 matched pairs. Note that even though some algorithms find solutions with 29 matched mentees in some iterations, the existence of random (decision) procedures in each algorithm leads to potentially different solutions in each iteration.

Figure 1 shows the average number of matched pairs, i.e., the number of matched mentees in our case (since we have less mentees than mentors), in addition with error bars indicating the standard deviation for the given 100 iterations. Several observations are notable. First, the Deferred Acceptance algorithm is outperformed by the others who specialize on finding a large stable match. Second, the heuristic using a Genetic Algorithm with mixed initial solutions and a subsequent Threshold Accepting approach (GATA Mixed) performs best, with the LocalSearchSMTI (LSMTI) and GSModified procedures being close behind. Third, a comparison of GATA (starting solutions computed by DA) and GATA Mixed (starting solutions with DA and approximation algorithms) reveals that adding a more diverse set of starting solutions for the Genetic Algorithm increases the ability of the heuristic to find good solutions in this case. In addition, using approximation algorithms as a seed for subsequent heuristics seems to be a profitable approach, as they outperform the initial approximation algorithms. A Kruskal–Wallis and subsequent Dunn test with Bonferroni adjustments for the algorithm differences based on the 100 simulation runs shows that GSModified, LocalSearchSMTI, and GATA-Mixed significantly increase the number of mentees matched ($p-value<0.001$), and that no statistical difference can be found between the three approaches.

Figure 1.

Number of matched pairs found by algorithms.

4.2. Welfare

The solution metric Welfare looks at how closely the average participant is matched to the most preferred solution. While calculating a theoretical optimum for the given preferences is infeasible (due to the NP-hardness), values closer to 1 (the most preferred match/preference rank) are better, allowing for a comparison between algorithms.

Figure 2 shows the Welfare for each algorithm, averaged over the 100 repetitions. Error bars with the standard deviation of Welfare scores are included as well. Note that the algorithms are sorted based on their performance to find a high number of matched pairs, i.e., their performance in Figure 1. Several things can be observed. First, the heuristics GATA and GATA-Mixed, which performed well/best for the first solution criterion, consistently outperform the other approaches. While they achieve an average matched rank of 1.81 and 1.86, respectively, the other algorithms achieve a Welfare of 1.95 and higher. Second, and particularly striking, is that the second best performing solution, LocalSearchSMTI, yields the worst Welfare results with a score of 2.53. In a direct comparison between GATA-Mixed and LocalSearchSMTI, the average user is matched 0.67 preference ranks worse in the latter algorithm. While LocalSearchSMTI does a superb job at finding additional matched pairs, apparently it does so by sacrificing the average matched rank of the participants. In contrast, the heuristic approach GATA-Mixed seems to find good solutions with simultaneous good characteristics in Welfare. The GSModified algorithm is closer to the GATA-Mixed welfare score, indicating a better performance as compared to LocalSearchSMTI. Similar as before, a Kruskal Wallis and follow-up Dunn test shows that GATA and GATA-Mixed significantly improve the Welfare score of the solution compared to the other algorithms ($p-value<0.001$).

Figure 2.

Welfare score as average matched rank for participants.

While the Welfare metric considers the average matched rank for all participants, it is also worthwhile to consider the solution quality with respect to the lowest rank that any mentee is matched with, i.e., the mentee that is worst off in the given solution. Figure 3 shows the worst preference rank for mentees over all matched pairs, averaged over the 100 repetitions. The error bars in the picture capture the standard deviation of this metric. Interestingly, it can be observed that DA yields, on average, the lowest worst rank, whereas the best performing algorithms for the other metrics, GSModified, LocalSearchSMTI, and GATA-Mixed, yield worse performance in this case. However, this seems to be a trade-off as the DA matches less mentees on average. The worse ranks for GSModified, LocalSearchSMTI, and GATA-Mixed in Figure 3 indicate that stable solutions which match more mentees in total lead to the situation where some of the mentees are matched with less preferred partners. From an overall perspective, however, the performance of GATA-Mixed with respect to number and welfare of matched mentees seems to be the preferred choice.

Figure 3.

Average worst preference rank for mentees.

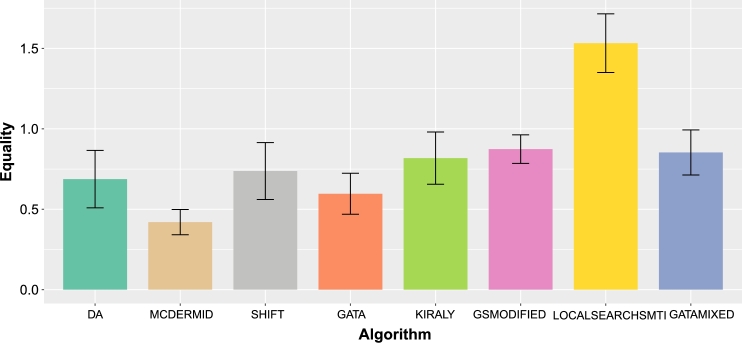
4.3. Equality

Considering Equality, i.e., if both mentors and mentees are treated equally by the solution with respect to the preference rank that their partners have, Figure 4 shows the respective equality scores. For example, an Equality score of 0.85 for GATA-Mixed indicates that, on average, the difference between the preference ranks for the partner that each mentor and mentee is matched with is 0.85. Interestingly, in this case the McDermid approximation algorithm seems to yield the most equal solutions, whereas the previously best performing algorithms GATA-Mixed, GSModified, and in particular LocalSearchSMTI yield less equal solutions.

Figure 4.

Average equality score for the algorithms.

This result shows again that there are trade-offs in the performance of the algorithms with respect to different metrics. Overall, however, when concentrating on the main criteria number of matched pairs and Welfare, GSModified, LocalSearchSMTI and especially GATA-Mixed seem to provide the best overall performance. Table 2 summarizes the results for the number of matched pairs, Welfare, as well as Equality.

Table 2.

Comparison of the algorithms with respect to number of matched pairs and welfare.

Algorithm	Average number of matched pairs	Average welfare	Worst matched rank	Equality score
DA	25.28	2.43	3.81	0.65
McDermid	26.66	1.97	3.91	0.44
Shift	27.20	2.06	4.1	0.72
Király	27.90	1.99	4.35	0.79
GATA	27.95	1.81	4.26	0.62
GSModified	28.67	1.95	4.78	0.87
LSMTI	28.72	2.53	4.68	1.48
GATA-Mixed	28.95	1.86	4.3	0.85

5. Related work

Related work in Two-Sided Matching can be broadly categorized into solutions for different preference properties and solution quality criteria, and the analysis of preference manipulation strategies.

Regarding preference properties and solution quality, we have to distinguish between complete and incomplete preferences as well as the introduction of ties (indifferences). On one hand, the DA can be used in all scenarios to compute a stable solution. On the other hand, including additional solution criteria leads to considerably more complex problems. For example, [15], [5] showed that the number of stable solutions for a given preference set can be large, sometimes even exponential. With the exception of complete preferences without ties, where there are polynomial-time algorithms to compute the welfare-best [16] and approximately fairness-best solutions [17], finding the welfare-best or fairness-best stable solution is generally an NP-hard problem and sometimes even hard to approximate [18]. For the most general case of incomplete preferences and allowed indifferences, the common goal is to find stable solutions that match as many participants as possible. For this specific case, approximation algorithms have been developed that provide lower-bound quality guarantees for the solutions [11], [10], [12]. In addition, other approaches that aim to increase the solution quality are heuristics such as Genetic Algorithms with multi-objective target functions [19], [20], [7]. While heuristics do not provide lower bound quality guarantees, they have been shown to work well on average and offer the flexibility to optimize multiple solution criteria simultaneously. In another approach, Erdil and Ergin [21] introduced an extension to the DA that can cope with ties in preferences. Their algorithm tries to find potential Pareto-improvement cycles in a given solution which might improve the overall quality of the solution.

A second line of research in Two-Sided Matching considers the occurrence and practical implications of preference manipulation. While finding stable solutions is the de-facto standard [22], it can be shown that algorithms which always find stable solutions are not incentive compatible [23], [2]. This implies that for these algorithms, at least some of the participants have an incentive to submit manipulated preferences that do not reflect their true preference ranking. Preference manipulation is an important consideration due to the effects on both participants and the overall solution quality. On one hand, individual participants have to decide whether or not and how to manipulate the preferences. While theoretical results show that preference manipulation is beneficial for some participants [24], the results do not provide guidance on how much and in which circumstances to manipulate. On the other hand, manipulation can also affect the overall solution quality. As the algorithms calculate stable solutions based on the submitted (and potentially manipulated) preferences, the resulting solution is not necessarily stable under the true preferences. The effects of manipulation can be severe, as evidenced by schools that have been closed due to being ranked low in the School Choice problem [25]. The most common manipulation strategy is truncation, where participants submit a shortened preference ranking by leaving out undesired potential matches. Theoretical and experimental studies have shown its prevalence and the implications on the overall system [26], [27], [28].

6. Discussion & conclusion

This article considers the matching of mentors and mentees, which can be substantially improved by applying Two-Sided Matching approaches. This guarantees stable matchings as well as near-optimal solutions with respect to secondary solution quality criteria such as the average matched rank of participants. With respect to algorithm choice, heuristic approaches perform best when it comes to number of matched participants as well as substantially outperform other approximation solutions with their ability to find solutions with high welfare quality, i.e., solutions where the average participant is matched close to their most preferred choice. Considering additional criteria such as Equality, the results show that there seems to be a trade-off between algorithm performance with respect to different metrics. Overall, the performance of the GATA-Mixed heuristic seems to be the best fit for the given set of preferences.

The work at hand can be extended in several directions. First, the overall approach can be adjusted to include additional constraints such as mentors who are willing to supervise mentees that do not find other mentors, but would prefer to remain unmatched otherwise. Second, additional solution criteria can be considered. A common additional criterion for Two-Sided Matching is Fairness, which compares the welfare for each participating side. If both sides, on average, are matched to similarly preferred partners, the solution is considered fair. Finally, an interesting endeavor is the explicit analysis of potential preference manipulation in this type of Two-Sided Matching. Through the use of questionnaires or other confidential means, participants can be asked to reveal if they adjusted their true preference ranking, and to provide their actual ranking. This would enable us to study how frequent and severe preference manipulation is, and also what the actual effects of manipulation on the overall solution quality (stability and welfare of the solution) are.

Declarations

Author contribution statement

Christian Haas: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Margeret Hall, Sandra Vlasnik: Conceived and designed the experiments; Performed the experiments; Contributed reagents, materials, analysis tools or data.

Funding statement

This work was partially sponsored by the Nebraska Research Initiative.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.