Skip to main content
PMC home page
Royal Society of Chemistry logoLink to Royal Society of Chemistry
. 2018 Jun 4;20(24):16817–16827. doi: 10.1039/c8cp03094d

X-ray-induced sample damage at the Mn L-edge: a case study for soft X-ray spectroscopy of transition metal complexes in solution†

Markus Kubin a, Jan Kern b, Meiyuan Guo c, Erik Källman c, Rolf Mitzner a, Vittal K Yachandra b, Marcus Lundberg c, Junko Yano b,✉, Philippe Wernet a,✉
PMCID: PMC6011208  NIHMSID: NIHMS974855  PMID: 29888772

graphic file with name c8cp03094d-ga.jpgDose-dependent damage to a Mniii complex in solution, induced by soft X-rays, is investigated with Mn L-edge X-ray absorption spectroscopy.

Abstract

X-ray induced sample damage can impede electronic and structural investigations of radiation-sensitive samples studied with X-rays. Here we quantify dose-dependent sample damage to the prototypical MnIII(acac)3 complex in solution and at room temperature for the soft X-ray range, using X-ray absorption spectroscopy at the Mn L-edge. We observe the appearance of a reduced MnII species as the X-ray dose is increased. We find a half-damage dose of 1.6 MGy and quantify a spectroscopically tolerable dose on the order of 0.3 MGy (1 Gy = 1 J kg–1), where 90% of MnIII(acac)3 are intact. Our dose-limit is around one order of magnitude lower than the Henderson limit (half-damage dose of 20 MGy) which is commonly employed for protein crystallography with hard X-rays. It is comparable, however, to the dose-limits obtained for collecting un-damaged Mn K-edge spectra of the photosystem II protein, using hard X-rays. The dose-dependent reduction of MnIII observed here for solution samples occurs at a dose limit that is two to four orders of magnitude smaller than the dose limits previously reported for soft X-ray spectroscopy of iron samples in the solid phase. We compare our measured to calculated spectra from ab initio restricted active space (RAS) theory and discuss possible mechanisms for the observed dose-dependent damage of MnIII(acac)3 in solution. On the basis of our results, we assess the influence of sample damage in other experimental studies with soft X-rays from storage-ring synchrotron radiation sources and X-ray free-electron lasers.

I. Introduction

X-ray induced damage to radiation-sensitive samples such as (metallo-) proteins in solution is a phenomenon well-known in X-ray crystallography and spectroscopy in the energy range of hard X-rays (1–100 keV), but is less well characterized in X-ray spectroscopic investigations with soft X-rays (0.1–1 keV). X-ray induced sample damage depends on the absorbed X-ray dose D = E/m which is the ratio of absorbed photon energy E and the absorbing mass m of the probed sample volume and it is measured in units of Gray (Gy, where 1 Gy = 1 J kg–1). In X-ray protein crystallography with synchrotron radiation sources a typical threshold known as the Henderson limit of 20 MGy (2 × 107 Gy) was defined, where for protein crystals at cryogenic temperatures half of the diffraction signal is lost due to sample damage.1 This limit was more recently refined by Garman et al., to be 30 MGy (3 × 107 Gy).2

Proposed explanations for this dose-dependent sample damage reflect the creation of electrons and radicals (“electron-gain centers” and “electron-loss centers”),3 initiated by the emission of Auger- and photoelectrons within the sample bulk after absorption of an X-ray photon. These “primary” electrons can scatter multiple times within the sample, creating a local cloud of radicals and “secondary” electrons.4 These can subsequently diffuse or tunnel and react, for example, with protein residues and cleave molecular bonds, leading to (irreversible) changes in the local molecular structures.5,6 These local changes can disrupt the long-range structure of a protein crystal (order of magnitude of 1 nm), explaining the loss of diffraction intensity. Dose-limits for 50% loss of diffraction intensity are reported between 1 and 40 MGy, depending on the experimental conditions such as, in particular, the sample temperature.2,7,8

In contrast to X-ray crystallography, X-ray spectroscopic methods based on hard9–11 and soft X-rays12–15 probe the local electronic structure which can be strongly affected by local chemical changes such as changes in bond distances and oxidation states, initiated by reactions with the radicals and electrons that are generated during the measurement.16,17 This specific kind of sample damage affects, in particular, high-valent 3d transition metals, many of which are relevant for catalytic processes in metalloproteins. X-ray absorption and emission studies of the photosystem II (PS II) protein have shown that high-valent MnIII and MnIV ions in the native oxygen evolving complex of PS II are reduced to MnII species upon irradiation with hard X-rays (Mn K-edge at ∼6.5 keV), where 50% of the Mn atoms are reduced to MnII at an X-ray dose between ∼0.1 and ∼10 MGy (half-damage dose), with a trend to higher dose-limits at cryogenic temperatures,18 and lower dose limits at room temperature.19

There are only a few studies of dose-dependent sample damage in the soft X-ray regime, mostly reporting damage to samples in the solid phase, with widely varying (half-damage) dose limits between 49 MGy and 4.2 GGy.20,21 We are not aware of any comparable work with soft X-rays on transition-metal complexes in solution and at room temperature, relevant for studying metalloproteins under ambient conditions and catalytic processes in solution without the influence of dose-dependent sample damage.22 Quantifying these dose limits and unraveling the underlying damage mechanism is expected to provide important information for the design and interpretation of the respective experimental approaches.

Here we bridge this gap with an investigation of dose-dependent sample damage, induced by soft X-rays to the MnIII(acac)3 complex in solution and at room temperature. We employ X-ray absorption spectroscopy (XAS) at the Mn L-edge to probe the local electronic structure at the Mn center via 2p–3d transitions. The (high-valent) MnIII complex is a valid prototype, as it is sensitive to sample damage and its damage-free L-edge XAS spectrum was characterized previously in solution.15,23 We use a static (non-flowing) transmission cell to quantify sample damage to MnIII(acac)3 by the occurrence of MnII and establish a dose limit above which sample damage starts to severely alter the spectra. We also extract the spectrum of the reduced species (MnII) and use ab initio calculations based on the restricted active space (RAS) approach24–29 to assess possible damage mechanisms. We apply our findings to validate our experimental approaches with liquid jets15,23 and start building a basis for the experimental design of damage-free L-edge XAS of transition-metal complexes and metalloproteins in solution, using soft X-rays from storage-ring synchrotron radiation facilities and X-ray free-electron lasers.

II. Materials and methods

Sample preparation

The data reported here is based on two sample preparation methods. Sample A was prepared from solid MnIII(acac)3 (manganese(3+) tris[(2Z)-4-oxo-2-penten-2-olate]), acetylacetonato ligands are abbreviated as (acac)–, purchased as a crystalline powder (technical grade) from Sigma-Aldrich and dissolved in acetylacetone (Sigma-Aldrich) with concentrations between 100 and 150 mM. Sample B was prepared from MnII(acac)2 (manganese(2+) bis[(2Z)-4-oxo-2-penten-2-olate]), purchased as a crystalline powder (technical grade) from Sigma-Aldrich and dissolved in acetylacetone (Sigma-Aldrich), with concentrations on the order of 50 mM. We find that upon solubilizing MnII(acac)2 in acetylacetone, the complex undergoes chemical changes that result in an L-edge absorption spectrum similar to that of MnIII(acac)3 (see Fig. S1 and Section 1 of the ESI†).

Experimental setup and data analysis

X-ray absorption spectra of the solution samples were measured in transmission mode with the transmission NEXAFS end-station30 at the undulator beamline UE52_SGM31 of the BESSY II synchrotron radiation facility. Solution samples were prepared in a transmission cell consisting of a holder with two X-ray transparent 100 nm thin Si3N4 membranes (purchased from Si-Mat Silicon Materials, Germany, membrane area 500 × 500 μm2). The thickness of the sample (excluding the membranes) varied between 1 and 6 μm and was adjusted by varying the pressure of the helium atmosphere in the experimental chamber between 780 and 1000 mbar. The experimental chamber was separated from the beamline vacuum by an additional 150 nm thin Si3N4 membrane. The cell and in particular the sample thickness was monitored as described in ref. 30. The size of the X-ray beam on the sample was determined to be 100 × 50 μm2 (horizontal × vertical), using knife-edge scans. A monochromator slit size of 20 μm was used, corresponding to a bandwidth of 50 meV (fwhm).

The photon flux ΦL(hν) after transmission through the solution sample of thickness L (plus the two 100 nm Si3N4 membranes and the He atmosphere with distances in the experimental chamber of 290 mm before and 45 mm after the transmission cell) was measured with a calibrated photodiode (Hamamatsu G1127-04 2K, placed on the X-ray beam axis 45 mm behind the transmission cell). The diode signal was read out by a Keithley Electrometer (model 6514B) and recorded as a function of the incident photon energy hν as scanned with the beamline monochromator. Reference spectra Φ0(hν) were recorded under equivalent conditions as the sample scans ΦL(hν) but on an empty transmission cell equivalent to the sample cell, both mounted on the same holder in the chamber. All diode signals were normalized by the storage ring current of the BESSY II synchrotron radiation facility and single outlier data points (on average four per single-scan) were corrected following the same procedure as in ref. 15. Each scan was taken in steps of 0.1 eV with 1 s integration time per step resulting in total acquisition times on the order of 10 min per single scan. Transmission spectra were obtained from the ratio TL(hν) = ΦL(hν)/Φ0(hν) of single scans ΦL(hν) with sample and reference scans Φ0(hν) without sample in the transmission cells.

The sample thickness L was determined separately for each scan by fitting the transmission of the pure solvent, as calculated from Henke's tables32,33 and using Beer–Lambert's law, to experimental data in the non-resonant spectral ranges (hν ≤ 637 eV and hν ≥ 654.5 eV). We estimate the uncertainty of the sample thickness by extracting a minimum and a maximum value from two separate fits at the low-energy (hν ≤ 637 eV) and the high-energy sides (hν ≥ 654.5 eV) of each transmission spectrum (thereby accounting for differences in the thickness at the beginning and at the end of the scan; see Fig. S2, ESI†).

Absorption spectra in units of the linear absorption coefficient α(hν) were calculated from the transmission spectra via αtot(hν) = –ln[TL(hν)]/L. Each Mn L-edge absorption spectrum αMn(hν) was obtained from αtot after correction for an absorption background αbg due to the solvent and due to slow drifts in the sample thickness by subtracting a low-order polynomial αbg(hν) (1st and 2nd order). This polynomial was fitted to the non-resonant parts at the low- and the high-energy sides of the spectrum (hν ≤ 637 eV and hν ≥ 654.5 eV) and was subtracted from the total absorption signal, so that αMn = (αtot – αbg). With this, we neglect information about the magnitude of the edge-jump (absorption beyond the L2-edge), which is acceptable for the purpose of this study and makes the resulting spectra comparable to our previous work.15

The axis of incident photon energy was calibrated as previously,15,22,23 by applying the same constant energy shift to all spectra in order to match the L3-edge maximum of intact MnIII(acac)3 sample with the maximum at 641.6 eV of the calibrated spectrum in ref. 15.

Calculation of absorbed X-ray doses

The dose D accumulated by the sample was calculated for all single-scan spectra at each data point by integrating over differential doses dD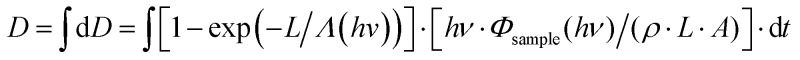Inline graphicover all scans on the sample, where hν (∼10–16 J) is the photon energy, dt (∼1 s) is the collection time per data point, L (∼1 to 6 μm) is the fitted sample thickness (only the solution), ρ = 0.98 g cm–3 is the density of the solvent, A = 500 × 500 μm2 is the surface area of the sample volume and Λ(hν) (∼1.14 μm at a photon energy of 640 eV) is the attenuation length of the solvent acetylacetone as obtained from Henke's tables.32,33 The flux incident on the sample, Φsample(hν), is calculated from Φsample(hν) = Φ0(hν)/[THe·TSi3N4] with the flux measured with an empty reference cell, Φ0(hν), after correction for the transmission THe of 45 mm He atmosphere at a pressure p(He) and for the transmission TSi3N4 of one 100 nm Si3N4 cell membrane. Both transmission curves THe and TSi3N4 were calculated from Henke's tables.32,33

We emphasize that all doses are calculated with respect to the mass of the full transmission cell volume V = L·A. With this, we assume that during a scan (10 min) diffusion evenly distributes reduced MnII species over the volume of the transmission cell. This is justified by estimating the diffusion length of the reduced MnII species in the liquid sample. For two-dimensional diffusion along the plane of the transmission cell,34 and using the diffusion coefficient reported for MnIII(acac)3 in solution, Ddiff ∼ 4 × 10–6 cm2 s–1,35 we estimate a diffusion length of 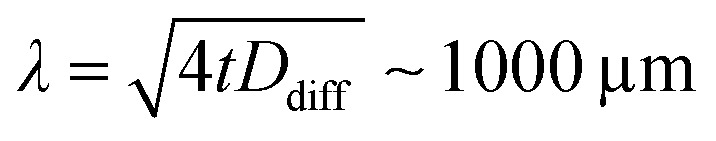Inline graphic for the duration of a single scan (t = 10 min). This length is comparable to the dimensions spanned by the transmission cell (500 × 500 μm2) and justifies our choice of the reference volume for calculating the dose. We note, however, that we systematically neglect diffusion-driven sample exchange with the reservoir surrounding the transmission cells (with extensions of several millimeters, see Fig. S3a in the ESI† and ref. 30), which occur on longer time scales of around 1 h (see Fig. S3b, ESI†). This is taken into account in the discussion of our results. We note also that under the conditions used here we do not have evidence for or against the formation or accumulation of photoproducts on the Si3N4 membranes.

As the accumulated dose increases with continuous X-ray illumination during each scan, assigning a distinct dose value to a given spectrum is not possible. We here assign scan-averaged doses and consider the range of doses surpassed during a scan (637–654.5 eV) as the systematic uncertainty. Combined with the thickness variations, these minimum-to-maximum uncertainties are represented by the error bars of the average doses.

Restricted active space (RAS) calculations

Spectra calculated with the RAS approach were performed with MOLCAS 7.936 at the RASPT2/ANO-RCC-VDZP level.23,27 The RAS calculations are based on molecular geometries obtained from DFT/B3LYP solvent optimization. As previously, to save computational cost, calculations for the tris-acetylacetonato species were performed on truncated structures where six terminal methyl groups were replaced by hydrogen atoms. We checked that this does not notably change the spectrum. Equivalent geometries were also used for the RAS calculations in ref. 15 and 23. A minimal valence active space consisting of the five metal-3d dominated orbitals were placed in the RAS2 space. The Mn 2p orbitals were placed in the RAS3 space and to ensure the hole stayed in these orbitals they were frozen in the RASSCF optimizations. For the final states, all possible configurations with one core hole were included. RASPT2 calculations were performed using the default ionization potential electron affinity (IPEA) shift of 0.25 Hartree. An imaginary shift of 0.1 Hartree was used to reduce the occurrence of “intruder states” in the core-excited states. Effects of model choices on spectral shape have been analyzed in ref. 37. All calculations were performed in a solvent environment that was modeled using the polarized continuum model (PCM) for the solvent acetylacetone. For comparison to the calculated spectra in ref. 15 we checked that changing the solvent from acetylacetone to ethanol has no effect on the calculated L-edge spectra. RAS spectra were broadened with a Gaussian with 0.3 eV fwhm and Lorentzian lifetime widths 0.2 eV and 0.7 eV (fwhm) for the L3 and L2-edges, respectively.38 The energy axis of all calculated spectra was corrected by a constant shift of –4.94 eV as determined previously for coinciding L3-edge peak maxima in experimental and calculated VDZP-quality spectra of MnII(acac)2.23

III. Results and discussion

Experimental setup

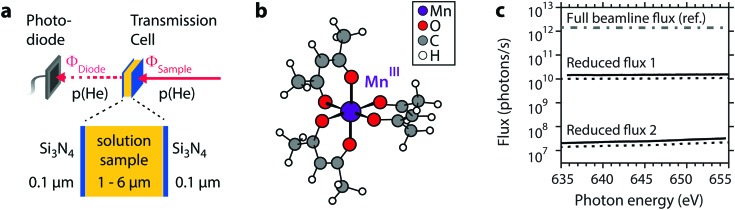
The experimental setup30 used for studying X-ray induced damage to MnIII(acac)3 solution samples with transmission-detected XAS is shown in Fig. 1a. The liquid sample is placed in a cell with Si3N4 membrane windows with a photodiode behind the cell which detects the transmitted intensity of the soft X-ray beam (normal incidence on the sample). The sample cell is used in a non-flowing operation mode which allows for the controlled accumulation of X-ray dose in the liquid sample for successive scans. The structure of the MnIII(acac)3 complex is shown in Fig. 1b. The central high-spin MnIII atom is coordinated by six oxygen atoms from the acetylacetonato ligands in a nearly octahedral Jahn–Teller distorted symmetry.15,23 For analyzing the changes in the spectra as a function of increasing X-ray dose, we used two different beamline settings; setting 1 with 102 times reduced flux and setting 2 with 105 times reduced X-ray flux, as compared to the typical maximum flux of the X-ray undulator beamline. Measured flux on the sample is compared in Fig. 1c for the energy range relevant to Mn L-edge XAS (for details on the determination of Φsample, see the Methods section). The typical maximum flux available for optimized undulator settings for the beamline is on the order of 1012 photons s–1.15 In setting 1, the flux on the sample was on the order of 1010 photons s–1. This was achieved as follows: by closing the beamline aperture (“beamline baffles”) between the monochromator and the refocusing optics to 600 μm (reduction factor ∼4), closing the monochromator slit to 20 μm (reduction factor ∼5 relative to ref. 15), and a reduction by 4–5 with respect to the full flux used in ref. 29 due to the attenuation by 290 mm He atmosphere at 750–1000 mbar in the experimental chamber and the 200 nm Si3N4 windows (calculated from Henke's tables32,33). In setting 1, the undulator was used in its optimized configuration, i.e. it was set up to follow the monochromator energy during a scan (undulator gap varying between 28.0 mm and 28.5 mm with monochromator energies 635–660 eV). In setting 2, we achieved a further reduction (by a factor 1000) to 107 photons s–1 by additionally detuning the undulator from this optimized configuration to a static gap distance of 29.4 mm. With this choice we took care to obtain a flat flux profile as a function of photon energy (Fig. 1c) as the X-ray photons originated from the spectrally flat wings of the undulator harmonics.

Fig. 1. (a) Schematic of the transmission-cell setup (ref. 30) for X-ray absorption spectroscopy at the L-edge of MnIII(acac)3 in solution. (b) Molecular structure of MnIII(acac)3 (cartoon based on the optimized structure used in ref. 15 and 23). (c) Experimental photon flux for different configurations of the undulator beamline UE52_SGM at the BESSY II synchrotron (solid: sample A; dotted: sample B) as compared to the full beamline flux (dash-dotted) from ref. 15.

Fig. 1

Open in a new tab

Damage to MnIII(acac)3 by soft X-rays

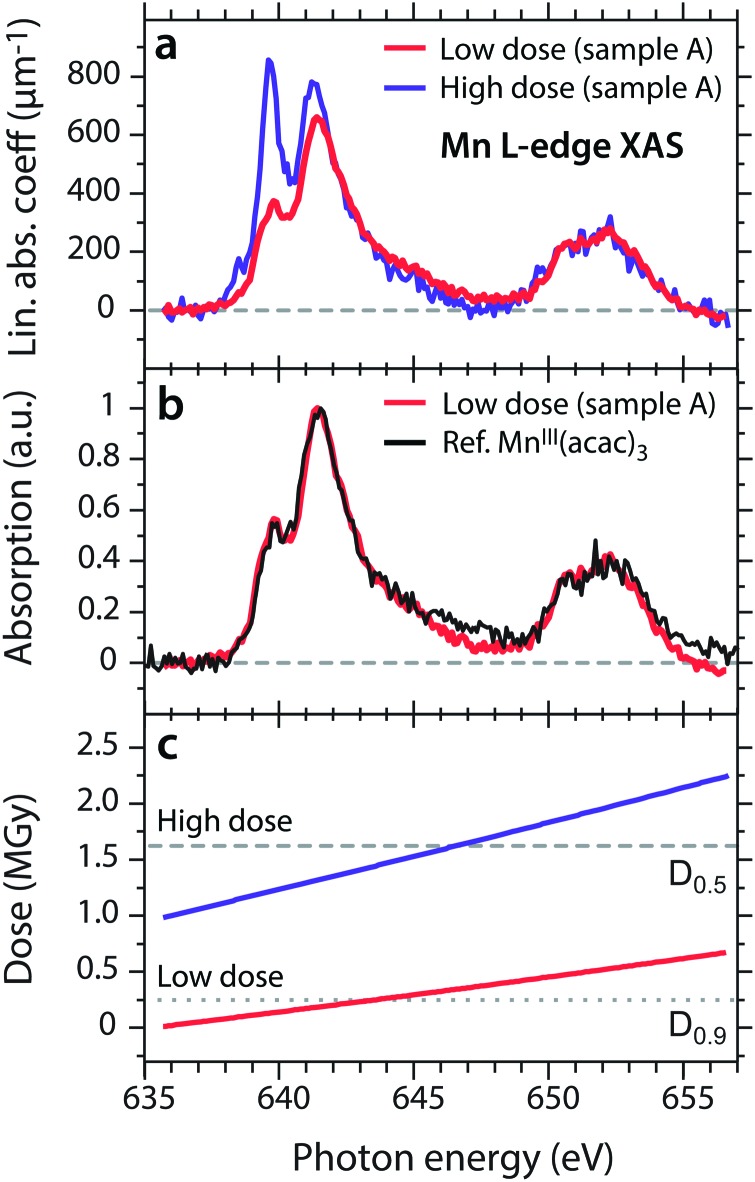
In Fig. 2a we compare two consecutive single-scan Mn L-edge XAS spectra of ∼150 mM MnIII(acac)3 in acetylacetone solution (sample A). Both spectra were recorded at flux setting 1 with ∼1010 photons s–1 on the same sample and the “low-dose” spectrum (first scan) was measured prior to the “high-dose” spectrum (second scan). The absorption spectra are shown in units of linear absorption coefficients αMn and are obtained from the raw transmission spectra as described in the Methods section. The thickness of the low-dose spectrum (measured in the center of the cell window) was determined to be between 5.8 μm and 6.1 μm (see Methods section and Fig. S2 in the ESI†) and that of the high-dose spectrum (measured closer to the edge of the cell window) was determined to be close to 2.6 μm. The linear absorption coefficients αMn of this ∼150 mM sample have peak values on the order of 600 μm–1 to 800 μm–1 which is consistent with our value of around 450 μm–1 reported for 100 mM damage-free MnIII(acac)3 in ref. 15.

Fig. 2. (a) Two subsequent scans of the same sample of MnIII(acac)3 in acetylacetone solution measured with the reduced flux setting 1 (see Fig. 1c), here shown in units of the linear absorption coefficient αMn (see Methods section). (b) Comparison of the spectrum measured at low dose from (a) to that of damage-free MnIII(acac)3 in ethanol (black), taken from ref. 15. Spectra are normalized to one at maximum. (c) X-ray dose accumulated by the sample volume, as calculated for each data point of the low-dose and the high-dose scans in (a). Doses are calculated with respect to the volume of the transmission cell with an area of 500 × 500 μm2 and thicknesses on the order of 6 μm (low dose, red) and 3 μm (high dose, purple).

Fig. 2

Open in a new tab

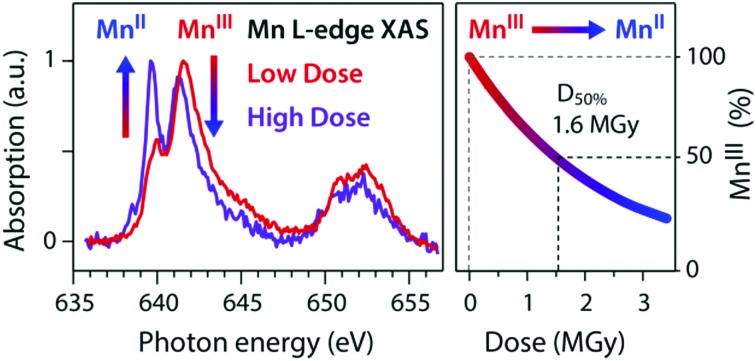
The shapes of the high-dose and low-dose spectra differ significantly in the L3 edge, in particular, by the sharp absorption maximum at 639.6 eV in the high-dose spectrum. Comparison to our previously reported Mn L-edge XAS spectra of MnII(acac)2 and MnIII(acac)3 in solution that were free of X-ray induced damage (this assessment is validated in a later section of this paper),15 clearly shows that this sharp peak is due to a reduced MnII species, occurring in the sample. The low-dose spectrum is almost identical to the damage-free spectrum of MnIII(acac)3 as shown by the direct comparison in Fig. 2b. Below 640 eV the high-dose spectrum with its sharp absorption peak maximum at 639.6 eV and the smaller peak at 638.5 eV is similar to the characteristic L-edge XAS spectrum of MnII species such as in MnII(acac)2 and [MnII(H2O)6]2+.15,39 These observations clearly show that the spectrum measured at the lower dose is almost free from X-ray induced damage, whereas the spectrum measured at the higher dose contains portions of reduced, spectrally distinct MnII species. This is consistent with observations from Mn K-edge XAS on the PS II protein, where the reduction of high-valent MnIII and MnIV sites to spectrally distinct, reduced MnII species is observed for increasing X-ray doses.18 A similar effect was reported for Fe L-edge XAS with the dose-dependent reduction of FeIII to FeII compounds.21,40

Starting from this qualitative picture of dose-dependent reduction of MnIII to MnII in MnIII(acac)3, we now aim for systematically quantifying the doses and the amounts of damaged species. In Fig. 2c, we show the accumulated dose, calculated for each data point in the spectra in Fig. 2a and increasing with X-ray irradiation time. We note that, while the scan of the low-dose spectrum starts at a dose of around 0 MGy, the scan of the high-dose spectrum starts at around 1 MGy due to the dose accumulated during the preceding scan. The average dose (see Methods section) calculated for the two spectra in Fig. 2a is 0.33 ± 0.28 MGy and 1.6 ± 0.6 MGy, respectively.

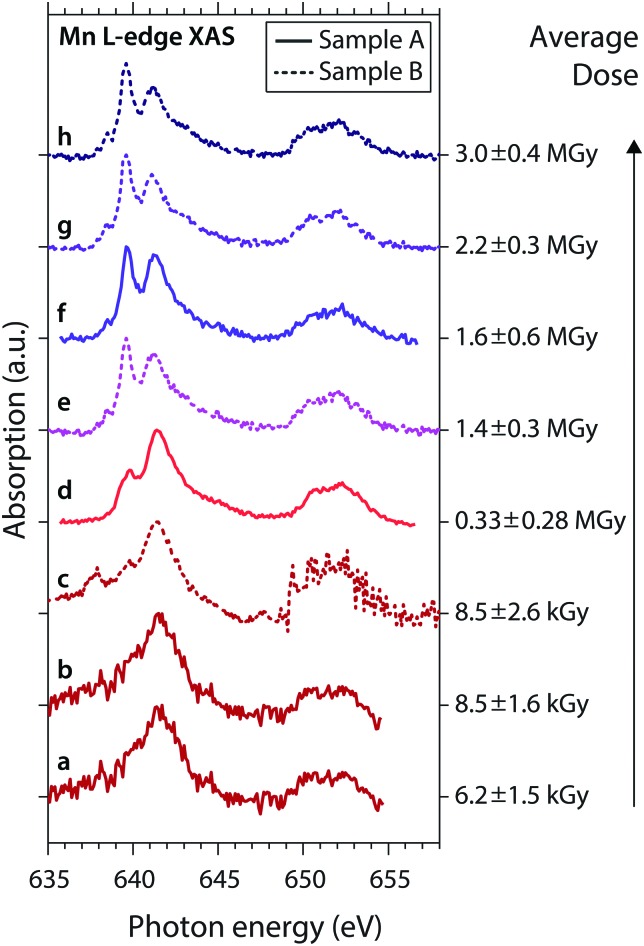
The general observations made here for the low- and high-dose spectra are also observed for low and high doses in the series of spectra shown in Fig. 3. Here we show consecutive scans of Mn L-edge XAS spectra of MnIII(acac)3 in solution of samples A (spectra “a”, “b”, “d”, “f”) and sample B (spectra “c”, “e”, “g”, “h”), sorted by average dose from bottom to top. Spectra “a”, “b” and “c” were scanned with flux setting 2 (∼107 photons s–1 on sample, diode currents ∼30–140 pA) at an average dose on the order of kGy (spectra at these low diode currents are affected by slow drifts and sudden jumps; spectrum “c” is corrupted for ≥649 eV due to an unintentional change of the dynamic range in the Keithley electrometer). These spectra agree with the undamaged spectrum of MnIII(acac)3.15 Spectra “d” to “h” were scanned with flux setting 1 (∼1010 photons s–1 on sample, diode currents ∼1–20 nA) and spectra “e” to “h” (with average doses ≥1.4 MGy) are similar to the damaged high-dose spectrum in Fig. 2a.

Fig. 3. Series of experimental Mn L-edge absorption spectra of MnIII(acac)3 solution samples A (solid) and B (dotted) with given average doses (error bars reflect the uncertainty of the sample thickness and the range of doses surpassed during a scan). Spectra (a) to (h) are sorted by the average dose values, spectra (d) and (f) are identical to the low-dose and high-dose spectra in Fig. 2a.

Fig. 3

Open in a new tab

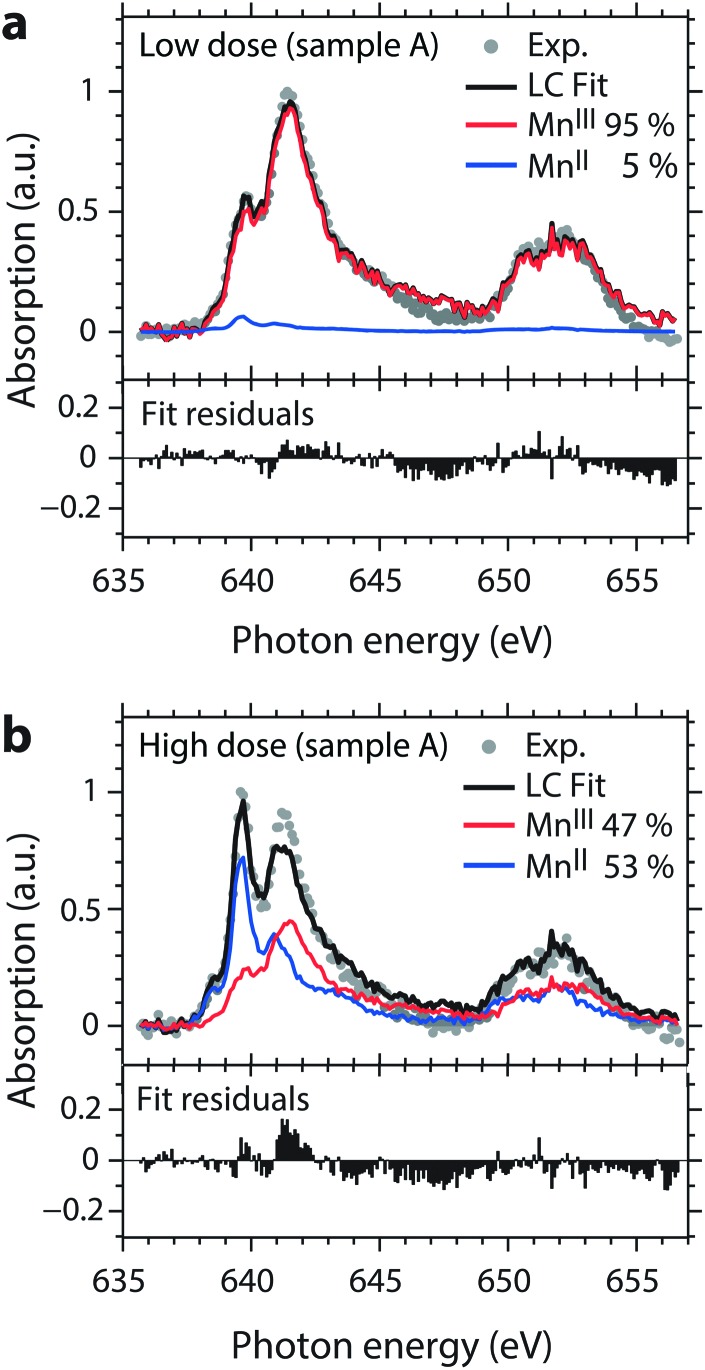
Fig. 4 illustrates how we further quantify the amount of the reduced MnII species in the sample, using the examples of the low- and high-dose spectra from Fig. 2. Our approach is a least-squares fit of a linear combination of damage-free spectra of MnII(acac)2 and MnIII(acac)3 taken from ref. 15. In these fits the ratio of integrated absolute absorption cross sections of the MnIII(acac)3 and MnII(acac)2 spectra of 1.16 ± 0.28 is maintained and the relative uncertainty of this way of determining the MnII/MnIII ratio governs the uncertainty of this fit. Within this approach, the fit curves in Fig. 4a and b reveal portions of 5% MnII (95% MnIII(acac)3) for the low-dose spectrum and 53% MnII (47% MnIII(acac)3) for the high-dose spectrum, both being in good agreement with the experimental spectra (see the small residuals of below 10% in the bottom panels of Fig. 4a and b, except for the mismatch at 641.6 eV in the high-dose spectrum). This also justifies using MnII(acac)2 as a model spectrum for the reduced MnII species (within the uncertainties of our approach we find the same MnII/MnIII ratios and comparably good fits when using MnIIaq. 39 as a model for the reduced MnII species39,41). This analysis was applied to all spectra shown in Fig. 3, with generally good agreement of the fits with the spectra measured at flux setting 1. Due to the poorer data quality of the spectra measured at flux setting 2 the fit of these spectra includes an additional estimated uncertainty of 30%.

Fig. 4. Fits (black) of normalized low-dose (a) and high-dose (b) absorption spectra (circles, taken from Fig. 2a) with linear combinations of damage-free spectra of MnII(acac)2 (blue) and MnIII(acac)3 (red) from ref. 15. Fit residuals are shown in the bottom panels.

Fig. 4

Open in a new tab

We note that a spectrum of MnIII(acac)3 reported in the literature has a similar spectral shape as the spectra of the damaged complex reported here. The MnIII(acac)3 spectrum reported in ref. 42 is similar to our “high-dose” spectrum at ∼1.6 MGy (Fig. 3). In Fig. S4a in the ESI† we show a least-squares fit (similar to the fits shown in Fig. 4) to this spectrum and find an amount of roughly 40% of MnII. Building theoretical analyses on this or other spectra of damaged species may consequently lead to erroneous choices of free parameters in the calculations and hence to biased conclusions about the studied sample.43,44 This example emphasizes the necessity of establishing experimental protocols and dose limits for X-ray spectroscopy, in particular for high-valent metal complexes, to avoid X-ray induced sample damage.

Dose-dependent reduction of MnIII(acac)3 in solution

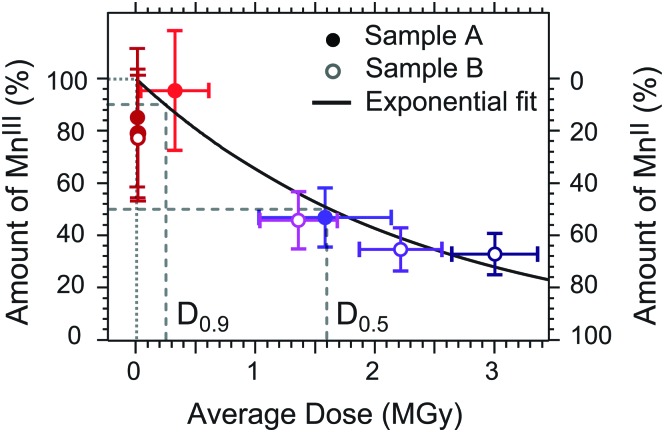
In Fig. 5 we combine the results from our least-squares fits of all spectra in one “dose plot”. At a dose close to zero we observe that around 100% of MnIII(acac)3 are present in the sample and the amount of MnIII(acac)3 decreases gradually to around 35% when the average dose increases to around 3 MGy. We employ a least-squares fit of the exponential decay function P(D) = P0·exp(–k·D), where P is the relative amount of MnIII(acac)3 in the sample, D denotes the average dose and k is the exponential decay parameter in units of Gy–1. With this we assume a first-order reduction reaction as a function of dose similar to the analysis in ref. 21 and as further justified in the following section. The decay constant resulting from this fit is k = (4.25 ± 0.85) × 10–7 Gy–1 (error bars are one standard deviation from the fit). The “half-damage” dose, D0.5, is 1.6 ± 0.4 MGy, where 50% of MnIII(acac)3 in the sample is reduced to MnII. As Mn L-edge spectra at this dose level are severely affected by X-ray induced sample damage (the high-dose spectrum in Fig. 2a represents the half-dose level), establishing a spectroscopically tolerable dose limit is useful.21 For example, at a conservative dose limit of D0.99 = 23 ± 5 kGy, 99% of the sample is intact. The spectra recorded at flux setting 2 (“a”, “b”, “c” in Fig. 3) are affected by a dose smaller than this conservative limit and are hence unaffected by damage. Our analysis of the low-dose spectrum from Fig. 2b and 4a shows that this spectrum is also almost unaffected by damage. The average dose assigned to this spectrum is close, for example, to the less conservative dose limit defined as D0.9 = 0.25 ± 0.05 MGy (average dose) where 90% of the sample is intact. The good agreement of this spectrum with the damage-free spectrum of MnIII(acac)3 (Fig. 2b) validates the choice of the less conservative dose limit of D0.9 here for spectroscopically tolerable dose in Mn L-edge XAS. We note that for transmission-detected XAS of non-flowing solution samples this dose limit of ∼0.25 MGy is reached within a fraction of a second at typical undulator beamlines, using a soft X-ray flux on the order of 1012 photons s–1.

Fig. 5. Dose plot combining the experimental results from this work, depicting the portion of MnIII(acac)3 as a function of average absorbed X-ray dose (circles with error bars). Horizontal error bars reflect the uncertainty of the sample thickness and the range of doses surpassed during a scan (minimum-to-maximum values), vertical error bars reflect systematic uncertainties. The color code reflects that of the spectra in Fig. 3. Solid line: exponential decay model fitted with a decay constant of k = (0.425 ± 0.085) × 10–7 Gy–1 with a half-damage dose of D0.5 = 1.6 ± 0.4 MGy and a spectroscopically tolerable dose of D0.9 = 0.25 ± 0.05 MGy (90% of the sample intact).

Fig. 5

Open in a new tab

In the above analysis we assumed that diffusion-driven exchange of liquid sample with the sample reservoir is negligible. However, if a solution sample is scanned sequentially with an accumulated duration of up to ∼1 h, taking into account these diffusion effects may be required when estimating the effective dose. Using the diffusion coefficient of D ∼ 4 × 10–6 cm2 s–1 reported for MnIII(acac)3 in solution,35 we estimate that the effective dose of a probed sample volume can be up to one order of magnitude smaller than the average dose values determined above. The reason for this is the continuous, diffusion-driven mixing of irradiated sample in the probing region with non-irradiated sample from the sample reservoir. In turn, the dose limits of D0.9 ∼ 0.25 MGy (D0.5 ∼ 1.6 MGy) reported here may be overestimated by up to one order of magnitude so that the same sample without diffusion-driven mixing could have dose limits on the order of D0.9 ∼ 0.03 MGy (D0.5 ∼ 0.2 MGy).

Mechanism for dose-dependent reduction

As shown in Fig. 5, an exponential decay function describing how the damage varies with dose agrees well with the experimental data, and a possible rationale for these data is as follows. Most of the photons absorbed by the sample are absorbed by light atoms in the sample (H, C, O) and generate fast (“primary”) Auger- and photo-electrons which scatter multiple times within the sample bulk. For a given sample volume, each absorption event generates a number of secondary electrons, proportional to the absorbed energy and thus to the dose absorbed by the sample volume. These electrons are the reactants driving the reduction of MnIII to MnII as expressed by the simplified equation MnIII + e– → MnII. This reaction is expected to follow a first order kinetic in time, described by an exponential decay as a function of time. The electrons are generated at low rates (at a dose of ∼1–103 Gy s–1, corresponding to a dose of ∼kGy to ∼MGy absorbed in 10 min), presumably lower than the rate of the reduction reaction, which occurs in picoseconds.45 This would justify that the progress of this reaction is dependent on the dose rather than the time and hence also that the first order reaction is a function of dose, as applied to the fit in Fig. 5.

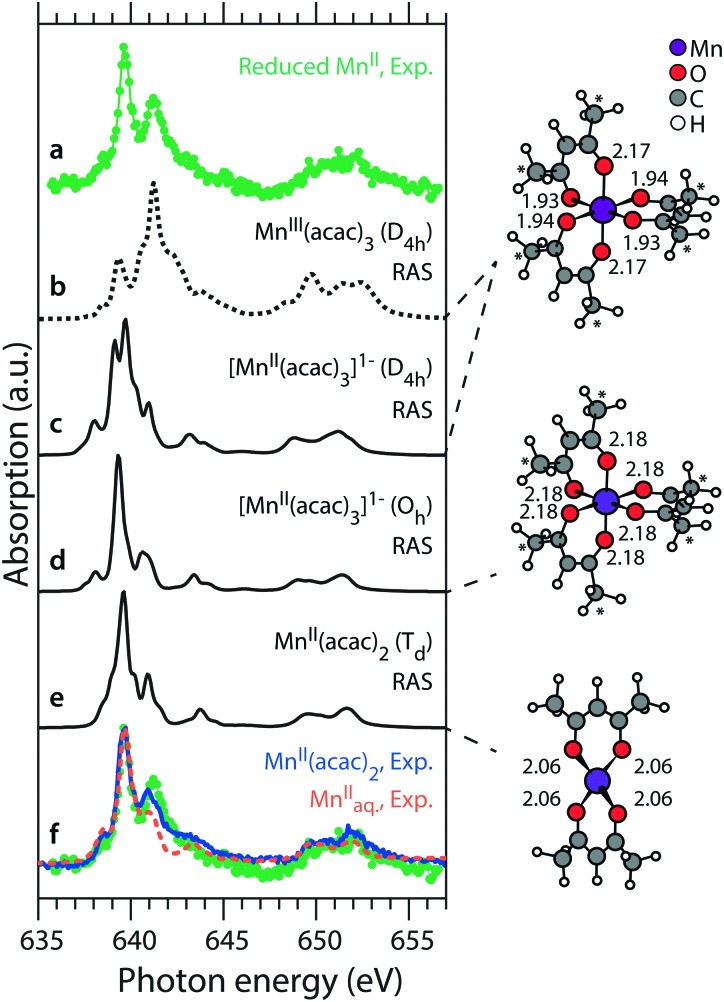
It is also important for understanding the reduction reaction to determine the chemical identity of the reduced MnII species resulting from the reduction of MnIII(acac). Within the limitations of our fitting model, we extract a spectrum of the reduced MnII species by subtracting from the high-dose spectrum (Fig. 4b) the undamaged spectrum of MnIII(acac)3 (Fig. 2b), scaled according to its contribution (47%) at the given dose level. This difference spectrum of the reduced MnII species is shown in Fig. 6 as spectrum “a” and we use it in the following to tentatively assess the chemical nature of the reduced species. The spectrum is compared to Mn L-edge XAS spectra calculated with the ab initio RAS approach for a series of Mn acetylacetonate complexes with different molecular geometries (see Methods section) and Mn oxidation states (Fig. 6). Spectra “b”, “c” and “e” are comparable to those in ref. 15 and 23. All spectra were calculated with a smaller basis set but show no significant differences to the spectra in the references. The energy axis of the spectra is calibrated as previously, their relative energies are plotted as calculated.

Fig. 6. Left: Spectrum of the reduced MnII species (a), obtained from subtracting the fitted portion of 47% damage-free MnIII(acac)3 from ref. 15 from the high-dose spectrum in Fig. 2b. This spectrum is compared to spectra from RAS calculations for different acetylacetonate complexes of MnIII (b) and MnII (c–e), with relative energies as calculated. In the bottom row (f) it is overlaid (gray) with experimental spectra of damage-free MnII(acac)2 in solution of ethanol (solid blue) from ref. 15 and of MnIIaq. (dashed orange) from ref. 39. Right: Molecular structures in the RAS calculations (Mn–O bond lengths in Å).

Fig. 6

Open in a new tab

We start with RAS spectrum “b”, calculated for the optimized structure of MnIII(acac)3 with a central Jahn–Teller distorted, nearly octahedral MnO6 cluster (Fig. 6, top right). For the MnIII complex no good agreement is found in the shape of the L3-edge as compared to the spectrum of reduced MnII. When going from “b” to “c”, changing the oxidation state from MnIII to MnII (while keeping the molecular structure constant) clearly improves the similarity. This is observed as a spectral shift of the L3-edge maximum between MnIII and MnII by 1.5 eV, consistent with previous studies.12,22,23 On this level of sensitivity, we note that the ability to predict the spectrum of a complex using ab initio RAS calculations is a powerful tool as it may indicate potential issues with X-ray induced sample damage in the experimental data. As compared to “c”, spectrum “d” differs in that the molecular structure is optimized (“allowed to relax”) for the oxidation state of MnII (Fig. 6, middle right). This slightly improves the similarity of theoretical and experimental L3-edge shapes with respect to the reduced MnII species. As a last step with RAS, with spectrum “e” we also compare the spectrum calculated for the optimized structure of MnII(acac)2 with a central, tetrahedral MnO4 cluster (Fig. 6, bottom right).15,23 The agreement of spectral shapes improves, if at all, only slightly. We find that the spectrum calculations with RAS confirm the MnII oxidation state of the reduced species, but predicted differences in spectra are not large enough to allow for assigning its molecular structure.

In row “f” of Fig. 6 we overlay spectrum “a” of the damage product (green) with the absorption spectrum of damage-free MnII(acac)2 in solution (solid blue)15 and find comparably good agreement in shape and energy of most spectral features (except for some deviation in the peak at 641.6 eV). This could imply that the final product of X-ray induced sample damage is MnII(acac)2 which has one acetylacetonate ligand less than the original MnIII(acac)3 complex. For comparison, we also show the spectrum of aqueous solution of ionic MnII (dashed orange) from ref. 39. This spectrum shows slightly less similarity to the spectrum of the reduced MnII species than that of MnII(acac)2, in particular with respect to the peak at 641.6 eV and to the high-energy side of the L3-edge. This comparison could support a tentative, but not significant assignment of the reduction product to MnII(acac)2. We note, however, that this assignment may be biased by the choice of our fit model (Fig. 4).

We summarize our analysis in a possible three- or four-step reaction mechanism, respectively, for the dose-dependent damage of MnIII(acac)3 in solution. First, an X-ray photon (hν) is absorbed by an atom or molecule A, predominantly (∼90% and more) by the abundant solvent molecules (∼104 mM as compared to sample concentrations around ∼102 mM with respective absorption cross sections at the Mn L-edge of ∼106 barns or 10–22 m2 for the solvent molecules,32,33 and up to ∼107 barns or 10–21 m2 for the solute15), and a fast Auger- or photoelectron (e–) with a kinetic energy Ekin is emitted from A.hν + A → A+ + e– + EkinEach of these fast, primary electrons scatters multiple times, each time transferring part of its kinetic energy to the scattering partners B (other atoms or molecules) creating a cascade of N Auger- and photoelectrons and N radicals B+.e– + Ekin + N·B → (N + 1)·e– + N·B+The resulting N + 1 electrons are slow as they have lost almost their entire kinetic energy. They can either recombine with their parent ions or migrate through the liquid sample (diffusion coefficient ∼5 × 10–5 cm2 s–1)46 and react with intact MnIII(acac)3 molecules, thereby reducing it to [MnII(acac)3]1– (since diffusion depends on temperature, the relative amounts of recombination and migration/reduction events can also depend on temperature).3MnIII(acac)3 + e– → [MnII(acac)3]1–So far this reaction mechanism seems substantiated by the spectral comparison in Fig. 6. The reduced molecule [MnII(acac)3]1– may then possibly dissociate to[MnII(acac)3]1– → MnII(acac)2 + (acac)1–where a potentially negatively charged acetylacetonate ligand could detach and be solvated by the structurally identical solvent. This may be supported by the slightly better but not significant spectral similarity of the reduced MnII species with MnII(acac)2 than with ionic MnIIaq. in the bottom row “f” of Fig. 6.

Comparison to dose limits from literature

The nature of how X-ray induced sample damage is reflected in Mn L-edge XAS, i.e. by local chemical changes leading to a reduced MnII species, differs from how damage affects X-ray diffraction (XRD) approaches, where long-range structural changes of the protein crystal are, for example, reflected in a decreased diffraction intensity.

For the assessment of our results from this work, in Table 1 we now compare our half-damage dose limit, D0.5 ∼ 1.6 MGy (with a potential overestimation by up to an order of magnitude, see above), to some half-damage dose-limits D0.5 reported in literature (or dose-limits extracted numerically from published data). We note that these dose limits often vary by an order of magnitude, even for similar samples and within a single study. We therefore keep our discussion on the level of an order of magnitude. Following Table 1 from top to bottom, we first compare with dose-limits reported in X-ray diffraction and X-ray spectroscopic studies with hard X-rays, and we then turn to spectroscopic results with soft X-rays. Dose-limits for hard and soft X-rays are herein compared directly, which is justified as for a given dose value the concentration of slow electrons in the probed sample volume, and thus the relative amount of damaged sample, is largely independent from the X-ray energy (see also definition above of the X-ray dose).

Table 1. Comparison of dose limits for X-ray induced sample damage in terms of half-damage doses D0.5 and spectroscopically tolerable doses D0.9 (where 90% of the sample is intact) from this work and published results using X-ray diffraction (XRD) methods, and X-ray absorption (XAS) and emission spectroscopies (XES).

Reference Sample conditions T (K) X-ray hν (keV) Observable k (Gy–1) D 0.9 (MGy) D 0.5 (MGy)
Proteins Hard X-ray diffraction
Henderson (1990)1 Proteins, frozen crystals 77 8, any XRD, 50% loss of signal 3 × 10–8* 3* 20
Owen (2006)2 Proteins, frozen crystals 100 13.2 XRD, 50% loss of signal 2 × 10–8* 7* 43
Liebschner (2015)7 Proteins, frozen crystals 100 6.3 XRD, 50% loss of signal 6 × 10–8* 2* 12*
13/19 3 × 10–8* 3* 21*
Southworth-Davies (2007)8 Protein, liquid solution 300 8.0 XRD, 50% loss of signal 2 × 10–6* 0.06* 0.4
4 × 10–7* 0.3* 1.8
Sutton (2013)6 Protein, frozen crystals 4 70 XRD, trapped radicals 4.2 × 10–6 0.03* 0.2*
XRD, reduced RSSR 1.7 × 10–6 0.06* 0.4*
Reference Sample conditions T (K) X-ray hν (keV) Observable k (Gy–1) D 0.9 (MGy) D 0.5 (MGy)
Proteins Hard Spectroscopic methods
Yano (2005)18 PS II protein, frozen crystals 10 13.3 XAS, amount of Mn(ii) 7 × 10–8* 1.5* 10*
100 13.3 XAS, amount of Mn(ii) 2 × 10–7* 0.4* 3*
PS II protein, frozen solution 100 13.3 XAS, amount of Mn(ii) 5 × 10–7* 0.2* 1*
100 6.6 XAS, amount of Mn(ii) 2 × 10–7* 0.5* 3*
Davis (2012)19 PS II protein, liquid solution 300 7.5 XES, amount of Mn(ii) 4 × 10–6* 0.03* 0.2*
1 × 10–6* 0.09* 0.6*
Meharenna (2010)48 CCP protein, frozen crystals 65 13 UV-vis, amount Fe(iv) 3 × 10–6* 0.035 0.2*
Reference Sample conditions T (K) X-ray hν (keV) Observable k (Gy–1) D 0.9 (MGy) D 0.5 (MGy)
Solution samples Soft Spectroscopic methods
This work Mn(iii) compound, solution 300 0.64 XAS, amount of Mn(ii) 4.3 × 10–7 0.25 ± 0.05 1.6 ± 0.4
(∼0.03)† (∼0.2)†
Reference Sample conditions T (K) X-ray hν (keV) Observable k (Gy–1) D 0.9 (MGy) D 0.5 (MGy)
Solid samples Soft Spectroscopic methods
George (2008)20 Fe(iii) compound, solid 135 0.40 XAS, amount of Fe(ii) 2 × 10–10* 500* 3000
Fe(iv) compound, solid 135 0.40 XAS, amount of Fe(ii) 2 × 10–9* 60* 410
Schooneveld (2015)21 Fe(iii) compound, solid 300 0.71 XAS, amount of Fe(ii) 1.4 × 10–8 7* 49
35 1.7 × 10–10 600* 4200
Open in a new tab

Typical D0.5 dose limits for the loss of diffraction signal and thus for long-range structural damage in X-ray diffraction studies of protein crystals with hard X-rays are reported between 0.4 and 43 MGy.1,2,7,8 These studies can be divided into two groups, first with frozen samples at cryogenic temperatures (dose limits D0.5 between 12 and 43 MGy)1,2,7 and, second, with solution samples at room temperature (dose limits D0.5 between 0.4 and 1.8 MGy).8 The well-known trend that dose limits are lower at room temperature than at cryogenic temperatures, may be explained with decreased (temperature-dependent) diffusion of electrons and radicals (electron-gain and electron-loss centers)3 driving the sample damage.47 As compared to long-range structural changes in the crystal lattice relevant for the loss of X-ray diffraction signal, dose-dependent effects of local chemical changes, e.g. the reduction of functional sites in (metallo-) proteins, were shown to occur already at lower doses. High-resolution X-ray diffraction experiments show, for example, that the local trapping of radicals and local reduction processes occur at doses around D0.5 ∼ 0.2–0.4 MGy (here at cryogenic temperatures) and thus appear to precede the loss of diffractivity.6

Local chemical changes, in particular the reduction of high-valent transition metal sites, are sensitively probed with X-ray and UV-vis spectroscopic studies of metalloproteins irradiated with hard X-rays.18,19,48 In those studies, the dose-dependent reduction of high-valent transition metal sites was observed to occur at dose-limits D0.5 between 0.2 and 10 MGy at cryogenic temperatures,18,48 and between 0.2 and 0.6 MGy at room temperature.19 We find that within the accuracy level of our discussion (one order of magnitude) both ranges of dose-limits, in particular for the reduction of high-valent MnIII and MnIV sites in PS II,18,19 are consistent with the dose-limit D0.5 of 1.6 MGy found here for the reduction of MnIII(acac)3 in room temperature solution.

Among the few studies of dose-dependent sample damage by soft X-rays, we are only aware of data from iron complexes in the solid phase where dose-limits D0.5 with large spreads were reported, ranging from 49 to 4200 MGy, even for the same compounds and within a single study.20,21 These dose limits reported for the reduction of FeIII and FeIV in the solid phase are two to four orders of magnitude larger than the limits determined here for the reduction of MnIII in solution. At this point, however, it remains an open question whether the nature and the oxidation state of the metal center (Fe or Mn), the sample temperature or the phase of the sample (solid vs. solution) determines these differences in the sensitivity to X-ray induced sample damage. We speculate that the apparent higher sensitivity of the solution sample studied here is due to a facilitated diffusion of electrons and radicals in solution samples as compared to the solid samples, where charge migration may be limited to tunneling effects. This decreased mobility of electrons and radicals in solid samples could explain an increased role of electron–ion recombination after the primary ionization event, counteracting diffusion-driven sample damage and leading to increased dose-limits as compared to solution samples. Comparable studies of high-valent meal complexes in the solid and the liquid phase and at different temperatures could further explain the above differences in sensitivity to dose-dependent sample damage.

The dose limits reported here for the reduction of MnIII in solution and at room temperature can be used to assess other experimental approaches and to validate other spectroscopic results for the influence of sample damage. In particular, we can validate our damage-free L-edge absorption spectra of MnIII(acac)3 in solution that were acquired with different types of fast-flowing liquid jets. For transmission-detected Mn L-edge XAS of MnIII(acac)3 using a transmission flatjet, we estimated an average dose of around 20 Gy,15 and for our results from partial fluorescence-yield (PFY) detected XAS we estimated an average dose on the order of 5 kGy.23 With the results from this work, we can therefore estimate amounts of less than 1% of damaged metal centers in those studies and validate the results as free from sample damage.

We also compare our current results with the data collected with femtosecond soft X-ray pulses from X-ray free electron lasers (XFEL),22 in which we collected PFY-detected Mn L-edge XAS of high-valent MnIII and MnIV complexes in solution and at room temperature. Based on spectral comparisons we concluded there that the spectra are free of X-ray induced sample damage. Each sample volume probed by the intense, 100 fs soft X-ray XFEL pulses was estimated to absorb an average dose of around 2–4 MGy.22 These dose values are much larger than the spectroscopically tolerable dose limit of ∼0.3 MGy (D0.9) determined here for MnIII(acac)3 in solution, using soft X-rays from a storage-ring synchrotron radiation source; one would expect sample damage on the order of 50% for comparable experiments at a synchrotron radiation sources. The fact that no X-ray induced reduction of Mn was observed in the XFEL data implies that, using an XFEL, the spectral information is probed on ultrafast time scales (100 femtosecond) and outruns the effects of diffusion-driven (dose-dependent) sample-damage that occur on the order of picoseconds.45

IV. Conclusions

In this paper, we analyze dose-dependent X-ray induced sample damage to MnIII(acac)3 in solution and at room temperature for the soft X-ray energy range. We employ X-ray absorption spectroscopy at the Mn L-edge to quantify the amount of damaged sample. Spectra measured at an average dose on the order of ∼0.3 MGy are nearly identical with damage-free spectra published previously. For a larger dose we observe increasing spectral contributions from a reduced MnII species resulting from the X-ray induced reduction of MnIII(acac)3. On the basis of calculated spectra from the ab initio restricted active space (RAS) approach and comparison to damage-free experimental spectra of MnII(acac)2 and MnIIaq. in solution, we discuss a possible mechanism for the X-ray induced reduction of MnIII(acac)3 in solution. We model the reduction reaction with a single-exponential dose-dependence and quantify an amount of 50% sample damage at 1.6 ± 0.4 MGy. We establish a spectroscopically tolerable dose limit of 0.25 ± 0.05 MGy, where 90% of the sample is intact. We discuss that diffusion-driven mixing of the liquid sample may cause a systematic overestimation of the effective dose-limit in this analysis by up to one order of magnitude. The dose limit reported here for the X-ray induced reduction of MnIII(acac)3 in room temperature solution by soft X-rays is hence around one order of magnitude smaller than the dose-limits typically used to delimit the loss of X-ray diffraction intensity in protein crystallography at cryogenic temperatures, but is consistent with dose-limits reported for the reduction of high-valent metal sites in metalloproteins, such as the oxygen evolving Mn complex in photosystem II, by hard X-rays. Comparison to other available studies with soft X-rays reveals an unexplained discrepancy by two to four orders of magnitude in dose between the experimental dose limits determined here for solution samples and those reported for iron complexes in the solid phase. Still, the observed photoreduction is expected to occur also in other high-valent transition metal complexes in solution. Using the dose limits determined here we validate other experimental approaches that promise damage-free soft X-ray absorption spectra of solution samples, relevant for studying catalysts and metalloproteins under ambient conditions. These approaches comprise fast-flowing liquid jets at synchrotron radiation sources and femtosecond pulses from X-ray free electron lasers, which outrun the time-scales of (dose-dependent) diffusion-driven sample damage.

Author contributions

Conceived the experiment: M. K., J. K., J. Y., V. Y., Ph. W. Designed the experiment: M. K., Ph. W. Prepared the samples: M. K. Carried out the experiment: M. K. Analyzed the data: M. K., under the supervision of Ph. W. Carried out ab initio restricted active space calculations: M. G., E. K., M. L. Wrote the paper: M. K. with contribution from all authors.

Conflicts of interest

There are no conflicts of interest to declare.

Supplementary Material

Click here for additional data file. (589.6KB, pdf)

Acknowledgments

We gratefully acknowledge the continuous support by the BESSY II staff and we thank HZB for the allocation of synchrotron radiation beamtime. We thank Simon Schreck (HZB) for advising us on the transmission NEXAFS setup and Christian Weniger (HZB) and Brian Kennedy (HZB) for the preparation of the transmission membranes. We acknowledge financial support from Human Frontiers Science Program (RGP0063/2013) (Ph. W., J. Y.), the Swedish Research Council (Grant No. 2012-3924), and the Knut and Alice Wallenberg Foundation (Grant No. KAW-2013.0020). The computations were performed on resources provided by SNIC through Uppsala Multidisciplinary Center for Advanced Computational Science (UPPMAX) under project snic2016-1-464 and National Supercomputer Centre at Linköping University (Triolith) under project snic2016-1-508. Parts of this research are supported by the Director, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences of the Department of Energy under contract DE-AC02-05CH11231 (J. Y., V. K. Y.), and by the NIH Grants GM110501 (J. Y.), GM126289 (J. K.) and GM55302 (V. K. Y).

Footnotes

†Electronic supplementary information (ESI) available: Details on sample preparation; data processing and analysis; diffusion-driven exchange with the sample reservoir; comparison to reference spectra. See DOI: 10.1039/c8cp03094d

References

  1. Henderson R. Proc. Biol. Sci. 1990;241:6–8. [Google Scholar]
  2. Owen R. L., Rudino-Pinera E., Garman E. F. Proc. Natl. Acad. Sci. U. S. A. 2006;103:4912–4917. doi: 10.1073/pnas.0600973103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. O'Neill P., Stevens D. L., Garman E. F. J. Synchrotron Radiat. 2002;9:329–332. doi: 10.1107/s0909049502014553. [DOI] [PubMed] [Google Scholar]
  4. Garman E. F. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2010;66:339–351. doi: 10.1107/S0907444910008656. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Weik M., Ravelli R. B. G., Kryger G., McSweeney S., Raves M. L., Harel M., Gros P., Silman I., Kroon J., Sussman J. L. Proc. Natl. Acad. Sci. U. S. A. 2000;97:623. doi: 10.1073/pnas.97.2.623. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Sutton K. A., Black P. J., Mercer K. R., Garman E. F., Owen R. L., Snell E. H., Bernhard W. A. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2013;69:2381–2394. doi: 10.1107/S0907444913022117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Liebschner D., Rosenbaum G., Dauter M., Dauter Z. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2015;71:772–778. doi: 10.1107/S1399004715001030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Southworth-Davies R. J., Medina M. A., Carmichael I., Garman E. F. Structure. 2007;15:1531–1541. doi: 10.1016/j.str.2007.10.013. [DOI] [PubMed] [Google Scholar]
  9. Glatzel P., Bergmann U. Coord. Chem. Rev. 2005;249:65–95. [Google Scholar]
  10. Bergmann U., Glatzel P. Photosynth. Res. 2009;102:255–266. doi: 10.1007/s11120-009-9483-6. [DOI] [PubMed] [Google Scholar]
  11. Beckwith M. A., Roemelt M., Collomb M. N., DuBoc C., Weng T. C., Bergmann U., Glatzel P., Neese F., DeBeer S. Inorg. Chem. 2011;50:8397–8409. doi: 10.1021/ic200970t. [DOI] [PubMed] [Google Scholar]
  12. Cramer S. P., DeGroot F. M. F., Ma Y., Chen C. T., Sette F., Kipke C. A., Eichhorn D. M., Chan M. K., Armstrong W. H. J. Am. Chem. Soc. 1991;113:7937–7940. [Google Scholar]
  13. Wasinger E. C., De Groot F. M. F., Hedman B., Hodgson K. O., Solomon E. I. J. Am. Chem. Soc. 2003;125:12894–12906. doi: 10.1021/ja034634s. [DOI] [PubMed] [Google Scholar]
  14. Kowalska J. K., Nayyar B., Rees J. A., Schiewer C. E., Lee S. C., Kovacs J. A., Meyer F., Weyhermüller T., Otero E., DeBeer S. Inorg. Chem. 2017;56:8147–8158. doi: 10.1021/acs.inorgchem.7b00852. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kubin M., Guo M., Ekimova M., Baker M. L., Kroll T., Källman E., Kern J., Yachandra V. K., Yano J., Nibbering E. T. J., Lundberg M., Wernet P. Inorg. Chem. 2018;57:5449–5462. doi: 10.1021/acs.inorgchem.8b00419. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Nagasaka M., Yuzawa H., Horigome T., Hitchcock A. P., Kosugi N. J. Phys. Chem. C. 2013;117:16343–16348. [Google Scholar]
  17. Risch M., Stoerzinger K. A., Han B., Regier T. Z., Peak D., Sayed S. Y., Wei C., Xu Z., Shao-Horn Y. J. Phys. Chem. C. 2017;121:17682–17692. [Google Scholar]
  18. Yano J., Kern J., Irrgang K. D., Latimer M. J., Bergmann U., Glatzel P., Pushkar Y., Biesiadka J., Loll B., Sauer K., Messinger J., Zouni A., Yachandra V. K. Proc. Natl. Acad. Sci. U. S. A. 2005;102:12047–12052. doi: 10.1073/pnas.0505207102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Davis K. M., Mattern B. A., Pacold J. I., Zakharova T., Brewe D., Kosheleva I., Henning R. W., Graber T. J., Heald S. M., Seidler G. T., Pushkar Y. J. Phys. Lett. 2012;3:1858–1864. doi: 10.1021/jz3006223. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. George S. J., Fu J., Guo Y., Drury O. B., Friedrich S., Rauchfuss T., Volkers P. I., Peters J. C., Scott V., Brown S. D., Thomas C. M., Cramer S. P. Inorg. Chim. Acta. 2008;361:1157–1165. [Google Scholar]
  21. van Schooneveld M. M., DeBeer S. J. Electron Spectrosc. Relat. Phenom. 2015;198:31–56. [Google Scholar]
  22. Kubin M., Kern J., Gul S., Kroll T., Chatterjee R., Löchel H., Fuller F. D., Sierra R. G., Quevedo W., Weniger C., Rehanek J., Firsov A., Laksmono H., Weninger C., Alonso-Mori R., Nordlund D. L., Lassalle-Kaiser B., Glownia J. M., Krzywinski J., Moeller S., Turner J. J., Minitti M. P., Dakovski G. L., Koroidov S., Kawde A., Kanady J. S., Tsui E. Y., Suseno S., Han Z., Hill E., Taguchi T., Borovik A. S., Agapie T., Messinger J., Erko A., Föhlisch A., Bergmann U., Mitzner R., Yachandra V. K., Yano J., Wernet P. Struct. Dyn. 2017;4:054307. doi: 10.1063/1.4986627. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kubin M., Guo M., Kroll T., Löchel H., Källman E., Baker M. L., Mitzner R., Gul S., Kern J., Föhlisch A., Erko A., Bergmann U., Yachandra V., Yano J., Lundberg M. and Wernet P., 2018, submitted. [DOI] [PMC free article] [PubMed]
  24. Josefsson I., Kunnus K., Schreck S., Föhlisch A., de Groot F., Wernet P., Odelius M. J. Phys. Lett. 2012;3:3565–3570. doi: 10.1021/jz301479j. [DOI] [PubMed] [Google Scholar]
  25. Pinjari R. V., Delcey M. G., Guo M., Odelius M., Lundberg M. J. Chem. Phys. 2014;141:124116. doi: 10.1063/1.4896373. [DOI] [PubMed] [Google Scholar]
  26. Malmqvist P. Å., Roos B. O., Schimmelpfennig B. Chem. Phys. Lett. 2002;357:230–240. [Google Scholar]
  27. Malmqvist P. Å., Pierloot K., Shahi A. R. M., Cramer C. J., Gagliardi L. J. Chem. Phys. 2008;128:204109. doi: 10.1063/1.2920188. [DOI] [PubMed] [Google Scholar]
  28. Preuße M., Bokarev S. I., Aziz S. G., Kühn O. Struct. Dyn. 2016;3:062601. doi: 10.1063/1.4961953. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Bokarev S. I., Khan M., Abdel-Latif M. K., Xiao J., Hilal R., Aziz S. G., Aziz E. F., Kühn O. J. Phys. Chem. C. 2015;119:19192–19200. [Google Scholar]
  30. Schreck S., Gavrila G., Weniger C., Wernet P. Rev. Sci. Instrum. 2011;82:103101. doi: 10.1063/1.3644192. [DOI] [PubMed] [Google Scholar]
  31. Miedema P. S., Quevedo W., Fondell M. Journal of large-scale research facilities JLSRF. 2016;2:70. [Google Scholar]
  32. Henke B. L., Gullikson E. M., Davis J. C. At. Data Nucl. Data Tables. 1993;54:181–342. [Google Scholar]
  33. CXRO, Center for X-ray Optics, X-ray Database, http://henke.lbl.gov/optical_constants/, accessed 06/01/2017, 2017.
  34. Berg H. C., Random walks in biology, Princeton University Press, 1993. [Google Scholar]
  35. Sleightholme A. E. S., Shinkle A. A., Liu Q., Li Y., Monroe C. W., Thompson L. T. J. Power Sources. 2011;196:5742–5745. [Google Scholar]
  36. Aquilante F., De Vico L., Ferre N., Ghigo G., Malmqvist P. A., Neogrady P., Pedersen T. B., Pitonak M., Reiher M., Roos B. O., Serrano-Andres L., Urban M., Veryazov V., Lindh R. J. Comput. Chem. 2010;31:224–247. doi: 10.1002/jcc.21318. [DOI] [PubMed] [Google Scholar]
  37. Pinjari R. V., Delcey M. G., Guo M., Odelius M., Lundberg M. J. Comput. Chem. 2016;37:477–486. doi: 10.1002/jcc.24237. [DOI] [PubMed] [Google Scholar]
  38. Ohno M., van Riessen G. A. J. Electron Spectrosc. Relat. Phenom. 2003;128:1–31. [Google Scholar]
  39. Mitzner R., Rehanek J., Kern J., Gul S., Hattne J., Taguchi T., Alonso-Mori R., Tran R., Weniger C., Schröder H., Quevedo W., Laksmono H., Sierra R. G., Han G., Lassalle-Kaiser B., Koroidov S., Kubicek K., Schreck S., Kunnus K., Brzhezinskaya M., Firsov A., Minitti M. P., Turner J. J., Moeller S., Sauter N. K., Bogan M. J., Nordlund D., Schlotter W. F., Messinger J., Borovik A., Techert S., de Groot F. M. F., Föhlisch A., Erko A., Bergmann U., Yachandra V. K., Wernet P., Yano J. J. Phys. Lett. 2013;4:3641–3647. doi: 10.1021/jz401837f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Risch M., Stoerzinger K. A., Regier T. Z., Peak D., Sayed S. Y., Shao-Horn Y. J. Phys. Chem. C. 2015;119:18903–18910. [Google Scholar]
  41. Cross sections from personal communication by S. Schreck and Ph. Wernet, Helmholtz-Zentrum Berlin, Germany, 2018. [Google Scholar]
  42. Grush M. M., Muramatsu Y., Underwood J. H., Gullikson E. M., Ederer D. L., Perera R. C. C., Callcott T. A. J. Electron Spectrosc. Relat. Phenom. 1998;92:225–229. [Google Scholar]
  43. Carlotto S., Sambi M., Vittadini A., Casarin M. Polyhedron. 2017;135:216–223. [Google Scholar]
  44. Carlotto S., Floreano L., Cossaro A., Dominguez M., Rancan M., Sambi M., Casarin M. Phys. Chem. Chem. Phys. 2017;19:24840–24854. doi: 10.1039/c7cp04461e. [DOI] [PubMed] [Google Scholar]
  45. Davis K. M., Kosheleva I., Henning R. W., Seidler G. T., Pushkar Y. J. Phys. Chem. B. 2013;117:9161–9169. doi: 10.1021/jp403654n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Buxton G. V., Greenstock C. L., Helman W. P., Ross A. B. J. Phys. Chem. Ref. Data. 1988;17:513–886. [Google Scholar]
  47. Garman E. Curr. Opin. Struct. Biol. 2003;13:545–551. doi: 10.1016/j.sbi.2003.09.013. [DOI] [PubMed] [Google Scholar]
  48. Meharenna Y. T., Doukov T., Li H., Soltis S. M., Poulos T. L. Biochemistry. 2010;49:2984–2986. doi: 10.1021/bi100238r. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (589.6KB, pdf)

Articles from Physical Chemistry Chemical Physics are provided here courtesy of Royal Society of Chemistry

RESOURCES