Overestimation of the adaptive substitution rate in fluctuating populations

Abstract

Estimating the proportion of adaptive substitutions (α) is of primary importance to uncover the determinants of adaptation in comparative genomic studies. Several methods have been proposed to estimate α from patterns polymorphism and divergence in coding sequences. However, estimators of α can be biased when the underlying assumptions are not met. Here we focus on a potential source of bias, i.e. variation through time in the long-term population size (N) of the considered species. We show via simulations that ancient demographic fluctuations can generate severe overestimations of α, and this is irrespective of the recent population history.

1. Introduction

The proportion of amino acid substitutions that are adaptive, α, is an important parameter routinely inferred in population genomic studies. Methods for estimating α usually rely on the McDonald & Kreitman principle, which is based on the comparison of polymorphic and fixed mutations at synonymous versus non-synonymous positions [1–5]. These methods, however, make various assumptions that are not always met in real data. One of them is that the stringency of purifying selection against deleterious mutations has been constant over the considered time period, so that the rate of non-adaptive (neutral and slightly deleterious) substitutions during divergence, ω_na, can be estimated based on polymorphism data. Sequence divergence, however, builds up across long periods of time. If the selection regime has changed in the past, so that polymorphism data are not representative of the average long-term process governing rates of divergence, then the estimation of α can be biased [6].

Importantly, the strength of purifying selection is determined by population size (N) [7], which likely varies in time. The geographical range of Palaearctic species, for instance, has expanded and contracted due to the alternation of glacial and interglacial periods during the Quaternary [8]. Species adapted to warm habitats, hereafter called ‘temperate’, have mainly subsisted in refuges during glacial periods, where their census population sizes were presumably reduced. Conversely, species adapted to cold habitats, hereafter called ‘alpine’, have presumably occupied larger ranges during cold periods than during warm ones [9,10]. Both types of species are particularly prone to exhibit discrepancies between current and average long-term N, which might bias estimations of α based on both divergence and polymorphism data that have not been generated under the same selection regime. More specifically, if the current population size is lower than the average long-term population size, we expect an underestimation of this statistic due to the presence of slightly deleterious mutations that are now segregating in polymorphism data, but have not contributed to divergence. If, however, current population size is higher than the average long-term population size, then we expect an overestimation of α due to an inflated rate of fixation of slightly deleterious mutations in the past, whereas these have been efficiently selected against recently.

Methods taking into account recent N changes that affect polymorphism in the estimation process have been developed and proved to perform well [2]. In contrast, ancient changes that affect divergence have been rarely investigated. Modelling single changes in N, Eyre-Walker showed that in presence of slightly deleterious mutations, an increase in N in the past could yield spurious evidence for positive selection, whereas a decrease in N can either increase or decrease α depending on when it happened [6].

To further explore the extent of the error one can make when estimating genome-wide adaptive rates, we simulated coding sequence evolution under plausible scenarios involving fluctuating N along with linkage effects, and tested the performance of the most recent implementations of the McDonald–Kreitman approach [4,5]. Our results reveal a substantial overestimation of α and of the adaptive rate ω_a in most scenarios, calling for a re-examination of the interpretation of the high values of α often reported based on these methods.

2. Material and methods

(a). Generating simulated data of temperate and alpine species

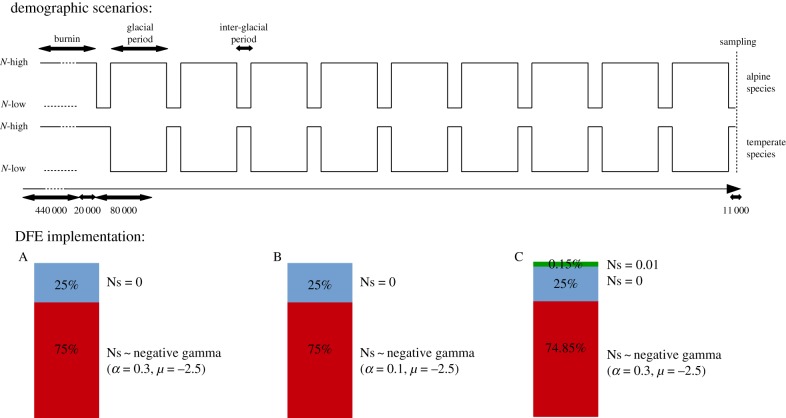
We simulated the evolution of coding sequences in a single population evolving forward in time using SLIM V2 [11]. We considered panmictic populations of diploid individuals whose genomes consisted of 1500 coding sequences, each of 999 base pairs. The mutation rate was set to 2.2 × 10⁻⁹ per base pair per generation [12] and the recombination rate to 1 × 10⁻⁸ per base pair per generation [13]. Simulations differed from one another with respect to the demographic scenario and the assumed distribution of the fitness effect of mutations (DFE) as shown in figure 1. The alternation of a high (10⁵) and a low N (10⁴) was assumed to follow quaternary climatic cycles, with temperate species having a high N during interglacial periods, and alpine having a high N during glacial periods. Each combination of parameters was replicated 50 times. SLIM allows tracking of all mutations arising during a simulation, along with their associated fitness effect and frequency, which can be 1 if the mutation has reached fixation. Each mutation that arose during a simulation was categorized as either synonymous (if the fitness effect was zero) or non-synonymous (if the fitness effect was different from zero). For each replicate simulation, we retrieved all fixed and segregating mutations and their population frequencies, and we computed non-synonymous and synonymous divergence and the unfolded site frequency spectra (SFS). An unfolded SFS is a vector of 2n − 1 entries corresponding to the counts of SNPs where the absolute frequency of the derived allele is 1, 2, …, 2n − 1, respectively, in a sample of n diploid individuals. Here samples of size n = 10 individuals were considered. From SLIM output we also calculated for each simulation the true (realized) values of the proportion of adaptive substitutions α, the rate of adaptive substitutions ω_a and the rate of non-adaptive substitutions ω_na.

Figure 1.

Demographic scenario and distribution of fitness effect (DFE) parameters used in the simulations. N-high is set to 10⁵ individuals, and N-low is set to 10⁴ individuals for the reference scenarios, and 10³ individuals for the ‘severe bottlenecks’ scenarios. DFE ‘A’ describes the reference DFE we use in the simulations, which did not include a positive component. DFE ‘B’ presents a change in the shape of the negative DFE, modelled as a gamma distribution, and DFE ‘C’ contains a positive DFE component. α and μ, respectively, stand for the shape and the mean parameter of a gamma distribution. (Online version in colour.)

(b). Computing estimates of α, ω_a and ω_na

We estimated α, ω_a and ω_na from simulated SFS and divergence data using two distinct programs introduced by Galtier [4] and Tataru et al. [5], denoted by G and T underscripts, respectively. Both programs re-implement and extend a method of estimation of the adaptive rate introduced by Eyre-Walker & Keightley [2]. Distinct DFE models were considered and fitted to SFS and divergence data. The model ‘Gamma’ includes the fitting of a gamma distribution for neutral and deleterious mutations, along with a fixed class of strongly adaptive substitution, whereas under model ‘GammaExpo’ the DFE includes both a negative (gamma) and a positive (exponential) component [4,5] (see electronic supplementary methods). Two approaches were taken for estimating ω_a, ω_na and α posterior to model fitting. In the first approach [2], the expected ω_na is estimated from the inferred DFE, whereas ω_a and α are obtained by subtracting ω_na from the observed dN/dS ratio (dN/dS = ω_a + ω_na and ω_a = α*dN/dS). In the second approach [4,5], divergence data were only used at the DFE model fitting step, ω_na, ω_a and α being estimated directly from the inferred DFE (see electronic supplementary methods). This approach is only applicable to DFE models including an explicit adaptive DFE component, such as GammaExpo. We called this procedure ‘GammaExpo*’. When estimating DFE model parameters, we jointly accounted for demographic effects by using nuisance parameters, which correct each class of frequency of the synonymous and non-synonymous SFS relative to the neutral expectations in an equilibrium Wright–Fisher population [14].

3. Results and discussion

(a). Influence of past demographic fluctuations on the estimations of the parameters of adaptation

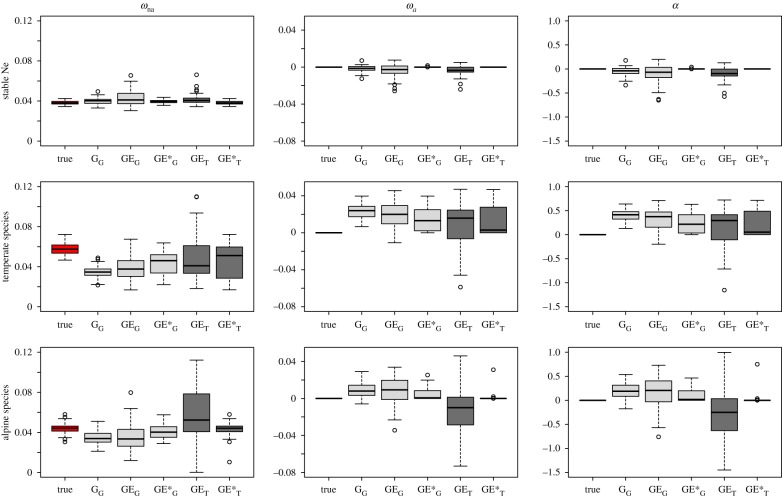
We report a substantial overestimation of α in the great majority of scenarios of fluctuating N, especially for temperate species, whereas methods tended to reliably infer positive selection when N was stable (figure 2 and table 1). In the worst case (inference made with the model Gamma_G, for a temperate species and simulation under a scenario with no adaptive evolution (DFE implementation ‘A’), all the replicates yielded estimated α values above 0.13, 54% of which being above 0.4, whereas the true α equalled 0 (figure 2). The overestimation of α for temperate species is caused by an underestimation of the non-adaptive substitution rate ω_na, indicating that this result is indeed due to the presence of slightly deleterious mutations. As for alpine species, for which the last episode of demographic fluctuation is a population decrease, we still observed inflated α values with some models, contrary to the findings of [6]. This might be because here the average expected coalescence time is longer than the last inter-glacial period (11 000 generations), so that polymorphism reflects a period that may span several cycles of fluctuations. Thus the long-term population size, which can be approximated by the harmonic mean through time, may not be greater than the recent N even in alpine species (see electronic supplementary material, table S1).

Figure 2.

ω_na, ω_a and α estimates according to different models (implementation of Galtier in light grey and implementation of Tataru in dark grey: ‘G’ stands for Gamma, ‘GE’ for GammaExpo and ‘GE*’ for GammaExpo*) for three main treatments: stable population size, temperate species and alpine species with the simulated DFE ‘A’ in figure 1, i.e. which does not include adaptive mutation. (Online version in colour.)

Table 1.

Statistic estimates according to different models for additional treatments with different DFE implementations (see the DFE descriptions in figure 1), different recombination rate and severeness of bottlenecks.

	scenario	true α	αGammG	dN/dS	πn/πs	true ωa	ωaGammG	true ωna	ωnaGammaG
temperate species	DFE C	0.58 [0.52;0.66]	0.61 [0.40;0.77]	0.15 [0.12;0.18]	0.079 [0.063;0.097]	0.085 [0.069;0.10]	0.090 [0.056;0.13]	0.062 [0.046;0.081]	0.057 [0.038;0.079]
	DFE B	0 [0;0]	0.16 [−0.030;0.33]	0.34 [0.31;0.37]	0.34 [0.29;0.38]	0 [0;0]	0.054 [−0.0094;0.11]	0.34 [0.31;0.37]	0.28 [0.22;0.32]
	DFE A N-low = 1000	0 [0;0]	0.69 [0.53;0.97]	0.099 [0.082;0.12]	0.056 [0.044;0.067]	0 [0;0]	0.069 [0.046;0.096]	0.10 [0.082;0.12]	0.030 [0.0034;0.043]
alpine species	DFE C	0.83 [0.79;0.87]	0.81 [0.73;0.98]	0.27 [0.25;0.30]	0.071 [0.055;0.084]	0.23 [0.20;0.25]	0.22 [0.12;0.28]	0.048 [0.034;0.059]	0.051 [0.0068;0.071]
	DFE B	0 [0;0]	0.084 [−0.074;0.24]	0.31 [0.28;0.34]	0.33 [0.30;0.36]	0 [0;0]	0.027 [−0.022;0.075]	0.31 [0.28;0.34]	0.28 [0.24;0.32]
	DFE A N-low = 1000	0 [0;0]	0.48 [0.29;0.72]	0.067 [0.055;0.077]	0.054 [0.042;0.065]	0 [0;0]	0.032 [0.019;0.051]	0.067 [0.055;0.077]	0.035 [0.019;0.048]
stable N	DFE C	0.73 [0.72;0.75]	0.65 [0.60;0.72]	0.23 [0.22;0.24]	0.10 [0.092;0.11]	0.17 [0.16;0.18]	0.15 [0.14;0.16]	0.062 [0.059;0.065]	0.080 [0.064;0.094]
	DFE A higher recombination rate	0 [0;0]	0.0022 [−0.21;0.15]	0.034 [0.030;0.037]	0.056 [0.053;0.059]	0 [0;0]	0.00019 [−6.5 × 10−3;5.5 × 10−3]	0.034 [0.030;0.037]	0.034 [0.029;0.038]
	DFE C higher recombination rate	0.90 [0.90;0.91]	0.87 [0.85;0.90]	0.41 [0.40;0.42]	0.069 [0.064;0.074]	0.37 [0.36;0.38]	0.36 [0.34;0.38]	0.040 [0.037;0.043]	0.051 [0.044;0.060]

(b). Comparison of the different methods of inference of α

Figure 2 shows that the five tested inference models are overall consistent, all showing an overestimation of α when there are past fluctuations of N. A significantly positive correlation was found between the two pairs of inference models GammaExpo and GammaExpo* of the implementations of Galtier and Tataru [4,5] (R = 0.59 and R = 0.73 respectively, and electronic supplementary material, figure S1). However, the models differed in terms of variance of the estimations and in the extent of the overestimation they produced. The model performing the best was GammaExpo*. This model uses the observed non-synonymous divergence count as a parameter when fitting the DFE to the data, and estimates ω_a from the inferred DFE. Consequently, the discrepancies between divergence and polymorphism data that could be entailed by past demographic fluctuations are mitigated, as the parameters of the DFE that lead to the estimation of ω_a are adjusted from the two sources of data. Ideally, using solely polymorphism data, such as developed in [5], removes all risks of discrepancies, but such a method needs high quality datasets, and estimation relying exclusively on SFS data pays a penalty because estimates will have inherently more sampling variance [5]. Nevertheless, with such a method, α estimates will reflect the recent proportion of adaptive substitutions, contrary to the α estimated by the other models.

(c). Control analyses

We explored how estimation of α and ω_a is influenced by changes in the DFE, as well as in recombination rate and the intensity of the bottlenecks (table 1). When adaptive mutation was part of the simulation, we observed a slight overestimation of α only for temperate species. This suggests that the estimation methods are particularly prone to strong biases particularly when the true adaptive substitution rate is low.

Additionally, we tested the influence of the shape of the negative part of the DFE modelled with a gamma distribution. Using a shape parameter of 0.3 instead of 0.1 decreased the true value of α and lead to a less severe overestimation of the adaptive rate (table 1). This is likely due to the fact that, as the shape parameter approaches zero, the assumed DFE becomes closer and closer to the neutral model—i.e. with a low prevalence of slightly deleterious mutations—so that dN/dS is less and less sensitive to N.

We tested the influence of the recombination rate by increasing it by a factor of 10 under stable N. This decreased the bias and reduced the variance of the estimations of α substantially for the simulations using the DFE ‘C’, but not for those using DFE ‘A’, where the bias was already very low (table 1).

Finally, we also tested the effect of the intensity of the fluctuations, by decreasing the population size to 1000 individuals in the bottlenecks. As expected, the extent of the overestimation was stronger, with estimations of α reaching a mean of 0.69 for temperate species.

4. Conclusion

We showed that under plausible demographic scenarios involving fluctuations in population size, current inference methods can severely overestimate α. This upward bias is exacerbated when the true adaptive substitution rate is low, when there are a lot of slightly deleterious mutations, and recombination rate is low. The upward bias is mainly caused by ancient demographic events which are likely to be essentially undetectable from current polymorphism data. Without any specific clue regarding the long-term demographic history of a population, we therefore call for caution when interpreting the results of such methods, especially when the estimated α is high.

Methods relying on an explicit model of adaptive evolution performed better in the case of population fluctuations and should probably be developed further in order to overcome this problem.

Data accessibility

The unfolded SFS and divergence counts of each replicate of the different simulation scenarios we generated are deposited in the Dryad Digital Repository (http://dx.doi.org/10.5061/dryad.85qb2r1) [15].

Authors' contributions

M.R. and M.M. performed the simulations, analysis and interpretations, under the supervision of N.G., B.N. and T.B. M.R. drafted the article, and M.M., N.G., B.N. and T.B. revised it critically for important intellectual content. M.R., M.M., B.N., T.B. and N.G. all approve the final version and all aspects of the work, and agree to be accountable for all aspects of the work, the content therein and approve the final version of the manuscript.

Competing interests

We have no competing interests.

Funding

This work was supported by Agence Nationale de la recherche grant no. ANR-15-CE12-0010 ‘DarkSideOfRecombination’.