Mechanistic models versus machine learning, a fight worth fighting for the biological community?

Abstract

Ninety per cent of the world's data have been generated in the last 5 years (Machine learning: the power and promise of computers that learn by example. Report no. DES4702. Issued April 2017. Royal Society). A small fraction of these data is collected with the aim of validating specific hypotheses. These studies are led by the development of mechanistic models focused on the causality of input–output relationships. However, the vast majority is aimed at supporting statistical or correlation studies that bypass the need for causality and focus exclusively on prediction. Along these lines, there has been a vast increase in the use of machine learning models, in particular in the biomedical and clinical sciences, to try and keep pace with the rate of data generation. Recent successes now beg the question of whether mechanistic models are still relevant in this area. Said otherwise, why should we try to understand the mechanisms of disease progression when we can use machine learning tools to directly predict disease outcome?

Machine learning models provide predictions on the outcomes of complex mechanisms by ploughing through databases of inputs and outputs for a given problem. Authors such as Tom Mitchell define machine learning as the computer-based process that improves its performance on a given task with the experience of it [1]. This experience may come from interactions with previously collected data or from an interaction with the environment while performing the task. While this approach strongly emphasizes the artificial intelligence perspective of machine learning, other fields, such as the database community, view machine learning as the algorithmic part of a much broader ‘knowledge discovery from databases’ process (a rather outdated term, now known as data mining) [2].

To provide accurate predictions, machine learning models require large amounts of data or an intensive interaction with the environment, the choice of an adequate algorithm, and the identification of inputs and outputs of interest. The ability to avoid the need to understand complex mechanisms, through the use of large-scale datasets, engenders machine learning algorithms scalable and efficient in making predictions in e.g. clinical settings. A recent clinical example is the application of Google's DeepMind technology to 1.6 million NHS patient records. This initiative led to the development of the smartphone app Streams, aimed at addressing ‘failure to rescue’, where warning signs of deteriorating health are not identified or acted upon quickly enough (https://deepmind.com/applied/deepmind-health/working-partners/how-were-helping-today/).

While machine learning models can be used to isolate relevant inputs from big datasets for a given output, mechanistic modelling relies on the generation of novel hypotheses for causal mechanisms that are generated through observations of the phenomenon of interest. Its purpose is to mimic real-life events through assumptions on the prominent underlying mechanisms. Typically, this involves constructing simplified mathematical formulations of causal mechanisms, and developing and/or using analytical tools to determine whether the range of possible input–output behaviours predicted by the model, and hence the causal hypotheses, are consistent with experimental observations. Like machine learning models, mechanistic modelling relies upon a two-stage process: first a subset of the available data is used to construct and calibrate the model; and subsequently, in a validation phase, further data are used to confirm and/or refine the model, thereby increasing its accuracy. Ideally the resulting mechanistic models can be leveraged for subsequent use in applications where experiments are either impossible or difficult to achieve.

A paradigm of the mechanistic modelling approach is provided by the work of Hodgkin & Huxley, first published in 1952 [3]. Hodgkin & Huxley's model of the generation of the nerve action potential is one of the most successful mathematical models of a complex biological process that has ever been formulated. Their model accounts phenomenologically for the dynamics of independent ion channels in which currents are carried entirely by ions moving down electrochemical gradients. It was calibrated and validated using a series of experiments to determine the macroscale parameters of the ion channels (e.g. conductances, equilibrium potentials, the dynamics of each type of ion channel). Hodgkin & Huxley's work, which won them the Nobel Prize in 1963, has seen widespread use, pushing forward the boundaries of our understanding of the electrical activity of cells on scales ranging from single-celled organisms right through to the neurons in our brains, as well as in cardiac mechanics. Hodgkin & Huxley were able to provide scientists with a basic understanding of how nerve cells work. In addition, their model stimulated a significant amount of research in applied mathematics through the derivation of simple caricature models of excitable systems.

Machine learning and mechanistic modelling approaches rely on different types of data and provide access to different types of information (table 1). In short, they are two different paradigms. We suggest that, in this sense, they should not be seen as direct competitors or one used at the direct exclusion of another. While mechanistic models provide the causality missing from machine learning approaches, their oversimplified assumptions and extremely specific nature prohibit the universal predictions achievable by machine learning. However, the pros of one are the cons of the other, which suggests that research efforts should be directed towards enabling a symbiotic relationship between both. Returning to the previous example, Hodgkin & Huxley focused on developing a quantitative model of the action potential produced by the squid giant axon, and multiple variations of this model have been subsequently developed to describe the dynamics of a large number of ion channels. However, efforts to calibrate Hodgkin–Huxley-type models to all possible neurons remain quixotic as this approach cannot be sustained against the recent acceleration in discoveries of new types of ion channels (http://channelpedia.epfl.ch). This is very much evidenced by the barriers to progress encountered by the existing worldwide initiatives in neuroscience. However, one can imagine in the future the realization of a universal model applicable to all ion channels where individual parameter calibration and model refinement would rely on a machine learning layer overtop the mechanistic framework. More generally, machine learning research could be harnessed to overcome the current scalability limitations of mechanistic modelling, while mechanistic models could be used by machine learning algorithms both as transient inputs and as a validating framework.

Table 1.

The advantages and disadvantages of mechanistic modelling and machine learning.

mechanistic modelling	machine learning
seeks to establish a mechanistic relationship between inputs and outputs	seeks to establish statistical relationships and correlations between inputs and outputs
difficult to accurately incorporate information from multiple space and time scales	can tackle problems with multiple space and time scales
capable of handling small datasets	requires large datasets
once validated, can be used as a predictive tool where experiments are difficult or costly to perform	can only make predictions that relate to patterns within the data supplied

However, such marriage is not always straightforward, especially in the clinical context. Any attempt by machine learning technologies to predict individual patient outcomes from past observations using a patient database is potentially able to identify which of existing treatments is most adequate, but intrinsically unable to suggest new treatment protocols or to provide accurate predictions for new treatments. In the literature, this aspect is referred as the ‘inductive capability’ of the learning algorithms (from past data, one can identify patterns happening in the data). This is vastly different from the deductive capability of mechanistic models, in which the combination of logical (mechanistic) principles enables extrapolation to predictions about behaviours not present in the original data [4]. In short, mechanistic models can provide insights and understanding into the mechanistic functions of treatments, and these are necessary to overcome the limitations of machine learning predictions. A recent example is the use of machine learning in predicting the success rate for endoscopic third ventriculostomy (used to treat hydrocephalus) [5]. While the algorithm could predict the success rate of the actual procedure, it was not able to take into account the risks for a particular patient of other general physiological variables to allow the procedure to be favoured over another. The exact risks for any patient depend on so many other variables that a clinical estimate of which procedure is preferable can only be made at the bedside. To be able to compare the global state of the patient, the future risks and the treatments necessary requires a ‘holistic’ understanding, and it cannot be provided using machine learning models built on patient data alone.

While the field of fundamental cell biology underpins all advances in our understanding of disease, it remains virtually unaffected by progress in machine learning technologies. One of the reasons for this is that it has traditionally relied on low-throughput means of generating data with a focus on establishing small numbers of input–output relationships. Mechanistic hypotheses generated from the identification of these relationships can often be naturally interrogated using simplified mechanistic models, and causal mechanisms established. More recently, the explosion in high-throughput methods of data collection has reinforced the, often negatively perceived, ‘butterfly-collecting’ nature of cell biology. Yet, the community remains focused on establishing mechanistic understanding. This dichotomy between data and purpose often leads to the development of a plethora of potential mechanistic models that explain small pieces of a much bigger picture. While these mechanistic models could potentially be assembled as inputs of larger machine learning algorithm, serious efforts in this direction are still lacking.

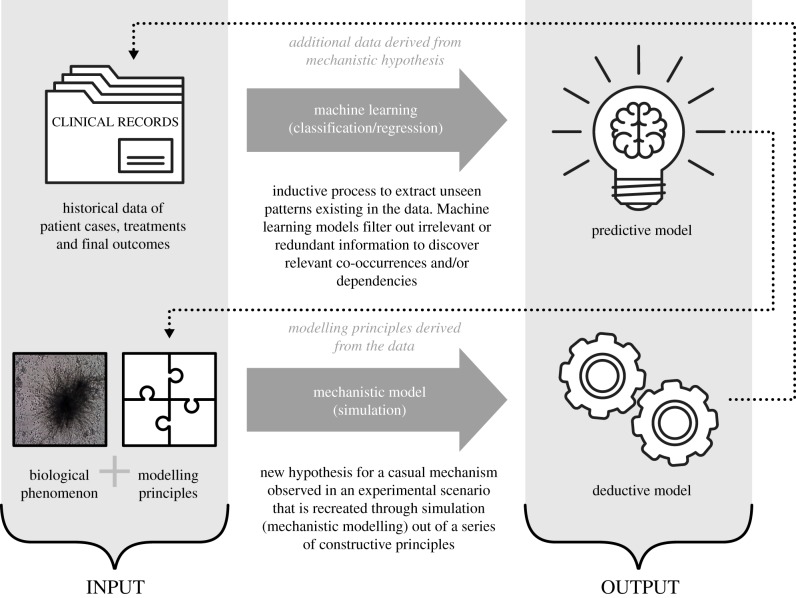
There are two synergic ways in which mechanistic and machine learning approaches may be combined (figure 1). Firstly, within the mechanistic modelling approach, specific components are learnt from the data [6]. An example is the use of multiscale simulations using surrogate models: a machine learning model obtained from the data produced by detailed simulations. Here, only a small number of simulations of the detailed model are run (in order to learn the model), and then the approximate surrogate model is used for future predictions. This approach is used mainly as a method to speed up expensive, computational, multiscale simulations. Secondly, within a machine learning-based pipeline, input information is raw data enriched by derived parameters generated by a mechanistic approach (in the same way improved probabilistic models get the benefit of more informative estimations of the ‘hidden variables’ [7]).

Figure 1.

The inputs and outputs from machine learning and mechanistic modelling approaches, and the potential for synergy between the two.

The integration of machine learning approaches and mechanistic modelling in cell biology can be found, for example, in the use of multivariate information measures such as partial information decomposition to identify putative functional relationships between genes from single-transcriptomic data [8]. The validity of the learnt (hypothesized) gene regulatory networks can then be tested using mechanistic modelling approaches, as part of the test–predict–refine–predict cycle so essential in the biological sciences. An example of the use of this approach is in the identification of how pluripotency regulatory networks are reconfigured during the early stages of embryonic stem cell differentiation [9]. However, there remains much work to be done in bringing together machine learning and mechanistic modelling approaches to best effect in the biological sciences.

The lack of progress towards integrating machine learning and mechanistic modelling approaches in fundamental biology studies is at odds with the widespread adoption of machine learning approaches by the clinical community. In fact, many new models and algorithms naturally find their first application in clinical scenarios. This discrepancy of collaboration certainly stems from the relative ease with which one can define the inputs and outputs of a clinical problem, as opposed to the complex fundamental problems tackled by cell biologists. Thus, many of the fast-changing computational approaches spearheaded by interdisciplinary collaborations in the clinical sciences end up escaping entirely this field. Fundamental biology should not choose between small-scale mechanistic understanding and large-scale prediction. It should embrace the complementary strengths of mechanistic modelling and machine learning approaches to provide, for example, the missing link between patient outcome prediction and the mechanistic understanding of disease progression. The training of a new generation of researchers versatile in all these fields will be vital in making this breakthrough. Only then can mechanistic models in cell biology find their real clinical use in the high-throughput world of the twenty-first century.

Data accessibility

This article has no additional data.

Authors' contributions

R.E.B. and A.J. conceived the manuscript. R.B., J.-M.P. and A.J. wrote the manuscript with inputs from J.J. All authors approved the final version of the manuscript and agree to be held accountable for the content therein.

Competing interest

There are no competing interests.

Funding

R.B. would like to thank the Leverhulme Trust for a Leverhulme Research Fellowship, the Royal Society for a Wolfson Research Merit Award, and the BBSRC for funding via BB/R00816/1. A.J. acknowledges funding from the European Union's Seventh Framework Programme (FP7 20072013) ERC Grant Agreement no. 306587 and from the EPSRC Healthcare Technologies Challenge Award EP/N020987/1.