Getting somewhere with the Red Queen: chasing a biologically modern definition of the hypothesis

Abstract

The Red Queen hypothesis (RQH) is both familiar and murky, with a scope and range that has broadened beyond its original focus. Although originally developed in the palaeontological arena, it now encompasses many evolutionary theories that champion biotic interactions as significant mechanisms for evolutionary change. As such it de-emphasizes the important role of abiotic drivers in evolution, even though such a role is frequently posited to be pivotal. Concomitant with this shift in focus, several studies challenged the validity of the RQH and downplayed its propriety. Herein, we examine in detail the assumptions that underpin the RQH in the hopes of furthering conceptual understanding and promoting appropriate application of the hypothesis. We identify issues and inconsistencies with the assumptions of the RQH, and propose a redefinition where the Red Queen's reign is restricted to certain types of biotic interactions and evolutionary patterns occurring at the population level.

1. ‘Down the rabbit hole’¹: introduction

The Red Queen hypothesis (RQH) was first proposed by Van Valen [1] to explain a pattern he argued was manifest in the fossil record involving component members of several major taxonomic groups: survivorship curves that were linear when plotted against geologic time. The RQH contains several additional elements Van Valen [1] derived from this pattern. First, in any taxonomic group that occupies the same adaptive landscape, the probability of survival is independent of age throughout its existence. Then, Van Valen [1] took this interpretation one step further and concluded that all members of such groups had an equal probability of extinction. This aspect of the RQH he termed the ‘Law of Constant Extinction’ which was held to be applicable across different organizational (e.g. population, community), and taxonomic (e.g. species, genera, families) levels. Finally, Van Valen [1] suggested that the RQH involved omnipresent competitive interactions among taxonomic groups; these were continually changing, but they were not getting relatively better in a competitive sense through time such that there was a zero-sum expectation (figure 1). Instead, they were metaphorically running in place and not getting anywhere: like the eponymous Red Queen from Lewis Carroll's ‘Through the Looking-Glass, and What Alice Found There’.

Figure 1.

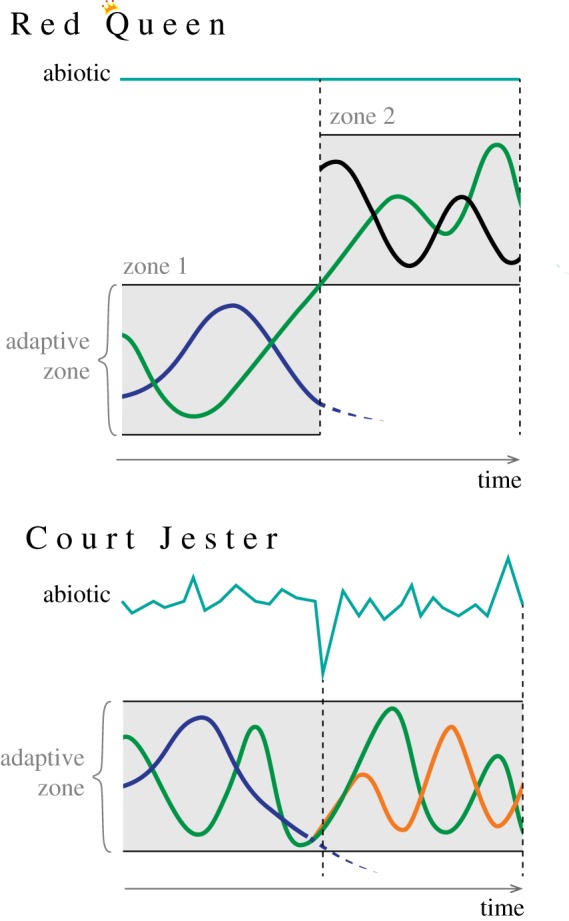
Evolutionary change under Red Queen hypothesis-type dynamics versus Court Jester hypothesis-type dynamics. The blue line represents the abiotic environment. Species A (green) represents a potential prey organism. Species B (purple) represents its potential predator. Species C (black) also preys on species A. Species D (orange) is a descendant taxon of species B. In both scenarios (Red Queen and Court Jester), species B goes extinct (represented by the dotted line). Under the Red Queen scenario (sensu Van Valen [1]), the extinction of species B is due to species A shifting from adaptive zone 1 to adaptive zone 2 as it moves towards a fitness optimum and ultimately exceeds the relevant traits of species B (traits relevant to the capacity of species B to capture and consume species A). The new adaptive zone that species A now occupies contains a different predator species (species C) whose fitness is affected by the arrival of species A, as per Van Valen's [1] zero-sum assumption. In this scenario, abiotic parameters remain unchanged and evolutionary change can still occur. In the Court Jester scenario, the extinction of species B is due to environmental changes that result in suboptimal conditions for species B. Populations within the species become isolated from one another, population sizes decrease, and almost all of the component populations die off, such that species B goes extinct; however, in one case an isolated population of species B diverges, survives and becomes a new species (species D). No changes in the adaptive zone of species A occur in this scenario, nor did they the cause the extinction of species B. Both hypotheses have different evolutionary and spatial scales. The RQH operates across individual populations on small spatial and short temporal scales, leading to differential survival of populations within communities. By contrast, the Court Jester hypothesis is tied to large-scale shifts in the physical environment, which would affect multifarious populations from species in different clades, with each population potentially responding individualistically to the perturbation [2].

Many aspects of Van Valen's findings have stimulated extensive debate and discussion. For instance, his purported link between extinction probability and species age has been disputed [3–7]. The RQH has also been the subject of reviews (e.g. [8–10]) and a variety of modelling-based studies (e.g. [11–15]). Some of these endorsed aspects of the core predictions of the RQH, others challenged them. Moreover, additional definitions of the RQH have been proposed [10] that differ from Van Valen [1]. Scientists have also attempted to use the RQH to explain phenomena beyond its original purview, for example, the dynamics of some host–parasite systems [16] and the role that these coevolutionary relationships may play in the maintenance of sexual reproduction [8,17–19].

Even as the scope of the RQH has broadened, at its core the RQH retains a key element: the primary drivers of macroevolution are held to be biotic interactions, in particular, the effects that the origin of a new trait in one group (populations, species, etc.) has on each group it interacts with [9]. This feature is not exclusive to the RQH. Further, there is an emphasis in the RQH on groups interacting with equal effect [1]. This is potentially problematic, as real ecological dynamics are usually far more complicated [20] and groups rarely have equal effects on each other [21].

Also, notably many studies [2,3,20–24] have disputed the validity of numerous aspects of Van Valen's [1] original RQH. Thus, it is perhaps surprising that the RQH continues to receive support and evolve as a concept [9,25–28]. In the light of these theoretical and conceptual peregrinations, we re-examine the RQH, discuss original and subsequent expositions and put forward a single definition, informed by Van Valen's [1] original exposition, that also accounts for subsequent treatments. The aim is to provide clarity to what has at times been a murky topic in evolutionary biology.

2. ‘It's no use going back to yesterday, because I was a different person then’: the RQH evolves

Stenseth & Maynard Smith [12] suggested rejecting the RQH's zero-sum expectation and proposed that RQH dynamics may only apply in ecosystems where evolutionary rates are greater than zero, where evolution is mediated by biotic interactions, and where the physical environment remains unchanged. The purpose of this was not to refute the RQH, but to provide the RQH with an alternate null hypothesis where environmental change is the impediment to evolutionary stasis, and evolutionary advances by one species need not necessarily result in a net negative effect of the same magnitude across other species. While this new hypothesis was not the RQH sensu Van Valen [1], it did open up the application of a RQH-like framework beyond its original domain and began a trend of placing different evolutionary phenomena under the banner of the RQH that did not entirely align with the RQH sensu Van Valen [1]. For instance, it is suggested that the RQH provides a mechanism for the evolution and maintenance of sex by explaining the value of recombination due to the negative frequency-dependent selection associated with parasitism [8,17,18], with sexual lineages better at evading parasites via genetic recombination, thereby forcing continual coevolution on the part of the parasite to maintain a constant level of virulence [16]. Similar types of continual coevolutionary patterns have also been proposed for predator–prey relationships [19], with predators maintaining sexual reproduction to preserve a constant level of predation success as variable prey populations within species shift in abundance between those with a greater capacity for obtaining nutrients and those better able to defend against predation.

In an attempt to clarify and categorize the growing body of RQH-influenced ideas, an important synthesis was provided by Brockhurst et al. [10], who argued that there were three distinct classes of concepts that aligned with the RQH based on the patterns they displayed and the processes involved. The work of Brockhurst et al. [10] also continued the trend of the RQH evolving beyond the original purview of Van Valen [1]. Brockhurst et al.'s [10] classes were designated the Escalatory, Fluctuating and Chase. The Escalatory-RQH occurs when species interactions lead to directional selection and both interacting species move towards a fitness optimum as each struggles to ‘exceed’ the relevant trait of the other species [10]. Such a dynamic is posited in the case of evolutionary arms races. The Fluctuating-RQH is associated with an oscillating mode of selection, where two antagonist species oscillate backwards and forwards between fitness optima, with one interactor always lagging behind the other [10]. This involves continual, yet non-directional, evolutionary motion for both antagonists, analogous to constrained stasis or a random walk in species morphology that produces no net change over the long term [29,30]. Finally, the Chase-RQH supposes that across the range of two interacting or co-evolving species, respective populations may be responding in different ways to the biotic milieu they experience [10]. As populations of the chased antagonist seek to escape co-occurring populations of the chaser through the evolution of novelty, diversity within populations becomes reduced but divergence between populations increases as they spread across a multidimensional phenotypic space. All three classes outlined by Brockhurst et al. [10] invoke biotic interactions among two groups as the drivers of evolutionary change. The Escalatory-RQH approximates the RQH sensu Van Valen [1]: a key difference is the latter focuses on higher taxa. The Chase-RQH, however, diverges from the RQH sensu Van Valen [1] because it involves several interacting component populations of different species, each evolving in varying directions due to distinct selective pressures. The Fluctuating-RQH also potentially diverges from the RQH sensu Van Valen [1] if the emphasis is placed on changes in specific fitness or phenotypic states, because species are hopping back and forth between distinct states rather than continually running in place. Alternatively, it is possible that if the change in question is migration across the evolutionary landscape, or changes in the dynamics of species interactions, then the relevant species are indeed running in place and the fluctuating-RQH can be considered equivalent to the RQH sensu Van Valen [1].

3. ‘Off with her head!’: problematic aspects of the RQH

Acceptance of the RQH has not been universal, and a number of authors have either implicitly or explicitly opposed Van Valen's [1] conclusions. For instance, the competitive species interactions invoked by the RQH have been shown as unlikely to result in persistent evolutionary change [31]. Questions have also been raised as to whether the taxonomic survivorship curves presented by Van Valen [1] are truly linear [5,7,32–35]. While evidence from planktic microfossils has been used to support log-linearity of species-level survivorship curves [11,36–39], results for planktic foraminifera have, by contrast, demonstrated a positive relationship between extinction risk and species age [6,40,41]. Mass extinction has been singled out as one significant phenomenon that causes groups to deviate from constant extinction over time (e.g. [35,42]). Van Valen [1] himself noted that mass extinctions in specific clades (e.g. ammonites) were exceptions to the ‘Law of Constant Extinction’ as they represent times of exceptional elevation of extinction rates. Intriguingly though, if mass extinctions truly eliminate large numbers of species effectively at random then, under certain circumstances of prior diversification, they could result in situations where the probability of extinction of species is independent of its duration [3].

Conceptual criticisms of the RQH have also focused on whether, even assuming taxonomic survivorship curves are linear, the ‘new evolutionary law’ Van Valen [1] erected was valid [3,4,43,44]. For example, McCune [3] concluded that, while the probability of extinction of taxa within a clade may be constant with respect to the duration of those taxa, this does not mean that the rate or the probability of extinction is constant per unit time. She thus argued that the RQH is only one of many potential phenomena that might explain linear taxonomic survivorship curves.

The RQH also depends upon substantive phyletic speciation and associated pseudoextinction [4,12]. This creates a paradox for the RQH because, if phyletic speciation is a primary evolutionary mode, this means that the rate of extinction will be directly correlated with the rate of evolution. Yet the RQH posits that species extinction should be independent of duration. As Vrba [4] recognized, the rate of phyletic speciation cannot be independent of itself.

4. ‘I'm not crazy. My reality is just different than yours’: abiotic alternatives to the RQH

Another significant criticism of the RQH stems from the limited role it imputes to abiotic factors as important drivers of evolutionary change [2,4,24]. Evidence from a variety of sources [45–51] uphold abiotic factors as important drivers of evolution and speciation. This has led to proposed alternatives to the RQH which focus on the physical environment as the main driver of evolution. The most prominent of these is the ‘Court Jester’ hypothesis [23] (figure 1), with the name chosen to highlight the capricious effects environmental changes can have on evolution. This is in contradiction to the more predictable effects that might be associated with the RQH. The Court Jester attempts to unite under one concept the plethora of previously proposed ideas that support abiotic factors as main drivers of evolutionary change (e.g. ‘turnover-pulse hypothesis’ [4]; ‘stationary model’ [12] and ‘coordinated stasis’ [52]).

Proponents of abiotic change as the chief driver of evolution have been particularly critical of the assertion that competition between groups at taxonomic ranks higher than the species, where the RQH sensu Van Valen [1] is focused, could result in these groups diverging or going extinct [2,4,24]. If and when the RQH does operate, it should be at the level of individual populations at small spatial and short temporal scales. Entities at higher hierarchical levels (sensu [2,4]), such as clades which consist of many species, should not be expected to respond as a unit ([45]; though see [53] for a divergent opinion). Indeed, there is scant evidence that the RQH operates at scales involving entire continents or millions of years [2,4,23,24]. Instead, individual populations of species living in different communities and climates would interact in different ways with numerous populations of other species across the totality of their ranges, and respond individualistically to any perturbations [2,4,23,24]. While refocusing the RQH onto the species, and especially the population level, would address these concerns [9], it is not the same as the RQH sensu Van Valen [1].

5. ‘Who in the world am I? Ah, that's the great puzzle’: what is the proper domain of the RQH?

As the RQH has been increasingly applied beyond Van Valen's [1] original focus, it has become increasingly difficult to evaluate its legitimacy. It is first and foremost necessary to ascertain whether the RQH sensu Van Valen [1] has been generally upheld. If it has been, then the RQH provides an explanation for how biotic interactions could drive phenotypic change, even if only under certain circumstances. However, if it is not generally upheld by most studies, then the question becomes which parts of the RQH should be retained in evolutionary theory and how should the RQH be viewed in the future?

It has been proposed that rejecting the RQH is only possible by demonstrating that evolutionary and ecological changes of organisms (presumably at the species or population level) are primarily due to abiotic change, while at the same time also considering the effect of biotic interactions or abiotic change that is biotically driven [9]. We diverge from this proposal as this set of conditions is probably unachievable, because a period of constancy of any potential abiotic factors is virtually absent from the geological record [14]. Another challenge to evaluating the RQH is that biotic and abiotic factors can interact to drive macroevolution [54,55], making it hard to differentiate primary biotically driven evolution from secondary biotically driven evolution instigated by abiotic forcing. Because of these challenges, here we focus on an alternative method to assess the validity of the RQH sensu Van Valen [1]. As would be the case for any hypothesis, if any (or several) of the core assumptions of the RQH are found to be spurious, then the hypothesis itself would be difficult to uphold, and usage should only be done with significant caution and caveats.

Upon consideration of the evidence for and against the RQH sensu Van Valen [1] as a valid macroevolutionary concept, potential problems with the hypothesis emerge. Of greatest concern are the evidence-based [5–7,32–35] and concept-based [3,4] refutations of the foundational assumption of the RQH that taxonomic survivorship curves are linear. This undercuts the very notion of Van Valen's [1] ‘Law of Constant Extinction’. These refutations are supported by an even larger body of the literature in palaeontology and community ecology, demonstrating that extinction is associated with a range of parameters that are not purely stochastic (e.g. geographical range size is a demonstrated key predictor of extinction [55]). Van Valen, despite erecting his ‘law’, acknowledged ‘the probability of extinction is not constant over geological time’ ([1], p. 18) and that constant extinction only prevails if extinctions associated with major perturbations are ignored. Mass extinctions, of course, are a significant feature of the history of life. If the assumption of constant extinction rates is invalid, and extinction probabilities are not age independent, this impugns the RQH as an explanation of macroevolutionary patterns. Evolutionary advances by one species need not produce a net negative effect of the same magnitude across all other coexisting species, because no mechanism is required to maintain equal extinction probabilities. The apparent difficulty of reducing macroevolutionary dynamics to a zero-sum process [12] finds meaning when the ‘Law of Constant Extinction’ is rejected [20,21].

There are additional issues that, when considered singularly, would not be enough to refute the foundational assumptions of the RQH but, when considered collectively, call into question their cogency. First, Van Valen [1] used data from groups that have subsequently been identified as paraphyletic, such that they lack evolutionary significance [56]. Second, only five of the 56 clades Van Valen [1] analysed were treated at the species level, with the remaining majority comprising either genera or families. The notion that competition, selection or anagenesis could involve higher taxa is inconsistent with basic evolutionary principles. For example, genera are arbitrary units that are not necessarily monophyletic or equivalent across clades [56] and it is unlikely evolutionary processes can be applied to them.

A further difficulty with upholding the RQH involves the phenomenon of pseudoextinction. Although Van Valen [1] noted that pseudoextinction is an infrequent process in the fossil record (at higher taxonomic levels), frequent pseudoextinction is perforce necessary in any system where the RQH is the explanatory mechanism for evolutionary change [4,12,57]. Like constant extinction, frequent pseudoextinction has been refuted in the literature [58], and does not make sense in light of modern phylogenetic understanding. Analyses of species origination for planktic foraminifera, a group where taxon durations can be accurately estimated at the species level, have demonstrated pseudoextinction to be a rare occurrence (less than 10%) at the macroevolutionary scale [58,59], and once putative ‘archetypal’ examples of anagenesis with concomitant pseudoextinction have subsequently been shown to involve cladogenesis [60].

Ultimately, given the challenges to the evidence and core assumptions underlying Van Valen's [1] RQH, it seems hard to advocate that his microevolutionary mechanism of intrinsic biotic conflicts is what drives the macroevolutionary trends observed in the fossil record. There may still be a place for a RQH-like framework but, if so, it operates at the level of populations within ecosystems [2,4,24] and is not the RQH sensu Van Valen [1].

6. ‘Everything's got a moral, if only you can find it’: a contemporary definition of the RQH

The paucity of support for the RQH sensu Van Valen [1] does not mean that we propose no conditions exist where biotic interactions could be a significant mechanism for evolutionary change. It also does not take away from the fact that Van Valen's [1] original RQH was highly valuable, stimulated a variety of important research and greatly furthered conceptual understanding. Antagonistic interactions are potential examples where a qualified version of the RQH could conceivably apply, such as populations of hosts and their parasites or predators and their prey [19,61].

We propose that were one to take Van Valen's RQH and modify it based on developments in evolutionary theory, palaeontology and phylogenetics made after 1973, then what results is Brockhurst et al.'s [10] Chase-RQH. Although Brockhurst et al. [10] did not go so far as to nominate the Chase-RQH (or any of their other classes of Red Queen) as a replacement of the RQH sensu Van Valen [1], we do so here (figure 2). It is not Van Valen's [1] RQH because it does not focus on constant extinction rates within higher taxonomic groups, nor does it claim that the probability of extinction of any taxonomic group is independent of its duration, but it does capture coevolutionary relationships where two interacting, antagonistic populations are continually changing yet neither is ‘improving’ relative to the other. It also parallels Thompson's [62] strongly supported view of coevolution, which emphasized the geographical mosaic of the phenomenon. Further, it agrees with Eldredge's [2], Vrba's [4], Barnosky's [23], Benton's [24] and Liow et al.'s [9] contention that the RQH be refocused at the species/population level and that Red Queen phenomena occur at the level of populations within ecosystems, not species or higher taxa across vast tracts of geographical space. Brockhurst et al.'s [10] Chase-RQH also resolves the problems with Van Valen's [1] RQH that pertain to pseudoextinction. In fact, the Chase-RQH can lead to cladogenesis, as individual populations may deviate from the species as a whole (figure 2), such that a descendant may evolve while its ancestor persists. This divergence among populations subject to different selection regimes places Chase-RQH within the tenets of modern microevolutionary theory. The Chase-RQH also aligns with models linking host–parasite interactions to the evolution and maintenance of sex. Most importantly, the Chase-RQH establishes a link between microevolutionary processes and macroevolutionary patterns that is internally consistent with current thinking in evolutionary biology.

Figure 2.

A contemporary definition of RQH based upon Brockhurst et al.'s [10] Chase Red Queen and informed by Vrba's [4] turnover pulse hypothesis and Barnosky's [23] Court Jester hypothesis. Two interacting co-evolving species (species A and B) have seemingly fixed relative fitness over time at the macroscale. A detailed examination (first box) shows at the microscale that actually species A is a chased antagonist pursued by species B across an adaptive zone, with a lag in the response of species B relative to the shifts in mean fitness of species A. These shifts in mean fitness for species A and B represent disparate reactions by individual populations of each species as they respond individualistically to biotic or abiotic perturbations (second box). As populations of the chaser seek to keep pace with co-occurring populations of the chased antagonist, individual populations deviate from the species mean trait values and may even go extinct (e.g. species B, pop 4). Because the mean relative fitness of the two species is constant over time, the relative fitness of co-occurring populations of species A versus species B must be maintained over time, but the relative fitness of non-co-occurring populations of species A versus species B need not remain static. Significant abiotic events can potentially alter this balance, with individual populations of either species becoming isolated and forming a new species, or the extinction of key populations leading to the overall extinction of either species (but not necessarily both).

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests

Funding

This research was supported by NSF ADBC-1206757 and DBI-1602067.