A meta-analysis approach with filtering for identifying gene-level gene-environment interactions

Abstract

There is a growing recognition that gene-environment interaction (GxE) plays a pivotal role in the development and progression of complex diseases. Despite a wealth of genetic data on various complex diseases/traits generated from association and sequencing studies, detecting GxE via genome-wide analysis remains challenging due to power issues. In genome-wide GxE studies, a common strategy to improve power is to first conduct a filtering test and retain only the genetic variants that pass the filtering step for subsequent GxE analyses. Two-stage, multi-stage, and unified tests have been proposed to jointly consider the filtering statistics in GxE tests. However, such GxE tests based on data from a single study may still be underpowered. Meanwhile, large-scale consortia have been formed to borrow strength across studies and populations. In this work, motivated by existing single-study GxE tests with filtering and the needs for meta-analysis GxE approaches based on consortia data, we propose a meta-analysis framework for detecting gene-based GxE effects, and introduce meta-analysis-based filtering statistics in the gene-level GxE tests. Simulations demonstrate the advantages of the proposed method – the ofGEM test. We apply the proposed tests to existing data from two breast cancer consortia to identify the genes harboring genetic variants with age-dependent penetrance (i.e., gene-age interaction effects). We develop an R software package ofGEM for the proposed meta-analysis tests.

1 Introduction

Complex diseases and traits arise as the consequence of many factors, including genetic factors, environmental exposures, and the interplay among them. Gene-environment interaction (GxE) effects may contribute to the “missing heritability,” and studying GxE can help to elucidate disease/trait aetiology [Thomas, 2010]. The detection of GxE effects and the identification of individuals or populations susceptible to specific environmental hazards are essential to the development of precision medicine [Collins and Varmus, 2015].

Despite the enthusiasm for detecting GxE effects via genome-wide scans of existing genome-wide association (GWA) or sequencing data, such endeavors are likely underpowered [Smith and Day, 1984; Murcray et al., 2009]. Only a limited number of GxE effects have been detected using data from individual association studies and stringent genome-wide significance thresholds [Thomas, 2010; Rothman et al., 2010]. There is also growing recognition that very large sample sizes are required in order to identify genetic variants that have effects modified by the environment [Smith and Day, 1984; McCarthy et al., 2008]. With the goal of identifying new genetic risk factors using large samples, many large consortia have been formed to study a wide-array of disease phenotypes using shared data resources [Hunter et al., 1982; Hu et al., 2013; Ahsan et al., 2014; Huo et al., 2016]. Novel and powerful meta-analysis approaches are needed to address the new challenges arising from the analysis of consortium data.

With data from a single GWA study, a common strategy to improve power for detecting GxE effects is to first filter out the majority of unpromising genetic variants based on some filtering test(s) and then consider only the remaining variants in the variant-level GxE tests. The genome-wide significant threshold is relaxed to the genome-wide error rate divided by the number of retained variants. The filtering test and the GxE test are required to be independent under the null to preserve the overall genome-wide error rate [Dai et al., 2012]. Such two-stage or multi-stage analysis strategies relax the stringent genome-wide significance thresholds and improve the power for detecting variants with GxE effects [Kooperberg and LeBlanc, 2008; Murcray et al., 2009]. In addition to variant-level analysis, gene-based or set-based approaches have been proposed to detect those individually-weak-but-collectively-strong GxE effects within a gene or a set. Many gene-based association tests [Wu et al., 2011; Chen et al., 2012] can be generalized to test for gene-level GxE effects. Chatterjee et al. [2006] proposed a Tukey’s 1-degree-of-freedom GxE test, which assumes GxE effects are proportional to the main effects of variants in a gene. Variance component methods have also been proposed for testing gene-level GxE effects [Lin et al., 2013; Tzeng et al., 2011; Zhao et al., 2015; Lin et al., 2016]. Jiao et al. [2013] proposed a gene-based GxE test in which the gene-environment (G–E) correlations are used to filter variants showing no promises of GxE effects in case-control studies. More recently, Liu et al. [2016] developed a unified gene-based GxE testing framework that simultaneously considers filtering on individual variants and testing for GxE effects on the retained variants in a gene. They calculate the estimated optimal filtering threshold for each gene (a set of variants) and show that the unified test with an adaptive filtering threshold generally improves the power for gene-based GxE analysis.

These aforementioned methods are proposed for GxE analyses in a single association study, but there are very few methods available for meta-analysis of GxE effects based on summary statistics from consortium data. Lee et al. [2013] proposed gene-based association tests for meta-analysis with rare variants, and the tests can also be applied to meta-analysis of GxE effects. In their work, they consider both fixed-effects and random-effects meta-analysis tests to aggregate all the genetic variants in a gene.

In this work, we propose to introduce filtering into the gene-based GxE tests in the meta-analysis setting. We first perform variant-level “meta-filtering” tests that combine the filtering statistics across multiple studies for each individual variant, and then use meta-analysis approaches to test for gene-based GxE effects on only the retained variants. We study both fixed-effects and random-effects meta-analysis approaches, and propose to combine the strengths of both into a unified test – the omnibus filtering-based GxE meta-analysis (ofGEM) test. We compare the proposed ofGEM test with competing methods and demonstrate the control of type I error rates as well as a power advantage. As an extension, we also suggest a gene-based GxE test for consortium data with more than one ethnic group. Note that unlike two-stage variant-level GxE tests, the overall genome-wide significance threshold is not relaxed in our unified gene-level test. If a gene has no variant passing the filtering, the gene will be assigned a p-value of 1 and is still considered in the multiple testing adjustment. Therefore, our method does not require independence between filtering and GxE testing. We apply the proposed tests to two data sets from breast cancer GWA consortia [Ahsan et al., 2014; Huo et al., 2016], with samples of European and African ancestries respectively, to identify the genes harboring variants with age-dependent penetrance (i.e., gene-age interaction effects). Both studies include multiple sub-cohorts or sub-populations, and as such a meta-analysis rather than a pooled analysis approach would better account for sample heterogeneity. We develop an R software package ofGEM for the proposed meta-analysis test.

2 Methods

In this work, we considered meta-analysis methods for jointly testing GxE effects of k variants in a gene or a set. Let θ_j be the interaction effect of the j-th genetic variant and the environmental exposure. We are interested in testing the null hypothesis of no interaction effect for any variant in the gene versus the alternative hypothesis of at least one variant in the gene having a non-zero interaction effect.

$$H_0:{\theta }_j=0\text{for}\text{all}j(j=1,\dots ,k)\text{versus}{H}_1:\text{at}\text{least}\text{one}{\theta }_j\ne 0.$$

The methods discussed in this section took variant-level filtering and GxE test statistics from each study as input. Those summary statistics can be calculated from general models, and are considered to be normally or approximately normally distributed. For example, in a casecontrol study one may fit a logistic regression to test for GxE effects on a binary outcome (Y ),

$$\text{logit}(Pr(Y=1))={\alpha }_0+{\alpha }_1·E+{\alpha }_2·G_j+{\theta }_j·G_j\times E+{\alpha }_3·\mathbf{C},$$

where E is the environmental variable, G_j is the genotype of the j-th genetic variant, G_j ×E is the statistical interaction term of genotype and environment with θ_j being the interaction effect, and C is a matrix of a set of covariates. For each variant j, we calculated the Wald statistic for testing H₀ : θ_j = 0, and denoted it as Z_j.

In case-control studies, a commonly-used variant-level filtering test for GxE is to test for gene-environment correlations in the combined case-control samples [Murcray et al., 2009]. For quantitative traits, one may test for equal variances across genotype groups to filter out the less-promising variants [Paré et al., 2010]. In the application section of the current work, we performed a meta-analysis of multiple case-control studies, and for the filtering statistics X_j ’s, we used the t-statistics for testing non-zero correlations of G_j’s and E in the combined case-control samples.

2.1 Testing for gene-based GxE effects with data from a single study

We first reviewed the gene-based GxE test with variant-level filtering and testing statistics from a single GWA study. A unique characteristic of GxE effects in association studies is that those effects are likely to be very sparse in the genome. By filtering out variants that are unlikely to have GxE effects, one may increase the ratio of variants with GxE effects to all variants in a gene and improve the power to detect genes with GxE effects [Jiao et al., 2013]. The power of this approach will depend on the filtering threshold used. Liu et al. [2016] further proposed a general framework for gene-based GxE test with adaptive filtering for each gene based on the following statistic:

$$T=\sum _{j=1}^k{w}_j{Z}_j^2·𝟙\{\mid X_j\mid \ge z_{\eta /2}\},$$

where w_j is the weight for variant j, X_j is the filtering statistic, Z_j is the statistic testing for GxE effects, z_η/2 is the (1 − η/2) × 100-th quantile of N(0, 1), and η is the adaptive filtering threshold for the gene being tested. The optimal filtering threshold primarily depends on the number of variants with GxE effects (k₁) and the total number of variants in a gene, i.e., the gene size (k).

2.2 Meta-analysis approaches for gene-based tests

To combine data from multiple studies, Lee et al. [2013] proposed and discussed a general framework for meta-analysis of gene-based tests in association studies. The proposed framework can also be applied to gene-based GxE tests. Assuming homogeneous GxE effects across multiple studies, they proposed a fixed-effects approach that first combined the score-statistics across different studies for each variant and then aggregated the squared collapsed score statistics of all variants in a gene:

$$Q_{\mathit{hom}-\mathit{meta}-\mathit{SKAT}}=\sum _{j=1}^k{\left(\sum _{s=1}^S{w}_{js}{Z}_{js}\right)}^2,$$ (1)

where w_js is the weight and Z_js is the GxE testing statistic for variant j in study s.

With heterogeneous GxE effects, they proposed a random-effects approach that combined the squared score statistics of all k variants across S studies:

$$Q_{\mathit{het}-\mathit{meta}-\mathit{SKAT}}=\sum _{j=1}^k\left(\sum _{s=1}^S{w}_{ks}^2{Z}_{js}^2\right).$$ (2)

2.3 Meta-analysis approaches for gene-based GxE tests with filtering

The meta-analysis tests proposed by Lee et al. [2013] aggregated the effects of all variants in a gene across studies. However, those tests did not fully utilize information that may help to filter out the variants that are unlikely to have GxE effects. In this subsection, we propose a meta-analysis approach with variant-level filtering and gene-level GxE testing based on summary statistics from S studies. Our method also considers different levels of heterogeneity of GxE effects across studies.

2.3.1 A meta-filtering strategy

When the sample size of an individual study is moderate to small, the power of filtering tests could be low. Applying filtering tests to each individual study may filter out many variants with potential GxE effects, and could hurt the overall power for testing GxE. As such, we propose to conduct filtering tests based on the combined data across studies. Let {X_js : j = 1, … , k; s = 1, … , S} be the filtering statistic for variant j in the s-th study.

For the fixed-effects model in (1) assuming homogeneous GxE effects, we propose a corresponding fixed-effects meta-filtering statistic for variant j across multiple studies:

$$X_j^{\text{MF-fixed}}=\sum _{s=1}^S{w}_{js}{X}_{js},$$ (3)

where MF stands for meta-filtering, and w_.s is the weight for each study. One may use the weight, $w_{.s}=\sqrt{n_s/N}$, where n_s is the sample size for the s-th study, and N = n₁ +…+n_S. Here we used equal weights for variants, w_.s = w_s. One may also set the variant-level weights to be proportional to the minor allele frequencies (MAFs), and those options have been extensively discussed elsewhere [Lee et al., 2013].

For the random-effects model in (2) assuming heterogeneous GxE effects, we propose a random-effects meta-filtering statistic as

$$X_j^{\text{MF-random}}=\sum _{s=1}^S{w}_{js}^2{X}_{js}^2.$$ (4)

2.3.2 The meta-analysis tests with meta-filtering

For meta-analysis assuming homogeneous GxE effects, we propose a gene-level fixed-effects statistic with the meta-filtering in (3) as below:

$$T_{hom-\text{MF-fixed}}=\sum _{j=1}^k{\left(\sum _{s=1}^S{w}_s{Z}_{js}\right)}^2/\sum _{s=1}^S{Z}_{js}^2·𝟙\{\mid X_j^{\text{MF-fixed}}\mid \ge z_{\eta /2}\},$$ (5)

where z_η/2 is the (1 − η/2) × 100-th quantile of N(0, 1) and η is the filtering threshold of p-values.

For meta-analysis assuming heterogeneous GxE effects across studies, we propose the gene-level random-effects statistic with the meta-filtering as in (4):

$$T_{\text{het-MF-random}}=\sum _{j=1}^k\left(\sum _{s=1}^S{w}_s^2{Z}_{js}^2\right)·𝟙\{X_j^{\text{MF-random}}\ge q_{\eta }\},$$ (6)

where q_η is the (1− η)×100-th quantile of a weighted χ² distribution under the null [Davies, 1980].

In comparison with the statistics in (1) and (2), the test statistics in (5) and (6) incorporate variant-level meta-filtering in the gene-based meta-analysis tests.

2.3.3 The omnibus filtering-based GxE meta-analysis (ofGEM)

The fixed- or random-effects tests have been shown to have better power when the effects of interest are homogeneous or heterogeneous, respectively, across studies [Lee et al., 2013]. In practice, the study heterogeneity is often unknown and could vary across genes.

The homogeneous fixed-effects test and the heterogeneous random-effects test are complementary tests. Each is better suited to detect a different type of gene with different levels of study heterogeneity. With unknown study heterogeneity, it is desirable to have a test that is powerful regardless of whether the true effects of interest are homogeneous or heterogeneous across studies. One may take the minimum of the two p-values (i.e., p-values from fixed- and random-effects tests) and adjust the significance by Bonferroni correction. More recently, Soave et al. [2015] proposed to use Fisher’s method to combine two independent and complementary tests. Here we adopted the Fisher’s method to combine the p-values based on tests (5) and (6), and we termed this approach as the omnibus filtering-based GxE meta-analysis (ofGEM) test. Note that here we used “omnibus”: in a broad sense to imply that the significance of either fixed- or random-effects tests may trigger the significance of the proposed test. Figure 1 presents a flowchart of the proposed test. When each Z_js is an independent normal variable with zero mean, ${\sum }_{s=1}^S{w}_s{Z}_{js}/\sqrt{{\sum }_{s=1}^S{Z}_{js}^2}$ is independent of ${\sum }_{s=1}^S{Z}_{js}^2$ [Lehmann and Romano, 2006], and the test statistics from (5) and (6) would be independent under the null.

Figure 1.

The flowchart of the proposed ofGEM test for meta-analysis of gene-level GxE, considering filtering statistics.

2.3.4 An extension: The meta-analysis GxE test for data from two or more ethnic groups

Some very large consortia may have samples and studies from different ethnic groups. In analyzing those data, it is expected that studies of the same ethnic group are more homogeneous, and studies across different ethnic groups are more heterogeneous.

Here we extend the filtering-incorporated fixed-effects test in (5) and propose a grouped fixed-effects GxE test for data from B ethnic groups. The grouped fixed-effects test first calculates the fixed-effects statistic with meta-filtering on studies within each ethnic group and then aggregates the statistics from multiple ethnic groups. The test statistic is given by

$$T_{\text{grp-MF-fixed}}=\sum _{b=1}^B{T}_{hom-\text{MF-fixed}}^b=\sum _{b=1}^B\sum _{j=1}^k{\left(\sum _{s\in {\mathrm{\Omega }}_b}{w}_s{Z}_{js}\right)}^2/\sum _{s\in {\mathrm{\Omega }}_b}{Z}_{js}^2·𝟙\{\mid X_{jb}^{\text{MF-fixed}}\mid \ge z_{\eta /2}\},$$ (7)

where Ω_b contains the study indices for studies from the b-th group (b = 1, 2, … , B), and $X_{jb}^{\text{MF-fixed}}$ is the meta-filtering statistic for variant j based on the studies from the b-th group. This grouped test applies the fixed-effects test in (5) to each ethnic group and then combines the group statistics as the overall statistic for a gene being tested.

Similarly, we propose the grouped random-effects tests, T_{grp-MF-random}. This test can be formulated by applying the random-effects tests in (6) to studies from each ethnic group and then combining the group statistics for the genes of interest. Additionally, one may further obtain the grouped ofGEM test, T_grp-MF-ofGEM, by combining the grouped fixed- and random-effects p-values using Fisher’s method.

2.4 The filtering thresholds

A major innovation of our proposed test is to incorporate filtering into meta-analysis of gene level GxE tests. It has been shown that in the analyses of individual studies, filtering can lead to an increase in the proportion of non-null variants in a gene, increasing the power to detect gene-level GxE effects [Jiao et al., 2013; Liu et al., 2016]. The filtering thresholds may affect the overall gene-level testing power. When the filtering threshold is too stringent, many of the variants with potential GxE effects may be filtered out and power could be reduced. When the filtering threshold is too liberal, power may not improve much compared to tests without filtering.

For gene-level GxE tests in a single association study, Jiao et al. [2013] employed a fixed filtering threshold of 0.1 for most of the genes in the genome. Liu et al. [2016] proposed to adaptively calculate the optimal filtering threshold for each gene in the genome. The calculated optimal filtering thresholds largely depend on the gene size, and the calculation requires specifying the assumed or expected GxE effect sizes.

For the fixed-effects model with meta-filtering in (5), the optimal filtering threshold can be calculated directly using the formula for a single study proposed in Liu et al. [2016], by specifying the assumed homogeneous effect sizes for all studies. This is because it has been shown that when GxE effects are homogeneous across studies, the power of the fixed-effects meta-analysis test with no filtering is almost identical to the power of the joint analysis of all samples pooled together [Lee et al., 2013]. The calculation of the optimal filtering threshold proposed in Liu et al. [2016] is based on the pooled analysis and can be used to obtain the approximated optimal threshold for meta-analysis with homogeneous GxE effects.

For the random-effects model with meta-filtering in (6), the calculation of the optimal filtering threshold would require the specification of heterogeneous effect sizes for different studies. The level of heterogeneity may heavily influence the calculated filtering threshold. In reality, the heterogeneity across variants and studies is often unknown and is hard to specify. Misspecification of those parameters could lead to a sub-optimal filtering threshold, which may not improve the power to detect GxE over a fixed filtering threshold. Therefore in the current work, for all the meta-analysis, regardless of fixed- or random-effects models, we followed Jiao et al. [2013] and adopted a fixed and liberal p-value threshold of 0.1 in the filtering tests.

2.5 Significance evaluation

The presence of linkage disequilibrium (LD) in real data makes it challenging to evaluate the significance of each gene based on the proposed tests. Moreover, most consortia would only share summary statistics of individual studies, and the raw genotype data are often not available. Permutation-based p-value calculation is not only computational prohibitive but also impractical.

Here we adopted the sequential sampling procedure proposed in Liu et al. [2016]. Specifically, with centered genotype and environmental data, and t-statistics (or other approximately normally distributed statistics) as the filtering and testing statistics, we can approximately sample the null variant-level statistics of each gene in S studies {(X_1s, …,X_ks), s = 1, … , S} and {(Z_1s, …,Z_ks)} from a multivariate normal distribution N(0,R), where R = (R_ij)_k×k, R_ij = cor(G_i,G_j) for any i and j, with G_i being the genotype at location i. In other words, one may use the LD matrix to approximate the correlation matrix of summary statistics of variants in a gene under the null hypothesis. After sampling the null sets of variant-level statistics from the multivariate normal distributions, we computed the null ofGEM statistics and calculated the p-value for each gene. The R matrix is the LD matrix of genotype correlations and can be estimated based on data from the 1000 Genomes Project or based on available samples in the consortia [Yang et al., 2012; Hu et al., 2013].

To further improve computational efficiency, for a given gene, if no variant passed the meta-filtering test, the p-value was set to 1 and no further sampling was needed. For genes with at least one variant passing the meta-filtering, we first drew L = 100 sets of null filtering and testing statistics from N(0,R). If the p-value calculated based on these 100 sets of null statistics was less than 0.1, then we drew 9 times more sets (i.e. L = 1000) to obtain a p-value with higher precision. We repeated this procedure until the p-value was greater than 10/L or the total number of sampling exceeded 10⁸ – the precision needed for reaching the genome-wide gene-level significance.

3 Simulations

3.1 Evaluation of type I error rate

In this subsection, we use simulations to assess the control of type I error rate of the proposed ofGEM test, in the presence of LD. Additionally, Lin et al. [2013] have shown that the single variant GxE test can be biased in the presence of the strong main effect and LD. Here we simulated data under the null in the presence of main genetic effects and LD to evaluate the control of type I error rates by different methods.

In the following simulation, we took the real genotype data and the age variable as a continuous “environmental” variable from the study by Ahsan et al. [2014] – the same data we analyze in the application section. We randomly selected 243 genes with 5–15 common variants (MAF ≥ 5%) in LD, which provided about 2,000 variants in total. To simulate a binary response variable affected by main genetic effects only, following Lu et al. [2017], we calculated the sum of minor allele count for each individual across all 2,000 variants, and then divided the samples into cases or controls based on the sums where nearly half of the samples were cases. We repeated the simulation 100 times and averaged the results for different sizes of genes. Table 1 shows the type I error rates for different competing tests at the p-value threshold of 0.05. In addition to comparing with fixed-effects and random-effects meta-analysis tests with the corresponding meta-filtering in (5) and (6), we also compared our method to a standard meta-analysis test – a fixed-effects gene-based test without filtering, and we calculated the p-values for this test based on the χ² distribution. In the presence of main effects and LD, the parametric test based on fixed-effects suffered from inflated type I error rates. In contrast, since our proposed tests (fixed- and random-effects tests with meta-filtering, and the ofGEM test) calculated the p-values based on a sequential sampling method accounting for LD, our tests controls the type I error rates.

Table 1.

Type I error rates for different tests at a p-value threshold of 0.05. The simulation is based on real genotype data in the presence of LD. We simulated case-control status affected by main genetic effects only. The results with inflated type I error rates arc in bold. The fixed-effects test with no filtering is based on the test statistic ${\sum }_{j=1}^k{\left({\sum }_{s=1}^S{w}_s{Z}_{js}\right)}^2$.

MAF	gene size	fixed-effects test with no filtering	random-effects test with meta filtering	fixed-effects test with meta-filtering	ofGEM
0.05–0.5	5	0.092	0.035	0.055	0.040
	5–10	0.105	0.043	0.059	0.054
	5–15	0.112	0.043	0.063	0.057
0.005–0.025	5	0.042	0.030	0.043	0.041
	5–10	0.039	0.034	0.056	0.052
	5–15	0.039	0.030	0.051	0.046

To evaluate the type I error rate for our method when applied to rare variants, we again took 243 randomly selected genes with 5–15 rare variants (0.5% ≤ MAF≤2.5%). We repeated the simulation on the rare variants. The parametric test based on the fixed-effects model with no filtering suffered from slightly deflated type I error rates. However, the proposed ofGEM test controls the type I error rates in analyses of rare variants.

3.2 Power Comparison

We compared the power of 1) our proposed ofGEM test, 2) the fixed- and random-effects tests with no filtering [Lee et al., 2013], 3) the fixed- and random-effects tests with filtering in individual studies, and 4) the fixed- and random-effects tests with meta-filtering. In particular, we examined the power comparison when there is either no or mild study heterogeneity and when there is moderate-to-strong study heterogeneity.

In each simulated data set, we simulated multiple case-control data representing individual studies, each with 1000 cases and 1000 controls sampled from a population with disease prevalence of 5%. We simulated a binary environmental factor with 50% probability of being 1. We simulated each genetic variant as an independent binomial variable with an MAF of 0.2. For each simulated data set, we simulated 1000 genes with different numbers of variants.

In the following 576 sets of simulation data, we varied the key parameters that may affect the power of the meta-analyses. These parameters are: the GxE effect size θ being log(1.2) or log(1.3); the number of studies (S) varying from 3 to 10; the number of variants in the gene (k) being 30 or 50; the number of variants with GxE effects (k₁) being 3 or 5; and the level of study homogeneity (ϕ) varying from 20% to 100%. Here the level of study homogeneity refers to the percentage of total studies that have a non-null GxE effect for a non-null variant in a gene. As an example, when θ = log(1.3), S = 8, k = 30, k₁ = 5 and ϕ = 50%, we simulated 1000 genes in 8 studies, each gene having 30 variants, 5 out of 30 variants having GxE effects being log(1.3) in 4 out of 8 studies (i.e., 50%), and the rest of the variants having no GxE effects. The 192 simulated data sets with a level of study homogeneity ϕ ≤ 40% were considered as data sets with moderate-to-strong heterogeneity.

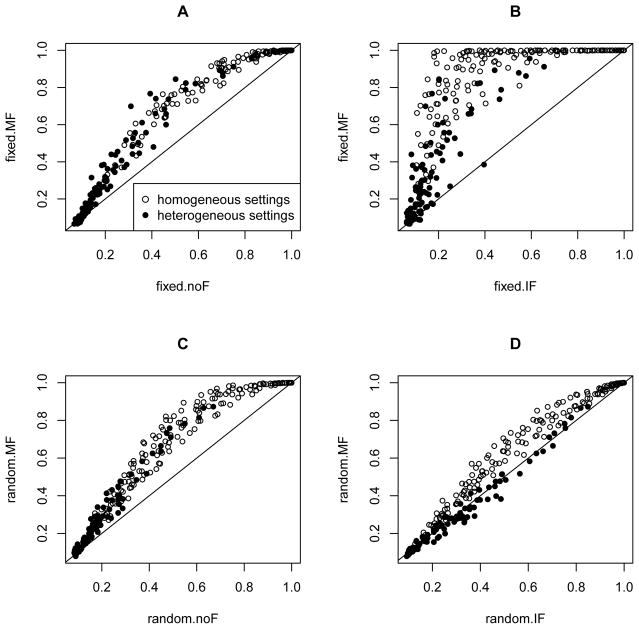
In Figure 2, we compared the power of the proposed methods and competing methods at a significance level of 0.05. We repeated the comparison at a significance level of 0.001, and the conclusions were unchanged (results not shown). Each dot in the figure represents the power of two competing methods at the significance level based on one simulated data set. The data sets with ϕ ≤ 40%, i.e., the heterogeneous studies, were plotted as filled circles, and the more homogeneous studies were plotted as unfilled circles. We first compared the power of fixed-effects tests with meta-filtering versus other filtering options, i.e., no filtering or filtering by individual study (Figure 2A and B). For both homogeneous and heterogeneous data sets, the power of the fixed-effects model with meta-filtering was much higher than no filtering or filtering by individual study. For the random-effects tests, the power of meta-filtering was also substantially improved over that of no filtering (Figure 2C). When comparing the random-effects model with meta-filtering to that with filtering by individual study (Figure 2D), we observed modest power improvement. The power improvement came from aggregating concerted GxE effects across studies in the filtering test. The lower power improvement in Figure 2D may be because the random-effects model already accounted for some degrees of study heterogeneity. For the extremely heterogeneous studies, the meta-filtering approach may have reduced filtering effectiveness compared to filtering by individual studies, and in those cases, meta-analyses would not be more powerful than analyses of individual studies.

Figure 2.

Power comparison of different filtering methods for fixed- and random-effects tests. We simulated 576 data sets, each with 1000 genes. We varied the effect sizes, the gene sizes, the numbers of studies, and the level of study heterogeneity. The filled circles denote the more heterogeneous data sets and the unfilled circles are the more homogeneous data sets. We compared the power of A) the fixed-effects test with meta-filtering (fixed.MF) versus no filtering (fixed.noF); B) the fixed-effects test with meta-filtering (fixed.MF) versus filtering by individual study (fixed.IF); C) the random-effects test with meta-filtering (random.MF) versus no filtering (random.noF); and D) the random-effects test with meta-filtering (random. MF) versus filtering by individual study (random.IF).

Regardless of fixed- or random-effects tests and the level of study heterogeneity, filtering out the unpromising variants improved the proportion of variants with true GxE effects (k₁/k) and the power to detect gene-level GxE effects, as shown in Figure 2A and Figure 2C. When individual studies had limited sample sizes, by combining all studies to conduct filtering we may improve the filtering effectiveness, and as such may improve the power of gene-level GxE testing. The power improvement largely depends on the study heterogeneity.

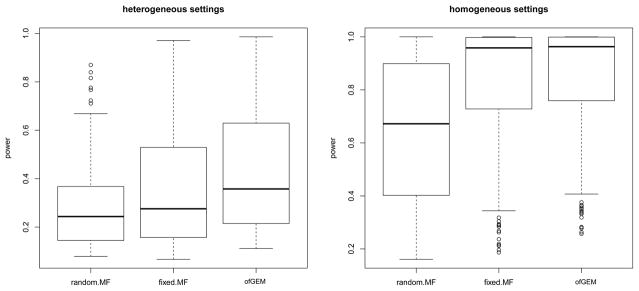
In Figure 3, we compared the power of the proposed ofGEM method versus the fixed- and random-effects tests with meta-filtering for homogeneous and heterogeneous data sets. The power of ofGEM was comparable or even higher than both the fixed- and random-effects tests. It has been shown in Soave et al. [2015] that when applying Fisher’s method to combine two complementary tests, if only one of the tests had power, then the combined test may have comparable power; and if both tests showed some power, then the combined test can be much more powerful than either. This finding matches with what we have observed in our simulation studies. In reality, the level of study heterogeneity is often unknown, and may also vary across genes. It is desirable to have a test that is powerful under different levels of study heterogeneity.

Figure 3.

Power comparison of fixed- and random-effects tests with meta-filtering versus the ofGEM test. Based on the 576 simulated data sets described in Section 3, we compared the power of fixed- and random-effects tests versus the proposed ofGEM test for heterogeneous (left) and homogeneous (right) settings. The ofGEM test is more powerful in most simulated data sets.

4 Applications: Detecting genes with age-dependent penetrance for breast cancer risk

The risk of breast cancer is relatively low in young women aged 50 or younger. But younger women with early onset breast cancer (EOBC) are more likely to have advanced stage cancers at diagnosis in comparison with older women with breast cancer. According to the American Cancer Society, the absolute risks of developing breast cancer in the next 10 years for women aged 20, 30, and 40 are 0.05%, 0.4%, and 1.5%, respectively; and up to age 85, the chance of developing breast cancer over a lifetime is up to 12 percent [American Cancer Society, 2013]. The risk of breast cancer increases with age. Some known germline mutations (for example, mutations in BRCA1 and BRCA2) have age-dependent penetrance. That is, the observed effects of those mutations on breast cancer risks depend on age, showing gene-by-age interaction effects. In this section, we analyzed two existing GWA consortium data sets as described by Ahsan et al. [2014] and Huo et al. [2016] with European and African ancestries, respectively, to detect genes with variants potentially interacting with age to affect breast cancer risk.

4.1 Detecting genes with age-dependent penetrance in an EOBC study

In the study by Ahsan et al. [2014], a total of 3,523 cases and 2,702 controls of non-Hispanic White (NHW) women were recruited. The cases were NHW women diagnosed with invasive breast cancer aged 20 to 50 and not known to carry pathogenic mutations in BRCA1 or BRCA2. The controls were NHW women between the ages of 20 and 50 years without a history of breast cancer. Among the eight sites in the study, we focused on the six sites contributing both controls and cases. Those women were recruited from the Breast Cancer Family Registry (BCFR) in Australia, Canada, and the United States; the Genetic Epidemiologic Study of Breast Cancer (GESBC) in Germany; the Long Island (LI) Breast Cancer Study Project; and the Surveillance, Epidemiology, and End Results (SEER) Program. After excluding the subjects with missing age, we restricted our analysis to 2,540 cases and 2,429 controls. Table 2 shows the number of cases and controls in each of the six study sites of the EOBC data.

Table 2.

Data summary by study site for the EOBC and the ROOT data.

Consortium	Study	Location	Cases	Controls	Total
EOBC	BCFR (AUS)	Australia	593	250	843
	BCFR (NCA)	Northern California, USA	204	156	360
	BCFR (Ontario)	Ontario, Canada	668	395	1,063
	GESBC	Germany	553	1,071	1,624
	LI	Long Island, New York, USA	225	229	454
	SEER	Seattle, Washington, USA	297	328	625
ROOT	NBCS	Ibadan, Nigeria	711	623	1,334
	BNCS	Barbados	92	229	321
	RVGBC	Philadelphia & Detroit, USA	145	257	402
	BBCS	Baltimore, Maryland, USA	95	102	197
	CCPS	Chicago, Illinois, USA	394	387	781
	SCCS	Southern United States	220	430	650

After genotype imputation and quality control, we obtained a total of 1,060,790 genetic variants on Chromosomes 1 to 22. For the gene-based test, we mapped the variants to genes based on the definition of the Single Nucleotide Polymorphism database (dbSNP, https://www.ncbi.nlm.nih.gov/projects/SNP/); and dbSNP assigns variants to genes if residing within 2,000 base pairs upstream and 500 base pairs downstream. For each gene, we then performed LD pruning at the threshold of r² > 0.9 to remove the variants in very high LD. After LD pruning, we considered only the genes with at least 5 variants. This resulted in a total of 14,631 genes for the analysis.

Due to sample heterogeneity among different study sites, we used meta-analysis methods (the fixed- and random-effects tests with meta-filtering, and the ofGEM test) to analyze this data. The goal was to test for non-zero gene-by-age interaction effects (i.e., age-dependent penetrance) at the gene-level across study sites. We first obtained the filtering and GxE testing summary statistics from each study site. For each study site, we calculated the t-statistics for testing correlations of age and genotype based on the combined case and control data as the filtering statistics. We calculated Wald statistics for testing gene-by-age interaction effects based on logistic regression models as the testing statistics. When calculating the filtering and testing statistics, we adjusted for the top ten principal components calculated from the genotype matrix. The summary statistics from each study site were then used in the meta-analysis tests. All the p-values were calculated based on the sequential sampling procedure described in Section 2.5.

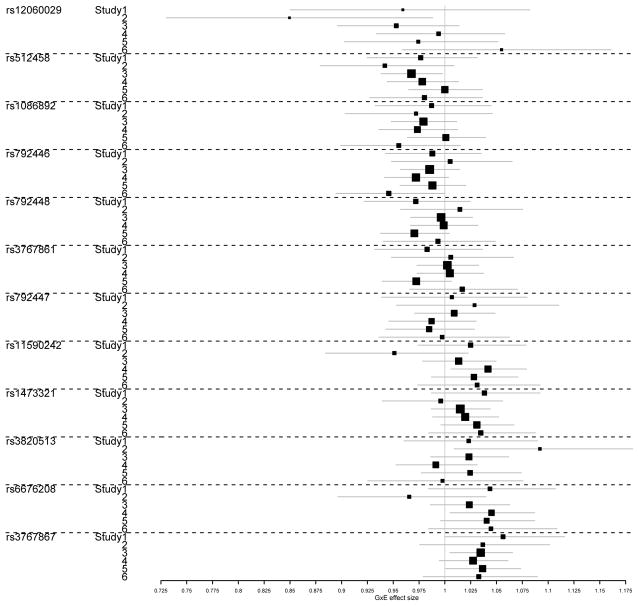
Table 3 lists the genes with suggestive evidence of gene-level GxE effects, with p-values below 10⁻⁵ for the ofGEM test. The gene TMEM206 was significant at the genome-wide significance threshold of 0.05 (p-value threshold = 0.05/14631 = 3.42×10⁻⁶). Figure 4 shows the forest plot of variant-level interaction effects for this gene in different study sites. Multiple SNPs showed interaction effects in at least one of the six EOBC studies. The function of this gene is relatively uncharacterized.

Table 3.

The p-values of genes with suggestive evidence of gene-level GxE effects in the- meta-analysis of gene-age interactions for the; EOBC and the ROOT data analysis. Genes with p-values less than 10⁻⁵ are listed. The gene TMEM206 is significant at the genome-wide significance threshold of 0.05 in the EOBC data analysis (p-value threshold = 0.05/14631 = 3.42×10⁻⁶). The gene LOC101928278 is significant at the genome-wide significance threshold of 0.05 in the ROOT data analysis (p-value threshold is 0.05/17547 = 2.85 × 10⁻⁶).

Consortium	Sample size (Case/Control)	Gene	Gene size (k)	p_random.MF	p_fixed.MF	p_ofGEM
EOBC	4,969 (2,540/2,429)	FAM91A1	9	5.13×10−3	7.80×10−5	6.30×10−6
		TMEM206	12	2.94×10−3	2.60×10−5	1.33×0−6
ROOT	3,685 (1,657/2,028)	LOG101928278	5	2.10×10−5	1.89×10−3	7.15×10−7
		SIAH2	11	3.60×10−2	1.20×10−5	6.77×10−6

Figure 4.

The forest plot of gene TMEM206 in sites from EOBC data.

4.2 Detecting genes with age-dependent penetrance in the ROOT study

The ROOT consortium consists of 3,686 women of African ancestry from six studies: the Nigerian Breast Cancer Study (NBCS), Barbados National Cancer Study (BNCS), Racial Variability in Genotypic Determinants of Breast Cancer Risk Study (RVGBC), Baltimore Breast Cancer Study (BBCS), Chicago Cancer Prone Study (CCPS), and Southern Community Cohort (SCCS). Table 2 shows the sample size of each study. Among the 3,685 women, 1,657 were cases and 2,028 were controls. Those women were 18 to 92 years old, and 2,114 (54.0%) were 50 years old or younger. This study also had a large proportion of women with breast cancer that occurred at younger ages. Supplementary Figure 1 shows the distributions of age in both EOBC and ROOT studies.

After quality control and filtering out variants with MAFs < 5%, we focused on 1,394,070 variants from Chromosome 1 to 22. Similar to the analysis of the EOBC data, we performed LD pruning at the threshold of r² > 0.9 for each gene, and restricted the analysis to the 17,524 genes with at least five variants. The largest gene in the analysis harbors 3210 variants.

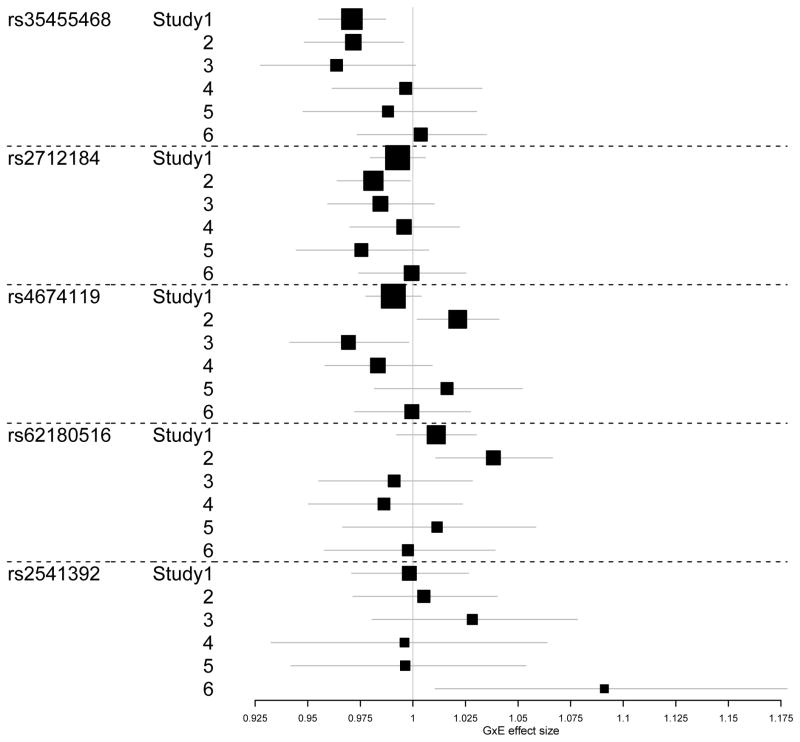
We applied the fixed- and random-effects tests with meta-filtering and the ofGEM test to the ROOT data to detect genes with variants showing age-interaction effects. Two genes, LOC101928278 and SIAH2, showed suggestive evidence of gene-level gene-by-age interaction effects with p-values less than 10⁻⁵ by the proposed ofGEM test. And the gene, LOC101928278, reached the Bonferroni-adjusted genome-wide significance threshold of 0.05/17547 = 2.85×10⁻⁶. The gene has been previously reported to have SNPs (Single Nucleotide Polymorphisms) associated with breast cancer risk. Huo et al. [2016] has identified a SNP, rs12998806 (imputed), in LOC101928278 as being associated with breast cancer risk in the ROOT data based on a variant-level analysis. Our analysis reports multiple variants (not including rs12998806) in the gene showing moderate gene-by-age interaction effects. Our results added supporting evidence that the gene may have multiple SNPs associated with breast cancer risk through main genetic effects or with age-dependent penetrance (age-interaction effects). Additionally, the gene and the 2q35 region it resides in have also been reported to be associated with breast cancer risk by other studies [Stacey et al., 2007]. The function of this gene is largely unknown. Figure 5 shows the forest plot of variant-level interaction effects of this gene in different study sites in the ROOT consortium. Multiple SNPs showed interaction effects in at least one of the six studies.

Figure 5.

The forest plot of gene LOC101928278 in sites from ROOT data.

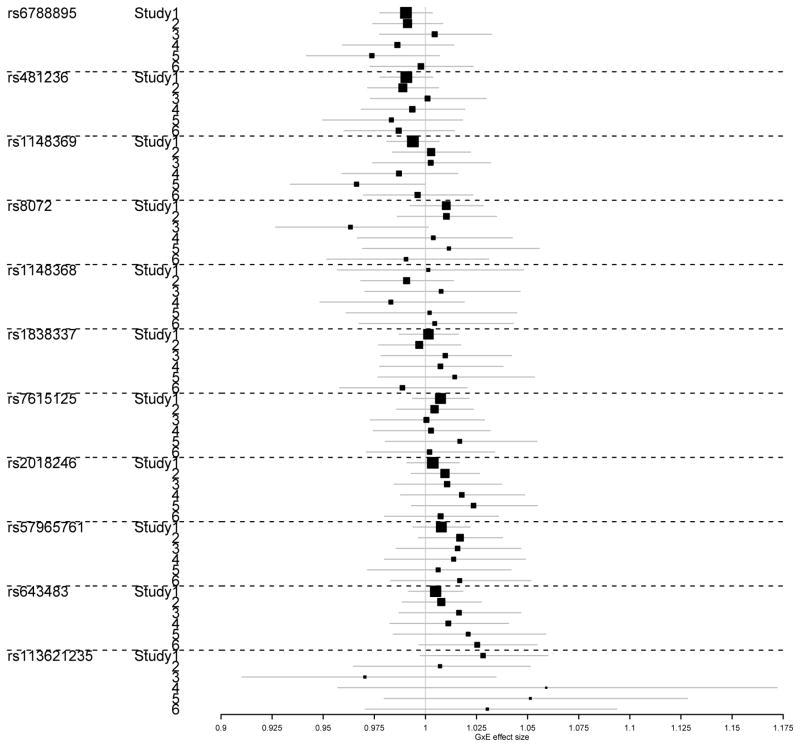
The gene, SIAH2, encodes a protein that is involved in ubiquitination and proteasome-mediated degradation of specific proteins. Its activity has been implicated in regulating cellular response to hypoxia. SNPs in this gene have also been reported to be associated with hormonal receptor-positive breast cancer in Japanese [Elgazzar et al., 2012]. In particular, the SNP rs6788895 has been replicated in an independent set of data. The SNP is a genotyped SNP in the ROOT data. We observed moderate and concerted gene-by-age interaction effects in multiple SNPs of this gene, including rs6788895 (Figure 6).

Figure 6.

The forest plot of gene SIAH2 in sites from ROOT data.

Furthermore, we jointly analyzed the EOBC and the ROOT data using the grouped tests for multiple ethnic groups proposed in Section 2.3.4. No gene reached the genome-wide significance threshold and none showed suggestive evidence of interaction effects. The lack of very significant findings across ethnicities echoed the well-known different breast cancer etiologies among women with European and African ancestries, and suggested that much of the age-dependent penetrance of breast cancer risk loci may be different in different ethnic groups.

Supplementary Figure 2 showed the QQ plots of the fixed-, random-effects and the ofGEM tests applied to each of the two consortia data and to the combined data.

5 Summary

In this work, we proposed gene-based meta-analysis tests with filtering to detect gene-environment interactions based on association data from large consortia. We first proposed to conduct filtering tests in a meta-analysis of GxE by combining all filtering summary statistics in the consortium data. The proposed meta-filtering method improved the overall power compared to no filtering or filtering by individual study, particularly when each individual study sample size is moderate to small. We then proposed the ofGEM test that combined the strengths of fixed- and random-effects tests with meta-filtering. With simulation studies, we showed that the proposed tests controlled the type I error rates even in the presence of main genetic effects and LD and were more powerful than competing tests in a wide range of settings with varying levels of study heterogeneity. Lin et al. [2013] have shown that single variant GxE tests can be biased in the presence of strong main genetic effects and LD. We did not observe strong inflation in the type I error rate. This may be because that we used a non-parametric sampling approach to calculate p-values, and that largely reduced the impact of LD. Also, the filtering test helped to filter out many variants that may contribute to the inflation. We further extended the proposed approaches to analyze data from multiple consortia and from multiple ethnic groups.

We applied the proposed meta-analysis tests to GWA data from two breast cancer consortia of European and African ancestries, to identify genes harboring variants with age-dependent penetrance. We identified some genes with suggestive evidence of gene-level GxE effects with p-values less than 10⁻⁵. By reviewing the forest plots, we observed that those genes harbored multiple variants with small-to-moderate age-dependent effects across studies. Those analyses also illustrated that our proposed tests are powerful in detecting individually-weak-but-collectively-strong interaction effects in a gene (or a set of SNPs).

By applying the proposed grouped ofGEM test to the combined data from two consortia of different ethnic groups, we did not identify any gene with concerted GxE effects across ethnicities. Our results largely echoed the well-known different etiologies of breast cancer among women with European and African ancestries.

The proposed tests can be applied to existing GWA or sequencing data from large consortia of complex diseases to detect interaction effects. Our methods require only summary statistics and can be cost-effective in recapitalizing on existing data.

6 Software

An R package ofGEM is hosted at GitHub (https://github.com/randel/ofGEM) and will be made available through R CRAN.