Combining energy and electron transfer in a supramolecular environment for the “green” generation and utilization of hydrated electrons through photoredox catalysis

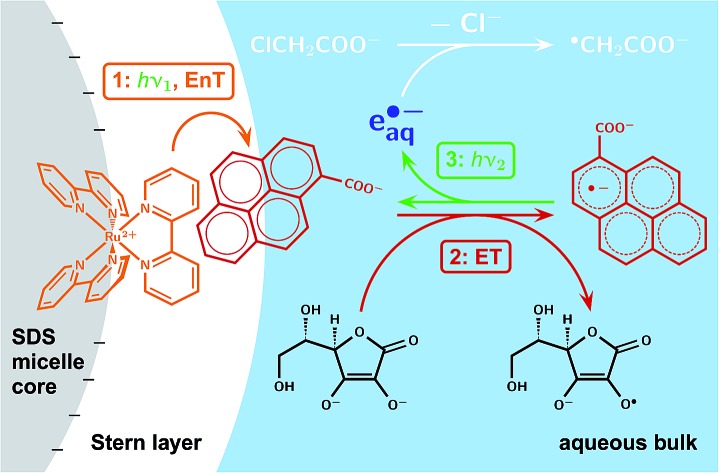
The interaction of an anionic micelle with the molecular charges and dipole moments ensures the desired sequence of processes and suppresses cross reactions in an “all-green” photoredox catalytic access to hydrated electrons e˙–aq, which reductively decompose nonactivated chloro-organics.

Abstract

We present a new mechanism that sustainably produces hydrated electrons, i.e., extremely strong reductants, yet consumes only green photons (532 nm) and the bioavailable ascorbate as sacrificial donor. The mechanism couples an energy-transfer cycle, in which a light-harvesting ruthenium polypyridine complex absorbs a first photon and passes the excitation energy on to a pyrene-based redox catalyst, with an electron-transfer cycle, in which the resulting triplet is reductively quenched and the energy-rich aryl radical anion is finally ionized by a second photon. Thus separating the roles of primary and secondary absorber permitted choosing a redox catalyst with a nonabsorbing ground state but efficiently ionizable radical anion; the quantum yield of the ionization step in our complex mechanism surpasses that in a simple photoredox cycle featuring only the metal complex by a factor of four. We suppressed undesired cross reactions through the noncovalent interactions of an anionic micelle with the charges of the reactants, intermediates, and products: the cationic light-harvesting complex remains affixed to the micelle surface, which blocks the access of the negatively charged sacrificial donor, aryl radical anion and hydrated electron, but allows the pyrene ground-state almost unhindered entry into the Stern layer despite a carboxylate substituent by virtue of its large dipole moment. We demonstrate the applicability of the mechanism to the reductive detoxification of halogenated organic waste, which hitherto required UV-C for electron generation, by decomposing the typical model compound chloroacetate.

1. Introduction

Visible-light driven photoredox catalysis is currently evolving into a remarkably versatile and powerful method for sustainable syntheses.1–7 Its operating principle is the activation of reactants through photoinduced electron transfer, so when the photon energy is insufficient for a desired process and shorter-wavelength radiation is unavailable, two photons must be pooled in an upconversion process, following Nature's precedent from photosynthesis. Examples of such upconversions in homogeneous photoredox catalysis are still extremely rare but were all reported very recently in high-impact journals,8–11 suggesting that the time is ripe for a broader application of this strategy.

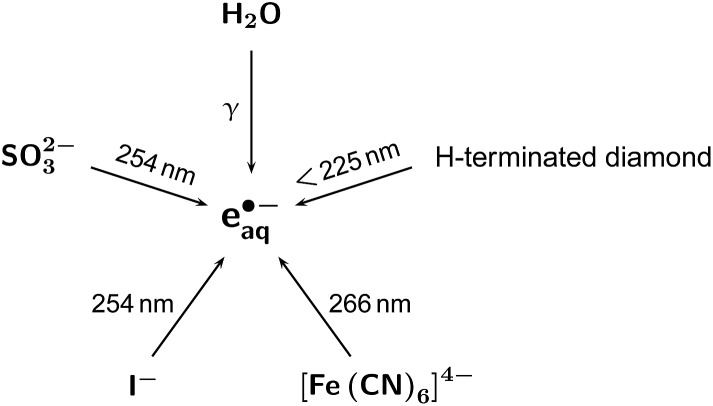
As two-photon energized forms, excited doublet states of photogenerated radical anions9 or excited singlet states afforded by triplet–triplet annihilation10,11 have been used to turn photoredox catalysts into “super reductants” with visible light. In an alternative concept, we have employed cyclic green-light ionizations of the catalyst molecules via their radical anions8 to liberate hydrated electrons e˙–aq, which then reductively attack any additives. Our present work again pursues this approach because the intermediacy of e˙–aq brings a twofold advantage: kinetically, the much longer natural life of e˙–aq (ref. 12) compared with excited doublets13–15 or singlets16 permits a concomitant reduction of the additive concentrations for the same degree of scavenging. Thermodynamically, the impressive reductive power of e˙–aq (2.77 V vs. normal hydrogen electrode NHE)12 allows not only the decomposition of non-activated chlorinated17,18 or even fluorinated19–21 organic molecules but also the direct reduction of molecular nitrogen22 or carbon dioxide.23 Up to now, e˙–aq for all these promising applications were only accessible by radiolysis17 or excitation in the UV-C (≈250 nm),18–23 as displayed in Fig. 1, but with the upconversion system of this report we shall demonstrate the first green-light driven degradation of chloroacetate, a typical model compound for chlorinated organic waste.18

Fig. 1. Previous pathways to e˙–aq for the applications listed in the Introduction.17–23 .

Our “all-green” electron source is a complex reaction scheme with a significantly improved quantum yield of the photoionization step over that of our previous attempt.8 Again inspired by Nature, we have assigned each absorption process to a different parent molecule, using a light-harvesting complex for the primary excitation and the radical anion of the redox catalyst for the photoionization proper. Such a separation greatly facilitates the independent optimization of each component for its main function; specifically, it opens up the possibility of including redox catalysts that do not absorb in the visible range before their conversion into radical anions.

The choice of our redox catalyst has been guided by the anticipation that, intrinsically, aryl radical anions should be efficiently photoionizable whenever thermodynamics permits because their rigid molecular skeletons favour electron detachment from an excited doublet state D_1…n by slowing down the competing radiationless deactivation.24 On the same grounds, the photoionization quantum yield should rise with increasing D₀–D₁ gap,25 that is, when the aromatic system shrinks; thereby, however, the parent molecule becomes more difficult to reduce, so demands progressively shorter wavelengths for a photochemical generation of the radical anion. This reasoning is borne out by our recent investigation of a naphthalene-derived radical anion,24 which exhibits the highest quantum yield of a green-light ionization known to date but is inaccessible with a single green photon; ref. 9 provides the other extreme with the much more extended π system of a perylene bisimide, whose radical anion is no longer photoionizable but easily available via green-light induced electron transfer.

The medium-sized pyrene chromophor, with its extremely slow radiationless deactivation16 as additional benefit, appears a near-perfect compromise because its high-lying radical anion can yet be prepared with green light through triplet sensitization followed by electron-transfer quenching. As we will show, neither the energetics nor optimized concentrations afford sufficient suppression of undesired reaction pathways in the resulting three-component system, but that problem is solved by the supramolecular environment of an anionic micelle, which fixes the light-harvesting complex on the core surface while allowing the redox catalyst to act as a relay between Stern layer and aqueous bulk.

2. Results and discussion

Our experimental method is one- and two-flash laser photolysis (532 nm) on a nanosecond timescale. Full particulars can be found in the ESI† (Section 1; hereafter abbreviated as ESI-1,† etc.), to which we will refer extensively in the following for details.

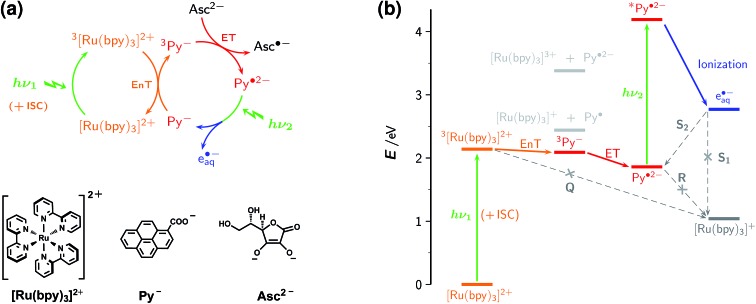
The mechanism consists of an energy-transfer cycle followed by an electron-transfer cycle, each driven by one green photon. It is displayed in Fig. 2a, together with the structural formulas of the key compounds; Fig. 2b gives an energy diagram; Table 1 lists the pertaining rate constant; and exhaustive information on spectroscopic and other relevant properties of the reactants and intermediates has been compiled in ESI-2 and ESI-3.†

Fig. 2. Operating principles of the green-light driven, sustainable source of hydrated electrons e˙–aq. (a) Reaction mechanism (top) and structural formulas (bottom) of the light-harvesting complex [Ru(bpy)₃]²⁺, the redox catalyst Py^–, and the sacrificial electron donor Asc^2–. (b) Thermodynamics relative to the sum of energies of [Ru(bpy)₃]²⁺, Py^–, and Asc^2– (or Asc˙^–; the difference26 is visually indiscernible), with pertinent triplet energies and redox potentials taken from the literature.12,16,26 Desired processes and intermediates are displayed in colour, unwanted ones in gray, with crosses denoting reactions that are suppressed by the micellar environment. Equations for the labeled reactions are given in Table 1. Further details, see text.

Table 1. Reactions relevant for the electron source of Fig. 2 including a model reaction (X) for the utilization of the product e˙–aq, their rate constants in homogeneous aqueous phase and aqueous SDS micellar solution, and cross reference with the ESI†.

Label a	Reaction	Rate constant b		Section of ESI† or reference
		In water	In SDS
	3[Ru(bpy)3]2+ natural life	2.0 × 106	1.5 × 106	3.5
EnT	3[Ru(bpy)3]2+ + Py– → [Ru(bpy)3]2+ + 3Py–	5.4 × 109	8.8 × 108 c	3.2
Q	3[Ru(bpy)3]2+ + Asc2– → [Ru(bpy)3]+ + Asc˙–	7.6 × 109	3.9 × 107	ref. 8
	3Py– natural life	4.0 × 104	4.0 × 104	3.2
ET	3Py– + Asc2– → Py˙2– + Asc˙–	4.9 × 108	2.5 × 108	3.3
	Py˙2– natural life	1.5 × 104	1.5 × 104	3.3
R:	Py˙2– + [Ru(bpy)3]2+ → Py– + [Ru(bpy)3]+	6.4 × 109	1.8 × 107	3.5
	e˙–aq natural life	3.8 × 105	3.8 × 105	3.6
S1	e˙–aq + [Ru(bpy)3]2+ → [Ru(bpy)3]+	5.0 × 1010	2.7 × 109	ref. 28
S2	e˙–aq + Py– → Py˙2–	1.5 × 1010	1.5 × 1010	ref. 29, 3.6
(X)	e˙–aq + ClCH2COO– → Cl– + ˙CH2COO–	1.3 × 109	1.3 × 109	3.6, 4.2

^aIn Fig. 2, where applicable. Desired reactions in bold, unwanted reactions in normal typeface.

^bIn s^–1 for first-order reactions (without labels in the first column), in M^–1 s^–1 for all others.

^cApparent rate constant for the concentrations used in this work.

For the electron-transfer cycle, we employ pyrene-1-carboxylate Py^– as a water-soluble redox catalyst and eject e˙–aq, with concomitant regeneration of Py^–, from its radical anion Py˙^2–. This energy-rich radical anion, which boasts of an intense absorption band in the blue–green, is conveniently prepared through electron transfer to the triplet ³Py^– from a sacrificial donor; as such, we use the bioavailable ascorbate (vitamin C) and maximize its reducing power by converting it into its dianion Asc^2– through working at a very high pH. Completing this cycle by direct excitation of Py^– is only feasible in the UV, however, as Py^– is transparent throughout the visible range.

To access ³Py^– also with visible light, we have prefixed the electron-transfer cycle with an energy-transfer cycle featuring the popular light-harvesting compound [Ru(bpy)₃]²⁺, which absorbs well into the green and upon excitation quantitatively transforms into its lowest triplet state ³[Ru(bpy)₃]²⁺ within picoseconds.27 Both oxidative and reductive quenching of ³[Ru(bpy)₃]²⁺ by Py^– are barred by thermodynamics, but energy-transfer quenching is weakly exergonic, so provides a viable indirect route to ³Py^–.

The whole sequence utilizes the energy of the first green photon (532 nm, 2.33 eV) in a remarkably economical way: only one-fifth is lost on the way to the electron precursor Py˙^2– (E°(Py^–/Py˙^2–) = –1.85 V vs. NHE).16 The stored remainder combines with the energy of the second green photon to give a total of 1.4 eV above the threshold of electron formation.

The hydrated electron is so reactive that it attacks not only the additive one intends to decompose but also the catalytic ingredient of each cycle, [Ru(bpy)₃]²⁺ and Py^–. This unwanted competition puts upper bounds on the catalyst concentrations to keep the mechanism useable as an electron source. Defining an order-of-magnitude reduction of the natural lifetime of e˙–aq by reaction S₁ or S₂ as an acceptable limit, these bounds are about 1 × 10^–4 M for [Ru(bpy)₃]²⁺ and 3 × 10^–4 M for Py^– in water. Below, we shall demonstrate that our supramolecular approach renders negligible reaction S₁ even with the mechanism of Fig. 2a in isolation; in a practical application, both S₁ and S₂ are suppressed by the competition with reaction X when the additive concentration is high enough.

As we found in homogeneous aqueous solution, the energy transfer from ³[Ru(bpy)₃]²⁺ to Py^– (reaction EnT) is quite fast despite its small driving force, such that the above maximum concentration of Py^– amounts to roughly the half-quenching concentration, whereas the electron-transfer quenching of ³Py^– by Asc^2– (reaction ET) is slower by an order of magnitude. When the concentration of [Ru(bpy)₃]²⁺ falls below one-fifth of that of Py^–, reaction EnT becomes practically irreversible already in the absence of Asc^2–, and that limit is reached even sooner when ³Py^– is removed from the equilibrium by reaction ET.

However, kinetic complications arise from two additional processes through each of which a reactant belonging to one cycle scavenges a pivotal intermediate of the respective other cycle. First, the sacrificial electron donor Asc^2– disturbs the energy-transfer cycle in that manner by reductively quenching not only the product ³Py^–, as projected, but also the energy donor ³[Ru(bpy)₃]²⁺, and the much more favourable Coulombic interaction causes that undesired reaction (Q) to be 16 times faster than reaction ET.8 Second, the energy-transfer sensitizer [Ru(bpy)₃]²⁺ in its ground state removes the key species Py˙^2– from the electron-transfer cycle by oxidizing it in a fast thermal reaction (R).

The seemingly simple answer to the first problem, namely, increasing the concentration of Py^– well above that of Asc^2–, is impracticable owing to the accompanying loss of e˙–aq through reaction S₂. Similarly, the second problem could be solved by reducing the concentration of [Ru(bpy)₃]²⁺, but only at the expense of absorbing fewer photons in the energy-transfer cycle, so ultimately producing fewer electrons.

As a general strategy to address both problems without these adverse side effects, we have used a supramolecular environment to decelerate strongly all electron-transfer reactions involving the light-harvesting complex in its ground or excited state, that is, reactions Q, R, and S₁. This end can be achieved simply by working in solutions of micelles with a negative surface charge, such as sodium dodecyl sulfate SDS. The doubly charged cationic species [Ru(bpy)₃]²⁺ and ³[Ru(bpy)₃]²⁺ associate very strongly30 with the anionic micelles, whereas the doubly negatively charged reductants Asc^2– and Py˙^2– are anticipated to be firmly repelled. Those predictions are vindicated by the rates of reactions Q and R, which we found to be 200 and 350 times lower than in homogeneous aqueous solution. By the same token, reaction S₁ featuring the singly charged reductant e˙–aq still becomes 20-fold slower in SDS, thus essentially sealing off that unwanted decay channel of e˙–aq.

In welcome contrast, the microheterogeneous environment decreases the rates of the two key reactions EnT and ET much less, by factors of only 6 and 2. This weak influence of SDS is most surprising at first glance: on one hand, Py^– must approach the anionic micelle from the aqueous phase to undergo reaction EnT with the micelle-bound metal complex, as follows from our observation of a predominantly dynamic quenching; the Coulombic repulsion by the micelle should thus decelerate reaction EnT to a similar degree as it does reaction S₁. On the other hand, as long as ³Py^– afforded by reaction EnT resides within the micelle, the subsequent reaction ET should be suppressed equally strongly by SDS as is reaction Q, because both involve the same dianionic quencher Asc^2–; the alternative, a fast exit of ³Py^–, seems irreconcilable with the fast entry of Py^– suggested by reaction EnT, given the quite similar charge distributions in ³Py^– and Py^– (compare, ESI-2†).

Ion–dipole interactions provide an explanation. Py^– has a dipole moment as high as 14 D,31 which is oriented in a direction (see, ESI-2†) practically coinciding with a line from C_10a to C_5a. The attractive interaction between that dipole and the negative surface charge of the micelle partly compensates the Coulombic repulsion and is maximized when Py^– moves toward the micelle in the manner displayed in Fig. 3a, that is, with its aromatic system first. As the size of the pyrene skeleton is comparable to the thickness of the Stern layer32 and the energy donor ³[Ru(bpy)₃]²⁺ is localized (Fig. 3a) such that it protrudes considerably into that layer,33,34 reaction EnT does not necessitate an entry of Py^– into the micelle interior but only requires that quencher to prick the Stern layer. This geometrical arrangement, with part of the pyrene system still outside, furthermore rationalizes why the ensuing reaction ET is almost as fast as in homogeneous aqueous phase despite the dianionic reductant Asc^2–: neither does that donor need to enter to Stern layer, nor is an exit of ³Py^– from the Stern-layer necessary; instead, by virtue of its partially embedded π system, the redox catalyst also serves as a switching relay that enables the energy and electron transfers in the order given by Fig. 2.

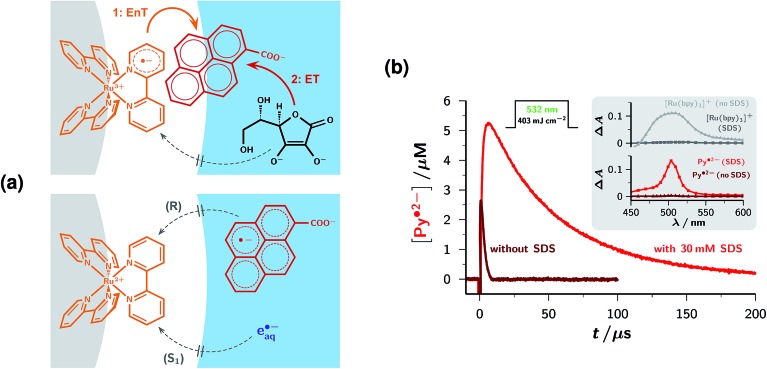
Fig. 3. Optimizing formation and decay of the radical anion Py˙^2– by an anionic micelle. (a) Drawn-to-scale pictures of the relevant zones of an SDS micelle (gray, core, radius 19.6 Å; white, Stern layer, diameter 6.8 Å)32 in water (blue) and calculated molecular sizes, illustrating the most probable locations of the reaction partners and intermediates. The light-harvesting complex is attached to the boundary of the micelle core,33,34 and (top) in its excited form ³[Ru(bpy)₃]²⁺ the ligand protruding farthest into the Stern layer has been turned into a radical anion.27 The high dipole moment31 of the redox catalyst Py^– helps overcome the Coulombic repulsion and enables Py^– to enter the Stern layer in the orientation shown in the upper drawing, such that it can acquire sufficient orbital overlap with ³[Ru(bpy)₃]²⁺ to undergo the Dexter energy transfer25 EnT. The sacrificial donor Asc^2– (top), as well as the delocalized radical anion Py˙^2– and the hydrated electron e˙–aq (bottom), can only reside in the aqueous phase. These properties ensure the unhindered sequence of reactions EnT and ET while strongly suppressing the undesired reactions Q, R, and S₁ (compare, Fig. 2b and Table 1). (b) Main plot, concentration traces of the electron precursor Py˙^2– in deoxygenated homogeneous aqueous solution (brown) and 30 mM aqueous SDS (red) in the photolysis of 6 × 10^–5 M [Ru(bpy)₃]²⁺, 3 × 10^–4 M Py^– and 1.5 mM Asc^2– at pH 12.7 with a single green pulse, intensity given above the traces. The increased yield and much longer life of Py˙^2– in the micellar environment are obvious. Inset, transient absorption spectra (top, [Ru(bpy)₃]⁺, gray in water, dark gray in SDS; bottom, Py˙^2–, same color coding as in the main plot) at 10 μs after the laser flash and separated by the procedure described in ESI-3.5,† demonstrating the practically exclusive presence of [Ru(bpy)₃]⁺ in homogeneous solution and that of Py˙^2– in the micellar system. Further information, see text.

This delicate localization balance is corroborated by the effects of a more lipophilic light-harvesting complex or redox catalyst. A replacement of [Ru(bpy)₃]²⁺ by the tris(4,7-diphenyl-1,10-phenanthroline)-ruthenium dication decelerated the energy transfer to Py^– by an order of magnitude despite an unchanged thermodynamic driving force (ESI-3.5†); this observation finds a natural explanation in the more lipophilic ligands, which drag the complex more towards the micelle interior, thus obstructing the access of Py^–. In contrast, supplanting the carboxylate Py^– by the butyrate, which is 35 times more strongly bound to SDS but practically identical to Py^– with respect to triplet energy and redox potential (ESI-3.1†), led to quasi-instantaneous energy transfer from ³[Ru(bpy)₃]²⁺ through static quenching but complete suppression of the desired electron transfer from Asc^2– to the resulting triplet.

Fig. 3b demonstrates the improvement achieved by the described supramolecular approach. Not only does the addition of SDS almost double the maximum concentration of the electron precursor Py˙^2–, which is mainly due to the deceleration of the competing reaction Q, but it also prolongs the life of that key intermediate by a factor of 30. When we omitted the green-light sensitizer [Ru(bpy)₃]²⁺ and excited Py^– direct with a 355 nm flash, we observed a further increase of the lifetime of Py˙^2– by 7% only, which bears out the virtual elimination of reaction R by the anionic micelles. The underlying cause, a difference in accessibility of the Stern layer to Py^– and Py˙^2–, is consistent with expectation because the conversion of Py^– into Py˙^2– both reduces the assisting dipole moment by a factor of 2.7 (ESI-2†) and adds an impeding negative charge, which is delocalized over the aromatic system. Including the green photoionizing flash in the two experiments of Fig. 3b provides verification that the analogous suppression of reaction S₁ by the surfactant solution prolongs the electron life accordingly. The spectra after completion of the primary photochemistry (see, the inset of Fig. 3b) finally establish that in homogeneous aqueous medium the reaction takes an unwanted deviation towards the reduced complex [Ru(bpy)₃]⁺, which can be prevented almost completely by the SDS micelles. All these findings show that the well-known [Ru(bpy)₃]²⁺ — pyrene dyads35–38 are unusable for our purpose despite their quasi-instantaneous analogue of reaction EnT, because after electron-transfer quenching of the redox-catalyst (i.e., pyrene) part the equivalent of reaction R would immediately relocate the excess electron to the light-harvesting moiety.

Fig. 4a turns to the green-light ionization of the redox catalyst Py˙^2–, the other cornerstone of the mechanism of Fig. 2. Concentration traces of Py˙^2– and e˙–aq in a representative experiment with two successive green laser flashes are displayed in the main plot. The first flash hits the pristine system containing the starting concentration of Py^– but no Py˙^2– yet, whereas the second flash arrives when Py˙^2– has reached its maximum concentration. The formation of more Py˙^2– from residual Py^– by that second flash has been blanked by the procedure explained in ESI-4.1,† thus exclusively filtering out the effect of green photons on Py˙^2–.

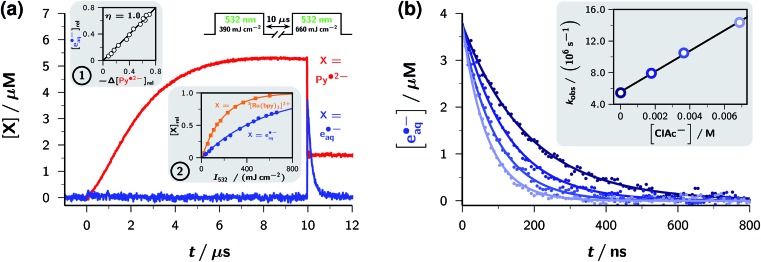
Fig. 4. Generating (a) and using (b) e˙–aq with the mechanism of Fig. 2a. (a) Main plot, concentration traces of Py˙^2– (red) and e˙–aq (blue) in an experiment with the pulse scheme displayed above the traces, on the solution of Fig. 3b with 30 mM SDS; Py˙^2– trace after the second pulse corrected with the procedure of ESI-4.1.† Inset 1, e˙–aq formation as function of Py˙^2– bleaching, with the concentration changes –Δ[Py˙^2–]_rel and [e˙–aq]_rel taken relative to the concentration of Py˙^2– immediately before the second pulse. Inset 2, relative actinometry of green-light ionization of Py˙^2– with excitation of [Ru(bpy)₃]²⁺ (formation of the emissive state ³[Ru(bpy)₃]²⁺) as reference reaction. Blue data points, [e˙–aq]_rel as in Inset 1 as function of the intensity I₅₃₂ of the second laser pulse. The monoexponential fit by the blue curve, 1 – exp[–I₅₃₂/(558 mJ cm^–2)], validates the monophotonic ionization mechanism. Orange data points and fit curve 1 – exp[–I₅₃₂/(187 mJ cm^–2)], intensity dependence of ³[Ru(bpy)₃]²⁺ emission normalized to maximum. The ratio of these best-fit constants times the ratio of the molar absorption coefficients of the species excited with 532 nm (³[Ru(bpy)₃]²⁺, 1000 M^–1 cm^–1; Py˙^2–, 6200 M^–1 cm^–1) gives the photoionization quantum yield, 0.054. (b) Decomposition of the model compound chloroacetate CICH₂COO^– by e˙–aq generated as in (a). Main plot, decay of e˙–aq in the presence of variable amounts of CICH₂COO^–; inset, resulting Stern–Volmer plot. The same colour coding of the concentrations has been used in the main plot and in the inset. Further explanation, see text and ESI-4.† .

Evidently, the first flash initiates the gradual buildup of Py˙^2– described above but generates no e˙–aq, whereas the second flash abruptly removes about 70% of Py˙^2– and instantaneously produces the equivalent amount of e˙–aq. The first inset of Fig. 4a confirms the validity of this 1:1 stoichiometric ratio between radical anion disappearance and electron formation for arbitrary intensities of the second laser flash, so pinpoints Py˙^2– as the direct electron precursor.

The dependence of the electron yield on the intensity of the ionizing flash (see, second inset of Fig. 4a) clearly features a linear low-intensity regime with zero intercept, which characterizes39 the green-light ionization of Py˙^2– as monophotonic. We regard this property as a precondition for the practical applicability of the mechanism of Fig. 2a as a green-light driven electron source: a biphotonic ionization of type 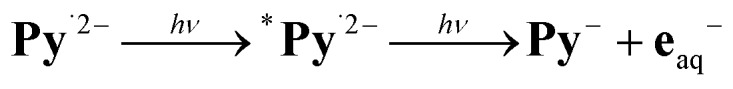would not only require one photon more than dictated by thermodynamics but also demand the absorption of two photons during the life of the excited state ^*Py˙^2–, that is, within nanoseconds or less, so could never be effected with a low-flux light source such as the sun.

Relative actinometry results are displayed in the second inset of Fig. 4a. The excitation of [Ru(bpy)₃]²⁺ served as the reference reaction at comparable optical density of the absorber and in the same medium but in the absence of the additives Py^– and Asc^2–, thus eliminating possible errors of absolute light intensities and illumination homogeneity. The use of the intensity dependences over the entire range, through the best-fit parameters, maximizes experimental precision and avoids saturation effects. The actinometry gave a quantum yield φ₅₃₂ of 0.054 for the process 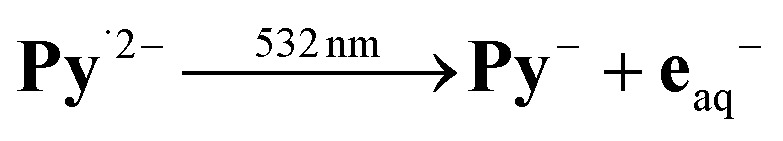. This outperforms φ₅₃₂ of the only other green-light driven, sustainable electron source known to date (via the one-electron reduced form [Ru(bpy)₃]⁺ of our light-harvesting complex)8 by a factor of four, and is only topped by φ₅₃₂ of a few aryl radical anions24,40 that cannot be accessed with green light. It also compares favourably with the formation of e˙–aq by the sulfite process, which has twice the quantum yield but only at twice the photon energy,18 that is, needs UV-C (254 nm), which is not contained in the terrestrial solar spectrum.

To test the applicability of our system as an “all-green” electron source for the decomposition of organic waste, we repeated the experiments of Fig. 4a in the presence of varying amounts of the chloroacetate anion CICH₂COO^–, a well-established model compound for such an assay.18,41 The main plot of Fig. 4b displays the electron decays under these circumstances. Increasing [CICH₂COO^–] clearly has no influence on the initial electron concentration but progressively shortens the electron life; hence, the additive does not interfere with the complex mechanism of Fig. 2a – in particular, reacts neither with Py˙^2– nor with ^*Py˙^2– – but scavenges only the product e˙–aq, as desired. The analysis shown as the inset of Fig. 4b yields the bimolecular rate constant for this dissociative electron transfer, which ejects the chlorine atom as its nontoxic anion (reaction X in Table 1). The result agrees with the reported value41 when the higher ionic strength of our medium is taken into account.

The aliphatic chloro-organic CICH₂COO^– is not sufficiently activated to be decomposable by the recently published two-photon redox catalysis via the excited radical anion ^*PD˙^– of a perylene diimide:9 the return of ^*PD˙^– to the ground-state perylene diimide supplies about 0.5 eV less than the oxidation of (unexcited) Py˙^2– to Py^–; as Py˙^2– obviously cannot reduce CICH₂COO^–, ^*Py˙^– cannot either. But even when such a process is thermodynamically feasible, such as between ^*Py˙^2– and CICH₂COO^– in the present work, the very short life13,15,42,43 limits the usefulness of an excited radical anion as an electron donor in a bimolecular process. This is borne out by the fact (Fig. 4b) that at millimolar concentrations CICH₂COO^– does not measurably quench the high-energy but short lived species ^*Py˙^2–, whereas it quenches up to 70% of the energetically lower but much longer lived e˙–aq. To quench ^*Py˙^2– to an appreciable degree, proportionally higher concentrations of CICH₂COO^– would thus have to be employed; conversely, this determines the levels to which [CICH₂COO^–] can be decreased by e˙–aq or ^*Py˙^2– within a reasonable amount of time. The monomolecular autoionization of ^*Py˙^2– is free from this constraint on the quencher concentration, and transforms the excited radical anion into the much more persistent but still extremely strong reductant e˙–aq; this suggests that whenever electron ejection from the excited radical anion is thermodynamically feasible, this pathway of a reductive two-photon catalysis is more efficient. Lifetime arguments also promise an inherent advantage over photoredox catalysis through triplet–triplet annihilation:10,11 cyclic photoionizations via radical anions do not rely on bimolecular processes between two excited species.

Since the light-harvesting complex is efficiently shielded by its micellar host, the fate of the radical anion of the redox catalyst determines the stability of our cyclic system. Under our conditions, Py˙^2– does not decay through recombination with Asc˙^– but through protonation by the solvent29 (ESI-3.3 and 3.4†). Although the resulting natural life of Py˙^2– is gratifyingly long (67 μs; compare, Fig. 3b), that slow reaction would ultimately destroy the catalyst. However, the photoionization blocks this by turning Py˙^2– into the indefinitely stable Py^–. Even at the wavelength available for this work, which does not match the sharp absorption band of the radical anion very well, more than two-thirds of Py˙^2– can be withdrawn by the photoionization (Fig. 4a), and thus protected against protonation; at the nearby (504 nm instead of 532 nm) maximum, where the molar absorption coefficient of Py˙^2– is an order of magnitude higher (see, ESI-3†), quantitative return to Py^– would be easily achievable.

To illustrate the advantage of using independent light absorbers for the two photons, we finally focus on an optimization of the light-harvesting complex. As has emerged, requirements already met satisfactorily by [Ru(bpy)₃]²⁺ comprise its absorption spectrum, its intersystem crossing quantum yield, its triplet energy, and its localization within the micelle, whereas its excited-state lifetime offers the biggest potential for improvement. To address this issue, we replaced [Ru(bpy)₃]²⁺ with the tris(phenanthroline) complex [Ru(phen)₃]²⁺, which is a perfect stand-in with respect to the former four properties but enjoys twice as long a life in its excited state ³[Ru(phen)₃]²⁺. Consistent with expectation, this substitution doubled the yield of Py˙^2–, as Fig. S8a of the ESI† shows.

3. Conclusions

In summary, the main characteristic of the described mechanism is the kaleidoscopic role of the redox catalyst, which successively acts as energy acceptor (Py^–), electron acceptor (³Py^–), and photon acceptor plus electron emitter (Py˙^2–). To expedite the first step of that sequence, a close proximity of the light-harvesting complex to Py^– is beneficial, whereas the suppression of cross reactions dictates that complex to be spatially separated from Py˙^2–, from the sacrificial donor Asc^2–, and from the product of the cycle e˙–aq. This dilemma is resolved by noncovalent interactions, which fix the complex on the core surface of an SDS micelle, allow Py^– and ³Py^– to shuttle between Stern layer and aqueous bulk, but bar the approach of all the other species. A recurrent theme is the prolongation of the “shelf life” of the stored photon energy by chemical transformations: for the first photon, reaction EnT achieves a factor of 35 and reaction ET a further factor of 3; with respect to the second photon, the electron ejection brings about an increase by at least three orders of magnitude. Harnessing visible-light photoredox catalysis thus into a tool for the production of e˙–aq provides access to one of the most potent reductants under extremely mild conditions and in a manner that can be controlled both spatially and temporarily.