Tissue growth constrained by extracellular matrix drives invagination during optic cup morphogenesis

Abstract

In the early embryo, the eyes form initially as relatively spherical optic vesicles (OVs) that protrude from both sides of the brain tube. Each OV grows until it contacts and adheres to the overlying surface ectoderm (SE) via an extracellular matrix (ECM) that is secreted by the SE and OV. The OV and SE then thicken and bend inward (invaginate) to create the optic cup (OC) and lens vesicle, respectively. While constriction of cell apices likely plays a role in SE invagination, the mechanisms that drive OV invagination are poorly understood. Here, we used experiments and computational modeling to explore the hypothesis that the ECM locally constrains the growing OV, forcing it to invaginate. In chick embryos, we examined the need for the ECM by (1) removing SE at different developmental stages and (2) exposing the embryo to collagenase. At relatively early stages of invagination (Hamburger–Hamilton stage HH14−), removing the SE caused the curvature of the OV to reverse as it ‘popped out’ and became convex, but the OV remained concave at later stages (HH15) and invaginated further during subsequent culture. Disrupting the ECM had a similar effect, with the OV popping out at early to mid-stages of invagination (HH14− to HH14+). These results suggest that the ECM is required for the early stages but not the late stages of OV invagination. Microindentation tests indicate that the matrix is considerably stiffer than the cellular OV, and a finite-element model consisting of a growing spherical OV attached to a relatively stiff layer of ECM reproduced the observed behavior, as well as measured temporal changes in OV curvature, wall thickness, and invagination depth reasonably well. Results from our study also suggest that the OV grows relatively uniformly, while the ECM is stiffer toward the center of the optic vesicle. These results are consistent with our matrix-constraint hypothesis, providing new insight into the mechanics of OC (early retina) morphogenesis.

1 Introduction

In the embryo, the eyes begin to develop as bilateral spherical protrusions called optic vesicles (OVs) that extend outward from the forebrain and soon contact the overlying surface ectoderm (SE). Within the region of contact, the OV and SE epithelia adhere and thicken to form the retinal and lens placodes, which then invaginate to create the bilayered optic cup (OC; future retina) and the lens vesicle, respectively (Fig. 1) (Hendrix and Zwaan 1974). Morphogenetic abnormalities during eye development can cause ocular defects such as coloboma (missing part of eye) and microphthalmia (abnormally small eye) (Mic et al. 2004). Studies suggest that SE invagination to create the lens is driven primarily by apical constriction (Plageman et al. 2011), but the biophysical mechanisms that drive OV invagination remain poorly understood.

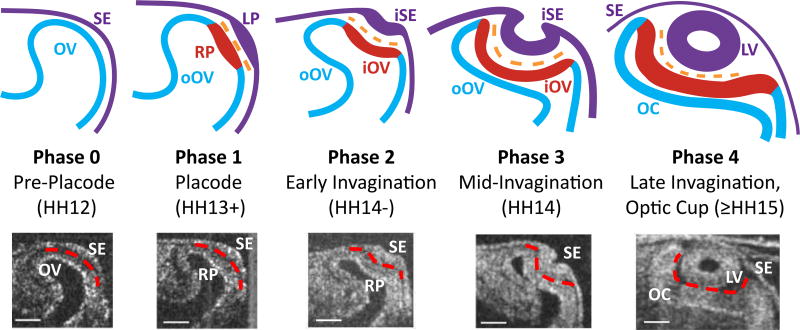
Fig. 1.

Morphology of optic cup in five phases. Top row Schematic diagram of phases of optic cup formation (OV = optic vesicle, blue; oOV = outer OV, blue; iOV = inner OV, red; SE = surface ectoderm, purple; iSE = inner SE, purple; RP = retinal placode, red; LP = lens placode, purple; ECM = extracellular matrix, orange). Bottom row Representative OCT images for each phase. Dashed red lines indicate boundary between the SE and OC. Phase 0, pre-placode The OV and SE are in contact but have not thickened. Phase 1, placode The two cell layers become tightly adhered via ECM and thicken to form the RP and LP. Phase 2, early invagination The OV and iSE begin to invaginate. Phase 3, mid-invagination Significant curvatures are apparent. Phase 4, late invagination The OC and LV have formed. Scale bars 100 µm

Previous experimental studies have provided valuable information needed to understand the mechanics of OC formation. First, it is important to note that actin is located primarily on the apical sides of both the SE and OV in chick and mouse, corresponding to the initial outer and inner surface, respectively, of these layers (Martinez-Morales and Wittbrodt 2009; Borges et al. 2011). The location in the SE is consistent with an apical constriction mechanism for lens placode invagination, but it is on the wrong side of the OV to drive retinal placode invagination. This process has been studied for over a century, with Spemann (1901) finding that contact between the OV and SE is required for lens invagination. More recently, Hyer et al. (2003) found that contact with the SE is needed only until the placode stage for invagination to occur in chick embryos, as ablating the lens after this time does not prevent OC formation. These findings indicate that the developing lens (SE) is not the main driver of OV (retinal placode) invagination and that actomyosin contraction does not play a major role in this process.

Another important mechanical consideration comes from the observation that the contact area between the OV and SE remains essentially constant during placode formation in chicken and mouse embryos (Zwaan and Hendrix 1973; Huang et al. 2011). Zwaan and Hendrix (1973) attributed this observation to the constraining effects of extracellular matrix (ECM) between these layers (Fig. 1). These authors also speculated that cell proliferation in the constrained region creates cell crowding, which causes the presumptive lens tissue of the SE to thicken into a placode that eventually buckles and invaginates. More recently, evidence obtained by Huang et al. (2011) indicates that the ECM constrains the spreading of both the OV and SE in their mutual region of contact as they grow, causing them to thicken locally and form placodes.

The present study extends these ideas to the process of OV invagination. In particular, we explore the hypothesis that OV growth, constrained by a relatively stiff extracellular matrix causes formation of the retinal placode, as well as subsequent invagination to create the OC. Consequently, the SE is involved only indirectly by secreting and inducing the OV to also secrete the necessary matrix. Rather than being a type of buckling, this represents a differential growth mechanism similar to that which bends a bimetallic strip, whereby one layer expands more than the other in response to an increase in temperature. Differential growth apparently plays a major role in the development of other organs, including the heart, brain, and gut (Taber 2014).

To test the physical plausibility of this hypothesis, we integrated experimental measurements of morphogenetic changes in geometry, as well as cell and matrix stiffness, with finite-element modeling of the invagination process. The model was tested experimentally using perturbations whereby the SE was removed from the OV and the matrix was degraded at various times during invagination. Consistent with our experimental results, the model indicates that the matrix is needed to initiate invagination but is no longer necessary for invagination to proceed after reaching a critical developmental stage. In addition, comparing experimental and numerical results suggests that the growth rate in the invaginating region of the SE is relatively uniform, while the ECM is stiffer near the center of the retinal placode. These details have subtle but potentially significant effects on OC (retinal) morphology.

2 Materials and methods

2.1 Embryo preparation and culture

Fertilized white Leghorn chicken eggs were incubated at 38 °C for 45–55 h to reach Hamburger–Hamilton stages 12–15 (HH12–HH15) (Hamburger and Hamilton 1951). Embryos were removed from the egg using a method in which the vitelline membrane adheres to a ring of filter paper (Whatman #2) to lift the embryo from the yolk. A second filter paper ring was placed on the ventral side of the embryo to keep the membranes from slipping. Embryos were cultured in approximately 1 ml chick media (Dulbecco’s modified Eagle’s medium with 10 % chick serum and 1 % antibiotics) in 35mmPetri dishes placed in a small plastic bag with a mixture of 95 % oxygen and 5 % carbon dioxide (Voronov and Taber 2002). To image further developed control embryos, additional eggs were incubated up to 80 h (HH21), and right eyes were imaged while in the yolk.

2.2 Removal of surface ectoderm and matrix

After embryos were removed from the egg, the SE was dissected from the right eye with the left eye serving as a control. During dissection, embryos were submerged in thin albumen collected from eggs. A small region of vitelline membrane was removed near the right eye with fine glass needles. Then <2 µl of 2 % Nile Blue sulfate was applied to the SE on and near the right eye with a glass capillary tube as described previously (Hyer et al. 2003; Yang and Niswander 1995). After a short time (<1 min), the SE blistered and was removed with a glass needle and forceps. The Nile Blue sulfate tended to have a stronger effect on SE blistering when embryos were submerged in thin albumen than in PBS (Dulbecco’s phosphate-buffered saline). After dissection, the albumen was replaced with PBS. After removal of the SE, a group of embryos was treated locally with 4 µl crude collagenase (1 mg/ml, C5138; Sigma-Aldrich, St Louis, MO, USA) to degrade the ECM on the basal surface of the OV.

2.3 Stiffness measurements

Tissue stiffness was measured in the eye using a custom-made microindentation device, consisting of a calibrated glass cantilever beam with a cylindrical tip (approximately 20 µm in diameter) at the end (Zamir et al. 2003; Xu et al. 2010). Motion of the cantilever was controlled by a piezoelectric motor, which moved the tip 200 µm in 5 s. The membranes surrounding the brain were removed for easier manipulation, and the heart was removed to eliminate motion caused by the heartbeat. With one OV held by suction onto a glass micropipette, the opposite eye was indented. Video recording of the indentation was used to quantify beam and tissue deflection as described in Zamir et al. (2003). Tissue stiffness before and after collagenase treatment was calculated as the slope of an average force–displacement curve at multiple indentation depths (10, 20 and 30 µm).

2.4 Imaging and measuring tissue morphology

Brightfield images and video recordings were captured with a Nikon EOS T3 camera on a Leica DMLB MZ 8 microscope. Optical coherence tomography (OCT) images were acquired with a Thorlabs (Newton, NJ, USA) OCT system (approximately 10 µm resolution).

Measurements of central curvature, invagination depth, and tissue thickness were made from OCT sections using ImageJ (National Institutes of Health, Bethesda, MD, USA). A circle was fit through approximately five markers near the center of the OV along the basal surface, and curvature was calculated as k = 1/r where r is the radius of the circle fit. Curvature was normalized by dividing values by the average, initial curvature at HH12. Normalized invagination depth, measured in the plane orthogonal to the optic stalk, is defined as the vertical distance between the top of the OV to the center of the neural retina (D) divided by the radius of the OV (R) defined by the distance from the center of the OV to the outer edge (see Fig. 8E, inset). To quantify thickness of the retinal placode, six measurements were made in each eye near the center of the OV (three measurements in two orthogonal planes). The thickness of the edge of the retinal placode region was measured by averaging four measurements at the dorsal edge in the plane through the optic fissure. The orthogonal plane did not have sufficient contrast at the placode edge to measure in this second plane. Cross-sectional area of the retinal placode was measured in two orthogonal planes for each eye in OCT images. Thickness and area were normalized by corresponding values at HH12.

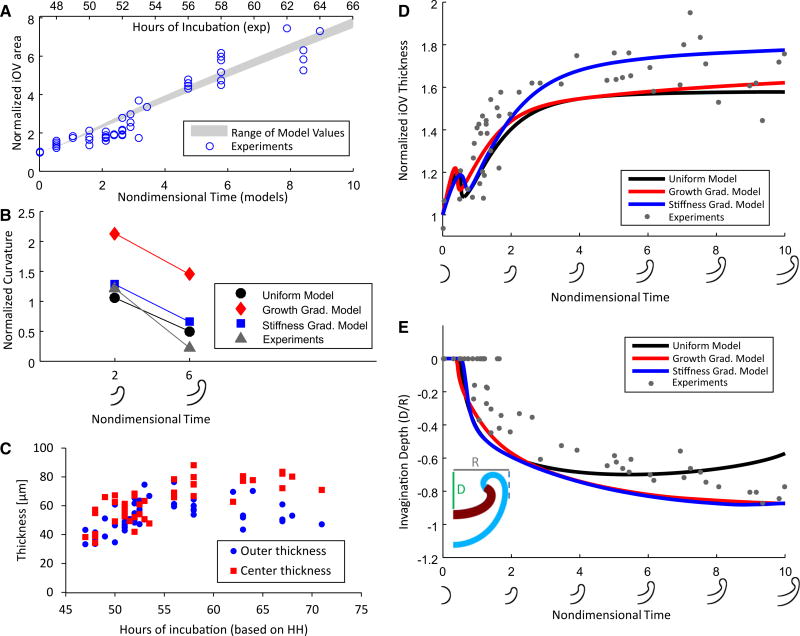
Fig. 8.

Comparison of experimental and model-predicted optic cup morphology. A Cross-sectional area of the iOV (normalized by average initial area), averaged from OCT images in two orthogonal planes, versus hours of incubation. Gray region shows the range of iOV area in the three models versus nondimensional time. A linear regression (R² = 0.996) through the model data was correlated with experimental area to determine corresponding times for the models. B Experimental curvature at center of iOV (normalized by initial curvature) decreased between t = 2 (Phase 3, HH14) and t = 6 (Phase 4, HH17). For all models, the curvature decreased a similar amount to the measurements, while the magnitude of the measured curvature was similar to that given by the uniform and stiffness gradient models but considerably lower than that of the growth gradient model. C Measured wall thickness at center and outer edge of the iOV. D Comparison of experimental and model wall thickness (normalized by initial thickness at Phase 0) at center of iOV as function of time. Thickness reached a local maximum early in each model as the placode flattened and increased afterward. Stiffness gradient model yields the best qualitative agreement with the data. E Comparison of experimental and model invagination depth versus time. Normalized invagination depth is defined as pit depth D divided by maximum OV radius R (see inset). In panels D and E, outlines of the stiffness gradient model mark each time point on the time axes. Stiffness and growth gradient models agree reasonably well with qualitative trends in the data

To better visualize the 3D morphology of the developing eye, the geometry of some OVs and OCs were reconstructed from OCT image stacks by tracing the surface of the OV in ImageJ. The segmented image volumes were then imported into the software package Caret (Essen et al. 2001) to create a smoothed surface from the outlines. The reconstructed volumes were then visualized in MATLAB (MathWorks, Natick, MA, USA).

2.5 Actin and matrix visualization

Embryos were stained after overnight fixation in 3.7 % formaldehyde. To visualize filamentous actin, embryos were first blocked in 0.1 % Triton X-100 (Sigma) and 1 % bovine serum albumin (BSA) in PBS and then stained with phalloidin (1:100, Alexa Fluor 488 phalloidin or Alexa Fluor 633 phalloidin, Molecular Probes) in PBS with 0.1 % Triton X-100 and 1 % BSA.

To visualize ECM, two separate fibronectin antibodies were used. Fixed chick embryos were permeabilized in 1 % Triton X-100 (Sigma) in PBS for 30 min and blocked in 5 % BSA in PBS for 3 h (Rifes and Thorsteinsdóttir 2012). Embryos were incubated with a primary antibody of mouse monoclonal anti-chick fibronectin (DSHB, clone B3/D6, 1:50) in 1 % BSA and 0.1 % Triton X-100 in PBS for 48 h at 4 °C. Embryos were rinsed in PBS and then incubated with the secondary antibody Alexa Fluor(R) 488 F(ab′)2 Fragment of Goat Anti-Mouse IgG (1:250, Invitrogen) in 1 % BSA and 0.1 % Triton X-100 in PBS for 48 h at 4 °C. Additional fixed embryos were rinsed in PBS, then soaked in blocking buffer (2 % goat serum with 0.1 % Triton X-100 in PBS) for 3 h. Samples were incubated in primary antibody in blocking buffer (Sigma F3648, 1:100) for 24 h at 4 °C, rinsed with PBS three times, and incubated with a secondary antibody of Alexa Fluor(R) 488 Goat anti-Rabbit IgG (H+L) (Invitrogen A11034, 1:100) in blocking buffer overnight at 4 °C. Samples were then rinsed with 0.1% Tween 20 (Sigma) and DAPI (Sigma) in PBS three times. The B3/D6 fibronectin antibody was developed by Fambrough and was obtained from the Developmental Studies Hybridoma Bank developed under the auspices of the NICHD and maintained by The University of Iowa, Department of Biology, Iowa City, IA 52242.

Actin-stained embryos were rinsed in PBS three times and then imaged using a fluorescence Leica DMLB microscope (5×, 20× objectives). Before imaging fibronectin distributions with confocal microscopy, tissues were embedded in 4 % agarose in PBS and cut into thick sections (120 µm) using a tissue slicer (Electron Microscopy Sciences, Hatfield, PA, USA). Confocal images were captured with a Zeiss LSM 510 or 710 confocal microscope (Carl Zeiss Microimaging, Inc., Thornwood, NY, USA).

Fibronectin distribution was analyzed by tracing the ECM between the SE and OV in ImageJ with a wide, segmented line. The line was then smoothed with the Fit Spline tool and the image straightened with the Straighten tool (see Online Resource 1, Fig. S1). The fluorescence intensity was calculated across the thickness of the ECM with respect to arc length with the Plot Profile tool, and data were exported to plot in Matlab. Arc length was normalized from 0 (the dorsal edge of the placode) to 1 (the center of the placode). Fluorescence intensity was normalized by dividing the raw data by the average intensity along the ECM for each sample.

2.6 Cell proliferation

Cell proliferation was quantified for the mouse OV from image data generously provided by the authors of Huang et al. (2011). As described in Huang et al. (2011), embryonic mice were exposed for 1 h to BrdU which incorporates into cells in S-phase. Fixed embryos were then sectioned and counterstained with hematoxylin. Using their images, we quantified cell proliferation in the OV in three equally sized regions of the retinal placode and in the outer OV at multiple stages of eye development. BrdU positive and negative cells were counted to calculate the percent of BrdU incorporation in each region of the mouse OV. Measurements were analyzed across stages and placode regions using two-way repeated measure ANOVA and post-hoc Tukey’s test in SigmaPlot (v12.5, Systat Software Inc.).

2.7 Finite-element models for morphogenesis

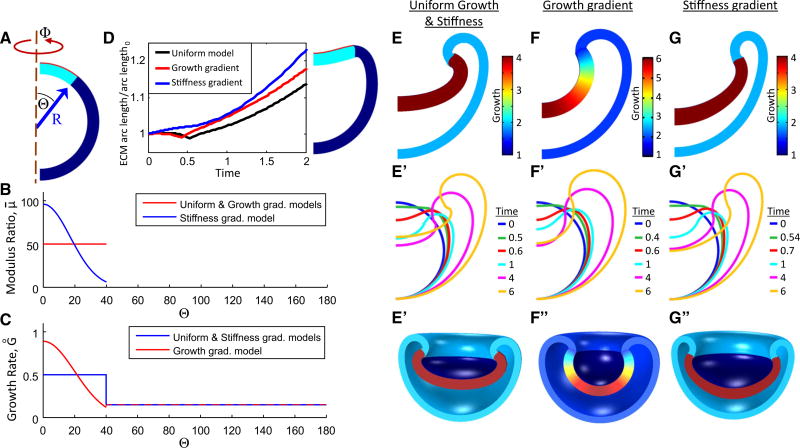
To simulate OV morphogenesis, we created axisymmetric finite-element models using COMSOL Multiphysics (Version 4.2a, COMSOL AB, Providence, RI, USA). The OV is modeled as a spherical shell with a normalized outer radius of 1 and wall thickness of 0.2. With OV and ECM geometries estimated from OCT images and fibronectin staining, respectively (e.g., Fig. 1, Fig. 2C), the model is divided into three regions representing the inner OV (placode region), the outer OV, and the ECM (Fig. 6B). The ECM is represented by a relatively thin layer of the outer wall spanning 1/10 the OV thickness and 80° of the circumference (future placode region) (see Fig. 7A). To prevent rigid-body motion, a point at the bottom of the OV is fixed. In some models, the invaginating region contacted the bottom of the OV. In these cases, the Contact Pair feature of COMSOL was used with a contact penalty factor of 2/h where h is mesh element size.

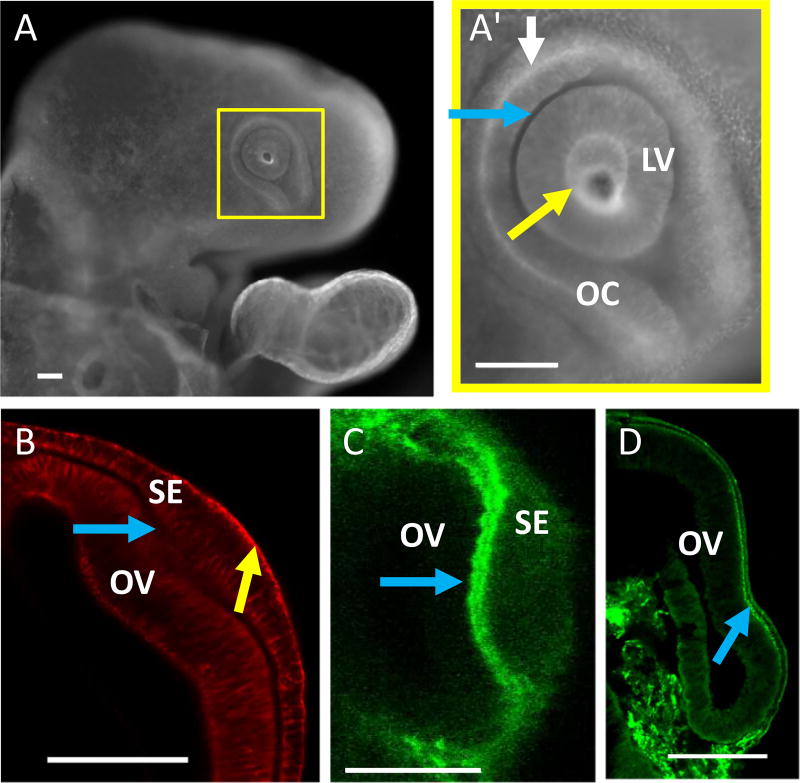
Fig. 2.

Distributions of actin and ECM in the eye. (A, HH14) Whole-mount stain of F-actin. (A’) is an enlarged view of yellow box in (A) showing concentrated actin along the apical surface of the SE (yellow arrow) and OC (white arrow) but not the basal surface of the OC (blue arrow). (B, HH13+) section during early invagination also showing F-actin concentrated mainly along the apical (initially convex) surface of the SE (yellow arrow). The basal (concave) side of the OV lacked substantial F-actin (blue arrow). (C, HH13+) section with fibronectin staining shows a bilayered ECM (blue arrow) between the invaginating OV and SE. (D, HH14−) ECM remained after SE removal (blue arrow). Scale bars 100 µm

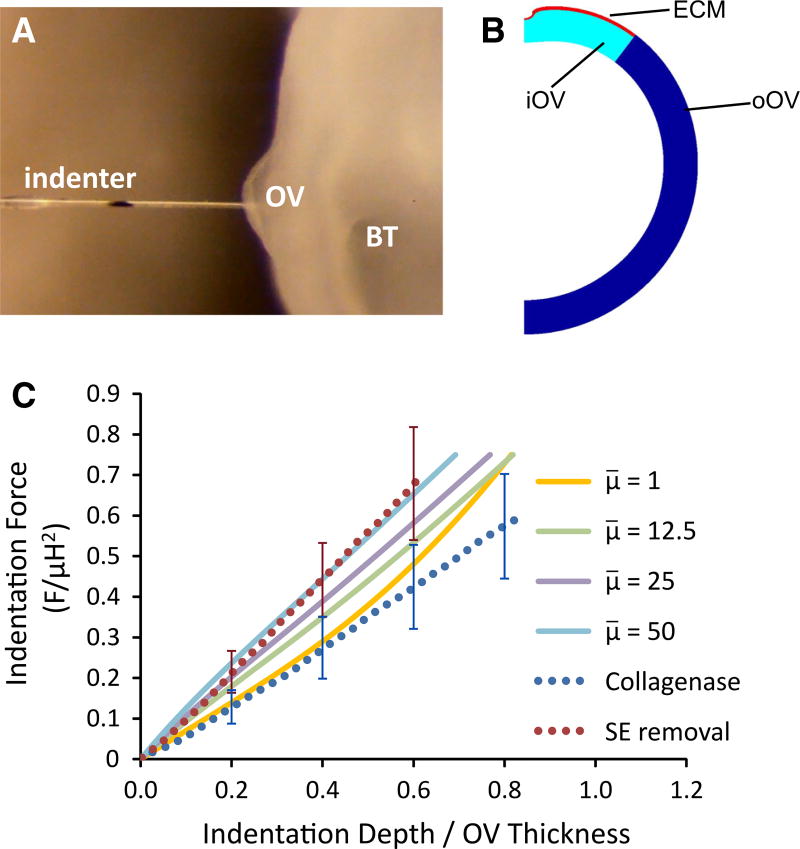
Fig. 6.

Microindentation testing to determine relative ECM stiffness. A Image of OV being indented (BT brain tube). Black mark on the indenter tip was tracked to determine displacement. B Finite-element model for OV indented at top. C Comparison of nondimensional force– displacement curves between experiment and model (F, indenter force; μ, shear modulus of OV; H, undeformed OV thickness). Model results are shown for various values of μ̄ = μ_ECM/μ_OV. Experimental curves represent the averages of three OVs without the SE before (red dots) and after (blue dots) collagenase treatment; error bars represent standard deviation. Indentation stiffness (slope) decreases after collagenase exposure

Fig. 7.

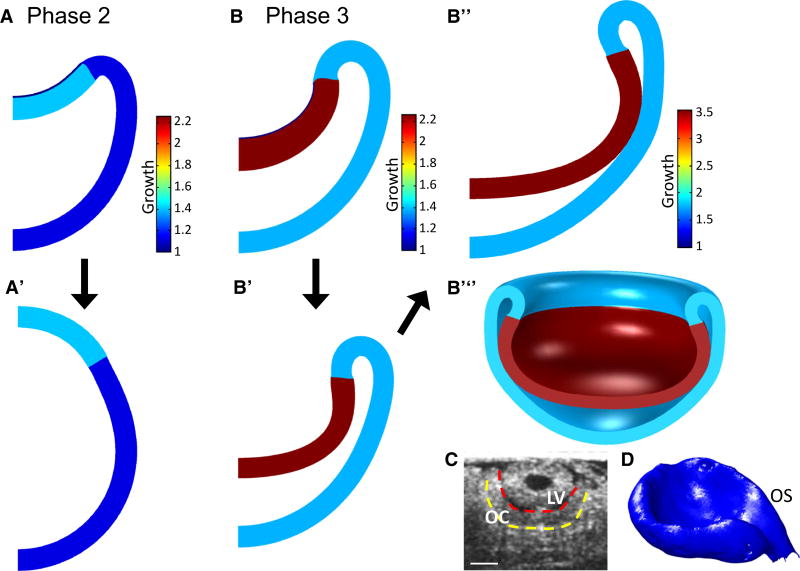
Three models for OV invagination. The models differ only in the distributions of growth and stiffness in the placode and ECM regions, respectively: (1) uniform growth and stiffness; (2) growth gradient with uniform stiffness; and (3) stiffness gradient with uniform growth. (A) Initial OV geometry is a spherical shell divided into three regions representing the iOV (light blue), oOV (dark blue), and ECM (red). (B, C) Spatial distributions of shear modulus ratio (μ̄ = μ_ECM/μ_OV) and growth rate in each model. (D) ECM arc length remains almost constant (1–2 % change) in each model as the placode flattens and begins to invaginate (t < 0.5), and then increases significantly with time. The uniform model is shown during early invagination (t = 0.55, right). (E–G) Invaginated shapes for each model at t = 6. (E’–G’) Outlines of models at various times. (E”–G”) 3D representations of each model

With all layers treated as pseudoelastic, growth is simulated by modifying the governing equations within COMSOL based on the theory of Rodriguez et al. (1994). Accordingly, the total deformation gradient tensor is defined as F = F^*·G, where F^* is the elastic deformation gradient tensor and G is the growth tensor. The Cauchy stress tensor is given by Taber (2004)

$$\mathit{\sigma }=\frac{2}{J^{\ast }}{\mathbf{F}}^{\ast }·\frac{\partial W}{\partial {\mathbf{C}}^{\ast }}·{\mathbf{F}}^{\ast \mathrm{T}},$$ (1)

where W is the strain–energy density function, C^* = F^*T·F^* is the right Cauchy–Green elastic deformation tensor, and J^* = det F^* is the elastic volume ratio. Details for incorporating growth in COMSOL 4.2a are provided in Hosseini et al. (2014).

Assuming the material properties for the OV are essentially the same as those for the rest of the brain tube during these stages, the strain–energy density function for each region is taken in the modified Blatz-Ko form (Xu et al. 2010; Taber 2004; Blatz and Ko 1962)

$$W=\frac{1}{2}\mu [I^{\ast }-3+\frac{1}{\alpha }(J^{\ast -2\alpha }-1\left)\right]$$ (2)

for an isotropic material, where μ is the shear modulus and α = ν/(1 − 2ν), with ν being Poisson’s ratio in the limit of small strain. In addition, I^* = tr C^* is the first strain invariant. For the OV, we set μ = 220 Pa and ν = 0.45 (Xu et al. 2010). Poisson’s ratio is taken the same for the ECM, but the shear modulus is larger as detailed later for each model.

In each region, the growth tensor is taken in the form

$$\mathbf{G}=G_R{\mathbf{e}}_R{\mathbf{e}}_R+G_{\mathrm{\Theta }}{\mathbf{e}}_{\mathrm{\Theta }}{\mathbf{e}}_{\mathrm{\Theta }}+G_{\mathrm{\Phi }}{\mathbf{e}}_{\mathrm{\Phi }}{\mathbf{e}}_{\mathrm{\Phi }}$$ (3)

where e_R, e_Θ, and e_Φ are undeformed unit vectors in spherical polar coordinates (Fig. 7A), and G_R, G_Θ, and G_Φ are specified functions of space and time. In all models, the ECM layer does not grow (G_R = G_Θ = G_Φ = 1), while, for axisymmetric deformation, the OV grows equally in the circumferential and meridional directions as defined by

$$G_{\mathrm{\Theta }}=G_{\mathrm{\Phi }}\equiv G,G_R=1$$ (4)

$$G=1+\mathring{G}(\mathrm{\Theta })t$$ (5)

where t is dimensionless time. The spatial distributions of the growth rate G̊ for each model are given in the Sect. 3.

3 Results

3.1 OCT imaging of eye morphology

At HH12 to HH13, the SE and OV are visible in OCT images as distinct cell layers of ectodermal origin (Fig. 1, bottom row). The lens placode and retinal placode form as these respective layers thicken locally in their mutual region of contact during stage HH13+. These placodes then invaginate to create the lens pit and bi-layered OC. The lens pit eventually closes to create the lens vesicle, the inner and outer regions of the OC become the neural retina and retinal pigment epithelium, respectively, and the part of the SE outside the lens fuses into a continuous sheet in contact with the lens (Fig. 1). The resolution of our OCT system (about 10 µm) is not fine enough to visualize the ECM between the OV and SE. The cell layers and ECM are depicted schematically in the top row of Fig. 1.

As embryonic structures acquire different shapes and functions, their names often change. During development, for example, a circular region of the SE becomes the lens placode, the lens pit, and the lens vesicle before becoming the lens itself. For simplicity, since this can be a source of confusion, we refer to the two main layers as the OV and SE at all stages. Each of these layers is composed of two regions. Regardless of the amount of invagination, we consider the OV as divided into the inner OV (iOV; retinal placode composed of neural ectoderm) and outer OV (oOV; retinal pigment epithelium), while the SE is divided into the inner SE (iSE; lens placode, lens pit, lens vesicle) and the outer SE (Fig. 1, top row).

In addition, we define the following developmental phases for the OV (Fig. 1):

• Phase 0: pre-placode (HH12) Phase 1: placode (HH13+)

• Phase 2: early invagination (HH14−)

• Phase 3: mid invagination (HH14)

• Phase 4: late invagination, optic cup (≥HH15)

Finally, it is important to note that the apical side of the SE becomes the concave side of this membrane in the invaginating region, while the basal side becomes convex. The opposite is true for the OV.

3.2 Actin and ECM staining

Tissues stained for F-actin were visualized with fluorescence microscopy in whole embryos (Fig. 2A, A’) and with confocal microscopy in sectioned embryos (Fig. 2B). Actin was concentrated primarily along the apical (initially convex then concave) side of the iSE, as has been previously reported in chick and mice (Zolessi and Arruti 2001; Smith et al. 2005; Chauhan et al. 2009). In the iOV, actin intensity was considerably weaker than in the iSE but was stronger on the apical (convex) side than the basal (concave) side.

Previous work in mice has shown that fibronectin is required for the lens placode to form, as well as for subsequent lens invagination. In mouse embryos, fibronectin is visible as a dual-layered ECM located between the SE and OV (Huang et al. 2011). Here, in chick embryos, the ECM was also typically visible as two layers between the SE and OV as shown by fibronectin staining (Fig. 2C).

3.3 Effects of SE and ECM removal

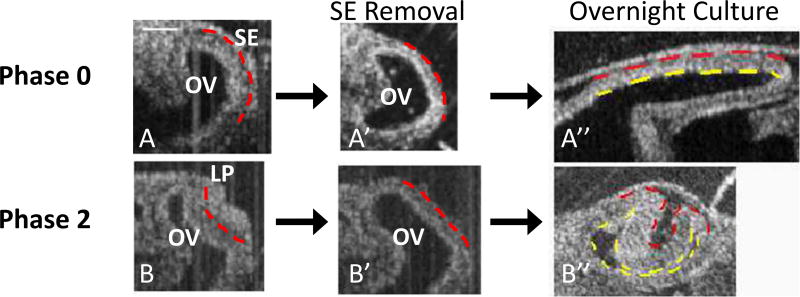
To determine whether the mechanics of OV invagination in the chick embryo are similar to those in mice, we first repeated the SE removal experiments of Hyer et al. (2003), who ablated the SE using a small amount of Nile Blue sulfate solution applied locally in ovo (see Sect. 2). We removed the iSE at multiple stages of eye development before, during, and after placode formation. The SE generally grew back as a thin layer, but this occurred a few hours after dissection or collagenase observations were made (longer if the ablated region was relatively large).

Consistent with the results of Hyer et al. (2003), removing the SE at Phase 0 (before placode formation) inhibited OC formation (Fig. 3A, A’, A”), while dissecting the SE after this time usually led to OVs invaginating into OCs without lens vesicles (Fig. 3B, B’, B”). In some embryos, the SE healed after several hours of culture and grew a small lens placode or lens vesicle from the newly created SE tissue.

Fig. 3.

OCT images of OV after SE removal and continued culture. Dashed red lines indicate the boundary between the SE and OV; dashed yellow lines indicate OV shape after overnight culture. (A, A’, A”) SE removal before placode formation had little effect on OV shape immediately after dissection (A, A’, Phase 0, HH12+) but inhibited subsequent invagination (A”). (B, B’, B”) Removing the SE after placode formation (B, B’, Phase 2, HH14−) caused immediate loss of concavity in most embryos (n = 24/34), but invagination still occurred in some embryos that were cultured overnight (n = 4/6) (B”), as reported by Hyer et al. (2003). Scale bar 100 µm

As shown later, although these results are crucial, the tissue behavior immediately after dissection yields important clues concerning the underlying morphogenetic mechanisms. Interestingly, the short-time behavior of dissected samples also depended on the stage of development. At Phase 0 and 1, the OVs maintained approximately the same shape just after SE removal (Fig. 3A, A’). At Phase 2, the concavity of OVs usually reversed, i.e., the invaginated region ‘popped out’ when the inner SE was ablated (24/34) (Fig. 3B, B’). At later phases of invagination (Phases 3 and 4), the OV typically remained invaginated after SE removal (15/40 popped out at Phase 3 and 0/15 at Phase 4) (e.g., see Fig. 4B, B’). Notably, some of the OVs that popped out after shallow invagination later resumed the invagination process to form relatively normal-looking OCs (Fig. 3B”).

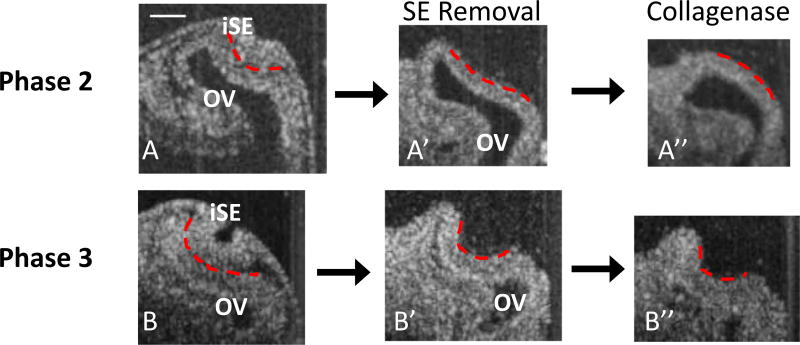
Fig. 4.

OCT images of OVs after SE removal and ECM degradation. Dashed red lines indicate outer surface of iOV. (A, A’, A”, HH14−) After removing the SE during early invagination, the OV sometimes remained concave (A’, n = 10/34 concave), but exposure to collagenase usually caused the remaining concavity to reverse (A”, n = 5/6 convex). (B, B’, B”, HH14+) At later phases of invagination, the OV typically remained concave after lens removal (B’, n = 25/40 concave) and usually remained concave after subsequent collagenase exposure (B”, n = 5/14 convex). At stages with a more developed optic cup (~HH15, not shown), concavity was maintained in all embryos after SE removal (n = 15/15 concave) and ECM degradation (n = 4/4 concave). Scale bar 100 µm

Taken together, these results suggest that OV invagination generally requires the presence of the SE through the period of placode formation (Phase 1), but not afterward. Evidence from a previous study suggests that the matrix secreted by the SE and OV (triggered by the contact between the two cell layers) rather than the SE itself, supplies a mechanical constraint needed for OV invagination (Huang et al. 2011). To explore this idea further, we disrupted the matrix at various stages of invagination (Phases 2–4).

First, to determine how SE removal affects the ECM, embryos were fixed and stained for fibronectin after SE ablation. A bilayered ECM was still visible in dissected embryos, indicating that the matrix was not destroyed in the process of removing the SE (Fig. 2D).

Next, we applied collagenase locally to degrade the ECM in eyes that remained invaginated after iSE removal and observed changes in morphology. The matrix between the OV and SE in the chick contains several components including collagen, fibronectin, laminin, and glycosaminoglycans (GAGs) (Hendrix and Zwaan 1974, 1975; Webster et al. 1983; Hilfer and Randolph 1993). Crude collagenase disrupts both collagen and fibronectin, which are major determinants of material properties in ECM (Oberhauser et al. 2002).

Within a few minutes of collagenase exposure, many of the Phase 2 OVs slowly reversed their concavity and became convex (5/6) (Fig. 4A, A’, A”). One became less invaginated but remained concave (1/6). Several eyes (9/14) at Phase 3 remained concave after collagenase treatment and showed relatively little change in morphology (Fig. 4B, B’, B”). To verify the effects of collagenase, in a few embryos both eyes were dissected, and only the right eye was treated with collagenase. The embryos were fixed and stained for fibronectin. As shown in Online Resource 1, Fig. S2, the crude collagenase decreased fibronectin staining and therefore degraded the ECM without affecting actin (see Online Resource 1, Fig. S3).

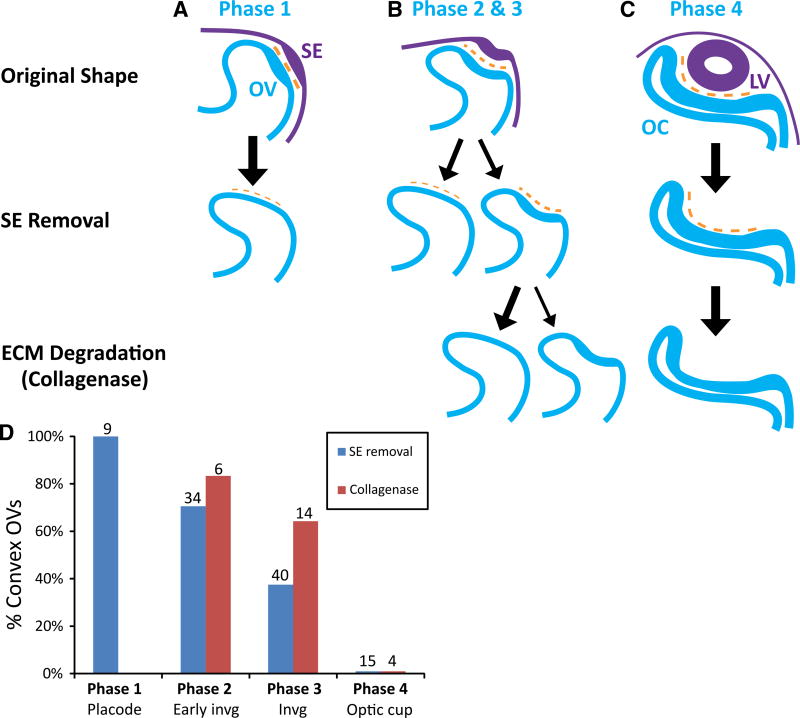
Figure 5 summarizes the main results of our SE and ECM perturbation studies. During early placode formation (Phase 1), OVs remained fairly unaltered following SE removal (Fig. 5A). At early to mid-stages of invagination (Phases 2– 3), many OVs became convex after SE removal, while others did not pop out until the ECM also was degraded (Fig. 5B). At Phase 2, 71 % of the OVs became convex after SE ablation (24/34), while this fraction dropped to 38 % at Phase 3 (15/40). For those Phase 2 OVs that remained concave after SE ablation, collagenase exposure caused 83 % (5/6) to become convex (Fig. 5D). By Phase 3, this fraction dropped to 64 % (9/14), and by Phase 4 all of the more developed OCs remained concave following SE removal (n = 15) and collagenase treatment (n = 4) (Fig. 5C, D).

Fig. 5.

Summary of shape changes in OV after SE removal and ECM degradation. A–C Schematics of observed shape changes (purple = SE, blue = OV, orange = ECM). Arrow size reflects the likelihood of each shape change as plotted in (D). (A, Phase 1) Removing the SE at the placode stage prior to invagination caused relatively little immediate shape change. (B, Phases 2 and 3) During OV invagination (HH14− to HH14+), SE (lens placode) removal sometimes caused the OV to lose its concave shape and become convex. Exposing the remaining concave OVs to collagenase caused most to pop out and become convex. (C, Phase 4) At later stages of invagination (about HH15 onward), lens removal and subsequent collagenase treatment had relatively little effect on the shape of the OC. (D) Fraction of OVs that became convex after treatment. As invagination deepened, optic cups were more likely to remain concave after SE removal (P < 0.001, Fisher’s exact test comparing Phases 2 and 3). However, collagenase had a similar effect at these two phases (P < 0.613, Fisher’s exact test). Numbers above bars indicate sample size. All OVs remained concave at Phase 4 after both SE removal and collagenase treatment

To determine whether the effects of SE removal and ECM degradation on OV shape were statistically significant, results were compared using Fisher’s exact test. After SE removal, a significantly higher fraction of OVs popped out at Phase 2 compared to Phase 3 (P < 0.001), indicating that the SE is more essential for invagination at the early phases. Although a higher percentage of Phase 3 OVs became convex after subsequent collagenase exposure, the difference relative to Phase 2 was not significant (P = 0.613), suggesting that the ECM is required for continued invagination at Phase 3.

Taken together, these results suggest that the presence of the SE is required to initiate OV invagination, but only the ECM is needed to continue the process at later stages. It would be interesting to conduct similar experiments in which the ECM is degraded without removing the SE, but our attempts to do so encountered technical difficulties.

3.4 Estimation of ECM stiffness

To explore the morphogenetic function of the ECM during OC formation, we measured mechanical properties and changes in geometry during invagination. These data were used to create and test finite-element models to assess the physical plausibility of the matrix-constraint hypothesis for OV invagination.

As shown later (see Fig. S4), results from our model suggest that the proposed mechanism requires the ECM to be considerably stiffer than the cells comprising the OV. Since it is not practical to measure the properties of the matrix directly, we estimated its modulus relative to that of the OV by conducting microindentation tests on partially invaginated OVs (Phases 2–3) with and without ECM (after removing the SE).

After indenting the center of the OV three times and averaging the results (see Fig. 6A), we repeated the tests on the same sample after several minutes of local collagenase exposure. Force–displacement curves for three embryos were averaged and fit to a quadratic polynomial for both conditions (with and without collagenase), and the slope of the curves at multiple indentation depths provided incremental stiffnesses. The measured force–displacement curves after SE removal and collagenase treatment were relatively linear (Fig. 6C). Degrading the ECM with collagenase decreased the average stiffness of the OV. At 20% indentation, the stiffness decreased about 38 % from 11.3 to 7.0 nN/µm, while at 40 % indentation the stiffness decreased about 42 % from 12.6 to 7.3 nN/µm.

To test for possible side effects of collagenase on the cells, Phase 0 embryos with intact SE tissue were indented before and after treatment. Collagenase had little effect on the stiffness of these OVs, presumably due to the lack of ECM between the OV and SE at these stages (data not shown). These results suggest that the softening effect of collagenase seen in our data was caused by degradation of the ECM and not by weakening of the cells.

To estimate the value of the ECM shear modulus relative to that of the OV, we created a finite-element model for the indentation test. As discussed in the Sect. 2, the OV was modeled as a spherical shell with the wall divided into three regions representing the iOV, the oOV, and the ECM (Fig. 6B). The shear modulus μ_OV is taken as uniform and equal in both regions of the OV. The force of a cylindrical indenter, with a radius 25 % of the OV thickness, was applied normal to the center of the ECM. Nondimensional force–displacement curves were computed for various values of μ̄ = μ_ECM/μ_OV and compared with experimental results (Fig. 6C).

These results indicate that the value μ̄ = 50 is reasonable for the intact OV with ECM but not SE (Fig. 6A). Moreover, the curve for μ̄ = 1 falls relatively close to the experimental curve for collagenase treatment, consistent with the assumption that collagenase effectively eliminates the ECM as a factor in the mechanics.¹

3.5 Computational models for OV invagination

Finite-element models were used to help answer the following questions: (1) Can the ECM constrain growth-driven OV expansion enough to cause invagination without the SE? (2) What distributions of placode growth and ECM stiffness produce the most realistic morphology during invagination?

To address these questions, the model from the indentation analysis was modified to include regional tissue growth (Fig. 7A). The shear modulus is taken as 220 Pa in both regions of the OV (Xu et al. 2010). We also assume that the ECM does not grow, while the OV grows only in the e_Θ and e_Φ directions (see Eqs. 3, 4). To give a realistic change in OV radius (R in Fig. 8E), the oOV is assumed to grow uniformly at the rate G̊ = 0.15 (see Eq. 5). This leaves ECM stiffness and iOV growth as free variables.

Here, we consider three models: (1) uniform model: uniform ECM modulus and uniform iOV growth; (2) growth gradient model: uniform ECM modulus and growth gradient in iOV (with higher growth rate at the center); and (3) stiffness gradient model: ECM stiffness gradient (with higher ECM stiffness at the center) and uniform growth in iOV. Values of the specified growth rate, G̊, and the ratio μ̄ = μ_ECM/μ_OV for each model are given in the following paragraphs. (For a given geometry, the behavior of the model depends on the ratio of the shear moduli, rather than their individual values).

For the first two models, we take μ̄ = 50 from our indentation data. In the third model, the distribution for the ECM was taken in the form (see Fig. 7B)

$$\overline{\mu }=96{\mathrm{e}}^{-\beta {(\mathrm{\Theta }/{\mathrm{\Theta }}_{\text{max}})}^2}$$ (6)

where β = 2.75 and Θ is the meridional angle from the axis of symmetry with Θ_max = 40° defining the margin of iOV (see Fig. 7A). This expression corresponds to an average ECM shear modulus of 50 μ_OV. The value for β was chosen to give a reasonably realistic thickness gradient in the iOV (see Fig. 8C and Online Resource 1, Fig. S5).

Cell proliferation in mouse eyes was higher in the iOV than the oOV during Phases 1 and 4 (see Fig. 9A). However, changes in cell size and cell death also can contribute to tissue growth. Hence, as discussed in the next subsection, the growth rate in the iOV was determined by matching experimental and numerical results for the temporal change in iOV cross-sectional area (see Fig. 8A). This procedure yielded G̊ = 0.5 for the (uniform) nondimensional growth rate in the uniform and stiffness gradient models. For the growth gradient model, we take

$$\mathring{G}=0.84{\mathrm{e}}^{-\gamma {(\mathrm{\Theta }/{\mathrm{\Theta }}_{\text{max}})}^2}$$ (7)

in the placode region with γ = 2 and the average growth rate maintained at GΠ = 0.5 (Fig. 7C). The value for γ was chosen based on morphology and curvature (see Online Resource 1, Fig. S6). All three models were run until the dimensionless time t = 10 at which point the growth G in the iOV reached 6 (or an average of 6 in the growth gradient model).

Fig. 9.

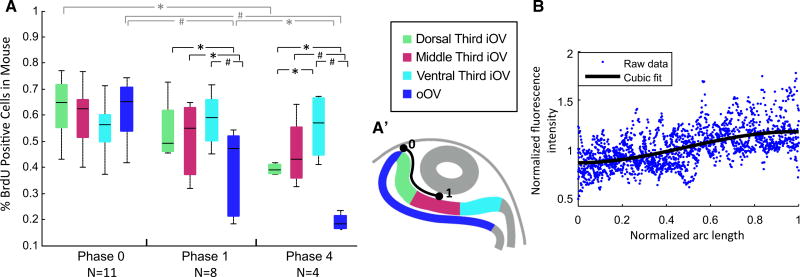
Cell proliferation and ECM distribution in embryonic eyes. (A) Cell proliferation at Phase 0 (E8.5), Phase 1 (E9.5), and Phase 4 (E10.5) was measured in the mouse embryo by counting the percent of BrdU positive cells in cross-sections in the oOV and three equal regions of the iOV (see A’). Horizontal black bars show significant differences between regions at a given phase, and gray bars between phases within a given region (two-way repeated measure ANOVA with Tukey’s test, ^*P < 0.05, ^# P < 0.001). Differences were significant between certain regions and stages with significant interaction between stage and region (P < 0.001). At Phases 0 and 1, proliferation in the three iOV regions was not significantly different suggesting uniform proliferation in the iOV. At Phase 4, proliferation of the dorsal third of the iOV was significantly lower than in the ventral third (P < 0.05). Proliferation significantly decreased in the oOV between each stage. (A’) Diagram shows the oOV and three regions of the iOV. The normalized arc length plotted in (B) is outlined in black from 0 to 1 (0 = dorsal contact point between OV and SE; 1 = center of the ECM, where the OV was most invaginated). (B) Fibronectin distribution between the OV and SE in the chick embryo at Phases 2–3. Fluorescence intensity was greater in the center than near the edge of the iOV (P < 0.001, t test comparing data between regions where arc length ≤0.1 and arc length ≥0.9), suggesting that the ECM is denser near the center of the iOV. Fluorescence intensity was normalized by average intensity in the ECM of each sample. A cubic polynomial was fit to the raw data (R² = 0.34, y = −0.71x³ + 1.05x² − 0.013x + 0.85)

All three models invaginate (Fig. 7E–G), suggesting that the ECM is stiff enough to produce an invagination without the SE. Moreover, there are some notable similarities as well as distinct differences in the morphogenetic behavior of these models.

In all three models, the iOV thickens into a relatively flat placode just prior to the start of invagination (Fig. 7E’–G’, green outlines). During this early phase, the placode thickness varies among the models (see below), but the radial arc length of the ECM-OV boundary remains relatively constant in all models (Fig. 7D). Near t = 0.5, the arc length reaches a local minimum in the growth gradient and uniform models and changes by only +2 % in the stiffness gradient model and −1 % in the other models. This behavior is consistent with measurements in chick and mouse embryos, where the contact area between the OV and SE remains relatively constant during placode formation (Zwaan and Hendrix 1973; Huang et al. 2011). As the invagination grows deeper, the ECM is stretched significantly by the growing iOV (Fig. 7D) as the oOV expands outward (Fig. 7E’–G’).

At the end of the simulation (t = 6), the center of the iOV is closest to the bottom of the oOV in the stiffness gradient model, while the uniform model has the largest gap (see Fig. 7E–G, E’–G’). In addition, the matrix inhibits tangential expansion of the growing placode region, with the added tissue volume causing the placode to thicken in all models. The wall thickness at the center of the OV increases most in the stiffness gradient model and least in the uniform model (Fig. 7E–G). As discussed below, quantitative comparisons of experimental and model geometries were used to determine the most realistic of these three models.

Cut-out 3D representations of the final shapes of the OC are shown in Fig. 7E”–G” and in animated videos in Online Resources 2–4. In addition, we conducted a parameter study to determine how changes in OV growth and relative ECM modulus affect invagination morphology. Decreasing μ̄ from 50 to 16 has relatively little effect on shape, but for μ̄ < 8 the iOV evaginates (see Online Resource 1, Fig. S4A). Between the values of 8 and 16, the model did not converge past early placode formation, possibly due to structural instability in the transition from convex to concave phenotype (Ramasubramanian and Taber 2008). Finally, increasing the growth rate in the oOV relative to that in the iOV does not change the shape of the iOV significantly, but the edge of the invaginating region within the oOV becomes less sharp (Fig. S4C). Modifying the parameters β in the stiffness gradient model and γ in the growth gradient model affects iOV curvature and invagination depth (see Online Resource 1, Figs. S5 and S6).

3.6 Stiffness gradient model best simulates optic cup formation

To determine which of the three models produces the most realistic behavior, we compared numerical results to experimental data acquired from chick embryos. Our evaluation is based on temporal changes in curvature, invagination depth, and wall thickness at the center of the iOV.

First, we correlated time scales using changes in cross-sectional area of the iOV. When normalized by initial area at Phase 0, the area obtained from OCT images increased approximately linearly with incubation time based on Hamburger–Hamilton staging (Fig. 8A) (Hamburger and Hamilton 1951). As mentioned above, when the average growth rate in the iOV is taken to be the constant value G̊ = 0.5 (see Eq. 5), the models yield area vs. time curves that agree reasonably well with the data (Fig. 8A).

Meridional curvature at the iOV surface (normalized by initial curvature), wall thickness (normalized by initial thickness), and invagination depth (normalized by OV radius) were measured over time (see Fig. 8B–E). Curvature was determined at t = 2 and t = 6 in the models and at comparable stages in the chick (HH14 and HH17). The growth gradient model produces the greatest curvature at both time points, while the uniform and stiffness gradient models more closely match the flatter curvature of the chick embryo (Fig. 8B).

Wall thickness and invagination depth at the center of the iOV change rapidly at first and then more slowly as the OV invaginates. Of the three models, the stiffness gradient model yields the best agreement with the thickness versus time data (Fig. 8D). In addition, although the thickness at the outer edge of the iOV was relatively difficult to measure accurately due to OCT resolution, the wall thickness near the center became higher than that near the edge as invagination proceeded (Fig. 8C). Only the stiffness gradient model captured this trend (see Fig. 7E–G).

Finally, the invagination depth versus time curves given by the growth gradient and stiffness gradient models are similar to each other but are quite different from the curve given by the uniform model at later stages (Fig. 8E). The trends provided by the two gradient models are a better match to experimental data (Fig. 8E). Note, however, that the early blip in the curves predicted by these models was not seen consistently in our data. This behavior is caused by a snap-through type of instability that occurs as the curvature reverses from convex to concave (Ramasubramanian and Taber 2008). Geometric imperfections in the actual OV would be expected to produce a smoother transition.

In summary, the stiffness gradient model is the only one of our three models that yields results in reasonably good agreement with all of our data. Taken together, therefore, the present results support the hypothesis that OV invagination is driven by uniform growth in the iOV constrained by a relatively stiff attached ECM. Our results also suggest that the stiffness of the ECM decreases with distance from the center of the OV. Although it is possible that the actual mechanism involves a combination of growth and stiffness gradients, our data indicate that the gradient in stiffness dominates the fundamental behavior.

We used other data to test the model predictions of uniform growth in the iOV and a stiffness gradient in the ECM. To examine the growth question, we used data from another study (Huang et al. 2011) to quantify cell proliferation in three regions of the iOV of the mouse embryo. No significant differences were found between regions at Phases 0 and 1 (two-way repeated measures ANOVA and post-hoc Tukey’s test) (Fig. 9A). There was a significant difference between the dorsal third and ventral third of the iOV by Phase 4 (P < 0.05), but these regions were not significantly different from the middle third. Although growth may not be caused by cell division alone and some differences exist in eye development between mouse and chick, these results suggest that a strong growth gradient in the iOV is unlikely. In addition, at Phases 1 and 4, proliferation in the oOV was significantly lower than the iOV, similar to published findings in the chick and at later stages of human eye development (Tsukiji et al. 2009; Božanić and Saraga-Babić 2004). These data are consistent with the different growth rates specified in the iOV and oOV of our model.

Using microindentation, we tried to measure regional stiffness variations in the iOV, but the relatively small size and concave curvature of this region made these measurements unreliable. Since fibronectin content has been found to correlate with tissue stiffness in arteries (Kakou et al. 2009), we used the intensity of fibronectin staining as an indicator of qualitative trends in ECM stiffness (see Online Resource 1, Fig. S1 for more details). Normalized intensity for six chick embryos is plotted as a function of normalized arc length from the dorsal edge to the center of the iOV (Fig. 9A’, B). Data for the ventral half of the iOV were quite irregular, possibly due to the developing optic stalk, and were ignored. Intensity was significantly higher near the center than near the dorsal edge (38 % higher in the cubic regression fit; P < 0.001, t test comparing data within 10 % of the total arc length from the center and edge). These results are consistent with the ECM being stiffer at the center than at the edge of the iOV.

Taken together, the cell proliferation and ECM staining data seem to support the stiffness gradient model for OV invagination. To compare morphology, the stiffness gradient model is superimposed over OCT images of the chick OV in Figure S7 (see Online Resource 1).

3.7 A stage dependent need for the ECM

As discussed above, our experiments have shown that degrading the ECM with collagenase during the early phases of invagination often caused the OV to pop out, converting the invagination into an evagination. At later phases, however, the invagination was more likely to remain concave after treatment (Fig. 5). We used this behavior to test the predictive ability of the stiffness gradient model. (Notably, the behavior of our other models is similar for this perturbation).

To simulate degradation of the ECM, growth was paused at a specified level of invagination, the shear modulus of the ECM was decreased to match that of the OV, and the value of G in the ECM layer was increased to match the value of the iOV (Fig. 10A, A’, B, B’). This procedure effectively eliminated the ECM from the model. Results from this procedure are shown for early invagination (Phase 2) and mid invagination (Phase 3). Consistent with our experiments, the OV reverted to a convex shape after ECM removal during early invagination (Fig. 10A, A’, Online Resource 5), but it remained concave after the deeper invagination (Fig. 10B, B’, Online Resource 6). Hence, the model captures this unexpected behavior reasonably well. Interestingly, removing the ECM at Phase 3 allowed the iOV to expand, decreasing its thickness and center curvature (Fig. 10B, B). In our collagenase experiments, thickness and curvature did not appear to change significantly, possibly due to cell remodeling. We attempted to find the critical invagination depth for popping out, but convergence issues near the critical point hindered this aspect of our study. However, the model results indicate that the critical point occurs between about HH13+ and HH14 (t = 0.9 to 2.1 in the model).

Fig. 10.

Simulation of ECM degradation (stiffness gradient model). To simulate matrix degradation, growth is paused at a specified invagination depth (A, B) and the ECM is converted to iOV tissue by decreasing its shear modulus and increasing its growth to match those of the iOV (A’, B’). (A, A’) Phase 2 (G = 1.4 in iOV); ECM degradation causes the OV to pop out, switching from concave to convex. (B, B’) Phase 3 (G = 2.25 in iOV); the OV remains invaginated. (B”) To simulate further invagination after the lens and optic cup have detached, growth is continued after ECM degradation of B’. (B”’) 3D representation of the model in B”. (C) Phase 4 (HH17) chick optic cup (OCT cross-section) shows the model qualitatively captures the flattening at the center of the iOV. (D) Reconstruction of optic cup from OCT images shows 3D shape with a groove along the optic stalk (OS). Scale bar 100 µm

Hendrix and Zwaan (1974) found that the density of the matrix increases through early OV invagination and then decreases as the lens pit begins to separate from the OC to close and form the lens vesicle. To simulate the later stages of invagination without the ECM, we restarted growth in the Phase 3 model without ECM (shown in Fig. 10B’). As invagination deepened, the iOV eventually contacted the oOV (Fig. 10B”, B”’) to form a bilayered OC with a shape similar to that seen in the chick at about HH17 (Fig. 10C, D).

4 Discussion

The results of the present study support the hypothesis that ECM-provided constraint on lateral expansion of the growing iOV is sufficient to drive the invagination that creates the OC. The behavior of our model indicates that invagination requires that the matrix be considerably stiffer than the cells in the OV (see Fig. S4), consistent with our stiffness measurements.² Our results also suggest that the shape of the invaginated iOV (neural retina) is regulated, in part, by a stiffness gradient in the ECM, which is stiffer near the center than near the margin of the iOV. This gradient affects the local curvature and thickness of the retina.

As mentioned in the Introduction, Zwaan and Hendrix (Zwaan and Hendrix 1973; Hendrix and Zwaan 1974) suggested a similar invagination mechanism for the iSE (lens), and they speculated that constrained growth may also be involved in OC development. However, although the ECM has been studied as a potential source of morphogenetic signals to the OV (Wride 1996), how the matrix might influence OV morphogenesis has remained poorly understood.

A mechanical function for ECM has been found in other problems in morphogenesis. In branching morphogenesis, for example, matrix is more abundant in cleft (concave) regions than in expanding (convex) regions (Daley and Yamada 2013). Treatment with collagenase can reverse cleft formation in salivary gland (Grobstein and Cohen 1965) and the early lung (Wessells and Cohen 1968), similar to the popping out effect we observed in the OV. During gastrulation in the sea urchin embryo, Lane et al. (1993) suggested that differential swelling of the ECM drives invagination, a mechanism supported by computer modeling (Davidson et al. 1995, 1999). Hence, accumulating evidence suggests that ECM plays a major biomechanical role in shaping the embryo.

4.1 Evidence supporting the constrained growth hypothesis for OV invagination

Most previous studies of early eye morphogenesis have focused on the lens, but some offer important clues for solving the OV problem. In Pax6^CKO embryos, for example, lens placode formation is absent, the ECM between the OV and SE is less abundant, and cell-matrix adhesion is reduced. As a result, the dividing cells spread laterally instead of maintaining constant contact area, and neither the lens nor the OV invaginate (Huang et al. 2011). Fibronectin knockout mice (Fn1^CKO) yield similar results (Huang et al. 2011). Fibronectin is a primary matrix constituent during eye development (Kwan 2014). These results suggest that placode formation is a prerequisite for invagination in the eye, as has been found in other morphogenetic problems (Huang et al. 2011; Jidigam and Gunhaga 2013), and that retinal and lens placode formation requires the ECM. However, they do not prove that the ECM is necessary for the invagination process itself.

The experiments of Hyer et al. (2003) provide further clues to our problem. As discussed in the Introduction, removing the SE prior to lens placode formation (Phase 1) blocks OV invagination, although the neuroepithelium of the iOV still differentiates, whereas OV invagination generally proceeds unimpeded when the lens placode is removed after Phase 1. We repeated these experiments and obtained similar results. To explain these findings, Hyer et al. (2003) speculated that the iSE must be present long enough to send a biochemical signal to the iOV that induces invagination. Once the signal is received, the iSE (lens) is no longer needed.

Here, we offer an alternative possibility. We found that dissecting the SE using the method of Hyer et al. (2003) leaves the matrix relatively intact in a considerable number of embryos (Fig. 2D; Online Resource 1, Fig. S2), and our computational model suggests that the ECM without the iSE provides sufficient constraint on OV expansion to cause invagination (Fig. 7). Moreover, once the invagination has reached a critical depth, invagination can proceed without the ECM (Fig. 10B, B’, B”). Accordingly, we speculate that the iSE is required only to generate sufficient matrix to reach the critical depth. Dissecting the iSE prior to the placode stage (Phase 1) removes the source of ECM before enough has accumulated to cause sufficient invagination, and the process does not complete. Later dissection, however, removes the source but leaves enough ECM intact to reach the critical stage. After this time, invagination can proceed even if the matrix degrades further.

This mechanism is also supported by our ‘popping out’ experiments. Removing the SE or disrupting the ECM during Phase 2 causes most OVs to immediately become convex (Fig. 5), as the mechanical constraint is lost. However, the fraction of OVs that remain concave after dissection or collagenase exposure increases at later times (Phases 3 and 4).³ By Phase 4, removing the iSE or the ECM no longer induces any OVs to pop out. The results given by our model are consistent with this behavior (Fig. 10).

The reason that the ECM is required to maintain invagination only until a certain depth can be understood by considering the behavior of the model as ECM degradation is simulated (see Fig. S8). When the constraint provided by the matrix is eliminated, the relatively large bending stresses generated near the edge of the invaginated region force the iOV toward reversing its curvature and pop out as these stresses are relieved. Since the iOV grows faster than the oOV, the increased surface area of the iOV must fit through a relatively smaller opening in the oOV during the transition from concave to convex curvature. Hence, the iOV pushes the edge of the spherical oOV radially outward, stretching it in the circumferential (hoop) direction. At Phase 2, the bending stresses can overcome these additional hoop stresses. By Phase 3, however, the growth disparity and corresponding hoop stresses are too large to overcome, and the iOV remains invaginated. Notably, this constraint is a consequence of the spherical geometry of the model; a cylindrical model would not provide such strong resistance to evagination.

Finally, it is important to note the following. While our study indicates that constrained growth likely drives OC formation on a global scale, the spatial distributions of growth and matrix stiffness can affect the more detailed shape of the invaginated iOV, i.e., the neural retina (Figs. 7E–G and S4–S6). While these gradients are not necessary for invagination to occur, a sharper gradient in ECM stiffness, for example, would produce an increased gradient in iOV thickness as well as a change in retinal curvature. Since the shape of the retina significantly affects vision, these morphogenetic factors should not be overlooked.

4.2 Possible alternative mechanism from stem cell studies

Recently, researchers have devised ways to generate self-assembling OCs in vitro using either mouse or human embryonic stem cells (Eiraku et al. 2011; Nakano et al. 2012). Notably, these structures invaginate without SE tissue, but laminin staining showed that ECM was present along the basal (outer) surface of the OV. Moreover, disrupting cell-matrix adhesion with anti-integrin-β1 antibody prevented OC formation in the mouse stem cell culture (Eiraku et al. 2011).

Although these results do not contradict the constrained growth hypothesis, Eiraku et al. (2011) proposed an alternative mechanism for OC formation based on growth and regulated actomyosin contraction along the apical surface of the OV. This mechanism, which does not require ECM, consists of four phases: (1) uniform contraction produces a spherical OV; (2) relaxation in the iOV creates a placode; (3) apical constriction at the iOV margin causes local cell wedging and a small invagination; and (4) growth of the iOV deepens the invagination. These investigators used staining of phosphorylated myosin, stiffness measurements, inhibitors of apical contraction, and a computer model to support their hypothesis (Eiraku et al. 2011, 2012).

While the elegant experimental and numerical results of Eiraku et al. (2011) offer strong support for this alternative hypothesis, it does not seem consistent with our ECM degradation experiments which suggest an important role for the matrix. We offer three possibilities. First, as discussed by Sasai et al. (2012), the mechanism of OV invagination may be fundamentally different in vitro. Second, a back-up mechanism may be triggered in vitro when the SE is not available to generate enough matrix to cause invagination. Third, the researchers may have uncovered a parallel mechanism that normally works in concert with constrained growth. In fact, other researchers have obtained evidence supporting a role for contraction in this process (Brady and Hilfer 1982; Plageman et al. 2011). Future studies are needed to evaluate these possibilities.

4.3 Limitations

With the focus here being mechanics, we did not consider the genetic and molecular signals involved in OV invagination. Reviews have explored the role of signals such as BMPs and FGF during eye development (Adler and Canto-Soler 2007; Fuhrmann 2010). Researchers have studied specification of the retina by signals from nearby tissues such as the mesenchyme and SE (Fuhrmann 2010). Knocking out BMP7, Six3, or Pax6 can cause various eye defects in mice (Fuhrmann 2010). Mutated genes such as SIX3, SHH, PAX6, and SMOC1, a BMP antagonist, have been associated with anophthalmia (missing eye) and microphthalmia (small eye) in humans (Slavotinek 2011). Future work could elucidate how these signals may disrupt the mechanical properties of the ECM or cell-matrix adhesion in the eye. For example, in an anophthalmic mouse strain ZRDCT-Ch, researchers have found decreased sulfated glycosaminoglycan staining on the basal side of the OV (Webster et al. 1984).

Mechanisms other than those considered here also may contribute to OC formation. For example, in those embryos that developed fully invaginated OCs without the iSE, the final morphology of the cultured lens-less OC sometimes was not completely normal. In some embryos, the iOV and oOV were not pressed together as seen in controls; this separation is also visible in the images of Hyer et al. (2003). This observation suggests that the invaginating lens may impart some secondary stresses that affect the final shape of the OC, e.g., by pushing against the OV. In addition, interkinetic nuclear migration may contribute to OV invagination by placing more cell nuclei near the apical side of the OV, causing it to expand (Zwaan et al. 1969; Norden et al. 2009) (see Online Resource 1, Fig. S1).

Further studies are needed to verify the distributions of growth and ECM stiffness suggested by our data. Our results indicate that the growth rate in the iOV is relatively uniform, but subtle differences in growth rate may exist. More precise estimates of growth distributions would require measuring local changes in tissue volume. In addition, the matrix and epithelial stiffnesses depend on their composition (material properties) and geometry (thickness). The ECM thickness could not be measured consistently due to sectioning difficulties. Moreover, the estimated shear moduli represent macroscopic averages of microstructural properties, but this is consistent with our tissue-level model. Although our microindentation tests indicate that the ECM shear modulus is high enough to provide the constraint on iOV expansion needed to drive invagination, technical challenges prevented us from using indentation to determine regional differences in ECM stiffness.

For the constrained growth mechanism to be feasible, the ECM must be tightly bound to the iOV. We did not examine the distribution of integrins connecting these layers, but we did notice that the center of the SE was more difficult to remove from the iOV than the outer region, especially at later stages, suggesting a stronger binding between the SE and OV near the center. Such a gradient in binding strength could also increase the effective ECM stiffness near the center of the iOV, thereby influencing retinal shape.

Finally, it is important to note that the mechanisms of eye morphogenesis may be considerably different in some species. In fish, for example, cells migrate over the rim from the oOV to the iOV during invagination (Li et al. 2000).

In conclusion, our results support the hypothesis that the ECM between the SE and OV plays a crucial role in OC formation. Our experiments and modeling suggest that the matrix constrains lateral expansion of the inner region of the growing OV, causing it to thicken and invaginate to create the primitive retina, while a gradient in ECM stiffness refines the final shape of the retina. Our study provides new understanding as well as poses new questions related to the mechanics involved in early eye development.