Identifying High Order Brain Connectome Biomarkers via Learning on Hypergraph

Abstract

The functional connectome has gained increased attention in the neuroscience community. In general, most network connectivity models are based on correlations between discrete-time series signals that only connect two different brain regions. However, these bivariate region-to-region models do not involve three or more brain regions that form a subnetwork. Here we propose a learning-based method to explore subnetwork biomarkers that are significantly distinguishable between two clinical cohorts. Learning on hypergraph is employed in our work. Specifically, we construct a hypergraph by exhaustively inspecting all possible subnetworks for all subjects, where each hyperedge connects a group of subjects demonstrating highly correlated functional connectivity behavior throughout the underlying subnetwork. The objective function of hypergraph learning is to jointly optimize the weights for all hyperedges which make the separation of two groups by the learned data representation be in the best consensus with the observed clinical labels. We deploy our method to find high order childhood autism biomarkers from rs-fMRI images. Promising results have been obtained from comprehensive evaluation on the discriminative power and generality in diagnosis of Autism.

1 Introduction

The brain can be partitioned into different regions according to various functions, and connectivity networks can be composed where information is continuously processed between these functionally linked brain regions [1]. In order to understand the pathological underpinnings of neurological disorder, many functional neuroimaging studies have been developed to investigate abnormal alternations among these brain connections. Recently, researchers have also used functional connectivity networks for diagnosing brain disease at individual level [2].

The brain is complex and oscillatory activities behind cognition are essentially the large-scale collaborative work among millions of neurons through multiple brain regions. The bivariate region-to-region interactions do not capture high order network architecture patterns that involve three or more brain regions in a subnetwork architecture. Recently, there is overwhelming evidence that brain network displays hierarchical modularity, making the investigation of high order network patterns more attractive to neuroscience and clinical practice than ever before.

Here, we propose a novel learning-based method to discover high order network connectome biomarkers that can be used to distinguish two clinical cohorts. Without doubt, there are thousands of high order connectome patterns varying from the number and combination of the involved brain regions. Considering the computational cost, we propose the following criteria to promote one high order network connectome to the biomarker: (a) Small subnetwork architecture. Since a triangle is one of the simplest types of subnetwork, we take a first step to discover high order connectome patterns that end up in the functional connectivity throughout the triangle cliques. (b) Entire functional connectivity flow. We examine the functional connectivity behavior throughout the subnetwork. Therefore, the connectome pattern is considered as a biomarker only if the entire functional connectivity flow inside the subnetwork, instead of particular predominant connection link, shows significant difference between two clinical cohorts.

To achieve it, we first construct a subnetwork repository that consists of all possible triangle cliques. The native solution is to measure and sort the significance of each triangle cliques via the independent statistical t-test. Since the subnetworks are highly correlated (e.g., large amount of overlap of edges among triangle cliques), independent statistical test can hardly be effective in looking for the critical subnetworks.

We utilize hypergraph technique to jointly find a set of the most significant high order connectome biomarkers by investigating subject-to-subject relationships based on functional connectivity flows in all possible subnetwork architectures. Specifically, each individual subject is treated as a vertex in the hypergraph. For each subnetwork architecture, a hyperedge is formed for each subject at a time that includes other subjects with similar functional connectivity flows throughout the same subnetwork architecture. Thus, the hypergraph eventually encodes a wide spectrum of high order connectome patterns in the population. The next step is to find the most significant biomarkers hiding behind thousands of subnetworks. Since each subject has the clinical label, the problem of seeking for high order biomarkers turns to the optimization of the weights on hyperedges such that the separation of subjects by the learned data representation (encoded by hypergraph) maximally agrees with the observed clinical labels. Intuitively, the learned weights reflect the significance in distinguishing two clinical cohorts. We have applied our learning-based method to discover the high order functional connectome patterns for childhood autism spectrum disorders (ASDs) and identify ASD individuals from ABIDE dataset. Promising classification results have been achieved which demonstrate the power of learned high order connectome patterns.

2 Method

Method Overview

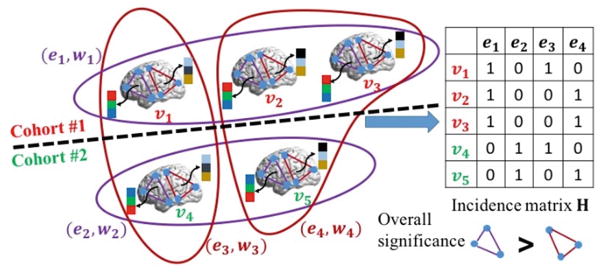
Figure 1 illustrates the intuition behind our proposed learning-based method. For clarity, we assume there are three subjects in one cohort (top left in Fig. 1) and two subjects in anther cohort (bottom left in Fig. 1). Only two possible subnetworks (triangle cliques in purple and red) are under investigation. The goal is to find out which subnetwork is able to separate subjects from two groups more accurately than the other, based on the functional connectivity flow inside the subnetwork. Eventually, the selected subnetworks are considered as biomarkers to identify other individual subjects.

Fig. 1.

The overview of our learning-based method to discover high order brain connectome patterns by hypergraph inference. (Color figure online)

Hypergraph is employed to measure the high order subject-wise relationships based on the functional connectivity flow running inside each subnetwork. Specifically, subjects are considered as vertices (v₁–v₅ in Fig. 1) in the hypergraph. In general, a set of subjects fall into the same hyperedge only if their functional connectivity flows in the same subnetwork show high correlations. Thus, hyperedge can accommodate high order relationship that is beyond two subjects in the conventional graph technique. For example, subject v₂ and v₃ stay in the same hyperedge e₁ with v₁ since their functional connectivity flows (designated by the black arrows) are very similar inside the purple triangle clique. The standard way to construct hyperedges is to exhaustively visit each subject per each subnetwork. As the example shown in Fig. 1, we obtain four hyperedges (e₁–e₄) that are displayed by curves. Note, the identical hyperedges are discarded and the color on each hyperedge indicates the associated subnetwork.

A hypergraph learning technique is used to jointly quantify the significance of each subnetwork based on the ground truth clinical label on each subject. Intuitively, the more label discrepancies occur within the hyperedges related to the underlying subnetwork, the lower the significance of that particular subnetwork becomes. Finally, the subnetworks with high overall significance value across related hyperedges are regarded as the biomarkers from rs-fMRI image. As shown in the left panel of Fig. 1, the labels in e₁ and e₂ (purple curves) are highly consistent, suggesting that the functional connectivity flow running on the purple triangle clique is a good biomarker to separate the subjects from two different groups. On the contrary, the functional connectivity flow inside the red triangle clique fails to be the biomarker since there are hyperedges built on the red triangle clique having subjects with different clinical labels, e.g., v₁ and v₄ are both in the hyperedge e₃.

2.1 Encode Subject-Wise Relationship in Hypergraph

Given a training set of N subjects {v_n|n = 1, …, N}, where each subject has already been partitioned to R anatomical regions. Without loss of generality, we use ‘+1’ and ‘−1’ to distinguish the label for two clinical groups, and thus form a column vector y =[y₁, y₂, …, y_N]^T. Considering the computational cost and efficiency, we first construct the pool of all possible subnetworks Δ = {Δ_j|j = 1, …, C}, where each triangle clique Δ_j is formed by three brain regions randomly picking up from totally R regions. Therefore, there are $C=\left(\begin{array}{c}R\\ 3\end{array}\right)$ combinations in total. Given subject v_n and particular subnetwork Δ_j, we can obtain a three-element vector of functional connectivity flow ${\alpha }_{n,j}=[{\alpha }_{n,j}^1,{\alpha }_{n,j}^2,{\alpha }_{n,j}^2]$, where each element in α_n,j is eventually the Pearson’s correlation degree of the mean rs-fMRI signals, from subject v_n, between any two brain regions within the triangle clique Δ_j.

Construct Hypergraph

Next, we construct hypergraph, as denoted by G =(V, E), where the hypergraph vertex set V = {v_n|n = 1, …, N} includes all subjects in the population. We use star-expansion algorithm to build a set of hyperedges by exhaustively visiting each vertex v_n for particular subnetwork Δ_j, thus forming the hyperedge set E = {e_n,j|n = 1, …, N, j = 1, …, C}. For each hyperedge e_n,j, we examine the similarity between functional connectivity flow α_n,j at current vertex v_n and α_n′,j (n′ = 1, …, N, n′ ≠ n) at all others vertices. The criteria of allowing v_n′ be in the hyperedge e_n,j (i.e., v_n′ ∈ e_n,j) are (a) the Euclidian distance $d_j(n,n^{\prime })={\Vert {\alpha }_{n,j}-{\alpha }_{n^{\prime },j}\Vert }_2^2$ between α_n,j and α_n′,j should be smaller than certain threshold; and (b) α_n′,j should be within the k-nearest neighborhood in terms of d_j(n, n′).

Encode Hypergraph in Incidence Matrix

In a conventional graph based method, the relationships among graph vertices are encoded in a N × N affinity matrix. In hyper-graph, instead, the relationships between vertices are encoded using an incidence matrix H, with the row and column denoting the vertices and hyperedges, respectively. Since each hyperedge e_n,j is related with both vertex v_n and subnetwork Δ_j, we use the column index θ to delegate the bivariate index (n, j), i.e., θ ↔ (n, j), where θ ranges from 1 to Θ = N · C. Thus, H is a N × Θ matrix. For each entry h(n, θ), we set h(n, θ)=1 if the vertex v_n is in hyperedge e(n, j). Otherwise, h(n, θ)=0. The example of incidence matrix is shown in the right panel of Fig. 1. Apparently, the incidence matrix conveys more information than the affinity matrix used in conventional approaches based on simple graphs.

Hyperedge Weights

For convenience, we use e_θ denote the particular hyperedge in the following text, instead of e_n,j. Each hyperedge e_θ has a non-negative weight w_θ. Furthermore, we construct a Θ × Θ diagonal matrix W where each diagonal element is the hyperedge weight w_θ. Given H and W, we can define the vertex degree $d(n)={\sum }_{\theta =1}^{\mathrm{\Theta }}{w}_{\theta }h(n,\theta )$ for each v_n and the hyperedge degree $\delta (\theta )={\sum }_{n=1}^{N}h(n,\theta )$ for each e_θ.

2.2 Discover High Order Brain Connectome Patterns by Hypergraph Learning

Our learning-based method aims to find out the biomarkers by inspecting the performance of each hyperedge in separating subjects from two groups. To that end, we first assume the label on each subject is not known yet. Thus, we use hypergraph learning technique to estimate the likelihood f_n for each subject v_n, which is driven by (a) the minimization of discrepancies between ground truth label vector y and the estimated likelihood vector f =[f₁, f₂, …, f_N]^T, and (b) the consistency of clinical labels within each hyperedge. The consistency requirement can be defined as:

$${\mathbf{\Omega }}_{\mathbf{f}}(\mathbf{W})={\sum }_{\theta =1}^{\mathbf{\Theta }}{\sum }_{n,n^{\prime }=1}^N\frac{w_{\theta }h(n,\theta )h(n^{\prime },\theta )}{\delta (\theta )}{\left(\frac{f_n}{\sqrt{d(n)}}-\frac{f_{n^{\prime }}}{\sqrt{d(n^{\prime })}}\right)}^2.$$ (1)

The regulation term Ω_f (W) penalizes the label discrepancy by encouraging the difference between the normalized likelihoods $f_n/\sqrt{d(n)}$ and $f_{n^{\prime }}/\sqrt{d(n^{\prime })}$ to be as small as possible if v_n and v_n′ are in the same hyperedge e_θ. It is clear that the regularization term Ω_f(W)is a function of both W and f, which eventually makes the optimization of W reflect the quality of each hyperedge being the biomarker. In order to avoid over-fitting, we use Frobenius norm on the weighting matrix W. Therefore, the objective function to look for high order connectome patterns is:

$$arg{min}_{\mathbf{W},\mathbf{f}}{\mathbf{\Omega }}_{\mathbf{f}}(\mathbf{W})+\lambda {\Vert \mathbf{y}-\mathbf{f}\Vert }_2^2+\mu {\Vert \mathbf{W}\Vert }_F^2.$$ (2)

where λ and μ are two scalars controlling the strength of data fitting term and Frobenius norm on the weighting matrix W, respectively.

Optimization

Ω_f(W)in Eq. (2) is called as hypergraph balance term in [3] and can be reformulated into a matrix form: Ω_f(W)=f^T (I − Λ)f = f^Tℒf, where ℒ is the normalized hypergraph Laplacian, I is the identity matrix, and $\mathbf{\Lambda }={\mathbf{D}}_v^{-\frac{1}{2}}{\mathbf{HWD}}_e^{-1}{\mathbf{H}}^T{\mathbf{D}}_v^{-\frac{1}{2}}$. Note, D_v = diag(d(n)) and D_e = diag(δ(θ)) are the diagonal matrices of the vertex degrees and the hyperedge degrees, respectively. It is clear that the objective function in Eq. (2) is not jointly convex with respect to W and f. Hence, we propose the following solution to find W and f, alternatively.

Solve Likelihood Vector f

Fixing W, the objective function becomes:

$$arg{min}_{\mathbf{f}}\varphi (\mathbf{f})={\mathbf{f}}^T\mathcal{L}\mathbf{f}+\lambda {\Vert \mathbf{y}-\mathbf{f}\Vert }_2^2.$$ (3)

Conventional hypergraph inference method can be used to estimate f by letting $\frac{\partial \varphi }{\partial \mathbf{f}}=0$, which leads to the deterministic solution: $\widehat{\mathbf{f}}={\left(\mathbf{I}+\frac{1}{\lambda }\mathcal{L}\right)}^{-1}\mathbf{y}$.

Optimize the Hypergraph Weight W

After discarding unrelated terms w.r.t. W in Eq. (2), we derive the objective function for hypergraph weight as:

$$arg{min}_{\mathbf{W}}\phi (\mathbf{W})={\mathbf{f}}^T\mathcal{L}\mathbf{f}+\mu {\sum }_{\theta =1}^{\mathbf{\Theta }}{(w_{\theta })}^2.$$ (4)

Since each w_θ in W is independent, we can yield the optimized hyperedge weight as ${\widehat{w}}_{\theta }=max\left(\frac{{\mathbf{f}}^T{\mathbf{D}}_v^{-\frac{1}{2}}\mathbf{H}{\mathbf{I}}_{\theta }{\mathbf{D}}_e^{-1}{\mathbf{H}}^T{\mathbf{D}}_v^{-\frac{1}{2}}\mathbf{f}}{2\mu },0\right)$ by letting the derivative $\frac{\partial \phi }{\partial w_{\theta }}=0$ and projecting ŵ_θ to meet the non-negative constraint. Note, I_θ is the Θ × Θ selection matrix which is zero everywhere except at entry (θ, θ).

Discover High Order Connectome Biomarkers

Since W and f are coupled in Eq. (2), the estimated hypergraph weights in W is driven to achieve (a) the least discrepancy between ground truth y and estimated likelihood f, and (b) highest label consistency within each hyperedge, which exactly matches with the important properties of imaging biomarkers. In our method, we sort the significance of the subnetworks according to the mean hyperedge weight over all subjects, i.e., ${\widehat{w}}_j={\sum }_{n=1}^N\widehat{w}(n,j)$. After that, a set of the critical subnetworks P = {Δ_j|j = 1, …, C, ŵ_j>ε}, as long as their mean hyperedge weights beyond certain threshold ε, are considered as the biomarkers where the functional connectivity flows running inside have significant difference between two clinical cohorts.

3 Experiments

3.1 Critical Subnetworks Learned by Hypergraph Inference

In this section, we applied our learning-based method to find critical subnetworks P based on 45 ASD and 47 typical control (TC) subjects from the NYU site of Autism Brain Imaging Data Exchange (ABIDE) database [4]. The first 10 obtained rs-fMRI images of each subject are removed to ensure magnetization equilibrium. After slice timing and head motion correction, the images are normalized into MNI space and then segmented into 116 regions-of-interest (ROIs) according to Automated Anatomical Labeling (AAL) template. Following this, the images underwent signal detrending and bandpass filtering (0.01–0.08 Hz). For each subject, the mean time series of each ROI is obtained by averaging the rs-fMRI time series over all voxels in that particular ROI. Note, the total number of possible subnetworks is $\left(\begin{array}{c}116\\ 3\end{array}\right)=253,460$. We jointly find the best parameters for λ and μ in Eq. (2) using the line search strategy with range from 0.1 to 10.0.

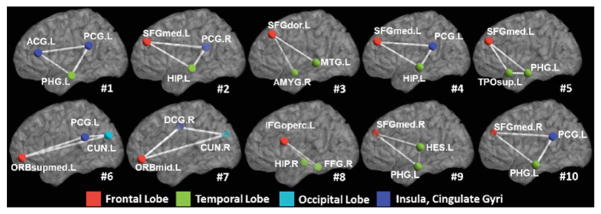
Figure 2 shows the top 10 most critical subnetworks (white triangle cliques) out of 253,460 candidates between ASD and TC cohorts. The color on each vertex differentiates the functions in human brain. It is clear (a) most of the brain regions involved in the selected top 10 critical subnetworks locate the key areas related with ASD, such as amygdala, middle temporal gyrus, superior frontal gyrus; and (b) most of the selected subnetworks travel cross the subcortical and cortical regions, which is in consensus with the recent discover of autism pathology in neuroscience community [5].

Fig. 2.

The top 10 selected subnetworks (white triangle cliques) where the functional connectivity flow running inside has significant difference between ASD and TC cohorts. (Color figure online)

3.2 Identification of ASD Subjects with the Learned Subnetwork

In the following experiments, we use functional connectivity flows on top 200 critical subnetworks as the feature representation (feature dimension: 200 × 3) to classify ASD and TC subjects. Then traditional Support Vector Machine (SVM) [6] is adopted to train the classifier directly based on the concatenated feature vector, denoted as Subnetwork-SVM. Since the functional connectivity flow comes from each subnetwork, it is straightforward to organize them to a tensor representation and use advanced Support Tensor Machine (STM) [7] to take advantage of the structured feature representation, denoted as Subnetwork-STM in the following experiments. In order to demonstrate the advantage of subnetwork over the conventional region-to-region connection in brain network, we compare with two counterpart methods Link-SVM (use the Pearson’s correlations on each link as the feature) and Toplink-SVM (select top 600 links by t-test and use the Pearson’s correlation on the selected links to form the feature vector).

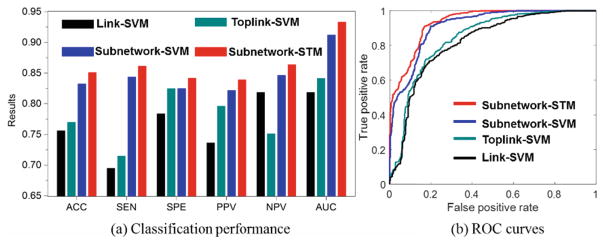
Evaluation on Discrimination Power

In this experiment, we use 10-fold cross validation strategy to evaluate the classification accuracy (ACC), sensitivity (SEN), specificity (SPE), positive predictive value (PPV), and negative predictive value (NPV) on 45 ASD and 47 TC subjects from NYU site in ABIDE database. As the classification performance plots and the ROC curves shown in Fig. 3, the classifiers trained on connectome features from our learned subnetworks have achieved much higher classification performance than those trained by the same classification tool but based on the connectome features from the conventional region-to-region connection links. Also, the substantial classification improvements by Subnetwork-STM over Subnetwork-SVM indicate the benefit of using structured data presentation in classification where such high order information is clearly delivered in the learned subnetworks.

Fig. 3.

Classification performance of four different classification methods.

Evaluation on Generality

To verify the generality of learned subnetworks, we directly apply the subnetworks learned on the NYU dataset to the classification of 44 ASD and 53 TC subjects from the UM (University of Michigan) site in ABIDE database. The accuracies obtained by Link-SVM and Toplink-SVM are 0.6086 and 0.6253, respectively, which is comparable to that in reference [8]. Our Subnetwork-SVM and Subnetwork-STM can improve the accuracy up to 0.6469 and 0.6610, respectively. Again, the classification methods using the features extracted from the learned top subnetworks achieve much higher classification accuracy than the counterpart Link-SVM and Toplink-SVM methods.

4 Conclusion

In this paper, we propose a novel learning method to discover high order brain connectome biomarkers which are beyond the widely used region-to-region connections in conventional brain network analysis. Hypergraph technique is introduced to model complex subject-wise relationships in terms of various subnetworks and quantify the significance of each subnetwork based on the discrimination power across clinical groups and consistency within each cohort. We apply our learning-based method to find the subnetwork biomarkers between ASD and TC subjects. The learned top subnetworks are not only in consensus with the recent clinical findings, but also able to significantly improve accuracy in identifying ASD subjects, strongly supporting their potential use and impact in neuroscience study and clinic practice.