Distributing coil elements in three dimensions enhances parallel transmission multiband RF performance: a simulation study in the human brain at 7 Tesla

Abstract

Purpose

We explore advantages of using a double-ring RF array and slice orientation to design parallel transmission (pTx) Multi-Band (MB) pulses for Simultaneous Multi-Slice (SMS) imaging with whole brain coverage at 7 Tesla (7T).

Methods

A double-ring head array with 16 elements evenly split in two rings stacked in the Z direction was modeled and compared to two single-ring arrays comprising 8 or 16 elements. The array performance was evaluated by designing band-specific pTx MB pulses with local SAR control. The impact of slice orientations was also investigated.

Results

The double-ring array consistently and significantly outperformed the other two single-ring arrays, with peak local SAR reduced by up to 40% at a fixed excitation error of 0.024. For all three arrays, exciting sagittal or coronal slices yielded better RF performance than exciting axial or oblique slices.

Conclusion

A double-ring RF array can be used to drastically improve SAR versus excitation fidelity tradeoff for pTx MB pulse design for brain imaging at 7T and, therefore, is preferable against single-ring RF array designs when pursuing various biomedical applications of pTx SMS imaging. With the stripline arrays compared, coronal and sagittal slices are more advantageous than axial and oblique slices for pTx MB pulses.

Introduction

Since its first successful demonstration for accelerating high resolution functional image acquisition in the human brain (1), Simultaneous Multi-Slice (SMS) imaging (2) using Multi-Band (MB) RF pulses has gained increasing popularity in the neuroimaging community for functional (fMRI) and diffusion MRI (dMRI) studies. Most importantly, it was adopted in the Human Connectome Project (HCP) (3,4), which aims to map the human brain macro-connectome using fMRI and dMRI data, primarily at 3 Tesla (3T) and to some extent at 7T (3,5). However, the optimum use of the technique, especially for 7T dMRI, is hampered by two RF related challenges, namely, transmit B1 (B1+) non-uniformities and Specific Absorption Rate (SAR) that increase with increasing magnetic field strength (6).

Several approaches have been proposed to address these two challenges. PINS (7) or DANTE (8) principle has been applied to design single-channel-transmit MB RF pulses to limit SAR or reduce the impact of B1+ inhomogeneity; representative methods include those using PINS (7,9), MultiPINS (10) and adiabatic PINS (11) pulses. Alternatively, parallel transmit (pTx) RF pulses that have the potential to simultaneously address both challenges have been pursued; in a 7T study, Wu et al. (12,13) introduced a design strategy for pTx MB pulses and demonstrated in the brain that these pulses can improve B1+ homogeneity while reducing total RF power (which closely relates to the global SAR) and local SAR, relative to the single-channel Circularly Polarized (CP) mode. In a 3T study, Poser et al. (14) demonstrated the ability of pTx MB pulses to create the same average flip angles across the brain but with 30% lower RF total power relative to conventional single-channel MB pulses operated in the CP mode.

RF coil geometries are intricately linked with pTx pulse design and resulting RF performance. Previous studies with Single-Band (SB) RF pulses have shown that a multi-ring RF transmit array, where coil elements are azimuthally arranged in two rings along the Z direction (15), can be utilized to further improve the RF performance of pTx pulses as compared to a single-ring array design (16–18). In one study, Wu et al. (17) demonstrated experimentally that using a double-ring array can improve RF excitation homogeneity across the entire brain at 7T when designing non-selective kT point pulses (19). In other studies, Guerin et al. (18) and Wu et al. (16) simulated different body coils at 3T and found that distributing coil elements in a multi-ring structure can enhance the RF performance when using single-slice pTx spoke pulses (20) or kT-points-based single-slab pTx pulses (16). Meanwhile, other researchers have been interested in calculating ideal current distributions for certain coil geometry to create the lowest possible or ultimate global SAR (21,22), in the hope that knowing the ideal current distribution may guide RF coil design to approach optimum performance; however, because of prohibitively huge computational burden, it is difficult for these theoretical calculations to consider local SAR, which is the actual limiting factor at ultrahigh fields.

In order to specifically investigate how multi-ring RF transmit array designs can enhance the performance of pTx MB pulses for SMS/MB imaging, we decided to simulate a double-ring head array at 7T and compared it to conventional single-ring arrays. The double-ring array was designed with 16 stripline coil elements evenly split in two rings stacked in the Z direction. Two single-ring arrays, comprised of 8 or 16 elements, were considered. The performances of all arrays were evaluated by designing recently introduced band-specific pTx MB pulses (12,13) with local SAR control. For each array, the impact of slice orientation was also investigated. The present paper reports the important findings of this effort and demonstrates how the double-ring RF head array and the choice of slice orientation can be used to improve RF performance of pTx MB pulses in terms of whole brain B1+ homogenization and local SAR reduction.

Methods

RF array electromagnetic modeling

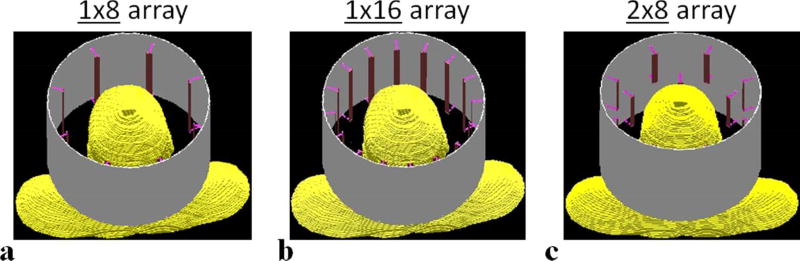
Three 7T head RF transmit arrays were simulated using electromagnetic (EM) modeling. The first array, referred to as the 1×8 array hereafter, comprised of eight stripline elements (23–25) arranged in a single-ring fashion (Fig. 1a). The eight elements, with their long axis aligned parallel to the main magnetic field (i.e., the Z direction), were placed on a cylindrical surface with a constant inter-element distance (i.e. the azimuthal angle spanned by any two adjacent elements within the XY plane was 45°).

FIG. 1.

Schematics of coil structure depicting the arrangement of individual coil elements for the 1×8 (a), 1×16 (b) and 2×8 (c) 7T head RF transmit arrays considered in the current study. For both 1×8 (8 elements in total) and 1×16 (16 elements in total) arrays, all coil elements are azimuthally distributed in a single ring, whereas for the 2×8 array the 16 elements are evenly split into two rings stacked in the Z direction.

The second array, referred to as the 1×16 array hereafter, was based on the same single-ring structure as the 1×8 array, but with 16 stripline elements evenly distributed on a cylindrical surface with azimuthal angles between any two adjacent elements being 22.5° (Fig. 1b).

The third array, referred to as the 2×8 array hereafter, also consisted of 16 stripline elements, but had its elements evenly split into two rings stacked along the Z direction (Fig. 1c). In each ring, the eight elements were evenly and azimuthally distributed in the XY plane as in the 1×8 array. To facilitate inter-ring decoupling, the two rings were separated in the Z direction by a 10-mm gap, and were rotated relative to each other by an azimuthal angle of 22.5° (with any element of one ring positioned in the middle of the two neighboring elements from the other ring).

For all three arrays, the cylindrical surface on which the coil elements were placed had the same diameter of 270 mm and was positioned inside a coaxed RF shield. The RF shield was made of a cylindrical copper sheet measuring 320 mm in diameter and 210 mm in length and also served as the ground. The dielectric substrate used in between the coil elements and the ground was air. The coil elements utilized for all three arrays were formed by a rectangular copper sheet of 12 mm in width. The length of the coil elements however was different between arrays and was much shorter in the 2×8 array than in the other two arrays – the element length measured 85 mm for the 2×8 array whereas 180 mm for the other two arrays.

All three RF arrays were simulated using a commercial finite difference time domain solver (XFDTD, Remcom, USA) for Maxwell’s equations. Each array was loaded with the same generic human tissue model comprising a medium-sized head and shoulders. In each case, the center of the brain was positioned at the isocenter of the array. The tissue model was composed of 17 tissue types and 680,391 tissue voxels defined with 2-mm in-plane and 2.5-mm through-plane resolutions. The whole brain including cerebrum, cerebellum and brain stem spanned 120 mm in the Z axis with 48 axial slices, 144 mm in the Y axis with 72 coronal slices, and 120 mm in the X axis with 60 sagittal slices. For each array, the EM maps of individual coil elements within the entire tissue model were simulated by driving one element at a time in the presence of all other elements. The maximum residual coupling between any two elements was −18 dB for the 1×8 array, −23 dB for the 1×16 array, and −26 dB for the 2×8 array.

For each array, the multi-channel electric field maps and the tissue electric properties (i.e., conductivity and mass density) were utilized to calculate the local 10-gram SAR (10g SAR) matrices (26). A voxel-specific 10g SAR matrix was calculated for each tissue voxel using a fast region growth algorithm (27) combined with an advanced computation approach (28) to ensure that the SAR is averaged within exactly 10 grams of tissue. The resulting 680,391 SAR matrices were then compressed to a largely reduced number of virtual observation points (VOP’s) following the recipe provided by Eichfelder and Gebhardt (29). For all three arrays, the same level of SAR overestimation was specified to create VOP’s, resulting in 63, 231 and 163 VOP’s for the 1×8, 1×16 and 2×8 arrays, respectively. These VOP’s were utilized to estimate the peak 10g SAR during the pulse design as described later.

pTx MB pulse design

To investigate the impact of the slice direction, we considered four axes as the slice direction and designed pulses to excite 1) axial, 2) coronal, 3) sagittal and 4) oblique slices. The oblique slice direction was manually chosen by identifying the shortest dimension of the brain of the tissue model used and was defined by tilting the axial slice direction 25° toward the posterior of the brain.

For pulse design, the original high-resolution multi-channel 3D B1+ maps were manipulated to create two sets of low-resolution (6 mm isotropic) B1+ maps. The first set was obtained by downsampling the original high-resolution B1+ maps and was used to design pulses for axial, coronal and sagittal slice directions. The second set of low-resolution B1+ maps was utilized to design pulses for the oblique slice direction and was generated by reslicing the original B1 maps along the oblique slice direction with affine transformation. The first set of B1+ maps contained 20, 24, and 20 brain slices in axial, coronal and sagittal slice directions, respectively, and the second set of B1+ maps had 18 brain slices in the oblique slice direction.

For each slice direction, pTx MB pulses for an MB factor of 2 (MB2) were designed in a slice-wise fashion to optimize the B1+ field within each brain slice (12). The number of pTx MB pulses to be designed was given by the number of brain slices divided by the MB factor. This led to the design of 10, 12, 10 and 9 pTx MB2 pulses for axial, coronal, sagittal and oblique slice directions, respectively. For each pTx MB2 pulse, the two constituting pTx SB pulse components were assigned a band-specific set of RF shim values (i.e., channel-specific RF magnitude and phase) to homogenize the B1+ field within respective brain slices.

For a given slice direction, the band-specific RF shim sets for individual SB components were designed jointly to promote the “SAR hopping” effect (30) and were calculated by solving a constrained minimization to minimize the local SAR while satisfying certain predefined excitation fidelity,

$$\stackrel{⌢}{w}=\text{arg }\underset{w}{\text{min}}{\text{SAR}}_{10\mathrm{g}}(w),\mathrm{s}.\mathrm{t}.\text{RMSE}(w)\le \epsilon$$ [1]

where w is a complex-valued vector concatenating individual RF shim sets, SAR_10g(w) denotes peak 10g SAR for a given w, RMSE(w) represents corresponding Root Mean Squared excitation Error (RMSE), and ε is a number used to constrain excitation error.

In this study, RMSE(w) was defined in a magnitude least square sense (31) as: $\text{RMSE}(w)={\Vert \left|\mathit{\text{Aw}}\right|-d\Vert }_2/\sqrt{N_{\text{ROI}}}$ where A is the complex-valued system matrix involving multi-channel B1+ maps within every brain slice as well as the base pulse shape to be used to assemble final pTx MB pulses; the vector d represents target excitation predefined within the region of interest (ROI); N_ROI is the number of voxels in the ROI.

As in Lee et al. (32), we solved Eq. [1] by casting it into an equivalent regularized minimization problem:

$$\stackrel{⌢}{w}=\text{arg }\underset{w}{\text{min}}[{\text{RMSE}}^2(w)+\lambda ·\text{SAR}(w)]$$ [2]

where λ is the regularization parameter. The term used to control local SAR was given by $\text{SAR}(w)={\sum }_{n=1}^{N_{\text{VOP}}}{\alpha }_n{\Vert S_{n}w\Vert }_2^2$ where N_VOP is the number of VOP’s and S_n a complex valued matrix involving the n-th VOP. A detailed description of how to construct the matrices and vectors can be found in Wu et al. (13). Eq. [2] was solved iteratively in a way similar to that described by Lee et al. (32) and Sbrizzi et al. (33).

For all pulse designs, the ROI only included brain voxels and the excitation target was uniform flip angles of 10°. The base pulse shape utilized was a 1-ms sinc pulse with a bandwidth-time-product of 6.

RF performance evaluation

L-curves quantifying the tradeoffs between resulting excitation errors and peak 10g SAR were created to evaluate the RF performances for various design scenarios (with different arrays and different slice directions). The L-curves were obtained by varying the excitation error constraint ε in Eq. [1]. For each ε value, the calculated RF shim sets were utilized to evaluate the resulting RMSE and peak 10g SAR. The RMSE was calculated by considering the resulting B1+ distributions across the entire brain. The peak 10g SAR was obtained by exhaustive search (i.e., by considering all 10g SAR matrices, not the VOP’s which were used only for pulse design) and were calculated assuming SMS single-shot echo planar imaging of the whole brain with a 1-s volume TR.

After qualitatively comparing different design scenarios based on a visual inspection of the L-curves, we conducted a more quantitative comparison based on peak 10g SAR values obtained at constant excitation fidelity determined by RMSE=0.024. The choice of RMSE=0.024 was arbitrary and was retrospectively made by following the L-curve criterion (34) which suggests that a solution near the corner of the L-curve be chosen so as to obtain preferable balance between excitation error and SAR. All calculations, except for the EM simulations of RF arrays, were performed in Matlab (Mathworks, USA).

Results

Impact of RF array design

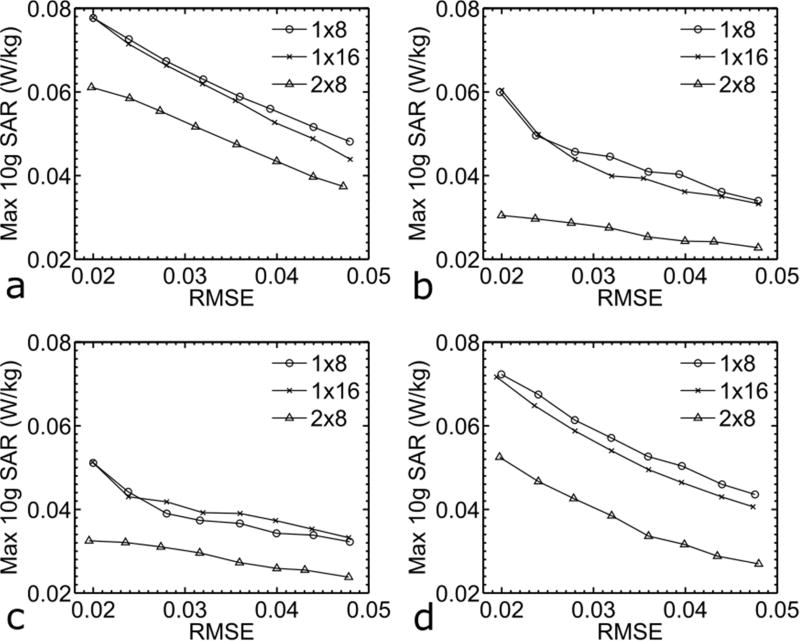
For each slice direction, the double-ring 2×8 array consistently outperformed the other two single-ring arrays in terms of local SAR reduction for the range of excitation fidelity investigated (Fig. 2). Quantitatively, at a constant excitation error of RMSE=0.024 the use of the 2×8 array reduced peak 10g SAR by 21% for axial, 40% for coronal, 27% for sagittal, and 30% for oblique slice excitation when compared to the 1×8 array, and by 18% for axial, 40% for coronal, 26% for sagittal, and 28% for oblique slice excitation when compared to the 1×16 array.

FIG. 2.

Impacts of RF array designs on excitation performance when designing pulses to excite axial (a), coronal (b), sagittal (c) or oblique (d) slices. L-curves quantifying the tradeoff between peak 10g SAR and root mean square excitation error (RMSE) are shown. For all cases, pTx MB pulses were designed for an MB factor of 2 (MB2) and with peak 10g SAR control. All local SAR numbers were calculated assuming single shot EPI image acquisitions with slice thickness=6 mm, pulse duration=1 ms, nominal flip angle=10 degrees and TR=1 s. Note that for each slice direction, the double-ring 2×8 array consistently outperformed the other two conventional single-ring arrays.

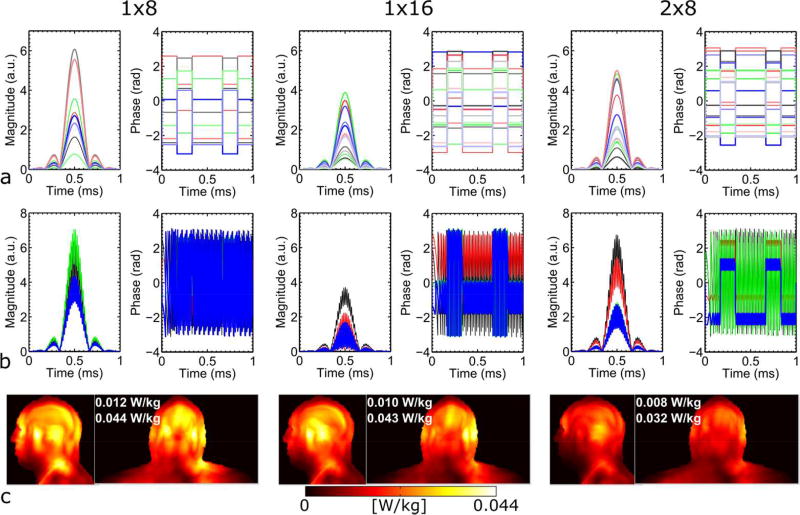
An example of channel-specific SB and MB pulses, along with the corresponding local SAR distribution, is given in Fig. 3 for the three RF arrays when designing pulses to excite sagittal slices at a constant RMSE of 0.024. The use of the 2×8 array also led to a lower global SAR than using the other two arrays.

FIG. 3.

Channel-specific single-band (a) and multiband (b) RF waveforms (magnitude and phase) and SAR (c). The RF waveforms shown are for those designed to excite sagittal slices and with a nominal RMSE of 0.024. For each array, channel-specific components of all channels for one pTx single-band pulse are shown, whereas channel-specific MB pulse components that would simultaneously excite two 6-mm thick, 6-cm separate slices are depicted only for four channels (i.e., every second channel for the 1×8 array and every fourth channel for the other two 16-element arrays). Also shown in (c) are both sagittal and coronal Maximum Intensity Projection (MIP) images of the final 10g SAR, along with the global and peak local SAR values.

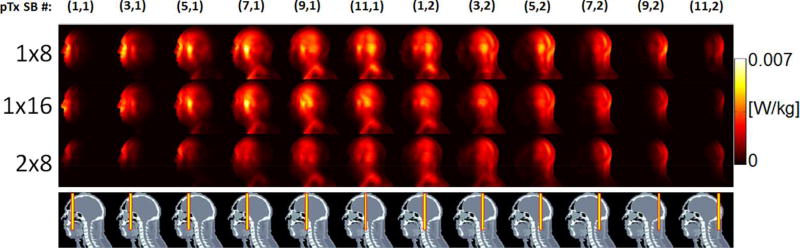
Further examining the local SAR spatial distributions of individual SB pulse components revealed that the SB pulses resulted in lower and more localized SAR hotspots for the 2×8 array than for the other two arrays (Fig. 4).

FIG. 4.

Local SAR distribution for the three RF arrays when designing pulses to excite coronal slices at a constant RMSE of 0.024. Sagittal Maximum Intensity Projection (MIP) images of 10g SAR of the two single-band (SB) pulses are depicted for each of the six odd numbered multiband (MB) pulses. The 12 SB pulse components for which SAR is shown are indexed by two numbers in parentheses, with the first number counting the MB pulses and the second number the SB component, e.g., (3,2) means it is the second SB component of the third MB pulse. The position of each of the 12 odd numbered target slices is indicated by a yellow box in the bottom row. Note that the SB pulses exhibited lower and more localized SAR for the 2×8 array than for the other two arrays.

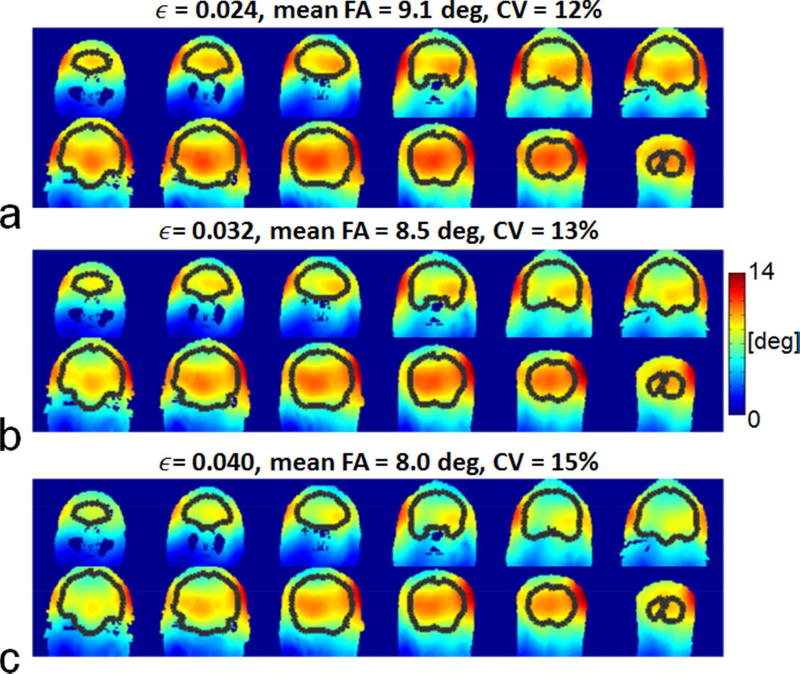
Fig. 5 displays the resulting flip angle (FA) distributions across the entire brain as a function of RMSE for the 2×8 array when designing pulses to excite coronal slices. The average FA decreased and the Coefficient of Variation (CV) of the FA increased with increasing RMSE.

FIG. 5.

Flip angle (FA) distributions across the brain for the 2×8 array when designing pulses to excite coronal slices for a nominal RMSE of 0.024 (a), 0.032 (b), and 0.04 (c). The resulting flip angles, obtained by running Bloch simulations with the original 2×2×2.5 mm3 resolution B1+ maps, are shown for every sixth coronal slice with brain regions indicated by black curves. Also shown are the coefficient of variation (i.e., std(FA)/mean(FA) and the mean FA calculated for the entire brain. Note that the flip angle decreased and the CV values increased with increasing RMSE.

Impact of slice directions

For each array, exciting sagittal or coronal slices yielded better RF performance than exciting axial or oblique slices over the range of excitation errors investigated (Fig. 2). Quantitatively, at a fixed excitation error of RMSE=0.024, exciting sagittal or coronal slices reduced peak 10g SAR by up to 40% for the 1×8 array, 39% for the 1×16 array and 48% for the 2×8 array as compared to exciting axial slices, and by up to 34% for the 1×8, 34% for the 1×16 and 36% for the 2×8 array as compared to exciting oblique slices.

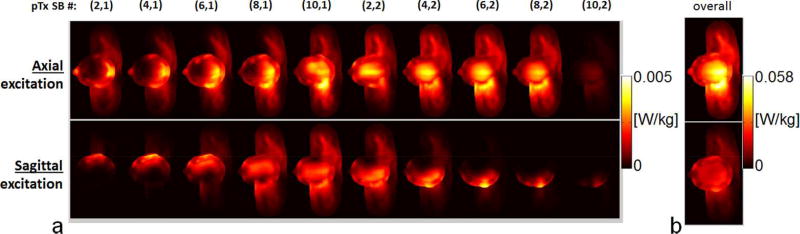
Taking the 2×8 array as an example, we found that exciting sagittal slices resulted in lower and more localized hotspots in the local SAR distributions of individual SB pulses than exciting axial slices (Fig. 6a), thereby reducing final SAR values (Fig. 6b).

FIG. 6.

Effects of slice directions on local SAR distributions for the 2×8 array when designing pulses to excite axial and sagittal slices for a nominal RMSE of 0.024. Transverse Maximum Intensity Projection (MIP) images of 10g SAR of the two single-band (SB) pulses are depicted in (a) for each of the five even numbered multiband (MB) pulses. The ten SB pulse components for which SAR is shown are indexed by two numbers in parentheses, with the first number counting the MB pulses and the second number the SB component, e.g., (6,1) means it is the first SB component of the sixth MB pulse. The MIP images of 10g SAR are also shown in (b) for the final SAR resulting from exciting all of the 20 axial or sagittal slices. Note that the SB pulses for exciting sagittal slices exhibited lower and/or more localized local SAR hotspots, thereby resulting in decreased final SAR.

Discussion

We investigated the performance of a double-ring RF head array with 16 coil elements azimuthally arranged within two rings stacked in the Z direction by designing pTx MB pulses targeting whole brain B1+ homogenization at 7T and demonstrated its advantages over two other conventional single-ring arrays with either 8 or 16 azimuthally arranged elements. Additionally, the impact of slice orientation in this pTx pulse design was examined. Our results using local-SAR-controlled pulse design based on multi-channel electromagnetic fields simulated for each array show that the doublering RF array can be used to largely reduce peak 10g SAR as compared to a single-ring array when achieving the same excitation fidelity across the whole brain. We also found that for all three arrays investigated, exciting sagittal or coronal slices led to significantly lower SAR values than exciting axial or oblique slices.

An important conclusion of this work is that increasing the transmit channel number from 8 to 16 can benefit pTx MB RF performance in whole brain SMS imaging at 7T. However this benefit can only be appreciated when the RF transmit array utilized is designed with the 16 coil elements distributed in three dimensions, i.e., with coils stacked in the Z-direction in addition to the X- and Y- directions. Similar results have been reported in an array comparison study by Guerin et al. (18) in which the authors compared the performance of different 3T body RF arrays designed with loop elements and found that a double-ring 2×8 array can be used to provide better RF performance than a single-ring 1×8 or 1×16 array when designing single-slice pTx spoke pulses for pelvic imaging. We also reported similar results, favoring a double-ring 2×8 RF array when searching for optimum body coil design for 3T MRI (16,35).

Another important finding of this study is that the choice of the slice direction plays a critical role in determining the RF performance of pTx MB pulses. Unlike single-channel MB RF pulses, pTx MB pulses may not necessarily achieve minimum SAR by choosing the slice direction to yield the least number of slices for whole volume coverage, which in the brain corresponds to coronal-axial-oblique direction that aligns with the shortest dimension of the brain. Rather they may reduce SAR more effectively by better capitalizing on the coil geometry through a different slice direction. Indeed, our results show that despite larger number of slices needed to cover the entire brain for a given resolution, designing pTx MB pulses to excite sagittal or coronal slices results in less SAR than to excite axial or oblique slices. The major reason is that exciting coronal or sagittal slices allows SAR hot spots of individual pTx SB pulses to spread out in the slice direction such that the hot spots are not spatially superimposed and do not add up in the final cumulative local SAR calculation (see Fig. 6).

In this study, single-spoke RF shim sets corresponding to RF shimming were calculated for the pTx MB pulses. Although demonstrated for a nominal flip angle of 10° using a sinc pulse with bandwidth-time-product of 6 as the base pulse shape, these band-specific RF shim sets can be used, without compromising the RF homogeneity, to assemble other pTx MB pulses using a different pulse shape or targeting a larger flip angle or both. In the case where the same pulse shape is used, the pTx MB pulses designed for lower flip angles can be scaled up in magnitude to achieve larger flip angles. For example, the magnitude of the pulse solution for Fig. 5a can be increased ~10 fold to make an average flip angle of 90° across the brain for the same pulse duration while benefiting from the same RF homogeneity with a CV of 12%; the corresponding local SAR can be obtained by multiplying 100 by the SAR already calculated for 9-degree flip angles. As in conventional imaging, when sinc pulses are scaled in magnitude to achieve higher flip angles, accompanying perturbations in performance, such as the well-known slice profile alterations, would remain also true for these MB pulses.

Although designed with 6-mm thick B1+ slices, the pTx MB2 pulses presented here can be used to excite thinner image slices. For example, the same 12 pTx MB2 pulses designed for coronal excitation can each be applied six times (13) to acquire a total of 144, 1-mm thick slices to cover the entire brain; correspondingly, the Specific RF Energy Absorption (SEA) will increase by six-fold as compared to those calculated for 6-mm slice thickness, indicating a six-fold increase in SAR for a given TR. Furthermore, the band-specific RF shim sets calculated for a given RMSE can be used to assemble pTx MB pulses for other MB factors. For example, considering coronal excitation, the same 24 band-specific RF shim sets can be used to form either eight MB3 or six MB4 pTx pulses; in either case, we note that the resulting SEA will remain unchanged whereas the SAR will increase with decreasing TR.

It is also possible to design pTx MB, multi-spoke pulses (36,37) for better excitation fidelity vs. SAR tradeoff. However, to retain excitation fidelity for large tip angles, more advanced and complex pulse design algorithms such as the optimal control method (38) need to be considered. Future work will investigate how pTx MB multi-spoke pulses can be designed for large tip angles and how these pulses compare to alternatives such as adiabatic MB pulses (11).

In the current study, the peak RF power is not controlled in pulse design. When using our method to design pulses for Spin Echo (SE)-like imaging with high MB factors, the required RF peak power for refocusing may become too high and exceed the limit of RF amplifiers. In this case, the high peak power may be reduced by time-shifting (39) and/or phase-scrambling (36,40) the pulse. Although the overall MB RF waveform for each channel will be altered with the use of time-shifting and/or phase-scrambling, these methods will not affect field interferences between RF channels for each single-band pTx pulse component; consequently, the excitation fidelity and SAR will remain unchanged. It is also possible to formulate the pulse design problem to minimize the excitation error while simultaneously constraining SAR and RF power (37,41,42).

For this initial study, we loaded the three RF arrays with a medium-sized head model. Our results suggest that the 2×8 array is beneficial in improving the RF performance of pTx MB pulses. However, this benefit may be compromised when a larger or a smaller head is used to load the arrays. With a smaller head, the impact of coil structures on the inter-element difference in field distributions within the brain may be reduced, whereas, with a larger head high local SAR in the skin, induced by coil elements now closer to the head, may become a dominating factor in determining RF performance. Comparing the actual impact of different head sizes for the three RF arrays presented here will be the subject of further investigation.

Our results suggest that distributing stripline elements in two vs. single Z-rings can effectively enhance the RF performance of pTx MB pulses. However, the RF performance may not be endlessly improved by increasing the number of rings. More rings imply using shorter elements to fit within the same coil dimension. In addition, the number of elements that can be distributed azimuthally in each ring is determined by the total number of transmit channels available and the number of rings desired along the Z direction. With increasing number of rings, the azimuthally distributed elements in each ring also become sparser. At some point, elements likely become too short and azimuthally sparse, thereby compromising transmit-efficiency and requiring a higher total RF power to achieve a same nominal flip angle in the middle of the brain. Such high power requirement may induce high, dominating local SAR in the vicinity of the coil element, thereby hampering the RF performance. This effect is already observed in another coil comparison study showing that the use of three vs. two rings is not advantageous when designing 3T body stripline arrays (16). Thus, building optimal coils with larger numbers of rings along the Z-direction is also tied to the availability and use of multichannel transmitters with higher numbers of pTx channels. Future work will investigate how pTx MB pulses would perform when using other types of coil elements (e.g., loops and/or dipoles) and/or arranging coil elements in a different multi-ring layout (e.g., in three rings) with appropriate numbers of azimuthally distributed coils unconstrained by the current 8- or 16-channel pTx systems.

In this study, we assumed the availability of full pTx hardware and designed band-specific pTx MB pulses to use the maximum degrees of freedom available. Alternatively, one may design band-joint pulses by calculating a common RF shim set for all single-band components of a pTx MB pulse. However, this band-joint design is not expected to provide as good an RF performance as the band-specific counterpart because of the reduced degrees of freedom it uses. This is confirmed by our additional comparison comparing band-joint with band-specific designs by designing MB2 pulses to excite coronal slices. The results for the three arrays show that using band-joint pulses could almost double the local SAR when achieving same excitation fidelity. However, these band-joint pulses are still expected to outperform single-channel MB pulses and represent a compelling choice for a simpler pTx system that uses phase and gain controllers to split the output of a single RF synthesizer. Comprehensive comparison of band-joint and band-specific pTx MB pulse designs is beyond the scope of the current study and is the focus of our future research.

We note that SMS/MB imaging requires an even more receiver coils to enable robust and reliable image reconstruction. For example, the current state-of-the-art SMS imaging protocols developed by the Washington University in Saint Louis – University of Minnesota consortium of the HCP (http://humanconnectome.org) utilize 32 receiver coils. These receiver coils are also arranged in three dimensions to maximize the signal-to-noise ratio and minimize the signal leakage (43) between simultaneously excited slices. Therefore, with the availability of a 16-channel pTx capability, an optimum RF coil design for 7T whole brain pTx SMS/MB imaging could be a double-ring 16-channel transmit array in combination with a multi-ring 32- or even 64-channel receiver array.

Conclusions

Based on electromagnetic simulations of stripline RF arrays, we have demonstrated that a double-ring layout with 16 coil elements evenly distributed in two rings stacked in the Z direction can be used to drastically improve SAR versus excitation fidelity tradeoff as compared to a single-ring, 8- or 16-element RF array when designing pTx MB pulses for 7T whole-brain SMS imaging, and therefore is a preferable stripline array design when pursuing various biomedical applications of pTx SMS brain imaging. With the stripline arrays compared, coronal and sagittal slices are more advantageous than axial and oblique slices for pTx MB pulses.