Abstract
Objective
Pulse transit time (PTT) is being widely pursued for ubiquitous blood pressure (BP) monitoring. PTT-based systems may require periodic cuff calibrations but can still be useful for hypertension screening by affording numerous, out-of-clinic measurements that can be averaged. The objective was to predict the maximum calibration period that would not compromise accuracy and acceptable error limits in light of measurement averaging for PTT-based systems.
Methods
Well-known mathematical models and vast BP data were leveraged. Models relating PTT, age, and gender to BP were employed to determine the maximum time period for the PTT-BP calibration curve to change by <1 mmHg over physiological BP ranges for each age and gender. A model of within-person BP variability was employed to establish the screening accuracy of the conventional cuff-based approach. These models were integrated to investigate the screening accuracy of the average of numerous measurements of a PTT-based system in relation to the accuracy of its individual measurements.
Results
The maximum calibration period was about 1 year for a 30 year old and declined linearly to about 6 months for a 70 year old. A PTT-based system with precision error of >12 mmHg for systolic BP could achieve the screening accuracy of the cuff-based approach via measurement averaging.
Conclusion
This theoretical study indicates that PTT-based BP monitoring is viable even with periodic calibration and seemingly high measurement errors.
Significance
The predictions may help guide the implementation, evaluation, and application of PTT-based BP monitoring systems in practice.
Index Terms: bias and precision error limits, blood pressure variability, calibration, cuff-less blood pressure, hypertension screening, pulse transit time, pulse wave velocity, wearable
I. Introduction
Pulse transit time (PTT) is inversely correlated with blood pressure (BP) in a person and can be measured simply via the relative timing between proximal and distal pulsatile waveforms. Hence, PTT is being widely pursued to achieve ubiquitous BP monitoring [1]–[18].
However, there are several outstanding issues in realizing a PTT-based BP monitoring system. One issue concerns the calibration period. That is, PTT in units of msec must be calibrated to BP in units of mmHg, but the calibration curve relating PTT to BP for a person will change over time with aging [1]. Hence, periodic construction of the calibration curve using cuff BP measurements may be needed. The maximum period between such cuff calibrations that would not compromise accuracy is unknown. It is even uncertain if this period is long enough to make the cuff-less system worthwhile. Another issue pertains to acceptable error limits. Because of the calibration step and since PTT measurements can vary independently of BP (due to, e.g., smooth muscle contraction) [1], a PTT-based system will likely yield higher BP errors than cuff devices. However, these errors may be countered by the capability of making many measurements over time with the ubiquitous system. Such measurements could be averaged to not only mitigate the errors but also to eliminate the substantial BP variations within a person. In this way, the PTT-based system may be able to provide an estimate of the actual underlying BP of the person that is reliable enough for hypertension screening despite large errors in any one of its measurements. Because many measurements can be exploited, the acceptable error limits are unknown.
The objective of this study was to make predictions on the maximum calibration period and acceptable error limits for PTT-based BP monitoring systems using well-known mathematical models and vast BP data from the literature. The results of this theoretical effort may help guide the implementation, evaluation, and application of PTT-based BP monitoring systems in practice.
II. Materials and Methods
A. Predictions on Maximum Calibration Period
The maximum calibration period (i.e., the longest time period between cuff calibrations that would not introduce significant BP error) was first predicted. For this prediction, PTT was assumed to precisely reflect diastolic BP, as PTT is conventionally detected from the “feet” of proximal and distal waveforms and therefore at the level of diastole [1].
The nonlinear model of the area-BP (A−P) relationship of the aorta developed by Wesseling et al. [19] was employed. This model was integrated into the Bramwell-Hill equation ( where τ is PTT, and ρ is the known blood density) to yield a parametric function relating diastolic BP (PD), age, and gender to PTT as follows:
| (1) |
| (2) |
| (3) |
Here, so that PD, τ, and age are in units of mmHg, msec/m, and years, respectively. Fig. 1(a) illustrates this function – as a diastolic BP versus PTT (per unit length) calibration curve – for different ages in males. (The function for females was, as expected, nearly the same.)
Fig. 1.
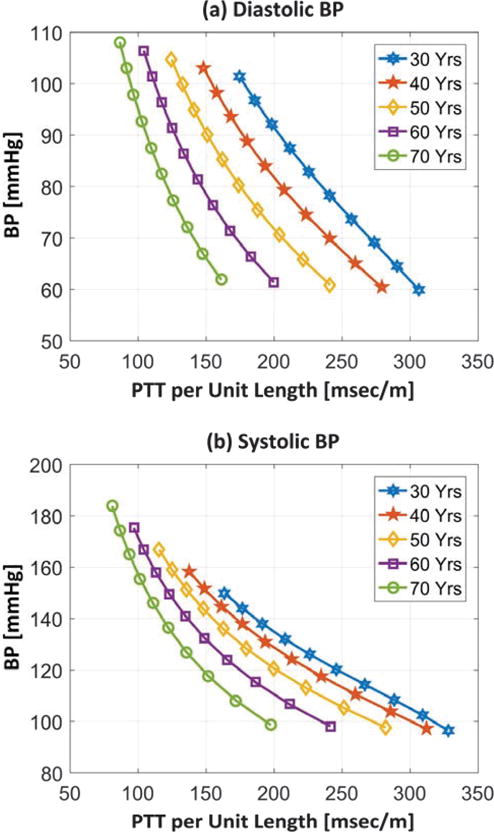
Calibration curves relating pulse transit time (PTT) per unit length to (a) diastolic blood pressure (BP) and (b) systolic BP in males.
To account for systolic BP, a phenomenological model relating diastolic BP to systolic BP (see [20] and references therein) was employed. This model is a line whose slope is typically greater than unity and increases with aging. The simple model has been verified repeatedly via observed correlation coefficients between systolic BP and diastolic BP of 0.7-0.8. The slope is believed to represent the differential arterial compliance at diastole divided by the differential arterial compliance at systole, while the intercept may account for stroke volume and arterial properties. In particular, a linear model relating diastolic BP, age, and gender to systolic BP (PS) was derived based on the data of Master et al. [21] as follows:
| (4) |
| (5) |
| (6) |
where PD > 50 mmHg and age = 30-70 years. Substituting Eqs. (4)-(6) into Eqs. (1)-(3) yields a function relating systolic BP, age, and gender to PTT. Fig. 1(b) illustrates this function – as a systolic BP versus PTT (per unit length) calibration curve – for different ages in males. (The function for females was similar.)
The functions in Fig. 1 indicate how the calibration curves evolve with aging. For a given age and gender, the maximum time period for each calibration curve to change by no more than ε mmHg over a relevant BP range was determined. More specifically, since BP levels vary with aging and differ between genders, age- and gender-dependent BP ranges were applied. According to statistical data provided in tables of [22], age is linearly related to the mean and standard deviation of systolic BP (R = 0.98 − 1) and, to a lesser extent, diastolic BP (R = 0.70 – 0.88) but the diastolic BP statistics are much less dependent on age. Hence, the BP mean ( , where X = D for diastolic and X = S for systolic) and standard deviation were computed as linear functions of age, where the slope and intercept are given in Table I for each BP level and gender. For each age, gender, and BP level, the calibration curve was specified over the BP range from to , as shown in Fig. 1. A second calibration curve was specified for a 0.1 year higher age over the corresponding BP range. The two curves were subtracted over the overlapping BP range, and the maximum absolute BP difference was determined. The age was then increased in increments of 0.1 year until the maximum absolute difference with the original curve reached ε mmHg (where ε 1, 2, or 3). The final age increase indicated the maximum calibration period for the given age, gender, and BP level.
Table I.
Slopes and intercepts of linear functions relating age (30-70 years) to diastolic blood pressure (BP), systolic BP, and between- and within-visit/time period BP variabilities. Values derived from [22] and [26].
| Diastolic BP | |||||
|---|---|---|---|---|---|
|
| |||||
| Race | Gender | Mean | Standard Deviation | ||
|
| |||||
| Slope | Intercept | Slope | Intercept | ||
| All | Male | 0.11 | 77.3 | 0.03 | 9.63 |
| Female | 0.22 | 68.4 | 0.05 | 8.68 | |
| White | Male | 0.08 | 78.4 | 0.03 | 9.27 |
| Female | 0.21 | 68.3 | 0.05 | 8.24 | |
| Black | Male | 0.16 | 78.0 | 0.01 | 12.5 |
| Female | 0.25 | 71.1 | 0.01 | 11.7 | |
| Diastolic BP | |||||
|---|---|---|---|---|---|
|
| |||||
| Race | Gender | Mean | Standard Deviation | ||
|
| |||||
| Slope | Intercept | Slope | Intercept | ||
| All | Male | 0.45 | 109.7 | 0.20 | 7.51 |
| Female | 0.86 | 85.6 | 0.27 | 5.35 | |
| White | Male | 0.45 | 109.7 | 0.21 | 6.80 |
| Female | 0.84 | 86.0 | 0.27 | 4.82 | |
| Black | Male | 0.49 | 110.9 | 0.14 | 12.5 |
| Female | 0.94 | 88.0 | 0.28 | 7.86 | |
| Diastolic BP | |||||
|---|---|---|---|---|---|
|
| |||||
| Race | Gender | Mean | Standard Deviation | ||
|
| |||||
| Slope | Intercept | Slope | Intercept | ||
| White | Male | −0.21 | 35.9 | 0.75 | 4.80 |
| Female | 0.05 | 21.0 | 1.10 | −0.90 | |
| Black | Male | −0.27 | 51.7 | 0.87 | 21.4 |
| Female | 0.10 | 21.6 | 0.86 | 22.0 | |
| Diastolic BP | |||||
|---|---|---|---|---|---|
|
| |||||
| Race | Gender | Mean | Standard Deviation | ||
|
| |||||
| Slope | Intercept | Slope | Intercept | ||
| White | Male | −0.04 | 9.30 | 0.09 | 10.6 |
| Female | −0.07 | 9.90 | 0.04 | 11.4 | |
| Black | Male | −0.11 | 14.0 | 0.18 | 7.80 |
| Female | 0.09 | 2.30 | 0.38 | −4.00 | |
B. Predictions on Acceptable Error Limits
About 45% of hypertensives in developed nations and about 55% of hypertensives in developing nations are unaware of their condition [23]. The main reason may be that many people do not have the means or interest to receive cuff BP measurements such as those in low resource settings or younger people who are not concerned with their health but who may be at risk for early development of hypertension [24], [25]. A secondary reason may be that hypertension detection in the office is challenging due to masked and white coat effects and large within-person BP variability [26]. A ubiquitous BP monitoring system would provide numerous, out-of-office measurements in the mass population so as to help increase hypertension awareness and possibly reduce the incidence of strokes and heart attacks. Hence, the principal, potential application of PTT-based BP monitoring systems is hypertension screening. A useful PTT-based system would be able to screen for hypertension with a level of accuracy that is at least comparable to the conventional cuff-based approach. A model of within-person BP variability [27] was first employed to establish the accuracy of conventional hypertension screening and therefore the “required” level of screening accuracy for PTT-based systems. The hypertension screening accuracy of these systems was then analyzed in relation to their BP measurement accuracy by integrating this model with the models in Section II.A so as to make predictions about the acceptable error limits with respect to manual cuff devices. Acceptable error limits of PTT-based systems were finally considered with respect to automatic cuff devices again based on various models. Methodological details follow.
1) Conventional Hypertension Screening and Model of Within-Person BP Variability
Conventional hypertension screening is based on the average of two cuff BP measurements made during a single office visit at the minimum [28]. A common decision rule is to conclude hypertension if the average systolic BP exceeds 140 mmHg and/or the average diastolic BP exceeds 90 mmHg. The accuracy of this screening approach is imperfect, because BP varies significantly in the short-term due to emotions, stress, physical activity, meals, and other factors, as well as masked and white coat effects in which patients present with BP levels that are not indicative of out-of-clinic settings. Indeed, an estimated 15-30% of people may have lower BP outside the office [29]. As a result, the office screening result is often confirmed via ambulatory or home cuff BP monitoring [28], which is cumbersome to the patient.
To estimate the accuracy of conventional hypertension screening, the three-way nested ANOVA model of within-person BP variability developed by Rosner et al. [27] was used. The model considers BP measurements via manual cuff (auscultation) devices and is given as follows:
| (7) |
where PX,ijk is the kth auscultation BP measurement (X = S for systolic and X = D for diastolic) at the jth clinic visit from the ith person; is the population mean value; and represents between-person variability; and represents between-visit variability for a specific person; and and represents within-visit variability for a specific person and visit. All random variables in the model are independent of each other. The values for and are again given as linear functions of age, where the slope and intercept values are provided in Table I for each BP level, gender, and race. Similarly, the values for and are dependent on the BP level and person’s attributes and may be approximated as linear functions of age based on data from two age groups provided in tables of Rosner et al. [27], where the corresponding slope and intercept values are also given in Table I. All linear equations in Table I are valid for ages of 30-70 years. This model treats the complex factors that cause within-person BP variability as random events. Note that the within-person systolic BP variances are larger than the within-person diastolic BP variances (see Table I), the between-visit variances are larger than the within-visit variances (see Table I), and averaging measurements from a single visit will reduce the within-visit variance but not the between-visit variance.
The screening accuracy of two auscultation measurements during a single clinic visit was computed using the ANOVA model. An average person in Table I (i.e., age of 50 years with mmHg2 for systolic BP and 26.2 mmHg2 for diastolic BP and mmHg2 for systolic BP and 7.1 mmHg2 for diastolic BP, where the averaging of variances was weighted assuming whites constitute 80% of the population) with long-term average auscultation BP in the office deviating by ±5 mmHg from the 140/90 mmHg threshold values (i.e., or 145 mmHg and or 95 mmHg) was assumed. The conventional screening accuracy was specifically computed as the probability of correctly detecting hypertension and normotension for the person.
2) Manual Cuff Device as the Reference
The BP measurement accuracy of a PTT-based system should be assessed using a manual cuff device as the reference, because auscultation is the proven cardiovascular risk factor. Further, an AAMI (Association for the Advancement of Medical Instrumentation) protocol is already available to assess the accuracy of automated devices against auscultation [30]. This protocol generally involves obtaining three successive measurements from each of 85 sufficiently diverse subjects with the test device and auscultation and computing the bias error (mean of the errors) and precision error (standard deviation of the errors) of the device. The device meets the AAMI accuracy standard, if the bias and precision errors are within 5 and 8 mmHg, respectively. Note that these limits were set based on the level of accuracy of auscultation with respect to intra-arterial catheters [30].
A PTT-based system could yield higher BP errors when tested according to the AAMI protocol but still afford the required screening accuracy, because many measurements could be readily obtained over time with the ubiquitous system and averaged. Averaging many measurements can help with hypertension screening for two reasons. Firstly, it will eliminate within-person BP variability, thereby providing an estimate of the actual underlying BP. In this regard, averaging many measurements may be more helpful for detecting systolic hypertension, which is more prevalent and often occurs in isolation [31], due to higher within-person systolic BP variability. Secondly, averaging can mitigate the BP error in individual PTT-based measurements. However, averaging cannot completely eliminate this error because of anticipated correlation in the errors. In particular, this error includes a random component, which can be averaged out, and a fixed component, which cannot be averaged out. A simplified, linear model is presented below to glean insight into these important error components and thereby make various predictions on the acceptable error limits.
Linearized Model of Individual and Average PTT-Based BP Measurement Errors
The model is illustrated in Fig. 2. The input to the model is either the true diastolic BP or true systolic BP of a person at a given time, and the output of the model is the corresponding diastolic BP or systolic BP measurement error via a PTT-based system. This model may therefore be used to help understand both BP measurement and hypertension screening accuracies of the system. The model is based on a set of assumptions and operates as follows.
Fig. 2.
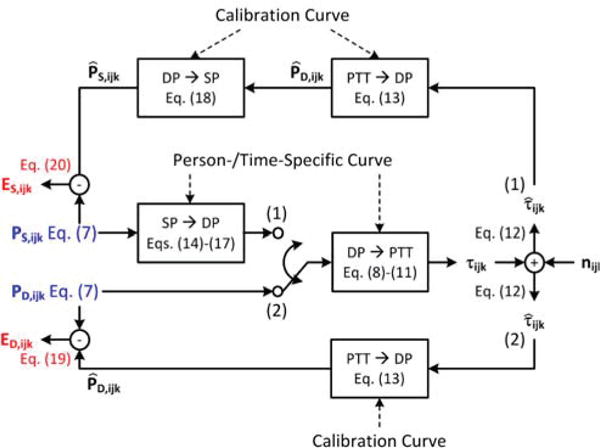
Model employed to predict the acceptable error limits for a PTT-based BP measurement system. The model input (blue) is either the true systolic BP or true diastolic BP, while the model output (red) is the corresponding measurement error of the PTT-based system. All mathematical symbols are completely defined in Eqs. (7)-(20).
The input to the model is a BP measurement described by the ANOVA model in Eq. (7). Hence, auscultation was assumed to provide BP without error. Further, since BP variability between office visits may be reflective of BP variability between different days or different times within a day (e.g., morning to evening), PX,ijk in this model represents the kth auscultation measurement at the jth distinct time period from the ith person. For simplicity, the model does not consider nighttime measurements, as nighttime dipping and the subsequent morning surge are largely deterministic events. However, a ubiquitous system could obtain nighttime BP measurements, which are of considerable value in detecting hypertensive risk [32].
Diastolic BP and PTT were again assumed to be precisely related. However, the nonlinear relationship in Eq. (1) was not used here, because it is too complicated (e.g., diastolic BP cannot be explicitly written in terms of PTT) to offer insight. Based on Fig. 1(a), PTT was instead assumed to be related to auscultation diastolic BP via a simple linear model as follows:
| (8) |
where ηD1,ijk and ηD2,ijk are the slope and intercept, which reflect arterial properties similar to P0 and P1 in Eq. (1). These coefficients were assumed to be person- and timespecific and represented by an ANOVA model analogous to Eq. (7) as follows:
| (9) |
| (10) |
Here, and are the population mean values; and represent between-person variabilities due to cardiovascular aging and disease; and represent between-time period variabilities for a specific person due to smooth muscle contraction; and and represent within-time period variabilities for a specific person and time period due to fast, neurally-mediated smooth muscle contraction. All terms with i, j, and/or k subscripts in each equation were assumed to be independent Gaussian distributed variables with zero-mean and some variance. Hence, like the ANOVA model of within-person BP variability in Eq. (7), this model treats the similar complex factors that cause withinperson smooth muscle contraction variability as random events. The true PTT (τijk) may then be determined from the auscultation diastolic BP input as follows:
| (11) |
A ubiquitous system would measure PTT with convenient sensing modalities (e.g., ballistocardiography for the proximal waveform and photoplethysmography for the distal waveform [11], [12]), which can be susceptible to measurement error. The PTT measured by the system was therefore assumed to be contaminated by additive noise as follows:
| (12) |
where nijk is independent Gaussian distributed noise with zero-mean and some variance.
Diastolic BP may then be computed from the noisy PTT measurement by the ubiquitous system via the following linear calibration curve:
| (13) |
where the values of and may be established based on, for example, the age and gender of the person similar to Eqs. (2) and (3).
To account for systolic BP, a linear model relating auscultation diastolic BP to auscultation systolic BP (see Section II.A) was employed as follows:
| (14) |
where ηS1,ijk and ηS2,ijk are the slope and intercept, which may again respectively indicate the ratio of the differential arterial compliance at diastole to the differential arterial compliance at systole and the stroke volume and arterial properties. Since these physiological variables likewise vary between people due to cardiovascular aging and disease and within a person due to, for example, neuro-humoral modulation caused by the aforesaid complex factors, the coefficients ηS1,ijk and ηS2,ijk were assumed to be person- and time-specific and represented by analogous models as follows:
| (15) |
| (16) |
Hence, within-person auscultation systolic BP and auscultation diastolic BP are imperfectly correlated in the model, which is consistent with the experimentally observed 0.7-0.8 correlation coefficients between the two BP levels. Auscultation diastolic BP may then be determined from the auscultation systolic BP input as follows:
| (17) |
The diastolic BP may thereafter be measured by the PTTbased system via Eqs. (12) and (13).
Finally, systolic BP may be computed from the diastolic BP measurement by the ubiquitous system via the following linear calibration curve:
| (18) |
where the values of and may be also derived based on, for example, the age and gender of the person as in Eqs. (5) and (6). Hence, both systolic BP and diastolic BP are obtained via the system by applying different linear calibration curves to the single PTT measurement.
The errors of the diastolic BP and systolic BP measured by the PTT-based system with respect to auscultation may be found using Eqs. (7), (12), (13), (17) and (18). Assuming small coefficients of variation for the involved variables, the equations may be simplified by neglecting second-order terms to give the following errors for diastolic BP (ED,ijk) and systolic BP (ES,ijk):
| (19) |
| (20) |
where and are the mean or long-term average of diastolic BP and systolic BP, respectively, for the ith person. These errors are Gaussian distributed with zeromean. The variances of the errors indicate the BP measurement accuracy. Note that the terms with the same subscripts (except for nijk) in each equation could possibly be correlated to each other (e.g., and or and ), as they are due to similar factors.
The errors of the average of many PTT-based BP measurements for the ith person may be determined via Eqs. (19) and (20) by noting that each term with subscript j and/or k are zero-mean random variables and that terms without such subscripts are effectively constants. These errors for diastolic BP and systolic BP may then be given as follows:
| (21) |
| (22) |
where J and K respectively denote the number of measurements during distinct time periods and within a time period and are large enough to average out the zero-mean random variables. For comparison with conventional hypertension screening, the error of the average of two auscultation measurements during a single office visit from the ith person is given as follows:
| (23) |
This equation arises from Eq. (7). The errors in Eqs. (21)–(23) are also Gaussian distributed with zero-mean. The variances of these errors indicate the hypertension screening accuracy.
Eqs. (19)-(22) constitute a linearized model of the sources of the BP measurement error associated with a PTT-based system. In particular, the sources of the random error component are: (i) within-person smooth muscle contraction variability ( , , , ); (ii) PTT measurement noise (nijk); and, for systolic BP only, (iii) imperfect within-person correlation between systolic BP and diastolic BP ( , , , ). The source of the fixed error component is the discrepancy between the PTT-BP calibration curves of the system and the long-term average of the person-specific curves relating PTT to BP ( , , , ). Also, the actual underlying BP levels of the person and the coefficient values in the population average curves impact the error magnitude.
Model Simulations
Simulations were performed with the model so as to provide a conservative prediction for the acceptable error limits of a PTT-based BP measurement system. However, rather than assuming the linear relationship between diastolic BP and PTT in Eqs. (8) and (13), the nonlinear relationship in Eqs. (1)-(3) was employed. In particular, the calibration curve relating measured PTT to diastolic BP was defined exactly by these equations (i.e., a universal calibration curve), whereas the person- and timespecific curve was specified in terms of the same equations but with the P0 and P1 parameters set analogously to Eqs. (9) and (10). Similarly, a universal calibration curve relating diastolic BP to systolic BP was defined as Eqs. (4)-(6). The remaining model parameter values were then selected as follows. The standard deviations of the fixed error components ( , , , ) were set to varying percentages (Y%) of their respective average values for the age and gender of the person ( , , , ). Due to the absence of experimental data, the Y values were assumed to be the same for each of the four components. The single Y value may be thought of as the average of the magnitudes of these components. That is, if different Y values were assigned to each fixed error component but the average of these four values was maintained, the average of the results may be similar to the results from the single Y value. The standard deviations of the random error components were set to either modest or observed values as follows: (i) standard deviation of nijk to 5% of τijk in Eq. (11); (ii) standard deviation of , which is an aggregate term arising from the linearization of Eq. (17), to a level that yields a correlation coefficient between the auscultation systolic BP input and auscultation diastolic BP in Eq. (17) of 0.75 for an average person; and (iii) standard deviations of and to 5% of and , respectively. The between-time period standard deviations in (ii) and (iii) accounted for 80% of the total standard deviations (similar to the within-person BP variances in Table I). For convenience, these ten error components were assumed to be independent of each other.
Simulations were performed for increasing values of Y. For each of these values, numerous AAMI and hypertension screening tests were simulated. For the AAMI tests, three consecutive auscultation and PTT-based BP measurements were simulated from 85 subjects, where the age, gender, and race of each subject were determined at random (uniform distribution between 30 and 70 years for age; Bernoulli distribution with p = 0.5 and 0.8 for gender and white). The BP measurement accuracy of the PTT-based system was then determined by averaging the resulting bias and precision errors over the many AAMI tests. For the hypertension screening tests, PTT-based BP measurements for an average person in Table I with long-term average auscultation BP deviating by ±5 mmHg from the 140/90 mmHg threshold values, as described earlier, were simulated for three successive measurements at 30 different time periods (e.g., daily measurements for a month or morning, afternoon, and evening measurements for 10 days) and then averaged. The screening accuracy was then determined by computing the fraction of the numerous tests for which hypertension and normotension were correctly detected via comparison of the averaged PTT-based measurements with the threshold values. The acceptable error limits were then predicted as the maximum bias and precision errors that allowed for the same screening accuracy as conventional auscultation.
A sensitivity analysis was performed to assess the robustness of the major predicted acceptable error limit. The standard deviation of each of the random error components (which represent the user-selected parameters in the simulations) was varied, one at a time, by ±50% relative to its nominal value or observed range. In particular, the standard deviation(s) of (i) nijk was set to 2.5 or 7.5% of τijk; (ii) was set so that the correlation coefficient between auscultation systolic BP and diastolic BP was 0.725 or 0.775 for an average person (observed range is 0.7-0.8); and (iii) and were set to 2.5 or 7.5% of and . The acceptable error limit for each of the six parameter settings was then similarly determined.
Finally, it is also of interest to examine the value added by a PTT-based system to auscultation in hypertension screening. Additional simulations were therefore performed to assess the screening accuracy of the average of the BP measurements from the PTT-based system and auscultation (using the nominal parameter settings).
3) Automatic Cuff Device as the Reference
While the BP measurement accuracy of a PTT-based system should be assessed against a manual cuff device, many developers may prefer initial testing using an automatic cuff device as a reference. In such convenient testing, the acceptable error limits may be higher because of significant error in the reference device. Predictions on the acceptable error limits with respect to an oscillometric device, which is the most popular automatic cuff device, were made as follows.
The error in a PTT-based system with respect to an oscillometric device may be expressed as the error in the PTTbased system with respect to auscultation minus the error in the oscillometric device with respect to auscultation. The bias error of the PTT-based system with respect to the oscillometric device is then simply the difference in the two bias errors with respect to auscultation. However, the precision error of the system with respect to the oscillometric device depends on the correlation between this pair of errors. The sources of the errors were analyzed to gain insight into the extent of the correlation and thereby make predictions on the acceptable bias and precision error limits with respect to an oscillometric device.
III. Results and Discussion
A. Predictions on Maximum Calibration Period
The predicted maximum calibration period turned out to be determined by the highest BP level in the age- and genderdependent BP range. Fig. 3 illustrates the predicted maximum calibration periods for each BP level as a function of age that yield peak BP calibration errors of ε mmHg (where ε = 1, 2, or 3) for males. (The predictions for females were similar.) For diastolic BP, the maximum calibration period decreased linearly with aging. Since diastolic BP increases only modestly with aging (see Table I), this age dependency was mainly due to the calibration curve becoming steeper at a fixed BP level with increased age (see Fig. 1(a)). For systolic BP, the maximum calibration period decreased more precipitously with aging. The stronger age dependency was due to the added effect of systolic BP increasing appreciably with aging (see Table I). Note that the maximum calibration period for systolic BP was often longer than for diastolic BP. This unexpected result occurred, because aging caused diastolic BP to be overestimated for a given PTT (see Fig. 1(a)) and systolic BP to be underestimated for a given diastolic BP (see increasing ηS1 with age in Eq. (5)) such that the two errors tended to offset each other. Hence, the diastolic BP result limited the predicted maximum calibration period. For negligible BP errors of <1 mmHg, the predicted maximum calibration period is therefore about 1 year for a 30 year old and decreases linearly to about 6 months for a 70 year old. This prediction means that a 30 year old would require the next cuff calibration at 31 years old; a 50 year old would require another cuff calibration at 50.75 years old; and a 70 year old would require the next cuff calibration at 70.5 years old. If BP calibration errors of <2-3 mmHg were tolerable, then the maximum calibration period would be 2-3 times longer.
Fig. 3.
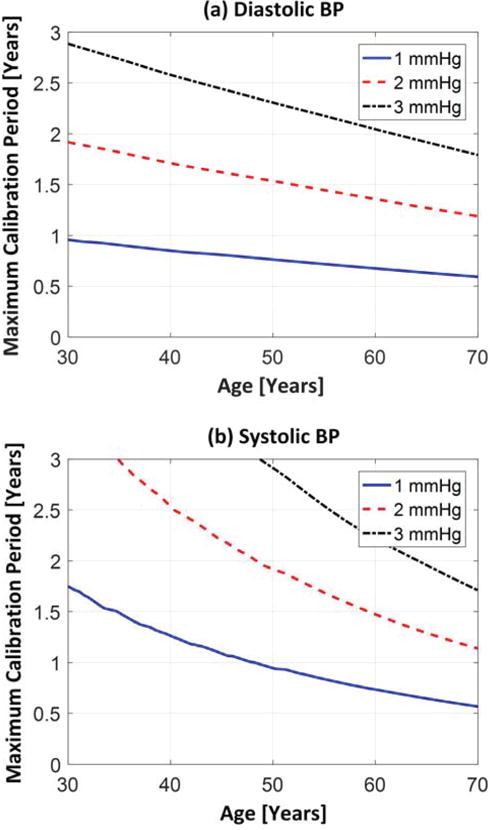
Predicted maximum calibration period as a function of age for (a) diastolic BP and (b) systolic BP in males. Here, 1, 2, and 3 mmHg correspond to the largest tolerable BP error over a physiological BP range.
It is important to emphasize that these maximum calibration period predictions may only be applicable to PTT measurements through the aorta. Peripheral arterial properties actually change less with aging than central arterial properties [33]. However, smooth muscle contraction is a significantly greater factor in the periphery [1]. Smooth muscle contraction is of concern, as it can change the calibration curve (e.g., the values for P0 and P1) even on the order of seconds to minutes due to neuro-humoral control mechanisms [1]. It therefore does not make sense to try to perform cuff calibrations to compensate for this fast phenomenon. The predictions ignore any smooth muscle contraction in the aorta and other confounding factors that can impact PTT-based BP measurement error (as described in Section II.B.2). These predictions are therefore reflective of the impact of only the age-induced changes in the calibration curve on the BP error.
B. Predictions on Acceptable Error Limits
1) Conventional Hypertension Screening
The screening accuracy afforded by two consecutive auscultation measurements was 0.74 for systolic BP and 0.82 for diastolic BP in an average person ( , where Φ is the cumulative Gaussian distribution function). Note that these accuracy levels indicate the minimum probability of correct hypertension and normotension screening in people whose underlying BP deviates by at least 5 mmHg from the threshold values. Also note that additional within-visit measurements (e.g., four) would increase the screening accuracy only little (e.g., 0.75 for systolic BP), because the within-visit BP variances are only about 25% of the between-visit BP variances (see Section II.B.1). Finally note that this simple calculation did not take into account auscultation measurement error (due to the auscultatory gap and observer bias) or masked and white coat effects. Hence, these accuracy levels essentially represent upper bounds for conventional hypertension screening.
2) Manual Cuff Device as a Reference
Predictions Based on the Linearized Model of PTT-Based BP Measurement Errors
To summarize the model in Section II.B.2, the PTT-based BP measurement error includes a random error component, which can be averaged out with many measurements via the ubiquitous system, and a fixed error component, which cannot be averaged out. The sources of the random error component are (i) within-person smooth muscle contraction variability; (ii) PTT measurement noise; and, for systolic BP only, (iii) imperfect within-person correlation between systolic BP and diastolic BP. The source of the fixed error component is the calibration error (i.e., the discrepancy between the PTT-BP calibration curves of the system and the long-term average of the person-specific curves relating PTT to BP). By simply examining this model, important predictions can be made as follows.
Prediction 1
Smooth muscle contraction and imperfect correlation between systolic BP and diastolic BP were originally thought – at least by the authors – to be completely problematic for a PTT-based system. However, the model here indicates that, while these sources are surely an issue from a BP measurement accuracy perspective, they can be averaged out with many measurements and may therefore be of little concern from a hypertension screening perspective. That said, smooth muscle contraction can affect the magnitude of the fixed error component. For example, suppose a personspecific PTT-diastolic BP calibration curve is constructed without error using cuff measurements from the person at a given time period. In this case, the calibration curve would not represent the long-term average person-specific curve but rather the person-specific curve under the particular smooth muscle contraction state. Therefore, the variances of fixed error terms ( and in Eqs. (9) and (10)) would equal the variances of random error terms ( and in the same equations). Hence, although smooth muscle contraction variability can be averaged out, a high degree of such variability could increase the magnitude of the fixed error component so as to reduce the hypertension screening capacity of a PTT-based system. Note that a universal PTT-BP calibration curve built upon person attributes such as age and gender (see Eqs. (1)-(3)) may be prone to nontrivial error because of between-person variability in cardiovascular aging due to lifestyle and otherwise [34]. PTT measurement through the aorta, wherein smooth muscle contraction is relatively sparse, may thus be preferable [1].
Prediction 2
Pulse arrival time (PAT) is often used as a surrogate for PTT in studies on cuff-less BP monitoring [1]. PAT equals PTT plus the pre-ejection period (PEP). PEP can vary significantly with arterial and ventricular properties [1]. The complex factors that cause within-person PEP variability may be emotions, stress, physical activity, etc. Hence, withinperson PEP variability may also be regarded as a random error component that could similarly be averaged out with many measurements. However, PEP also introduces a fixed error component. For example, a calibration curve relating measured PAT to diastolic BP could include, in addition to the calibration parameters relating PTT to diastolic BP (see and in Eq. (13)), an extra parameter reflecting the longterm average of PEP for the given person (which could possibly be derived based on age and gender [35]). Although the random variations in the PEP component of the PAT measurement about its mean value may be averaged out, the discrepancy between the long-term average of PEP for the person and the value assumed by the extra calibration parameter would represent another fixed error component that compromises hypertension screening accuracy. Measurement of PTT rather than PAT may thus be preferable.
Prediction 3
The variances of the errors in two auscultation measurements with respect to the long-term average (see Eq. (23)) for an average person are 58.5 mmHg2 for systolic BP and 29.8 mmHg2 for diastolic BP. Hence, the variances of the corresponding fixed error component of a PTT-based system (see Eqs. (21) and (22)) can be as high as these values without compromising hypertension screening accuracy. The variances of the random error components (see Eqs. (19) and (20)), which are independent of the fixed error components (due to the different subscripts), can be arbitrarily high without affecting hypertension screening accuracy provided that enough measurements can be made to average out these components. In sum, the acceptable precision error limits of the ubiquitous system are – at the very minimum – 7.6 mmHg for systolic BP and 5.5 mmHg for diastolic BP (i.e., square root of the above variances). Because there must be nontrivial random error components, these limits will be appreciably higher. Further, if errors in office auscultation measurements (due to the auscultatory gap, observer bias, and white coat and masked effects) and nighttime measurements by the ubiquitous system were taken into account, the error limits would rise even further.
Prediction 4
It is important to again emphasize that the model and its predictions pertain specifically to PTT measurements through the aorta. As mentioned above, this particular time delay may represent the best-case scenario for PTT-based BP monitoring. Further, insight about other time delays of interest, but for which well-established models are not available, can be gleaned from the quantitative framework. As an example, for the popular PAT, the PEP term introduces additional fixed and random error components. In general, when adding a random error component, the acceptable precision error limits will increase. On the other hand, when adding a fixed error component, the acceptable precision error limits will not change, but the magnitudes of the fixed error components needed to achieve the error limits will decrease. Since PAT may correlate better with systolic BP than diastolic BP [1], the error components may be smaller for systolic BP. In sum, the acceptable precision error limits for PAT relative to aortic PTT may be higher, but these error limits may be more difficult to achieve, especially for diastolic BP.
Simulations for Prediction of Acceptable Error Limits
Fig. 4 shows the screening accuracy versus the AAMI precision accuracy for systolic BP measurements via a PTT-based system (where the accuracies were again varied by sweeping Y, which represents the relative magnitude of the fixed error component) along with the “required” screening accuracy of 0.74. The bias errors were only 0-2 mmHg (results not shown), so each screening accuracy level largely reflected both sensitivity and specificity. These predictions suggest that the AAMI precision error for systolic BP can be near 12 mmHg (i.e., where the red and blue curves intersect) without loss of hypertension screening accuracy compared to conventional auscultation. Note that this acceptable precision error limit is significantly higher than the AAMI precision limit of 8 mmHg for automatic cuff devices. The predictions also suggest that the AAMI precision error for diastolic BP can be near 8 mmHg and satisfy the required screening accuracy of 0.82 (results not shown). Note that the Y value that yielded the required screening accuracy was near 7% for systolic BP (i.e., Y equals about 7% where the red and blue curves intersect) and near 16% for diastolic BP. Hence, although the acceptable systolic BP precision error limit is appreciably higher, the acceptable diastolic BP precision error limit may be more achievable. Also note that these predictions are quite conservative, yet still relatively high for systolic BP, for two reasons. Firstly, the magnitudes of the random error components were set to modest values (e.g., only 5% smooth muscle contraction variability, which may be low even for aortic PTT). Secondly, the predictions again ignore error in office auscultation measurements and do not consider nighttime measurements. The acceptable bias error limits may be regarded as 5 mmHg similar to automatic cuff devices.
Fig. 4.
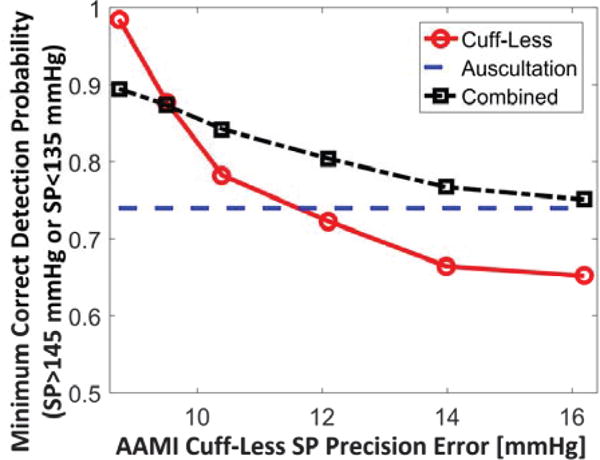
Predicted hypertension screening accuracy versus precision accuracy for systolic BP measurements via a PTT-based system as well the PTT-based system and conventional auscultation combined. Hypertension screening accuracy is quantified in terms of the probability of correctly detecting systolic BP >145 mmHg or <135 mmHg via many measurements from the PTT-based system and two consecutive auscultation measurements for the combined system. Precision accuracy is quantified in terms of the standard deviation of individual measurements from the PTT-based system in an AAMI protocol.
When the magnitude of each of the user-selected parameters in the simulations was perturbed by ±50% relative to its nominal value or observed range, the predicted acceptable systolic BP precision error limit in Fig. 4 changed from about 11 to 13 mmHg (i.e., −3.5 to +9.5% of the predicted value of about 12 mmHg from the nominal parameter value settings). Hence, the major prediction may be quite robust to reasonable perturbations in the parameter choices.
When a PTT-based system was combined with conventional auscultation, the screening accuracy was improved by at least 0.05 over auscultation alone provided that the precision errors of the PTT-based system were within about 13 mmHg for systolic BP (i.e., where the black curve equals 0.79 in Fig. 4) and about 9 mmHg for diastolic BP (results not shown). In sum, the predicted acceptable precision error limits are about 12 mmHg for systolic BP and about 8 mmHg for diastolic BP when the PTT-based system is viewed as an alternative to auscultation and about 1 mmHg higher when the system is considered in addition to auscultation.
3) Automatic Cuff Device as a Reference
The error sources for PTT-based systems may be discrepancies in the calibration curve with respect to the actual curve, PTT measurement noise, and, for systolic BP only, variations in the within-person relationship between diastolic BP and systolic BP. According to modeling and experimental studies (see [36] and [37] and references therein), the major error sources for automatic oscillometric cuff devices may be variations in the width of the brachial artery compliance curve around zero transmural pressure and variations in pulse pressure. Although the sources of error for both methods implicitly or explicitly include variations in arterial compliances, the ranges of BP for the compliance values are different (i.e., transmural pressure of 0 mmHg for an oscillometric device and nominally 100 mmHg for a PTTbased system). Even over the same BP range, the correlation coefficient between the compliance of the aorta, which may be the preferred PTT measurement site, and the brachial artery (as measured in terms of pulse wave velocity) is only about 0.36 [38]. Both methods also implicitly or explicitly share within- and between-person pulse pressure variations as sources of systolic BP error. However, within-person pulse pressure variations may translate into a relatively small component of the errors, and a PTT-based system may be more robust to between-person pulse pressure variations via person-dependent calibration. Hence, the correlation between the errors of a PTT-based system and oscillometric device may be small enough to reasonably approximate the precision error of a PTT-based system with respect to an oscillometric device as the square root of the sum of the error variances of the two methods with respect to auscultation.
The acceptable error limits of a PTT-based system with respect to an automatic cuff device in subjects with characteristics similar to AAMI protocol subjects may be as follows. If the acceptable bias and precision limits of the system with respect to auscultation were 5 and 8 mmHg, which are the conservative bias and precision limits for diastolic BP from the model simulations and the current AAMI standard for automatic cuff devices, then the acceptable bias and precision limits with respect to an oscillometric device would be ±5 mmHg minus the bias of the latter device, as published in its brochure, and the square root of 64 mmHg2 plus the square of the published precision error of this device, respectively. In this case, for oscillometric devices that meet the AAMI standard, the maximum acceptable bias and precision limits would be 10 mmHg in magnitude and 11 mmHg (=√(64+64)), respectively. If the acceptable precision limit of a PTT-based system with respect to auscultation were 12 mmHg for systolic BP, as conservatively predicted via the model simulations, then the acceptable systolic BP precision error limit with respect to an oscillometric device would be above 14 mmHg. This predicted acceptable error limit is considerably higher than a naïvely assumed limit of 8 mmHg.
As a final comment on acceptable error limits, a standard protocol may not always suffice for testing the accuracy of PTT-based systems that require cuff calibration. For example, suppose a system is calibrated with cuff measurements for a subject, and the calibration curve yields similar BP levels despite appreciable variations in measured PTT (e.g., is small in Eq. (13)). Then, when the system is tested in the same subject at a later time, its error may simply reflect the variability in the cuff measurements. This variability could be within the acceptable error limits predicted here, especially when young white males who are typically included in PTTbased BP measurement studies [1], form the study group (see Table I). Hence, PTT-based systems that require cuff calibration should be tested for accuracy using interventions that alter BP significantly (and in different ways) such as postexercise and cold pressor [1]. That is, the system should first be calibrated for a subject during a baseline and then tested in the same subject during the BP maneuvers. In this case, the demonstrated accuracy may be more compelling, and the predicted acceptable error limits may be more applicable. This suggestion is consistent with the IEEE Standard 1708-2014 – Wearable Cuffless Blood Pressure Measuring Devices.
IV. Conclusion
A most important potential application of PTT-based, ubiquitous BP monitoring systems is hypertension screening. That is, by affording numerous, out-of-clinic BP measurements in the mass population, such systems may enhance hypertension awareness and thereby help reduce the incidence of strokes and heart attacks. However, several questions are commonly put forth when discussing the viability of PTT-based BP monitoring systems. One question is: how often do these systems need to be calibrated with cuff measurements and is the period between such calibrations even long enough to make the systems worthwhile? Another question is: what are the acceptable error limits of these systems? This latter question comes up, because PTT-based systems could effectively screen for hypertension, despite serious error in individual measurements due to calibration and otherwise, by mitigating the error and eliminating nontrivial within-person BP variability via averaging of the many measurements. In this study, answers to these difficult questions were sought by making predictions on the maximum calibration period (i.e., the longest period between cuff calibrations that would not compromise accuracy) and acceptable error limits (i.e., the maximum error in individual BP measurements that would still permit, through measurement averaging, a hypertension screening accuracy that is comparable to the current cuff-based approach) via mathematical models and BP data from the literature.
The major predictions of this theoretical investigation were as follows:
The maximum calibration period for PTT measurements is at least 6 months.
The acceptable precision error limit for systolic BP, which is most important for hypertension screening [31], is >12 mmHg in an AAMI protocol with a manual cuff device as a reference. The corresponding acceptable bias error limits and diastolic BP precision error limit may be, at the minimum, similar to the current standard for automatic cuff devices. However, the diastolic BP error limits may actually be easier to achieve in practice.
The acceptable bias and precision error limits for systolic BP can be up to 10 mmHg in magnitude and >14 mmHg, respectively, with respect to an automatic cuff device. The corresponding limits for diastolic BP can be up to 10 mmHg in magnitude and >11 mmHg.
The acceptable error limits for the popular PAT may be higher but more difficult to achieve in practice, especially for diastolic BP.
Interestingly, this study also yielded predictions that may not have been obvious as follows:
The maximum calibration period for PTT measurements declines significantly with aging (e.g., from about 1 year at 30 years old to about 6 months at 70 years old).
For hypertension screening, the deleterious effects of smooth muscle contraction, PEP, and within-person variations in the systolic BP-diastolic BP relationship can be mitigated (but not eliminated in the case of person-specific calibration) via measurement averaging.
The predictions as well as other information provided herein may be of some value in guiding the implementation, evaluation, and application of PTT-based BP monitoring systems in practice. Examples follow. For implementation, the predictions indicate that cuff calibrations should be performed more frequently with increasing age. For evaluation, the predictions suggest that PTT-based systems showing bias and precision errors significantly above the standard 5 and 8 mmHg limits, especially with respect to automatic cuff devices, should not be readily dismissed, because these systems could still screen for hypertension just as effectively as the current cuff-based approach or enhance the screening accuracy when combined with this approach. Moreover, the pivotal evaluation of PTT-based systems should be a hypertension screening accuracy test rather than a measurement accuracy test. Such an evaluation may be most easily conducted by employing the system in a group of subjects with previously diagnosed hypertension and normotension and showing that its hypertension screening accuracy in this group is comparable or adds values to that of the manual cuff-based approach. For application, the predictions suggest that the system would be better off in reporting a running average of many BP measurements instead of individual measurements so as to indicate the true underlying BP of the person. Further, the screening results of the system should be confirmed with ambulatory or home cuff BP monitoring before any clinical treatment is prescribed.
In sum, the results of this theoretical study indicate that the PTT-based BP monitoring approach may be viable even with periodic calibration and seemingly high measurement errors. This information, which would have been difficult to ascertain experimentally, could possibly be helpful in achieving ubiquitous BP monitoring in practice.
Acknowledgments
This material is based upon work supported by the National Institutes of Health under Grant EB018818.
Biographies

Ramakrishna Mukkamala (M’02) received the B.S.E. degree in Biomedical/Electrical Engineering from Duke University, Durham, NC, in 1993 and the S.M. and Ph.D. degrees in Electrical Engineering and Computer Science from the Massachusetts Institute of Technology, Cambridge, MA, in 1995 and 2000, respectively. He was a Postdoctoral Fellow/Research Engineer at the Harvard-MIT Division of Health Sciences and Technology, Cambridge, MA, from 2000 to 2002. Since then, he has been on the faculty of the Department of Electrical and Computer Engineering at Michigan State University, East Lansing, MI, where he is currently a Professor. His research interests include biomedical signal processing and identification, modeling of physiologic systems, cardiovascular physiology, and patient monitoring. Dr. Mukkamala was a recipient of an AHA Scientist Development Grant, an NSF CAREER Award, an MSU Teacher-Scholar Award, and an MSU College of Engineering Withrow Teaching Excellence Award. He is an Associate Editor of the IEEE Transactions on Biomedical Engineering, the Editor of the Cardiovascular and Respiratory Systems Engineering Theme of the IEEE EMBS Conference Proceedings, and a member of the IEEE EMBS Technical Committee on Cardiopulmonary Systems.

Jin-Oh Hahn (M’08) received BS and MS degrees in mechanical engineering from Seoul National University, Seoul, Korea, in 1997 and 1999, and PhD degree in mechanical engineering from Massachusetts Institute of Technology, Cambridge, MA, USA, in 2008. He is currently with the University of Maryland, College Park, MA, USA, where he is an Assistant Professor in the Department of Mechanical Engineering. Dr. Hahn is a recipient of the Young Investigator Program Award from the Office of Naval Research in 2014, and the Young Investigator Grant Award from the Korean-American Scientists and Engineers Association in 2013. His current research interests include systems and controls approach to health monitoring, diagnostics and maintenance of dynamic systems.
Contributor Information
Ramakrishna Mukkamala, Department of Electrical and Computer Engineering, Michigan State University, East Lansing, MI, USA.
Jin-Oh Hahn, Department of Mechanical Engineering, University of Maryland, College Park, MD, USA.
References
- 1.Mukkamala R, et al. Towards Ubiquitous Blood Pressure Monitoring via Pulse Transit Time: Theory and Practice. IEEE Trans Biomed Eng. 2015;62(8):1879–1901. doi: 10.1109/TBME.2015.2441951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ding XR, et al. Continuous Blood Pressure Measurement From Invasive to Unobtrusive: Celebration of 200th Birth Anniversary of Carl Ludwig. IEEE J Biomed Heal Informatics. 2016;20(6):1455–1465. doi: 10.1109/JBHI.2016.2620995. [DOI] [PubMed] [Google Scholar]
- 3.Buxi D, Redouté J, Yuce MR. A survey on signals and systems in ambulatory blood pressure monitoring using pulse transit time. Physiol Meas. 2015;36:R1–R26. doi: 10.1088/0967-3334/36/3/R1. [DOI] [PubMed] [Google Scholar]
- 4.Buxi D, Redout J. Blood Pressure Estimation Using Pulse Transit Time From Bioimpedance and Continuous Wave Radar. IEEE Trans Biomed Eng. 2017;64(4):917–927. doi: 10.1109/TBME.2016.2582472. [DOI] [PubMed] [Google Scholar]
- 5.Kachuee M, Member S, Kiani MM, Member S. Cuffless Blood Pressure Estimation Algorithms for Continuous Health-Care Monitoring. IEEE Trans Biomed Eng. 2017;64(4):859–869. doi: 10.1109/TBME.2016.2580904. [DOI] [PubMed] [Google Scholar]
- 6.Lin H, Xu W, Guan N, Ji D, Wei Y, Yi W. Noninvasive and Continuous Blood Pressure Monitoring Using Wearable Body Sensor Networks. IEEE Intell Syst. 2015;30(6):38–48. [Google Scholar]
- 7.Ding X, Zhang Y, Liu J, Dai W, Tsang HK. Continuous Cuffless Blood Pressure Estimation Using Pulse Transit Time and Photoplethysmogram Intensity Ratio. IEEE Trans Biomed Eng. 2016;63(5):964–972. doi: 10.1109/TBME.2015.2480679. [DOI] [PubMed] [Google Scholar]
- 8.Da He D, Winokur ES, Sodini CG. An Ear-Worn Vital Signs Monitor. IEEE Trans Biomed Eng. 2015;62(11):2547–2552. doi: 10.1109/TBME.2015.2459061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thomas SS, Nathan V, Zong C, Soundarapandian K, Shi X, Jafari R. BioWatch: A Noninvasive Wrist-Based Blood Pressure Monitor That Incorporates Training Techniques for Posture and Subject Variability. IEEE J Biomed Heal Informatics. 2016;20(5):1291–1300. doi: 10.1109/JBHI.2015.2458779. [DOI] [PubMed] [Google Scholar]
- 10.Zheng Y-L, Yan BP, Zhang Y-T, Poon CCY. An Armband Wearable Device for Overnight and Cuff - Less Blood Pressure Measurement. IEEE Trans Biomed Eng. 2014;61(7):2179–2186. doi: 10.1109/TBME.2014.2318779. [DOI] [PubMed] [Google Scholar]
- 11.Martin SL, et al. Weighing Scale-Based Pulse Transit Time is a Superior Marker of Blood Pressure than Conventional Pulse Arrival Time. Sci Rep. 2016;6:39273. doi: 10.1038/srep39273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kim CS, Carek AM, Mukkamala R, Inan OT, Hahn JO. Ballistocardiogram as proximal timing reference for pulse transit time measurement: Potential for cuffless blood pressure monitoring. IEEE Trans Biomed Eng. 2015;62(11):2657–2664. doi: 10.1109/TBME.2015.2440291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sola J, et al. Noninvasive and nonocclusive blood pressure estimation via a chest sensor. IEEE Trans Biomed Eng. 2013;60(12):3505–3513. doi: 10.1109/TBME.2013.2272699. [DOI] [PubMed] [Google Scholar]
- 14.Giassi P, Okida S, Oliveira MG, Moraes R. Validation of the inverse pulse wave transit time series as surrogate of systolic blood pressure in MVAR modeling. IEEE Trans Biomed Eng. 2013;60(11):3176–3184. doi: 10.1109/TBME.2013.2270467. [DOI] [PubMed] [Google Scholar]
- 15.Chandrasekaran V, Dantu R, Jonnada S, Thiyagaraja S, Subbu KP. Cuffless differential blood pressure estimation using smart phones. IEEE Trans Biomed Eng. 2013;60(4):1080–1089. doi: 10.1109/TBME.2012.2211078. [DOI] [PubMed] [Google Scholar]
- 16.Gao M, Cheng H-M, Sung S-H, Chen C-H, Olivier NB, Mukkamala R. Estimation of pulse transit time as a function of blood pressure using a nonlinear arterial tube-load model. IEEE Trans Biomed Eng. 2017;64(7):1524–1534. doi: 10.1109/TBME.2016.2612639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Seeberg T, et al. A novel method for continuous, non-invasive, cuffless measurement of blood pressure: Evaluation in patients with nonalcoholic fatty liver disease. IEEE Trans Biomed Eng. 2016 doi: 10.1109/TBME.2016.2606538. [DOI] [PubMed] [Google Scholar]
- 18.Addison PS. Slope transit time (STT): A pulse transit time Proxy requiring only a single signal fiducial point. IEEE Trans Biomed Eng. 2016;63(11):2441–2444. doi: 10.1109/TBME.2016.2528507. [DOI] [PubMed] [Google Scholar]
- 19.Wesseling KH, Jansen JRC. Computation of aortic flow from pressure in humans using a nonlinear, three-element model. J Appl Physiol. 1993;74(5):2566–2573. doi: 10.1152/jappl.1993.74.5.2566. [DOI] [PubMed] [Google Scholar]
- 20.Gavish B, Bendov IZ, Bursztyn M. Linear relationship between systolic and diastolic blood pressure monitored over 24 h: assessment and correlates. J Hypertens. 2008;26:199–209. doi: 10.1097/HJH.0b013e3282f25b5a. [DOI] [PubMed] [Google Scholar]
- 21.Master AM, Lasser RP. The relationship of pulse pressure and diastolic pressure to systolic pressure in healthy subjects 20–94 years of age.pdf. Am Heart J. 1965;70(2):163–171. doi: 10.1016/0002-8703(65)90063-3. [DOI] [PubMed] [Google Scholar]
- 22.National Center for Health Statistics. Drizd T, Dannenberg AL, Engel A. Blood Pressure Levels in Persons 18-74 Years of Age in 1976 – 80, and Trends in Blood Pressure From 1960 to 1980 in the United States. 1986 [PubMed] [Google Scholar]
- 23.Ibrahim MM, Damasceno AA. Hypertension in developing countries. Lancet. 2012;380:611–619. doi: 10.1016/S0140-6736(12)60861-7. [DOI] [PubMed] [Google Scholar]
- 24.Yano Y, et al. Isolated systolic hypertension in young and middle-aged adults and 31-year risk for cardiovascular mortality: The Chicago heart association detection project in industry study. J Am Coll Cardiol. 2015;65(4):327–335. doi: 10.1016/j.jacc.2014.10.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Weber MA. Interpreting blood pressure in young adults. J Am Coll Cardiol. 2015;65(4):336–338. doi: 10.1016/j.jacc.2014.11.016. [DOI] [PubMed] [Google Scholar]
- 26.Pickering TG, Shimbo D, Haas D. Ambulatory Blood-Pressure Monitoring. N Engl J Med. 2006;354(22):2368–2374. doi: 10.1056/NEJMra060433. [DOI] [PubMed] [Google Scholar]
- 27.Rosner B, Polk BF. Predictive values of routine blood pressure measurements in screening for hypertension. Am J Epidemiol. 1983;117(4):429–442. doi: 10.1093/oxfordjournals.aje.a113561. [DOI] [PubMed] [Google Scholar]
- 28.U.S. Preventive Services Task Force. Final Recommendation Statement: High Blood Pressure in Adults: Screening. [Online]. Available: https://www.uspreventiveservicestaskforce.org/Page/Document/RecommendationStatementFinal/high-blood-pressure-in-adults-screening.
- 29.Piper M, Oregon Evidence-based Practice Center (Center for Health Research (Kaiser-Permanente Medical Care Program. Northwest Region)), United States. Agency for Healthcare Research and Quality, and U.S. Preventive Services Task Force Screening for high blood pressure in adults: a systematic evidence review for the US Preventive Services Task Force. 2014 [PubMed] [Google Scholar]
- 30.Non-invasive sphygmomanometers - Part 2: Clinical validation of automated manometer type. International Organization for Standardization; 2009. [Google Scholar]
- 31.Franklin SS, Jacobs MJ, Wong ND, L’Italien GJ, Lapuerta P. Predominance of isolated systolic hypertension among middle-aged and elderly US hypertensives: Analysis based on national health and nutrition examination survey (NHANES) III. Hypertension. 2001;370(3):869–874. doi: 10.1161/01.hyp.37.3.869. [DOI] [PubMed] [Google Scholar]
- 32.Boggia J, et al. Prognostic accuracy of day vs. night ambulatory blood pressure: a cohort study. Lancet. 2007;370:1219–1229. doi: 10.1016/S0140-6736(07)61538-4. [DOI] [PubMed] [Google Scholar]
- 33.Nichols W, O’Rourke MF, Vlachopoulos C. McDonald’s Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles. CRC Press; 2011. [Google Scholar]
- 34.Tanaka H, Dinenno FA, Monahan KD, Clevenger CM, DeSouza CA, Seals DR. Aging, habitual exercise, and dynamic arterial compliance. Circulation. 2000;102(11):1270–1275. doi: 10.1161/01.cir.102.11.1270. [DOI] [PubMed] [Google Scholar]
- 35.Montoye HJ, Willis PW, Howard GE, Keller JB. Cardiac preejection period: age and sex comparisons. J Gerontol. 1971;26(2):208–16. doi: 10.1093/geronj/26.2.208. [DOI] [PubMed] [Google Scholar]
- 36.Liu J, Hahn JO, Mukkamala R. Error mechanisms of the oscillometric fixed-ratio blood pressure measurement method. Ann Biomed Eng. 2013;41(3):587–597. doi: 10.1007/s10439-012-0700-7. [DOI] [PubMed] [Google Scholar]
- 37.Liu J, Cheng H, Chen C, Sung S, Hahn J, Mukkamala R. Patient-specific oscillometric blood pressure measurement: Validation for accuracy and repeatability. IEEE J Transl Eng Heal Med. 2017;5:1900110. doi: 10.1109/JTEHM.2016.2639481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tillin T, et al. Measurement of pulse wave velocity: site matters. J Hypertens. 2007;25(2):383–389. doi: 10.1097/HJH.0b013e3280115bea. [DOI] [PubMed] [Google Scholar]


