DTI BASED STRUCTURAL DAMAGE CHARACTERIZATION FOR DISORDERS OF CONSCIOUSNESS

Abstract

MRI Diffusion Tensor Imaging (DTI) has been recently proposed as a highly discriminative measurement to detect structural damages in Disorders of Consciousness patients (Vegetative State/Unresponsive Wakefulness Syndrome-(VS/UWS) and Minimally Consciousness State-MCS). In the DTI analysis, certain tensor features are often used as simplified scalar indices to represent these alterations. Those characteristics are mathematically and statistically more tractable than the full tensors. Nevertheless, most of these quantities are based on a tensor diffusivity estimation, the arithmetic average among the different strengths of the tensor orthogonal directions, which is supported on a symmetric linear relationship among the three directions, an unrealistic assumption for severely damaged brains. In this paper, we propose a new family of scalar quantities based on Generalized Ordered Weighted Aggregations (GOWA) to characterize morphological damages. The main idea is to compute a tensor diffusitivity estimation that captures the deviations in the water diffusivity associated to damaged tissue. This estimation is performed by weighting and combining differently each tensor orthogonal strength. Using these new scalar quantities we construct an affine invariant DTI tensor feature using regional tissue histograms. An evaluation of these new scalar quantities on 48 patients (23 VS/UWS and 25 MCS) was conducted. Our experiments demonstrate that this new representation outperforms state-of-the-art tensor based scalar representations for characterization and classification problems.

1. INTRODUCTION

After a traumatic or non-traumatic brain injury, some patients will fall into a coma state, and possibly brain death. However, some others will “awaken”(i.e., recover sleep-wake cycles) from their coma, but with absence of any behavioral signs of awareness (i.e., will only show reflex movements without command following) [1]. This state is known as unresponsive wakefulness syndrome or Vegetative State (VS/UWS) [1]. In contrast, other patients evolve to a Minimally Conscious State (MCS) showing non-reflexive and purposeful behaviors but they are unable to communicate [2]. From the clinical perspective, the diagnosis of these Disorders of Consciousness (DoC) is a very challenging task, reflected in the high rate of misdiagnoses of the VS/UWS patients (approximately 40%) [3]. Recently, some neuroimages experiments have tried to establish accurate biomarkers of the consciousness level in VS/UWS and MCS [4, 5, 6]. Nevertheless, a complete disease characterization of the neuroimaging is still a very difficult problem [7, 5].

Main etiologies of DoCs include Traumatic Brain Injury (TBI) and Anoxic Brain Injury (ABI) [2]. In TBI brain structures are damaged by external forces. For example, rapid accelerations or decelerations in a car accident can generate strong shearing forces that will affect the axon bodies in white matter [8]. The ABI results from a lack of oxygen supply to the brain, with consequent neuronal cell death [9]. These instantaneous damages are followed by complex physiological processes that, over the course of hours, days or even months, can lead to inflammatory processes, neuronal and axonal death. As a consequence, these patients frequently present very severe cortical and subcortical atrophies secondary hydrocephalus (i.e, enlarged ventricles [10]. All these physiological processes could dramatically change local and global morphological brain properties [11].

Recently, some biomarkers based on DTI have been proposed to quantify in-vivo structural changes that correlate with the level of consciousness in DoC patients [12, 5]. In particular, the amount of diffusion estimated by the mean diffusivity, has been identified as a low level scalar representation of the diffusivity water properties related to the morphological damage [5, 12]. This scalar seems to provide a good characterization capacity to discriminate VS/UWS and MCS patients [5]. Nevertheless, this quantity is implicitly assuming that different tensor orthogonal directions (one axial, two radial) are linearly related and have the same importance for the mean diffusivity estimation. This can be an unrealistic assumption in severely damaged brains where the level of atrophy and neuronal death probably affects each tensor direction in a different way [13]. This suggests that usual DTI scalar maps are likely non-optimal representations of damaged tissue, at least in these pathological brains.

In this paper we propose a new family of mean diffusivity estimations for damaged tissue in DoC patients. The main contribution of this work is the use of Generalized Ordered Weighted Aggregations (GOWA) to obtain a more realistic diffusivity estimation for the tensors located in damaged tissue. We show that classic tensor maps could be reformulated and even generalized in this new setting. Six different new quantities to capture different relationships between axial and radial diffusivities were formulated. Using these quantities a highly discriminant feature to distinguish VS/UWS and MCS patients was proposed. Results show that these new features outperforms state-of-the-art DTI based scalar quantities in real data.

2. METHODS

In DTI information related with strength of water diffusion is described by a tensor S. Several scalar measures can be derived from S to describe the structural damage in the brain. Common measures include the eigenvalues λ = (λ₁, λ₂, λ₃), λ₁ ≥ λ₂ ≥ λ₃, that characterize disruption in the orientation of the brain structures, the mean diffusivity (MD):

$$MD=\langle \mathrm{\lambda }\rangle =\frac{{\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_3}{3}$$ (1)

which represents the increase of overall molecule displacement and several kinds of anisotropy indices, for instance the volume ratio - VR and the fractional anisotropy - F A:

$$\begin{gathered} VR=\frac{{\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_3}{{\langle \mathrm{\lambda }\rangle }^3} \\ FA=\frac{\sqrt{3\left({\left({\mathrm{\lambda }}_1-\langle \mathrm{\lambda }\rangle \right)}^2+{\left({\mathrm{\lambda }}_2-\langle \mathrm{\lambda }\rangle \right)}^2+{\left({\mathrm{\lambda }}_3-\langle \mathrm{\lambda }\rangle \right)}^2\right)}}{\sqrt{2\left({\mathrm{\lambda }}_1^2+{\mathrm{\lambda }}_2^2+{\mathrm{\lambda }}_3^2\right)}} \end{gathered}$$ (2)

that quantify the level of disorder in oriented structures in the tissue [14]. Importantly, most of these quantities depend upon the estimation of the overall diffusivity in S, an arithmetic average of the eigenvalues (equation 1). For the morphological damage characterization problem, this estimation is assuming that all tensor orthogonal information is equally relevant. Additionally, the use of an arithmetic mean is assuming the existence of a linear relationship among the three eigenvalues [15]. Two assumptions that could be violated in severely damaged brains, resulting in a non-robust estimation of the mean diffusivity in the damaged tissue.

It is worthy to note that the weight selection $\frac{1}{3}$ in equation 1 is based on the Laplace principle of insufficient reason, i.e., if there is no data to consider that one environmental state is more likely than the other, then prior probabilities of environmental states have to be equal (the spherical tensor model) [16]. However, because of the inhomogeneity in the tensor shapes coming of complex inflammatory and reabsorption processes in DoC patients, we believe that this symmetrical assumption is not valid. For example, histological evidence in TBI suggests that when axons are rapidly stretched they become brittle, and the axonal cytoskeleton can be broken. Then axonal transport is blocked in the breaking point of the cytoskeleton, leading to an accumulation of transport products and local swelling. Swelling can tear the axon at the site of the break in the cytoskeleton, causing it to drawback toward the cell body and form a bulb called a retraction ball [17]. By choosing equally probable weights in equation 1, it is assuming that these retraction balls are uniformly distributed on the volume measured by DTI. This symmetry could be naturally captured by the spherical tensor model, that has been proved to be appropriate in healthy tissue [18]. However, histological evidence suggests that this symmetry is not preserved anymore in the damaged brain tissues [17], therefore spherical tensor model could not be valid anymore. Additionally, the aritmetic average in equation 1 is assuming a linear tensor shape, i.e., tensor orthogonal directions are linearly scaled [15]. However, the successful log-euclidian metrics in DTI suggest that the tensor nature could be exponentially related rather than linear [19]. To capture these two phenomena, 1) the non-uniform distributions of the structural damages and 2) the non-linear watter difussivity in the volume measured by DTI, we here assume non-isotropic tensor models for the estimation of the mean diffusivity.

To our knowledge, there is not extensive information about lesion tissue morphology on TBI and ABI to build a full disease related tensor model [13]. We therefore model some plausible damaged tensor shapes involving different diffusivity axis relevance: axial and radial. In addition, we model different relationships among the different tensor orthogonal directions: linear or exponential. This problem could be formulated using generalized ordered weighted aggregations (GOWA) operators [20]. These operators are widely used in computational intelligence because they provide a unified framework to aggregate multiple ordered information by using different weights to model different relevance of input information. GOWA operators also include several primitives of aggregation to capture different relationships between input information, for instance, linear or exponential [20]. A GOWA mapping M on a set of positive real numbers λ₁, λ₂, …, λ_n is defined by

$$M_{w,p}\left({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2,\dots ,{\mathrm{\lambda }}_n\right)={\left({\displaystyle \sum _{j=1}^n{w}_j{\theta }_j^p}\right)}^p$$ (3)

where w = (w₁, w₂, …, w_n) is a collection of weights satisfying w_j ∈ [0, 1] and ${\displaystyle {\sum }_{j=1}^n{w}_j=1}$, p is a parameter such that p ∈ [−∞, ∞], θ_j is the jth largest of the λ_j. This operator is a generalized weighted average on the set of input re-ordered data. Because this re-ordering step, a particular aggregate λ_i is not associated with a particular weight w_i, but rather a weight is associated with a particular ordered position of aggregate.

We build different tensor diffusivity estimations by using these operators over the eigenvalues. Note that usual scalar maps could be written with these operators, for example if p = 1 and $w_j=\frac{1}{3}$ we obtained $MD=M_{\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right),1}\left({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2,{\mathrm{\lambda }}_3\right)$. The VR could be written as the power three of the ratio of two GOWA mappings, one with p → 0 and $w_j=\frac{1}{3}$, were we obtain the geometrical average $M_{\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right),0}=\left({\mathrm{\lambda }}_1^{1/3}{\mathrm{\lambda }}_2^{1/3}{\mathrm{\lambda }}_3^{1/3}\right)$, and other for the denominator using the MD GOWA, i.e.:

$$VR={\left(\frac{M_{\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right),0}}{M_{\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right),1}}\right)}^3$$

Other DTI scalar quantities could be similarly derived, for instance, λ₁ = M_(1,0,0),1, λ₂ = M_(0,1,0),1 and λ₃ = M_(0,0,1),1.

As observed, in the GOWA setting determining the associated weights w and the power term p of the operator are the most important tasks. Two options have been proposed in this case, the first is to use a set of training samples to estimate the parameters [21, 22], the second is to model explicitly the aggregation [21]. For this problem, because of the inhomogeneity of the tensor shapes coming from complex inflammatory and athrophy processes, selection of good training samples of damaged tissue could be a difficult task [13]. We propose to model four different GOWA operators to capture some plaussible tensor shapes. Firstly, $M{D}_{\perp ,1}=M_{\left(\frac{2}{3},\frac{1}{3},0\right),1}$ to model the high relevance of axial information compared to radial diffusivity. The last weight is set to zero to avoid highly noise input effects usually observed in the third eigenvalue of DTI [23]. Similarly, a mapping to model the opposite effect could be formulated, i.e., high radial information compared to axial diffusivity $M{D}_{-,1}=M_{\left(\frac{1}{3},\frac{2}{3},0\right),1}$. In both cases, by using p = 1 a linear relationship between the different orthogonal dimensions of the tensor is assumed. However, an exponential shape could be modeled in both cases by using weighted geometrical averages $M{D}_{\perp ,0}=M_{\left(\frac{2}{3},\frac{1}{3},0\right),0}$, $M{D}_{-,0}=M_{\left(\frac{1}{3},\frac{2}{3},0\right),0}$.

Interpretation of these quantities are as follows, for instance $M_{\left(\frac{1}{3},\frac{2}{3},0\right),0}$ is capturing the value of the average diffusitivity under the assumption that the tensor has a radial shape and their orthogonal directions have an exponential growing. We observed that tensors with high values for this mapping are likely in agreement with this tensor shape. This idea could be used to contrast two very different tensor models:

$$V{R}_{\perp /-}={\left(\frac{M_{\left(\frac{2}{3},\frac{1}{3},0\right),0}}{M_{\left(\frac{1}{3},\frac{2}{3},0\right),1}}\right)}^3,V{R}_{-/\perp }={\left(\frac{M_{\left(\frac{1}{3},\frac{2}{3},0\right),0}}{M_{\left(\frac{2}{3},\frac{1}{3},0\right),1}}\right)}^3$$

these quatities are natural extensions of the volume ratio (equation 2) and can be also be used as scalar maps.

2.1. DTI based scalar features

Overall, these patients present macrostructural lesions [24]. This condition could result for instance from hydrocephaly and atrophy processes that change dramatically the geometrical brain configuration [25]. Because of these large spatial deformations, recent approaches for characterization and classification based on DTI normalization could fail [26]. In neuroimages group studies severely deformed brains sometimes need to be excluded [5, 26]. Nevertheless, in the clinical practice it is of paramount importance to keep these data for diagnosis/prognosis [26]. In order to avoid such limitation, in this work we introduce an automatic global invariant affine characterization based on histograms to describe DTI information without any spatial normalization. In particular, we characterize white matter and gray matter volumes. An automatic brain segmentation was computed in the patient space by segmenting the DTI data using a multichannel expectation maximization algorithm [27]. The λ₃ and MD were used to obtain [28, 27]: Cerebral Spinal Fluid (CSF), Gray Matter (GM) and White Matter (WM) volumes. CSF was removed from the analysis to avoid hydrocephaly confounds [29]. Histograms for each scalar map inside each volume (WM and GM) were computed and normalized to sum 1. The histogram shape was described using the first four statistical moments (mean, variance, skewness and kurtosis) and the maximum peak of the histogram.

2.2. Experimental settings

We evaluated how discriminative were the proposed scalar GOWA maps compared with state-of-the-art scalar maps on two tasks: discrimination at the group level (VS/UWS vs. MCS) and patient-per-patient classification (VS/UWS vs. MCS). A sample of 48 severely brain-injured patients (23 VS/UWS and 25 MCS) of varying etiologies, who met the criteria defining the VS/UWS and MCS [30], was used to evaluate the proposed characterization. Clinical examination was performed using the Coma Recovery Scale-Revised (CRS-R) [30]. DTI data were acquired using 3T MRI Scanner (Allegra, Siemens) 64 non-collinear directions using a b-value = 1000 s/mm² and two b=0 images (TR= 5700 ms, TE= 87 ms, matrix size=128 × 128, 45 slices, slice thickness=3 mm, gap=0.3 mm) at the University Hospital of Liége, Belgium. Images were processed using the FMRIB Software Library (FSL, version 4.1.6; Oxford Centre for Functional MRI of the Brain (FMRIB), UK; http://www.fmrib.ox.ac.uk/fsl/). Several DTI Based scalar maps were constructed from the DTI data [14], namely tensor eigen-values (λ₁, λ₂, λ₃), mean diffusivity (MD), fractional anisotropy (FA), volume ratio (VR), the recently proposed ellipsoid area ratio (EAR) [31], and the six proposed scalar quatities (MD_⊥,1, MD_−,1, MD_⊥,0, MD_−,0, VR_⊥/−, VR_−/⊥). For the group level study we reported the results of a two-tailed t-tests comparing the five computed quantities per scalar map (Bonferroni corrected for multiple comparisons, p < 0.01). For the classification task we used a k-nearest neightborhood (k-NN) classifier (k = 3). A 10-folding cross-validation was used to evaluate generalization performance. A total of ten different 10-folding cross-validations were performed. The area under the Receiver Operational Curve (ROC) was computed as summary statistic in each fold experiment [32]. Two additional experiments of classification were performed to explore the discrimination capacity of the complete set of features with and without GOWA based scalar maps, one with all features and one using feature selection previous to the training process [33].

3. RESULTS

Table 1 reports the p-values of the five histogram features of each scalar map. The third moment of the second eigen value λ₂ and the third moment of MD_⊥,0 provided the best discrimination between VS/UWS and MCS in white matter. In gray matter the best discrimination was given by the maximum probability peak of proposed contrasts scalar map VR_−/⊥. Finally, when both white matter and gray matter were used to compute the histogram of damage the best discrimitation was given by the third moment of the MD_⊥,0. Using this global characterization (WM-GM), the best discrimination values (FA, EAR, MD_⊥,0) were obtained. EAR outperformed FA. The proposed scalar feature MD_⊥,0 outperformed both.

Table 1.

Best differences between vegetative/unresponsive (VS/UWS) and minimally conscious state (MCS) patients for differences DTI scalar maps in white matter (WM), gray matter (GM) and both (GM-WM). In parentheses the histogram feature ((1) mean, (2) variance, (3) skewness, (4) kurtosis and (5) maximum probability peak) that provides the best discrimination between VS/UWS and MCS.

		DTI Scalar Maps
		λ1	λ2	λ3	MD	FA	VR	EAR	MD⊥,1	MD−,1	MD⊥,0	MD−,0	VR⊥/−	VR−/⊥
p-value	WM	0.0184 (3)	0.0022 (3)	0.0025 (3)	0.0026 (3)	0.0569 (5)	0.1046 (2)	0.0474 (5)	0.0026 (3)	0.0047 (3)	0.0022 (3)	0.0035 (3)	0.1087 (5)	0.0794 (2)
	GM	0.0099 (1)	0.0064 (1)	0.0073 (1)	0.0070 (1)	0.0218 (5)	0.0234 (1)	0.0132 (5)	0.0071 (1)	0.0082 (1)	0.0067 (1)	0.0075 (1)	0.0067 (2)	0.0062 (5)
	WM-GM	0.0095 (1)	0.0056 (1)	0.0057 (1)	0.0064 (1)	0.0017* (2)	0.0081 (2)	0.0015* (2)	0.0066 (1)	0.0078 (1)	0.0062 (1)	0.0073 (1)	0.0010* (3)	0.0020 (3)

^*Bonferroni corrected (p < 0.01).

Figure 1 shows the performance for a patient classification task (VS vs. MCS) using whole brain (WM-GM) histogram features with different DTI scalar maps features. The proposed contrast scalar map VR_−/⊥ outperforms other scalar maps with an average classification performance of 0.68 ± 0.026 (best classification 0.72). The EAR based feature provided the best average classification performance 0.66 ± 0.043 (best classification 0.72) among the evaluated state-of-the-art scalar features. Two additional experiments were performed to assest the discrimination capacity the complete set of the scalar features. The first experiment (All − No − GOWA) evaluated the discrimination capacity of the classifier using all state-of-the-art scalar features (λ₁, λ₂, λ₃, MD, FA, VR, EAR) including the GOWA based scalar maps (All − GOWA). In figure 1, classification performance improves from 0.57 ± 0.048 (best classification 0.64) to 0.66 ± 0.041 (best classification 0.75) by using the complete set of features including the GOWA maps. For the second experiment including that included the feature selection method, the average classification performance decreased to 0.49 ± 0.031 by using this feature selection step on the state-of-the-art scalar features (All − No − GOWA^†). With the same selection procedure applied over the complete set of scalar features, including the GOWA based scalar maps (All − GOWA^†), the best average classsification performance 0.74 ± 0.032 (best classification 0.79) was obtained. This improvement in the classification performance is statistically significant (p < 0.0001).

Fig. 1.

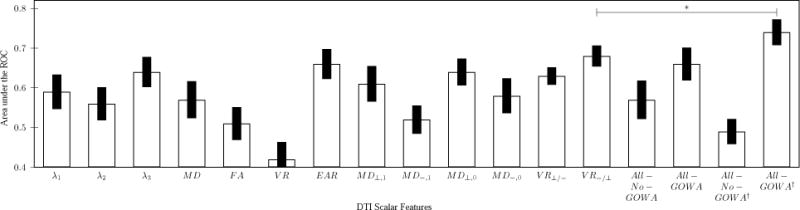
Area under the ROC for a whole brain brain classiffier (± standard deviation) using different the DTI scalar features. *Bonferroni corrected (p < 0.0001).

4. CONCLUSIONS

We here proposed a new family of diffusion tensor scalar quantities based on GOWA to characterize morphological damages in severely damaged brains. Using these scalar maps we constructed a global affine invariant DTI tensor feature based on regional tissue histograms. We demonstrated on different experimental settings that the new representation is suitable to characterize the severity of damage in DoC patients.