Why do disordered and structured proteins behave differently in phase separation?

Abstract

Intracellular membraneless organelles and their myriad cellular functions have garnered tremendous recent interest. It is becoming well accepted that they form via liquid-liquid phase separation (LLPS) of protein mixtures (often including RNA), where the organelles correspond to a protein-rich, droplet phase coexisting with a protein-poor, bulk phase. The major protein components contain disordered regions and often also RNA-binding domains, and the disordered fragments on their own easily undergo LLPS. In contrast, LLPS for structured proteins has been observed infrequently. The contrasting phase behaviors can be explained by modeling disordered and structured proteins, respectively, as polymers and colloids. These physical models also provide better understanding on the regulation of droplet formation by cellular signals and dysregulation leading to diseases.

MLOs: disordered proteins as drivers and myriad cellular functions

Whereas the roles of most membrane-bound organelles have been established over a century, characterization of the molecular and physical features of membraneless organelles (MLOs; see Glossary) has started only in recent years. Already, they have been associated with a wide range of biological functions, including RNA processing, ribosome biogenesis, and sequestration of mRNA (for later translation), proteins (for signaling), and compacted chromatin (for gene silencing) [1-3]. It is now well accepted that MLOs form via liquid-liquid phase separation (LLPS; Box 1), whereby they emerge from the cytoplasm or nucleoplasm as protein-rich droplets [4-8]. Like their membrane-bound counterparts, each type of MLO contains many different species of macromolecules, but the MLO identity can often be associated with one or more “driver” proteins that are most responsible for the assembly and function of the organelle [9]. For example, fibrillarin (FIB1) and nucleophosmin (NPM1) are putatively driver proteins for the subcompartmentalized organization of the nucleolus, an organelle with a primary function in ribosome pre-assembly [10]. In a number of better-characterized cases, the driver proteins always have extended, intrinsically disordered regions (IDRs), which sometimes also have RNA-binding ability (Figure 1a); quite often though, one or more separate RNA-binding domains, such as RNA-recognition motifs (RRMs), are present as well [11] (Table 1). Many studies with deletion constructs have shown that the IDRs are sufficient and perhaps necessary for LLPS [10, 12-23]. It has been speculated that intrinsic disorder may promote LLPS by enabling multiple, weakly attractive interactions [12, 14, 17, 24, 25], but the mechanism largely remains unclear.

Box 1. Phases and determination of coexistence curves.

For simple molecules like water, the separation between two phases occurs when the molecules can achieve the same low free energy by adopting two distinct types of configurations, with different densities and different extents of intermolecular contacts (Figure Ia). The low free energy may result from high entropy in one phase (e.g., with high translational freedom for the molecules) and strong negative enthalpy in the other phase (e.g., with favorable intermolecular interactions). A homogeneous mix of the two phases, with a density falling in the gap between the two phases, would have a higher free energy and hence only be metastable relative to the coexistence of the two phases. The three common phases are gas, liquid, and solid (Figure Ib).

For two phases to coexist, they have to satisfy thermodynamic conditions, namely, equality of temperature T, pressure P, and chemical potential μ, since the two phases are in contact and are equally stable. The chemical potential itself is a function of

T and P, so the equality in μ between the phases defines a relation between T and P, i.e., a coexistence curve in the T – P plane that separates the two phases (Figure Ib). On one side of the coexistence curve, one phase has a lower chemical potential and hence is the stable phase; the opposite is true on the other side of the coexistence curve. Phase boundaries can continue indefinitely, or terminate at a certain point. In particular, the boundary between the gas and liquid phases starts at the “triple” point (where gas, liquid, and solid coexist) and ends at the critical point (where the distinction between gas and liquid vanishes). The density ρ is also a function of T and P, but typically experiences a discontinuity across a phase boundary. So on the ρ – T plane, a coexistence curve between two phases has two branches; the regions outside the two branches correspond to two stable phases whereas the region within the two branches is only metastable (Figure Ic).

The determination of the phase boundary requires the calculation of the free energy as a function of density for a given temperature. In the double-tangent construction, one plots f ≡ F/V, the Helmholtz free energy per unit volume, as a function of density. Phase separation occurs when f is tangent to a single line at two points (Figure Ia). The two points of tangency identify the respective densities of the two coexisting phases; the slope of the line gives the chemical potential (because μ = ∂f/ ∂ρ); and the negative of the intercept with the f axis yields the pressure (because f = μρ – P). Equivalently, the densities of the two coexisting phases can be identified by the Maxwell construction in the μ – ρ plane, involving a horizontal line that intersects the isotherm loop with equal areas above and below.

The principle outlined above applies equally to protein-solvent mixtures. The role of the solvent can be treated as modifying the interactions between protein molecules; the pressure relevant for phase equilibria is the osmotic pressure due to the protein rather than the total pressure of the protein mixture, and vanishes at zero protein concentration (as would be true also for an ideal gas at zero density). Accordingly proteins can also exist in three phases. The typical aqueous solutions of proteins correspond to the liquid phase; solutions of structured proteins at high concentrations can crystalize, creating the solid phase; lastly, solutions of disordered proteins often can easily separate into two phases, with protein-rich droplets coexisting with a protein-poor solution. This LLPS isreminiscent of liquid-gas coexistence for simple molecular fluids. Light scattering by the protein droplets (typically microns in size) gives the protein solution a cloudy appearance (in the same way as our eyes see clouds in the sky).

Figure I.

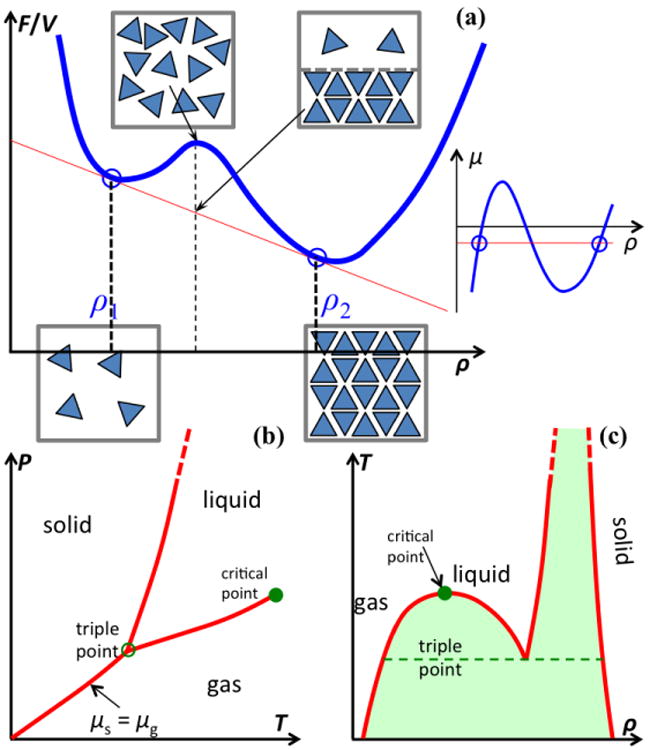
Phase boundaries. (a) Free energy per unit volume, f ≡ F/V, as a function of density, ρ. Two phases emerge when this function (blue curve) is tangent to a single line (in red) at two points (indicated by circles). The two bottom boxes illustrate molecular configurations in two stable phases; the top left box represents a metastable configuration, whereas the top right box represents the separation of two phases. On the far right is an illustration of the Maxwell construction in the μ – ρ plane, where the red line dissects the isotherm (blue curve) with equal areas. (b) Boundaries, on the T – P plane, between three common phases. (c) Coexistence curves on the ρ – T plane. Metastable regions between phases are shaded.

Figure 1.

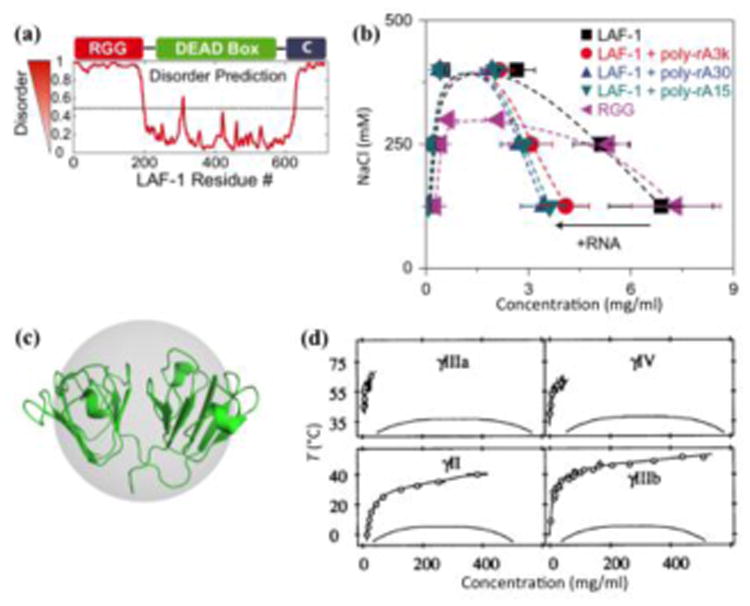
Disparate phase diagrams of disordered and structured proteins. (a) LAF-1 consists of two terminal disordered regions and a structured domain. The N-terminal disordered region (RGG) can bind RNA. Reproduced from ref [13]. (b) Liquid-liquid coexistence curves of LAF-1 and its disordered RGG region, in the presence and absence of polyadenylate RNA (poly-rA) of 15, 30, and 3000 nucleotides. A leftward arrow labeled with “+RNA” indicates the shift of the droplet branch in the presence of RNA. Reproduced from ref [29]. (c) Structure of γII-crystallin, embedded in a sphere to emphasize the globular shape. (d) Phase diagrams of 4 types of γ-crystallins, which are members of a highly homologous family of proteins. Symbols and the associated upper curves represent the fluid branch of the fluid-solid phase diagram, and lower curves are fits to liquid-liquid coexistence data from ref [36]. The fact that the liquid-liquid coexistence curve lies entirely below the fluid branch indicates metastability of the liquid-liquid phase separation relative to the fluid-solid phase separation (cf Box 3 Figure I). Reproduced from ref [78].

Table 1. Disordered regions and RNA-binding domains of proteins that drive the formation of membraneless organelles.

Driver proteina	IDRsb	Enriched AAs	RNA binding	MLOs	References
DDX3_CAEEL (708) D0PV95 LAF-1/DDX3	1-202 620-708	9-168: R/G 624-691: G	N-term IDR (RGG repeats)	P granule	[13, 29]
DDX4_HUMAN (724) Q9NQI0 DDX4	1-257	58-234: G	N-term IDR?	Nuage	[17]
FBRL_CAEEL (352) Q22053 FIB1/fibrillarin	1-122	8-114: DMA/G	N-term IDR? Fibrillarin domain (119-346)?	Nucleolus	[10]
FUS_HUMAN (526) P35637 FUS	1-286 356-526	1-165: Q/G/S/Y 166-267: G 371-526: R/G	RRM (287-365)	Stress granule Paraspeckle DNA damage site	[12, 14, 16, 47]
IF4F2_YEAST (914) P39936 eIF4G2	1-104 111-389 454-581 812-914	32-97: N 459-510: R/S 840-863: R/S	MIF4G (567-810)	Stress granule	[14]
LSM4_YEAST (187) P40070 LSm4	88-187		LSM (5-81)	P body	[14]
NPM_XENLA (299) P07222 NPM1/nucleophosmin	116-258	1-7: M 122-137: D/E 160-187: D/E	NPM1-C (246-294)	Nucleolus	[10, 24]
PTBP1_HUMAN (531) P26599 PTB/HNRNP I		316-323: A only	RRM (59-143) RRM (184-260) RRM (337-411) RRM (454-529)	Nuclear speckle	[5]
PUB1_YEAST (453) P32588 Pub1	1-64 211-330 410-453	8-16: Q 243-288: N 442-453: Q	RRM (77-146) RRM (164-234) RRM (343-407)	Stress granule	[14]
ROA1_HUMAN (372) P09651 HNRNPA1	177-372	195-372: G	RRM (16-85) RRM (107-176) C-term IDR	Stress granule Paraspeckle	[14, 15]
TADBP_HUMAN (414) Q13148 TDP-43	258-414	274-413: G	RRM (106-172) RRM (193-243)	Stress granule Paraspeckle	[15, 22]
TIA1_HUMAN (386) P31483 TIA-1	331-386		RRM (9-77) RRM (108-178) RRM (216-280)	Stress granule	[14, 60]
WHI3_YEAST (661) P34761 WHI3	1-102 196-314 324-580 608-661	247-277: Q	RRM (540-613)	Stress granule	[19]
ROA2_HUMAN (341) P22626-2 hnRNPA2	171-341	190-341: G	RRM (11-80) RRM (102-171)	Stress granule	[18, 23]
NPHN_HUMAN (1241) O60500 Nephrin	1095-1171			Nuclear body	[20]
Q9TXM1_CAEEL (862) Q9TXM1 MEG-3	1-382 395-606	S	Entire length	P granule	[21]
G5EBV6_CAEEL (693) G5EBV6 PGL-3	518-693		RGG repeats (634-693)	P granule	[32]

^aEach protein is identified by the UniProt entry name (with length given in parentheses) and accession number, as well as the common name.

^bDisorder was predicted by PONDR-VSL2 [77], with the threshold score set at 0.8 for reliability.

A hallmark of LLPS (in contrast to, e.g., protein aggregation) is thermodynamic reversibility, consistent with the liquid-like character of the droplet phase. That is, droplets can easily dissolve upon raising temperature or salt concentration and can reform when conditions are reverted. The reversibility comes because the two phases, droplet and dispersed, are in thermodynamic equilibrium (Box 1). Phase separation occurs when molecules can achieve the same low free energy by adopting two distinct types of configurations, with disparate concentrations and extents of intermolecular contacts [26]. The low free energy is achieved by distinct means in the two phases: e.g., high entropy (due to low concentration) in the dispersed phase but strong favorable (i.e., negative) enthalpy (from intermolecular contacts) in the droplet phase. Raising temperature or salt concentration leads to reduced stabilization of the droplet phase by intermolecular contacts. Beyond a critical point, the distinction between the two phases vanishes, and hence droplets dissolve. In general, the more strongly attractive the intermolecular interactions are, the wider the range of conditions for phase separation is (corresponding to raised critical temperature or critical salt concentration).

Synthetic polymers have long been known to undergo LLPS [27]. As with other thermodynamic properties of intrinsically disordered proteins (IDPs) [28], polymer models have been invoked to analyze phase boundaries. Specifically, the Flory-Huggins theory and its extensions (Box 2) have been used to fit experimental data or construct phase diagrams, providing explanations for the effects of salts, RNA, and sequence charge patterns on phase boundaries [17, 29-31]. Salt ions can screen charge-charge attraction between protein residues, and hence droplets dissolve above a critical salt concentration. Several studies have shown that the addition of RNA promoted LLPS, indicated by either reduced threshold protein concentrations for droplet formation or increased critical salt concentrations [5, 10, 14, 15, 21, 24, 32]. On the other hand, Zhang et al. [19] and Banerjee et al. [33] observed that RNA promoted LLPS only up to a point in RNA concentration, with further increase in RNA leading to LLPS suppression. In yet another variation, Wei et al. [29] recently found that, for LAF-1, a disordered driver protein for P granules [13], RNA had little effects on the threshold protein concentration and critical salt concentration, but significantly reduced the protein concentration in the droplet phase (Figure 1b). These conflicting reports were resolved in a recent theoretical study [34] (see below).

Box 2. Free energy calculation: lattice models and mean-field treatment.

Lattice models, where particles occupy sites on a defined lattice, have been very useful in illustrating basic physical ideas by simplifying free energy calculations [61]. For example, consider a lattice with each site occupied by one and only one molecule, of which there are two types, A and S, representing solute and solvent, respectively (Figure Ia top). Suppose that the numbers of A and S molecules are M_A and M_S, respectively, and the volume of each lattice site is ν₁. Then the volumes occupied by A and S molecule are V_A = M_Aν₁ and V_S = M_Sν₁, respectively, and the total number of sites is M = M_A + M_S and the total volume of the lattice is V = V_A + V_S = Mν₁. Relative to the unmixed case (where the A and S molecules each occupy their own lattices with respective volumes V_A and V_S), the lattice of a totally random A-S mixture has an increase, ΔS_mix, in entropy,

$$\mathrm{\Delta }{\mathrm{S}}_{\text{mix}}=M_{\mathrm{A}}{k}_{\mathrm{B}}ln(V/V_{\mathrm{A}})+M_{\mathrm{S}}{k}_{\mathrm{B}}ln(V/V_S)$$ [I]

similar to what happens upon the expansion of an ideal gas. Here k_B denotes the Boltzmann constant. In terms of the volume fraction ϕ = V_A/V of the solute, we have

$$\frac{\mathrm{\Delta }{S}_{\text{mix}}}{M{k}_{\mathrm{B}}}=-\varphi ln\varphi -(1-\varphi )ln(1-\varphi )$$ [II]

Note that the rate of entropy change with respect to ϕ is the greatest as ϕ → 0 or 1.

To obtain the free energy, we still need the average energy of the A-S mixture. To that end, we assume that each molecule has z neighbors, and the interaction with each neighbor makes an energetic contribution of ε_AA, ε_AS, or ε_SS, depending on the identities of the molecules in the pair. This “mean-field” treatment leads to the following average energy for the mixture:

$$U=\frac{1}{2}{M}_{\mathrm{A}}z[\varphi {\varepsilon }_{\text{AA}}+(1-\varphi ){\varepsilon }_{\text{AS}}]+\frac{1}{2}{M}_{\mathrm{S}}z[\varphi {\varepsilon }_{\text{AS}}+(1-\varphi ){\varepsilon }_{\text{SS}}]$$ [III]

The change in energy relative to the unmixed case is

$$\beta \mathrm{\Delta }U/M=\chi \varphi (1-\varphi )$$ [IV]

where β = 1/k_BT and

$$\chi =\frac{1}{2}\beta ({\varepsilon }_{\text{AA}}+{\varepsilon }_{\text{SS}}-2{\varepsilon }_{\text{AS}})z$$ [V]

which measures the magnitude of the effective attraction between two A molecules. Combining Equations [II] and [IV], we find the Helmholtz free energy as

$${\upsilon }_1\beta f=\varphi ln\varphi +(1-\varphi )ln(1-\varphi )+\chi \varphi (1-\varphi )+\varphi {\upsilon }_1\beta f_{\mathrm{A}}+(1-\varphi ){\upsilon }_1\beta f_{\mathrm{S}}$$ [VI]

where the second line represents the free energy of the unmixed case. The A-S mixture can separate into an A-poor phase and an A-rich phase (Figure Ib). The critical point, where the two branches of the coexistence curve coalesce, can be found by requiring both the second and third derivatives of f with respect to ϕ to vanish, yielding ${\varphi }_{\mathrm{c}}=\frac{1}{2}$ for the critical volume fraction and χ_c = 2 for the critical value of χ. Phase separation occurs only when χ ≥ χ_c (i.e., A-A attraction must exceed a critical strength); here the two branches of the coexistence curve are symmetric with respect to ϕ = ϕ_c.

Flory and Huggins [27] developed a lattice model for calculating the entropy for mixing polymer chains with solvent molecules. Each lattice site was occupied by either a monomer unit (like an A molecule) of a polymer or a solvent molecule; two adjacent monomer units along a polymer occupied neighboring sites (Figure Ia bottom). Suppose that there are N polymers, each with chain length L. The entropy of the polymer-solvent mixture can be calculated by counting the number of ways that the polymers can be placed in the lattice. For the first polymer, the first monomer unit has M choices for its site; the second unit has z choices; and all subsequent units each have z – 1 choices. However, the fact that no more than one monomer unit can occupy the same site reduces the number of choices; the reduction factors are (M – 1)/M for the second unit, (M – 2)/M for the third unit, etc. Therefore the total number of ways for placing the first polymer is

$$\begin{array}{c}{\upsilon }_1=M\frac{z(M-1)}{M}\frac{(z-1)(M-2)}{M}\cdots \frac{(z-1)(M-L+1)}{M}\\ \approx {\left(\frac{z-1}{M}\right)}^{L-1}\frac{M!}{(M-L)!}\end{array}$$ [VII]

Similarly, if n polymers have already been placed, occupying nL sites, the total number of ways for placing the (n + 1)th polymer is

$${\upsilon }_{n+1}={\left(\frac{z-1}{M}\right)}^{L-1}\frac{(M-nL)!}{[M-(n+1)L]!}$$ [VIII]

The total number of ways for placing N polymers on a lattice with M sites is then

$$\Omega (N,M)=\frac{1}{!N}\prod _{n=1}^N{\upsilon }_n=\frac{1}{N!}{\left(\frac{z-1}{M}\right)}^{N(L-1)}\frac{M!}{(M-NL)!}$$ [IX]

where a factor 1/N! has been inserted to account for the indistinguishability of the polymers. Finally the mixing entropy is

$$\frac{\mathrm{\Delta }{S}_{\text{mix}}}{k_{\mathrm{B}}}=ln\frac{\mathrm{\Omega }(N,M)}{\mathrm{\Omega }(N,Nl)\mathrm{\Omega }(0,M-NL)}$$ [X]

or

$$\frac{\mathrm{\Delta }{S}_{\text{mix}}}{M{k}_{\mathrm{B}}}=-\frac{\varphi }{L}ln\varphi -(1-\varphi )ln(1-\varphi )$$ [XI]

where ϕ = NL/M is the volume fraction of the polymers. Notice that the last expression correctly reduces to Equation [II] when L = 1. At a high degree of polymerization (i.e., L ≫ 1), the rate of entropy change with respect to ϕ near ϕ = 0 is significantly less than that for the A-S mixture, because the polymers, due to chain connectivity between monomer units, are significantly less mixed with the solvent. Combined with the mean-field treatment of the average energy (see Equation [VI]), the free energy of the polymer-solvent mixture is

$${\upsilon }_1\beta f=\frac{\varphi }{L}ln\varphi +(1-\varphi )ln(1-\varphi )+\chi \varphi (1-\varphi )+\varphi {\upsilon }_1\beta f_{\mathrm{p}}+(1-\varphi ){\upsilon }_1\beta f_{\mathrm{s}}$$ [XII]

where χ now represents the magnitude of the monomer-monomer attraction, and the second line represents the free energy of the unmixed case. Effects beyond the mean-field treatment, including monomer density fluctuation and three-body or sequence-dependent interaction, have also been treated theoretically [31, 62].

For the polymer solution, the coexistence curve between the polymer-poor and polymer-rich phases becomes asymmetric (Figure Ib), due to the reduced mixing entropy at ϕ near 0 (relative to the counterpart at ϕ near 1). The critical point is at ϕ_c = 1/(1 + √L) and ${\chi }_{\mathrm{c}}=\frac{1}{2}{(1+1/\sqrt{L})}^2$. As the polymer chain length increases from 1 to ∞, the critical volume fraction decreases from 0.5 to 0 while χ_c decreases from 2 to 0.5 (the latter change corresponding to a 4-fold increase in the critical temperature T_c). So for long polymer chains, LLPS occurs at low concentrations and over a wide range of temperatures.

The latter is a qualitatively important result for polymer solutions. However, the lattice model underlying the Flory-Huggins theory provides only a very crude account of excluded-volume effects (in particular, resulting in unphysically high ϕ values in the polymer-rich phase shown in Figure Ib). Moreover, the mean-field treatment yields only a rough estimate for the effects of solute-solute attraction. Box 3 and Box 4 present much more realistic calculations of these effects for colloids and polymers, respectively.

The Flory-Huggins theory predicts only upper critical solution temperature (UCST), a situation where T_c is the upper bound of temperatures for phase separation. Polymers are also known to have lower critical solution temperature (LCST), in which case T_c is the lower bound of temperatures where LLPS occurs. By making k_BT_χ dependent on T and/or ϕ, LCST can be predicted. LCST has been observed on synthetic peptides and on some proteins [63-66]; better physical understanding of such observations will be desirable.

Figure I.

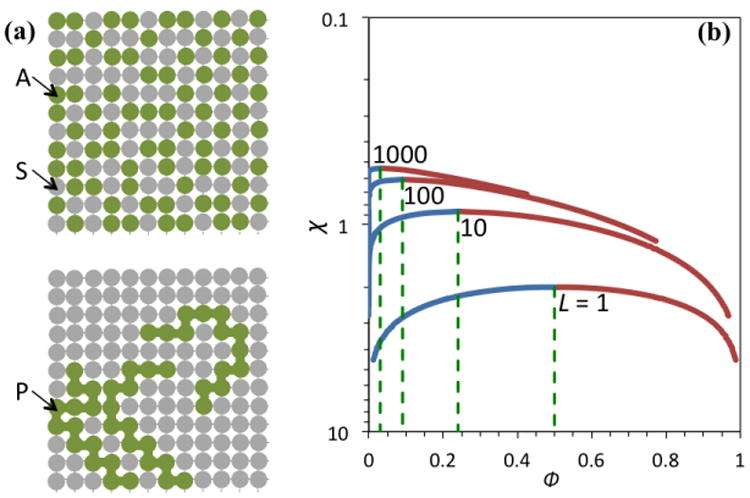
Lattice models and their liquid-liquid phase separation. (a) Lattice models for a mixture of A molecules (top) or polymers (bottom) with S molecules. Each A or S molecule as well as each monomer of the polymers occupies one and only one site on the lattice. (b) Coexistence curves for polymers chains of various lengths. The polymer-poor and polymer-rich branches are in blue and cayenne, respectively. The L = 1 case is equivalent to the A-S mixture.

Wei et al. [29] noted that the LAF-1 concentrations in the dissolved and droplet phases, approximately 0.1 and 5 mg/ml, respectively, are orders of magnitude lower than the counterparts of structured proteins including lysozyme [35] and γ-crystallins (Figure 1c,d) [36]. This contrast buttresses the notion that LLPS occurs much more easily for disordered proteins than for structured proteins, which is a focus of the present review.

LLPS of structured proteins: metastability relative to fluid-solid transition

LLPS was actually first observed on structured proteins, as a metastable step on the way to crystallization [37, 38]. The metastability (Figure 1d) can be attributed to the small ratio between the range of attractive interactions and diameter of proteins, as demonstrated on spherical models of colloidal particles (Box 3). Kinetically, the metastable droplets rich in proteins can facilitate nucleation and thereby accelerate crystallization [39-42].

Box 3. Free energy calculations: perturbation theory for colloids.

Both simple molecular fluids and colloidal suspensions have often been modeled by an inter-particle interaction comprising a hard-core repulsion and a short-range attraction. The square-well potential is an example of such an interaction:

$$u(r)=\{\begin{array}{cc}\infty ,& r<\sigma \\ -\varepsilon ,& \sigma <x<\sigma +\delta \\ 0,& r>\sigma +\delta \end{array}$$ [I]

where r is the inter-particle distance, σ is the diameter of hard core, and δ and ε are the width and depth, respectively, of the attraction. Without the attraction, the particles are hard spheres, for which an accurate expression for the free energy per particle is [67]

$$\frac{\beta F_{\text{HS}}}{N}=ln(\rho {\upsilon }_Q)-1+\frac{\varphi (4-3\varphi )}{{(1-\varphi )}^2}$$ [II]

where ν_Q is an arbitrary constant with the dimension of volume, and ϕ = ρν_p, with ν_p = πσ³/6 denoting the volume of each particle, is the volume fraction of the particles. The first two terms of Equation [II] constitute the “ideal” part of the free energy whereas the last term is the excess part due to hard-core repulsion. The effect of the attraction can be obtained by a perturbation theory [68]. To the first order, the theory predicts

$$\frac{\beta F}{N}=\frac{\beta F_{\text{HS}}}{N}-\frac{1}{2}\beta \varepsilon \rho {\int }_{\rho }^{\sigma +\rho }{g}_{\text{HS}}(r)4\pi r^{2}dr$$ [III]

where g_HS(r) is the radial distribution function, representing the relative density of other hard spheres around a tagged hard sphere. On a per unit volume basis, we have [35]

$${\upsilon }_{\mathrm{p}}\beta f=\varphi ln\left(\frac{\varphi {\upsilon }_{\mathrm{Q}}}{{\upsilon }_{\mathrm{p}}}\right)-\varphi +\frac{{\varphi }^2(4-3\varphi )}{{(1-\varphi )}^2}-\chi {\varphi }^2$$ [IV]

The parameter

$$\chi =12\beta \varepsilon {\int }_1^{1+\delta /\sigma }{g}_{\text{HS}}(x\sigma )x^2\mathit{\text{dx}}\equiv 12\beta \varepsilon I(\varphi ;\delta /\sigma )$$ [V]

as in Box I, measures the strength of inter-particle attraction. The integral I(ϕ; δ/σ) [69] can be fitted to a quadratic function b₀ + b₁ϕ + b₂ϕ², and the coefficients b₀, b₁, and b₂ are 0.178, 0.258, and 1.01, respectively, at δ/σ = 0.15 for ϕ < 0.49. The corresponding expression for the chemical potential is

$$\beta \mu =ln\left(\frac{\varphi {\upsilon }_{\mathrm{Q}}}{{\upsilon }_{\mathrm{p}}}\right)+\frac{\varphi (8-9\varphi +9{\varphi }^2)}{{(1-\varphi )}^3}-24\beta \varepsilon \varphi (b_0+3b_1\varphi /2+2b_2{\varphi }^2)$$ [VI]

Equation [IV] leads to LLPS (Figure I). The critical point would be at ϕ_c = 0.13 and χ_c = 10.6 if I(ϕ; δ/σ) (and hence χ) were independent of ϕ (as would be in a mean-field treatment) [35]. Note that a ϕ-independent −χ can be viewed as the lowest order coefficient, (B₂ – B_2;HS)/ν_p, of a “perturbative” virial expansion of ν_pβf, where B₂ is the second virial coefficient and B_2;HS = 4ν_p is the counterpart for the hard-sphere reference. The preceding χ_c value corresponds to −B₂(T_c)/ν_p = 6.6; a near constancy of −B₂(T_c)/ν_p around 6 was first proposed by Vliegenthart and Lekkerkerker [70]. It is apparent from Equation [V] that the critical temperature increases with increasing magnitude and range of the attraction. For example, as δ/σ increases from 0.05 to 0.15, k_BT_c/ε increases from 0.286 to 0.670 when the ϕ dependence of χ is accounted for. Hard-sphere liquids, corresponding to χ = 0, do not have LLPS.

Hard spheres do undergo a fluid-solid phase transition, forming crystals with a face-centered cubic (FCC) unit cell. The free energy in the solid phase can be estimated from a free-volume approach [71] as

$$\frac{\beta F_{\text{HS}}^{\mathrm{S}}}{N}=ln\left(\frac{{\upsilon }_{\mathrm{Q}}}{{\upsilon }_{\mathrm{F}}}\right)$$ [VII]

where a subscript “s” indicates the solid phase, and

$${\upsilon }_{\mathrm{F}}=\frac{8}{\sqrt{2}}{(R_1-\sigma )}^3$$ [VIII]

is the volume accessible to a hard sphere in the FCC lattice. In the last expression, R₁ denotes the distance between nearest neighbors, which is related to the density of the crystal via $1/\rho =\frac{1}{\sqrt{2}}{R}_1^3$. With Equations [II] and [IV] for the free energies of the fluid and solid, the coexistence volume fractions are found to be 0.49 and 0.56, respectively, for the two phases.

The effect of the inter-particle attraction in the solid phase can also be obtained by a perturbation theory, similar to Equation [III] [72]. After fitting the integral of the radial distribution function of the hard-sphere FCC solid [73] to a quadratic function of ϕ (cf. Equation [V]), the free energy is

$$\frac{\beta F^{\mathrm{S}}}{N}=\frac{\beta F_{\text{HS}}^{\mathrm{S}}}{N}-12\beta \varepsilon \varphi [c_0-c_1{(\varphi -{\varphi }_0)}^2]$$ [IX]

where the parameters c₀, c₁, and ϕ₀ are 0.767, 12.8, and 0.643, respectively, at δ/σ = 0.15 for 0.52 ≤ ϕ ≤ 0.73. Using Equations [III] and [IX], the coexistence curve between the fluid and solid phases can be determined (Figure I). Note that the coexistence curve for LLPS falls entirely in the metastable region for fluid-solid phase separation. Therefore for colloids and structured proteins that can form crystals, the thermodynamically stable coexistence is between a dissolved phase and a crystalline phase, not between two liquid phases. Whereas the ranges of attraction are comparable for macromolecular particles and simple molecules, the much smaller hard-core diameters of the latter increase the order of magnitude of the ratio δ/σ from 0.1 to 1. For such higher δ/σ, the coexistence curve for LLPS emerges above the fluid branch of the fluid-solid coexistence curve [39, 72], and hence simple molecules have three stable phases (i.e., gas, liquid, and solid).

Under conditions for slow crystallization, the LLPS coexistence curves of several structured proteins have been determined, including arachin [37], lysozyme [35], γ-crystallins (Figure 1d) [36, 43], with critical protein concentrations ranged from 180 to 276 mg/ml. The critical concentrations of immunoglobulin G (IgG) antibodies were somewhat lower, at approximately 90 mg/ml, which was attributed to the nonspherical shape of the antibody molecules [44]. Recently a peptide oligomer was found to phase separate with an even lower critical concentration of 50 mg/ml; loose packing within the oligomer was suggested as an explanation [45].

The high concentrations required pose one difficulty for observing LLPS of structured proteins. Structured proteins also tend to have low critical temperatures (T_c). When T_c is below the freezing point of the protein solution, it is not possible to directly observe LLPS. Crowding agents like polyethylene glycol (PEG) have been found to promote LLPS, raising T_c to above the freezing point [43, 45]. By extrapolating, one can deduce the coexistence curve for the protein in the absence of crowding.

Transient bonding networks: common organizational principle for protein droplets

So far there has been very little crosstalk between the growing community of scientists working on LLPS of MLO-driving disordered proteins and the more established counterpart on LLPS of structured proteins. Connecting the research in the two communities will help us establish a common physical basis for phase separation of proteins, exchange knowledge between the two communities, and identify what are unique about IDPs and about structured proteins.

Droplet formation requires a sufficient extent of attraction between protein molecules to provide stability. On the other hand, to be in a liquid phase, individual interactions between two molecules must be easily breakable and hence relatively weak. Therefore, by necessity, proteins, whether structured or disordered, in the droplet phase form weakly attractive interactions with multiple partners, resulting in transient bonding networks (Figure 2a) [46].

Figure 2.

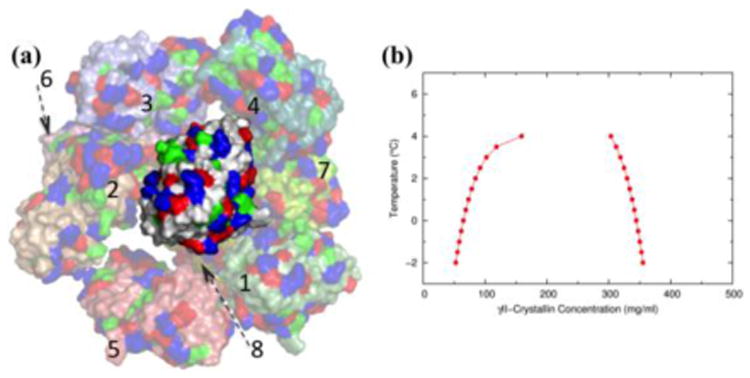
Atomistic view of liquid-liquid phase separation (LLPS) for γII-crystallin. (a) Snapshot of a transient bonding network. The γII-crystallin molecule at the center presently is in contact with four other molecules (numbered 1-4); four molecules (numbered 5-8) further into the background and in contact with the bonding partners of the central molecule are also shown, but bonding partners of the central molecule in the foreground are not displayed. Molecules are displayed as surface, with acidic (Asp/Glu), basic (Arg/Lys), and hydrophobic (Leu/Ile/Val/Met/Phe) residues in blue, red, and green respectively. (b) Calculated LLPS coexistence curve for γII-crystallin. Reproduced from ref [46].

For rigid structured proteins, it has become possible to use an all-atom representation in simulating phase separation and calculating coexistence curves (Figure 2) [46]. These simulations provide an atomistic view of the bonding networks in protein droplets. With atomistic calculations of coexistence curves, it is possible to test whether ideas such as nonspherical shape and loose packing are correct in explaining low critical concentrations for some structured proteins. Moreover, even highly homologous γ-crystallins can differ in T_c in excess of 30 °C (Figure 1d). The calculations afford an opportunity to relate changes in phase behavior to changes in amino acid sequence. Such relations may provide valuable insight for understanding how mutations (e.g., ones associated with diseases) and posttranslational modifications affect LLPS of MLO-driving proteins (see below).

In addition to changes in amino acid sequence, the presence of other macromolecules can also influence the bonding networks of droplet-forming proteins and hence their phase behaviors. As noted, PEG has been used to raise T_c for structured proteins [43, 45]. Similarly, crowding agents such as PEG, Ficoll, and dextran have been found to promote LLPS of MLO-driving proteins [14, 15, 47].

Crowders promote LLPS by preferentially partitioning in the dispersed phase, and therefore displacing proteins into the droplet phase to strengthen bonding networks there [34]. A macromolecular component, e.g., another protein or RNA, starts to partition in the droplet phase if it has attraction for the droplet-forming protein. When the macromolecule-protein attraction is mild, the presence of the macromolecule in the droplet phase serves to disrupt the bonding networks of the protein and thereby suppress LLPS. Such an effect was observed for human and bovine serum albumin, respectively, on the phase separation of an IgG antibody [44] and hnRNPA1 [48]. On the other hand, when the macromolecule-protein attraction is stronger than the protein-protein attraction, the macromolecule can strengthen the protein bonding networks and thus promote LLPS. This is likely the reason for the effects of RNA in several studies [5, 10, 14, 15, 21, 24, 32]. However, the promotional effects persist only up to a certain RNA-to-protein molar ratio, beyond which RNA displaces too much of the protein from the droplet phase and thereby again disrupts the bonding networks. Such dual effects of RNA have been observed by Zhang et al. [19] and Banerjee et al. [33].

It should be noted that MLO-driving proteins often contain both IDRs and structured domains (including those binding RNA; see Table 1). Several studies have shown that IDRs and structured domains can act synergistically in promoting phase separation [24, 48-50].

Physical basis for contrasting phase behaviors of disordered and structured proteins

A common physical basis notwithstanding, structured and disordered proteins nevertheless exhibit very different phase behaviors, in terms of high T_c and low critical concentrations for the latter proteins and the general ease in observing LLPS for them. Whereas structured proteins can form crystals and LLPS for them is often metastable relative to the fluid-solid transition, disordered proteins cannot form crystals and hence do not have a similar fluid-solid transition for competition [26]. Disordered proteins can form solid-like condensates such as gels and fibrils.

The contrast in T_c and critical concentration between structured and disordered proteins is reminiscent of the differing phase behaviors of colloid particles (Box 3) and polymer chains (Box 4). We represent colloid or polymer concentration by the volume fraction ϕ. Relative to a colloid that models globular proteins, a 100-residue polymer, which could serve as a model for IDPs, has a T_c that is 4.2 times higher and a critical concentration (ϕ_c) that is 5.1 times lower. How can we understand these differences?

Box 4. Free energy calculations: perturbation theory for polymers.

A different type of perturbation theory has been developed for polymer solutions, with unchained monomers as reference and their bonding as perturbation [74]. This idea has been improved, with short blocks as reference and inter-block bonding as perturbation [75, 76]:

$${\mu }^{\text{ex}}(L)=(L/l_{\mathrm{r}}){\mu }^{\text{ex}}(l_{\mathrm{r}})+(L/l_{\mathrm{r}}-1){\mu }^{\text{bond}}(l_{\mathrm{r}})$$ [I]

where L (or l_r) is the chain length of the actual polymers (or reference blocks), μ^ex(l) represents the excess chemical potential of pure l-mers at the same monomer density as the L-mers, and μ^bond(l_r) represents the free energy for forming a bond between two l_r-mer blocks. A further approximation is

$${\mu }^{\text{bond}}(l_{\mathrm{r}})={\mu }^{\text{ex}}(2l_{\mathrm{r}})-2{\mu }^{\text{ex}}(l_{\mathrm{r}})$$ [II]

since the obvious difference between one 2l_r-mer and two l_r-mers is a single bond. Therefore

$$\frac{{\mu }^{\text{ex}}(L)}{L}=\frac{{\upsilon }^{\text{ex}}(l_{\mathrm{r}})}{l_{\mathrm{r}}}+(1-l_{\mathrm{r}}/L)\frac{{\mu }^{\text{ex}}(2l_{\mathrm{r}})-2{\mu }^{\text{ex}}(l_{\mathrm{r}})}{l_{\mathrm{r}}}$$ [III]

which has been written on a per monomer basis. Equation [III] works well whether the polymers are purely repulsive or also have an attractive component. Escobedo and de Pablo [76] recommended using l_r = 4.

We now specialize to polymers modeled as fully flexible chains of tangent spheres interacting via a square-well potential (Box 3 Equation [I], but with the hard-core diameter of the monomers denoted here by d). To gain deeper insight, let us decompose μ^ex(L) into a term μ^rep(L), due to hard-core repulsion, and a term μ^att(L), due to attraction:

$${\mu }^{\text{ex}}(L)={\mu }^{\text{rep}}(L)+{\mu }^{\text{att}}(L)$$ [VI]

The repulsion term, according to Equation [III], can be written as

$$\frac{{\mu }^{\text{rep}}(L)}{L}=\frac{{\mu }^{\text{rep}}(l_{\mathrm{r}})}{l_{\mathrm{r}}}+(1-l_{\mathrm{r}}/L)\frac{{\mu }^{\text{rep}}(2l_r)-2{\mu }^{\text{rep}}(l_r)}{l_r}$$ [V]

Escobedo and de Pablo [76] fitted their Monte Carlo simulations data for μ^rep(l)/l at l = l_r and l = 2l_r to rational functions of the volume fraction ϕ. Note that μ^rep(l) is the work required to insert an l-mer into a solution of repulsive l-mers, and is an increasing function of ϕ. Because of the chain connectivity between the two l_r-mer blocks in the 2l_r-mer, μ^rep(2l_r) is always less than 2μ^rep(l_r), and the deficit grows with increasing ϕ. Consequently the rise of μ^rep(L)/L with increasing ϕ becomes moderated at larger L.

The attraction term can be similarly written as

$$\frac{{\mu }^{\text{att}}(L)}{L}=\frac{{\mu }^{\text{att}}(l_{\mathrm{r}})}{l_{\mathrm{r}}}+(1-l_{\mathrm{r}}/L)\frac{{\mu }^{\text{att}}(2l_{\mathrm{r}})-2{\mu }^{\text{att}}(l_{\mathrm{r}})}{l_{\mathrm{r}}}$$ [VI]

The simulation results of Escobedo and de Pablo [76] for μ^att(l_r)/l_r and [μ^att(2l_r) – 2μ^arr(l_r)]/l_r at δ/d = 0.5 are, up to ϕ = 0.35, approximated well by

$$\frac{{\mu }^{\text{att}}(l_{\mathrm{r}})}{l_{\mathrm{r}}}=-24\varepsilon \varphi (b_{10}+b_{10}\varphi )$$ [VII]

$$\frac{{\mu }^{\text{att}}(2l_{\mathrm{r}})-2{\mu }^{\text{att}}(l_{\mathrm{r}})}{l_{\mathrm{r}}}=24\varepsilon \varphi (b_{20}+b_{21}\varphi +b_{22}{\varphi }^2)$$ [VIII]

where the coefficients b₁₀, b₁₁, b₂₀, b₂₁, and b₂₂ are 0.450, 1.70, 0.225, 0.205, and -1.60, respectively. The LLPS coexistence curves for polymers with lengths at 10, 50, 100, and 200 are shown in Figure I. Compared to the prediction of the Flory-Huggins theory (Box 2 Figure I), the coexistence curves are further skewed toward ϕ = 0. More importantly, the volume fractions of polymers in the droplet phase now fall into the physically accessible range.

At phase equilibrium, the dispersed and droplet phases must have equal chemical potentials. The chemical potential can be decomposed,

$$\mu ={\mu }^{\text{id}}+{\mu }^{\text{rep}}+{\mu }^{\text{att}}$$ [1]

The first term on the right-hand side is the ideal part, which is the chemical potential if intermolecular interactions were totally absent, given by

$${\mu }^{\text{id}}=k_{B}Tln\varphi$$ [2]

The second term, μ^rep, is the contribution from steric repulsion between colloids or polymers; this would be the only contribution from intermolecular interactions if the molecules were purely repulsive toward each other. This term is positive and an increasing function of ϕ, reflecting the difficulty in inserting a molecule into an already crowded solution. The third term, μ^att, is the contribution from intermolecular interactions beyond steric repulsion, and does not have to be purely enthalpic. The μ^id and μ^rep terms favor the dispersed phase, whereas μ^att favors the droplet phase and must become sufficiently negative at increasing ϕ for LLPS to occur. (Note that, when crowders are present, they preferentially partition into the dispersed phase and raise μ^rep there; then μ^att does not need to be as negative as in the absence of crowders.) In general T_c increases with increasing magnitude of μ^att.

In Figure 3, Key Figure we compare the component and total chemical potentials of the colloid and 100-residue polymer. Each monomer unit of the polymer can have attractive interactions with all other monomers (in the same chain or in other chains), in a way similar to attractive interactions between colloid particles. Therefore μ^att for the polymer accumulates over the monomer units, leading to a much higher T_c than that of the colloid. Due to the same reason, the chemical potential results for the polymer are shown in Figure 3b on a per monomer basis (i.e., divided by the chain length L), and at a temperature that is 4 times higher than for the colloid. For the colloid, μ^id has a rapid rise near ϕ = 0, and subsequently, μ^rep takes off; μ^att catches up with μ^id + μ^rep only at a high ϕ. That explains why the concentrations of colloids (and, by inference, globular proteins) in the droplet phase are high. The concentrations of colloids in the dispersed phase cannot be too low either, since that would make the dispersed phase too stable (due to a strongly favorable μ^id) compared with the droplet phase.

Figure 3. Key Figure.

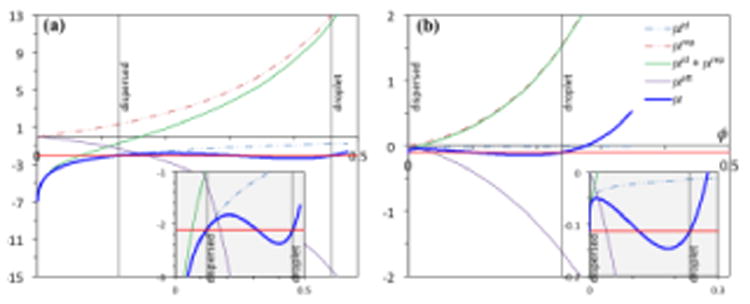
Decomposition of the chemical potentials of colloid and polymer models. (a) The chemical potential (μ) of a colloid suspension is given by Box 3 Equation [VI], with the ideal (μ^id; assuming ν_Q = ν_p), repulsive (μ^rep), and attractive (μ^rep) components, respectively, represented by the three terms on the right-hand side. Results for δ/σ = 0.15 and k_BT/ε = 0.6 are shown. (b) The chemical potential of a polymer solution is shown on a per monomer basis (L = 100). μ^id/L = (1/L) ln ϕ; μ^rep/L is given by Box 4 Equation [V]; and μ^att/L is given by Box 4 Equations [VI] – [VIII] (for δ/d = 0.5 and k_BT/ε = 2.4). Abscissa: volume fraction ϕ; ordinate: chemical potentials and their components in units of k_BT. Horizontal red lines dissect the μ versus ϕ curves (blue) with equal areas; ϕ values for the dispersed and droplet phases are indicated by vertical black lines; the ϕ value for the dispersed phase of the polymer solution is so small that a vertical line cannot be distinguished from the ordinate axis. A view of the dissection, enlarged in the vertical direction, is shown as insets (gray shading).

In contrast, for the polymer, on a per monomer basis, μ^id/L is small, and the rise of μ^rep/L is much less rapid than μ^rep for a colloid particle (the two would be the same were the monomer units not connected into a chain). Therefore μ^att/L can catch up with μ^id/L + μ^rep/L at relatively low ϕ. That explains why the concentrations of polymers (and, by inference, IDPs) in the droplet phase are low.

The polymer model also predicts a much higher T_c than the colloid model (see Box 3 Figure I and Box 4 Figure I). This difference is related to the fact that each monomer unit in a polymer chain has the freedom to interact with all the monomer units in any other chain. Therefore the flexible polymer chains, as well as IDPs, can easily form multivalent interactions.

Figure I.

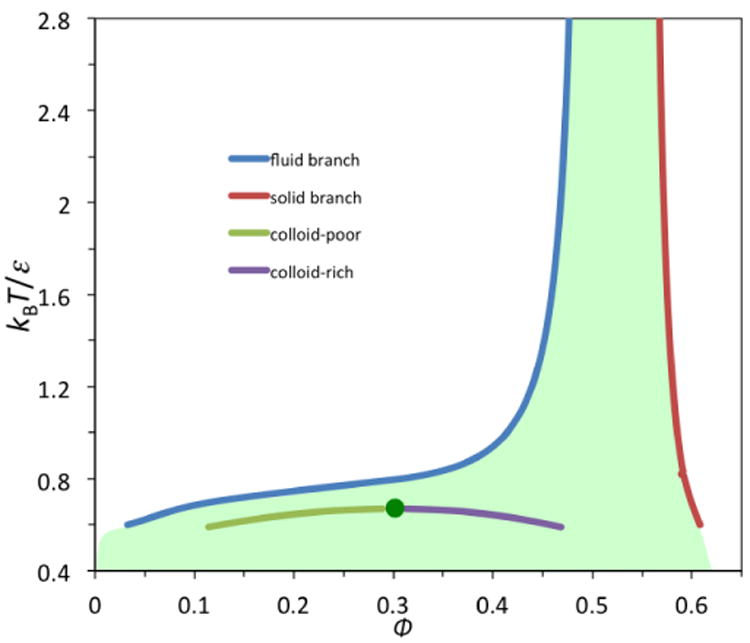
Coexistence curves for colloid particles modeled by a square-well potential. Note that the coexistence curve for liquid-liquid phase separation (LLPS) falls inside the metastable region (shaded) for fluid-solid phase separation. The critical point for LLPS is indicated by a green circle.

Figure I.

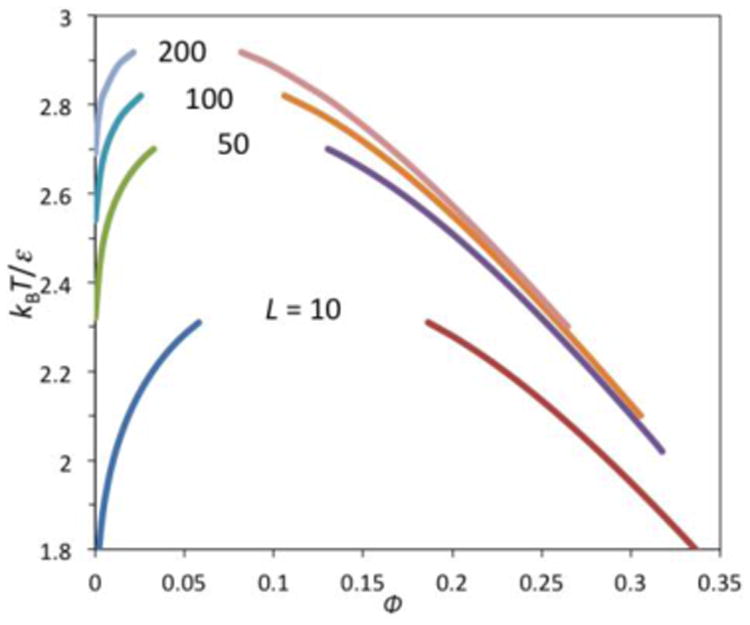
Coexistence curves for liquid-liquid phase separation of polymers, modeled as flexible chains of tangent square-well spheres.

Regulation of MLO formation by cellular signals

The foregoing presentation makes it easy to explain how various cellular signals can regulate protein droplet formation. Environmental stress can be transmitted into changes in intracellular osmotic pressure or temperature [17, 51], and these basic physical changes can bring proteins into or out of LLPS conditions. Effects of varying salt concentrations and pH on LLPS, by modulating the magnitude of μ^att, have been amply demonstrated in in vitro studies, and are likely exploited in vivo. Interestingly, cells may also perturb μ^rep, by changing the level of macromolecular crowding through an increase or decrease in cell size [52].

LLPS occurs below the critical point but only when protein concentrations are above a threshold. Therefore intracellular protein concentration provides another means for regulating MLO formation [15]. RNA in particular can promote phase separation, but only within a certain range, and hence RNA expression level can also control whether MLOs form. Molecules that compete for RNA binding with droplet-forming proteins can limit the amount of RNA that enter into droplets and thus provide yet another layer of regulation [21, 32].

Posttranslational modifications (PTMs) regulate molecular structural organizations at all levels, and MLOs are no exception. The IDRs of droplet-forming proteins provide ready accessibility for PTMs, and the PTMs can promote or suppress LLPS by enabling or disrupting intermolecular interactions. For example, Tyr phosphorylations of the nephrin C-terminal IDR enable multivalent binding with Nck SH2 domains, and thereby promote LLPS of the Nck/N-WASP system [5]. On the other hand, Ser/Thr phosphorylation and phosphomimetic (Ser/Thr to Glu) mutation of the FUS N-terminal IDR disrupt transient intermolecular interactions and suppress LLPS [53]. Similarly, Ser phosphorylation of the MEG group of IDPs promotes P granule disassembly whereas dephosphorylation promotes granule assembly [54]. Arg methylations of both the hnRNPA2 C-terminal IDR [23] and the DDX4 N-terminal IDR [17] were found to suppress LLPS. An alternative splicing of the DDX4 N-terminal IDR also abrogated LLPS [17].

Droplets of structured proteins can nucleate crystal growth and have been associated with the genesis of protein condensation diseases such as cataract [38, 55, 56] and sickle cell anemia [57, 58]. Similarly, LLPS of disordered proteins can facilitate further transition to solid-like condensates such as gels and fibrils, either as normal cellular response [59] or for pathogenesis [15, 22, 23, 47, 53, 60]. Disease-associated mutations may either promote LLPS or accelerate liquid-to-solid transition.

Concluding remarks

The physical basis for the LLPS of proteins, both structured and disordered, is becoming clear. Proteins are driven into the dispersed and droplet phases by different forces: translational freedom of the individual molecules and steric repulsion between them for the dispersed phase whereas intermolecular attraction for the droplet phase. It is important to recognize that the phase equilibrium is determined by the balance of steric (or crowding) and attractive interactions. Macromolecular crowders, by preferentially partitioning into the dispersed phase, can have significant effects on LLPS, as demonstrated in computational and in vitro experimental studies, and very likely on in vivo MLO formation. Other macromolecules, in particular RNA, can partition into the droplet phase, thereby strengthening or disrupting transient bonding networks there and affecting the phase equilibrium.

Macromolecular crowders and RNA are respective examples of species that are excluded from and recruited into protein droplets. MLOs contain multiple components and are surrounded by many more non-component species. Moreover, different types of MLOs may be immiscible and may even organize into core-shell structures (droplet inside droplet) [10]. A fruitful direction would be to characterize the differential partitioning of various species and their effects on MLO assembly and disassembly (see Outstanding Questions).

Outstanding Questions.

• Disordered proteins drive the formation of membraneless organelles (MLOs), but many other components help regulate the assembly/disassembly and functions of MLOs. The recruitment of certain macromolecular species into MLOs and the exclusion of many others, and the consequence on MLO assembly/disassembly are only starting to be understood in terms of intermolecular interactions. Polymer crowding agents and RNA serve as extreme examples, but the effects of the differential partitioning of many more species, their mutual influences, and their individual and collective effects on MLO structure and function are yet to be well characterized.

• Transient bonding networks appear to be a general mechanism for the internal structural organization of MLOs. Expanding the knowledge in this area is potentially a new frontier for structural biology and computational biophysics.

• Liquid-liquid coexistence curves have been determined experimentally for some proteins and more should be done. Even more urgently, calculations of coexistence curves, based on realistic modeling of proteins and rigorous implementation of thermodynamic principles, can bring tremendous physical insights to, in particular, the effects of posttranslational modifications and disease-associated mutations, but will require solutions to technical challenges.

• Pathogenesis of MLO proteins often involves transition to solid-like condensates. Physical models are needed to gain a foundational understanding of this process.

Our knowledge about transient bonding networks inside protein droplets is still scant. Here computation can well complement structural biology techniques. For structured proteins, computation at the all-atom level is already feasible [46], but for disordered proteins, conformational flexibility has limited computation to a coarsegrained level [23]. For subtle effects of PTMs and disease-causing mutations, an all-atom representation may be necessary for quantitative prediction. All-atom computation for IDP LLPS will be a great challenge for the future.

Transitions of IDP droplets into solid-like condensates (e.g., gels and fibrils) are implicated both in normal cellular responses and in diseases. A general physical model for such transitions is yet to be developed, in part because they often appear irreversible. Once again one may have to go to the colloid and polymer literature for some guidance.

Highlights.

• Phase separation leading to protein droplets and membraneless organelles (MLOs) is determined by the balance among translational entropy of protein molecules and steric and attractive interactions between molecules.

• Colloids and polymers serve as good models for understanding the different phase behaviors of structured and disordered proteins. Disordered proteins are characterized by both extensive attraction and low energetic cost from steric repulsion, contributing to easy observation of phase separation.

• Protein molecules form transient bonding networks in the droplet phase. The networks can be strengthened or disrupted by posttranslational modifications and disease-associated mutations and by other macromolecular species such as RNA, leading to assembly and disassembly of MLOs.

Glossary

Coexistence curve

a relation between two thermodynamic properties, such as temperature and pressure or temperature and concentration, that is followed when two phases are at equilibrium. Also known as phase boundary.

Critical point

a unique thermodynamic condition at which distinction between two fluid phases (gas and liquid for simple molecular fluids or dispersed and droplet for macromolecular solutions) vanishes. In particular, the concentrations of the two phases become identical and are known as the critical concentration. Phase separation occurs only on one side of the critical point, e.g., below the critical temperature.

IDR

intrinsically disordered region

IDP

intrinsically disordered protein

LLPS

liquid-liquid phase separation

MLO

membraneless organelle

PTM

posttranslational modification

RRM

RNA-recognition motif, an amino-acid sequence motif that consists of approximately 90 residues and forms a structural fold with a four-stranded β-sheet packed against two α-helices