Lung Mass Density Analysis using Deep Neural Network and Lung Ultrasound Surface Wave Elastography

Abstract

Lung mass density is directly associated with lung pathology. Computed Tomography (CT) evaluates lung pathology using the Hounsfield unit (HU) but not lung density directly. We have developed a lung ultrasound surface wave elastography (LUSWE) technique to measure the surface wave speed of superficial lung tissue. The objective of this study was to develop a method for analyzing lung mass density of superficial lung tissue using a deep neural network (DNN) and synthetic data of wave speed measurements with LUSWE. The synthetic training dataset of surface wave speed, excitation frequency, lung mass density, and viscoelasticity from LUSWE (788000 in total) was used to train the DNN model. The DNN was composed of 3 hidden layers of 1024 neurons for each layer and trained for 10 epochs with a batch size of 4096 and a learning rate of 0.001 with three types of optimizers. The test dataset (4000) of wave speeds at three excitation frequencies (100, 150, and 200 Hz) and shear elasticity of superficial lung tissue was used to predict the lung density and evaluate its accuracy compared with predefined lung mass densities. This technique was then validated on a sponge phantom experiment. The obtained results showed that predictions matched well with test dataset (validation accuracy is 0.992) and experimental data in the sponge phantom experiment. This method may be useful to analyze lung mass density by using the DNN model together with the surface wave speed and lung stiffness measurements.

Introduction

Interstitial lung disease (ILD), manifested as fibrotic and stiffened lung parenchyma, can result in symptoms such as dyspnea and may lead to respiratory failure [1]. ILD usually affects the peripheral, sub-pleural regions of the lung [2, 3]. ILD can be induced by autoimmune diseases, genetic abnormalities, and long-term exposures to hazardous materials yet its cause is mostly unknown and lung manifestations are characterized as idiopathic interstitial pneumonia.

It has been shown that lung mass is not uniformly distributed in the lung, with greater density in the lower lobes. Moreover, lung mass increases with the degree of fibrosis [4, 5]. Currently, there are no clinical imaging modalities to directly measure lung mass density. High-resolution computed tomography (HRCT) is the clinical standard for diagnosing lung fibrosis given the specific radiation attenuation properties of the lung tissue [6, 7]. Numerous studies have shown that the extent of emphysema measured by pathology scores in resected lung tissue is well correlated with lung density values obtained from preoperative CT of the lung [8, 9]. Two objective measures of CT lung density, so-called densitometric parameters (the percentile density and relative area of emphysema), were used to correlate emphysema on CT to the extent of emphysema in the corresponding resected lobes. CT images have been used to quantify lung density to some extent [10–12]. Computed tomography (CT) is the major clinical imaging modality for assessing various lung diseases. The mechanism of CT is based on the changes of tissue mass density but the CT system uses the Hounsfield unit (HU) but not lung density to image the lung. Yet, it exposes patients to a high dose of radiation.

Data-driven clinical predictions are not new in medical practice. Combined with modern machine learning, clinical data enable us to generate prediction outcomes for different clinical applications. Machine learning techniques are particularly suitable for predictions based on existing data. These approaches are able to discover and identify patterns and relationships between them from complex datasets, while they are able to effectively predict future outcomes [13, 14]. In supervised learning, a labeled set of training data is used to estimate or map the input to the desired output. In the case of regression problems, a learning function maps the data into a real-valued variable. For each new sample, the value of the predictive variable can be estimated [15].

It is well known that lung tissue is normally filled with air and the difference in acoustic impedance between air and tissue is large, resulting that most of the energy of the ultrasound wave is reflected from the lung surface. We have recently developed a lung ultrasound surface wave elastography technique (LUSWE) for measuring the surface wave speeds of superficial lung tissue [16–18]. The estimation of viscoelasticity of lung tissue is also dependent on mass density of lung tissue. However, the data of mass density of lung is very limited, especially when the lung tissue is diseased (such as ILD) or at various pulmonary pressures (such as at total lung volume). The purpose of this study is to develop a method to analyze the lung density using a deep neural network algorithm and the LUSWE measurements.

Materials and methods

Synthetic dataset

In order to generate the database for training the DNN model, analytical simulations were carried out for different sets of material parameters.

The surface wave speed model is used,

$$c_s=\frac{1}{1.05}\sqrt{\frac{2({\mu }_1^2+{\omega }^2{\mu }_2^2)}{\rho ({\mu }_1+\sqrt{{\mu }_1^2+{\omega }^2{\mu }_2^2})}}$$ (1)

where μ₁, μ₂ and ρ are shear elasticity, shear viscosity, and mass density of the material, while ω and c_s are the excitation frequency and corresponding surface wave speed [19–21]. Lung density of healthy subjects obtained via x-ray was reported to be 0.24 g/cm³. For the patients with pulmonary congestion and edema, the lung density was 0.33-0.62 g/cm³ [22]. We could not find lung density data for ILD patients or at the total lung volume. Young’s modulus of normal lung tissue was reported to be 1-5 kPa [23]. Fibrotic lung tissue was reported 20 times stiffer than normal lung tissues [24]. The ranges of material parameters were: μ₁ = (2 kPa, 14 kPa), μ₂ =(2 Pa·s, 17 Pa·s) [25], ρ = (240 kg/m³, 620 kg/m³). A certain number of random numbers in a normal distribution were generated within the range of material parameter (20 for μ₁, 20 for μ₂ and 3200 for ρ). For each set of material properties (μ₁, μ₂ and ρ), three excitation frequencies (100, 150, and 200 Hz) were used to generate the wave speeds at corresponding frequencies. 792000 data sets were obtained in total. The dataset is divided into three parts: training data (630400), validation data (157600), testing data (4000). The features available for us to use are the shear wave speeds of lung tissue at three excitation frequencies and shear elasticity of lung tissue. The only label is the mass density of superficial lung tissue.

Deep neural network model

The synthetic dataset is used to train a DNN model. The proposed architecture is composed of 5 fully-connected layers as described in Fig. 1. The DNN model trained by back propagation consists of 4 neurons in the input layer, 1024 neurons in each of three hidden layers, and 1 neuron in the output layer. The surface wave speeds at three frequencies and shear elasticity (c_{s_100}, c_{s_150}, c_{s_200} and μ₁) of lung tissue are imported as input layer. For our Deep Neural Network, we used the ‘DNNRegressor’ with rectified linear activation unit (ReLU). To reduce overfitting, regularizer L2 was used for each fully-connected layer [26]. The training of DNN is composed of two parts: a training objective and an optimization algorithm to minimize this objective function. In this study, we evaluated the performance of 3 optimizers, Adam, Stochastic gradient descent (SGD) and AdaGrad, to minimize the mean square error (MSE) [27, 28]. The MSE represents the dissimilarity of the approximated output distribution from the true distribution of labels. Learning rate was 0.001. The neuron in the output layer corresponds to the predicted lung mass density and is compared with the predefined lung mass density (TargetsData). The evaluation of performance of different optimizers was based on a train-validation-test scheme. The actual training of the approach was carried out on the training dataset, while the validation dataset (cross-validation ratio is 0.2) was used for fine tuning of hyper-parameters; the overall performance of each optimizer was evaluated on the test dataset [29].

Figure 1.

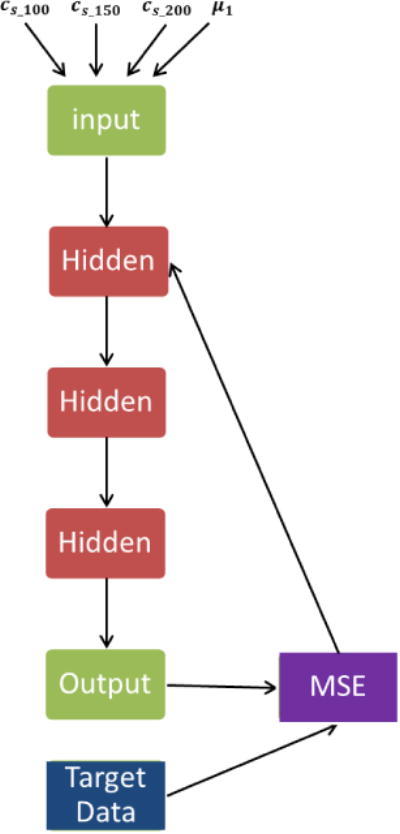
Schematic of a deep neural network.

The trainable weights are initialized with the Xavier initialization [30]. The weight updates are performed in mini-batches and the number of samples per batch was set to 4096. The training ends when the network does not significantly improve its performance on the validation set for a predefined number of epochs. This number is set to 10 and the performance is evaluated in terms of loss and accuracy [31]. Loss is mean square error, which is dissimilarity of the approximated output distribution from the true distribution of labels. $\text{Loss}=\text{MSE}=\frac{1}{\mathrm{n}}{{\displaystyle {\sum }_{\text{i=1}}^{\mathrm{n}}\left({\mathrm{Y}}_{\mathrm{i}}-{\widehat{\mathrm{Y}}}_1\right)}}^2$. Accuracy is calculated in terms of coefficient of determination R2, which is calculated as, ${\mathrm{R}}^2=1-\frac{{{\displaystyle {\sum }_{i=1}^n\left({\mathrm{Y}}_{\mathrm{i}}-{\widehat{\mathrm{Y}}}_{\mathrm{i}}\right)}}^2}{{{\displaystyle {\sum }_{i=1}^n\left({\mathrm{Y}}_{\mathrm{i}}-\overline{\mathrm{Y}}\right)}}^2}$. Y_i is the training data, ${\widehat{\mathrm{Y}}}_{\mathrm{i}}$ is the prediction from the model, $\overline{\mathrm{Y}}$ is the mean value of training dataset. An improvement is considered significant if the relative increase in performance is at least 0.5%.

The DNN was implemented using the Python API of TensorFlow and TFLearn framework. Graph visualization of data flow for the network was shown in Figure 1.

LUSWE on sponge phantom

A cellulose sponge (Ocelo utility sponge, 3M, St. Paul, MN, USA) was cut into a 3.0 cm × 1.9 cm × 8.0 cm rectangular piece. The volume and weight of the dry sponge were measured to calculate its density. The sponge was put into a customized metal holder with a fixed inner width of 2.0 cm (Figure 2). It was then injected with tap water at an interval of 3 ml from 0 to 30 ml and the corresponding mass density of sponge was calculated. After each injection, a sinusoidal signal of 0.1s duration was generated using a function generator (33120A, Agilent Technologies, Inc., Santa Clara, CA, USA) and amplified with amplifier (Pyle PCA4 stereo power amplifier, Pyle audio inc., Brooklyn, NY, USA) at five frequencies 100, 150, 200, 250 and 300 Hz [32]. This signal drives a mechanical shaker (FG-142, Labworks Inc., Costa Mesa, CA, USA) which applied a harmonic vibration on the sponge phantom surface. A Verasonics Vantage system with a L11-5v probe (6.4 MHZ) was used to capture the motion of the sponge. Each measurement was repeated three times at each injection and frequency. The surface wave speed of the sponge was analyzed by the change in wave phase with distance. For the details of procedures for measuring the surface wave speed of the sponge phantom, readers are encouraged to read reference [18, 19]. The viscoelasticity of the sponge at each injection was calculated using the Voigt model [33]. Given the surface wave speed at different excitation frequency and viscoelasticity of the sponge at different level of water injection, the mass density of the sponge was predicted using the trained DNN model. It was then compared with the measured mass density of the sponge phantom at different level of water injection.

Figure 2.

Experimental setup of the LUSWE on the sponge phantom

Results

The convergence of the three different optimizers is demonstrated in terms of the validation loss over the epochs in Fig. 3(a). The loss drops dramatically in the first few steps for Adam yet soon stops. For SGD and AdaGrad, the loss gradually drops toward the end. The validation accuracy of model was plotted in Fig. 3(b). Both SGD and AdaGrad gradually approach 0.86 with AdaGrad converging faster than SGD while Adam gradually approaches 1 from approximately 0.7. MSE and accuracy of the validation dataset of three different optimizers were shown in Table 1. Minimizing the MSE by the Adam optimizer yielded the best results in a small number of iterations. AdaGrad follows with about 5% lower performance and SGD with even a higher drop in performance of 8%. Predefined and predicted lung densities of different optimizers for the test dataset were shown in Table 2. It showed that the prediction matched well with the predefined densities using Adam yet not good with SGD or AdaGrad.

Figure 3.

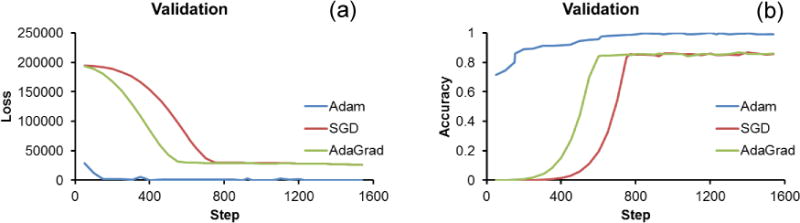
Comparison of the convergence speed between three optimizers. Loss (a) and accuracy (b) curves during the supervised learning of the proposed system.

Table 1.

Comparison in metrics of the proposed technique with different optimizers.

Metrics	Adam	SGD	AdaGrad
MSE Loss	8	26062	26422
Val_acc	0.992	0.856	0.862

Table 2.

The comparison of different optimizers in the test dataset between predefined and predicted densities of lung tissue.

Predefined density (kg/m3)	378	491	544	479	495	548	463	275	249	439
Adam	375	490	544	478	494	548	461	274	249	437
SGD	507	582	578	583	581	577	448	477	483	451
AdaGrad	511	577	573	579	577	573	456	488	496	459

The predicted density from the DNN matched well with the measured density of the sponge phantom (Table 3). The validation accuracy is 0.92.

Table 3.

The comparison between measured and predicted densities of sponge phantom at different level of water injection in the LUSWE.

Measured (kg/m3)	82	184	255	334	408	481	553	622	686	755	831
Predicted	107	219	288	353	429	458	573	649	710	770	830

Discussions

The aim of this study was to develop a deep neural network (DNN) model to predict the lung density for ILD patients based on measurements of wave speeds obtained from LUSWE. Ranges of viscoelasticity and densities of lung tissue covering both healthy controls and ILD patients were predefined to generate synthetic data in terms of wave speeds of lung tissue at three vibration frequencies to train the DNN model. Then, the DNN model was used to predict lung density based on wave speeds of lung tissue at three frequencies and shear elasticity of lung tissue. This model was also validated using a LUSWE on a sponge phantom. The obtained results show that DNN can be used to predict lung mass density with high accuracy.

Ultrasonography is not widely used in clinical practice for lung evaluation because lung tissue is filled with air and most energy of the ultrasound wave is reflected from the lung surface. However, lung ultrasonography can be used for diagnosing various thoracic diseases and especially useful in the emergency and critical care settings [34–36]. In order to noninvasively measure lung viscoelastic property, we have developed an ultrasound-based LUSWE technique to quantify superficial lung tissue stiffness [37, 38]. In LUSWE, a small, local 0.1 second harmonic vibration is generated by the indenter of a handheld shaker on the skin of the subject at three frequencies (100, 150, and 200 Hz). The ultrasound probe is placed approximately 5 mm away from the indenter in the same intercostal space to measure the generated surface wave propagation on the lung surface in that intercostal space. The wave propagation speed of superficial lung tissue is determined by the change in wave phase with distance.

At first, we used linear regression to identify lung mass density based on surface wave speeds of lung tissue at different excitation frequencies, yet got pretty poor results (data not shown). The DNN Regressor is a fully connected feed-forward model that is connected with a rectified linear activation unit (ReLU) [39]. It has been shown that activation function greatly affects the speed of convergence. The use of the ReLU function has been proven to be able to accelerate the training process compared with the sigmoid alternative. SGD is a stochastic approximation of the gradient descent optimization and iterative method for minimizing an objective function that is written as a sum of differentiable functions. AdaGrad is a modified stochastic gradient descent with per-parameter learning rate. It works well with sparse gradients. However, for noisy objectives, higher-order optimization is not suited. Adam is a method for efficient stochastic optimization that only requires first-order gradients with little memory requirements. It computes individual adaptive learning rates for different parameters from estimates of first and second moments of the gradients. Adam adapts learning rates for different layers instead of manually hand picking. Adam employs a preconditioner that adapts to the geometry of the data. Adam adapts the advantage of AdaGrad for sparse gradients. Moreover, its magnitudes of parameter updates are invariant to rescaling of the gradient, its step sizes are approximately bounded by the step size hyper-parameter, it does not require a stationary objective, and it performs a form of step size annealing [27, 40].

Lung CT scanning has widely been used to quantify lung density for emphysema [8]. Parenchyma of patients with pulmonary fibrosis was imaged with HRCT to evaluate lung density based on gray scale histogram [10]. HRCT is essential in quantitative analysis of ILD in terms of regional volumetric quantities [41]. However, HRCT substantially increases radiation exposure for patients and the potential for frequency HRCT use is limited by its expense. In future studies, HRCT could be used to validate the prediction of lung density with DNN. Lung density measurements via CT scanning was well correlated with pulmonary function tests [11]. However, CT or HRCT does not directly measure lung density. We could extend this DNN model together with CT and pulmonary function test (PFT) for analyzing patient’s LUSWE data. PFT can provide the global lung stiffness and LUSWE can provide local region lung stiffness measurements in various intercostal spaces. The novelty of this study was to develop a method for analyzing the lung mass density using DNN and measurements from LUSWE. In future studies, we will evaluate novel DNN techniques and their applications to our problems. We will increase the number of layers of neural network and use deep-residual-networks to improve the accuracy of prediction.

The wave speed on the lung surface was determined by analyzing ultrasound data directly from lung surface. Hence, the wave speed measurement is local and independent of the location of excitation. The wave speeds of superficial lung tissue in LUSWE are obtained at total lung capacity when a subject is taking a deep breath and holds for a few seconds. The lung density is also dependent on the pulmonary pressure. In future studies, in vitro studies can be conducted on porcine lungs to investigate the relationship between lung density and pulmonary pressure based on LUSWE and DNN.

Most soft tissues are incompressible and their mass densities are close to 1000 kg/m³. Lung parenchyma is a porous material filled with air and with a void ratio of approximately 0.7 [42, 43]. The range of lung mass between 240 kg/m³ and 620 kg/m³ was studied in this research based on the available data from literature. Sponge phantom has been shown to have similar microstructure as lung parenchyma [44, 45]. With its availability, relevant phantom models for a systemic study of induced disease states, such as pulmonary edema, can be generated. Pulmonary edema is a fundamental feature of congestive heart failure and inflammatory conditions such as acute respiratory distress syndrome [46]. The presence of extravascular lung water (EVLW) predicts worse prognosis in critically ill patients [47] and increased risk of death or heart failure readmission [48]. The lung density should increase for lung edema. In future, we plan to evaluate the DNN model for patients with pulmonary edema.

Conclusion

In this work, we propose to use a deep neural network model for lung mass density prediction of superficial lung tissue based on LUSWE. The synthetic data was obtained by calculating surface wave speeds of superficial lung tissue at different excitation frequencies given viscoelasticity and density of lung tissue. The training was performed by minimizing the mean square error of the training set and validation set with the different optimizers. The proposed method is evaluated on the synthetic dataset and validated on the sponge phantom experiment. The DNN model is able to predict lung tissue density with high accuracy using the Adam optimizer.

Highlight.

• Developing a method to analyze lung mass density using a deep neural network model and experimental data with lung ultrasound surface wave elastography (LUSWE).

• Synthetic data was generated in terms of surface wave speed from excitation frequency, lung mass density and viscoelasticity from LUSWE to train the deep neural network model.

• The obtained results showed that predictions matched well with test dataset (validation accuracy is 0.992).

• This model was validated in a lung phantom model using sponges.