Abstract
Background
The variation and covariation for many cardiometabolic traits have been decomposed into genetic and environmental fractions, by using twin or single‐nucleotide polymorphism (SNP) models. However, differences in population, age, sex, and other factors hamper the comparison between twin‐ and SNP‐based estimates.
Methods and Results
Twenty‐four cardiometabolic traits and 700,000 genotyped SNPs were available in the study base of 10 682 twins from TwinGene cohort. For the 27 highly correlated pairs (absolute phenotypic correlation coefficient ≥0.40), twin‐based bivariate structural equation models were performed in 3870 complete twin pairs, and SNP‐based bivariate genomic relatedness matrix restricted maximum likelihood methods were performed in 5779 unrelated individuals. In twin models, the model including additive genetic variance and unique/nonshared environmental variance was the best‐fitted model for 7 pairs (5 of them were between blood pressure traits); the model including additive genetic variance, common/shared environmental variance, and unique/nonshared environmental variance components was best fitted for 4 pairs, but estimates of shared environment were close to zero; and the model including additive genetic variance, dominant genetic variance, and unique/nonshared environmental variance was best fitted for 16 pairs, in which significant dominant genetic effects were identified for 13 pairs (including all 9 obesity‐related pairs). However, SNP models did not identify significant estimates of dominant genetic effects for any pairs. In the paired t test, twin‐ and SNP‐based estimates of additive genetic correlation were not significantly different (both were 0.67 on average), whereas the nonshared environmental correlations from these 2 models differed slightly from each other (on average, twin‐based estimate=0.64 and SNP‐based estimate=0.68).
Conclusions
Beside additive genetic effects and nonshared environment, nonadditive genetic effects (dominance) also contribute to the covariation between certain cardiometabolic traits (especially for obesity‐related pairs); contributions from the shared environment seem to be weak for their covariation in TwinGene samples.
Keywords: biomarker, cardiac metabolism, environment, genes, heritability
Subject Categories: Biomarkers, Etiology, Genetics, Epidemiology
Clinical Perspective
What Is New?
This was a comprehensive investigation about the relative importance of genes and environment for the covariation between cardiometabolic traits, by using both twin‐ and single‐nucleotide polymorphism–based models within the same study base.
What Are the Clinical Implications?
The contributions of genetic and environmental effects vary by different clusters of cardiometabolic traits.
Additive genetic effects and nonshared environmental effects influence the covariation between blood pressure traits.
Beside additive genetic effects and nonshared environmental effects, dominant genetic effects are important for the covariation between obesity traits.
Contributions from shared environment seem to be weak between these cardiometabolic traits.
Levels of cardiometabolic traits vary more between than within individuals, and most of them are normally distributed in the population, indicating complex regulation by both genes and environment. The concept of “heritability” reflects the relative importance of genes (in contrast to environment) for complex traits.1 Univariate heritability is defined as the proportion of a trait's phenotypic variation explained by genetic effects, whereas bivariate heritability is the proportion of phenotypic covariation between 2 traits explained by genetic effects.2
Several methods have been developed to partition the variation and covariation of human complex traits into genetic and environmental components. The twin study is the classic family‐based design, relying on comparing the within‐pair similarity between monozygotic and dizygotic twins.3 As a result of genome‐wide association studies, many common single‐nucleotide polymorphisms (SNPs) associated with complex traits (eg, cardiometabolic biomarker levels) have been identified.4 Since 2010, several SNP‐based methods for heritability estimation have been developed; the genomic relatedness matrix restricted maximum likelihood (GREML) and linkage disequilibrium score regression (LDSC) are the most frequently used SNP‐based methods.5, 6, 7
To date, the univariate heritabilities of >17 800 traits/diseases have been estimated from twin studies8; SNP‐based univariate heritabilities of >700 traits/diseases have been estimated by GREML or LDSC.9, 10 A general finding has been that SNP‐based estimates tend to be considerably lower than corresponding estimates from twin studies. The causes of this gap are topics for continuing discussions and investigations.11 Although heritability often turns out comparable across populations, it varies by the actual distribution of age, sex, and other factors in the investigated population sample.12 Therefore, the only straightforward and strictly valid way to investigate the “heritability gap” between the twin and SNP model is to compare the twin‐ and SNP‐based estimates in the same population sample at the same time point.
By comparing univariate heritabilities of 18 human complex traits within the same study base, we observed that common SNPs captured 70% of the narrow‐sense heritability estimated from twin models, when the power in the twin model was high enough to declare and distinguish the dominant from additive genetic variation.13 However, similar comparisons for the bivariate estimates between cardiometabolic traits have not been undertaken. This study quantifies the extent of genetic (additive and dominant) and environmental (shared and nonshared) contributions to the covariation between cardiometabolic traits, by applying both twin and SNP models within the same study base.
Methods
The data and study materials are available to other researchers on application and approval from the steering group of the Swedish Twin Registry.14 Access to the analytic methods may be requested from the corresponding author.
Study Population
All participants in this study were from the TwinGene project, a Swedish population‐based cohort of twins born between 1911 and 1958.15 From 2004 to 2008, 12 614 twins donated venous blood samples after overnight fasting and had a health checkup at their local healthcare facility. Blood samples were sent to Karolinska Institutet Biobank before the weekend by overnight post. The TwinGene project was approved by the local ethics committee at Karolinska Institutet, and all participants gave informed consent.
Phenotypes
Twenty‐four continuous cardiometabolic traits were measured or calculated for ≈12 000 TwinGene participants. Serum levels of apolipoprotein (apo) A1 and B, total cholesterol (TC), low‐ and high‐density lipoprotein (LDL and HDL, respectively), triglycerides, hemoglobin, C‐reactive protein, and fasting glucose were measured by routine methods on semiautomated biochemistry analyzer (Beckman Coulter, CA). Non‐HDL was calculated as TC minus HDL. Hemoglobin A1c was measured by ion exchange chromatography. Creatinine was measured by an enzymatic method using Arcitect c8000 and Arcitect c16000 immunoassay analyzers (Abbott, IL). Cystatin C was measured by particle‐reinforced immunoturbidimetric method using Architect ci8200, and estimated glomerular filtration rate was calculated as 79.901×(cystatin C [mg/L])−1.4389. Height, weight, and waist and hip circumference were measured without shoes and in light clothing. Body mass index was calculated as weight (kg)/height (m)2, and waist/hip ratio (WHR) was calculated as waist circumference (cm)/hip circumference (cm). Systolic and diastolic blood pressures (SBP and DBP, respectively) were measured in mm Hg, mean arterial pressure (MAP) was calculated as 0.33 SBP+0.67 DBP, and pulse pressure (PP) was calculated as SBP minus DBP. The same transformation was used to make all cardiometabolic traits comparable and to achieve standard normal distribution: the raw values were adjusted for age, sex, and 10 genetic principal components in a linear regression model, after which the residuals were rank order normalized and used as phenotypes in the further analyses. Subjects with missing values (after adjustments) for >5 blood biomarkers or who had unknown zygosity were excluded; finally, 10 682 twins remained to constitute the study base.
Genotypes
Genomic DNA was extracted from whole blood samples by using Puregene extraction kit (Gentra Systems, Minneapolis, MN). After excluding subjects with DNA concentration <20 ng/mL, DNA samples of other available dizygotic twins and 1 twin from each monozygotic twin pair (n=9896) were sent for genotyping. SNPs were genotyped by using Illumina OmniExpress BeadChip (700K), with quality controls as follows: individual missingness ≤0.03, genotype missingness ≤0.03, minor allele frequency ≥0.01, Hardy‐Weinberg equilibrium P≥10−7, no sex mismatch, no excess heterozygosity (individuals with an F‐statistic beyond 5 SDs from the sample mean), and no cryptic (unknown) relatedness. Finally, 9617 individuals and 644 556 SNPs were kept.
Twin and SNP Models
For each cardiometabolic trait and highly correlated trait pair (absolute phenotypic correlation coefficient |rP|≥0.4), twin‐based structural equation model (SEM) and SNP‐based GREML (dominant) method were performed to get the twin‐ and SNP‐based estimates, respectively. Paired t test was used to test the agreement (or difference) between significant twin‐ and SNP‐based estimates.
From the study base, 3870 complete twin pairs (1088 monozygotic, 1443 same‐sex dizygotic, and 1339 opposite‐sex dizygotic pairs) were used in twin models. The zygosity was determined by DNA markers (for 57% of the study sample) or by using an algorithm on self‐reported childhood resemblance data.15 Twin studies are based on 3 main assumptions: cotwins within monozygotic pair share 100% while cotwins within dizygotic pair share 50% of segregating genes, and cotwins within the same pair share 100% of the raising environment.2 By using OpenMx 2.8.3 package in R 3.4.1, twin‐based SEMs were constructed to partition phenotypic variation of each trait and covariation between traits into genetic and environmental components.16 Akaike information criterion was used to compare the goodness of model fitting, in which the parameters of the covariance matrices were estimated by maximum likelihood methods.17
The GREML(d) method implemented in genome‐wide complex trait analysis tool, version 1.26.0, was used to get SNP‐based estimates.5, 18 The method relies on comparisons between measured phenotypic similarities and estimated genetic sharing. All directly genotyped SNPs (passing the quality controls) were fitted as random effects in a mixed linear model. To avoid bias from shared environment, 1 twin from each twin pair was randomly removed first, and remaining related individuals (relatedness >0.025) were further removed on the basis of pair‐wise genomic relationship matrix. Finally, 5779 unrelated individuals from the same study base were used in SNP‐based GREML(d) model. Restricted maximum likelihood approach was used to calculate the parameter values with the best probability, and likelihood ratio test was used to test for the best model fitting.
For each trait, the phenotypic variation can be mainly partitioned into the following: additive genetic variance (a2; sum of individual effect of each locus or SNP), dominant genetic variance (d2; interactions between alleles at the same locus or SNP) or common/shared environmental variance (c2; contributes to the similarities between relatives who live together, only from twin model), and unique/nonshared environmental variance (e2; specific to individuals, contributes to the dissimilarities between family members).
To decompose the covariation between 2 correlated traits, bivariate “Cholesky model” was constructed in twin‐based SEM,2 and SNP‐based bivariate GREML(d) analyses were performed in genome‐wide complex trait analysis.6 The phenotypic correlation between 2 traits can be decomposed into bivariate a2 (proportion explained by additive genetic effects), bivariate d2 (proportion explained by dominant genetic effects) or bivariate c2 (proportion explained by shared environment, only from twin model), and bivariate e2 (proportion explained by nonshared environment). The overlaps of genetic and environmental effects (to what extent it is the same effects in action) were investigated by estimating additive and dominant genetic correlations (rA and rD, respectively), as well as shared and nonshared environmental correlations (rE).
Results
General characteristics of 10 682 twins in the study base are presented in Table 1. The distribution of each cardiometabolic trait was similar between the 3870 complete twin pairs and the 5779 unrelated individuals (Table 2). Results from the univariate models for 17 of the 24 traits from the same sample have been published previously (Table S1).13 In short, for all traits, but not apolipoprotein A1 and height, the intrapair correlation coefficients were more than twice larger in monozygotic than dizygotic twin pairs. In the univariate twin SEM, the model including a2 and e2 (AE) was the best‐fitted model for HDL, apolipoprotein A1, DBP, MAP, and PP; the model including a2, c2, and e2 components (ACE) was the best‐fitted model for height; the model including a2, d2, and e2 (ADE) was the best‐fitted model for the remaining 18 traits. SNP‐GREML(d) identified significant d2 for triglycerides and waist circumference. Except for C‐reactive protein, waist circumference, and WHR, the twin‐based a2 values were larger than the corresponding SNP‐based estimates; SNP‐based a2 was not significant for SBP, DBP, and MAP.
Table 1.
General Characteristics of Participants in the Study Base
| Characteristics | All | Men | Women |
|---|---|---|---|
| Participants | 10 682 (100) | 5074 (47.50) | 5608 (52.50) |
| Age, ya | 64.89±8.08 | 65.45±7.99 | 64.38±8.13 |
| Triglycerides, mmol/La | 1.20 (0.86–1.60) | 1.20 (0.88–1.70) | 1.10 (0.84–1.60) |
| Total cholesterol, mmol/La | 5.77±1.12 | 5.52±1.10 | 6.00±1.09 |
| Low‐density lipoprotein, mmol/La | 3.76±0.99 | 3.65±0.98 | 3.86±0.99 |
| Apolipoprotein B, g/La | 1.08±0.25 | 1.07±0.24 | 1.10±0.25 |
| Non‐high‐density lipoprotein, mmol/La | 4.37±1.07 | 4.28±1.06 | 4.44±1.07 |
| High‐density lipoprotein, mmol/La | 1.41±0.42 | 1.24±0.34 | 1.56±0.42 |
| Apolipoprotein A1, g/La | 1.64±0.30 | 1.53±0.26 | 1.75±0.30 |
| Hemoglobin, g/dLa | 14.26±1.21 | 14.87±1.13 | 13.72±1.00 |
| Hemoglobin A1c, %a | 4.82±0.68 | 4.85±0.74 | 4.78±0.61 |
| Glucose, mmol/La | 5.59±1.22 | 5.76±1.33 | 5.44±1.08 |
| Creatinine, μmol/La | 75 (66–86) | 84 (76–93) | 68 (62–76) |
| Cystatin C, mg/La | 0.97 (0.86–1.11) | 0.99 (0.88–1.14) | 0.95 (0.84–1.09) |
| eGFR, mL/min per 1.73 m2 a | 83.55±21.88 | 80.74±21.94 | 86.08±21.53 |
| C‐reactive protein, mg/L | 1.70 (0.72–3.50) | 1.70 (0.73–3.40) | 1.70 (0.72–3.60) |
| Height, ma | 1.69±0.10 | 1.76±0.09 | 1.63±0.08 |
| Weight, kga | 74.94±13.81 | 81.77±12.33 | 68.75±12.05 |
| Body mass index, kg/m2 a | 26.31±7.33 | 26.59±6.83 | 26.07±7.75 |
| Waist circumference, cma | 91.78±12.18 | 97.16±10.26 | 86.91±11.72 |
| Hip circumference, cm | 103.26±8.93 | 103.20±8.06 | 103.30±9.64 |
| Waist/hip ratioa | 0.89±0.15 | 0.94±0.13 | 0.84±0.16 |
| Systolic blood pressure, mm Hga | 139.07±19.80 | 140.10±19.43 | 138.20±20.10 |
| Diastolic blood pressure, mm Hga | 82.10±10.61 | 83.19±10.63 | 81.12±10.49 |
| Mean arterial pressure, mm Hga | 101.09±12.22 | 102.20±12.11 | 100.10±12.24 |
| Pulse pressure, mm Hg | 56.97±15.94 | 56.89±15.65 | 57.04±16.19 |
Values are in number (percentage) for sex, mean±SD for the normal distribution, or median (25th–75th percentile) for the skewed distribution. eGFR indicates estimated glomerular filtration rate.
The difference between men and women is statistically significant (P<0.05) from t test, in which triglycerides, creatinine, cystatin C, and C‐reactive protein are log transformed before performing the t test.
Table 2.
General Characteristics of Subjects in Twin and SNP Models
| Characteristics | Complete Twin Pairs in Twin Model | Unrelated Individuals in SNP Model | ||
|---|---|---|---|---|
| N | Value | N | Value | |
| Men, % | 3653 | 47.20 | 2755 | 47.67 |
| Age, y | 7740 | 65.03±7.75 | 5779 | 64.91±8.33 |
| Triglycerides, mmol/L | 7739 | 1.20 (0.86–1.60) | 5778 | 1.20 (0.85–1.60) |
| Total cholesterol, mmol/L | 7740 | 5.78±1.13 | 5779 | 5.76±1.11 |
| Low‐density lipoprotein, mmol/L | 7639 | 3.77±0.99 | 5704 | 3.75±0.98 |
| Apolipoprotein B, g/L | 7738 | 1.09±0.25 | 5776 | 1.08±0.25 |
| Non‐high‐density lipoprotein, mmol/L | 7740 | 4.38±1.07 | 5779 | 4.35±1.06 |
| High‐density lipoprotein, mmol/L | 7740 | 1.41±0.42 | 5779 | 1.41±0.42 |
| Apolipoprotein A1, g/L | 7738 | 1.64±0.30 | 5776 | 1.64±0.30 |
| Hemoglobin, g/dL | 7726 | 14.26±1.19 | 5769 | 14.26±1.21 |
| Hemoglobin A1c, % | 7727 | 4.82±0.66 | 5770 | 4.82±0.68 |
| Glucose, mmol/L | 7736 | 5.59±1.20 | 5775 | 5.59±1.19 |
| Creatinine, μmol/L | 7534 | 75 (66–86) | 5634 | 76 (66–87) |
| Cystatin C, mg/L | 7534 | 0.97 (0.86–1.11) | 5634 | 0.97 (0.86–1.12) |
| eGFR, mL/min per 1.73 m2 | 7534 | 83.62±21.50 | 5633 | 83.09±22.26 |
| C‐reactive protein, mg/L | 7738 | 1.70 (0.74–3.50) | 5777 | 1.70 (0.71–3.50) |
| Height, m | 7685 | 1.69±0.10 | 5701 | 1.69±0.10 |
| Weight, kg | 7684 | 74.74±13.67 | 5699 | 75.06±13.69 |
| Body mass index, kg/m2 | 7679 | 26.29±7.48 | 5695 | 26.26±6.72 |
| Waist circumference, cm | 7671 | 91.70±12.12 | 5693 | 91.89±12.13 |
| Hip circumference, cm | 7655 | 103.24±8.83 | 5680 | 103.41±8.77 |
| Waist/hip ratio | 7652 | 0.89±0.15 | 5680 | 0.89±0.10 |
| Systolic blood pressure, mm Hg | 7334 | 139.11±19.79 | 5420 | 139.42±20.01 |
| Diastolic blood pressure, mm Hg | 7333 | 82.14±10.68 | 5420 | 82.13±10.67 |
| Mean arterial pressure, mm Hg | 7333 | 101.13±12.30 | 5420 | 101.23±12.31 |
| Pulse pressure, mm Hg | 7333 | 56.96±15.78 | 5420 | 57.28±16.13 |
Values are in number (percentage) for sex, mean±SD for the normal distribution, or median (25th–75th percentile) for the skewed distribution. eGFR indicates estimated glomerular filtration rate; SNP, single‐nucleotide polymorphism.
The phenotypic correlation pattern for the investigated cardiometabolic traits was also similar between the complete twin pairs and samples restricted to unrelated individuals (Figure 1). Twenty‐seven pairs (9 for blood lipids, 4 for metabolic biomarkers, 9 for obesity traits, and 5 for blood pressure traits) showed strong or moderate phenotypic correlations (|rP|≥0.40), and they were selected for further investigation in the bivariate analyses.
Figure 1.

Phenotypic correlation matrix among 24 cardiometabolic traits. Statistically significant (P<0.05) estimates of Pearson correlation coefficient (r) are boldfaced. Estimates in the top triangle are from the 3870 complete twin pairs used in twin models, and estimates in the bottom triangle are from the 5779 unrelated individuals used in single‐nucleotide polymorphism models. apoA1 indicates apolipoprotein A1; apoB, apolipoprotein B; BMI, body mass index; Crea, creatinine; CRP, C‐reactive protein; CysC, cystatin C; DBP, diastolic blood pressure; eGFR, estimated glomerular filtration rate; Glu, fasting glucose; Hb, hemoglobin; HDL, high‐density lipoprotein; Hip, hip circumference; LDL, low‐density lipoprotein; MAP, mean arterial pressure; PP, pulse pressure; SBP, systolic blood pressure; TC, total cholesterol; TG, triglycerides; WC, waist circumference; WHR, waist/hip ratio.
Negative phenotypic correlation was found between triglycerides and HDL (rP=−0.46), but positive phenotypic correlations were found for the other 8 pairs of blood lipids (average rP=0.85, Table 3). AE was the best‐fitted twin model for triglycerides‐HDL and TC‐apoB. ACE was the best‐fitted model for HDL–apolipoprotein A1, LDL‐apoB, and apoB–non‐HDL, but the estimates of bivariate c2 were close to zero. In twin models, significant contributions of dominance genetic effects were identified for 3 lipids pairs (TC‐LDL, TC–non‐HDL, and LDL–non‐HDL), and the average bivariate d2 was 23% and rD was 0.96. For these 9 pairs of blood lipids, the average estimates of bivariate a2 were 42% from the twin models, whereas the SNP models provided lower estimates of 16%.
Table 3.
Bivariate Analyses Between Blood Lipids in Twin and SNP Models
| Pairs | rP (SE) | BM | Bivariate a2 (SE), % | Bivariate d2 (SE), %a | rA (SE) | rD (SE)a | rE (SE) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Twin | SNP | Twin | Twin | SNP | Twin | Twin | SNP | |||
| Triglycerides‐HDL | −0.46 (0.01)b | AE | 66 (3)b | 29 (6)b | ··· | −0.51 (0.02)b | −0.48 (0.13)b | ··· | −0.39 (0.02)b | −0.45 (0.11)b |
| Triglycerides–non‐HDL | 0.41 (0.01)b | ADE | 33 (14)b | 11 (6) | 23 (15) | 0.43 (0.15)b | 0.23 (0.20) | 0.49 (0.51) | 0.38 (0.03)b | 0.46 (0.05)b |
| HDL‐apoA1 | 0.84 (0.02)b | ACEc | 66 (2)b | 21 (6)b | ··· | 0.89 (0.01)b | 0.88 (0.06)b | ··· | 0.85 (0.01)b | 0.84 (0.05)b |
| TC‐LDL | 0.94 (0.02)b | ADE | 25 (8)b | 15 (6)b | 21 (9)b | 0.92 (0.04)b | 0.92 (0.04)b | 0.94 (0.06)b | 0.95 (0.00)b | 0.94 (0.04)b |
| TC‐apoB | 0.87 (0.02)b | AE | 46 (2)b | 14 (6)b | ··· | 0.83 (0.01)b | 0.82 (0.09)b | ··· | 0.91 (0.00)b | 0.87 (0.07)b |
| TC–non‐HDL | 0.93 (0.02)b | ADE | 25 (8)b | 13 (6)b | 22 (9)b | 0.88 (0.05)b | 0.89 (0.05)b | −0.96 (0.04)b | 0.96 (0.00)b | 0.94 (0.05)b |
| LDL‐apoB | 0.91 (0.02)b | ACEc | 47 (2)b | 14 (6)b | ··· | 0.91 (0.01)b | 0.89 (0.06)b | ··· | 0.92 (0.00)b | 0.91 (0.05)b |
| LDL–non‐HDL | 0.97 (0.02)b | ADE | 23 (8)b | 14 (6)b | 25 (9)b | 0.94 (0.03)b | 0.95 (0.03)b | 0.98 (0.02)b | 0.96 (0.00)b | 0.96 (0.03)b |
| ApoB–non‐HDL | 0.94 (0.02)b | ACEc | 47 (2)b | 14 (6)b | ··· | 0.95 (0.01)b | 0.96 (0.03)b | ··· | 0.95 (0.00)b | 0.93 (0.03)b |
a2 Indicates additive genetic variance; ACE, model including a2, common (c2), and nonshared environmental (e2) components; ADE, model including a2, d2, and e2; AE, model including a2 and e2; apoA1, apolipoprotein A1; apoB, apolipoprotein B; BM, best‐fitted model according to Akaike information criterion; d2, dominant genetic variance; HDL, high‐density lipoprotein; LDL, low‐density lipoprotein; rA, additive genetic correlation; rD, dominant genetic correlation; rE, nonshared environmental correlation; rP, phenotypic correlation; SNP, single‐nucleotide polymorphism–based genomic relatedness matrix restricted maximum likelihood model; TC, total cholesterol.
Bivariate d2 and rD are not significantly identified from SNP models for any pairs.
Statistically significant estimates (P<0.05).
ACE is the best‐fitted model, but bivariate c2=0% (SE=1%).
ADE was the best‐fitted twin model for 3 of 4 pairs of metabolic biomarkers (hemoglobin A1c–glucose, creatinine–cystatin C, and creatinine–estimated glomerular filtration rate), but bivariate d2 and rD were only significantly identified for hemoglobin A1c–glucose (Table 4). ACE model was best fitted for cystatin C–estimated glomerular filtration rate, whereas bivariate c2 was also close to zero. For these 4 pairs of metabolic biomarkers, the average twin‐ and SNP‐based bivariate a2 values were 43% and 23%, respectively.
Table 4.
Bivariate Analyses Between Metabolic Biomarkers in Twin and SNP Models
| Pairs | rP (SE) | BM | Bivariate a2 (SE), % | Bivariate d2 (SE), %a | rA (SE) | rD (SE)a | rE (SE) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Twin | SNP | Twin | Twin | SNP | Twin | Twin | SNP | |||
| HbA1c‐glucose | 0.51 (0.01)b | ADE | 29 (11)b | 23 (6)b | 49 (11)b | 0.51 (0.15)b | 0.61 (0.16)b | 0.76 (0.12)b | 0.32 (0.03)b | 0.48 (0.14)b |
| Creatinine‐CysC | 0.56 (0.01)b | ADE | 44 (10)b | 22 (6)b | 18 (11) | 0.65 (0.09)b | 0.59 (0.13)b | 0.48 (0.16)b | 0.53 (0.02)b | 0.59 (0.13)b |
| Creatinine‐eGFR | −0.53 (0.01)b | ADE | 39 (11)b | 25 (6)b | 22 (12) | −0.57 (0.11)b | −0.57 (0.13)b | 0.54 (0.23) | −0.50 (0.02)b | −0.55 (0.13)b |
| CysC‐eGFR | −0.95 (0.02)b | ACEc | 58 (2)b | ··· | ··· | −0.98 (0.00)b | ··· | ··· | −0.97 (0.00)b | ··· |
a2 Indicates additive genetic variance; ACE, model including a2, common (c2), and nonshared environmental (e2) components; ADE, model including a2, d2, and e2; BM, best‐fitted model according to Akaike information criterion; CysC, cystatin C; d2, dominant genetic variance; eGFR, estimated glomerular filtration rate; HbA1c, hemoglobin A1c; rA, additive genetic correlation; rD, dominant genetic correlation; rE, nonshared environmental correlation; rP, phenotypic correlation; SNP, single‐nucleotide polymorphism–based genomic relatedness matrix restricted maximum likelihood model.
Bivariate d2 and rD are not significantly identified from SNP models for any pairs.
Statistically significant estimates (P<0.05).
ACE is the best‐fitted model, but bivariate c2=0% (SE=1%).
For all of the 9 pairs of obesity traits, bivariate d2 (48% on average) and rD (0.84 on average) were significantly identified from twin models (Table 5). However, bivariate a2 was not significant for weight‐WHR, body mass index–WHR, or waist circumference–WHR. For the remaining 6 obesity‐related pairs, on average, the twin‐ and SNP‐based bivariate a2 values were 26% and 21%, respectively.
Table 5.
Bivariate Analyses Between Obesity Traits in Twin and SNP Models
| Pairs | rP (SE) | BM | Bivariate a2 (SE), % | Bivariate d2 (SE), %a | rA (SE) | rD (SE)a | rE (SE) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Twin | SNP | Twin | Twin | SNP | Twin | Twin | SNP | |||
| Weight‐BMI | 0.86 (0.02)b | ADE | 25 (8)b | 18 (6)b | 45 (8)b | 0.68 (0.08)b | 0.66 (0.09)b | 1.00 (0.00)b | 0.89 (0.01)b | 0.93 (0.09)b |
| Weight‐WC | 0.82 (0.02)b | ADE | 25 (8)b | 22 (6)b | 47 (8)b | 0.83 (0.09)b | 0.87 (0.06)b | 0.93 (0.04)b | 0.74 (0.01)b | 0.82 (0.06)b |
| Weight‐Hip | 0.83 (0.02)b | ADE | 33 (8)b | 28 (6)b | 40 (8)b | 0.91 (0.05)b | 0.99 (0.04)b | 0.90 (0.04)b | 0.70 (0.02)b | 0.78 (0.04)b |
| Weight‐WHR | 0.42 (0.01)b | ADE | 14 (13) | 7 (6) | 54 (14)b | 0.26 (0.51) | 0.14 (0.19) | 0.62 (0.12)b | 0.38 (0.03)b | 0.49 (0.20)b |
| BMI‐WC | 0.81 (0.02)b | ADE | 21 (8)b | 17 (6)b | 50 (8)b | 0.80 (0.14)b | 0.76 (0.09)b | 0.93 (0.04)b | 0.70 (0.02)b | 0.83 (0.08)b |
| BMI‐Hip | 0.77 (0.02)b | ADE | 26 (8)b | 21 (6)b | 46 (9)b | 0.76 (0.10)b | 0.78 (0.08)b | 0.89 (0.05)b | 0.66 (0.02)b | 0.78 (0.08)b |
| BMI‐WHR | 0.47 (0.01)b | ADE | 15 (12) | 10 (6) | 56 (13)b | 0.36 (0.51) | 0.24 (0.20) | 0.66 (0.11)b | 0.37 (0.03)b | 0.52 (0.18)b |
| WC‐Hip | 0.76 (0.02)b | ADE | 23 (8)b | 22 (6)b | 46 (9)b | 0.94 (0.09)b | 0.90 (0.08)b | 0.80 (0.05)b | 0.66 (0.02)b | 0.73 (0.08)b |
| WC‐WHR | 0.73 (0.01)b | ADE | 12 (9) | 10 (6) | 48 (9)b | 0.64 (0.51) | 0.46 (0.19)b | 0.80 (0.06)b | 0.72 (0.01)b | 0.79 (0.19)b |
a2 Indicates additive genetic variance; ADE, model including a2, d2, and nonshared environmental (e2) components; BM, best‐fitted model according to Akaike information criterion; BMI, body mass index; d2, dominant genetic variance; Hip, hip circumference; rA, additive genetic correlation; rD, dominant genetic correlation; rE, nonshared environmental correlation; rP, phenotypic correlation; SNP, single‐nucleotide polymorphism–based genomic relatedness matrix restricted maximum likelihood model; WC, waist circumference; WHR, waist/hip ratio.
Bivariate d2 and rD are not significantly identified from SNP models for any pairs.
Statistically significant estimates (P<0.05).
AE was the best‐fitted twin model for all 5 pairs of blood pressure traits (Table 6). The average estimates of bivariate a2 were ≈40% in the twin models, whereas in SNP models, they were smaller and significant only for SBP‐PP (bivariate a2=11%; 95% confidence interval, 0%–22%). The twin‐ and SNP‐based estimates of rA and rE were similar for SBP‐MAP, SBP‐PP, and DBP‐MAP (>0.80); SNP‐based estimates of rA and rE were not significant for SBP‐DBP or MAP‐PP.
Table 6.
Bivariate Analyses Between Blood Pressure Traits in Twin and SNP Models
| Pairs | rP (SE) | BM | Bivariate a2 (SE), % | rA (SE) | rE (SE) | |||
|---|---|---|---|---|---|---|---|---|
| Twin | SNP | Twin | SNP | Twin | SNP | |||
| SBP‐DBP | 0.67 (0.01)a | AE | 41 (3)a | 7 (6) | 0.71 (0.02)a | 0.55 (0.34) | 0.63 (0.01)a | 0.67 (0.50) |
| SBP‐MAP | 0.92 (0.02)a | AE | 40 (2)a | 9 (6) | 0.92 (0.01)a | 0.88 (0.11)a | 0.89 (0.01)a | 0.90 (0.16)a |
| SBP‐PP | 0.84 (0.02)a | AE | 39 (2)a | 11 (6)a | 0.85 (0.01)a | 0.83 (0.13)a | 0.81 (0.01)a | 0.83 (0.10)a |
| DBP‐MAP | 0.93 (0.02)a | AE | 38 (2)a | 7 (6) | 0.93 (0.01)a | 0.88 (0.11)a | 0.92 (0.00)a | 0.92 (0.22)a |
| MAP‐PP | 0.51 (0.01)a | AE | 42 (3)a | 9 (6) | 0.57 (0.03)a | 0.46 (0.35) | 0.46 (0.02)a | 0.51 (0.34) |
a2 Indicates additive genetic variance; AE, model including a2 and nonshared environmental components; BM, best‐fitted model according to Akaike information criterion; DBP, diastolic blood pressure; MAP, mean arterial pressure; PP, pulse pressure; rA, additive genetic correlation; rE, nonshared environmental correlation; rP, phenotypic correlation; SBP, systolic blood pressure; SNP, single‐nucleotide polymorphism–based genomic relatedness matrix restricted maximum likelihood model.
Statistically significant estimates (P<0.05).
The overall agreements between significant twin‐ and SNP‐based estimates for these highly correlated cardiometabolic pairs are plotted in Figure 2. The twin‐based bivariate a2 (36% on average) was significantly larger than SNP‐based estimates (19% on average). The estimates of rA were not significantly different between twin‐SEM and SNP‐GREML (both were 0.67 on average). However, the twin‐based rP (0.66 on average) and rE (0.64 on average) values were slightly but significantly different from the SNP‐based rP (0.65 on average) and rE (0.68 on average) values.
Figure 2.
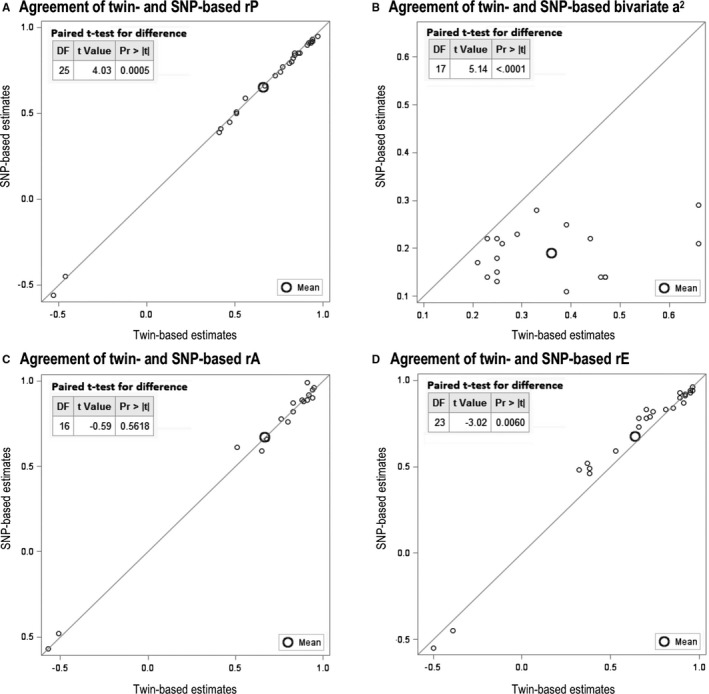
Paired test for agreement between significant twin‐ and single‐nucleotide polymorphism (SNP)–based estimates. a2 Indicates additive genetic variance; Pr, probability; rA, additive genetic correlation; rE, nonshared environmental correlation; rP, phenotypic correlation.
Discussion
This study mainly aims to quantify the contribution of genetic and environmental effects to the covariation between cardiometabolic traits and to compare the estimates obtained from both twin and SNP models within the same study base. Beside additive genetic effects and nonshared environment, the twin models also find significant contributions of dominant genetic effects to the covariation between certain cardiometabolic traits (especially for obesity‐related pairs); contributions of shared environment generally seem to be weak for their covariation. The results show that the twin model captures significantly more bivariate additive genetic variance than SNP model, whereas the estimates of additive genetic correlation from these 2 models are not significantly different.
Twenty‐seven highly correlated pairs of cardiometabolic traits were investigated in this study. They were grouped into 4 biological clusters: blood lipids, metabolic biomarkers, obesity traits, and blood pressure traits. The magnitudes of rP, rA, and rE are similar for each pair (Figure 2), perhaps because the correlated traits are calculated from each other, represent similar features, or are involved in the same biological process. For example, apoB is the primary apolipoprotein of LDL, LDL constitutes the majority of TC, and non‐HDL is calculated as TC minus HDL; thus, apoB–LDL–TC–non‐HDL are strongly and positively correlated.
ApoA1 is the major component of HDL, and genetic effects contribute more (66%) to their phenotypic correlation than environment in twin model. Similarly, twin model also indicates that 66% of the negative correlation between triglycerides and HDL is explained by genes (Table 3). On the contrary, environmental factors contribute more (≈60%) than genes to the phenotypic correlations for 5 pairs of blood pressure traits (Table 6), perhaps because blood pressure fluctuates more from environmental or behavioral factors (eg, physical activity, smoking, alcohol drinking, and psychological stress) than genes.19
On the basis of different assumptions, twin and SNP models are used to estimate the relative importance of genes and environment for complex traits (represented by the concept of heritability). Twin studies have historically been the most frequently used design to provide estimates of “traditional heritability.” By using directly genotyped SNPs in unrelated individuals, GREML(d) estimates the so‐called “chip heritability.” LDSC uses the summary genome‐wide association study results (including both directly genotyped and imputed SNPs) to estimate the “SNP heritability.” For most cardiometabolic traits in our study, a trend can be found that the estimates of traditional heritability ≥ chip heritability ≥ SNP heritability (Table S1). A similar significant trend was also observed for bivariate heritabilities (Figure 2). The causes of the gap between twin‐ and SNP‐based estimates of heritability are of direct relevance for the discussions about the “missing” or “hidden” heritability.11, 20
The issue of missing heritability was raised because of the fact that robustly associated genome‐wide significant SNPs generally explain <5% of traits’ variation.20 However, the explained variance becomes larger (≈50%) when all common SNPs are taken into account in GREML methods.21 Our previous study also indicated that genome‐wide common SNPs could capture large proportions (≈70%) of the “traditional narrow‐sense heritability (a2)” if the power in the twin model was enough to identify and discriminate dominant from additive genetic contributions.13
Classic twin studies based solely on monozygotic and dizygotic twins reared together are unable to simultaneously estimate shared environmental variance (c2) and dominant genetic variance (d2). However, because c2 and d2 are likely to coexist in reality, it is fully possible that both of them contribute simultaneously to similarities between twins and relatives. Whenever c2 and d2 are both present, their contributions will tend to mask each other in the twin model; thus, the net effect may appear as contribution from neither. Although an extended twin‐family study design including more family members (eg, parents, offspring, and nontwin siblings) is the optimal design to detect the existence of nonadditive genetic effects, such materials of adequate sample size are exceptionally rare.22, 23, 24
The identification of true d2 depends heavily on the sample size. Most previous twin studies are small, <1000 twin pairs on average.8 It might lead to inadequate power to significantly declare contributions from less prominent variance components; thus, d2 or c2 may be attributed to a2 instead.13 This is in line with the observation that most previous twin studies report the estimates from the most parsimonious AE model.8
There are 3870 complete twin pairs in present study, and bivariate d2 is significantly distinguished from bivariate a2 for 13 of 16 ADE best‐fitted pairs. Among these pairs, the directly genotyped common SNPs captured 75% of twin‐based bivariate a2 (narrow‐sense heritability). Previous genome‐wide association studies have identified 47 loci that associated with both LDL and TC25; the significant bivariate d2 for TC‐LDL in our twin model suggests potential interactions between the alleles within the same locus. However, our SNP model did not identify significant dominant genetic effects for any pairs, perhaps because of the inadequate power for bivariate GREML(d). Therefore, more SNPs in larger samples need to test such potential interactions.
For ADE fitted traits or pairs, the separation between additive and dominant genetic variation is important to understand the gap between twin‐ and SNP‐based univariate or bivariate narrow‐sense heritability. Even so, the twin‐based bivariate a2 values are still significantly higher (on average 25% for ADE fitted pairs and 48% for all pairs) than SNP‐based estimates. Potential explanations might be the following: twin‐based SEM captures all genetic effects, whereas GREML(d) is just based on common SNPs; other mutations, like rare SNPs, copy number variations, insertions, or deletions, will not be taken into account; and violations of the assumptions of twin studies (monozygotic and dizygotic twin pairs share environment to the same extent, minimal gene‐environment correlations or interactions) may inflate the twin‐based heritability estimation.26
For all ACE best‐fitted pairs, estimates of bivariate shared environmental variance (c2) are close to zero, perhaps reflecting the relative old age of the participants in our study base (65±8 years on average). It is reasonable to assume that most cotwins of old age live separately and that the influences of shared environment decrease with age. A weaker contribution from c2 may lend d2 less masked and thus more prominent at older ages. Therefore, the influence on twin similarity stemming from c2 can be expected to be largest during childhood, with subsequent diminishing importance with advancing age. However, a thorough investigation of the potential role of age for the relative importance between c2 and d2 (eg, the age‐related changes in contribution from c2 and d2 to trait covariation) requires even larger sample size.
Previous twin studies, including small numbers of monozygotic twins reared apart, identified that shared environmental effects contribute to the variation of some cardiometabolic traits27, 28; this occurs perhaps because such study setting allows researchers to directly use ACE decomposing model rather than choosing the best‐fitted one among ACE, ADE, and AE models. After removing pairs with relatedness >0.025, it is unlikely to have contributions from c2 in GREML(d). Therefore, the estimates from SNP‐GREML(d) represent a lower bound of a2. In Table S1, the estimates of univariate heritability from SNP‐based GREML(d) (22% on average, using 644 556 directly genotyped SNPs in our samples) are significantly higher than LDSC‐based estimates (14% on average, including up to ≈10 million directly genotyped and imputed SNPs in LD Hub). Both GREML(d) and LDSC assume that heritability is independent of linkage disequilibrium pattern, which has been suggested to underestimate the SNP‐based heritability.29, 30 However, the estimates of rA from LDSC were >1 for 4 pairs of blood lipids, indicating potential inflation in signal, potentially resulting from using overlapped individuals (Table S2) or imputed SNPs to capture the covariation. Recently, a study suggested that rA estimates from LDSC are less accurate than rA obtained by GREML(d), perhaps because of the uncertainty of homogeneity among combined data sets.31 Still, our twin‐SEM and SNP‐GREML(d) models give estimates of rA and rE largely in agreement with each other for most correlated cardiometabolic pairs.
In summary, this study indicates that contributions of genetic and environmental effects vary by different clusters of cardiometabolic traits. Contributions from the shared environment seem to be weak between these cardiometabolic traits. Additive genetic effects and nonshared environmental effects influence the covariation between blood pressure traits. Dominant genetic effects are important between obesity traits, and the gap between twin‐ and SNP‐based bivariate narrow‐sense heritability would become smaller if dominance can be significantly distinguished from additive genetic effects. However, larger sample size of unrelated individuals is still required to test the significance of dominant genetic effects from SNP‐based models.
Sources of Funding
The Swedish Twin Registry is managed by Karolinska Institutet and receives funding through the Swedish Research Council (grant 2017‐00641). This study was supported by the Swedish Heart‐Lung Foundation (grant 20070481) and China Scholarship Council (grant 201306210065).
Disclosures
None.
Supporting information
Table S1. Univariate Analyses in Twin and SNP Models
Table S2. LDSC‐Based Estimates of Cardiometabolic Traits From European Ancestry Data in the LD Hub
(J Am Heart Assoc. 2018;7:e007806 DOI: 10.1161/JAHA.117.007806.)29669715
References
- 1. Tenesa A, Haley CS. The heritability of human disease: estimation, uses and abuses. Nat Rev Genet. 2013;14:139–149. [DOI] [PubMed] [Google Scholar]
- 2. Neale MC, Maes HHM. Methodology for Genetic Studies of Twins and Families. Dordrecht, Netherlands: Kluwer Academic Publishers BV; 2004. [Google Scholar]
- 3. van Dongen J, Slagboom PE, Draisma HH, Martin NG, Boomsma DI. The continuing value of twin studies in the omics era. Nat Rev Genet. 2012;13:640–653. [DOI] [PubMed] [Google Scholar]
- 4. Visscher PM, Wray NR, Zhang Q, Sklar P, McCarthy MI, Brown MA, Yang J. 10 years of GWAS discovery: biology, function, and translation. Am J Hum Genet. 2017;101:18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Yang J, Lee SH, Goddard ME, Visscher PM. GCTA: a tool for genome‐wide complex trait analysis. Am J Hum Genet. 2011;88:76–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Lee SH, Yang J, Goddard ME, Visscher PM, Wray NR. Estimation of pleiotropy between complex diseases using single‐nucleotide polymorphism‐derived genomic relationships and restricted maximum likelihood. Bioinformatics. 2012;28:2540–2542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Bulik‐Sullivan BK, Loh PR, Finucane HK, Ripke S, Yang J; Schizophrenia Working Group of the Psychiatric Genomics Consortium , Patterson N, Daly MJ, Price AL, Neale BM. LD score regression distinguishes confounding from polygenicity in genome‐wide association studies. Nat Genet. 2015;47:291–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Polderman TJ, Benyamin B, de Leeuw CA, Sullivan PF, van Bochoven A, Visscher PM, Posthuma D. Meta‐analysis of the heritability of human traits based on fifty years of twin studies. Nat Genet. 2015;47:702–709. [DOI] [PubMed] [Google Scholar]
- 9. Ge T, Chen CY, Neale BM, Sabuncu MR, Smoller JW. Phenome‐wide heritability analysis of the UK Biobank. PLoS Genet. 2017;13:e1006711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Zheng J, Erzurumluoglu AM, Elsworth BL, Kemp JP, Howe L, Haycock PC, Hemani G, Tansey K, Laurin C; Early Genetics and Lifecourse Epidemiology (EAGLE) Eczema Consortium . Pourcain BS, Warrington NM, Finucane HK, Price AL, Bulik‐Sullivan BK, Anttila V, Paternoster L, Gaunt TR, Evans DM, Neale BM. LD Hub: a centralized database and web interface to perform LD score regression that maximizes the potential of summary level GWAS data for SNP heritability and genetic correlation analysis. Bioinformatics. 2017;33:272–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Tropf FC, Lee SH, Verweij RM, Stulp G, van der Most PJ, de Vlaming R, Bakshi A, Briley DA, Rahal C, Hellpap R, Nyman A, Esko T, Metspalu A, Medland SE, Martin NG, Barban N, Snieder H, Robinson MR, Mills MC. Hidden heritability due to heterogeneity across seven populations. Nat Hum Behav. 2017;1:757–765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Visscher PM, Hill WG, Wray NR. Heritability in the genomics era: concepts and misconceptions. Nat Rev Genet. 2008;9:255–266. [DOI] [PubMed] [Google Scholar]
- 13. Chen X, Kuja‐Halkola R, Rahman I, Arpegard J, Viktorin A, Karlsson R, Hagg S, Svensson P, Pedersen NL, Magnusson PK. Dominant genetic variation and missing heritability for human complex traits: insights from twin versus genome‐wide common SNP models. Am J Hum Genet. 2015;97:708–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. The Swedish Twin Registry . https://ki.se/en/research/the-swedish-twin-registry. Accessed March 25, 2018.
- 15. Magnusson PK, Almqvist C, Rahman I, Ganna A, Viktorin A, Walum H, Halldner L, Lundstrom S, Ullen F, Langstrom N, Larsson H, Nyman A, Gumpert CH, Rastam M, Anckarsater H, Cnattingius S, Johannesson M, Ingelsson E, Klareskog L, de Faire U, Pedersen NL, Lichtenstein P. The Swedish Twin Registry: establishment of a biobank and other recent developments. Twin Res Hum Genet. 2013;16:317–329. [DOI] [PubMed] [Google Scholar]
- 16. Neale MC, Hunter MD, Pritikin JN, Zahery M, Brick TR, Kirkpatrick RM, Estabrook R, Bates TC, Maes HH, Boker SM. OpenMx 2.0: extended structural equation and statistical modeling. Psychometrika. 2016;81:535–549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. deLeeuw J. Introduction to Akaike (1973) Information Theory and an Extension of the Maximum Likelihood Principle. New York, NY: Springer; 1992. [Google Scholar]
- 18. Zhu Z, Bakshi A, Vinkhuyzen AA, Hemani G, Lee SH, Nolte IM, van Vliet‐Ostaptchouk JV, Snieder H, LifeLines Cohort S, Esko T, Milani L, Magi R, Metspalu A, Hill WG, Weir BS, Goddard ME, Visscher PM, Yang J. Dominance genetic variation contributes little to the missing heritability for human complex traits. Am J Hum Genet. 2015;96:377–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Brook RD. The environment and blood pressure. Cardiol Clin. 2017;35:213–221. [DOI] [PubMed] [Google Scholar]
- 20. Maher B. Personal genomes: the case of the missing heritability. Nature. 2008;456:18–21. [DOI] [PubMed] [Google Scholar]
- 21. Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, Madden PA, Heath AC, Martin NG, Montgomery GW, Goddard ME, Visscher PM. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 2010;42:565–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Keller MC, Coventry WL, Heath AC, Martin NG. Widespread evidence for non‐additive genetic variation in Cloninger's and Eysenck's personality dimensions using a twin plus sibling design. Behav Genet. 2005;35:707–721. [DOI] [PubMed] [Google Scholar]
- 23. Rettew DC, Rebollo‐Mesa I, Hudziak JJ, Willemsen G, Boomsma DI. Non‐additive and additive genetic effects on extraversion in 3314 Dutch adolescent twins and their parents. Behav Genet. 2008;38:223–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Rahman I, Bennet AM, Pedersen NL, de Faire U, Svensson P, Magnusson PK. Genetic dominance influences blood biomarker levels in a sample of 12,000 Swedish elderly twins. Twin Res Hum Genet. 2009;12:286–294. [DOI] [PubMed] [Google Scholar]
- 25. Willer CJ, Schmidt EM, Sengupta S, Peloso GM, Gustafsson S, Kanoni S, Ganna A, Chen J, Buchkovich ML, Mora S, Beckmann JS, Bragg‐Gresham JL, Chang HY, Demirkan A, Den Hertog HM, Do R, Donnelly LA, Ehret GB, Esko T, Feitosa MF, Ferreira T, Fischer K, Fontanillas P, Fraser RM, Freitag DF, Gurdasani D, Heikkila K, Hypponen E, Isaacs A, Jackson AU, Johansson A, Johnson T, Kaakinen M, Kettunen J, Kleber ME, Li X, Luan J, Lyytikainen LP, Magnusson PK, Mangino M, Mihailov E, Montasser ME, Muller‐Nurasyid M, Nolte IM, O'Connell JR, Palmer CD, Perola M, Petersen AK, Sanna S, Saxena R, Service SK, Shah S, Shungin D, Sidore C, Song C, Strawbridge RJ, Surakka I, Tanaka T, Teslovich TM, Thorleifsson G, Van den Herik EG, Voight BF, Volcik KA, Waite LL, Wong A, Wu Y, Zhang W, Absher D, Asiki G, Barroso I, Been LF, Bolton JL, Bonnycastle LL, Brambilla P, Burnett MS, Cesana G, Dimitriou M, Doney AS, Doring A, Elliott P, Epstein SE, Eyjolfsson GI, Gigante B, Goodarzi MO, Grallert H, Gravito ML, Groves CJ, Hallmans G, Hartikainen AL, Hayward C, Hernandez D, Hicks AA, Holm H, Hung YJ, Illig T, Jones MR, Kaleebu P, Kastelein JJ, Khaw KT, Kim E, Klopp N, Komulainen P, Kumari M, Langenberg C, Lehtimaki T, Lin SY, Lindstrom J, Loos RJ, Mach F, McArdle WL, Meisinger C, Mitchell BD, Muller G, Nagaraja R, Narisu N, Nieminen TV, Nsubuga RN, Olafsson I, Ong KK, Palotie A, Papamarkou T, Pomilla C, Pouta A, Rader DJ, Reilly MP, Ridker PM, Rivadeneira F, Rudan I, Ruokonen A, Samani N, Scharnagl H, Seeley J, Silander K, Stancakova A, Stirrups K, Swift AJ, Tiret L, Uitterlinden AG, van Pelt LJ, Vedantam S, Wainwright N, Wijmenga C, Wild SH, Willemsen G, Wilsgaard T, Wilson JF, Young EH, Zhao JH, Adair LS, Arveiler D, Assimes TL, Bandinelli S, Bennett F, Bochud M, Boehm BO, Boomsma DI, Borecki IB, Bornstein SR, Bovet P, Burnier M, Campbell H, Chakravarti A, Chambers JC, Chen YD, Collins FS, Cooper RS, Danesh J, Dedoussis G, de Faire U, Feranil AB, Ferrieres J, Ferrucci L, Freimer NB, Gieger C, Groop LC, Gudnason V, Gyllensten U, Hamsten A, Harris TB, Hingorani A, Hirschhorn JN, Hofman A, Hovingh GK, Hsiung CA, Humphries SE, Hunt SC, Hveem K, Iribarren C, Jarvelin MR, Jula A, Kahonen M, Kaprio J, Kesaniemi A, Kivimaki M, Kooner JS, Koudstaal PJ, Krauss RM, Kuh D, Kuusisto J, Kyvik KO, Laakso M, Lakka TA, Lind L, Lindgren CM, Martin NG, Marz W, McCarthy MI, McKenzie CA, Meneton P, Metspalu A, Moilanen L, Morris AD, Munroe PB, Njolstad I, Pedersen NL, Power C, Pramstaller PP, Price JF, Psaty BM, Quertermous T, Rauramaa R, Saleheen D, Salomaa V, Sanghera DK, Saramies J, Schwarz PE, Sheu WH, Shuldiner AR, Siegbahn A, Spector TD, Stefansson K, Strachan DP, Tayo BO, Tremoli E, Tuomilehto J, Uusitupa M, van Duijn CM, Vollenweider P, Wallentin L, Wareham NJ, Whitfield JB, Wolffenbuttel BH, Ordovas JM, Boerwinkle E, Palmer CN, Thorsteinsdottir U, Chasman DI, Rotter JI, Franks PW, Ripatti S, Cupples LA, Sandhu MS, Rich SS, Boehnke M, Deloukas P, Kathiresan S, Mohlke KL, Ingelsson E, Abecasis GR; Global Lipids Genetics Consortium . Discovery and refinement of loci associated with lipid levels. Nat Genet. 2013;45:1274–1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Mayhew AJ, Meyre D. Assessing the heritability of complex traits in humans: methodological challenges and opportunities. Curr Genomics. 2017;18:332–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Elder SJ, Lichtenstein AH, Pittas AG, Roberts SB, Fuss PJ, Greenberg AS, McCrory MA, Bouchard TJ Jr, Saltzman E, Neale MC. Genetic and environmental influences on factors associated with cardiovascular disease and the metabolic syndrome. J Lipid Res. 2009;50:1917–1926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Heller DA, de Faire U, Pedersen NL, Dahlen G, McClearn GE. Genetic and environmental influences on serum lipid levels in twins. N Engl J Med. 1993;328:1150–1156. [DOI] [PubMed] [Google Scholar]
- 29. Yang J, Zeng J, Goddard ME, Wray NR, Visscher PM. Concepts, estimation and interpretation of SNP‐based heritability. Nat Genet. 2017;49:1304–1310. [DOI] [PubMed] [Google Scholar]
- 30. Speed D, Cai N; UCLEB Consortium , Johnson MR, Nejentsev S, Balding DJ. Reevaluation of SNP heritability in complex human traits. Nat Genet. 2017;49:986–992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Ni G, Moser G, Wray NR, Lee SH. Estimation of genetic correlation using linkage disequilibrium score regression and genomic restricted maximum likelihood. bioRxiv. 2017. DOI: 10.1101/194019. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1. Univariate Analyses in Twin and SNP Models
Table S2. LDSC‐Based Estimates of Cardiometabolic Traits From European Ancestry Data in the LD Hub


