Single‐Beat Estimation of Right Ventricular Contractility and Its Coupling to Pulmonary Arterial Load in Patients With Pulmonary Hypertension

Abstract

Background

An accurate assessment of intrinsic right ventricular (RV) contractility and its relation to pulmonary arterial load is essential for the management of pulmonary hypertension. The pressure‐volume relationship with load manipulation is the gold standard assessment used for this purpose, but its clinical application has been hindered by the lack of a single‐beat method that is valid for the human RV. In the present study, we sought to validate a novel single‐beat method to estimate the preload recruitable stroke work (PRSW) and its derivative for ventriculoarterial coupling in the human RV.

Methods and Results

A novel single‐beat slope of the PRSW relationship (M_sw) was derived by calculating the mean ejection pressure when the end‐systolic volume was equal to volume‐axis intercept of the PRSW relationship. In addition, by using a mathematical transformation of the equation representing the linearity of the PRSW relationship, a novel index for ventriculoarterial coupling, M_sw/mean ejection pressure, was developed. RV pressure‐volume relationships were measured in 31 patients (including 23 patients with pulmonary hypertension) who were referred for right‐sided heart catheterization. In this cohort, the single‐beat M_sw was strongly correlated with the multiple‐beat M_sw (r=0.91, P<0.0001). Moreover, a significant correlation was observed between the single‐ and multiple‐beat M_sw/mean ejection pressure (r=0.53, P=0.002), with a stronger correlation in those with greater RV systolic pressure (r=0.70, P=0.003).

Conclusions

The novel single‐beat approach provided an accurate estimation of indexes for the PRSW relationship and ventriculoarterial coupling. It may be particularly useful in assessing RV adaptation to increased pressure overload.

Clinical Perspective

What Is New?

• Pulmonary impedance describes both steady and pulsatile afterloads, but it has been unable to be summarized by a single number. Right ventricular (RV) mean ejection pressure/stroke volume represents a comprehensive marker for pulmonary impedance.

• Balance between RV contractility and pulmonary arterial (PA) afterload (ie, RV‐PA coupling) can be assessed using a simple index: preload recruitable stroke work/mean ejection pressure.

• Preload recruitable stroke work and its coupling to PA load can be estimated from a single beat without changing loading conditions, which can help improve the diagnosis and treatment of diseased RV in humans.

What Are the Clinical Implications?

• Whether preload recruitable stroke work–based RV‐PA coupling index predicts clinical outcomes better than traditional RV‐PA coupling indexes warrants future investigations.

• Molecular mechanisms of RV adaptation to pressure overload need to be studied further using the new preload recruitable stroke work–based measure of RV adaptation.

Pulmonary arterial (PA) hypertension (PAH) can lead to pathologic remodeling of the pulmonary vasculature and progressive increases in the PA load. Although the right ventricle (RV) attempts to adapt by compensatory hypertrophy and dilation, adaptation can become insufficient, leading to right‐sided heart failure and ultimately death.1 Accordingly, prognosis in PAH is strongly related to RV compensation rather than to the degree of the vascular injury itself.1, 2, 3 Thus, accurate assessment of intrinsic RV contractility and its relation to the PA load is essential for refining risk stratification and optimizing treatment in these patients.1, 3 However, commonly used indexes of RV contractility, such as the RV ejection fraction (EF) and tricuspid annular plane systolic excursion, are limited by considerable load dependence.4

Pressure‐volume (PV) relationships provide relatively load‐insensitive measures of contractility, such as end‐systolic elastance (E_es), preload‐recruitable stroke work (PRSW), and E_es/arterial elastance (E_a), a key metric that describes RV‐PA coupling.5, 6, 7 However, measuring E_es or PRSW requires generating a family of PV relationships over a wide range of volumes using means such as inferior vena cava occlusion or the Valsalva maneuver, which can be time‐consuming and difficult to measure. Single‐beat estimates of RV E_es have been proposed; however, these methods have not been validated for use in the human RV,8, 9, 10 and unfortunately this estimate did not correlate with clinical outcomes in 2 recent studies.11, 12 The PRSW (M_sw), defined as the slope of ventricular stroke work (SW) versus end‐diastolic volume measured across a range of ventricular volumes, arguably provides the most load‐insensitive measure of RV contractility.13 Compared with E_es, the PRSW relationship is reported to be more strictly linear, more reproducible, and less dependent on chamber size or afterload.14 However, its clinical application has also been limited because of the lack of a single‐beat method that is valid for the human RV.

We recently reported a novel single‐beat approach for estimating M_sw in the canine left ventricle (LV).15 This method may also be applicable to the human RV because it does not necessarily depend on conditions that are specific to the LV. In addition, we predicted, for the first time, that the M_sw could be coupled with ventricular afterload using a simple new index, M_sw/the mean ejection pressure (P_m), to assess RV‐PA coupling. Thus, the present study sought to validate our novel single‐beat method for M_sw and our newly described measure of RV‐PA coupling in a cohort of subjects with invasively measured RV PV relationships.

Methods

The individual data will not be made available to other researchers for purposes of reproducing the results. The analytic methods, however, are presented as Supplementary Materials to assist other researchers in replicating the procedure.

Study Subjects

We retrospectively analyzed data from consecutive patients who underwent PV studies during right‐sided heart catheterization for the diagnosis or management of pulmonary hypertension (PH) at the Johns Hopkins Hospital (Baltimore, MD) from November 1, 2012 to June 30, 2015. The research protocol was approved by Institutional Review Board of the Johns Hopkins School of Medicine, and informed consent was obtained from all patients.

PV Loop Analysis

After standard right‐sided heart catheterization, a PV catheter (model SPC‐570‐2; Millar Instruments, Houston, TX) was advanced through the right internal jugular vein and positioned at the RV apex to measure instantaneous RV volume. The RV conductance signal was calibrated to match the RV EF, which was independently determined by same‐day cardiac magnetic resonance imaging (CMR) and thermodilution cardiac output. PV loops and relationships were constructed both at baseline and during phase 2 of the Valsalva maneuver (period of preload decline), as validated previously.10, 16 PV data were digitalized at 500 Hz using a custom‐designed data acquisition system and stored for subsequent offline analysis. Extraction of the conventional hemodynamic parameters from the PV loops was performed using custom analysis programs (WinPVAN‐3.5.10). Further analyses involving multiple‐beat E_es and PRSW were conducted using R version 3.0.1.

Calculation of E_es and the PRSW Relationship Using Multiple Beats

The end‐systolic points for a series of loops during the Valsalva maneuver were determined as those with maximal elastance and were fitted against the linear end‐systolic PV relationship (ESPVR) using the linear least‐squares method, with the use of an iterative method to calculate the multiple‐beat E_es, as previously reported.17 Effective E_a was determined by dividing the end‐systolic pressure by the stroke volume (SV), and RV‐PA coupling was assessed as E_es/E_a. The PRSW relationship was also determined by a linear regression analysis of SW versus end‐diastolic volume data obtained during the Valsalva maneuver, according to the following equation:

$$\text{SW}={\mathrm{M}}_{\mathrm{SW}}\times ({\mathrm{V}}_{\mathrm{ed}}-{\mathrm{V}}_{\mathrm{SW}})$$ (1)

where M_sw and V_sw are the slope and volume‐axis intercept, respectively.13 The PRSW coefficients determined from multiple‐beat data are specifically denoted as M_sw(MB) and V_sw(MB).

Outline of the Single‐Beat Estimation of the ESPVR and the PRSW Relationship

Our single‐beat approach for estimating RV M_sw, hereby described, involves the following: (1) an estimation of the ESPVR from the single‐beat late systolic PV relation and (2) a determination of M_sw on the basis of a novel link between the PRSW relationship and the ESPVR. These have been validated previously for the LV in an animal study.15

(1) Estimation of the curvilinear ESPVR from the single‐beat late systolic PV relation

We used a single‐beat method to estimate a curvilinear ESPVR on the basis of the concept of maximum systolic myocardial stiffness, as previously proposed by Mirsky et al.15, 18 We modified the original ESPVR formula of Mirsky et al¹⁸ to implement a CMR‐measured wall volume into the formula, as outlined in detail in Data S1, 19:

$${\mathrm{P}}_{\mathrm{es}}({\mathrm{V}}_{\mathrm{es}})=\mathrm{A}\times \text{In}(\frac{{\mathrm{V}}_{\mathrm{es}}}{{\mathrm{V}}_0})\times \text{In}(\mathrm{1}+\frac{{\mathrm{V}}_{\mathrm{wall}}}{{\mathrm{V}}_{\mathrm{es}}})$$ (2)

where A is an amplification factor and V₀ is the volume‐axis intercept of the ESPVR, which represents the chamber volume when the fiber stress is assumed to be zero. The RV wall volume was measured using CMR or can be calculated from end‐diastolic volume by assuming a constant RV wall‐volume ratio when measured wall volume is not available. Figure 1 shows that the single‐beat ESPVR was estimated by fitting the points between the peak systolic pressure and the end‐systolic point on the signal‐averaged baseline loop against equation (2) using the nonlinear least‐squares method. This provides a zero‐stress volume (V₀) on the basis of the single‐baseline beat, which was denoted as V_0(SB).

Figure 1.

Single‐beat estimation of the end‐systolic pressure‐volume relationship (ESPVR). A, Multiple‐beat ESPVR (black curve). The end‐systolic points for a series of loops were determined as those with maximal stress/strain ratio (open black circles) and were fitted against the equation for the ESPVR $(\mathrm{P}=\mathrm{A}\times \text{In}(\frac{\mathrm{V}}{{\mathrm{V}}_0})\times \text{In}(\mathrm{1}+\frac{{\mathrm{V}}_{\mathrm{wall}}}{\mathrm{v}}))$ using a nonlinear least‐square method, with the use of an iterative method to determine the zero‐stress volume, V_0(MB). B, Single‐beat ESPVR (red curve) was estimated by fitting points between the peak systolic pressure and the end‐systolic points (red open points) on the signal‐averaged baseline loop against the equation, $\mathrm{P}=\mathrm{A}\times \text{In}(\frac{\mathrm{V}}{{\mathrm{V}}_0})\times \text{In}(\mathrm{1}+\frac{{\mathrm{V}}_{\mathrm{wall}}}{\mathrm{v}})$ (equation (2) in the main text) using the nonlinear least‐squares method. The end‐systolic point (ie, the last point used for the curve fitting; black closed point) in this figure has been determined uniformly using an algorithm on the basis of an iterative method, as described in detail in Figure S5. The red closed point represents the zero‐stress volume of the single‐beat ESPVR (V_0[SB]).

(2) Determination of M_sw from the estimated ESPVR

The principle for estimating the RV M_sw using a single beat is based on a novel physiologic link detected between the ESPVR and the PRSW relationships.15 We defined the P_m as SW/SV:

$$\text{SW}={\mathrm{P}}_{\mathrm{m}}\times \text{SV}$$ (3)

Combining equations (1) and (3) yields

$${\mathrm{P}}_{\mathrm{m}}\times \text{SV}={\mathrm{M}}_{\mathrm{sw}}\times ({\mathrm{V}}_{\mathrm{es}}+\text{SV}-{\mathrm{V}}_{\mathrm{sw}})$$ (4)

which can be rearranged to

$$({\mathrm{P}}_{\mathrm{m}}-{\mathrm{M}}_{\mathrm{sw}})=\frac{{\mathrm{M}}_{\mathrm{sw}}}{\text{SV}}\times ({\mathrm{V}}_{\mathrm{es}}-{\mathrm{V}}_{\mathrm{sw}})$$ (5)

More important, this equation indicates that when the end‐systolic volume is equal to V_sw, P_m should be equal to M_sw. If one conceptualizes M_sw and V_sw as a PV coordinate, then the linearity of the PRSW relationship dictates that this coordinate (V_sw, M_sw), when placed on the PV plane, must be on the PV relationship between P_m and V_es, as defined in equation (5), which is hereby referred to as the end‐systolic P_m‐volume relationship (EMPVR) (see Figure 2A). This relationship is conceptually similar to the ESPVR, but with end‐systolic pressure replaced by P_m. We assumed that the EMPVR:P_m(V_es) function has a curvilinear characteristic similar to that of the ESPVR:end‐systolic pressure(V_es) (equation (2)) with a common V₀ but a different amplification factor, as follows:

$${\mathrm{P}}_{\mathrm{m}}({\mathrm{V}}_{\mathrm{es}})=\frac{{\mathrm{P}}_{\mathrm{m}\_\mathrm{sb}}}{{\mathrm{P}}_{\mathrm{es}}({\mathrm{V}}_{\mathrm{es}\_\mathrm{sb}})}\times {\mathrm{P}}_{\mathrm{es}}({\mathrm{V}}_{\mathrm{es}})=\mathrm{B}\times \text{In}(\frac{{\mathrm{V}}_{\mathrm{es}}}{{\mathrm{V}}_0})\times \text{In}(\mathrm{1}+\frac{{\mathrm{V}}_{\mathrm{wall}}}{{\mathrm{V}}_{\mathrm{es}}})$$ (6)

where P_{m_sb} and V_{es_sb} are known P_m values and end‐systolic volumes of the baseline single beat, respectively, and B is an amplification factor.

Figure 2.

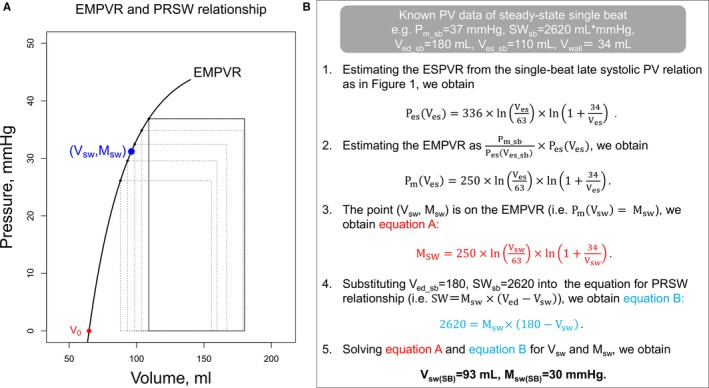
Outline of the single‐beat estimation of the preload recruitable stroke work relationship. A, A novel physiologic feature that links the end‐systolic mean ejection pressure (P_m)‐volume relationship (EMPVR) and the preload recruitable stroke work (PRSW) relationship. The squares represent the rectangular‐transformed pressure‐volume (PV) loops that have the same area (ie, stroke work [SW]) and width (ie, stroke volume [SV]) as the original PV loops. The trajectory of the left‐upper corners of the squares was denoted as the EMPVR. The bottoms of the squares were aligned at the volume axis; hence, the height of the square represents the absolute value of the P_m (SW/SV). The units for volume‐axis and the slope of the PRSW relationship (V_sw and M_sw) are mL and mm Hg, respectively. When the point (V_sw, M_sw) is plotted as a blue point on the PV plane, this point is on the EMPVR curve, as demonstrated mathematically in the main text. B, Schematic flow chart of an example of single‐beat estimation of M_sw. The P_m of the baseline single beat (P_{m_sb}=37 mm Hg) was calculated as the SW of the baseline single beat (SW_sb=2620 mL×mm Hg) divided by the SV of the baseline single beat (=70 mL). The right ventricular wall volume (V_wall) was obtained from the cardiac magnetic resonance imaging. ESPVR indicates end‐systolic pressure‐volume relationship; M_sw(SB), slope of the PRSW relationship estimated from the baseline single beat; V₀, volume‐axis intercept of the ESPVR; V_{ed_sb}, end‐diastolic volume of the baseline single beat; V_{es_sb}, end‐systolic volume of the baseline single beat; and V_sw(SB), volume‐axis intercept of the PRSW relationship estimated from the baseline single beat.

Once the ESPVR is estimated from a single beat, the EMPVR can also be determined as in equation 6 using V_0(SB). As P_m is equal to M_sw when end‐systolic volume is equal to V_sw [ie, P_m(V_sw)=M_sw], substituting V_sw for V_es in equation 6 yields,

$${\mathrm{M}}_{\mathrm{sw}}=\mathrm{B}\times \text{In}(\frac{{\mathrm{V}}_{\mathrm{sw}}}{{\mathrm{V}}_{0(\mathrm{SB})}})\times \text{In}(\mathrm{1}+\frac{{\mathrm{V}}_{\mathrm{wall}}}{{\mathrm{V}}_{\mathrm{sw}}})$$ (7)

Also, from equation (1),

$${\text{SW}}_{\mathrm{sb}}={\mathrm{M}}_{\mathrm{sw}}\times ({\mathrm{V}}_{\mathrm{ed}\_\mathrm{sb}}-{\mathrm{V}}_{\mathrm{sw}})$$ (8)

where SW_sb and V_{ed_sb} are the known SW and end‐diastolic volume of the baseline single beat, respectively. By solving the 2 simultaneous equations for M_sw and V_sw (equations (7) and (8)), we finally obtain single‐beat estimates of the PRSW coefficients (M_sw[SB] and V_sw[SB]). A schematic flow chart using an example case for single‐beat estimation of M_sw is summarized in Figure 2B. An algorithm using this outlined approach was generated in R version 3.0.1 (R Foundation) and used to calculate the M_sw uniformly from each signal‐averaged single‐beat loop.

Proposal of a Novel Index of Ventriculoarterial Coupling

We propose the use of the ratio of contractility (ie, the M_sw) to P_m as a novel index of RV‐PA coupling. By rearranging equation (5), we obtain

$$\frac{{\mathrm{M}}_{\mathrm{sw}}}{\text{SV}}=\frac{({\mathrm{P}}_{\mathrm{m}}-{\mathrm{M}}_{\mathrm{sw}})}{({\mathrm{V}}_{\mathrm{es}}-{\mathrm{V}}_{\mathrm{sw}})}={\mathrm{E}}_{\mathrm{es}}^{\prime }$$ (9)

where $\frac{({\mathrm{P}}_{\mathrm{m}}-{\mathrm{M}}_{\mathrm{sw}})}{({\mathrm{V}}_{\mathrm{es}}-{\mathrm{V}}_{\mathrm{sw}})}$ represents the local slope of the EMPVR and is denoted as ${\mathrm{E}}_{\mathrm{es}}^{\prime }$, as shown in Figure 3. More important, equation (9) indicates that ${\mathrm{E}}_{\mathrm{es}}^{\prime }$ is consistently equal to the M_sw adjusted by the SV (ie, contractility). On the other hand, pulmonary vascular impedance can be represented by the slope of a diagonal line across the rectangular PV loop, as in Figure 3, which is denoted as ${\mathrm{E}}_{\mathrm{a}}^{\prime }$:

$${\mathrm{E}}_{\mathrm{a}}^{\prime }=\frac{{\mathrm{P}}_{\mathrm{m}}}{\text{SV}}=\frac{\text{SW}}{{\text{SV}}^2}$$ (10)

Figure 3.

A novel ventriculoarterial coupling framework on the basis of the end‐systolic mean ejection pressure (P_m)‐volume relationship (EMPVR). If the preload recruitable stroke work relationship can be assumed to be linear, ${\mathrm{E}}_{\mathrm{es}}^{\prime }$, the slope of the red segment between the end‐systolic point of the baseline square (V_es, P_m) and the point (volume‐axis intercept of the preload recruitable stroke work [PRSW] relationship [V_sw], slope of the PRSW relationship [M_sw]) is equal to $\frac{{\mathrm{M}}_{\mathrm{sw}}}{\text{SV}}$, as shown in equation (9) in the text. Moreover, the effective arterial elastance for the rectangular pressure‐volume loop (${\mathrm{E}}_{\mathrm{a}}^{\prime }=\frac{{\mathrm{P}}_{\mathrm{m}}}{\text{SV}}$, black slope) represents the vascular impedance that accounts for both steady and pulsatile afterload, as shown in Data S2. The pump performance of the ventricle can be determined by ${\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime }$ in a similar way to E_es/E_a. Furthermore, ${\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime }$ can be simply formulated as M_sw/P_m, as shown in equation (11) in the text. SV indicates stroke volume.

As shown in Data S2, ${\mathrm{E}}_{\mathrm{a}}^{\prime }$ is transformed into an integrated form of vascular impedance on the basis of the concept that the external ventricular work (ie, SW) is equal to the hydraulic energy imparted to the blood.1, 20 The pumping performance of the ventricle can be determined by ${\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime }$ in a similar way to E_es/E_a coupling, as shown in Figure 3.7 Thus, this novel ${\mathrm{E}}_{\mathrm{es}}^{\prime }-{\mathrm{E}}_{\mathrm{a}}^{\prime }$ coupling framework, on the basis of the EMPVR, directly relates the intrinsic contractility with the vascular impedance. Multiplying both sides of equation (9) by SV/P_m yields

$$\frac{{\mathrm{M}}_{\mathrm{sw}}}{{\mathrm{P}}_{\mathrm{m}}}=\frac{({\mathrm{P}}_{\mathrm{m}}-{\mathrm{M}}_{\mathrm{sw}})}{({\mathrm{V}}_{\mathrm{es}}-{\mathrm{V}}_{\mathrm{sw}})}/\frac{{\mathrm{P}}_{\mathrm{m}}}{\text{SV}}=\frac{{\mathrm{E}}_{\mathrm{es}}^{\prime }}{{\mathrm{E}}_{\mathrm{a}}^{\prime }}$$ (11)

Therefore, the M_sw can be linked with the arterial load simply as M_sw/P_m to determine the RV‐PA coupling $({\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime })$ in the PV plane. Single‐ and multiple‐beat M_sw/P_m were calculated as M_sw[SB]/P_m and M_sw[MB]/P_m, respectively.

Statistical Analysis

Data were presented as mean±SD. The PRSW estimates, on the basis of the single‐beat approach, were compared with the multiple‐beat PRSW measurements (ie, the V_sw[MB] and M_sw[MB]) using Pearson's correlation coefficient and a linear regression analysis. Bland‐Altman analysis was used to assess the agreement between single‐ and multiple‐beat measurements. Statistical analyses were conducted with R version 3.0.1.21

Results

Study Population

Of the 41 patients enrolled, we evaluated data from 31 who had successful studies for PV loops and CMR (6 patients did not complete the study for safety or technical reasons, and 4 patients were excluded because of insufficient preload reduction with the Valsalva maneuver). The analyzed cohort included 23 patients with PH (idiopathic PAH, n=6; systemic sclerosis PAH, n=13; systemic sclerosis with PH attributable to heart failure with preserved EF or interstitial lung disease, n=4) and 8 patients without PH (systemic sclerosis without PH, n=6; no PH, n=2). Patient characteristics are shown in Table 1.

Table 1.

Patient Characteristics

Characteristics	Value (n=31)
Diagnoses, n (%)
IPAH	6 (19.4)
SSc‐PAH	13 (42.0)
SSc‐PH attributable to HFpEF or ILD	4 (12.9)
SSc without PH	6 (19.4)
No PH	2 (6.5)
Age, y	61±12
Female sex, n (%)	28 (90)
Body surface area, m2	1.84±0.21
NYHA class III/IV, n (%)	12 (39)
Heart rate, bpm	74±13
Systemic arterial pressure, mm Hg	94±14

Continuous variables are shown as mean±SD. Bpm indicates beats per minute; HFpEF, heart failure with preserved ejection fraction; ILD, interstitial lung disease; IPAH, idiopathic PAH; NYHA, New York Heart Association; PAH, pulmonary arterial hypertension; PH, pulmonary hypertension; SSc, systemic sclerosis.

Multiple‐beat data

Table 2 shows that the PV data were obtained from patients with variable hemodynamic statuses. The RV end‐diastolic wall‐to‐chamber volume ratio was 0.17±0.06. During phase 2 of the Valsalva maneuver, 6.0±2.2 PV loops were obtained. Variable multiple‐beat E_es (0.14–1.9 mm Hg/mL) and E_a (0.29–2.3) resulted in variable RV‐PA coupling (E_es/E_a[MB]), which ranged from 0.23 to 4.5 (1.0±0.91). The PRSW relationship was highly linear (r=0.97±0.02), and the M_sw(MB) ranged from 14 to 64 mm Hg. The ratio between M_sw(MB) and P_m (M_sw[MB]/P_m=${\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime }$), our novel index of RV‐PA coupling, was 0.75±0.16. The M_sw(MB)/P_m (=${\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime }$) ranged from 0.51 to 1.17, as a result of variable ${\mathrm{E}}_{\mathrm{es}}^{\prime }$ (M_sw[MB]/SV, range, 0.18–1.3) and ${\mathrm{E}}_{\mathrm{a}}^{\prime }$ (=P_m/SV, range, 0.23–1.7). Although both indexes of RV‐PA coupling (E_es/E_a[MB] and M_sw[MB]/P_m) were significantly correlated with each other (r=0.53, P=0.002, Figure S1), the range of change differed considerably. The RV‐PA coupling ratio in patients with PH was significantly lower than that in those without PH (P=0.03 for multiple‐beat E_es/E_a, and P=0.003 for M_sw[MB]/P_m).

Table 2.

Hemodynamic Data

Variable	Total (n=31)
Conventional right‐sided heart catheterization data
Cardiac output by thermodilution, L/min	4.70±0.91 (2.8–6.3)
Pulmonary arterial pressure, mm Hg	31±13 (14–67)
Pulmonary arterial wedge pressure, mm Hg	10±4.0 (4.0–19)
Pulmonary vascular resistance, Wood units	4.8±3.8 (1.2–19)
RV systolic pressure, mm Hg	50±22 (26–109)
RV end‐diastolic pressure, mm Hg	11±5.2 (2.1–21)
dP/dtmax, mm Hg/s	441±131 (305–937)
Cardiac magnetic resonance imaging data
RV end‐diastolic volume, mL	144±40 (71–245)
RV ejection fraction, %	53±9.1 (34–71)
RV wall volume, mL	22.8±6.64 (12.8–40.6)
RV pressure‐volume study data
Multiple‐beat Ees, mm Hg/mL	0.64±0.43 (0.14–1.9)
Ea, mm Hg/mL	0.80±0.45 (0.29–2.3)
Multiple‐beat Ees/Ea	1.0±0.91 (0.23–4.5)
Stroke work, mm Hg/mL	2465±1064 (881–5200)
Multiple‐beat Msw, mm Hg	27±12 (14–64)
Multiple‐beat Vsw, mL	50±23 (8.1–97)

Continuous variables are shown as mean±SD (range). dP/dt_max indicates maximum rate of RV pressure increase; E_a, effective arterial elastance; E_es, end‐systolic elastance; M_sw, the slope of the preload recruitable stroke work relationship; RV, right ventricular; V_sw, x‐axis intercept of the preload recruitable stroke work.

Single‐beat estimation of the PRSW relationship and RV‐PA coupling

An iterative algorithm yielded an average of 20 points (range, 9–56 points) on a steady‐state PV loop to be used for single‐beat ESPVR estimation. Figure 4 shows that the zero‐stress volumes of the single‐ and multiple‐beat ESPVRs were strongly correlated (r=0.86, P<0.0001). The single‐beat estimation of the PRSW slope (M_sw[SB]) estimated from the signal‐averaged baseline PV loop was strongly correlated with the multiple‐beat PRSW slope, M_sw(MB) (Figure 5A, r=0.91, P<0.0001). Even when the RV end‐diastolic wall‐to‐chamber volume ratio was assumed (a mean value of 0.17), the single‐beat approach provided an accurate estimation of M_sw(MB) without individual information on the RV wall volume (Figure 5B, r=0.91, P<0.0001). Bland‐Altman plots showed a mild overestimation by 3.7 (SEM, 0.92) mm Hg and limits of agreement from −6.5 to 14.0 mm Hg (Figure 5C and 5D).

Figure 4.

Single‐ and multiple‐beat end‐systolic pressure‐volume relationship (ESPVR). Scatterplots comparing zero‐stress volumes of single‐ vs multiple‐beat ESPVRs (V_0[SB] and V_0[MB], respectively).

Figure 5.

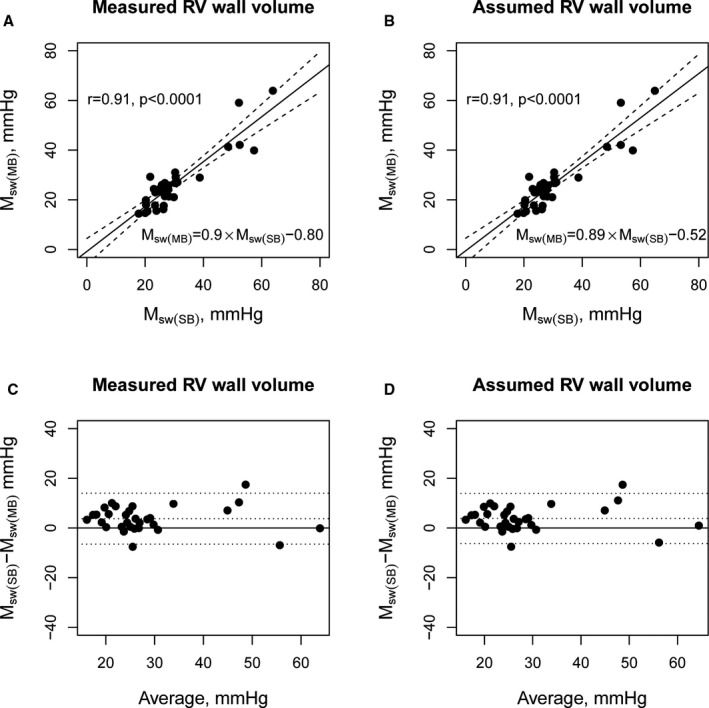
Estimated and measured preload recruitable stroke work slope, M_sw. A, Scatterplots comparing the estimated preload recruitable stroke work (PRSW) slope (M_sw[SB]) on the basis of the single‐beat method using measured right ventricular wall volume to the multiple‐beat PRSW slope (M_sw[MB]). B, Similar analysis using the assumed right ventricular (RV) end‐diastolic wall/chamber volume ratio. C, Bland‐Altman plots for M_sw(SB) on the basis of the single‐beat method using measured RV wall volume. D, Bland‐Altman plots for M_sw(SB) using the assumed RV end‐diastolic wall/chamber volume ratio.

Although estimated and measured ${\mathrm{E}}_{\mathrm{es}}^{\prime }$ (ie, M_sw[SB]/SV and M_sw[MB]/SV) strongly correlated with each other (r=0.95, P<0.0001, Figure S2), the correlation between estimated and measured RV‐PA coupling on the basis of the ${\mathrm{E}}_{\mathrm{es}}^{\prime }$ (ie, single‐ versus multiple‐beat ${\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime }$ calculated as M_sw[SB]/P_m versus M_sw[MB]/P_m) was only moderate (r=0.52, P=0.002, Figure 6A), with a stronger correlation in patients with greater RV systolic pressure (red circles; RV pressure ≥ median of 44.12 mm Hg, r=0.68, P=0.004). Even when the M_sw(SB) on the basis of the assumed RV end‐diastolic wall‐to‐chamber volume ratio was used to estimate RV‐PA coupling, the correlation between estimated and measured RV‐PA coupling was moderate (r=0.53, P=0.002), with a stronger correlation in those with greater RV systolic pressure (r=0.70, P=0.003), as shown in Figure 6B.

Figure 6.

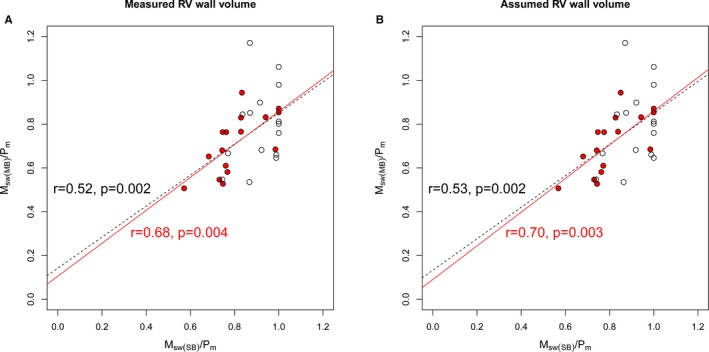
Single‐beat estimation of a novel index of right ventricular–pulmonary arterial coupling. A, Scatterplots comparing single‐ and multiple‐beat slope of the preload recruitable stroke work (PRSW) relationship (M_sw)/mean ejection pressure (P_m), calculated using measured right ventricular (RV) wall volume. A stronger correlation was observed in those with greater RV systolic pressure (median of 44 mm Hg or greater; closed red points). B, Similar analysis using the assumed RV end‐diastolic wall/chamber volume ratio. M_sw(MB) indicates the multiple‐beat PRSW slope; and M_sw(SB), the estimated PRSW slope from a single beat.

Validation analyses for our single‐beat method

To test the validity of the basic principle of our estimation method that the point (V_sw, M_sw) is on the EMPVR curve, PRSW coefficients that were determined from the multiple‐beat EMPVR (as a point on the EMPVR) were compared with the actual multiple‐beat PRSW coefficients (ie, M_sw[MB] and V_sw[MB]). The actual and EMPVR‐based PRSW coefficients derived from the same set of multiple‐beat data were robustly correlated with each other (r=0.98, P<0.0001 for V_sw and r=0.99, P<0.0001 for M_sw estimation, Figure S3). More important, a similar analysis, assuming that the EMPVR was linear, reduced the robustness (r=0.93 for M_sw and r=0.56 for V_sw), which highlights both the importance of selecting an appropriate EMPVR model and the validity of our model (equation 6).

Finally, as a sensitivity analysis, our single‐beat method was applied to the first PV loop during phase 2 of the Valsalva maneuver, instead of the signal‐averaged baseline PV loop. A strong correlation was still observed between the estimated and measured M_sw (r=0.89, P<0.0001).

Discussion

The present study showed, for the first time, that the slope of the PRSW relationship (ie, M_sw) can be accurately estimated from a single beat in the human RV by combining the following: (1) an estimation of the curvilinear ESPVR and EMPVR from the late‐systolic PV relationship and (2) a novel physiologic link between the EMPVR and PRSW relationship (which identifies the M_sw by determining the P_m when the end‐systolic volume is equal to V_sw). Moreover, our single‐beat approach is the first to successfully link the M_sw with the impedance of the vascular system to generate the ratio M_sw/P_m, thereby providing a simple yet reliable estimate of RV‐PA coupling. These attractive features of our single‐beat method should be of great clinical value for the assessment of RV contractile function and RV‐PA coupling, and thus can help improve the diagnosis and treatment of diseased RV in humans.

Single‐Beat Estimation of Human RV E_es and M_sw

Assessment of RV function is increasingly recognized because of growing recognition that RV function is strongly related to outcomes in several cardiovascular diseases, including PH, congenital heart disease, and left‐sided heart failure.2 However, commonly used clinical indexes of RV contractility, such as RV EF or tricuspid annular plane systolic excursion, are limited by their considerable load dependence.4 Both E_es and M_sw provide measures of an intrinsic contractile state that are largely independent of loading conditions, even for the RV,6, 14 but the clinical application of these indexes has been extremely limited by the need to record multiple beats over a wide volume range. Although several single‐beat methods for such indexes have been developed and validated for the LV,17, 22 the application of such methods to the RV has not necessarily been successful in the human RV. A single‐beat approach for estimating E_es using the sine‐wave fit, originally developed for the LV by Sunagawa et al,23, 24 is believed to work for the RV. This belief is based on indirect evidence from an animal study that the maximal pressure of isovolumetric contraction (during pulmonary artery clamping) can be predicted from sine‐wave fitting of the isovolumetric phase of RV pressure.8 However, this single‐beat method has never been validated in the human RV and was shown to agree poorly with measured E_es in an animal study.25 Furthermore, this estimate was not found to be associated with clinical outcomes in 2 recent studies.11, 12

This is the first study to demonstrate a single‐beat method that is valid for use in the human RV. We used a novel approach to estimate both the ESPVR and PRSW relationship, which has already been validated for the LV in our animal study.15 Because the ESPVR and PRSW relationships have different hemodynamic characteristics, using both relationships would be ideal to enhance clinical interpretation. The curvilinear ESPVR used in the present study is based on the concept proposed by Mirsky et al that the maximal myocardial stiffness (ie, stress/strain ratio of the ventricular wall) attained at end systole is constant throughout short‐term changes in preload and afterload.18 The estimation of ESPVR from the late systolic PV relation is based on the notion that the late systolic PV relation can be approximated as a set of PV data achieving maximal myocardial stiffness (ie, ESPVR).15 In fact, in our RV data, a near‐maximal myocardial stiffness (97.7% of the maximal myocardial stiffness on average) was already attained during late systole (ie, before end systole), which supports the use of a late systolic PV relation to estimate ESPVR in the human RV. Although the late systolic period can be short in some patients with PH, sufficient data acquisition for curve fitting was possible in the present study. We showed that the V₀ of the ESPVR can be accurately estimated using 20 data points on average (range, 9–56 points). Although curvilinear ESPVR models have been shown to provide a more reliable trajectory of the ESPVR than linear ESPVR,18, 26 it has not been widely acknowledged because it does not provide single numbers for contractility and for ventriculoarterial coupling, such as E_es and E_es/E_a. However, in the present study, because of a novel link between the ESPVR and the PRSW relationship that has been validated for the first time in the RV, the curvilinear ESPVR model was able to provide another load‐insensitive measure of contractility, the M_sw. Because the M_sw has many advantages over E_es, including its strong linearity over a wide range of physiologic loads and independence of chamber size and volume signal gain, our single‐beat method may be of great clinical value in assessing RV contractility in diseases of the right side of the heart.

Assessment of RV‐PA Coupling Using the M_sw

Despite the attractive features of the M_sw, as previously noted, one important limitation of the M_sw thus far has been the inability to relate it to PA loads in the PV plane to assess RV‐PA coupling. In the present study, we have resolved this long‐standing problem with the M_sw by developing a novel index of M_sw‐based RV‐PA coupling: M_sw/P_m, which is equal to the ${\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime }$ in the PV plane. Figure 3 shows that ${\mathrm{E}}_{\mathrm{es}}^{\prime }$ is the local slope of the EMPVR, which is analogous to a linear approximation of the curvilinear ESPVR and reflects intrinsic contractility (ie, M_sw adjusted by SV). More important, the afterload (${\mathrm{E}}_{\mathrm{a}}^{\prime }$) that is coupled with the ${\mathrm{E}}_{\mathrm{es}}^{\prime }$ represents an integrated form of vascular impedance (Data S2), which is known to provide a comprehensive description of both steady and pulsatile afterloads (including PA resistance and compliance). Thus, the ${\mathrm{E}}_{\mathrm{es}}^{\prime }-{\mathrm{E}}_{\mathrm{a}}^{\prime }$ framework is physically meaningful because it is derived mathematically from well‐established measures of contractility and vascular load. This is in contrast to the E_es‐E_a framework, wherein E_a is only indirectly related to vascular impedance.27 By considering P_m, rather than end‐systolic pressure (ie, at EMPVR rather than at ESPVR), one can assess RV‐PA coupling on the basis of ${\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime },$ in a similar way to E_es/E_a. Although a minor difference between end‐systolic pressure and P_m is expected in the LV, where the pulsatile component of the external ventricular power is far less than the steady component, a significant difference would exist for the RV, where the pulsatile power is reported to account for as much as 23% of the total ventricular power.20 This was clearly shown by only a moderate correlation (r=0.53) and a considerable difference in the range of change between multiple‐beat E_es/E_a and ${\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime }$ (ie, E_es/E_a[MB] and M_sw/P_m[MB]), as shown in Figure S1. We speculate that the optimal value for the novel index of RV‐PA coupling is ≈0.8 to 1.0, which was attained by those without PH (Figure S1). Although E_es/E_a is an established marker of RV‐PA coupling, ${\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime }$ potentially provides an even better characterization of RV‐PA coupling, considering the significantly pulsatile PA load caused by enhanced PA wall stiffness and its substantial impact on survival in PAH.28 Because survival in PAH is closely related to RV adaptation to the increased pressure overload (ie, RV‐PA coupling),1 whether the PRSW‐based RV‐PA coupling index (ie, M_sw/P_m or ${\mathrm{E}}_{\mathrm{es}}^{\prime }/{\mathrm{E}}_{\mathrm{a}}^{\prime }$) predicts clinical outcomes better than the traditional RV‐PA coupling indexes, such as RV EF or an ESPVR‐based index (E_es/E_a), warrants future investigations.

In the present study, although the agreement between estimated and measured ${\mathrm{E}}_{\mathrm{es}}^{\prime }$ on the basis of our single‐beat method was excellent, the correlation between measured and estimated RV‐PA coupling on the basis of the ${\mathrm{E}}_{\mathrm{es}}^{\prime }$ was only moderate for the whole population. This was mainly because the estimation of RV‐PA coupling was less accurate in those with low afterload, wherein a small estimation error in contractility would result in a relatively large estimation error in RV‐PA coupling (ie, ratio of contractility/afterload). However, RV‐PA coupling is of clinical issue for those with elevated RV pressure in the setting of PH. For such patients, our single‐beat method provided a better estimation of RV‐PA coupling (r=0.70).

Study Limitations

First, this was a retrospective single‐center study that enrolled a comparatively small number of patients. The sensitivity of our single‐beat M_sw to short‐term changes in inotropic status was not investigated in the present study, which needs to be elucidated in future investigations. Second, the formula used for modeling the curvilinear ESPVR in the present study was developed under the assumption of the ventricular shape to be prolate spheroid, and thus, the applicability of such a formula to the RV was not guaranteed.19 However, our single‐beat approach was capable of estimating the M_sw much more accurately than those based on a generally used linear ESPVR model, which provides strong evidence for the validity of our model. In addition, our single‐beat method has an advantage of allowing selection of any other ESPVR formulas for further refinement. Third, the algorithm of our single‐beat method may be somewhat complicated compared with that of the conventional single‐beat method for E_es using sine‐wave fitting. However, when the conventional sine‐wave fit was applied to our data,8, 25 the correlation between single‐ and multiple‐beat E_es was low (r=0.41), as shown in Figure S4, which would preclude a reliable assessment of contractility. A program to automate the data processing of our single‐beat method is provided in Data S3 for the readers’ wide use. Finally, our single‐beat approach still requires measurement of instantaneous PV data. A combination of the pressure recording of the normal right‐sided heart catheterization and flow/volume data on CMR would possibly provide a good approximation of the late systolic PV relation as well as the baseline SW necessary for our single‐beat approach. This needs further study.

Conclusions

A load‐insensitive measure of contractility, M_sw, for the human RV and its coupling to PA afterloads can be accurately estimated using our single‐beat approach. This approach would help in precisely assessing RV adaptation to increased pressure overload and thereby help improve the management of patients with PH.

Disclosures

None.

Supporting information

Data S1. End‐systolic pressure volume relationship based on maximum myocardial stiffness.

Data S2. Relationship between ${\mathrm{E}}_{\mathrm{a}}^{\prime }$ and pulmonary impedance.

Data S3. R code for our single‐beat method.

Figure S1. Relationship between conventional and novel indices of right ventricular–pulmonary arterial coupling.

Figure S2. Estimated and measured E_es.

Figure S3. Consistency assessment within multiple‐beat data.

Figure S4. Conventional single‐beat estimation of end‐systolic elastance (E_es) based on sine‐wave fit.

Figure S5. Iterative method used for single‐beat estimation of the end‐systolic pressure–volume relationship.

(J Am Heart Assoc. 2018;7:e007929 DOI: 10.1161/JAHA.117.007929.)29739798