Social contact patterns can buffer costs of forgetting in the evolution of cooperation

Abstract

Analyses of the evolution of cooperation often rely on two simplifying assumptions: (i) individuals interact equally frequently with all social network members and (ii) they accurately remember each partner's past cooperation or defection. Here, we examine how more realistic, skewed patterns of contact—in which individuals interact primarily with only a subset of their network's members—influence cooperation. In addition, we test whether skewed contact patterns can counteract the decrease in cooperation caused by memory errors (i.e. forgetting). Finally, we compare two types of memory error that vary in whether forgotten interactions are replaced with random actions or with actions from previous encounters. We use evolutionary simulations of repeated prisoner's dilemma games that vary agents' contact patterns, forgetting rates and types of memory error. We find that highly skewed contact patterns foster cooperation and also buffer the detrimental effects of forgetting. The type of memory error used also influences cooperation rates. Our findings reveal previously neglected but important roles of contact pattern, type of memory error and the interaction of contact pattern and memory on cooperation. Although cognitive limitations may constrain the evolution of cooperation, social contact patterns can counteract some of these constraints.

1. Introduction

From purchasing rounds of drinks at the local bar to helping a neighbour with a house repair, cooperative behaviour is a hallmark of human society. Yet, the emergence of cooperation seems to be a puzzling phenomenon: although it increases the greater good, it incurs costs to donors. To solve this puzzle, researchers have attempted to identify the factors that lead to the evolution of cooperation. One important determinant is the ability to reciprocate a partner's previous actions [1].

Because reciprocity requires repeated interactions with partners [2], cooperation depends on the social networks in which individuals interact, as they structure the pattern of interactions [3–5]. For instance, in networks with highly interconnected clusters of reciprocal cooperators, the benefits of mutual cooperation are particularly high [6].

To date, investigations on the influence of network structure on cooperation have primarily focused on the arrangement of connections between agents. However, the strength (or weight) of the connections—that is, the frequency of contact between agents—can critically impact network dynamics as well [7,8]. Past contact frequency is critical to cooperation because it increases the probability of future interactions [9–11] and thus should influence whether reciprocal cooperation can evolve. For simplicity, most models of cooperation assume equal contact frequencies with all partners. Empirical investigations, by contrast, have found that patterns of contact frequencies in social networks are skewed, with most interactions occurring with only a small fraction of their network's members [10,12]. It is currently unclear how differences in contact patterns—that is, whether the distribution of interactions across the members of one's network is equal or skewed—impact the evolution of cooperation. On the one hand, skewed contact patterns may create clusters of interactions and promote cooperation [6,13]. On the other hand, simulations of scale-free social networks have suggested that cooperation decreases with higher heterogeneity in connection weights [14]. This study, however, used arbitrary distributions of connection weights. Here we use agent-based simulations to investigate how empirically based skew in contact patterns influences cooperation and interacts with memory.

Many cooperative strategies rely on memory to track the agent's and/or the partner's past behaviour [15–17]. Tit-for-tat, for example, copies the partner's behaviour from the previous interaction, requiring that the agent remember whether the partner cooperated or defected [2]. Therefore, imperfections in memory due to forgetting can degrade cooperation for reciprocal strategies [18–20]. Yet, existing models have not investigated how these cognitive factors interact with the social environment (contact patterns) to influence the evolution of cooperation, so they may fail to capture a critical factor in these situations. We test the hypothesis that the impact of forgetting on cooperation may depend on the pattern of contact with one's partners.

Finally, we consider that the impact of forgetting on cooperation may differ depending on which type of memory error is assumed. In existing models, an agent forgets its partner's action with a particular error rate and then chooses cooperation and defection with equal probability [18–20]. When agents randomly guess actions like this, they will misremember half of the time. We propose a type of error that is new to models of cooperation in which, rather than randomly choosing an action, the agent skips the forgotten event and instead retrieves the memory of the most recent preceding event that is remembered. Whereas existing models of cooperation have considered only replacing forgotten interactions with random actions (guessing errors), here we also investigate memory errors that involve skipping entire episodes (skipping errors), providing a novel and more complete account of memory's role on cooperation. These guessing and skipping errors map onto errors of commission and omission, respectively. Distinguishing between these two kinds of errors led to important developments in the field of memory (e.g. the reliability of eye-witness testimony and memories of childhood sexual abuse), but the consequences of this distinction have yet to be been considered in investigations of the evolution of cooperation [21].

Using agent-based, evolutionary simulations [22], we study how patterns of contact in an agent's social network and memory failures affect the evolution of cooperation and, in particular, how these two components interact. We hypothesize that contact pattern will interact with the quality of memory to influence the evolution of cooperation. When contact frequency differs between network members, there is variation in the number of intervening interactions with other network members that occur between the interactions of a specific pair. When memory is imperfect, the contact pattern should influence the evolution of cooperation because the distribution of contacts determines the number of intervening interactions: the higher the relative frequency of interactions with a network member, the more recently, on average, the last interaction with that member will have occurred. As memory is more accurate for more recent events [23], there will be fewer memory errors for the interactions with network members with whom interactions are frequent. Better memory should promote the evolution of cooperation, but the size of the effect may depend on the contact pattern.

In our approach, we focus on repeated prisoner's dilemma situations [2,24]. In the simulations, each agent employed one of nine commonly modelled strategies [2,20] when interacting with other agents. When two agents interacted, they chose an action (cooperate or defect) and received a payoff based on the classic prisoner's dilemma payoff matrix [2]. At the end of one generation of interactions, the total payoff received by each agent determined how frequently that agent's strategy was represented in the next generation, thereby allowing the distribution of strategies to evolve over generations.

We implemented three types of contact pattern between agents (electronic supplementary material, figure S1). In the no-skew condition, the agents interacted with the members of their personal network with equal frequency. Many species, however, do not have the same number of interactions with everyone in their social network. In humans, the distribution of contact frequency is highly skewed, such that we frequently interact with some network members but infrequently interact with most network members [10,12]. Therefore, our simulations also included two skewed contact patterns: one (high skew) used a distribution of contacts that matched the empirical distribution in humans estimated by Pachur et al. [10], and the other (low skew) used a distribution with skew intermediate between high and no skew (electronic supplementary material, figure S1).

When two agents interact, they may use information about previous interactions, and accessing this information requires memory. A previous agent-based simulation investigated the evolution of cooperation across a wide range of forgetting error rates [20]. The results demonstrated that cooperation could evolve with very low levels of forgetting, but defection dominated with forgetting rates higher than 5%. Therefore, in addition to varying the contact pattern, we varied the forgetting rate, using a standard forgetting function from cognitive psychology [25,26] (electronic supplementary material, figure S2). We used empirical estimates of these parameters from humans [20], along with higher and lower rates. To investigate the interplay of contact pattern and forgetting in shaping the evolution of cooperation, we considered memory errors of both guessing and skipping.

In sum, our simulation investigated how cooperation evolves under different combinations of contact patterns (no, low or high skew), forgetting rates and types of memory error (guessing and skipping errors).

2. Methods

(a). Agents

Each simulated agent was assigned one of nine different strategies: all cooperate, all defect, tit-for-tat, tit-for-two-tats, generous tit-for-tat, contrite tit-for-tat, grim trigger, win-stay-lose-shift and random (electronic supplementary material, table S1). These are commonly used strategies in the literature [20] that represent a range of reactions to partner actions. Each simulation run started with an equal number of agents using one of the nine strategies. The population size was fixed at 90, with 10 agents for each strategy.

(b). Variation of memory

We varied memory of agents on two dimensions: probability of forgetting and type of memory error. We modelled the probability that individuals correctly remembered an interaction in the past based on the idea that an agent's intervening interactions increased forgetting. Specifically, we set the probability of correctly remembering a previous interaction (p) to a modified version of Wickelgren's [25] forgetting function [26]: p = λ(k + 1)^−ψ, where λ and ψ are parameters defining the starting point and the decay rate of the forgetting function, and k represents the number of interactions between the target and the current interaction. We created seven different forgetting rates by varying the two parameters (electronic supplementary material, figure S2).

We also varied the type of memory error. When skipping encounters, agents completely forgot the interaction (both the agent's and partner's action) and thus consulted the past history of interactions to replace the forgotten information with the actions from the immediately preceding interaction that was remembered to determine the current action. With random guessing, the agent replaced the memory of a forgotten interaction with a random memory of actions (cooperate or defect with equal probability) for both itself and its partner. For both types of error, these replacement actions were incorporated into the agent's history of interactions and used to select the next action based on its strategy.

(c). Contact patterns

For the simulation, we considered a population of 90 agents. These agents were placed on a network such that each agent had 10 neighbours. In the no-skew distribution, agents played an equal number of 10 rounds against all of their neighbours, such that each agent participated in 100 interactions in total. The other two environments redistributed the total of 100 interactions per player. Specifically, we considered the following distribution of interactions illustrated by three vectors that give the number of interactions with each partner: no skew 〈10, 10, 10, 10, 10, 10, 10, 10, 10, 10〉, low skew 〈19, 16, 14, 11, 10, 8, 7, 6, 5, 4〉 and high skew 〈33, 23, 15, 10, 7, 5, 3, 2, 1, 1〉 (electronic supplementary material, figure S1). Each agent's interaction pattern exactly matched the vector corresponding to its respective skew condition. To create the complete set of interactions for all agents in a population, an algorithm first paired each agent with its 10 partners as specified by the skew vector. Then, it appended all of these interactions into a single list and randomly shuffled all of the interactions.

(d). Simulation setup

The actions of the two agents determined the payoffs received for an interaction, based on the classic prisoner's dilemma payoff matrix [2] (table 1). We summed the payoffs for each agent's 100 interactions to generate its fitness score, which determined the distribution of strategies in the following generation using a roulette-wheel selection operator [27]. The chance of replicating a specific agent's strategy was proportional to its share of the total fitness scores among all agents. We repeated this procedure for 250 generations, and for each environment we conducted 1000 replicates. In addition, we conducted sensitivity analysis simulations that varied the number of interactions per agent (200, 500 and 1500), the payoff matrix and the selection operator. We report the distribution of strategies and the proportion of cooperative choices in the final (250th) generation averaged across 1000 trials for each environment.

Table 1.

Payoff matrix for agent based on agent's and partner's action.

		partner
		C	D
agent	C	3	0
	D	5	1

(e). Data analysis

We conducted the simulations in MATLAB and analysed the data using R v. 3.4.4 [28]. MATLAB code, data and R code and packages used are available in electronic supplementary material and at the Dryad Data Repository [29] and the Open Science Framework (https://osf.io/a7d3b/).

3. Results

(a). Cooperation rates

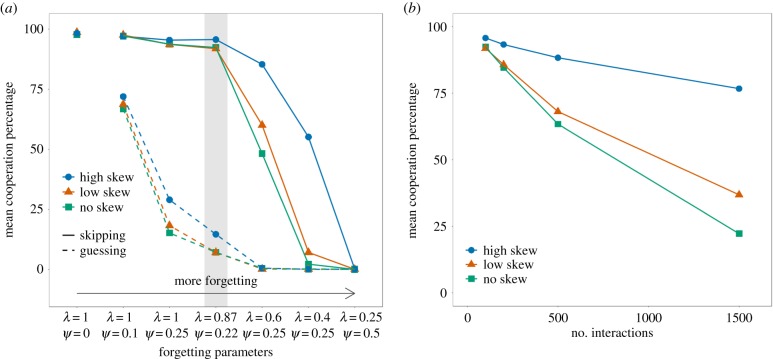
Figure 1 illustrates the effect of contact pattern, forgetting rate and memory error type on cooperation rates in each of our 39 environments (each point in the figure represents one environment). Cooperation rates peaked at 98% when there was no forgetting. As forgetting increased, cooperation rates dropped, replicating other work showing the fragility of cooperation when faced with forgetting [18–20]. The rate of cooperation evolved differently depending on the type of memory error used. Collapsed across all conditions, mean cooperation rates were higher for errors caused by skipping (62%) than for errors caused by guessing (17%). This probably reflected the fact that, compared to the skipping condition, agents in the guessing condition were more likely to select a different action than that expected with perfect memory, which also resulted in more defection (electronic supplementary material, figure S3). Thus, when information was lost, memory that reverted to records of previous interactions with that partner rather than randomly choosing an action led to higher levels of cooperation.

Figure 1.

(a) Mean cooperation rate across all strategies in the final generation varied based on level of skew in contact pattern (no skew, low skew, high skew), forgetting rate (λ specifies starting point, ψ specifies decay rate) and type of memory error (guessing or skipping). Each agent experienced 100 interactions spread across 10 partners. Shaded area highlights the empirically derived forgetting parameters. Standard error of the mean error bars are not shown because they are smaller than the data point symbols. (b) Mean cooperation rate across all strategies in the final generation varied based on the number of interactions that partners experienced (100, 200, 500 and 1500) and contact pattern skew for the λ = 0.87, ψ = 0.22 skipping condition. (Online version in colour.)

Importantly, the detrimental effects of forgetting on the evolved cooperation rate depended on the degree of skew in the contact pattern. Specifically, in the conditions with a highly skewed distribution, the decline in the rate of cooperation across forgetting rates was less steep than in the conditions with low- or no-skew contact patterns. In other words, a skewed distribution buffered the detrimental effects of forgetting on cooperation. The magnitude of this buffering effect depended on the forgetting rate and type of memory error. For illustration, with guessing errors, simulations with forgetting parameters of λ = 1, ψ = 0.25 and no skew reduced cooperation rates by 85% compared to perfect memory. The high-skew condition, however, reduced cooperation rates by only 71%, thus buffering the drop in cooperation by 14 percentage points. At forgetting rates approximating empirically measured ones (λ = 0.87, ψ = 0.22), high skew buffered the drop in cooperation by 7 percentage points. With skipping errors, the buffering effect of a skewed contact pattern was even stronger, up to 53 percentage points. Overall, these results demonstrate that the emergence of cooperation was strongly affected by the pattern of contact frequency in an agent's social network. In addition, the contact pattern buffered negative effects of forgetting on the evolution of cooperation. These findings replicated both with a more cooperation-friendly payoff matrix (electronic supplementary material, figures S4 and S5) and with two other selection operators (electronic supplementary material, figure S6).

For computational reasons, our simulation only included 10 social partners per agent. But many social animals, including humans, have many more social partners than this. To determine whether the buffering effect of contact pattern on forgetting is influenced by the number of partners, we increased the number of interactions that the agents experienced in their lifetime. We inserted these interactions as ‘filler’ interactions without actually assigning partners or calculating their payoffs. Instead, they acted as additional intervening interactions, thus mimicking an increase in the number of partners without substantially increasing the computational load of the simulation (see electronic supplementary material for details). Increasing the number of interactions decreased the cooperation rate. Most importantly, however, the decrease in cooperation with increasing numbers of interactions was again buffered by skew: agents in the no-skew condition showed a much steeper drop in cooperation with interaction number than those in the high-skew condition (figure 1). The condition with 1500 interactions is analogous to a social network size of 150 individuals, which matches Dunbar's [30] estimate for the size of human social groups. Thus, with an empirically estimated social network size (1500 interactions or 150 individuals) and contact pattern (high skew), cooperation is maintained at high levels, even with empirically estimated forgetting rates.

(b). Strategy composition

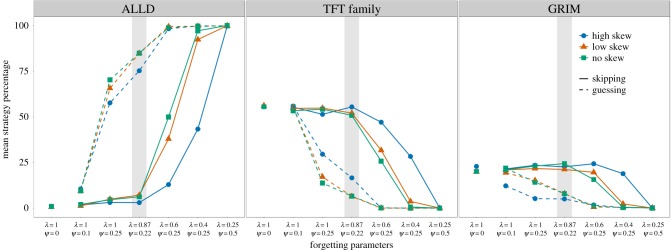
Cooperation rates are determined by the composition and interaction of strategies in the population, so the observed effects on cooperation rates depend on the architecture of the decision strategies. To examine how the impact of contact pattern on the detrimental effect of forgetting depends on the decision strategy, we also investigated how the individual strategies responded to variations in our environments. Figure 2 illustrates the effects of contact pattern, forgetting rate and type of memory error on three strategies whose performance in a previous study [20] depended on forgetting rates (electronic supplementary material, figure S7 includes all strategies). All defect (ALLD) showed the opposite pattern to the cooperation rate in figure 1: (i) less defection with high skew and intermediate error rates, and (ii) less defection with skipping errors than guessing errors. The tit-for-tat-derived strategies showed similar patterns to each other, so we aggregated them into a TFT family. The results for the TFT family mirrored those of the cooperation rate, suggesting that the TFT-derived strategies underpinned the buffering effects on cooperation rates. The third major strategy influencing cooperation rates was grim trigger (GRIM). With skipping errors, skewed contact pattern also buffered GRIM against memory errors. This was not the case, however, with guessing errors: GRIM performed worst, with a highly skewed distribution. Therefore, the effects of contact pattern, forgetting rate and memory error type interacted to have differential effects on different strategies.

Figure 2.

Mean percentage of each strategy in the population varied based on level of skew in contact pattern (no skew, low skew, high skew), forgetting rate (λ specifies starting point, ψ specifies decay rate) and type of memory error (guessing or skipping). ALLD represents all defect strategy. TFT family sums the percentages from strategies tit-for-tat, tit-for-two-tats, generous tit-for-tat and contrite tit-for-tat. GRIM represents grim trigger strategy. Standard error of the mean error bars are not shown because they are smaller than the data point symbols. (Online version in colour.)

4. Discussion

Our simulation results provide several major contributions to understanding the evolution of cooperation. First, our simulations (1) integrate into models of cooperation manipulations of contact pattern, forgetting rate and type of memory error, and (2) use empirically derived estimates of these measures in humans. Our estimates provide empirically based evaluation of the cognitive and environmental conditions relevant for the evolution of cooperation.

Second, our results demonstrate that skewed distributions of contact can enhance cooperation by buffering effects of forgetting. This key finding qualifies previous analyses of the evolution of cooperation and the detrimental role of cognitive limitations. Our results indicate that future empirical studies of cooperation should measure patterns of contact across species and future theoretical studies of cooperation should incorporate empirically derived distributions of contact frequency in their models.

Third, the effect of contact patterns and forgetting on cooperation is mainly driven by TFT-derived strategies (though win-stay-lose-shift can increase with other payoff matrices; electronic supplementary material, figure S5). At intermediate forgetting rates, cooperative strategies (particularly members of the TFT family) perform better with a highly skewed contact pattern than with low- or no-skew distributions. Skewed contact patterns allow cooperative strategies to interact more with other cooperative strategies because more of their total encounters are allocated to a subset of network members who cooperate. This parallels a similar phenomenon in scale-free networks in which clusters of cooperators are created [13]. This buffering effect of skew is modulated by the type of memory error, with better performance observed with skipping than guessing.

Fourth, different strategies react differently to the two types of memory error. The TFT-family strategies are more successful with highly skewed than non-skewed contact patterns across both types of forgetting. Though GRIM shows an increase in frequency with skew for skipping errors, it shows a decrease in frequency with skew for guessing errors. This results from GRIM's trigger rule of constant defection following a single defection by the partner. With guessing errors, when GRIM forgets, it randomly chooses between cooperation and defection, thereby resulting in a 75% chance of triggering constant defection for the future unless another error occurs. This prevents it from taking advantage of the cooperative nature of the TFT-family strategies. With skipping errors, however, when GRIM forgets, it simply goes back one more interaction. Assuming the partner cooperated in that interaction, this prevents GRIM from triggering constant defection and allows it to maintain cooperation with cooperative strategies. Thus, the effectiveness of cooperative strategies depends critically on specific cognitive processes such as memory.

Fifth, we test a form of memory error that plays an important role in human memory but has not been incorporated into models of cooperation. Skipping errors provide a stronger buffering effect than guessing errors. Compared with guessing errors, skipping errors result in a lower percentage of interactions in which agents select a different action than that expected with perfect memory (electronic supplementary material, figure S3). Skipping back to previous memories results in more benign errors than randomly guessing, thereby maintaining cooperation. Currently, the norm in theoretical analysis is to implement memory errors only in terms of random guessing. This, however, is only one way in which memory error might be implemented, and our results underscore that different implementations of errors can lead to different results.

Researchers of cooperation have treated forgetting as an impediment that may constrain the evolution of cooperation. A certain rate of forgetting, however, may provide fitness benefits. For instance, forgetting can be an adaptive response to a changing environment [9,21,31]. Thus, evolved rates of forgetting might depend on the structure of interactions. When there are skipping errors, for example, forgetting can actually benefit GRIM when interacting with cooperative strategies. Forgetting a mistaken defection by a partner can rescue both players from perpetual defection. Therefore, we must treat forgetting not as a fixed constraint on the evolution of cooperation but as a dynamic trait that may co-evolve with cooperative strategies. This is evidenced by empirical work demonstrating that, in some circumstances, people remember defection better than cooperation [32,33]. Future modelling efforts could incorporate differential forgetting rates for cooperation and defection. In addition, it could be useful to empirically investigate memory processes for cooperation (e.g. differential position effects for cooperators and defectors) in greater detail. Further, the types of memory error might also co-evolve, such that, when there are strong selective pressures for cooperation, memory may evolve to be relatively robust against guessing errors. Future work is needed to further understand the co-evolution of cognition and cooperation.

Both social networks [34] and cognition [35] are complex, dynamic systems whose components yield emergent behaviour. Combining these two complex systems can produce difficult-to-predict interactions. Yet, understanding the evolution of behaviour requires the joint study of the behavioural environment and cognition, as proposed by Simon's [36] notion of bounded rationality. For Simon, understanding decision-making requires the investigation of both the ‘structure of task environments and the computational capabilities of the actor’ ([36], p. 7). Simon's admonition to study both the environment and cognition suggests that these two components of bounded rationality must be integrated to fully understand behaviour. Our results support this notion by demonstrating an interaction between the environment and cognition—both must be included to understand the evolution of cooperation. To fully grasp when and why humans and other species cooperate, we must model both the structure of the environment and the cognitive capabilities of the actors together. With these models in hand, we can make new predictions about the likelihood of cooperation and the frequency of cooperative strategies evolving across a wide range of species and environments.

Data accessibility

MATLAB code, data and R code and packages used are available in electronic supplementary material and at the Dryad Data Repository [29] and the Open Science Framework (https://osf.io/a7d3b/).

Author's contributions

J.R.S., J.K.W., L.J.S. and T.P. designed research; J.K.W. and S.L. performed research; J.R.S. and J.K.W. analysed data; and J.R.S, J.K.W., L.J.S. and T.P. wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

We would like to thank the Max Planck Society for funding this project.