A computational approach for predicting off-target toxicity of antiviral ribonucleoside analogues to mitochondrial RNA polymerase

Abstract

In the development of antiviral drugs that target viral RNA-dependent RNA polymerases, off-target toxicity caused by the inhibition of the human mitochondrial RNA polymerase (POLRMT) is a major liability. Therefore, it is essential that all new ribonucleoside analogue drugs be accurately screened for POLRMT inhibition. A computational tool that can accurately predict NTP binding to POLRMT could assist in evaluating any potential toxicity and in designing possible salvaging strategies. Using the available crystal structure of POLRMT bound to an RNA transcript, here we created a model of POLRMT with an NTP molecule bound in the active site. Furthermore, we implemented a computational screening procedure that determines the relative binding free energy of an NTP analogue to POLRMT by free energy perturbation (FEP), i.e. a simulation in which the natural NTP molecule is slowly transformed into the analogue and back. In each direction, the transformation was performed over 40 ns of simulation on our IBM Blue Gene Q supercomputer. This procedure was validated across a panel of drugs for which experimental dissociation constants were available, showing that NTP relative binding free energies could be predicted to within 0.97 kcal/mol of the experimental values on average. These results demonstrate for the first time that free-energy simulation can be a useful tool for predicting binding affinities of NTP analogues to a polymerase. We expect that our model, together with similar models of viral polymerases, will be very useful in the screening and future design of NTP inhibitors of viral polymerases that have no mitochondrial toxicity.

Introduction

The mitochondria contain their own circular dsDNA genome that encodes 13 proteins involved in the electron transfer chain, in addition to 2 rRNAs and 22 tRNAs (1). This genome is replicated by mitochondrial DNA polymerase γ and transcribed by human mitochondrial DNA-directed RNA polymerase, known as POLRMT.³ These polymerases are themselves encoded by nuclear DNA.

The inhibition of viral polymerases by nucleoside analogues has been the cornerstone of therapies against multiple pathogenic viruses, including HIV, hepatitis B virus, hepatitis C virus (HCV), and Herpesvirus. In particular, many viruses possessing RNA genomes, such as HCV, use RNA-dependent RNA polymerases for replication, which have been very successful targets for the development of antiviral drugs including ribonucleoside analogues. Ribonucleoside analogue drugs are converted to their active ribonucleoside triphosphate form by human kinases. After more than a decade of research aimed at identifying an anti-HCV ribonucleoside analogue, sofosbuvir was approved for medical use in the United States in 2013. Along the way, multiple attempts to develop ribonucleoside antivirals had to be discontinued because of toxicity, including NM283, R1626, PSI-938, and BMS-986094 (2–5). It had been known for years that deoxyribonucleoside analogues were associated with side effects caused by mitochondrial toxicity and off-target interactions with mitochondrial DNA polymerase in particular (6). However, it was not until 2012 that research performed by Arnold et al. (3) established that POLRMT is a major source of off-target toxicity for nucleoside analogue antivirals aimed at inhibiting microbial RNA polymerases. This work emphasized the need for setting up accurate screening tests for the interactions of ribonucleoside antivirals with POLRMT. One serious concern cited was that although nuclear RNA polymerase II has a proofreading mechanism through the activity of TFIIS, there does not seem to be any nucleotide excision mechanism in place for POLRMT (3). Pyrimidine nucleotide analogues pose an even greater risk for POLRMT inhibition than ATP derivatives, because CTP and UTP are present at 1–2 orders of magnitude lower concentrations in the mitochondria than ATP (1).

On the computational side, one previous predictive model of the mitochondrial toxicity of pharmaceutical drugs has focused on a cheminformatics approach (7). Here we describe the development of a computational model based upon the available crystal structure (8) that allows for the accurate prediction of relative binding affinities of NTPs to the POLRMT structure.

The detailed molecular structure of POLRMT as a closed-product elongation complex bound to template DNA and a small RNA transcript has been provided by X-ray crystallography, allowing for insights into NTP binding within the active site (Protein Data Bank code 4BOC) (8). The closed product is one of four stages of the nucleotide addition cycle of polymerases. In this cycle, an NTP first binds to the open post-translocated state of the polymerase, the complex undergoes a conformational change to the new pre-translocated insertion state, chemical reaction occurs leading to the closed product state, and finally translocation returns the system to the open product complex (9). To assess POLRMT inhibition, we had to create a model of the pre-translocated insertion state. We therefore adjusted the 4BOC structure to make it representative of the insertion state by using the crystal structure of the insertion state of the bacteriophage T7 RNA polymerase to which POLRMT is evolutionarily related (10, 11), to model the nucleoside triphosphate CTP and that of T7 DNA polymerase to model the active site metal ions (12). We also constructed models with each of ATP and GTP in the POLRMT nucleotide-binding site.

In our model development and validation, we take advantage of the experimentally determined dissociation constants for a panel of NTP analogues that were determined using a biochemical assay by Arnold et al. (3). The binding free-energy differences of these NTP analogues are determined relative to the binding free energies of the respective natural NTPs using the FEP methodology. FEP has the advantage over other less rigorous methods of being formally exact in the limit of complete phase-space sampling but requires lengthy simulations (13–17). Although using FEP to determine binding free energies is quite well-studied (16, 18), to the best of our knowledge this study is the first one to report the use of FEP to calculate binding free energies of NTP analogues to a polymerase.

Binding free energies of NTP analogues to polymerases are particularly hard to compute as averages over molecular dynamics simulations because of the high negative charge of −4e on nucleoside triphosphates; that is, the response in the fluctuation of the environment to fluctuations in the positions of the charged phosphates and metal ions may be expected to occur on a slower time scale than for systems with less charge polarization, leading to slow convergence of computed binding free energies. To converge results, we have performed lengthy simulations on our IBM Blue Gene Q supercomputer (see below for details). We note that in FEP, only relative binding free energies are calculated, i.e. binding free-energy differences between different NTPs, instead of absolute binding free energies. This facilitates convergence because fluctuations in energy caused by fluctuations in charge density cancel out when the energetic difference is calculated for two NTPs. Relative binding free energies are determined using a thermodynamic cycle, i.e. from the difference between the free energy change for the transformation of the natural NTP to its analogue in aqueous solution and the corresponding free energy change within the solvated protein-bound environment (19).

The FEP approach presented here can be applied to the rational salvaging of drug candidates found to inhibit POLRMT and moreover can be extended to applications to viral polymerases in general. When combined with experimental testing, it suggests an efficient strategic means for identifying nucleoside antivirals with high specificity and affinity for viral polymerases, leading to the design of safe and effective drugs.

Results

Molecular dynamics simulations of the NTP insertion state of POLRMT

We have performed molecular dynamics simulations of our model of the POLRMT NTP insertion state, which is based on the 4BOC (8) crystal structure of the POLRMT elongation complex. POLRMT is a 1230-amino acid protein consisting of three domains, namely the N-terminal extension (NTE) located at the very N terminus of the protein (residues 1–368), the N-terminal domain (residues 369–647) that follows the NTE in the primary sequence, and the C-terminal polymerase domain (residues 648–1230) (1). The polymerase domain has the classic structure resembling a cupped right hand as is seen in the RNA-dependent polymerases of viruses and bacteriophages and in DNA polymerases (Fig. 1). It has 41% sequence similarity and 25% sequence identity to T7 RNA polymerase (20). The pentatricopeptide repeat, making up the C terminus of the NTE, the N-terminal domain, and the C-terminal domain all are present in the 4BOC crystal structure and in our model.

Figure 1.

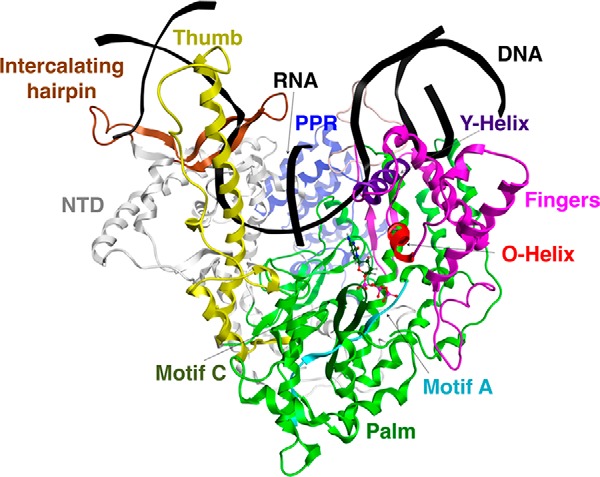
Molecular model of the nucleotide insertion state of POLRMT. Shown is a ribbon representation of our computational model of POLRMT in complex with DNA template and nontemplate strands, an RNA transcript, and an incoming CTP, with important domains and subdomains, which are discussed in the text, labeled. The upstream end of the template DNA is on the left-hand side of the figure, and the downstream end is on the right. Part of the nontemplate DNA forming the bubble region is missing from our model. PPR, pentatricopeptide repeat; NTD, N-terminal domain.

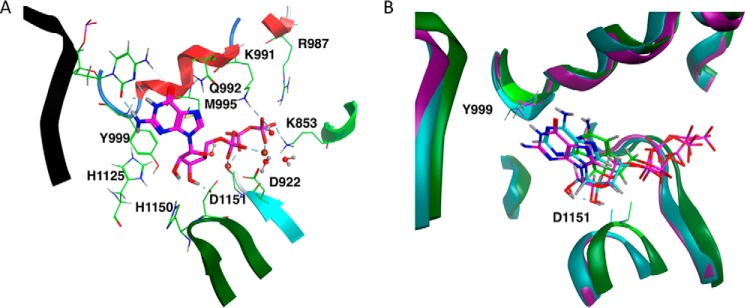
The NTP-binding pocket is located on top of the center of the palm and is formed mainly by structural motifs A and C, and the helical motif B, also known as the O-helix, belonging to the fingers region (Fig. 2A). Conserved residues within the active site contribute to the formation of the catalytic complex. Several residues are involved in coordinating the two active site Mg²⁺ metal ions, A and B (Fig. 2A). In our model (Fig. 2A), the side chains of two conserved Asp residues, Asp⁹²² and Asp¹¹⁵¹, respectively, belonging to motifs A and C help to coordinate metal A, along with the 3′OH O atom of the NTP, an α-phosphoryl O atom of the NTP, the main-chain carbonyl O atom of Gly⁹²³, and a water molecule. Metal B is coordinated by β- and γ-phosphoryl O atoms of the NTP, the Asp⁹²² side chain, and three water molecules. The NTP is bound to the polymerase principally by the electrostatic interaction between the highly charged triphosphate group and positively charged residues in the active site, namely Lys⁸⁵³, Arg⁹⁸⁷, and Lys⁹⁹¹ (8). As seen in Fig. 2A, the NTP is also stabilized by a sulfur-π interaction with residue M995 belonging to the O-helix in our model.

Figure 2.

Active site of our computational model of the POLRMT complex. A, active site of the GTP-bound complex, with conserved catalytic residues, and residues and water molecules important in coordinating active site Mg²⁺ metal ions displayed in line representation and GTP in stick mode. Metal ion A is to the left of metal ion B, and both are shown as spheres. B, comparison between the active sites of the GTP-, ATP-, and CTP-bound POLRMT complexes averaged over simulation trajectories, shown in magenta, teal, and green, respectively. For each system, the NTP molecule is shown in stick mode, and α and β carbons of the catalytic residues Tyr⁹⁹⁹ and Asp¹¹⁵¹ are shown in line mode.

A bound NTP is thought to be distinguished from a deoxyribonucleoside triphosphate because of the hydrogen bond formed by the NTP 2′OH to residue Tyr⁹⁹⁹ (8) (Fig. 2). In Fig. 3, we plot the distance between the hydroxyl H atom of the Tyr⁹⁹⁹ side chain and the 2′-hydroxyl O atom of the bound ribonucleotide as a function of time for the second half of the simulation of the CTP-bound complex (A) and for the ATP- and GTP-bound complexes (B and C, respectively). Based on the plots, whereas the hydrogen bond is largely maintained throughout all three simulations, the hydrogen bond distance is significantly larger on average for the CTP-bound complex than for the two purine-nucleotide-bound complexes. This hydrogen bond is particularly stable for the ATP-bound complex.

Figure 3.

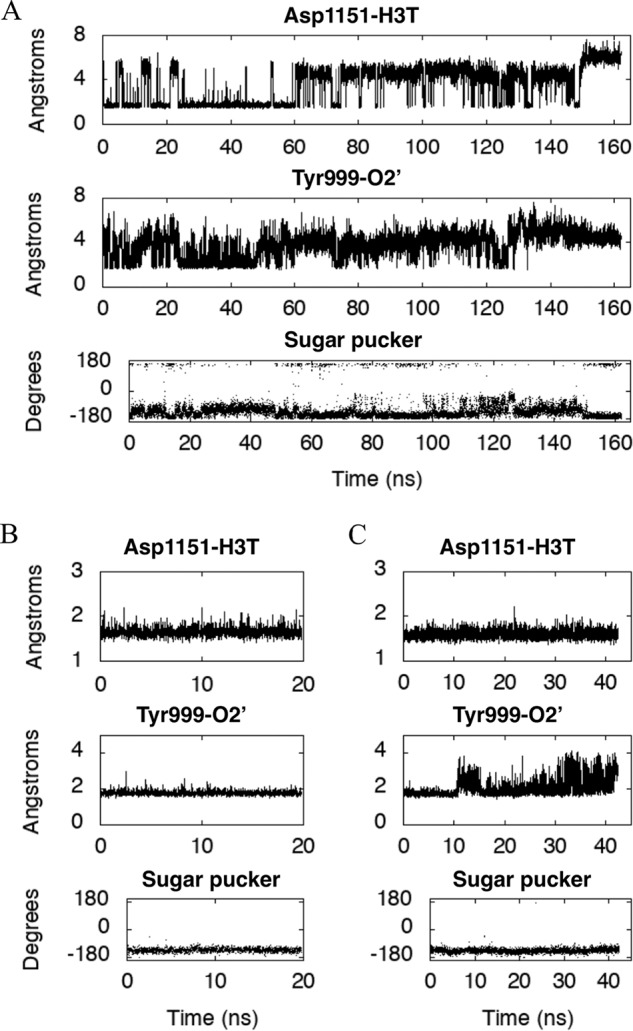
Geometric parameters characterizing the structure of our POLRMT model. Shown are the distances (Å), plotted for our model of the POLRMT complex as a function of simulation time (ns) between the acidic O atom of the Asp¹¹⁵¹ side chain and the 3′-hydroxyl H atom H3T of the bound NTP (top panels) and between the hydroxyl H atom of the Tyr⁹⁹⁹ side chain and the 2′-hydroxyl O atom O₂′ of the bound NTP (middle panels). In the bottom panels, the sugar pucker of the ribose belonging to the bound NTP is plotted as a function of simulation time (ns). The bound NTP is CTP in A, ATP in B, and GTP in C.

The nucleotidyl transfer mechanism of POLRMT includes two proton transfer reactions, and conserved residues help to catalyze this mechanism (21–23). The first proton transfer occurs during the nucleophilic attack of the RNA transcript's 3′ hydroxyl O atom on the α-phosphate of the incoming NTP to create a new phosphodiester bond. During this step, a proton is transferred from the 3′-hydroxyl O atom to a catalytic base, thought to be Asp¹¹⁵¹ (8) (Fig. 2). In Fig. 3, we plotted the distance between the acidic O atom of the Asp¹¹⁵¹ side chain and the 3′-hydroxyl H atom H3T of the bound nucleotide as a function of time for each of the CTP-, ATP-, and GTP-bound complexes; note that this distance is on average much closer for both the purine-nucleotide-bound complexes than for the CTP-bound complex. Metal A stabilizes this proton transfer by lowering the pkA of the 3′-hydroxyl group. In the course of the nucleotide addition reaction, the pyrophosphate leaving group also becomes protonated in the second proton-transfer reaction, with a residue from the O-helix acting as the proton donor (1), and metal B helping to stabilize this acid-catalysis step.

In Fig. 3, we also plot the ribose pucker, or pseudorotation angle, as a function of time for the NTP molecule belonging to each of the three nucleotide-bound complexes. In the case of the ATP- and GTP-bound complexes, the pseudorotation angle generally lies in the interval from −144 to −108°, known as the C4′-endo configuration. For CTP-bound POLRMT, the pseudorotation angle is generally either in the C4′-endo configuration or in the C3′-exo configuration (−180 to −144°) or more rarely in the C2′-endo configuration (144 to 180°) or in the O4′-exo configuration (−108 to −72°) (24).

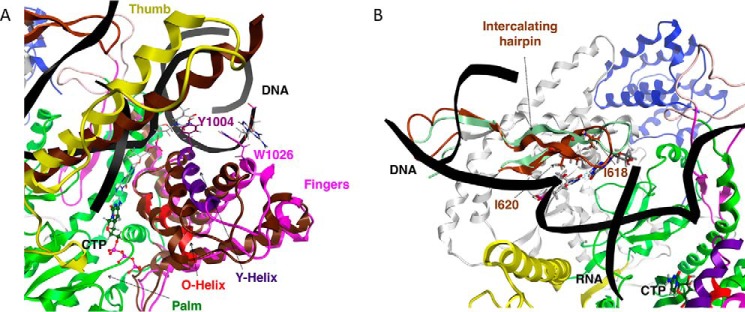
As mentioned above, during nucleotide addition, the POLRMT catalytic complex cycles from an open state to a closed state and back. It has been suggested that this cycling is driven by the interaction between the O-helix and the incoming NTP (1). As the NTP enters, the complex is in an open state and later forms a catalytically competent closed or clenched state in which the fingers, including the Y-helix, reposition, and the entrance to the active site is temporarily blocked (1). This closed structure, seen in the crystallized structure of the closed product state (8), is known as a clenched conformation. Tyr¹⁰⁰⁴, belonging to the Y-helix, and Trp¹⁰²⁶, belonging to another helix of the fingers domain, base-stack with the base at the +1 position in the template DNA and the base at the 0 position in the nontemplate DNA, respectively. These interactions between the fingers domain and the DNA maintain the separation of the two strands of the downstream DNA (8). In Fig. 4A, we show a comparison between the positions of the fingers in our model of the CTP-bound POLRMT complex and their corresponding positions in the aligned 4BOC structure of the closed product complex. As might be expected, the fingers take on a somewhat more open configuration in our model of the nucleotide insertion state compared with in the closed-product elongation complex.

Figure 4.

Nucleic acid strand separation in our model of the CTP-bound POLRMT complex. A, the separation of downstream DNA strands by conserved residues in the fingers subdomain. The positions of the fingers and thumb subdomains are compared with their corresponding positions in the 4BOC starting structure, shown in dark brown. Line representation is used to show Tyr¹⁰⁰⁴ and Trp¹⁰²⁶, and the DNA template and nontemplate bases that interact with Tyr¹⁰⁰⁴ and Trp¹⁰²⁶, respectively; CTP is shown in ball-and-stick mode. B, the separation of the upstream DNA template from the RNA transcript by conserved residues belonging to the intercalating hairpin. The position of the intercalating hairpin is compared with its corresponding position in the 4BOC starting structure, shown in light green. Line representation is used to show Ile⁶¹⁸ and Ile⁶²⁰, and the RNA transcript and DNA template bases that interact with Ile⁶¹⁸ and Ile⁶²⁰, respectively; CTP is shown in ball-and-stick mode.

We have also computed the tilt angle as a function of time for the bundle of helices in the fingers domain including the O- and Y-helices and the helices composed of residues 954–974, 1024–1044, and 1044–1064, respectively, for the CTP-bound POLRMT complex (Fig. 5). It may be seen from the figure that all of the helices reorient within the bundle. The O and Y helices and the 1044–1064 helix eventually settle into new stable conformations, whereas the helices composed of residues 954–974 and 1024–1044, respectively, continue to undergo large fluctuations in helical tilt during the second half of the simulation.

Figure 5.

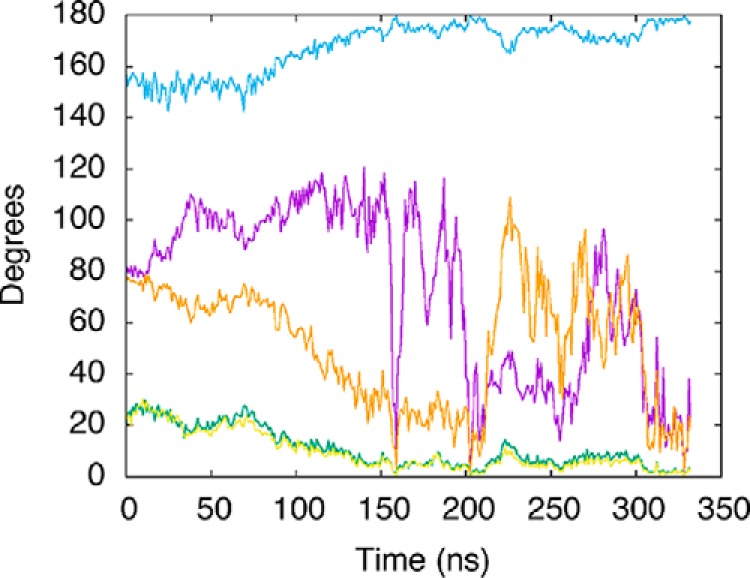
Tilt of axes corresponding to a bundle of helices in the POLRMT finger subdomain. Tilt, with respect to the average axis, is plotted as a function of time for the CTP-bound POLRMT complex. These helices include the helix composed of residues 954–974 (purple line), the O-helix (residues 986–997, green line), the Y-helix (residues 1002–1016, blue line), and the helices composed of residues 1024–1044 (orange line) and 1044–1064 (yellow line).

The thumb domain (residues 705–790) contains a long α-helix that interacts with and stabilizes the DNA template during transcript elongation (1, 8, 25). In Fig. 4A, we compare its position in our model of the insertion state to its position in the crystal structure of the closed product state. Like the fingers domain, it also appears more open in our model of the insertion state compared with in the closed product complex.

The intercalating hairpin of POLRMT (residues 591–624) separates the upstream DNA template strand from the RNA transcript in the elongation complex. The separation of upstream DNA from the transcript allows for the displacement of the transcript and its exit through a channel toward the back of the complex oriented as shown in Figs. 1 and 4. This interaction involves residues Ile⁶²⁰ and Ile⁶¹⁸ in the 4BOC crystal structure (8), and these interactions are retained in our model (Fig. 4B). In our model in Fig. 4B, the intercalating hairpin, colored in brown, has moved closer to the template DNA strand by comparison to its position in 4BOC, shown in light green.

Binding affinities from FEP

Our model contains two active site histidine residues, one of which, His¹¹⁵⁰, is near the ribose moiety of the bound NTP molecule, and the other of which, His¹¹²⁵, is separated from the NTP by residue Tyr⁹⁹⁹. Because the charge states of these two histidine residues may impact the strength of nucleotide binding in our calculations, we first sought to determine these charge states by performing explicitly solvated constant pH molecular dynamics simulations. Simulations were performed both for the ATP-bound POLRMT complex and for the apo POLRMT complex. For both simulations, His¹¹²⁵ was found to have a charge of +1, and His¹¹⁵⁰ was found to be neutral for almost the entire trajectories. On the other hand, when we performed implicitly solvated constant pH molecular dynamics simulations at pH 7.8 of the ATP-bound complex, we found that His¹¹²⁵ was neutral for 89% of the trajectory, whereas His¹¹⁵⁰ was again found to be neutral throughout almost the entire simulation. Because implicitly solvated simulations are expected to be less accurate than explicitly solvated simulations, it is likely that His¹¹²⁵ has a charged state of +1.

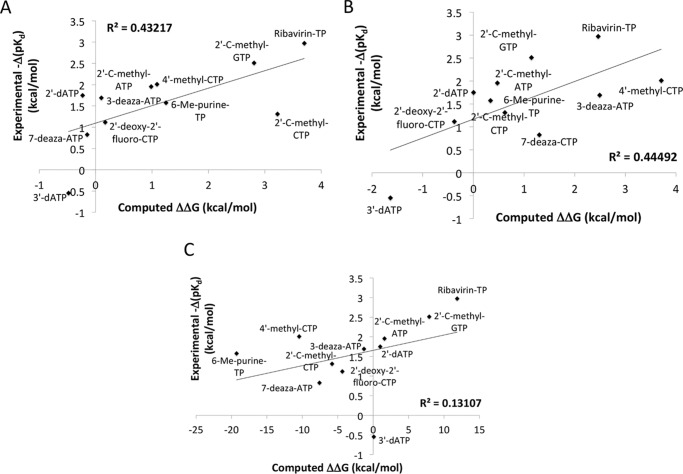
Starting with our model of the CTP-bound POLRMT complex obtained by clustering our 333-ns-long MD trajectory as described under “Experimental procedures” or with the final structure from our simulation of either the ATP or the GTP bound complex, we ran lengthy FEP simulations in which the corresponding natural nucleotide was slowly converted into each of a set of nucleotide analogues previously studied experimentally by Arnold et al. (3). FEP simulations were then run in the opposite direction, and the results of forward and backward simulation were averaged. The results are given in Table 1. In Fig. 6A we show the correlation between our computational results and the experimental results corresponding to the natural logarithms of the K_D values determined by Arnold et al. (3). For each nucleotide analogue, we calculated the experimental value of ΔΔG as the difference between the ln(K_D) value determined for that nucleotide analogue and the value of the same expression for the corresponding natural nucleotide. The average unsigned error is 0.97 kcal/mol, with a maximum unsigned error of 2.0 kcal/mol. The R² value calculated for the linear fit, which is much less relevant than the error for the narrow data range considered here, is 0.43 (r = 0.66). Part of the error is due not only to experimental noise, which has been estimated to typically lie in the range of 0.3–0.5 kcal/mol (18, 26), but also to differences in the sequence of the RNA/DNA hybrid used in the experiments compared with the sequence of the one present in the crystal structure that was used in our computations. These results demonstrate that FEP can be applied to determine relative binding free energies of NTP analogues to a polymerase with a significant degree of accuracy.

Table 1.

Comparison of calculated relative binding free energies of NTP and dNTP analogues to experimental values

Compound	ΔΔGMOE	ΔΔGFEPa	ΔΔGFEPb	−Δ(pKd)experimentalc	ErrorFEPb
	kcal/mol	kcal/mol	kcal/mol	kcal/mol	kcal/mol
3′-dATP	0.1	−1.6	−0.5	−0.5	0.0
7-Deaza-ATP	−7.6	1.3	−0.2	0.8	−2.0
2′-Deoxy-2′-fluoro-CTP	−4.4	−0.4	0.2	1.1	−0.9
2′-C-Methyl-CTP	−5.8	0.6	3.2	1.3	1.9
6-Methylpurine-TP	−19.3	0.3	1.2	1.6	−0.4
3-Deaza-ATP	−1.3	2.5	0.1	1.7	−1.6
2′-dATP	1.0	0.0	−0.2	1.8	−2.0
2′-C-Methyl-ATP	1.6	0.5	1.0	2.0	−1.0
4′-Methyl-CTP	−10.4	3.7	1.1	2.0	−0.9
2′-C-Methyl-GTP	7.9	1.1	2.8	2.5	0.3
Ribavirin-TP	11.9	2.5	3.7	3.0	0.7

^a Calculated under the condition of H1125 having a neutral charge state.

^b Calculated under the condition of H1125 having a +1 charge state.

^c Experimental results of Arnold et al. (3), except in the case of 2′-C-methyl-ATP; −Δ(pK_d)_experimental is taken from the average of the two values reported in Ref. 55.

Figure 6.

Correlation between results computed using FEP or single-point energy calculations with experimental values. We show the correlation with experiment of FEP results calculated under the condition of His¹¹²⁵ having +1 (A) and neutral (B) charge states, respectively, and of single point free energy calculations (C). R² values for the linear fit, or correlation, are shown on each of the three graphs. Experimental results are those of Arnold et al. (3) or in the case of 2′-C-methyl-ATP the averages of the two values reported in Ref. 55.

Because there was some doubt concerning the protonation state of residue His¹¹²⁵, in Fig. 6B we show the same correlation, this time calculated under the condition of His¹¹²⁵ being neutral. Here the average unsigned error (1.14 kcal/mol) is slightly higher than for His¹¹²⁵ protonated, and the R² value (0.44) is approximately the same, supporting the protonated state of His¹¹²⁵.

Comparison to other binding affinity calculations

We also performed single-point free-energy calculations of the NTP-binding affinities to POLRMT in the molecular operating environment (MOE) program for comparison. An implicit solvent representation was used in this approach, namely the reaction field method. The range of computed values falls far outside of the experimental range, and the square of the correlation coefficient R² between the resulting affinities and the experimental values is only 0.13 (Fig. 6 and Table 1). Thus the FEP results are much more accurate than the quick single-point free-energy predictions. Calculations performed in MOE could, however, be useful in a preliminary screen for nucleotide analogues binding to a polymerase, prior to FEP screening, by narrowing the search space.

In a previous study on a related topic, Florian and co-workers (27) applied FEP to compute the difference between the binding free energy of dCTP and dTTP to a DNA duplex. In that study it was concluded that at least 20 ns of simulation time was required for sufficient sampling (∼80 ns was used for each compound in the present study). In addition to the availability of adequate computational resources, another difficulty that has hindered efforts at performing free energy perturbation calculations is the intricacy of the setup, because programs such as NAMD do not offer automated scripts for creating the required dual topology files. In the present work, we have taken advantage of state-of-the-art computing power and in-house scripts to show that FEP can be effective at predicting nucleotide-binding free energies to a polymerase.

The value of FEP computations in pharmaceutical lead optimization is becoming increasingly appreciated as new improvements are being made to computer speed and efficiency. In a recent study the accuracy of FEP was tested by Schrodinger, Inc., across eight targets and 199 ligands (18). Depending upon the target, the mean unsigned errors ranged from 0.75 to 1.16 kcal/mol. Although that study used the Desmond simulation program (28) with the OPLS 2.1 (29) force field, the reported accuracy is similar to what we find here for our NAMD (30) calculations with the CHARMM/MATCH (31–34) force field.

Discussion

Mitochondrial toxicity is linked to the malfunction of multiple organs including the heart and brain (1) and thus is potentially a serious danger when developing ribonucleoside antivirals (and potentially even some deoxyribonucleotide triphosphate analogues). Thus the predictability of the binding of NTP analogues to POLRMT is an area warranting further advancement. Because POLRMT has been crystallized as a closed product complex and because POLRMT, T7 RNA polymerase, and T7 DNA polymerase have homologous catalytic domains (35), we were able to use the crystal structure of the nucleotide insertion state of T7 RNA polymerase (36), superimposed upon the homologous T7 DNA polymerase structure (12) and simultaneously upon POLRMT (8), to create a model of the POLRMT nucleotide insertion state.

MD simulations were used to analyze structural features of our model of the NTP-bound POLRMT complex. These revealed important details including the coordination of metal ions, interactions of the NTP with conserved active site residues, and the difference in the conformations of the fingers and thumb domains in the NTP-bound complex compared with their conformations in the closed product state.

We judiciously selected a panel of 11 NTP drugs and calculated their binding free energy differences, by FEP, relative to the binding free energies of the natural CTP, ATP, and GTP, ranging from −0.5 to 3.7 kcal/mol. Our computations correctly predicted ribavirin and 3′-dATP as the weakest and strongest binders, respectively, relative to the natural nucleotides and overall matched well with experimental values (3), with a mean unsigned error of only ∼1 kcal/mol and an R² value of 0.43. FEP is a formally exact method, meaning that there are no errors caused by approximations in the theory. Sources of error include contributions caused by the initial structure, by the force field, by the boundary conditions applied, and by imperfect sampling. Thus the close correspondence between our results and experimental values is attributable to the availability of not only low-resolution crystal structures but also highly accurate force fields and superb high-performance computing resources.

The application of FEP to model interactions between NTP analogues and the catalytic site of mitochondrial RNA polymerase will be of use, along with mitochondrial RNA polymerase catalytic assays, to identify potential inhibitors and also in the rational design and salvaging of inhibitory drugs. Moreover, applying this technology to viral-encoded and other pathogen-encoded polymerases and other key replicative enzymes will aid in the rational design of specific small molecule inhibitors, as well as being of value in the rational design of specific inhibitors of various host cell and cancer targets.

Experimental procedures

System setup and equilibration

Our model of POLRMT is based upon the 4BOC crystal structure of the protein in complex with a 28-mer dsDNA including a bubble region of 9 bases and a 14-mer RNA transcript (8). The crystal structure has a resolution of 2.65 Å and shows the entire DNA template except for the 5′ base and all of the nontemplate DNA except for the 5′ base and the bubble region. It includes a 9-bp DNA/RNA hybrid. Because a few loops were missing from the crystal structure of the protein, we used homology modeling in MOE (37) to complete this structure, for which the DNA and RNA were used as an environment for the induced fit. To model the incoming CTP and Mg²⁺ ions, the position of the base of the 3′-terminal RNA nucleotide was preserved, whereas the ribose and triphosphate atoms were modeled based on the 1QLN structure of the insertion state of RNA polymerase from bacteriophage T7 (36), simultaneously superimposed on 4BOC, and on the 1T7P structure of the homologous T7 DNA polymerase (12), because this structure includes active site Mg²⁺ ions.

Residue protonation states were assigned at a pH of 7.8 by the MOE program (37), corresponding to mitochondrial pH (although mitochondrial pH has been shown to fluctuate, depending upon metabolic state, from 7.5 to 8.2 (38)). The protonation states of the active site histidine residues 1125 and 1150 were evaluated using constant pH molecular dynamics (CphMD) (39, 40). Simulations were performed for both the ATP-bound POLRMT complex and for the apo-complex in explicit solvent and for the apo-complex in implicit solvent. During explicitly solvated CphMD simulations (40), protonation state changes were periodically attempted every 100 steps with a time step of 2 fs, i.e. every 0.002 ps, and production simulations (following heating and equilibration) were conducted for 800 ps (ATP-bound) or 500 ps (apo state). During implicitly solvated CphMD simulations (39), protonation state changes were attempted at every time step (2 fs), and production simulations were conducted for 2 ns.

Simulation setup was performed in the leap module of the AMBER 14 program package (41). We used parameters for CTP kindly provided by Francois-Yves Dupradeau through the RED database (42). The protein and nucleic acid were parameterized by the AMBER ff12SB force field (43–46). A cubic box of pre-equilibrated explicit TIP3P water was added extending to a distance of 15 Å from the protein. The total charge on the system was neutralized by the addition of Na⁺ ions, and then an additional 137 Na⁺ ions and the same number of Cl⁻ ions were added, bringing the ionic concentration to 150 mm. Molecular dynamics simulations were performed with periodic boundary conditions using the pmemd.MPI module of AMBER 14 (41). The water surrounding the molecular system was first relaxed, and then the entire system was relaxed. Next, restraining all solute atoms by a force constant of 25 kcal/mol, the system was heated to a final temperature of 300 K at a constant volume over a period of 50 ps using a Langevin thermostat. Restraints were then gradually relaxed to zero over 100 ps with a time step of 2 fs at constant pressure, and then a 2 ns equilibration was performed also at constant pressure.

We then ran a total of 333 ns of MD simulations in NAMD (30). The plot of active site root-mean-square deviation (RMSD) versus time became relatively flat approximately halfway through the simulation (Fig. 7A), and thus the last 135 ns of the trajectory was used in cluster analysis. Trajectory snapshots were clustered with respect to positions of active site residues into 18 sets (based on Davies Bouldin index (DBI) values and SSR/SST values (the ratio of the sum of squares regression to the total sum of squares)). A representative of the largest cluster was chosen as our starting model for binding free-energy simulations. This model of the CTP-bound POLRMT complex was also used for our depictions in Figs. 1, 2A, and 4.

Figure 7.

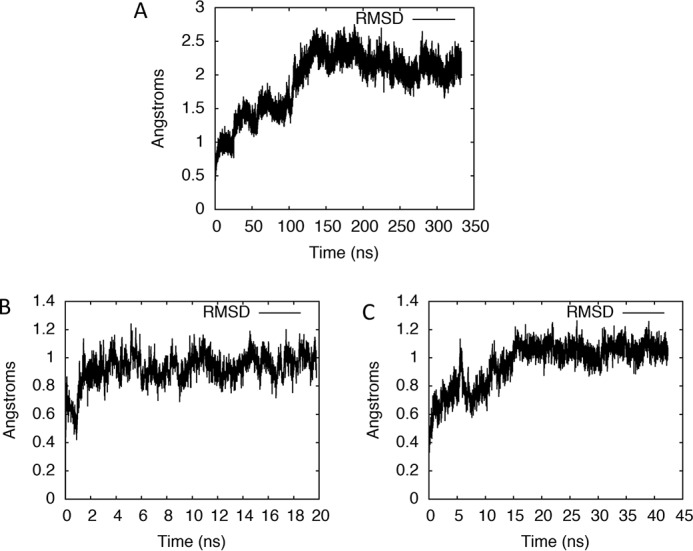
RMSD plots showing convergence and stability of simulations. Shown is the RMSD, relative to the starting structure, of the active site of our computational model of the POLRMT complex bound by CTP, A, as a function of simulation time. RMSD plots for simulations initiated after replacing the CTP in the active site by ATP or GTP at the end of the MD simulation of the CTP-bound complex are shown in B and C, respectively.

Starting with our model of the CTP-bound POLRMT complex, the CTP residue and its base-pairing dG residue in the template DNA strand were manually mutated to GTP-dC and ATP-dT pairs, respectively. We then performed MD simulations of the GTP- and ATP-bound POLRMT complexes, respectively. Because the active site RMSD stabilized very fast for the ATP-bound complex, this MD simulation was run for only 20 ns (Fig. 7B), whereas the simulation of the GTP-bound complex, which took longer to equilibrate based on the RMSD plot, was carried out for 42 ns (Fig. 7C). The final structures from our simulations of the ATP or the GTP-bound complexes, respectively, were used as starting models for free-energy simulations.

Free-energy simulations

Free-energy simulations were performed using the free energy perturbation method implemented in NAMD (30). Ligands were parameterized with the MATCH program (31), whereas protein and nucleic acid residues were parameterized using CHARMM22 (32) and CHARMM27 (33, 34), respectively. Dual topology files and coordinates were then created in NAMD. For each system, two sets of input files were created: one for simulation of the ligand in aqueous 0.150 m NaCl solution and another for simulation of the same ligand within the solvated protein-bound environment also containing 0.150 m NaCl, so that binding free energies could then be determined using a thermodynamic cycle. The computational details were as follows.

Systems were first minimized for 2000 steps and then gradually heated to 300 K (to match experimental conditions) using a Langevin thermostat over 60 ps with harmonic restraints. The restraints were gradually released over a period of 250 ps, and afterward systems were equilibrated for 1 ns, using a 0.5-fs time step. The coupling parameter, λ, which describes the fractional potential energy character of the second molecule associated with each window, was then scaled from 0 to 1 by increments of 0.02, i.e. over 50 simulation windows. In each window, equilibration was performed over 200,000 steps followed by 200,000 steps of data collection, with a time step of 2 fs. We made use of a “soft core” potential, i.e. van der Waals and electrostatic potentials were scaled separately to prevent atom clashes, which might occur if atoms appear or disappear in a highly charged state. The particle mesh Ewald method was used to treat long-range electrostatics, and SHAKE (47) was used to constrain bonds involving hydrogen atoms. The system energy was sampled every 10 steps. After having performed 40-ns simulations in the forward direction from the corresponding natural NTP to the nucleotide analogue, simulations were also run in the backward direction for 40 ns for each system, and the two results were averaged. For each alchemical transformation, the free-energy difference ΔΔG is found as (13–15, 30),

$$\Delta \Delta G=-k_{\text{B}}T{\displaystyle {\sum }_{i=1}^N\ln \langle \exp \left[-\left(H\left(x,\hspace{0.17em}p,\hspace{0.17em}{\lambda }_{i+1}\right)-H\left(x,\hspace{0.17em}p,\hspace{0.17em}{\lambda }_i\right)\right)/k_{\text{B}}T\right]\rangle }$$ (1)

where H is the system Hamiltonian; N is the number of windows, in our case 50; k_B is the Boltzmann constant; T is absolute temperature; and the angle brackets denote averaging over all sampled phase space points (x, p).

Single-point free-energy calculations

For single-point free-energy calculations, we used the MOE program (37) with the reaction field solvation model and the AMBER 10:EHT force field. In this force field, parameters of proteins and nucleic acids are taken from the AMBER ff10 force field (48), and those for small molecules are parameterized using 2D extended Hueckel theory (49). Energy minimizations were performed on nucleotide analogues placed in the NTP binding site of POLRMT prior to calculations of binding affinities.

Trajectory analysis

RMSD values of the active site relative to the initial configuration were calculated using the AMBER analysis tool cpptraj (50) for the 333-ns MD simulation of the CTP-bound POLRMT complex, the 20-ns MD simulation of the ATP-bound POLRMT complex, and the 42-ns MD simulation of the GTP-bound POLRMT complex. The active site was defined as all residues, not including the bound NTP, within 6 Å of the bound NTP. Selected distances, pucker angles, and average structure files were also calculated using cpptraj (50) along the entire trajectories of the ATP-bound and GTP-bound POLRMT complexes and for the second half of the simulation of the CTP-bound complex. Average structure files are used in our depictions in Fig. 2B.

The Gromacs (51–53) analysis tool gmx_bundle was employed in analyzing the bundle of helices belonging to the POLRMT finger subdomain, to calculate their axial tilts with respect to the average axis. Prior to applying this tool, the 333-ns NAMD trajectory of the CTP-bound catalytic complex was converted to Gromacs format with the acpype-0.1.0 program (54).

Author contributions

H. F. and M. H. conceptualization; H. F. and P. W. software; H. F. formal analysis; H. F. investigation; H. F. visualization; H. F. methodology; H. F. writing-original draft; H. F., P. W., J. T., D. L. T., and M. H. writing-review and editing; J. T., D. L. T., and M. H. supervision; D. L. T. and M. H. funding acquisition.