Cooperation of mono- and bi-articular muscles: human lower limb

Abstract

Objectives:

The aim of this study was to create and analyze a Pareto-optimal problem that would describe cooperation between mono- and bi-articulate lower limb muscles in sagittal plane.

Methods:

Equations describing the problem were derived and analyzed, additional constrains were introduced and experimental verification based on gait video analysis was performed.

Results:

Uncertainty of Pareto-optimal solution is shown for the muscular-skeletal system. An explanation of this situation is presented and discussed. Moreover, this theoretical observation is compared with a lack of gait reproducibility. Small but noticeable differences in gait cycles are shown and explained.

Conclusions:

A muscular system redundancy is shown and explained by the meaning of Pareto problem. Theoretical considerations were confirmed through a gait analysis. This leads to the conclusion, that during muscle cooperation each movement cycle can be different from the previous one, however due to physiological restrictions only a narrow equivalence class of the possible solutions exists.

Introduction

The structures of biological and artificial systems, which mean functional and structural similarities, are complex, i.e. muscles are working in groups, there are mono- and multi-articular muscles, and they can have different functions and arrangements[1-3]. This causes serious and challenging problems in their control, due to the dynamics phenomena, the complexity of structure and some computational problems[4]. The occurred imperfections, external actions on human or humanoid robot, some disturbances or fatigue of muscular-skeletal systems, method of minimization of the locomotion energetic cost[5] affect trajectories of motion, their speed and precision of repetitions. On the other hand, the variability of human gait parameters is obvious and evaluating it can help, for example in assessing the risk of falling[6]. It is conjectured that a movement of biological system is not determined along one fixed trajectory, what is also a well-known fact, for both upper and lower limb[7].

The skeletal muscles can be divided into: mono-articular, bi-articular and multi-articular[8]. Mono-articular muscles can generate a movement only in one joint, bi-articular – in two adjacent joints, multi-articular – in many joints. This complexity of functions and structures creates a challenge for their control and the cooperation between them. Sometimes, the muscle contraction causes movement/joint rotation, sometimes its role is to stabilize the joint or segment position. One of the papers[9] confirms the observations of muscle cooperation during movement. The authors have presented a measurement of Electromyography (EMG) signals, which shows that in the case of movement in one or two joints, an activation of muscles that span a joint that does not move, was observed.

From the point of view of mechanics, it is a redundant system[10,11], which, during the movement, leads to muscular-skeletal indeterminacy. Namely, from the mathematical standpoint, there is an infinite number of solutions which implies that a muscular-skeletal system has an infinite number of admissible paths of moving from one point to another, limited by the physiological restriction. In fact, theoretically an infinite number of muscle activation patterns exisit[11], but humans are using the relatively repeatable ones. In literature, there are a few hypotheses on how and why these patterns are chosen, i.e. due to the optimization of different parameters or by solving the problem of muscle synergy[12].

The aim of this work is to formulate a Pareto-problem that describe the cooperation between mono- and bi-articulate joint muscles of the human lower limb over chosen static state. This model is universal and can be used to illustrate the way of cooperation between any number of single and bi-joint flexors or extensors of both biological and artificial limb. Moreover, the inability to determine a unique trajectory, which is a Pareto-optimal solution for the existing limitations, is also shown, contrary to other publications, where ways of optimizing or choosing the trajectories are considered. It is also proved that the set of admissible trajectories is narrow. The obtained theoretical results are verified in an experiment based on the repeatability of the human gait. In order to record the trajectories of movement the motion capture system was used.

Description of the problem

Geometry and considered muscular-skeletal system

In the scope of the study it was assumed a human-like lower limb movement in a sagittal plane. In the described case, the system consists of (Figure 1):

Figure 1.

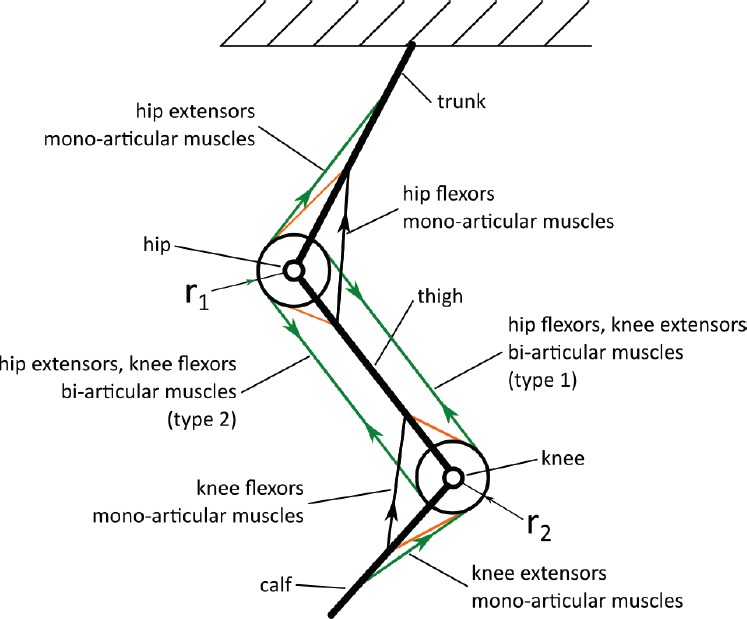
Example of the mono- and bi- articulate muscle system – a kinematic scheme; arrows indicate direction of muscle force, r_i - radius of hip and knee

1. trunk,

2. thigh,

3. calf,

4. hip joint,

5. knee joint,

6. mono-articular muscles: hip flexors and extensors and knee flexors and extensors,

7. bi-articular muscles: knee extensors and hip flexors (hereinafter called type 1 muscles),

8. bi-articular muscles: hip extensors and knee flexors (hereinafter called type 2 muscles).

It is also assumed, that according to the muscle physiology a muscle can only contract. Moreover, a simplification is used, that each muscle can generate a force that has the same value both on its origin and insertion. External influences are neglected.

[Figure 2] presents the analyzed movement: the calf is rotating while thigh and trunk remain in a state of immobility.

Figure 2.

Example of described movement, where a - angle between horizontal axis and trunk, β - angle between trunk and thigh, γ - angle between calf and thigh.

Mathematical notation

Let us introduce a problem of a leg movement which follows muscle actions. The notation as below is applied:

1. a,b – number of one joint flexors muscles of hip and knee, respectively;

2. c – number of two joint muscles: hip flexors, knee extensors (type 1);

3. d, e – number of one joint extensors of hip and knee, respectively;

4. f – number of two joint muscles: hip extensors and knee flexors (type 2).

Moreover we denote:

1. fh1 – one joint hip flexors, i ∈ (1,…., a);

2. fk1 – one joint knee flexors, i ∈ (1,…., b);

3. f1 – muscles type 1 (two joint muscles: hip flexors, knee extensors), i ∈ (1,…., c);

4. eh1– one joint hip extensors, i ∈ (1,…., c);

5. ek1 – one joint knee extensors, i ∈ (1,…., d);

6. e2 – muscles type 2 (muscles: hip extensors and knee flexors), i ∈ (1,…., e).

Contraction of the flexors causes flexion of the limb, while its extension results from the contraction of the extensors, assuming that chosen groups of muscles can act stronger than their antagonistic groups. To perform an accurate movement they have to cooperate in an appropriate way[1,2,8,9,13-17,22], i.e. by stabilizing the joint. In this study, it is assumed, that the movement is admissible in only one of the chosen joint (knee).

Formulation of the mathematical problem

Let us consider a knee flexion in the sagittal plane, when thigh and trunk should remain in an immobile state. In order to do that, one joint knee flexor muscles (fk1) and type 2 muscles (e2) have to contract, whereas the one joint knee extensors muscles (ek1) and type 1 muscles (f1) have to reduce their force. If the contraction of muscle will be strong enough and will not be compensated by type 1 muscles (f1), then we will also observe an extension in a hip joint, which is undesirable in this case. To prevent this movement a contraction of one joint hip flexors (fh1) muscles has to occur. This will compensate a moment of two joint muscles causing a movement of a calf only. In the considered model it is assumed that each of the muscle existing in the system contributes to the creation of the moment acting at the joint. We define it as follows:

where r_i means the arm of the F_i force acting with respect to the joint axis of rotation (Figure 2). In the presented system, the following moments are acting at the knee joint:

i. knee flexion:

ii. knee extension:

At the same time, the following moments are acting on the hip joint:

i. hip flexion:

ii. hip extension

It is worth noticing that a moment that causes the knee extension as the product of force F_i and constant radius block r₂ is a simplification – in biological systems radius varies and axis of rotation is moving[18].

Hence it follows, that the resultant moments acting on the joints are:

for the knee joint:

for the hip join:

A rotation in one joint is caused by the change of muscle force, which is involved in the movement[2,8,9]. This means that in order to describe the movement correctly we have to consider the equations (2) and (3) as a system of equations.

In order to simplify the description let us introduce the following notation:

The system, in a static case, is governed by the following system of equations:

This yields:

From the equation (4) it can be concluded that two-joint muscles do not compensate a movement in an adjacent joint. Transforming this equation into a quotient form and assuming (according to physiological behavior) that F_h+E_h ≠ 0, we obtain:

From that we can observe that, when the knee flexor forces increased, the force of the muscles (what implies to change in moment acting on the joint) E_k had to decrease or the sum of F_h+E_h have to increase.

However, on these conditions there is an infinite number of solutions. This is reflected in the actual behavior of the neuro-muscular-skeletal system. During the movement, the scheme of behavior is not unique. It can be explained by muscular redundancy problem optimization, solved by human nervous system[11], muscle coordination, their fatigue or other physiological or environmental reasons.

From the mathematical standpoint, the unique scheme of cooperation means that there exist one solution of this problem. In order to obtain an optimal one, certain optimization methods are used. The problem can be minimized by the cost function of energy, muscle force, excitation level or muscle fatigue[5,19], assuming that individual muscles cannot exceed the maximum physiological tension. It is also possible to consider the optimization problem based on minimizing the tension σ of a muscle.

Let us consider the following Pareto minimization problem:

where σ_i means i-th muscle tension and F_i is a force generated by i-th muscle, S_{i anat} stands for its anatomical cross section.

We denote by J the following objective function:

We minimize the function J with the following conditions:

where

and M is the moment generated by the knee flexors. Moreover, we assume:

Even if we know σ_imax, i=1, …, n, a, ∈ (0, π), S_i the problem is still indeterminate, which means that there exist infinitely many solutions. For obvious reasons some solutions are more proper than others. To reduce their number an additional criterion have to be added, that is the objective function (for example the function of energy Ε(δ), which limits the number of solutions) has to be supplemented by a scalar function. Moreover, it is also possible to enter additional, physiological restrictions (see Section 3), so the set of admissible solutions becomes narrower.

Physiological movement restrictions

One of the type of the mechanical restrictions concerns the limbs range of motion, and they are provided in the [Table 1].

Table 1.

Range of chosen lower limb joint angles according to the International Standard Orthopedic Measurements Norm in sagittal plane.

Joint	Active range of motion [deg]
Hip	15-0-125
Knee	0-0-130

This introduces certain restrictions concerning the angles of flexion/extension of the limb or its segments. It is worth mentioning, that during normal, daily activities, we are using the so-called “comfort range of motion” which limits the maximum values even more. This restriction can be combined with a stress distribution on the individual muscle. Another physiological condition is the phenomenon of the optimal length of the muscles and increase in the tissue (ex. joint ligaments or antagonist muscles) resistance in the extreme positions of the limb or joint[20].

An example of theoretical simulation results for flexors and extensors combined with other tissues that surround the joint are presented in [Figure 3]. A knee like joint simplified with the constant joint radius and muscle model (presented in paper[21]) was used for calculations. This graph explains the phenomenon of using comfortable range of motion during daily activities: in case of the extreme joint position, a pronounced growth of strain in antagonist muscles and tissues that surround the joint is observed. The range from value 0 (fully extended joint) to the point of intersection of the curves represents an active range of motion (movement made by the examined person). From this point to value 1 (fully flexed joint) a passive range of motion is observed (additional range of motion, when external moment is applied on the joint). This can be compared with results obtained by other authors[22].

Figure 3.

Theoretical results of the force of flexors (dashed curve), extensors and other tissues surrounding the joint (continuous line) during flexion of theoretical knee joint; data are normalised[20].

Overlapping of the aforementioned conditions like maximal range of motion, speed and acceleration of the limb segments (both linear and angular) leads to a reduction of possible solutions. However, as mentioned, additional restrictions should allow to obtain the solution possible. Not cost-effective ones (for example: energy or due to excessive stretching of tissue) will be eliminated by the central nervous system[11]. So there will be some narrow family of solutions. This is confirmed by the experiments, the results of which are presented in the following section.

Experimental verification of the theoretical prediction

Characteristic points of the lower limb joints and segments (big toe, heel, ankle, knee, hip and center of gravity (COG)) were marked with reflective, passive markers. During the test, their coordinates were determined using authorial numerical algorithm, specially developed for this purpose. Obtained results show that in presented case of treadmill walk with constant speed of 4.5 km/h there are no fixed trajectories (Figure 4). It can be observed that the cycles are similar, but slightly different according to the marker positions and intersegmental coordination. Thus we can conclude, that in case of this biological system, we do not have well-determined trajectory. Even if the purpose of the movement (e.g., putting a foot in a particular place) is strictly defined, the path to that goal is not repetitive, and the achievement of that goal is subject to some inaccuracy. The amount of that “unrepeatability” can be estimated i.e. by analyzing changes in step length, for example. For the case presented in Section 5, mean value of step length equals 0.659 m while its standard deviation σ=0.018.

Figure 4.

Repeatability of gait cycles on the treadmill, of lower limb trajectories during subsequent cycles. (an example), X - anterio-posterio axis, Y - longitudinal (vertical) axis.

Figure 5.

Step length repeatability during subsequent cycles (dots); linear regression with R²=0.0049 dashed line.

Conclusions

A biological muscle-system and muscle-like system redundancy problem was described. Its indeterminacy by applying Pareto-optimization was considered, i.e. lack of a unique solution was shown. This leads to the conclusion that during muscle cooperation each movement cycle will be slightly different from the previous one, because there exist as many solutions as combinations that meet a specified target. However, due to physiological restriction they are in a narrow equivalence class. Also due to many factors like muscle fatigue, external forces and other, human and environmental factors, each registered gait cycle during experiment was different. It was also found that for each of movement the strategy was different (different phases of motion at different speeds, different maximal flexion angles of the limb), but proper (in terms of achieving the intended global goal – effective locomotion).

From this we can conclude that muscles were contracting in different way in each cycle, what illustrates the problem of muscle cooperation uncertainty (see also [7]). For each cycle, a volunteer make the movement in a slightly different manner. In this particular case, there are also some biological and physiological constraints such as maximum flexion/extension angles of the joints, the maximum force that can generate muscle action.

More sophisticated/specialized models, in this line, can be applied to analyze any system of the repeatable movement of other limbs (like in reference [23]), human body or humanoid robots. In case of dynamics analysis, additional parameters and variables should be taken into consideration, like variable moment of inertia caused by muscle mass movement, ground reactions forces, realistic geometry etc.

What needs to be emphasized is that with both methods (theoretical and experimental) it was shown that there is no one fixed trajectory for the cyclic movement. The movement patterns can be very similar, but they will be different each time, i.e. a different angular and linear velocity, acceleration and step length can be observed.