TRAPEZIOMETACARPAL JOINT CONTACT VARIES BETWEEN MEN AND WOMEN DURING THREE ISOMETRIC FUNCTIONAL TASKS

Abstract

Trapeziometacarpal (TMC) joint osteoarthritis (OA) affects women two to six times more than men, and is influenced by stresses and strains in the cartilage. The purpose of this study was to characterize sex and age differences in contact area and peak stress location of the healthy TMC joint during three isometric tasks including pinch, grasp and jar twist. CT images of the hand from 50 healthy adult men and women were used to create a statistical shape model that was used to create finite element models for each subject and task. Forcedriven simulations were performed to evaluate cartilage contact area and peak stress location. We tested for sex and age differences using principal component analysis, linear regression, and linear discriminant analysis. We observed sex differences in peak stress location during pinch (p=0.0206), grasp (p=0.0264), and jar twist (p=0.0484). The greatest sex differences were observed during jar twist, where 94% of peak stresses in men were located in the centre compared with 50% in the central-volar region in women. These findings show that peak stress locations are more variable in women during grasp and jar twist than men, and suggest that women may employ different strategies to perform these tasks.

Introduction

The TMC joint is susceptible to OA, and women are two to six times more likely to develop TMC OA compared to men [1–3]. Mechanical factors such as contact forces and contact area are likely to be important contributors to the onset, progression, and sex-disparity of TMC OA [4–6]. Prior studies hypothesised that the smaller wrists of women would experience higher stress than men during activities of daily living that require similar overall contact forces, such as pinch, grasp, and jar twist, due to smaller contact areas [6–9]. Cartilage stresses and strains are dependent upon both the size and location of the contact area, and these in turn are influenced by the articulating surface geometry, joint posture, and contact forces.

The few studies that have investigated the location of TMC joint contact report contradictory findings. Several studies report contact on the volar-radial side of the trapezium [10–13], while Eaton and Littler [14] reported dorsal contact areas, and Ateshian, Ark [15] reported volar-ulnar contact areas. Most of these studies were performed in vitro using cadavers and did not consider important factors such as realistic kinematics. Furthermore, the small size and saddle shape of the TMC joint make it unsuitable for Tekscan (Tekscan Inc., Boston, MA, USA) or pressure film experiments, making direct measurement of contact pressure location difficult. Halilaj, Moore [10] investigated different postures in vivo, but used a surrogate measure (joint space centroid) to infer joint contact. To understand the contact area and peak stress location in the TMC joint, and how these locations differ between men and women, the articulating surface geometry and joint kinematics should ideally be accounted for. This can be performed using a suitable computational model with medical imaging data such as clinical CT scans of quasi-static poses.

We recently performed a statistical shape modelling study using CT scans from a cohort of 50 individuals and found that the trapezial and first metacarpal bones of men and women differed only in size and not in shape [8]. These results suggest that size alone is a key difference between the TMC joints of men and women. However, the resulting contact area is influenced by the orientation of the bones during a functional task. Halilaj, Rainbow [16] reported that the variability in TMC joint kinematics is large, but found no statistical difference between men and women. In their study, older subjects had 2° greater adduction-abduction compared to younger subjects during pinch, grasp, and jar twist tasks. In vivo kinematic and morphological integration will benefit our understanding of contact area and peak stress location in the TMC joint as it relates to OA development.

The purpose of this study was to characterise sex and age differences in the contact area and peak stress location of the TMC joint cartilage during pinch, grasp, and jar twist. To achieve this we developed a parameter optimisation method using population-based FE models to evaluate cartilage contact in a cohort of 50 subjects.

Methods

Subject Information

Data from an ongoing study was obtained for this analysis [8, 10, 16–18]. After Institutional Review Board approval and informed consent, the dominant wrists and thumbs consisting of 40 right hands and 10 left hands of 50 healthy non-osteoarthritic (radiographic and asymptomatic) volunteers (23 men, aged 35.6 year ± 13.7 year and 27 women, aged 42.9 year ± 15.3 year) were imaged with a 16-slice clinical CT scanner (GE LightSpeed 16, General Electric, Milwaukee, WI) (Figure 1) [16]. Prior to enrolment, an orthopaedic surgeon examined each subject to rule out conditions that alter TMC joint morphology or kinematics, such as inflammatory arthritis, metabolic bone disease, traumatic injury, surgery, signs of TMC or hand OA, or other non-osteoarthritic diseases of the hand [8, 10, 16–18].

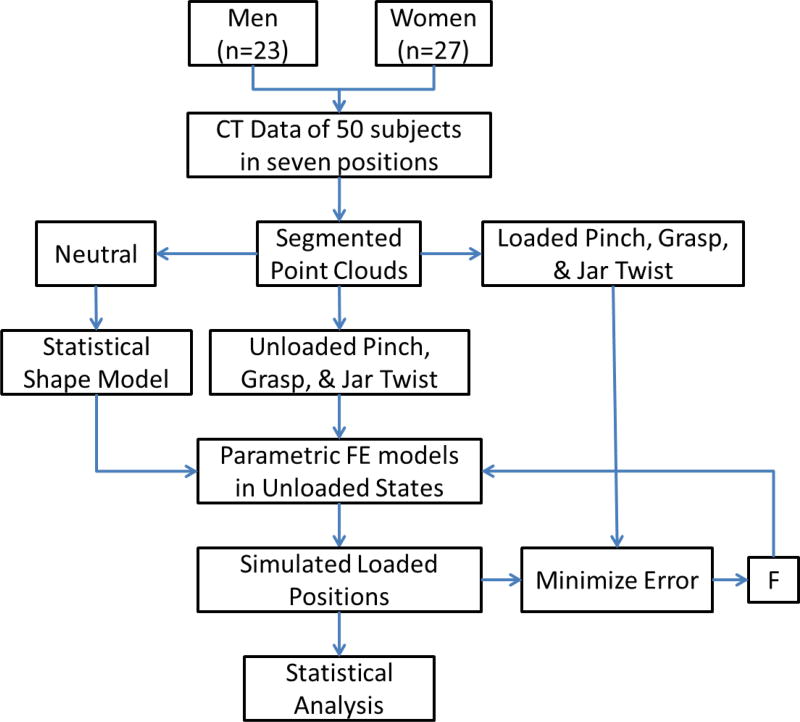
Figure 1.

Overview of the method: Clinical CT of 50 healthy adult men and women in seven positions (including neutral, unloaded pinch, unloaded grasp, unloaded jar twist, loaded pinch, loaded grasp, and loaded jar twist) were segmented into point clouds. Neutral point clouds were used as a training set to create a statistical shape model (SSM) of the bones. The SSM was used to create parametric finite element (FE) models of the trapezium and first metacarpal bones and were initialized in the unloaded state. Force-driven FE simulations were performed to simulate the loaded posture. The force vector, F, was optimized to minimize the error between the simulated postures and the actual loaded posture from CT. The results were analysed statistically.

Imaging Protocol

Each subject was imaged in seven positions with custom rigs [16]. The seven positions included clinical neutral position, unloaded pinch position, loaded pinch position at 80 % maximum effort, unloaded grasp position, loaded grasp position, unloaded jar twist position, and loaded jar twist position [16]. The settings used on the scanner were: tube parameters at 80 kVp and 80 mA, slice thickness of 0.625 mm, and in-plane resolution of 0.4 mm × 0.4 mm. The mean total radiation burden from seven scans for each subject was approximately 0.35 mSv. The trapezia and the first metacarpals were segmented semi-automatically using Mimics v12.11 (Materialise, Leuven, Belgium) and 3-D bone models were exported as meshed surfaces. The vertices of these surfaces were extracted to produce a training set of point clouds for SSM generation.

Statistical Shape Model Generation

Methods from a previous study were used to generate our SSM for parameterising the TMC bones [8, 19]. In summary, a custom template mesh with cubic-Lagrange elements [20] was designed to preserve articular surface boundaries of TMC joint bones. This template mesh was fitted to all data clouds in the training set via an iterative fitting process to produce maximally correspondent (parametric) bone meshes. PCA was performed on the correspondent meshes to create the SSM.

Finite Element (FE) Mesh Generation

Metacarpal and trapezial bone FE meshes were generated by discretising the higher order cubic Lagrange meshes obtained from the SSM into triangulated simplex meshes that were compatible with the FEBio [21] solver.

The articular surface region of the bone mesh was discretised to create a quadrilateral mesh, which was embedded in the SSM such that the mesh would morph with the shape model. Since the TMC cartilage was not visible in the CT images, the cartilage meshes for each subject were obtained by extracting the quadrilateral mesh from the SSM of each TMC bone, and lofting a uniform thickness [5] (0.7 mm) normal to the surface to create a hexahedral cartilage mesh three elements deep. A convergence test with 4 elements found little difference in the contact area (RMS Error < 1.7 mm²) and location of peak stresses (RMS Error < 0.5 mm), which indicated that 3 elements were sufficient for our purposes [22].

FE Model Setup

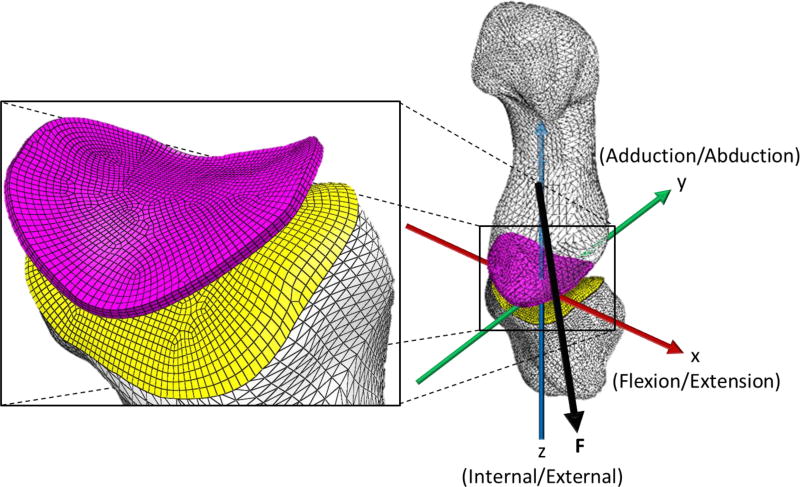
A custom python script was used to prepare the FE model to be solved by FEBio [21] for each dataset performing each task. For each task the posture of the TMC joint bones was initialised in the unloaded position with the centroid of the trapezium fixed at the origin (Figure 2). The joint was aligned such that the vector from the centroid to a landmark on the radial side of the trapezium was aligned with the x-axis (flexion-extension axis), and the vector from the centroid of the trapezium to the centroid of the metacarpal was aligned with the z-axis (internal-external rotation axis), and the cross-product of these two vectors was aligned with the y-axis (abduction-adduction axis).

Figure 2.

Finite element model showing: an unconstrained first metacarpal, fixed trapezium, coordinate system (x,y,z) aligned with the kinematic axes, and the force vector (F) passing through the centroid of the metacarpal towards the trapezium.

The kinematics of cartilage deformation was based on finite, or large, deformation theory. Since we were interested only in pure loading problems without unloading or cycling loading, cartilage can be modelled with sufficient accuracy as an elastic material. The stress-strain relationship of the cartilage was described using the neo-Hookean constitutive law. The stress-strain derived from this constitutive model exhibits a non-linear relationship for relatively large strain intervals. The parameters used in the constitutive model were: Young’s modulus = 10 MPa and Poisson’s ratio = 0.4 [23–25]. The deformed state of tissues for each task was obtained by solving the corresponding FE models. Contact was imposed using an augmented Lagrangian method [21]. Subsequently, the displacement, contact area and strain energy density (SED) of each tissue layer were calculated.

Cartilage meshes were tied to the subchondral surfaces of the corresponding bones which were modelled as rigid bodies [21]. The two contacting surfaces were not conforming, in which case an augmented Lagrangian method was used to enforce tied contact [21]. The trapezium was fixed in all degrees of freedom, while the metacarpal was unconstrained in all 6 degrees of freedom. The resultant force vector of all external forces onto the joint was passed through the centroid of the first metacarpal towards the trapezium to bring the two cartilage surfaces into contact. We assumed no contribution from ligaments during these postures [28].

Parameter Optimization

Because we did not explicitly model the muscle forces for each simulation, we performed an optimisation to identify a force vector that allowed the simulated loaded posture of the metacarpal with respect to the trapezium to be in the same position and orientation as that measured in the loaded CT scan. To achieve this, a custom python library was used to export the FE model to a file format compatible with FEBio (*.feb). FEBio v2.4 was used to solve for the displacements, contact area, and resulting cartilage stress (here we used SED as a combined measure of stress and strain, as it is a scalar quantity that is invariant to the reference frame) during contact as a result of the force vector. We used a bounded BFGS nonlinear minimisation algorithm to optimise for the force vector that minimised the corresponding RMS error between the nodes of the first metacarpal in final simulated position, and the nodes of the first metacarpal in segmented loaded position for each task. Simulations with a RMS error larger than 0.5 mm, or exhibited edge loading, were omitted from the statistical analysis.

Statistical Analysis

Contact Area

We performed a linear regression between contact area (predicted from the FE simulation), and age for each task. We also performed a t-test between contact area and sex for each task.

Peak Stress Location

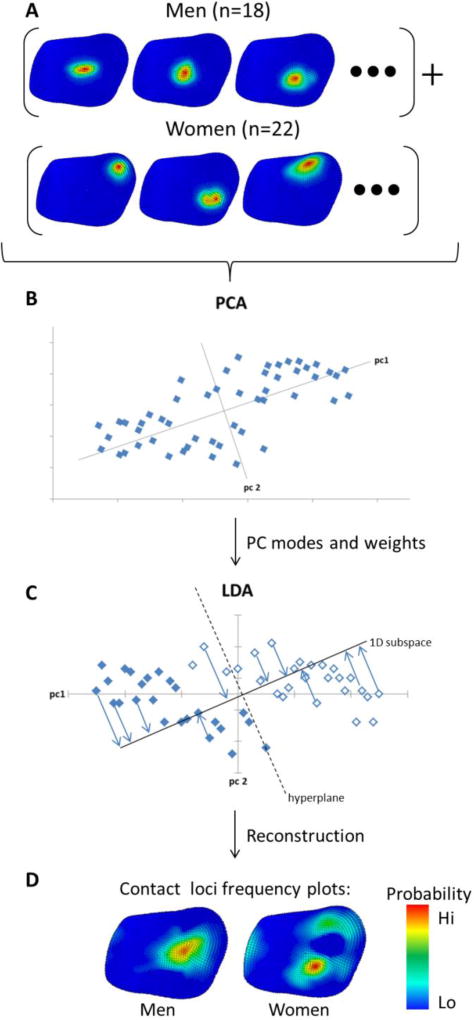
We extracted the stress distribution of all subjects, normalised the distributions to the peak stress such that we could compare the distributions parametrically (Figure 3A), and performed PCA on the normalised stress for each task (Figure 3B). We performed a linear regression between the PCA weights and age. Next, we performed a LDA on the PCA weights for each task against sex (Figure 3C). LDA classified men and women as positive and negative LDA weights respectively. A t-test was performed between the LDA weights of men against those of women. We explored the minimum number of PCA modes to include in the LDA to classify men and women successfully. This was done to prevent over-fitting. Finally, we reconstructed spatial frequency plots of contact for each group (Figure 3D) by shifting along the normal vector to the hyperplane that separates the PC weights between men and women until we had 100 % classification accuracy for that sex. These plots show the expected contact for each group, reconstructed with the minimum number of modes that display a significantly different distribution between groups (p < 0.05). The minimum number of modes was selected to avoid both over-fitting in the model and the introduction of noise.

Figure 3.

Overview of the process used for analysing differences in cartilage stress distributions between men and women for jar twist. Cartilage stress distributions were normalized by peak stress (A). Principal Component Analysis (PCA) was performed on the set of normalized distributions (B) to produce PC modes and weights. Linear Discriminant Analysis (LDA) of PC weights classified sex differences (C). LDA weights were used to reconstruct classification criteria for men and women (D). Red indicates a high probability of contact, and blue indicates a low probability.

Results

Average simulation convergence RMS errors for pinch, grasp, and jar twist were 0.293 mm, 0.325 mm, and 0.405 mm respectively. These errors were within the spatial resolution of the CT scans.

Contact Area

Results from linear regression indicated that age was a poor predictor of contact area (pinch R² = 0.0197, grasp R² = 0.0214, jar R² = 0.0195). We found no differences in the contact area between men and women during the three isometric tasks (Table 1). We found differences in the contact areas between pinch and grasp (p = 0.0003), and pinch and jar twist tasks (p = 0.0002).

Table 1.

Mean (± standard deviation) contact areas in the trapezial cartilage of the TMC joint during pinch, grasp and jar twist for men and women. Note that the number of simulations (n) for each condition was not consistent due to some simulations being omitted (as described in methods).

		Pinch		Grasp		Jar Twist
	n	Area (mm2)	n	Area (mm2)	n	Area (mm2)
Men	16	20.85 ± 5.91	19	11.90 ± 6.04	18	14.91 ± 4.77
Women	17	19.93 ± 4.90	20	13.00 ± 6.24	22	12.83 ± 4.34
Men vs. Women		p = 0.639		p = 0.590		p = 0.167

Peak Stress Location

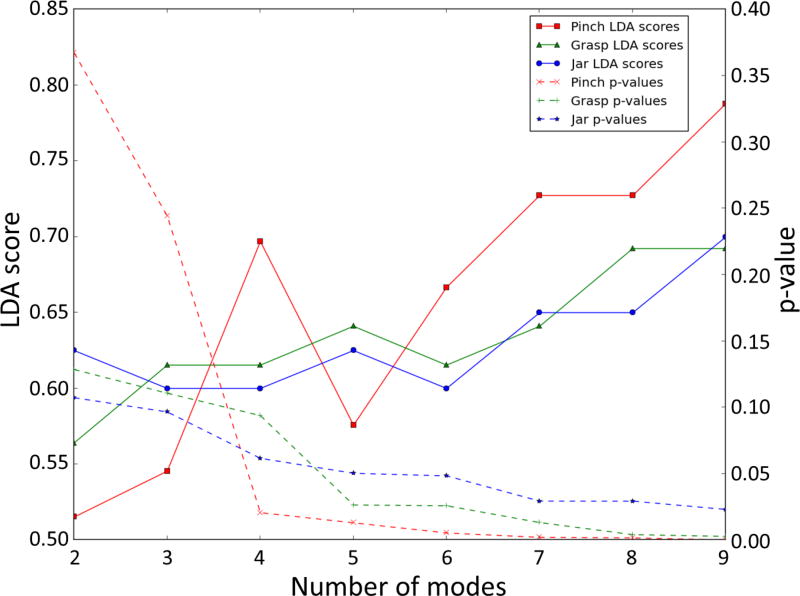
We found no correlation between age and peak stress location for all tasks (pinch R² = 0.280, grasp R² = 0.305, jar R² = 0.438). We found sex differences in the peak stress location during all three tasks. The inclusion of more modes in the LDA had two effects. Firstly, classification accuracy (LDA score) increased, and secondly, p-values from t-tests between the LDA weights of men and women decreased (Figure 4). Four, five, and six PC modes were the minimum number of modes required to classify a difference between men and women (p-value < 0.05) for pinch (p-value = 0.0206), grasp (p-value = 0.0264), and jar twist (p-value = 0.0484), respectively, without overfitting.

Figure 4.

Linear Discrimant Analysis (LDA) score, and p-value between men and women, against number of modes for pinch, grasp, and jar twist. The minimum number of modes that are required for the LDA model to classify a difference (p<0.05) in location of contact between men and women for pinch, grasp, and jar twist, was four, five and six modes, respectively.

For all three isometric tasks considered, the frequency plots of peak stress location between men and women show peak cartilage stress in different regions of the joint (Figure 5). For women performing pinch tasks, peak contact stress was located centrally in 53 % of women, with some spread to the radial-volar region and ulnar region. In men, 44 % of pinch contact was located central radially with some dorsal spread. A smaller percentage (19 %) of men experienced contact close to the ulnar ridge.

Figure 5.

Expected locations of peak cartilage stress in men and women for pinch, grasp, and jar twist, where red indicates the most likely location of peak stress and blue indicates the least likely location of peak stress. Black points indicate location of peak cartilage stresses in individual subject FE models.

Peak stress locations during the grasp task were more consistent than during pinch for men, as indicated by the focused frequency plot (Figure 5). In men, the majority of contact occurred radial from the centre (68 %), with 5 % experiencing contact at the ulnar region. In contrast, location of peak contact stress during grasp in women was less consistent and found in one of three regions. In decreasing order of frequency, these were the radial-volar region (60 %), the dorsal-radial region (10 %), and the ulnar-volar region (10 %), with 20 % scattered across the remaining region.

Of the three tasks tested, jar twist produced the most consistent results in men, with 94 % of peak cartilage stress located in a central to dorsal-radial spread. In contrast, women experienced three regions of contact. In decreasing order of frequency, these were the central-volar region (50 %), the dorsal-radial region (32 %), and the ulnar region (18 %).

Discussion

The purpose of this study was to determine sex and age differences in the contact area and peak stress locations of the TMC joint cartilage during pinch, grasp, and jar twist. Our study used a SSM, FE modelling and parameter optimisation, as well as data reduction techniques on a population of healthy men and women to investigate sex differences in contact in silico. Our findings show that the apparent natural variation in peak stress location is higher in women during grasp and jar twist tasks than in men (Figure 5). Our findings show that men and women exhibit differences in the location of peak cartilage stress for all three isometric tasks studied. However, contact area was not significantly different between men and women during these tasks. Furthermore, age was a poor predictor of contact area and peak stress location. Our findings show a difference in the peak stress location between men and women during pinch (Figure 5). For pinch, the most common peak stress location in men was in the central-radial region of the cartilage with some spread to the dorsal-radial region. This finding was consistent with the dorsal-radial contact areas reported by Ateshian, Ark [15]. However, these investigators also reported volar-ulnar contact areas during pinch, which was only exhibited in 6 % of men. Although 6 % of women experienced contact in the volar region, pinch contact in women was primarily located in the centre, consistent with the work of Halilaj, Moore [10]. Our results disagree with the reports of primarily palmar contact areas during lateral pinch [26]. The variation in pinch peak stress location might be explained by the higher overall motion (5 in pinch, compared to 0.5 to 2 in grasp and jar twist) involved in performing pinch and the high variability (s.d. of ± 8) in pinch kinematics across the population [16].

Current TMC literature is limited in descriptions of the contact area and peak stress location for grasp and jar twist tasks. To the authors’ knowledge, the study by Halilaj, Moore [10] is the only report which has estimated contact locations using joint space centroid. Using a FE method, we estimated locations of peak stress within the cartilage, which we believe is an important parameter to understand the potential degeneration of the tissue. Men and women exhibited different locations of peak stress during grasp and jar twist tasks. During grasp, the majority of men experienced contact in the central-radial and central-volar regions. This is consistent with contact locations reported by Halilaj, Moore [10] In contrast, peak stress locations in women were less consistent during grasp, indicating a greater variability in how this task was performed among women.

Jar twist tasks performed by men produced the most consistent peak stress locations in this study. Halilaj, Moore [10] found contact to consistently occur in the central-radial region for all men, which is in agreement with our peak stress results. In contrast, peak stress locations in women varied more (Figure 5). One possible explanation for the greater variability in peak stress locations is that since women have smaller hands and TMC joint bones [8], and the jar and grasp rigs were of a fixed diameter [16], different kinematics were required to execute the same task. This is often the case with activities of daily living where object size is constant and does not scale with hand size. When analysing the kinematics involved in jar twist, Halilaj, Moore [10] found a difference of six degrees in the abduction-adduction between men and women which might explain why peak stress location was more variable in women than in men [16]. Muscle weakness, poor neural coordination and pre-pathological kinematics might also be responsible for this difference. However, considering our healthy subjects, without further investigation we can only conclude that the apparent natural variation in peak stress location for these tasks is highly variable, especially amongst women.

Although men had greater bone size compared to women, contact area was not different between men and women [8]. Contact areas in men and women performing the same tasks overlapped significantly, but were different across tasks (Table 1). This suggests that size of the contact area does not depend on bone size, but depends on the posture of the joint during contact.

Both men and women experienced peak cartilage stress in regions that correlate to known wear patterns observed in TMC OA. Momose, Nakatsuchi [27] reported that degenerative change was frequently observed in the radial, volar [6], and ulnar regions of the trapezium. The primary location of peak stress in women performing grasp was the volar-radial region (Figure 5), which was reported to be the quadrant with most significant cartilage wear in TMC OA [5]. Location of peak stress on the ulnar side was not common, but occurred in a minority of men during pinch and grasp, and in women during pinch, grasp, and jar twist. During pinch, 19 % of men, and 18 % of women experienced peak stress in the ulnar region, whereas in grasp, 5 % of the peak stress in men and women was located ulnarly, and 18 % of peak stress during jar twist was located in the ulnar region in women. This loading profile correlates with known wear patterns in the ulnar region of the trapezium [27]. These results suggest that several subtypes of thumb OA may exist, explaining outlier contact zones with varied tasks in both sexes. Cartilage degeneration may occur through divergent mechanisms rather than a single progression pattern [9].

The strengths of our method include identifying the differences in peak stress locations between men and women in silico, and visualising the spatial spread of the expected contact location for each group. Although our findings were consistent with the work of Halilaj, Moore [10], our unique method allowed our results to provide supplementary and quantitative information regarding the cartilage stress and the distribution of cartilage stress across the joint. Second, since our results were obtained through solving force-controlled mechanics problems (with all degrees of freedom unconstrained), the joint postures, contact areas, and contact locations calculated were not susceptible to small errors in kinematics. In contrast, prescribing displacement boundary conditions for a small joint with thin cartilage often results in non-physiological forces. Lastly, our method of using a parametric mesh derived from a population model allows us to compare FE results from individuals within the population in the same reference frame. This allows us to compare high resolution contact data parametrically, without the need for grouping data into quadrants, and simplifies future surrogate models to represent cartilage stress.

Our method also has several limitations, which are worth mentioning. Firstly, the data collected were from static, isometric postures of the TMC joint during 80 % maximum pinch, grasp, and jar twist and may not represent the typical forces produced during dynamic activities of daily living. Rather than explicitly model the muscle and joint contact force, we optimised a force vector which stabilised the TMC joint in the imaged orientation. The assumption underlying this method was that the final static orientation and position of the metacarpal is a result of the combined muscle, joint contact, and ligament forces. However, ligament contribution to this force is thought to be minimal, as prior studies show TMC ligaments to be lax during the ranges of motion studied [28]. Since the TMC cartilage was not visible in the CT images, we represented cartilage as a uniform thickness of 0.7 mm with neo-hookean properties. Thus, variation in the cartilage height distribution has been neglected. We considered this assumption to be reasonable since Koff et al. has previously shown that the cartilage in early osteoarthritic (stage I) and even stage II and III osteoarthritic TMC joints exhibited less than 10 % variation in cartilage thickness across quadrants [5]. Similarly, Conconi, Halilaj [29] assumed that the subchondral bone was a reasonable measure for calculating joint congruence distribution in the neutral position using a contact based congruence measure. In healthy TMC cartilage, the mean thickness is less than 1 mm, and variation from the mean is small enough to not significantly affect the outcomes of a force controlled FE analysis. Thus, our findings appear to give reasonable characterisation of peak stress location and contact area size. Furthermore, using a hip joint model, Anderson, Ellis [30] showed that predicted cartilage contact pressure magnitudes and distributions were comparable when using a FE model with subject-specific cartilage geometry compared to a FE model with uniform cartilage thickness, so long as the underlying bone geometry was accounted for. At the ankle joint, Anderson, Goldsworthy [31] generated a cartilage contact model by uniformly extruding cartilage elements from a bone surface obtained from CT data and showed close agreement with measured pressure distributions from Tekscan data. We tested the effect of varying the cartilage thickness within ± 0.2 mm throughout the study and did not find a clinical difference in the investigation of sex and age differences in contact area size (RMS Error < 2.5 mm²) and location (RMS Error < 1.2 mm²). Lastly, we do not believe that the contact area size and location would be significantly affected by a more complex constitutive model of cartilage (e.g. Mooney-Rivlin) [21].

Our findings show that the location of peak cartilage stress in the TMC joint of men and women performing pinch, grasp, and jar twist tasks are different; men perform the tasks more consistently than women during grasp and jar twist. Contact areas do not appear to vary with age or sex, but are dictated by the task being performed. Furthermore, a subset of peak cartilage stress locations have been correlated with known wear patterns. This work has implications in terms of musculoskeletal modelling, understanding joint pathology, and tools that may potentially aid in clinical diagnosis of joint disorders. We envision a clinical tool which can automatically predict and diagnose joint degeneration based on morphology, kinematics and patient demographics. Further work should evaluate the kinematics of subjects that produce atypical cartilage stress locations and to evaluate and compare to subjects with early OA.

Highlights.

• Sex and age are poor predictors of contact area size in the trapeziometacarpal joint.

• The location of peak cartilage stress varied by sex for pinch, grasp, and jar twist tasks.

• Peak cartilage stress was more variably located in women than in men during grasp and jar twist.