Modular deconstruction reveals the dynamical and physical building blocks of a locomotion motor program

Abstract

The neural substrates of motor programs are only well understood for small, dedicated circuits. Here we investigate how a motor program is constructed within a large network. We imaged populations of neurons in the Aplysia pedal ganglion during execution of a locomotion motor program. We found that the program was built from a very small number of dynamical building blocks, including both neural ensembles and low-dimensional rotational dynamics. These map onto physically discrete regions of the ganglion, so that the motor program has a corresponding modular organization in both dynamical and physical space. Using this dynamic map, we identify the population potentially implementing the rhythmic pattern generator and find that its activity physically traces a looped trajectory, recapitulating its low-dimensional rotational dynamics. Our results suggest that, even in simple invertebrates, neural motor programs are implemented by large, distributed networks containing multiple dynamical systems.

Introduction

The concept of the motor program, a fixed sequence of automatically-executed movements, is widely assumed to underlie automatic motor control in both vertebrates (Mink, 1996; Grillner et al., 2005; Summers and Anson, 2009; Esposito et al., 2014) and invertebrates (Wu et al., 1994; Frost and Katz, 1996; Kupfermann and Weiss, 2001; Jing et al., 2004; Flood et al., 2013; Schoofs et al., 2014). Its neural basis has been most clearly elucidated in the reconstructions of dedicated circuits that initiate, generate, and execute a specific rhythmic behaviour in invertebrates (Selverston, 2010). Deep understanding of these circuits has been possible because each comprises the inter-connections between a few identifiable neurons that are common to every animal. These have illuminated general principles of the neural architectures, dynamics and modulation underlying motor control (Getting, 1989; Katz et al., 1994; Yuste et al., 2005; Selverston, 2010). However, in larger nervous systems the limited genetic capacity for specifying individual neurons and their connectivity means that dedicated circuits give way to stochastically wired networks. The existence of multifunctional motor networks in both Aplysia and the medicinal leech, in which the same neural system supports more than one distinct motor program (Tsau et al., 1994; Wu et al., 1994; Briggman et al., 2005; Briggman and Kristan, 2006), suggests that even in simple invertebrates neural motor programs are implemented in large, distributed networks rather than dedicated circuits (Getting, 1989; Wu et al., 1994). Understanding the distributed network implementation of a motor program would thus bridge the gap between dedicated circuits and the general principles of motor control.

How a distributed network implements a single motor program is unclear. Its implementation is potentially built from a mixture of systems (Getting, 1989; Jing et al., 2004; Rokni and Sompolinsky, 2012), including at least one pattern generator for rhythmic output (Selverston, 2010; Rokni and Sompolinsky, 2012; Churchland et al., 2012), a set of motorneurons for translating rhythmic output to muscle commands (Brezina et al., 2000; Rokni and Sompolinsky, 2012), and neuromodulators of both generator and motorneuron output (Getting, 1989; Brezina et al., 2000). Each of these “building blocks” (Getting, 1989) could form a functionally separate population within the network, or two or more could be combined into a single functional population. Each building block could implement a different dynamical system, such as neural ensembles (Wickens et al., 1994; Mattia et al., 2013) or low-dimensional attractors (Schoener and Kelso, 1988; Briggman et al., 2005; Churchland et al., 2012). Consequently, the distributed network implementation of a motor program has many unknowns: whether it is a mixture of functionally independent dynamical building blocks or a single integrated circuit; how these are organised in the network; and what dynamics they implement.

To address these issues, we imaged populations of neurons in the pedal ganglion of the sea-slug Aplysia while reliably eliciting its motor program for locomotion. The pedal ganglion contains approximately 1600 neurons (Cash and Carew, 1989), and wholly contains the rhythmic pattern generator (Jahan-Parwar and Fredman, 1979, 1980), motorneurons (Hening et al., 1979; Fredman and Jahan-Parwar, 1980) and associated neuromodulatory neurons (Hall and Lloyd, 1990; McPherson and Blankenship, 1992) for locomotion, thus making it a tractable target for mapping a motor program to the dynamics and structure of its underlying distributed network. This mixture of systems means that population-imaging of the Aplysia pedal ganglion is representative of the analytical challenges that will become increasingly common for large-scale recordings of complex neural systems (Cunningham and Yu, 2014), as we know that the recorded populations will have captured multiple dynamical systems within them. We thus had to develop new dimension-reduction approaches to deconstruct population recordings into the motor program’s component systems.

In this paper, we report that the locomotion motor program is built from a very small number of dynamical building blocks that are common to every execution. These include both ensembles and low-dimensional dynamics. We show that this dynamical decomposition unexpectedly maps onto physically discrete regions of the ganglion, such that the motor program is built from physical as well as functional building blocks in a distributed network. Using this dynamic map, we identify a population with rotational dynamics potentially implementing the rhythmic pattern generator. We further show that its activity physically traces a looped trajectory. These findings shed light on the general principles of implementing motor programs in distributed networks, place strong constraints on circuit mechanisms underlying locomotion in Aplysia, and pave the way for targeted studies of attractor-like dynamics in neural systems.

Results

Optical recordings reveal variation within and between motor program executions

We used a setup that was designed to simultaneously record neural populations at high temporal and spatial resolution during execution of a single motor program (Hill et al., 2010) (Fig. 1; see Experimental Procedures). Aversive tail stimuli elicit escape locomotion in Aplysia, which consists of a rhythmic series of head reaches and muscular contraction cycles that roll head to tail down the length of the animal (Jahan-Parwar and Fredman, 1979; Hening et al., 1979). Sharp-electrode studies showed rhythmically bursting motorneurons located mostly in the pedal ganglion’s rostro-medial quadrant (Hening et al., 1979) and phase-locked to the rhythmic muscle contractions (Hening et al., 1979; Fredman and Jahan-Parwar, 1980). The ganglion’s functional and physical organization during locomotion is otherwise largely unknown.

Figure 1. Imaging and analyzing Aplysia’s locomotion motor program.

A Experimental setup. Left: Head reach in Aplysia’s rhythmic escape locomotion. Middle: Preparations consisted of the ring ganglia (Ce: cerebral; Pl: pleural; Pd: pedal), with a stimulating electrode connected to peripheral nerve Pd9. Some recordings also used a suction electrode connected to pedal nerve 10 (Pd10) to monitor the neck contraction phase of locomotion. Right: Imaged area of the dorsal pedal ganglion, aligned to the photodiode array of 464 diodes (red outline). B Analysis stages for deconstructing the motor program. Fast voltage-sensitive dye recordings captured simultaneous cellular-level activity and the location of every neuron. Step 1: each motor program recording is decomposed into its component ensembles using modularity-detection (panel C). We map the physical location of the ensembles in each recording, seeking a “dynamic map” of each execution of the program. Step 2: ensembles are classified across recordings into groups of statistically similar firing patterns, seeking the dynamical building blocks of the motor program. Step 3: we map the physical location of the ensemble groups over all recordings, seeking the physical layout of the motor program’s dynamical building blocks. C Modularity detection of ensembles (step 1 in panel B). Schematic illustration of the steps for decoding neural ensembles using community detection with consensus clustering. Key is modelling the pairwise correlation matrix as a network: each node is a neuron, each link’s weight is the correlation between that pair of neurons. Community detection algorithms – so-called by analogy with the division of social networks into communities – provide a general solution to the problem of separating an arbitrary network into its component modules: here each module is thus an ensemble of strongly, mutually correlated neurons. Choice of time-scale and type of correlation thus define a “neural ensemble”. Here we convolve each spike-train with a Gaussian window whose width is defined by the characteristic period of the locomotion-related activity (Experimental Procedures; Supplemental Fig. 1), and correlate each pair of convolved spike-trains.

Using an isolated brain preparation, we reliably elicited fictive locomotion by stimulation of pedal nerve 9, while simultaneously recording the spike-trains of individual neurons across the entire ganglion at high temporal resolution (1.6 kHz) using voltage-sensitive dye imaging with a photodiode array (Fig. 1A) (Hill et al., 2010). We simultaneously recorded 57-125 neurons in each of 12 preparations, a total of 1145 neurons, with each record truncated to the initial 80 seconds in which each preparation consistently showed locomotion-related activity. We accurately mapped the location of every recorded neuron in the 2-dimensional imaging plane (see Supplemental Experimental Procedure 3; Fig. 3A).

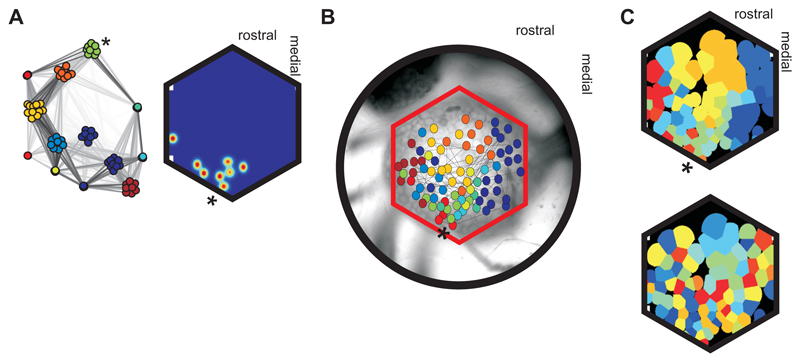
Figure 3. Modular deconstruction of the physical substrate.

A Mapping neuron location. Left: layout of a recorded functional network; the asterisk (∗) indicates the example neural ensemble corresponding to physical positions in panels A-C. Right: Estimated position of all 8 neurons in the example ensemble; each position estimate is plotted as a two-dimensional Gaussian, with blue-red indicating minimum-maximum probability of location. B Projection of the functional network onto physical space. We plot the mean estimated position of all neurons, color-coded by ensemble membership, onto the approximate extent of the ganglion covered in this recording. Links show a sample of the network (within ± 1 s.d. of mean correlation). C Map of neural ensemble locations on the photodiode array (top) showing physical contiguity of the ensembles in a recording: each region of the array is claimed by the closest neuron; all regions belonging to the same neural ensemble are merged (same color). Bottom: example control map, generated by randomly assigning neurons to the same number and size of neural ensembles. Supplemental Figure 3 compares data and randomized maps across all recordings.

Decomposing the motor program required combining recordings to identify dynamical building blocks common to each execution of the program. However, recorded executions varied in both time-scale (Supplemental Fig. 1A-C) and intensity (the distribution of firing rates significantly differed between 55 of the 66 unique pairs of recordings; K-S test at α = 0.05). This variation between recordings, combined with the likely mixture of dynamics within each recording, made analysis with standard dimension reduction techniques challenging (Machens, 2010). Illustrating this difficulty, we found that applying principal components analysis (Briggman et al., 2005; Levi et al., 2005) to each recording revealed hints of attractor-like dynamics (Supplemental Fig. 1D-E), but the number of principal components capturing 95% of the variance in a recording ranged from 2-12, indicating that each recording captured different sets of dynamics within the same motor program.

To solve these problems, our starting point was to seek the existence of neural ensembles within each recording. Finding these would provide evidence of ensembles within a distributed network implementation of a motor program; as we will show, these also provide a basis for solving the problem of combining information across variable recordings to decompose the dynamic systems within a program. Our analysis strategy for decomposing the motor program is illustrated in Figure 1B; below we detail the new algorithms introduced at each step.

Each motor program execution is comprised of functional neural ensembles

As there are an unknown number and size of ensembles in each execution – potentially zero – we developed an unsupervised algorithm for ensemble detection (Experimental Procedures). Each recording is characterized as a functional network of correlations between neuron pairs (Figure 1C), where each node is a neuron and each link encodes correlation strength. Our algorithm is based on the concept of community detection in arbitrary networks: it separates each functional network into modules (“communities”) of nodes by directly optimizing the modularity score Q, which is maximized by grouping nodes into modules that have dense connections within them and sparse connections between them (Newman, 2006b; Humphries, 2011). These modules are thus groups of neurons whose activity patterns are more similar to each other than to any other neuron, and give a quantitative definition of “neural ensemble” (or “cell assembly”) (Wehr and Laurent, 1996; Harris, 2005; Peyrache et al., 2009; Niessing and Friedrich, 2010). To solve the problem of reliably clustering each recording for later between-recording comparison, we developed a new consensus-clustering approach to community detection (Supplemental Experimental Procedure 1).

Consensus community detection was highly effective in organizing the raw recording traces into separate ensembles of temporally correlated neurons (illustrated in Fig. 2A-C). We found that each execution of the locomotion motor program decomposed into multiple neural ensembles. The recordings captured between 7 and 18 ensembles each (total of 147), ranging in size from 2–24 neurons (median 8 neurons; Fig. 2D). Every ensemble was highly self-similar (Fig. 2E), indicating that the algorithm was very successful at separating each functional network into its component modules. The modularity of each preparation was approximately the same (mean Q = 0.18 ± 0.05 s.d.), confirming that the recordings were sampling the correlation structure of the circuit in a consistent manner. The number of ensembles scaled with the number of recorded neurons in the preparation (Fig. 2F), suggesting that each recording is sampling a subset of all simultaneously present ensembles.

Figure 2. Modular deconstruction of a motor program recording.

A Raster plot of an example optical recording of 102 neurons over 80 seconds. B The corresponding functional network. Each node is a neuron; gray-scale intensity of the links indicates similarity of that pair of neurons. The 12 detected modules within the network are color-coded. Distance between modules indicates their average similarity. C Raster plot from panel A ordered and color coded by module membership in panel B, showing the 12 ensembles. D Distribution of ensemble size across all recordings. Red line indicates median value. E Distribution of median intra-group similarity over all preparations; red line indicates median of distribution. F Correlation between number of neurons in each recording and number of ensembles detected (linear regression, n = 12). (see also Supplemental Fig. 2).

Supplemental Figure 2 shows that our detected ensemble structures are robust to order of magnitude changes in the time-scale of correlation, and to using an adaptive time-scale that accounts for population firing rate changes over the recording.

Each motor program execution is comprised of physical neural ensembles

To understand how each motor program execution is distributed across the network, we then sought the physical layout of the ensembles in each recording. Our use of voltage-sensitive dye imaging with a photodiode array and independent component analysis to isolate the spike-trains (Hill et al., 2010) allowed us to recover the location of each neuron within the two-dimensional imaging plane of the ganglion (Fig. 3A; Supplemental Experimental Procedure 3). Across all recordings we found that most ensembles (100/147) were physically cohesive (P < 0.05, permutation test), as illustrated in Figure 3A, such that strongly correlated neurons were physically close.

We then asked whether this physical cohesiveness meant that ensembles comprising a single execution of the program were intermingled or discretely arranged. As each recording sampled a subset of all likely ensembles, to check for discreteness we needed to solve the problems of incomplete data, of unknown, likely irregular physical shapes of ensembles, and of possible noise in the clustering. To do so we developed a parameter-free method for interpolating the physical extent of each ensemble, illustrated in Fig. 3B-C (see Supplemental Experimental Procedure 3).

We found most ensembles (110/147) had at least half their neurons in one continuous patch of space, and so were highly discrete (Supplemental Fig. 3). Most strikingly, as illustrated in Fig. 3C the physical arrangement of ensembles in each recording was also highly discrete (mean proportion of neurons in a single continuous patch was between 52% and 92%; all were greater than 95% confidence interval, permutation test). Functionally-defined ensembles thus correspond to physically separate neuron groups: a single execution of the locomotion motor program is distributed across the network as a set of physically discrete neural ensembles.

Different classes of ensembles correspond to different dynamical systems within the motor program

Having characterized each execution, we turn to the central problem of combining recordings to identify the dynamical building blocks of the motor program (Fig. 1B, Step 2). We had identified a database of 147 ensembles across all recordings. We classified these ensembles into one of four classes defined by significant peaks or troughs in their autocorrelograms (Fig. 4; Experimental Procedures), which allowed us to capture their oscillation pattern invariant to the time-scale or intensity of the motor program execution to which they belonged. We show below that this broad classification allowed us to isolate dynamical systems within each recording.

Figure 4. Classes of ensemble.

Four classes of ensemble were defined by the presence or absence of significant peaks or troughs in their auto-correlograms: the non-oscillatory class had no significant peaks or troughs; “oscillators” had both; “bursters” had significant peaks but not troughs, indicating repeated phasic firing without repeated silence; “pausers” had significant troughs but not peaks, indicating repeated silence without repeated stereotyped bursts. Auto-correlogram (top) and raster (bottom) plotted for an example ensemble of each class. The red lines plot the upper and lower bounds on expected spike-count predicted by a shuffled inter-spike interval model; peaks are contiguous bins above the upper bound, troughs are contiguous bins below the lower bound. We also plot the “dynamic map” of each oscillatory class, with heat intensity (blue-red) indicating the proportion (%) of recordings in which that location belonged to that oscillatory class of ensemble; white indicates no membership of that class detected. All maps plotted for the left ganglion.

We found all four possible classes of oscillation pattern existed within the locomotion motor program (Fig. 4). Most ensembles (85%) fell into the three classes of oscillator: “oscillatory” (63%); “bursters” (19%); and “pausers”(3%). The remaining 15% of ensembles had no strong oscillation, yet neurons in these ensembles were recruited by the onset of the motor program (Supplemental Fig. 4). These data suggest that a neural motor program also incorporates neural ensembles that are not manifestations of some oscillation.

We found that the oscillator and burster classes identified separate dynamic systems. For each recording, we selected the subset of ensembles belonging to a particular class, and then projected all neurons in that selected population into a low-dimensional space using PCA, to visualize the population dynamics (Briggman et al., 2005; Levi et al., 2005).

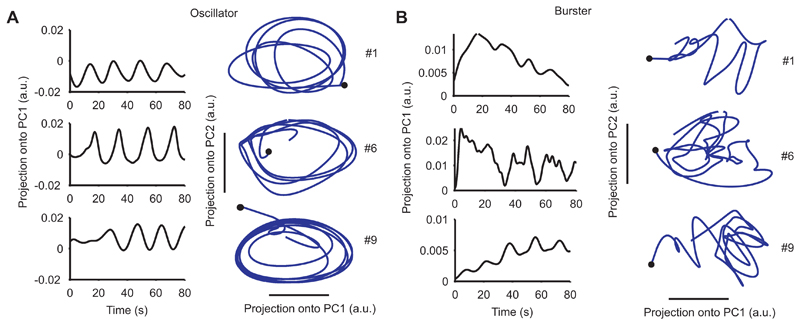
In most recordings we found that the oscillator-class population was dominated by an oscillation of constant amplitude and frequency throughout the program’s execution, shown by the first principal component (Fig. 5A). Projecting the population onto the first two principal components showed that this constant oscillation corresponded to a constant rotation of population activity (Fig. 5A). Such consistent rotation in two dimensions indicates that the underlying oscillatory activity in this population was phaselocked throughout the recording

Figure 5. Separate dynamical systems within the locomotion motor program.

A Oscillator-class ensembles. We plot the projection onto the first principal component (PC1, left) and onto the first two PCs (right) for the population of neurons in oscillator-class ensembles in three recordings (1, 6, and 9). Black dot indicates time zero. B Burster-class ensembles. Layout as for panel A, plotted for the population of neurons in burster-class ensembles in the same three recordings.

In recordings with sufficient numbers of identified burster-class ensembles, we found that the burster-class population was dominated by evolving activity over the course of the program, shown by the first principal component (Fig. 5B). To confirm this, we correlated the projection onto the first principal component against time, and found a strong relationship (median r² = 0.34, n = 11 recordings), consistent with a change in baseline activity over time. Projecting the population onto the first two principal components showed that this evolving oscillation did not correspond to a constant rotation of population activity (Fig. 5B).

Our identification of four classes of oscillation pattern shows that the locomotion motor program can be decomposed into at least three dynamic systems, one showing correlated firing but not oscillating (“non-oscillators”); one that implements a constant oscillator (“oscillators”); and one that evolves over the program’s execution (“bursters”). The pauser class may correspond to a fourth separate dynamic system, but no single recording contained sufficient numbers for us to check.

Dynamic mapping of the motor program

Having identified these four classes of dynamical building blocks of the motor program, we then sought to understand how they are distributed over the physical network (Fig. 1B, Step 3). To do so, we took the map of extrapolated ensemble locations for each recording (such as the example in Fig. 3C) and labeled each location with the oscillatory class of that ensemble. We then combined these re-labeled maps across all recordings. We plot the resulting “dynamic map” for each oscillatory class in Figure 4.

We see that the four classes of ensemble defined solely by oscillation pattern map to different locations on the ganglion. In particular, the oscillator class ensembles are predominantly located in the caudo-lateral quadrant, whereas the burster class ensembles are predominantly located in the rostro-medial quadrant. Thus, the separate dynamical systems identified by the oscillation patterns of neural ensembles correspond to a physical separation within the pedal ganglion network. We note that this clear separation is not a trivial result of the discreteness of the individual ensembles: the execution of a single program has discrete ensembles, showing that correlated neurons are located within a single, discrete region of the ganglion network; but ensembles of different oscillation classes could themselves be intermingled – our maps show that this is not the case.

Rotational dynamics of oscillator ensembles corresponds to a physical looped trajectory of activity

Aplysia locomotion represents a particular challenge in understanding motor control. In many invertebrates and some vertebrates locomotion is driven by a rolling wave of neural activity that causes sequential muscle contractions. This rolling wave is most often realized by the sequential firing of linked segmental networks (Cacciatore et al., 2000; Eisenhart et al., 2000; Gjorgjieva et al., 2013), but in Aplysia the entire neural apparatus is contained within the single pedal ganglion network. It is otherwise unknown how this single network can implement the rhythmic pattern generator necessary to generate the slow rolling wave.

The oscillator ensembles are potentially the observable portion of the unidentified rhythmic pattern generator for locomotion. Our dynamic map localized these to the caudolateral quadrant (Fig. 4) where few motorneurons are found (Hening et al., 1979), and where the single reported example of an oscillatory interneuron was found (Fredman and Jahan-Parwar, 1980). Within each recording, we have shown that the activity of the oscillator-ensemble population of neurons can be well-described by a perfect rotation in a two-dimensional space, despite the variations over a single motor program execution and between each execution (Fig. 5A).

Our mapping of the physical ensembles in each recording allowed us to ask if we could observe directly the rotation in the two-dimensional space as a rolling wave of activity in physical space. We again selected the oscillator ensembles in each recording, and plotted the position of their spatially-averaged activity over time (Fig. 6A; Experimental Procedures). We consistently found that this “activity packet” repeatedly traced a looped trajectory in the ganglion network during a single execution of the motor program (Fig. 6B; Supplemental Video 1), recapitulating the low-dimensional rotational dynamics of the population.

Figure 6. Rotational dynamics correspond to physical rotations of activity.

A Projection of oscillator-class activity onto physical space. Top: Sequence of firing of 4 representative oscillator ensembles in recording #1. Bottom: center of each of the 4 ensembles. Eligible recordings had 5-12 oscillator ensembles. B Looped trajectories of the activity packet in space. Top: the activity packet from recording #1 (panel A) describes an elliptical orbit (red) on the plane of the ganglion; black line: best-fit ellipse; scale bar: 1 diode spacing (∼ 60µm). Bottom: best-fit ellipses showing trajectories from all recordings with sufficient oscillator ensembles to uniformly span phases of a motor program cycle. C Looped trajectory corresponds to phasic motor output. Top: Extracellular recording from pedal nerve 10 (Pd10). Bottom: firing of Pd10 mapped onto the looped trajectory. Dark red represents peak firing, corresponding to bursts in the upper panel (see Supplemental Fig. 5). D Hypothesised control of the pedal wave for locomotion. Cycling activity on the network is plotted schematically as an ellipse. Activity on specific portions of the trajectory is proposed to recruit motorneurons (M) projecting to muscles in the foot and body wall, whose axons contribute to the suggested nerves. One cycle of the trajectory would thus generate the pedal wave for locomotion by sequentially activating the neck/anterior, middle, then posterior nerves.

If this was a physical realisation of the rhythmic pattern generator, the activity packet trajectory should correlate with specific phases of movement. Consistent with this picture, in further recordings we found that burst firing of pedal nerve 10, correlated with neck contraction (Xin et al., 1996), in turn correlated with a specific portion of the looped trajectory of activity in the ganglion network (Fig. 6C; Supplemental Video 2). Clustering these recordings showed that phasic activity of our detected ensembles was temporally aligned with the nerve’s activity, and so correlated with motor output during locomotion (Supplemental Fig. 5). Our results thus suggest the intriguing possibility that ensembles in the caudolateral quadrant are a network implementing a rhythmic pattern generator.

The motor program is comprised of a few dynamical building blocks

The classification of the 147 ensembles into four classes of oscillator allowed us to decompose and map the dynamical building blocks of the motor program, but had some limitations. Such a classification forced all ensembles into four pre-defined classes, thus pre-determining that there could only be a few dynamical building blocks. In addition, visual inspection of our recordings revealed a wider variety of spike-train structure than could be captured by oscillation pattern, and it is likely that each recording captured one or more entirely unknown types of ensemble. To address these issues, starting with the same database of 147 ensembles we repeated steps 2 (classify) and 3 (map) of the analysis (Fig. 1B) using a new unsupervised classification approach based on spike-train structure, thus not presuming any number of dynamical building blocks. We thus develop here a solution to the general problem of clustering ensembles across preparations.

To capture the wide variety of spike train structure we used a statistical approach (Compte et al., 2003; Wohrer et al., 2013). Each ensemble was described by its firing rate and regularity, respectively captured by the distribution of inter-spike intervals (ISIs) and the distribution of the local regularity measure CV₂ (Fig. 7A). Capturing each ensemble’s dynamics using these complete distributions precludes the use of conventional clustering methods to classify ensembles. To solve this, we developed an approach that clusters in a “fit space” (Experimental Procedures). We fit N models to each distribution and compute the probability that each model was the best fit to the distribution, combined into the length N vector P (model). Here we use N = 6 models, covering unimodal (exponential, normal, gamma, log-normal) and bimodal (normal, gamma) distributions (see Supplemental Experimental Procedures 2 for specification). By concatenating the vectors for its ISI distribution and for its CV₂ distribution, each ensemble is then represented as a point in the (2×N)-dimensional space of rate and regularity properties. Distances between pairs of ensembles in this fit-space are then used as the basis for unsupervised clustering, resulting in groups of ensembles defined by the statistical similarity of their spike-train structure.

Figure 7. Unsupervised clustering of ensembles in the “fit-space”.

A Ensemble characterization. Histograms show ISI or CV₂ distributions for three example ensembles, and red lines plot their best-fit models. A distribution for an ensemble was created by pooling distributions for each spike-train in the ensemble. B Clustering ensemble groups by spike-train structure. Top-left we plot two examples of concatenated P(model) vectors defining the 12-dimensional “fit-space”. Bottom-right: visualization of the network defined by distances between ensembles in this fit-space, and the nine identified ensemble-groups within it (colors); symbols indicate some common properties of the nine groups. Grayscale intensity of lines indicates similarity of nodes.

We found that the 147 ensembles reduced to nine ensemble groups defined by their spike-train structure (Fig. 7B), supporting the hypothesis that the locomotion motor program is constructed from a limited number of dynamical building blocks. No single recording captured ensembles from all groups (median 4 types of group per recording, range 2-6), showing that our unsupervised “fit space” approach was able to integrate information from across recordings. Figure 8 summarizes the properties of each group. Three groups have bimodal distributions of both ISIs and CV₂ (Groups 1, 2 & 8, totalling 119 of 147 ensembles in the database), consistent with the strongly oscillatory firing in the system. Together these account for the majority of “oscillator” and “burster” classes (Supplemental Fig. 6). A unique ensemble-group (Group 7; 3/147 ensembles) have a bimodal distribution of ISIs, implying that these ensembles are bursting, yet had a uniform distribution of regularity meaning that each burst is a Poisson process. Such highly-irregular firing may indicate that these neurons’ afferent network is in the “balanced” state of many asynchronous excitatory and inhibitory inputs (Berg et al., 2007).

Figure 8. Groups of ensembles defined by spike-train structure.

We found nine groups of ensemble distinguished by their firing rate and regularity; percentages on the far left give the proportion of ensembles in each group. In the left-most column we plot the map of all locations containing that ensemble group, with heat intensity (blue-red) indicating the proportion of recordings in which that location contained an ensemble of that group; white indicates no membership of that group detected. Further columns illustrate an example ensemble of each group: the four most-similar spike-trains in that ensemble (80 s duration); and the cumulative distributions for the interspike intervals (ISIs) and the irregularity metric (CV₂) for the ensemble. Black line: data; red line: best fitting model (highest P(model) out of the 6 candidates). Note different scaling of x-axes for cumulative plots. Supplemental Figure 6 maps these ensemble groups defined by spike-train structure onto the distribution of ensembles according to oscillator-class.

Strikingly, two groups of ensembles have a unimodal ISI distribution (Groups 4 & 9, 7/147 ensembles), implying tonic firing throughout their recordings. These confirm that ensembles of neurons with correlated but non-oscillatory firing are a dynamical system present during the locomotion motor program. The lack of oscillatory firing implies that such ensembles do not directly encode the program’s sequence of movements, but may play a modulatory role. We further discuss the relationship between the spike-train properties of the nine groups detected here and the known properties of the pedal ganglion in the Supplemental Text.

Using the same approach as the oscillator classes, we plot the resulting “dynamic map” for each ensemble group in Figure 8. We see that these groups are also physically segregated in the ganglion. As an example of the consistency in the mapping across recordings, we see that the ensembles of the Poisson-burst group (Group 7) are found in the same, precise location of the rostro-medial quadrant (Fig. 8). These maps show that, when defined through unsupervised clustering of their spike-train statistics, the dynamical building blocks of the locomotion motor program are physically segregated in the ganglion’s network.

Discussion

The implementation of a single motor program in a distributed network is modular, deconstructable into separate dynamical building blocks that are recapitulated in physical space (Figs. 4 and 8). These modules exist at two scales: the individual, discrete ensembles of neurons; and the larger-scale discrete mapping of the different dynamical systems within the pedal ganglion. This doubly-modular nature represents a dramatic dimension reduction: here our data-set of 1145 neurons comprised 147 neural ensembles, which in turn reduced to 9 groups of ensembles with statistically-similar firing. Our results thus support the idea (Koch, 2012) that detecting neural modularity will be highly effective in reducing the dimensional complexity of the brain.

Modular deconstruction of large-scale neural recordings

In tackling the problem of decomposing a motor program, we have developed an analysis pipeline for dynamical mapping of a neural circuit (Fig. 1B). As the pedal ganglion network’s implementation of the locomotion motor program contained many unknowns, the key here was to use entirely unsupervised analysis that allowed us to discover components within the large-scale recordings. Placed in sequence (Fig. 1B), the unsupervised steps of ensemble detection and classification allow for a data-driven breakdown of any set of large-scale, cellular-level recordings. Supplemental Fig. 2 shows that ensemble detection using our consensus clustering algorithm is robust to order-of-magnitude or dynamic changes in correlation time-scale, suggesting our methods are generalizable to systems with richer, faster dynamics. Code implementing all stages of the analysis is supplied in the Supplemental Software; Supplemental Experimental Procedures 1-3 outline the supplied functions. Ongoing developments of the MATLAB toolboxes are available at: for spike-train community detection: https://github.com/mdhumphries/SpikeTrainCommunitiesToolBox; and for analysis and classification of neural ensembles: https://github.com/mdhumphries/NeuralEnsembleAnalysis.

We used two different approaches to classifying ensembles, as they give complementary insights. Categorization by oscillation pattern (Fig. 4) allowed us to isolate dynamical systems within a single population recording, and yet identify them across all recordings. The unsupervised classification by spike-train statistics (Figs. 7-8) allowed us to both show that the groupings of ensembles exist independent of any experimenter assumptions, and use the extra statistical power gained by pooling across all recordings to identify unique ensembles that appear in only a small subset of recordings. Both are generally applicable to the output of any ensemble detection method.

Identified hypotheses for locomotion control in Aplysia

Generating rhythmic motor behavior requires solving the general problem of generating the underlying repeating cycle of neural activity. The solution for locomotion adopted by many invertebrate brains is to link many segmental ganglia following the longitudinal axis of the animal (Cacciatore et al., 2000; Eisenhart et al., 2000; Gjorgjieva et al., 2013). Their sequential firing then sequentially recruits motorneurons, causing a wave of muscle contractions. The single network of the Aplysia pedal ganglion must solve the problem in a different way.

The pattern generator and motorneurons appear to be distinct components in the pedal ganglion (Fredman and Jahan-Parwar, 1980). The motorneurons are not synaptically coupled (Hening et al., 1979; Fredman and Jahan-Parwar, 1980), ruling out the possibility that they are the internal pattern generator, generating and co-ordinating their own bursting activity (Fredman and Jahan-Parwar, 1980). The dominance of excitatory post-synaptic potentials underlying the firing of motorneurons (Hening et al., 1979; Fredman and Jahan-Parwar, 1980) and pedal-peptide neurons (Hall and Lloyd, 1990) points to an excitatory interneuron network within the ganglion. As there are around 1600 neurons in the pedal ganglion (Cash and Carew, 1989), and communication between neurons is predominantly via chemical synapses, a large network of synaptically-connected interneurons could feasibly exist. With this limited prior knowledge of the network, our unsupervised analyses rapidly identified a set of testable functional hypotheses for Aplysia locomotion control.

First, our data supports the hypothesis that the rhythmic pattern generator for Aplysia locomotion is realized by a network of interneurons in the caudo-lateral quadrant of the pedal ganglion. Here we identified a set of oscillator ensembles (Fig. 4), whose population activity traces a perfect rotation in low-dimensional dynamical space (Fig. 5), recapitulated in the physical space of the ganglion (Fig. 6). These rotations arise because individual neurons within the population had phase-locked oscillatory activity throughout the recordings. It is possible that the richness of observed oscillatory activity across this quadrant is not wholly intrinsic to the pattern generator, as inputs from the intact pleural and cerebral ganglion are known to respectively modulate the amplitude of oscillation (Jahan-Parwar and Fredman, 1979, 1980) and contain the command neurons for self-initiation of locomotion (Fredman and Jahan-Parwar, 1983).

From these data we can sketch a model for locomotion control in Aplysia, in which activity in each portion of the loop recruits motorneurons projecting to different muscle groups (as we showed for nerve P10 in Fig. 6C). We illustrate this idea schematically in Figure 6D, concentrating on the known nerves that project from the pedal ganglion to different portions of the foot (and thus control the pedal wave component of locomotion). One prediction of this model is that simultaneous suction electrode recordings from the identified nerves should map onto relatively discrete portions of the trajectory of activity. We do not expect them to be literally as discrete as shown; rather, pedal nerves innervate overlapping areas of the foot, presumably to allow smooth execution of the pedal wave (Fredman and Jahan-Parwar, 1980). As Aplysia locomotion includes both crawling and faster galloping (Jahan-Parwar and Fredman, 1979), this model suggests that these locomotion modes correspond to the rate of oscillation in the activity loop.

A second hypothesis is that the rotational dynamics recapitulated in dynamical and physical space are consistent with the direct observation of a cyclical attractor network (Eliasmith, 2005; Rokni and Sompolinsky, 2012; Yoon et al., 2013). This class of networks generate and self-sustain a moving packet of activity (consistent with our observations in Fig. 6, and Supplemental Videos 1-2), and have been proposed to underlie a wide-range of neural systems’ dynamics, including grid-cell generation (Yoon et al., 2013) and head-direction representation (Zhang, 1996). Compared to the cyclical attractors embodied by small, fixed central pattern generator circuits (Selverston, 2010), the theoretical advantage for locomotion of a network implementation lies in the ability to produce flexible motor programs of differing speed and/or muscle recruitment by the speed and trajectory of activity in the attractor network (Eliasmith, 2005; Rokni and Sompolinsky, 2012). This cyclical attractor could be representative of the general solution to generating rhythmic activity in a large neuronal network (Yuste et al., 2005; Yoon et al., 2013).

Under this hypothesis, our oscillator ensembles are the observable manifestations of the attractor network’s moving activity packet. An alternative explanation of the physical trajectory is that the pattern generator comprises a series of independently oscillating neuron groups: if they were physically arranged in phase order, the location of the activity packet would follow the layout of the groups. To be consistent with our observations, the independent oscillators would be laid out in a loop. Future testing of the attractor-network hypothesis will thus require making use of critical tests for dynamical systems using perturbation. One crucial test would be to perturb the activity of the oscillator-ensembles during an ongoing locomotion program: if they do form an attractor network, then the perturbed activity should return to the same cyclical trajectory. Another crucial test would be to target stimulation to a section of the oscillator-ensemble region at rest: if that section was part of a cyclical attractor network, then sufficiently intense stimulation should initiate the sustained activity packet.

A third hypothesis is that the burster-class ensembles are integrators, as they reliably form an evolving dynamical system over the motor program (Fig. 5B). These ensembles were in the ganglion’s rostro-medial quadrant, where motorneurons are predominantly located (Hening et al., 1979). One possibility is that the motorneurons captured in these ensembles are integrating the output of the putative pattern generator together with other modulatory inputs to turn the constant oscillation into a smoothly varying pattern of muscle contractions. Another is that the burster-class represents a subset of neurons integrating input for or against the decision to engage a different behavior (Briggman et al., 2005). Testing these hypotheses in future work requires more thorough sampling of the motorneuron population in this quadrant.

Outlook

Traditionally, functional mapping studies were based on sharp electrodes, typically placing them into at most a few neurons at a time to assess firing patterns during motor programs of interest. Reconstructing networks this way is labor-intensive and takes immense time, often involving successive generations of scientists focused on single model preparations. Locked within the large-scale cellular-level recordings during behavior newly available from a variety of species (Seelig et al., 2010; Ahrens et al., 2012, 2013; Larsch et al., 2013) are the data necessary to reconstruct neural circuits’ functional connectivity from single sets of recordings. The data-driven, unsupervised analysis pipeline developed here could unlock this data’s potential, reducing the time needed to identify key neuronal components for a given neural circuit by orders of magnitude.

Here we have demonstrated the use of modularity as a static concept to deconstruct the mapping between a motor program and its neural implementation. However, in common with many other neural populations’ activity (Briggman et al., 2005; Churchland et al., 2012), the locomotion motor program evolves over its time-course (Hill et al., 2012), displaying moment-to-moment functional reconfiguration. The next, greater challenges are to fully characterize such functional dynamic modularity and the mechanisms underlying it.

Experimental Procedures

Voltage-sensitive dye imaging in the fictive escape locomotion preparation

The cerebral, pleural and pedal ganglia were dissected out and pinned to the bottom of a Sylgard (Dow Corning) lined chamber containing Instant Ocean artificial seawater (Aquarium Systems). The loose connective tissue surrounding the ganglia and nerves was removed while keeping the sheath intact. The preparation was then transferred and pinned to the floor of a Sylgard-lined recording chamber with a coverslip bottom used for optical recording (PC-H perfusion chamber, Siskiyou). To maximize the number of neurons in focus, the ganglion to be imaged was partially flattened by lightly pressing a shard of cover slip upon it. The shard was held in place with small bits of silicon earplug (Mack’s) adhered to the recording chamber floor.

For imaging, the preparation was maintained at 15 – 17°C, using Instant Ocean passed through a feedback-controlled in-line Peltier cooling system (Model SC-20, Warner Instruments). Temperature was monitored with a BAT-12 thermometer fitted with an IT-18 microprobe (Physitemp, Inc) positioned near the ganglion being imaged. For staining, the room was darkened and the perfusion saline was switched to saline containing the fast voltage sensitive absorbance dye RH-155 (Anaspec). The preparation was perfused with 0.03 mg/ml RH-155 in Instant Ocean for 1 hour at 15°C. An Olympus BX51WI microscope equipped with a 10X 0.6NA water immersion objective was used for imaging. Trans-illumination was provided with light from a 735 nm collimated LED (ThorLabs) which was passed through a 0.9 NA flip top achromat Nikon condenser. The light from the objective was 100% directed either to an Optronics Microfire digital camera used for focusing or to the parfocal focusing surface of a 464-element photodiode array (NeuroPDA-III, RedShirtImaging) sampled at 1600 Hz.

Optical data from the 464 elements were bandpass filtered in Neuroplex (5 Hz high pass and 100 Hz low pass Butterworth filters), and then spike-sorted with independent component analysis (ICA) in MATLAB to yield single neuron action potential traces (the independent components), as detailed in Hill et al. (2010). We recently validated the accuracy of ICA spike sorting using simultaneous intracellular and optical recordings from neurons in various central ganglia of Tritonia diomedea and Aplysia californica (Hill et al., 2010).

Our set-up and spike-sorting minimizes potential issues caused by light-scattering in optical imaging studies. In invertebrate tissue, our combination of a photodiode array and light wavelength are known to give a scattering radius close to the diameter of single neurons (Cohen and Lesher, 1986; Zochowski et al., 2000). Scattering is minimized further by our imaging with a very shallow depth-of-field, high NA lens, which limits the recording mostly to those neurons visible on the surface, and by our use of a coverslip pressed down onto the ganglion surface, which flattens it and maximizes the number of neurons in focus. The further potential issue of merging neurons with similar activity into one signal is unlikely to arise as individual neurons are defined in our study, not by user outlined regions of interest, but in unsupervised fashion by our ICA spike sorting method.

Rhythmic locomotion motor programs were elicited using 5-10 V 5 ms monophasic pulses delivered in trains from 2-10 Hz for 2-5 s via suction electrode to pedal nerve 9. In some experiments, a separate suction electrode was attached to pedal nerve 10 to continuously monitor the locomotion rhythm (Xin et al., 1996).

Time-scale of each motor program execution

To characterize the time-scale of each motor program execution we sought the time-scale δ that maximized both in- and anti-phase correlation between the whole population’s activity, and so captured the time-scale of repeated states of the motor program. Each recording was divided into vectors of neuron activity at time [t, t+δ], each vector containing one entry for each neuron’s spike count in that time window. We correlated all pairs of vectors and computed the dispersion of correlation as D(δ) = {mean absolute deviation of correlation matrix} / { median of correlation matrix }; we picked δ giving the maximum dispersion (Supplemental Fig. 1).

To represent individual spike-trains on this characteristic time-scale, each was convolved with a Gaussian of width σ and unit area over support ±5σ, giving the “spike density” function f. We converted $\sigma =\delta /\sqrt{12}$ (see Humphries, 2011).

PCA of motor program activity

We used standard principal components analysis (PCA) on both the entire set of spike-density functions for each recording, and on sub-sets chosen according to the oscillatory classes found in each recording. See (Briggman et al., 2005) for a tutorial on using PCA to study neural population dynamics. The first few principal components define a set of orthogonal axes that maximally account for the covariance in the data. Each principal component U_i of an analyzed set of spike-density functions contains one entry per neuron in the analyzed population, whose magnitude gives the contribution of that neuron to that component: thus pairs of neurons with anti-phase activity will have large contributions to two different principal components. Note that in such recordings of mixed dynamics, neurons without strongly phasic activity are not strictly orthogonal to others, and so would not be well isolated by PCA. Projections of data onto the ith principal component allow us to visualize the population’s dynamics, and are defined at time t by: $z_i(t)={\displaystyle {\sum }_{k=1}^n{U}_i^k{f}^k(t),}$ where the sum is taken over all n neurons in the analyzed population.

Consensus algorithm for detection of neural ensembles

We defined functional networks of zero-lag correlations between each pair of neurons. To do so, we computed the correlation coefficient C_ij between the spike-density functions (f) for each pair of neurons. The weighted functional network was then: W_ij = C_ij if C_ij > 0 and W_ij = 0 otherwise.

Maximizing modularity Q of this network decomposed the recording into its constituent neural ensembles (Fig. 1C), where modularity is informally defined (Newman, 2006a) as Q = {number of links within a module} - {expected number of such links}. An important challenge for us was to produce solutions that individually have high Q yet that can also later be combined across recordings (in steps 2 and 3 of Fig. 1B). To solve this, we extended our previous algorithm (Humphries, 2011) for maximizing Q to produce a consensus clustering of modules for each recording (see Supplemental Experimental Procedure 1). Key advantages of this algorithm over standard clustering approaches include that it automatically determines the number and size of modules; and it can give null answers, as Q ≤ 0 signals the absence of ensembles (Humphries, 2011). A MATLAB toolbox for this family of algorithms is part of the Supplemental Software. Development of these spike-train community detection algorithms is ongoing at: https://github.com/mdhumphries/SpikeTrainCommunitiesToolBox.

Network visualization was done using the MATLAB toolbox of Traud et al (Traud et al., 2009): http://netwiki.amath.unc.edu/VisComms/VisComms.

Physical organization of the neural ensembles

The ICA weight matrix allowed estimation of the two-dimensional co-ordinates of each neuron (Supplemental Experimental Procedures 3). For each recording, we discretized the diode array and constructed ensemble maps by assigning grid squares to neurons in the same ensemble. Contiguous patches of space were defined by all adjacent squares assigned to the same ensemble. See Supplemental Experimental Procedure 3 for details; the code is also part of the Supplemental Software. Dynamic maps of classes and groups were created on a template of the left ganglion oriented with rostral north, so each individual recording’s ensemble map was rotated and/or mirrored to that template if necessary.

Finding types of functional ensembles

We classified ensembles according to their pattern of oscillation. We computed an auto- correlogram A with 1 s bins up to a maximum lag of 20 s; the bin-size was chosen to be smaller than the characteristic time-scale of the motor program in every recording (Supplemental Fig. 1). Significance of oscillations in the auto-correlogram was assessed using a permutation test. We shuffled the inter-spike intervals of the spike train 100 times to produce 100 permuted auto-correlograms A*, and determined their mean and standard deviation in each bin i. To remove rate-dependence, A was Z-transformed: Z(i) = [A(i) - mean(A*(i))] / std(A*(i)). We considered a Z-scored bin significant if Z(i) > 3 for positive-valued bins and Z(i) < −2 for negative-valued bins; note the asymmetry necessary to detect negative correlations in point processes. To further account for noise, two consecutive bins had to meet criterion to qualify as a significant peak or trough.

The“fit-space” approach to clustering each ensemble using the full statistical distributions of its spike-trains is detailed in Supplemental Experimental Procedure 2. This method generalizes to an arbitrary number N of models fit to any choice of S spike-train metrics, giving N vectors for P(model) and an N × S vector defining each ensemble’s position in the “fit space”. One key advantage is that the vector acts both as a space in which to classify types and as a mixture-of-models – if the true model is not amongst the N specified, P(model) uniquely weights the contribution of each specified model to the true model. The code for fitting distributions and clustering in the fit-space is part of the Supplemental Software. Further development of these ensemble analysis and classification tools are ongoing at: https://github.com/mdhumphries/NeuralEnsembleAnalysis.

Trajectories of motor program activity

We checked the motor program’s evolution in space using the oscillator class ensembles. Each ensemble’s activity was characterized by its average spike density function f*, obtained by taking the mean over the spike density functions f of its neurons. To ensure uniform sampling of the motor program’s cycle, we computed the phase-lag between f*s for all pairs of oscillator ensemble in a recording; phase spread was estimated by von Mises κ, and we chose only recordings with κ = 0 indicating uniform spread of phase (7/12 recordings). The estimated trajectory of the activity packet on the pedal ganglion was then computed. To make ensemble activity comparable, each f* was normalized to its maximum rate, giving ${\widehat{f}}^{\text{*}}$. We found the center (x, y) of the largest physical patch of each oscillator ensemble, and computed the current x-axis position x*(t) of the activity packet by taking the weighted center-of-mass at time t as $x*(t)={\displaystyle {\sum }_i^n{x}_i\widehat{f}{*}_i(t)}$ over all n oscillator ensembles, and similarly computed y*(t) for y-axis position. Ellipses were fit to trajectories using the direct least-squares method (Fitzgibbon et al., 1999). Mapping of pedal nerve 10 activity was also based on its spike density function f, generated by convolving its spikes with a Gaussian of the same width used for the population recording.

Highlights.

• Neural ensembles code the Aplysia locomotion motor program

• Stable and rotational dynamics differentiate classes of ensemble

• Different dynamical classes map to physically separate and discrete regions

• Low-dimensional rotations of activity are recapitulated in physical space