Proterozoic Milankovitch cycles and the history of the solar system

Significance

Periodic variations in Earth’s orbit and rotation axis occur over tens of thousands of years, producing rhythmic climate changes known as Milankovitch cycles. The geologic record of these climate cycles is a powerful tool for reconstructing geologic time, for understanding ancient climate change, and for evaluating the history of our solar system, but their reliability dramatically decreases beyond 50 Ma. Here, we extend the analysis of Milankovitch cycles into the deepest stretches of Earth history, billions of years ago, while simultaneously reconstructing the history of solar system characteristics, including the distance between the Earth and Moon. Our results improve the temporal resolution of ancient Earth processes and enhance our knowledge of the solar system in deep time.

Abstract

The geologic record of Milankovitch climate cycles provides a rich conceptual and temporal framework for evaluating Earth system evolution, bestowing a sharp lens through which to view our planet’s history. However, the utility of these cycles for constraining the early Earth system is hindered by seemingly insurmountable uncertainties in our knowledge of solar system behavior (including Earth–Moon history), and poor temporal control for validation of cycle periods (e.g., from radioisotopic dates). Here we address these problems using a Bayesian inversion approach to quantitatively link astronomical theory with geologic observation, allowing a reconstruction of Proterozoic astronomical cycles, fundamental frequencies of the solar system, the precession constant, and the underlying geologic timescale, directly from stratigraphic data. Application of the approach to 1.4-billion-year-old rhythmites indicates a precession constant of 85.79 ± 2.72 arcsec/year (2σ), an Earth–Moon distance of 340,900 ± 2,600 km (2σ), and length of day of 18.68 ± 0.25 hours (2σ), with dominant climatic precession cycles of ∼14 ky and eccentricity cycles of ∼131 ky. The results confirm reduced tidal dissipation in the Proterozoic. A complementary analysis of Eocene rhythmites (∼55 Ma) illustrates how the approach offers a means to map out ancient solar system behavior and Earth–Moon history using the geologic archive. The method also provides robust quantitative uncertainties on the eccentricity and climatic precession periods, and derived astronomical timescales. As a consequence, the temporal resolution of ancient Earth system processes is enhanced, and our knowledge of early solar system dynamics is greatly improved.

Quasiperiodic variations in insolation, known as Milankovitch cycles, serve as a primary control on climate change over timescales of 10⁴–10⁶ y (1). Their expression in the stratigraphic record provides a powerful tool for reconstructing geologic timescales, or astrochronologies, and evaluating Earth history. Extending this astronomical metronome into the Precambrian, however, has proven challenging due to shortcomings in both theory and geologic data. From the perspective of the geologic archive, a major limitation is the lack of sufficient independent time control (e.g., radioisotopic dates) to unambiguously calibrate the observed spatial rhythms to astronomical (temporal) periods. In terms of theory, the periods of Earth’s astronomical cycles also become more poorly constrained during the Precambrian due to uncertainties in the evolution of the solar system (2). Although it is established that the dominant eccentricity and climatic precession cycles derive from fundamental frequencies associated with the orbits of the five innermost planets (g₁ to g₅; ref. 2) and the precession constant k, these values are not precisely determined because of the chaotic nature of the solar system (2, 3) and because the history of tidal dissipation of the Earth–Moon system is not well known (2, 4). In fact, the validity of theoretical astronomical solutions that underpin astrochronology are limited to the past 50 My (2, 5), although “floating” astrochronologies have been proposed for older intervals, and the 405-ky-long orbital eccentricity cycle is expected to be relatively stable with an uncertainty of 0.2% by 250 Ma (2).

Recent advances in astrochronologic assessment yield a partial solution to the challenges noted above (6–8), in providing statistical approaches that explicitly consider and evaluate timescale uncertainty in terms of the accumulation rate of a given sedimentary record. However, these methods require assumptions about the astronomical frequencies associated with the Earth’s orbital eccentricity, axial tilt, and climatic precession (the Milankovitch cycles). In the present study, we build upon prior work to formulate a Bayesian inversion approach that quantitatively links astronomical theory with geologic observation, thus overcoming limitations associated with each. At the core of this approach are three components: (i) the TimeOpt method (8), which explicitly considers timescale uncertainty, and utilizes multiple attributes of the astronomical signal to increase statistical reliability; (ii) the underlying astronomical theory, which links observed climatic precession and orbital eccentricity rhythms to fundamental frequencies of the solar system and Earth–Moon evolution (2, 4) (Table 1); and (iii) a Bayesian Markov Chain Monte Carlo approach that allows explicit exploration of the data and model space and uncertainties. The result is a robust methodology for astrochronology that is suitable for the Proterozoic, and greatly enhances the astronomical knowledge that we can obtain from younger strata (e.g., the early Cenozoic). We refer to this approach as TimeOptMCMC. We emphasize that although TimeOptMCMC provides a rigorous quantification of the uncertainties in astrochronologic results, the method does not by itself reduce these uncertainties. Ultimately, uncertainties in astrochronology can only be decreased by additional information provided by measured data.

Table 1.

Source of the climatic precession and eccentricity periods, as derived from the fundamental frequencies and precession constant

Parameter	Source	Period (ky)—Today*
p1	k + g5	23.678
p2	k + g2	22.371
p3	k + g4	18.951
p4	k + g3	19.103
p5	k + g1	23.120
e1	g2 − g5	405.091
e2	g4 − g5	94.932
e3	g4 − g2	123.945
e4	g3 − g5	98.857
e5	g3 − g2	130.781

^*Precession and eccentricity estimates from ref. 2.

We apply the TimeOptMCMC method to evaluate two cyclostratigraphic records that are of special importance. The first is the 1.4-billion-year-old Xiamaling Formation from the North China Craton (9), one of the oldest proposed records of astronomical forcing (Fig. 1A). The second is the well-studied ∼55-million-year-old record from Walvis Ridge (ref. 10 and Fig. 1E), which is notable because it includes the Paleocene–Eocene Thermal Maximum, and it just exceeds the temporal limits of the available theoretical astronomical solutions [<50 Ma (2, 5)]. The methodology allows us to address two primary research objectives: (i) to provide well-constrained geologic estimates of the climatic precession and eccentricity periods for both the early Eocene and Proterozoic (including uncertainties); and (ii) to quantify length of day and Earth–Moon distance during the Proterozoic (via the precession constant k), at a time when extrapolation of the present-day rate of tidal dissipation would imply a condition near Earth–Moon collision (11).

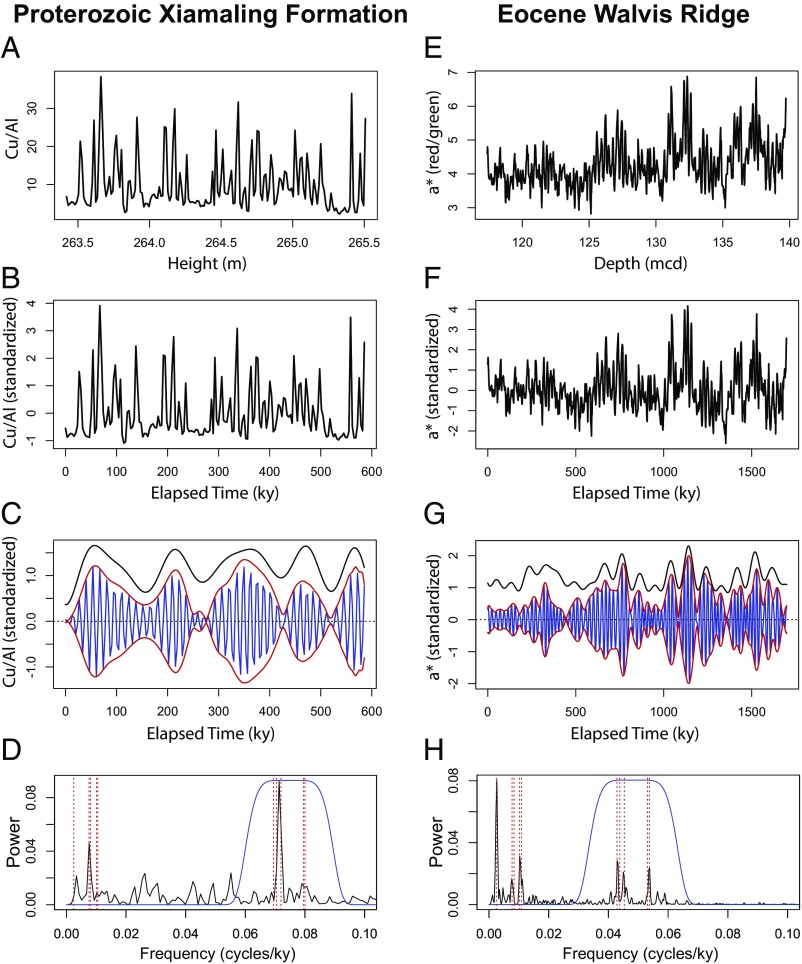
Fig. 1.

TimeOptMCMC results for the ∼1.4 Ga Proterozoic Xiamaling Formation Cu/Al data (9) and the ∼55 Ma Eocene Walvis Ridge a* (red/green) data (10). (A) Xiamaling Cu/Al data versus stratigraphic height. (B) Astronomically tuned Xiamaling Cu/Al data, using the TimeOptMCMC derived posterior mean sedimentation rate (Table 2). The data series has been standardized to unit variance, and a linear trend has been removed. (C) Xiamaling Cu/Al data precession envelope (red line) for the posterior mean sedimentation rate, and precession filter output (blue line). The black line illustrates the TimeOpt reconstructed eccentricity model. (D) Xiamaling Cu/Al data power spectrum (squared Fourier transform) using the posterior mean sedimentation rate. The vertical dashed red lines indicate the reconstructed target periods (mean posterior values in Table 2) for climatic precession and eccentricity, and the blue line illustrates the frequency response of the bandpass filter for precession modulation evaluation. (E) Eocene Walvis Ridge a* data versus meters composite depth (mcd). (F) Astronomically tuned Walvis Ridge a* data, using the TimeOptMCMC derived posterior mean sedimentation rate (Table 2). The data series has been standardized to unit variance, and a linear trend has been removed. (G) Walvis Ridge a* data precession envelope (red line) for the posterior mean sedimentation rate, and precession filter output (blue line). The black line illustrates the TimeOpt reconstructed eccentricity model. (H) Walvis Ridge a* data power spectrum (squared Fourier Transform) using the posterior mean sedimentation rate. The vertical dashed red lines indicate the reconstructed target periods for climatic precession and eccentricity (Table 2), and the blue line illustrates the frequency response of the bandpass filter for precession modulation evaluation.

Results

We focus our analysis of the Xiamaling Formation on a 2-m-thick section of rhythmically bedded black shale and chert (“unit 3” of ref. 9) that has been interpreted to reflect changes in upwelling and biological productivity. Paleogeographic reconstructions place this site in a subtropical/tropical marine environment that was under Hadley cell influence, suggesting an astronomical forcing scenario involving migration of the intertropical convergence zone (9). We investigate the published Cu/Al record (9), a proxy for productivity/redox state (12), which demonstrates high fidelity (SI Appendix, Fig. S6 and SI Appendix). Initial screening of the high-resolution dataset using the TimeOpt method with tentative (nominal) Proterozoic values for the climatic precession and eccentricity periods (2, 4) (SI Appendix, Table S2) reveals a highly significant astronomical signal (r²_opt = 0.300; P < 0.005, 2,000 simulations; SI Appendix, Fig. S6) at a sedimentation rate of 0.33 cm/ky. This sedimentation rate is consistent with radioisotopic data in an overlying 52-m-thick interval (SI Appendix). The statistically significant TimeOpt result is an important finding, as it overcomes the problem of false signal detection that complicates spectrum evaluation (13, 14) and provides an independent confirmation of the astronomical interpretation of Zhang et al. (9).

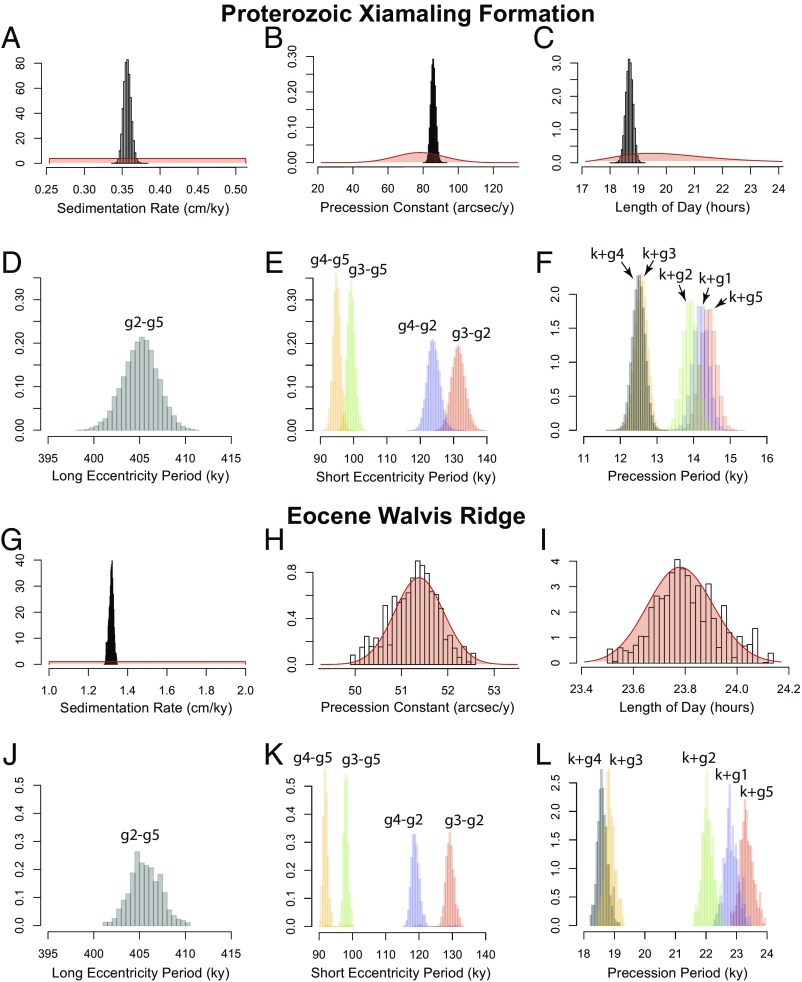
Bayesian inversion of the Xiamaling Cu/Al record is constrained by prior distributions for the fundamental frequencies g₁ to g₅, the precession constant k, and sedimentation rate (SI Appendix, Tables S3 and S4). Prior distributions for the fundamental frequencies g₁ to g₅ are based on the full range of variability in the model simulations of Laskar et al. (2) computed over 500 My. The prior distribution for the precession constant is derived from the recent study by Waltham (ref. 4; 78 ± 28 arcsec/y, 2σ), and sedimentation rate is permitted to vary across all plausible values for which it is possible to robustly identify a full astronomical signal, given the available data resolution. The posterior distribution from the TimeOptMCMC analysis indicates a precession constant of 85.79 ± 2.72 arcsec/y (2σ; Fig. 2B), consistent with an Earth–Moon distance of 340,900 ± 2,600 km (2σ) and length of day of 18.68 ± 0.25 h (2σ; Fig. 2C and Table 2). Climatic precession periods range between 12.5 and 14.4 ky (Fig. 2F and Table 2), with a dominant cycle of ∼14 ky in the study interval (Fig. 1D). The Proterozoic analog of the long eccentricity cycle, which has a duration of 405 ky in theoretical models for the Cenozoic (2), and is expected to be the most regular of the eccentricity cycles because it involves interaction between the very stable Jupiter and relatively stable Venus, has a duration of 405.1 ky (401.3–408.9 ky, 2σ; Fig. 2D). Finally, the reconstructed Proterozoic short eccentricity periods (Fig. 2E) are consistent with those observed in the theoretical models for the Cenozoic (2) (95–131 ky), with a dominant period of ∼131.4 ky in the study interval (Fig. 1D). It is notable that the posterior distributions for sedimentation rate (Fig. 2A) and the precession constant (Fig. 2B) are much narrower than their prior distributions, and the prior and posterior distributions of the fundamental frequencies g₁ to g₅ are nearly identical (SI Appendix, Fig. S7). Notwithstanding little improvement in the posterior uncertainties of the fundamental frequencies, the coupled nature of the eccentricity and climatic precession cycles, which share common g terms (the climatic precession terms also share a common k term) allows resolution of the Proterozoic Milankovitch periods with low uncertainty (Fig. 2 D–F and Table 2).

Fig. 2.

Summary of TimeOptMCMC prior and posterior distributions for the ∼1.4 Ga Proterozoic Xiamaling Formation Cu/Al data (9), and the ∼55 Ma Eocene Walvis Ridge Site 1262 a* (red/green) data (10). (A–F) Prior (red line) and posterior (histogram) probability distributions for Xiamaling Formation sedimentation rate, precession constant, length of day, long eccentricity period, short eccentricity periods, and climatic precession periods (C). (G–L) Prior (red line) and posterior (histogram) probability distributions for Eocene Walvis Ridge Site 1262 sedimentation rate, precession constant, length of day, long eccentricity period, short eccentricity periods, and climatic precession periods (I). See Table 1 for the relationship between g, k, and observed astronomical periods. See Table 2 for the mean posterior values associated with each distribution shown in this figure.

Table 2.

TimeOptMCMC reconstructed sedimentation rate, precession and eccentricity frequencies, fundamental frequencies (g terms), precession constant (k), and Earth–Moon distance, for the Proterozoic Xiamaling Formation and the Eocene Walvis Ridge

Parameter	Today*	Xiamaling Formation†	±σ	Walvis Ridge‡	±σ
Sedimentation rate (cm/ky)	—	0.357	0.005	1.316	0.011
p1, ky	23.678	14.392	14.178–14.613	23.335	23.121–23.554
p2, ky	22.371	13.899	14.407–13.983	22.066	21.874–22.261
p3, ky	18.951	12.497	12.673–12.327	18.613	18.448–18.781
p4, ky	19.103	12.569	12.744–12.398	18.848	18.685–19.013
p5, ky	23.120	14.192	14.407–13.983	22.827	22.608–23.050
e1, ky	405.091	405.077	406.971–403.201	405.613	403.969–407.270
e2, ky	94.932	94.912	96.028–93.821	91.975	91.099–92.867
e3, ky	123.945	123.955	125.868–122.100	118.946	117.483–120.447
e4, ky	98.857	99.211	100.386–98.064	98.009	97.161–98.871
e5, ky	130.781	131.392	133.467–129.380	129.236	127.752–130.755
k, arcsec/y	50.475838	85.790450	1.362320	51.280910	0.515371
Earth–Moon distance, km × 103	384.4§	340.855800	1.293260	383.110800	0.822051
h/d¶	23.93447	18.684750	0.126679	23.804850	0.123398
g1, arcsec/y	5.579378	5.531285	0.129246	5.494302	0.128076
g2, arcsec/y	7.456665	7.456848	0.014886	7.452619	0.013001
g3, arcsec/y	17.366595	17.320480	0.152805	17.480760	0.115325
g4, arcsec/y	17.910194	17.912240	0.158683	18.348310	0.135346
g5, arcsec/y	4.257564	4.257456	0.000020	4.257451	0.000020

^*Precession, eccentricity, g, and k estimates from ref. 2.

^†Results from the Xiamaling Formation are based on 50 MCMC simulation chains of length 1 × 10⁶ each.

^‡Results from the Walvis Ridge are based on 150 MCMC simulation chains of length 2 × 10⁵ each.

^§Semimajor axis.

^¶Sidereal day.

To provide a baseline assessment from the early Cenozoic, we investigate Eocene reflectivity data (a*, red/green) from the Walvis Ridge (10) (Ocean Drilling Program Site 1262; Fig. 1E). This dataset has been previously evaluated with the TimeOpt approach (8), and a statistically significant astronomical signal (P < 0.005) is identified at a sedimentation rate of 1.33 cm/ky (SI Appendix, Fig. S9). Application of the TimeOptMCMC algorithm allows a rigorous assessment of the uncertainty in the Eocene Milankovitch periods, in the underlying g and k terms, and in the sedimentation rate (Fig. 2, Table 2, and SI Appendix, Figs. S10 and S11). In this case, the posterior distributions for sedimentation rate (Fig. 2G) and for the fundamental frequencies g₃ (Earth) and g₄ (Mars) show the greatest change relative to their prior distributions (SI Appendix, Fig. S10 E and G). Most notably, the posterior mean value for g₄ (Mars) is greater than the maximum value observed in the modeling study of Laskar et al. (2). This discrepancy in g₄ is also expressed in the e₂ (91.98 ky) and e₃ (118.95 ky) eccentricity terms at Walvis Ridge (Fig. 2K and SI Appendix, Fig. S11 C and E), both of which share the g₄ term and are notably shorter than those observed in the astronomical model simulations of Laskar et al. (2) (Table 2). A possible explanation for these differences in g₃ and g₄ is that the frequencies reported in figure 9 of Laskar et al. (2) are averaged over 20-My intervals, whereas the Walvis Ridge record spans a shorter interval of about 1.7 My.

Discussion

Comparison of the Proterozoic and Eocene results highlights how the TimeOptMCMC approach combines cyclostratigraphic data and astronomical theory to improve model parameters. In the case of the Proterozoic, where the deviation of k from its present value is expected to be substantial due to the large uncertainties in the Earth–Moon history, the Xiamaling Cu/Al data provides strong constraints to improve our knowledge of the precession constant. In the case of the Eocene, the expected changes in k are much smaller, and the cyclostratigraphic data more strongly improve our knowledge of the fundamental frequencies g₃ and g₄. For both the Proterozoic and Eocene examples, the sedimentation rate (and hence the duration of the stratigraphic interval) is highly constrained by the Bayesian inversion.

Although stratigraphic-based estimates of the fundamental frequencies of the solar system are rare [g₁ to g₅; however, see Olsen and Kent (15)], numerous studies have attempted to reconstruct the precession constant and/or the Earth–Moon distance and length of day using geologic data. These approaches include inferences from the evaluation of tidal deposits and of growth patterns in marine invertebrate fossils and stromatolites throughout the past 2.5 billion years (16), and for the late Cenozoic (<25 Ma), the application of astronomical-based methods (1, 17, 18). In addition, a number of theoretical modeling exercises have been conducted to constrain the Earth–Moon history (2, 4, 16, 19, 20). In Fig. 3, we compare our astronomical-based results for the Proterozoic and Eocene to a number of Earth–Moon separation models, and also to two tidalite datasets that are considered to be of high quality (16): rhythmites from the Big Cottonwood Formation (∼900 Ma; refs. 21 and 22), and the Elatina Formation and Reynell Siltstone (∼620 Ma; refs. 16 and 23). It should be noted that the interpretation of tidalite (and also bioarchive) datasets in terms of Earth–Moon history remains a contentious issue due to problems with cycle recognition and the potential for missing laminations (4, 16), thus the TimeOptMCMC approach provides an independent means for their validation. To supplement our comparison, SI Appendix, Fig. S12 includes some additional more controversial estimates from Phanerozoic bioarchives, and a datum from the Weeli Wooli Formation rhythmite (∼2,450 Ma; refs. 11, 16, and 24).

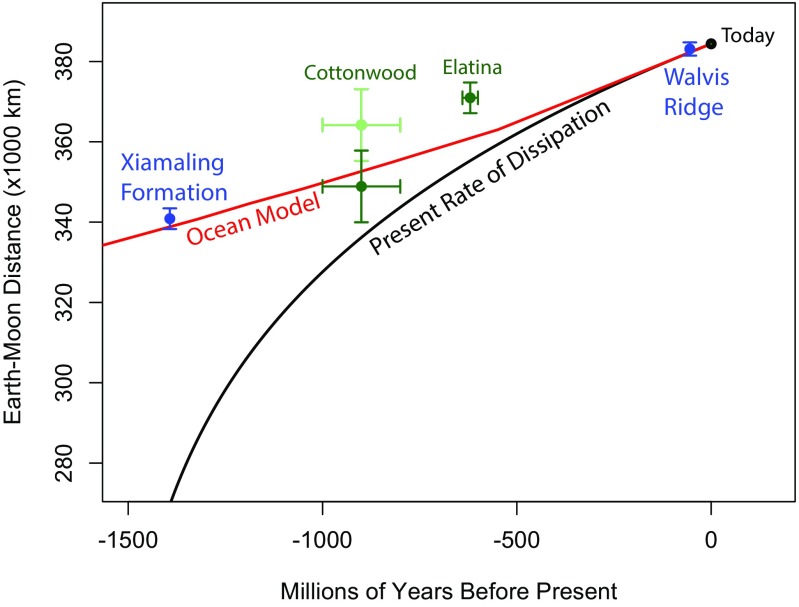
Fig. 3.

TimeOptMCMC reconstructed Earth–Moon distance, compared with two tidalite-based estimates and two models. Uncertainties in Earth–Moon distance are ±2σ and age uncertainties span minimum and maximum values. The Bayesian posterior TimeOptMCMC estimates for the Proterozoic Xiamaling Formation and Eocene Walvis Ridge are indicated with blue symbols. Note the significant improvement in precision between posterior (blue) and prior estimates for the Xiamaling data (prior = 319,743 to 380,309 km; 2σ). Age uncertainties for the Xiamaling and Walvis Ridge results fall within the size of the blue symbols. Tidalite estimates from the Big Cottonwood Formation (∼900 Ma; ref. 22) and Elatina Formation and Reynell Siltstone (∼620 Ma; ref. 23) are shown with dark green symbols (based on the updated analyses of ref. 16). The light green Big Cottonwood Formation estimate (364,192 km) is an alternative value reported by ref. 21 with uncertainties from the 348,884-km estimate (dark green symbol). The ocean model (red line), and a model using the present rate of tidal dissipation (black line), derive from ref. 20.

The TimeOptMCMC reconstructed Earth–Moon distance from the Xiamaling Formation (340,900 ± 2,600 km, 2σ; Table 2) is consistent with that derived from ocean models (20) that imply smaller torques, reduced tidal dissipation, and slower lunar retreat rates in the distant past, ultimately related to a less efficient excitation of the ocean’s normal modes by tidal forcing on an Earth with a faster rotation rate (Fig. 3). The Xiamaling result is also compatible with a model that employs an average tidal dissipation rate that is 60% of the present value (SI Appendix, Fig. S12). If the Elatina and Cottonwood tidalite data are taken at face value, either of these Earth–Moon separation models are possible, depending on the tidalite record considered. However, the small uncertainty of the Xiamaling estimate excludes a range of other potential models that are permitted by the tidalite data, such as one that employs a tidal dissipation rate that is 40% of the present value, and furthermore, the 60% model is inconsistent with estimates from the Weeli Wooli Formation (SI Appendix, Fig. S12). It should also be noted that the 40% and 60% rate models violate the constraint provided by modern observed Moon retreat rate, in contrast to the ocean model (20) and present rate model. Finally, the astronomical-based Bayesian reconstruction is consistent with a length of day (18.68 ± 0.25 h, 2σ), which is shorter than that of published Proterozoic estimates from geologic data (16), and is at the low end of existing model length of day estimates (4), but has a greatly reduced uncertainty (Fig. 2C).

The methodology presented here is not affected by problems inherent in previous estimates of the precession constant, associated with ambiguity in the interpretation of bioarchives and tidal deposits (4, 16). Furthermore, the technique should be widely applicable, given the abundance of relatively continuous records of astronomically forced sedimentation. An important feature of this quantitative approach is a comprehensive treatment of uncertainties, facilitated by the explicit coupling of astronomical theory with geologic observation. The quantification of prior and posterior distributions allows for a rigorous treatment of astrochronologic uncertainties, addressing a major weakness in prior work and providing an objective way to integrate astrochronologies with radioisotopic data, from the Proterozoic to the Cenozoic. Application of this methodology to sedimentary records that span Earth history will facilitate improvement in the calibration of the geologic time scale, will constrain the history of the Earth–Moon system in deep time, and shows promise of reconstructing the evolution of the fundamental orbital frequencies of the solar system over billions of years.

Materials and Methods

We utilize the recently developed TimeOpt regression framework (8) to evaluate two features that are diagnostic of an astronomical fingerprint in strata: the concentration of spectral power at the proposed astronomical frequencies (25) (e.g., climatic precession and eccentricity), and the amplitude modulation of climatic precession (26), which is caused by variations in eccentricity. For the Bayesian inversion, TimeOpt is reformulated in terms of likelihood functions (27) (SI Appendix), and Markov Chain Monte Carlo (MCMC) simulation is utilized to sample values of the solar system secular frequencies g₁ to g₅, precession constant k, and sedimentation rate that are physically plausible and agree with the stratigraphic data. This allows evaluation of the five dominant eccentricity and five dominant climatic precession cycles that are observable in sedimentary strata, which depend on sums or differences of the g terms and/or k (Table 1). For example, the 405-ky-long eccentricity term of the Cenozoic originates from the difference between g₂ (Venus) and g₅ (Jupiter), and one of the strongest climatic precession cycles (23.7 ky in the Cenozoic) corresponds to g₅ + k.

A complete description of the approach, including evaluation and calibration with a synthetic astronomical test series, is in the SI Appendix. All analyses were conducted using the free software R (28), and an implementation of the TimeOptMCMC algorithm is available in the Astrochron package (29).