Robust nonequilibrium pathways to microcompartment assembly

Significance

The structure of the carboxysome resembles a viral capsid, but, unlike many viruses, the monomers of its shell do not appear to fit together in a uniquely preferred way. As a result, the size and shape of this bacterial microcompartment must be determined by the dynamics of its self-assembly process. Using theory and simulation of a model system, we show that the mechanism of assembling such a structure can proceed through nonequilibrium dynamics that are both reliable and controllable. We identify experimentally tunable parameters that modulate the shape and size of the assembled structure, advancing strategies to repurpose natural microcompartments and to create synthetic mimics.

Abstract

Cyanobacteria sequester photosynthetic enzymes into microcompartments which facilitate the conversion of carbon dioxide into sugars. Geometric similarities between these structures and self-assembling viral capsids have inspired models that posit microcompartments as stable equilibrium arrangements of the constituent proteins. Here we describe a different mechanism for microcompartment assembly, one that is fundamentally nonequilibrium and yet highly reliable. This pathway is revealed by simulations of a molecular model resolving the size and shape of a cargo droplet and the extent and topography of an elastic shell. The resulting metastable microcompartment structures closely resemble those of carboxysomes, with a narrow size distribution and faceted shells. The essence of their assembly dynamics can be understood from a simpler mathematical model that combines elements of classical nucleation theory with continuum elasticity. These results highlight important control variables for achieving nanoscale encapsulation in general and for modulating the size and shape of carboxysomes in particular.

Spatial segregation is an ubiquitous strategy in biology for organizing the crowded, active viscera of the cell (1–4). Viral capsids exemplify this organization at very small scales, sequestering genetic material from the cytosol and recapturing it for delivery to new hosts. Extensive work has explored the structure, stability, and assembly dynamics of viruses, highlighting generic design principles and physical origins of the spontaneous assembly process (5–10). Overall capsid structure typically follows from the arrangements of neighboring proteins that are preferred by their noncovalent interactions. Strong preferences yield regular and highly stable structures, but at the same time impair kinetic accessibility by producing deep kinetic traps (11).

Bacterial microcompartments serve a very different biomolecular purpose from viruses but have striking structural similarities, namely, a quasi-icosahedral protein shell that assembles around a fluctuating cargo (2, 12–14). This comparison raises the question, Do the same assembly principles, based on a balance between equilibrium stability and kinetic accessibility, apply to microcompartments as well? Here we focus on a paradigmatic example of a microcompartment, the carboxysome. Carboxysomes play an essential role in the carbon fixation pathway of photosynthetic cyanobacteria (15). The shell proteins of the carboxysome, which have hexameric and pentameric crystallographic structures, assemble to encapsulate a condensed globule of protein including the enzymes RuBisCO and carbonic anhydrase (16–18). These vital, organelle-like structures regulate a microscopic environment to enhance catalytic efficiency, which has made them an attractive target for bioengineering applications (19–22).

Like some viral capsids, carboxysomes feature pronounced facets and vertices, and crystal structures of shell components suggest highly symmetric local protein arrangements (16, 18, 23). Unlike in viral capsids, however, these apparent preferences do not directly indicate the assembled structure, nor do they clearly point to a characteristic microcompartment size (24). Indeed, experimental evidence has not constrained a particular mechanism for assembly: Live cell images support the notion that the cargo assembles first and is subsequently coated by the shell (12), while direct observations of partially formed carboxysomes in electron micrographs point to a cooperative mechanism for assembly (25). Identifying essential variables for controlling or emulating carboxysome assembly awaits a clearer understanding of its dynamical pathways and underlying driving forces.

Theoretical and computational models for nanoshell assembly have primarily followed approaches inspired by viral capsid assembly. These approaches have emphasized the role of preferred shell curvature and shell–cargo interactions as a template for the final structure (26). For example, irreversible growth of shells comprising monomers that prefer a bent binding geometry has been shown in simulations to successfully assemble empty shells (27, 28). The assumption of such a preferred local curvature, however, is at odds with structural models of the carboxysome based on crystallography of shell proteins, which feature tiling of the shell by hexameric proteins that appear to bind optimally with zero curvature (18, 25, 29). Indeed, a number of experimental measurements bolster the view that bacterial microcompartments are bounded by protein sheets that are essentially flat away from localized regions of high curvature. The predominant constituents of diverse microcompartments (e.g., $\beta$-carboxysomes, $\alpha$-carboxsyomes, eut microcompartments, and pdu microcompartments) crystallize as layers of flat sheets comprising hexamers whose lateral contacts are genetically conserved (18). Recent atomic force microscopy measurements have demonstrated that these constituents also form flat monolayers in physiological buffer conditions (29). Furthermore, in vivo tomography data strongly suggest that biological carboxysomes have extended flat faces with curvature sharply localized at the joint of a facet (25).

Here we introduce and explore a model based on a mechanistic perspective that is fundamentally different from the one commonly applied to virus assembly and that does not require assuming an innately preferred curvature for contacts between shell proteins. The basic components are a cargo species that is prone to aggregation, a shell species that spontaneously forms flat, hexagonally symmetric elastic sheets, and an attractive interaction between the inside of the shell and the cargo, depicted in Fig. 1A and SI Appendix, Figs. S1–S3. These ingredients appear to be the essential constituents for carboxysome biogenesis in vitro—mutagenesis experiments have shown that pentameric proteins sometimes presumed to stabilize shell curvature are in fact not necessary for the formation of faceted shell structures (24). For such a basic model, thermodynamic considerations imply that finite encapsulated structures have negligible weight at equilibrium (SI Appendix, section S3). Nevertheless, we show that regularly sized microcompartments can emerge reliably in the course of natural dynamics.

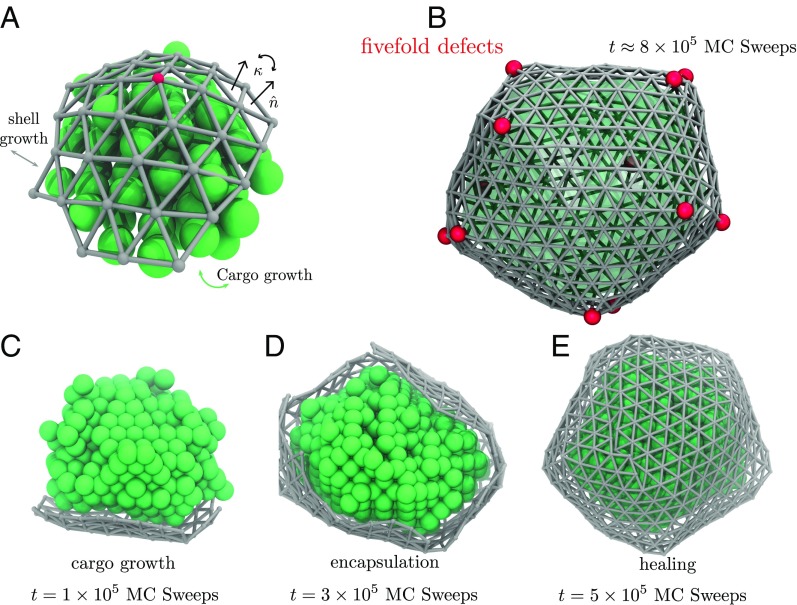
Fig. 1.

Model dynamics of microcompartment assembly. (A) Cargo monomers (green spheres) in our molecular model occupy sites of an FCC lattice, experiencing short-ranged attraction to their nearest neighbors and also to protein monomers composing the shell. Each shell monomer corresponds to a triangle in a discretized shell (gray) that resists bending and stretching according to an elastic Hamiltonian. Closure of the shell requires the presence of topological defects in the triangulated surface, vertices that are connected to only five neighbors. Red spheres in A and B highlight the locations of these defects. (B) A fully assembled microcompartment includes at least 12 of these defects. In B and E, we show the boundary of the cargo droplet as a translucent green surface. (C) At early time $t$ in the assembly process, high curvature of the cargo droplet limits shell growth to an area that is relatively flat while maintaining contact with the cargo. (D) Droplet growth reduces curvature until encapsulation becomes thermodynamically favorable and kinetically facile (Movie S1). (E) The nearly closed shell effectively halts cargo aggregation, but the approach to a simply connected envelope proceeds slowly as defects reposition and combine to heal grain boundaries.

Methods

We regard the protein shell of a growing carboxysome as a thin elastic sheet, whose energy can be discretized and expressed as a sum over the edges $ij$ of a triangulated surface (30). Its Hamiltonian is

$${\mathcal{H}}_{\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{l}\mathrm{l}}=\frac{ϵ}{2}\sum _{ij}{\left(l_{ij}-l_0\right)}^2+\frac{\kappa }{2}\sum _{ij}1-\cos \left({\theta }_{ij}\right)+{\mathcal{H}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{c}},$$ [1]

where $l_{ij}$ is the length of an edge, whose deviations from the preferred length $l_0$ experience a restoring force with stiffness $ϵ$. The bending rigidity $\kappa$ sets the energy scale for developing a nonzero angle ${\theta }_{ij}$ between normal vectors of triangles sharing the edge $ij$ (30).

We associate each triangular face in the discretized sheet with a protein monomer. The term ${\mathcal{H}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{c}}$ in Eq. 1 imposes steric constraints that prevent overlap of these monomers, by placing a hard sphere of diameter $0.45l_0$ at the center of each triangle in the sheet. Because the deformations of individual shell proteins are expected to be small relative to the bending fluctuations between adjacent monomers, we work in a limit where $ϵl_0^2\gg \kappa .$ The cohesive interactions that bind adjacent shell proteins in the sheet are accounted for separately, with an energy ${\mathcal{H}}_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}$ that tightly associates the vertices of contacting monomers. In the limit that bound vertices coincide exactly, the thermodynamic influence of ${\mathcal{H}}_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}$ depends only on the connectivity of the sheet, contributing a binding affinity factor $K$ for each constrained vertex, as described in SI Appendix, section S1.

We represent aggregating cargo as an Ising lattice gas on an face-centered cubic (FCC) lattice with chemical potential ${\mu }_{\text{c}}$, restricted to configurations with a single connected cargo droplet. Nearest neighbors are coupled through an interaction energy ${ϵ}_{\text{c}}$,

$${\mathcal{H}}_{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{o}}=-{\mu }_{\text{c}}\sum _{i=1}^{N_{\text{L}}}{\sigma }_i-{ϵ}_{\text{c}}\sum _{⟨ij⟩}{\sigma }_i{\sigma }_j,$$ [2]

where ${\sigma }_i=\left\{\mathrm{0,1}\right\}$ for occupied and unoccupied lattice sites, respectively, $⟨ij⟩$ indicates that the sum is taken over nearest neighbors, and $N_{\text{L}}$ is the number of lattice sites. The lattice spacing used throughout is $l_0,$ the average length of a shell monomer edge. The primary cargo species in a carboxysome, the protein RuBisCO, has a diameter $L_0$ that is larger than $l_0$; adopting a finer lattice spacing amounts to averaging approximately over configurational fluctuations of RuBisCO about a close-packed lattice.

Interactions between cargo and shell species in our model mimic a short-ranged directional attraction suggested by structural data (31) and the steric repulsion intrinsic to compact macromolecules. For a particular lattice site $i$ and shell monomer $j$,

$${\mathcal{H}}_{\text{int}}\left({\sigma }_i,{\widehat{n}}_j\right)=\left\{\begin{array}{cc}-{\gamma }_{\text{in}}\hspace{1em}\hfill & \text{if}-{\widehat{n}}_j\in \mathcal{V}\left(i\right)\text{and}{\sigma }_i=1\hfill \\ +{\gamma }_{\text{out}}\hspace{0.17em}\hfill & \text{if}{\widehat{n}}_j\in \mathcal{V}\left(i\right)\text{and}{\sigma }_i=1\hfill \\ 0\hspace{0.17em}\hfill & \text{otherwise},\hfill \end{array}\right.$$ [3]

where ${\widehat{n}}_j$ is the outward-facing normal vector of shell monomer $j$. The notation $\in \mathcal{V}\left(i\right)$ means that the point specified by the vector lies within the volume $\mathcal{V}\left(i\right)$ occupied by lattice cell $i.$ The full interaction is the sum of $H_{\text{int}}$ over all $i$ and $j$. This interaction, which contributes a favorable energy if the inward-facing normal lies within a cargo-occupied lattice site and an unfavorable energy if the outward-facing normal vector does so, is depicted schematically in SI Appendix, Fig. S5.

The thermal relaxation of a shell with a fixed number of vertices and fixed connectivity, subject to the energetics described above, can be simulated with straightforward Monte Carlo dynamics. In each move, a single vertex is chosen at random. As depicted in SI Appendix, Fig. S2, a random perturbation in 3D space is made to the selected vertex, attempting to change its position from $a$ to $a\prime .$ The resulting energy difference, ${\mathrm{\Delta }\mathcal{H}}_{\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{l}\mathrm{l}}+{\mathrm{\Delta }\mathcal{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}$, is used in a standard Metropolis acceptance criterion,

$$\text{acc}\left(a\to a\prime \right)=min\left[1,e^{-\beta \left({\mathrm{\Delta }\mathcal{H}}_{\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{l}\mathrm{l}}+{\mathrm{\Delta }\mathcal{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\right)}\right].$$ [4]

This procedure ensures that the configurations sampled in the Markov chain are consistent with a Boltzmann distribution.

Monte Carlo dynamics for growth of the shell are significantly more involved. For the procedure to satisfy detailed balance, care must be taken to ensure that every step is reversible and that algorithmic asymmetries of forward and reverse moves are fully accounted for. Our goal is to draw samples from a grand canonical distribution,

$$p\left(X,N_{\mathrm{s}},\left\{\sigma \right\}\right)={\mathrm{\Xi }}^{-1}{z}_{\mathrm{s}}^{N_{\mathrm{s}}}{e}^{-\beta \left({\mathcal{H}}_{\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{l}\mathrm{l}}+{\mathcal{H}}_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}+{\mathcal{H}}_{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{o}}+{\mathcal{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\right)},$$ [5]

where $\mathrm{\Xi }$ denotes the grand canonical partition function, $X$ gives the coordinates of the shell protein configuration, $N_{\text{s}}$ is the number of shell monomers, and $z_{\text{s}}\propto e^{\beta {\mu }_{\text{s}}}$ is an activity set by the concentration of free shell monomers in solution. We implement two types of Monte Carlo moves that allow the structure to grow, increasing the number of monomers by adding new vertices at the edge of the shell. Fusion of preexisting vertices can also occur, representing the binding between monomers in the shell that are nearby in space but not necessarily in connectivity. Details of these moves and their reverse counterparts, along with acceptance criteria that ensure detailed balance with respect to $p\left(X,N_{\text{s}},\left\{\sigma \right\}\right)$, are described in SI Appendix, section S1. In microcompartment growth simulations, they are performed in tandem with standard trial moves that change the occupation state of the cargo lattice, acting to grow or shrink the cargo droplet.

The routes of Monte Carlo trajectories propagated in this way are influenced by energetic parameters like $ϵ$, $\kappa$, and $\mu$ and by the shell-binding affinity $K$. The pathways are also shaped by the relative frequencies of proposing each type of move. A basic timescale $\tau$ is set by the duration of a “sweep” in which each vertex experiences a single attempted spatial displacement (on average). For every $n_{\text{c}}$ sweeps we attempt roughly $N_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}}$ moves that add or remove material at the surface of the cargo droplet, where $N_{\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}}$ is the number of lattice sites defining the droplet surface. This procedure establishes an effective rate $k_{\text{c}}^0={\left(2n_{\text{c}}\tau \right)}^{-1}$ at which cargo monomers arrive from solution at a given surface site. Similarly, a basic rate $k_{\text{s}}^0={\left(2n_{\text{s}}\tau \right)}^{-1}$ for shell monomer arrival at a given site on the shell’s perimeter is established by attempting $N_{\text{perim}}$ shell monomer addition/removal moves for every $n_{\text{s}}$ sweeps, where $N_{\text{perim}}$ is the number of edges at the shell boundary. In experiments these arrival rates are approximately proportional to the solution concentrations of the respective monomers. As a result, microcompartment mass changes slowly on the timescale of elastic fluctuations. Dynamics of vertex fusion and fission also proceed much more rapidly than growth. In essence, all processes other than monomer addition and removal follow along adiabatically. For the fate of assembly, the key dynamical parameter in our model is therefore the ratio $k_{\text{c}}^0/k_{\text{s}}^0$ of arrival rates for cargo and shell species.

Molecular Simulations

Fig. 1 depicts an example assembly pathway of this molecular model. Trajectories are initiated with a small droplet of cargo (comprising a few hundred cargo monomers) and a handful of proximate shell monomers, as described in SI Appendix, section S5. Under conditions favorable for assembly, such a droplet faces no thermodynamic barrier to growth; absent interactions with the shell, its radius $R$ would increase at a constant average rate as cargo material arrives from the droplet’s surroundings. Growth of the shell, on the other hand, is impeded by the energetic cost of wrapping an elastic sheet around a highly curved object. In early stages of this trajectory, shown in Fig. 1C, the net cost of encapsulation is considerable, and the population of shell monomers remains small as a result.

As the droplet grows, this elastic penalty is eventually overwhelmed by attractions between shell and cargo, similar to the mechanism of curvature generation by nanoparticles adsorbed on membrane surfaces (32–34). At a characteristic droplet size $R^{*}$, encapsulation becomes thermodynamically favorable. If the arrival rate of shell monomers is much higher than that of cargo (e.g., due to a higher concentration in solution), then a nearly complete shell will quickly develop (Fig. 1D), hampering the incorporation of additional cargo. The nascent shell that results, while sufficient to block cargo arrival, is highly defective and far from closed. A slow healing process ensues, dominated by relaxation of grain boundaries between growth faces (Fig. 1E). This annealing process is, in part, achieved by relocating topological defects in the structure, a phenomenon that has been previously encountered in ground-state calculations for closed elastic shells (35).

In the vast majority of the hundreds of assembly trajectories we have generated, healing leads ultimately to a completely closed structure with exactly 12 fivefold defects. Placement of these defects is often irregular and unlikely to yield minimum elastic energy, but further evolution of the structure is extraordinarily slow. Subsequent defect dynamics could produce more ideal shell structures as in ref. 35, and transient shell opening could allow additional cargo growth. But these relaxation processes require the removal of shell monomers that are bound to several others and that interact strongly with enclosed cargo. Under the conditions of interest, the timescale for such a removal is vastly longer than the assembly trajectories we propagate. Our model microcompartments are equilibrated with respect to neither shell geometry nor droplet size, yet they are profoundly metastable, requiring extremely rare events to advance toward the true equilibrium state.

In addition to generating molecular trajectories of microcompartment assembly, we performed umbrella-sampling simulations to compute the equilibrium free energy of the molecular model as a function of $N_{\text{s}}$ and the number $N_{\text{c}}$ of cargo monomers. Results, presented in SI Appendix, section S4, underscore the mechanistic features described above: a small critical nucleus size for cargo condensation and a size-dependent thermodynamic bias on encapsulation that becomes sharply favorable at a characteristic length scale. In Minimalist Model we examine the origins and consequences of these features in a more idealized context.

Minimalist Model

The scenario described above for our molecular model can be cast in a simpler light by considering as dynamical variables only the amounts of cargo and shell material in an idealized geometry. In this minimalist approach we focus on the radius $R$ of a spherical droplet and the polar angle $\theta$ subtended by a contacting spherical cap of shell material, as depicted in Fig. 2A. Taking the cargo and shell species to have uniform densities $\rho$ and $\nu$ within the droplet and cap, respectively, the geometric parameters$R$ and $\theta$ can be simply related to the monomer populations $N_{\text{c}}=\left(4\pi \rho /3\right)R^3$ and $N_{\text{s}}=2\pi \nu R^2\left(1-\cos \theta \right)$.

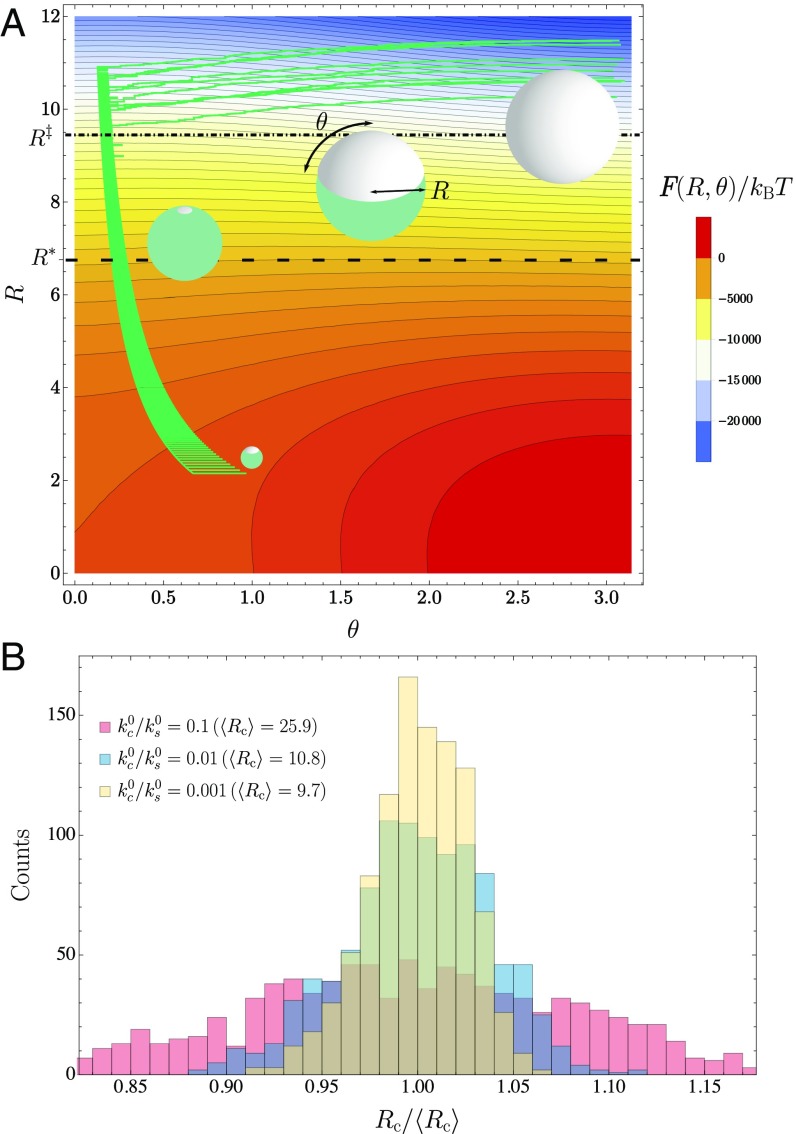
Fig. 2.

Minimalist model for dynamics of cargo growth and encapsulation. (A) Our phenomenological model resolves only the radius $R$ of a cargo droplet and the polar angle $\theta$ of a spherical cap that coats it. As in Fig. 1, the green spherical droplet represents the cargo, and the gray coating represents the shell. Black contours indicate lines of constant free energy $F\left(R,\theta \right)$. Green lines show the course of 10 kinetic Monte Carlo trajectories under conditions favorable for microcompartment assembly ($k_{\text{c}}^0/k_{\text{s}}^0=0.001$, all other parameters given in SI Appendix, section S4). Several structures along the assembly trajectory are shown near the corresponding values of $R$ and $\theta$. Encapsulation is thermodynamically favorable for $R>R*$ (lower dashed line). The free energy barrier to encapsulation is smaller than the thermal energy $k_{\mathrm{B}}T$ for $R>R^{‡}$ (Eq. S43) (dotted-dashed line). (B) Histograms of microcompartment radius when $\theta$ reaches $\pi$ (at which point dynamics cease). Ten thousand independent trajectories were collected for $k_{\text{c}}^0/k_{\text{s}}^0$ = 0.1, 0.01, and 0.001. Radius values are given in a unit of length $\ell$ that is comparable to the shell monomer size (Eq. S37).

In the spirit of classical nucleation theory, we estimate a free energy landscape in the space of $R$ and $\theta$ through considerations of surface tension and bulk thermodynamics. For our system these contributions include free energy of the condensed cargo phase, surface tension of a bare cargo droplet, free energy of a macroscopic elastic shell, and line tension of a finite shell, together with the energetics of shell bending and shell–cargo attraction. As shown in SI Appendix, section S3, this free energy $F\left(R,\theta \right)$ can be written in the form

$$\begin{array}{ccc}\hfill F\left(R,\theta \right)=a_{\text{c}}\left[{\left(\frac{R}{R_{\text{c}}}\right)}^2-{\left(\frac{R}{R_{\text{c}}}\right)}^3\right]& +\hfill & a_{\text{s}}\left[\left\{{\left(\frac{R^{*}}{R_{\text{s}}}\right)}^2-{\left(\frac{R}{R_{\text{s}}}\right)}^2\right\}\right.\hfill \\ \hfill & \hfill & \times \left.\left(1-\cos \theta \right)+\frac{R}{R_{\text{s}}}\sin \theta \right],\hfill \end{array}$$ [6]

where the energy scales $a_{\text{c}}$ and $a_{\text{s}}$ and the length scales $R_{\text{c}}$, $R^{*}$, and $R_{\text{s}}$ (all of which can be related to parameters of the molecular model) transparently reflect the thermodynamic biases governing growth and encapsulation. The function $F\left(R,\theta \right)$ can be minimum only at $R=0$ and $R=\infty$. As in the molecular model, finite microcompartments can appear and persist only as kinetically trapped nonequilibrium states.

Contours of this schematic free energy surface, plotted in Fig. 2A, are consistent with basic thermodynamic trends observed for the molecular model. Most importantly, they manifest the prohibitive cost of encapsulating small droplets. Only for radii $R>R^{*}$ is shell growth thermodynamically favorable. This characteristic length scale is determined by a straightforward balance among the shell’s bending rigidity, the macroscopic driving force for flat shell growth, and the attraction between shell and cargo, as detailed in SI Appendix, section S3. Whether encapsulation occurs immediately once the droplet exceeds the critical size $R^{*}$ depends on kinetic factors that are only partly governed by $F\left(R,\theta \right)$. Line tension of the shell, represented by the final term in Eq. 6, effects a barrier to encapsulation. As the droplet size increases, the height of this barrier declines, and encapsulation becomes facile only when it is sufficiently low. As with our molecular model, the subsequent dynamics may deviate significantly from equilibrium expectations based on the free energy surface. To explore these nonequilibrium outcomes, we must supplement the free energy surface $F\left(R,\theta \right)$ with a correspondingly minimal set of dynamical rules.

We take the rate of shell monomer addition to be a product of the per-edge rate of monomer arrival $k_{\text{s}}^0$ and the number of edges that can bind new monomers,

$$k_{\text{s}}^{+}\left(N_{\text{s}},N_{\text{c}}\right)=k_{\text{s}}^0\frac{2\pi R}{l_0}\sin \theta .$$ [7]

Similarly accounting for the number of sites where cargo can be added, we take the rate of cargo monomer addition to be

$$k_{\text{c}}^{+}\left(N_{\text{s}},N_{\text{c}}\right)=k_{\text{c}}^{0}4\pi \rho L_0{R}^2\left(1+\cos \theta \right).$$ [8]

The ratio of addition and removal rates is completely specified by the constraint of detailed balance. Defining the shell monomer and cargo monomer free energy differences

$$\mathrm{\Delta }{F}_{\text{s}}=F\left(N_{\text{s}},N_{\text{c}}\right)-F\left(N_{\text{s}}-1,N_{\text{c}}\right),$$ [9]

$$\mathrm{\Delta }{F}_{\text{c}}=F\left(N_{\text{s}},N_{\text{c}}\right)-F\left(N_{\text{s}},N_{\text{c}}-1\right),$$ [10]

we require that the rates of monomer removal satisfy

$$k_{\text{s}}^{-}\left(N_{\text{s}},N_{\text{c}}\right)=k_{\text{s}}^{+}\left(N_{\text{s}}-1,N_{\text{c}}\right)e^{\beta \mathrm{\Delta }{F}_{\text{s}}},$$ [11]

and

$$k_{\text{c}}^{-}\left(N_{\text{s}},N_{\text{c}}\right)=k_{\text{s}}^{+}\left(N_{\text{s}},N_{\text{c}}-1\right)e^{\beta \mathrm{\Delta }{F}_{\text{c}}}.$$ [12]

Stochastic trajectories for this minimalist description were generated by advancing the populations $N_{\text{s}}$ and $N_{\text{c}}$ in time with a kinetic Monte Carlo algorithm based on the transition rates $k_{\text{s}}^{+}$, $k_{\text{c}}^{+}$, $k_{\text{s}}^{-}$, and $k_{\text{c}}^{-}$. By construction, these rates are consistent with the equilibrium statistics implied by Eq. 6, but the geometry dependence of addition and removal rates ensures that typical trajectories do not simply follow a gradient descent on the free energy surface $F\left(R,\theta \right)$. The sampled paths shown in Fig. 2A (initiated with $N_{\text{s}}=1$ and $N_{\text{c}}=10$ and terminated when $N_{\text{s}}\ge 2N_{\text{c}}^{2/3}$ as described in SI Appendix, section S4) indeed exhibit strong geometric biases.

Most notably, $\theta$ increases rapidly at late times in these successful assembly trajectories, despite equilibrium forces that encourage droplet growth at the expense of reduced shell coverage. This route reflects an imbalance in the base addition rates $k_{\text{c}}^0$ and $k_{\text{s}}^0$ of cargo and shell material, which suppresses droplet growth while the shell develops. If the addition of shell material does not outpace that of cargo, then the angle $\theta$ decreases in time—the microcompartment grows but never advances toward closure (SI Appendix, Figs. S5 and S6. Since the addition rate of cargo scales with the droplet’s surface area, while the rate of adding shell material scales only with the shell’s perimeter, successful encapsulation generally requires that the imbalance in addition rates be substantial, which could be straightforwardly achieved through a large excess of shell monomers in solution relative to cargo. When the shell is able to envelop the cargo with only modest changes in droplet size, the distribution of sizes can be quite narrow, as shown in Fig. 2B.

Discussion

The minimalist model defined by Eqs. 7–12 explains the general course of our more detailed molecular assembly trajectories. But its assumption of ideally spherical geometry is a rough approximation, as evidenced by asymmetric droplet shapes in the molecular trajectory of Fig. 1. Fluctuations in cargo droplet shape are discouraged by its surface tension, but they are inevitable on small length scales. In extreme cases they lead to highly aspherical microcompartments akin to distended structures that have been observed in experiments (24). More common shape fluctuations have mechanistic influences that are more subtle but nonetheless important. These act to reduce local curvature and thus facilitate growth of a nearly flat shell patch over considerable areas even in the early stages of assembly. Enveloping the entire cargo globule still awaits sufficient cargo growth to reduce the average curvature below a threshold of roughly $1/R^{*}$. The necessary curvature that ultimately develops in the shell is also spatially heterogeneous. Protein sheets, which generally resist stretching more strongly than bending, tend to concentrate curvature at topological defects and along lines connecting them (36). As a kinetic consequence, bending is advanced primarily by discrete, localized events, in particular the formation of fivefold defects during shell growth. Indeed, the dynamics of encapsulation are noticeably punctuated by the appearance of topological defects, as shown in Movie S1.

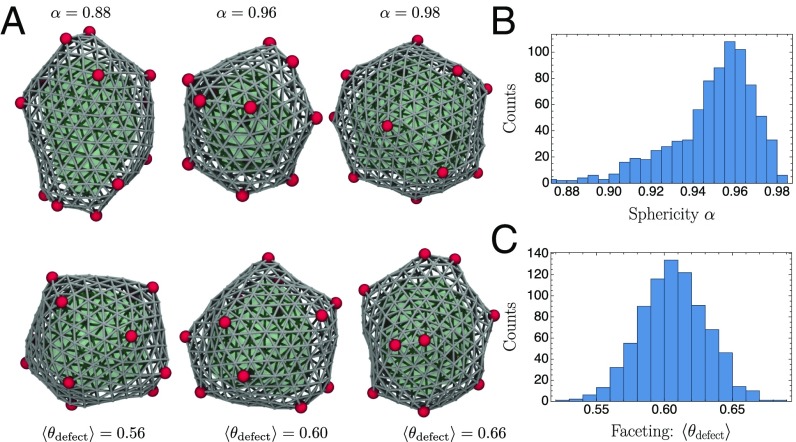
Systems out of equilibrium often support rich spatial and temporal patterns, but in many cases they are highly variable and challenging to harness or control. By contrast, the encapsulation process we have described is quite reliable. Fig. 3A shows closed structures resulting from assembly trajectories of our molecular model. They are not perfectly icosahedral (SI Appendix, Fig. S6 A and B), echoing the discernibly nonideal geometries observed in electron micrographs of carboxysomes (25). Our assemblies are nonetheless roughly isotropic and distinctly faceted, as quantified by the distributions of sphericity and defect angles shown in Fig. 3B. Gently curved regions do sometimes appear, as they do in the laboratory. In our model this smoothness reflects the presence of paired defects (one fivefold and one sevenfold) that sometimes form in the process of shell closure, screening the elastic interactions that give rise to faceting (36).

Fig. 3.

Structural variation among microcompartments generated by our molecular model. As in Fig. 1, the cargo is shown in green, the shell is shown in gray, and topological defects are shown in red. (A) Structures from the ensemble evincing the distinct regimes of sphericity and faceting. Note that two-dimensional projections can obscure some of the variation. (B) Typical assemblies are not substantially elongated, indicated by a histogram of the sphericity $\alpha$ (SI Appendix, section S7). (C) Faceting necessitates relatively sharp angles between shell monomers surrounding a fivefold defect (SI Appendix, section S7). A histogram of this angle $⟨{\theta }_{\text{defect}}⟩$ (averaged over all defects in an assembled structure) underscores the typically strong faceting visible in A.

In published work, Hagan and coworkers (26) computationally examined assembly dynamics of microcompartments stabilized by spontaneous curvature of the protein shell. Experimental data suggest that key shell proteins of the carboxysome tend, by contrast, to bind in an unbent geometry. But existing measurements do not definitively exclude a role for mechanically preferred curvature in carboxysome assembly. Quantitative characterization of the elastic properties of shell protein sheets in the absence of cargo would help clarify this issue. Systematic measurement of microcompartment geometry as a function of protein concentrations would provide a more stringent test of our nonequilibrium mechanistic hypothesis, which can be achieved with reconstitution experiments.

The nonequilibrium assembly mechanism revealed by our model has a particularly spare set of essential requirements: One needs only a monomer that assembles planar, elastic sheets and has a directional affinity for cargo that is prone to aggregation. Tuning the concentrations of these components provides a direct route to generating monodisperse, nanoscale, self-organizing structures. The simplicity of the process presents opportunities to investigate the dynamics of shell assembly in highly controlled experimental settings, for example using colloidal particles. Such a platform has already been demonstrated for a related example of kinetically defined microstructure assembly, namely bicontinuous gels stabilized by colloidal interfaces (37). Our results suggest that kinetic control can be used for precise, nanoscale assembly in a surprisingly general context.