Nonlinear Optical Methods for Characterization of Molecular Structure and Surface Chemistry

Abstract

The principles, strengths and limitations of several nonlinear optical (NLO) methods for characterizing biological systems are reviewed. NLO methods encompass a wide range of approaches that can be used for real-time, in-situ characterization of biological systems, typically in a label-free mode. Multiphoton excitation fluorescence (MPEF) is widely used for high-quality imaging based on electronic transitions, but lacks interface specificity. Second harmonic generation (SHG) is a parametric process that has all the virtues of the two-photon version of MPEF, yielding a signal at twice the frequency of the excitation light, which provides interface specificity. Both SHG and MPEF can provide images with high structural contrast, but they typically lack molecular or chemical specificity. Other NLO methods such as coherent anti-Stokes Raman scattering (CARS) and stimulated Raman scattering (SRS) can provide high-sensitivity imaging with chemical information since Raman active vibrations are probed. However, CARS and SRS lack interface and surface specificity. A NLO method that provides both interface/surface specificity as well as molecular specificity is vibrational sum frequency generation (SFG) spectroscopy. Vibration modes that are both Raman and IR active are probed in the SFG process, providing the molecular specificity. SFG, like SHG, is a parametric process, which provides the interface and surface specificity. SFG is typically done in the reflection mode from planar samples. This has yielded rich and detailed information about the molecular structure of biomaterial interfaces and biomolecules interacting with their surfaces. However, 2-D systems have limitations for understanding the interactions of biomolecules and interfaces in the 3-D biological environment. The recent advances made in instrumentation and analysis methods for sum frequency scattering (SFS) now present the opportunity for SFS to be used to directly study biological solutions. By detecting the scattering at angles away from the phase-matched direction even centrosymmetric structures that are isotropic (e.g., spherical nanoparticles functionalized with self-assembled monolayers or biomolecules) can be probed. Often a combination of multiple NLO methods or a combination of a NLO method with other spectroscopic methods is required to obtain a full understanding of the molecular structure and surface chemistry of biomaterials and the biomolecules that interact with them. Using the right combination methods provides a powerful approach for characterizing biological materials.

Introduction

Nonlinear optics is used in a wide range of applications. One process that many people have experience with is the frequency doubling 1064 nm light to 532 nm light in green laser diodes. In fact, a variety of nonlinear optical processes are common in different laser systems, such as optical parametric generation and amplification, difference frequency generation, and frequency doubling. These processes are used to tune and amplify intense laser light into the desired frequencies with high conversion efficiencies. Nonlinear optical processes are often complex and typically much time and effort have been required to gain the understanding needed for researchers to take advantage of them in material characterization. For instance, much of the early work on vibrational sum-frequency generation (SFG) spectroscopy was focused on small molecules at simple interfaces and well-controlled systems such as self-assembled monolayers.[1–5] Also, even though the stimulated Raman scattering phenomenon had been known since 1962, [6,7] it was not until 2008 that it was used to image biomedical samples.[8] Nowadays, many of the challenges of nonlinear optical techniques have been sorted out to the extent that their application to biological samples are becoming increasingly popular.[9–15] It is therefore the focus of this review to discuss the basic principles behind some of the most common nonlinear optics techniques and highlight their application to characterize various biomaterial structures and interfaces.

The structural integrity and mechanical properties of cells and tissues are to a large extent provided by protein fibers, such as the collagen fibers that are an essential part of the extracellular matrix.[16–18] A detailed understanding of the structure, interaction, orientation, conformation, and dynamics of these fibers is important for the development of new and improved strategies in the fields of tissue engineering and regenerative medicine, among others.[19,20] Other fibrillar structures, such as amyloids, are associated with severe diseases like diabetes, Alzheimer’s disease, and Parkinson’s disease.[21,22] Insights into how the environment affects their formation and how the mature fibers interact with their surrounding are essential for understanding disease development and could guide the pursuit of new drugs and biomarkers for the conditions.[23]

Functionalized nanoparticles and liposomes are two other important types of biomaterials, commonly used in drug delivery, biosensing assays, and as models for complex cellular systems.[24,25] Optimizing their performance in various applications requires careful control of their surface chemistry. Development of proper preparation and functionalization protocols are thus crucial; however, access to analytical techniques that can interrogate the presence, orientation, conformation, and interactions of chemical groups at the surface of the structures is equally important.

For most techniques, there are often limitations and challenges when characterizing the structure and surface chemistry of protein fibers, nanoparticles, or liposomes. While X-ray photoelectron spectroscopy and time-of-flight secondary ion mass spectrometry provide detailed chemical information with high surface specificity, [26–28] the techniques typically require ultra-high vacuum and sample preparation constraints that limit the type of systems that can be studied. Quartz crystal microbalance with dissipation and surface plasmon resonance are label-free techniques capable of real-time probing of biomolecular adsorption on solid/liquid interfaces, [29–33] but without chemical specificity. Infrared (IR) and spontaneous Raman spectroscopies, on the other hand, do provide chemical information;[34] however, the interfacial specificity is often poor or nonexistent and structures in biological environments are difficult to access for analysis. The techniques mentioned above, and many others, have provided much important information for understanding, developing and optimizing of the performance of biomaterials. However, it is clear that additional techniques with both chemical and interfacial specificity, as well as capable of analyzing biomaterials in aqueous and biological environments are desired - something that can be realized with nonlinear optics.[35–39]

Nonlinear optics is a field that includes a wide range of approaches for non-invasive characterization of materials with high-intensity lasers. Multiphoton excitation fluorescence (MPEF) is commonly used for high-quality imaging based on electronic transitions, while coherent anti-Stokes Raman scattering (CARS) and stimulated Raman scattering (SRS) can be performed in microscopy mode and provide images with contrast for specific wavenumbers in a vibrational spectrum.[38] While powerful, these techniques typically lack specificity for interfacial features, which is one of the main virtues of second-harmonic generation (SHG) and sum-frequency generation (SFG).[36] The former is commonly used for label-free imaging of ordered structures in complex biological samples, while the latter is often employed in reflection-mode for vibrational spectroscopy of light-accessible interfaces. This typically requires the use of two-dimensional surface models, which has been and continues to be a very useful approach. However, it is not clear how accurately such models capture key characteristics, such as dynamics and interactions, of biomaterials normally found in three-dimensional biological environments. For instance, the edge and corner atoms that separate facets on small metallic nanoparticles and the curvature of liposomes may affect the packing, organization and dynamics of species at their interfaces, [40–42] which can lead to behaviors that would not be predicted based on the results from the two-dimensional surface models. There is thus a need for approaches that are not limited to probing only planar interfaces.

The origin of the interfacial specificity in SHG and SFG is that net ordering of the probed transition dipole moments is required, which normally precludes solvent molecules and other isotropically distributed bulk species from contributing to the signal.[35–37] However, even isotopic objects such as spherical nanoparticles can produce SHG and SFG signals when the mixing light beams are scattered away from the phase-matched direction, resulting in a phase-shift across the scattering objects as well as a significant reduction in the coherence length. This means scatterers that include ordered species can produce 2^nd order nonlinear optical signals detectable in the far field, allowing for spectroscopic analysis of biomaterial interfaces in biological environments.[43,44] When applied in this mode, the techniques are called second-harmonic scattering (SHS) and sum-frequency scattering (SFS) and they were first introduced in the late 1990s and early 2000s, respectively.[45,46] Specialized and expensive equipment as well as complex or non-existent theoretical models have been prohibitive factors for the application of SHS and SFS to samples of biological relevance. However, continuous efforts during the last decade have now provided a theoretical framework that makes analyses of more complex samples feasible, such as biomaterials and biomacromolecules in aqueous and biological environments.

Nonlinear Optics

As mentioned above, nonlinear optics is a field that includes a broad range of techniques, which all have a nonlinear response to the total electric field intensity in the sample. The response is proportional to the square of the induced polarization as given by Eq. 1,

$$I\propto {\mid P\mid }^2={|{\epsilon }_0({\chi }^{(1)}{E}_i+{\chi }^{(2)}{E}_i{E}_j+{\chi }^{(3)}{E}_i{E}_j{E}_k\dots )|}^2$$ (1)

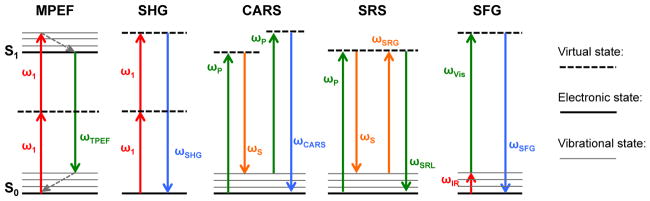
where I is the intensity of the response, P is the induced polarization, χ⁽ⁿ⁾ is the susceptibility factor for the n^th order mixing, and E represents the electric fields of the incoming laser beams. Normally, the susceptibility factors for higher-order induced polarization are very small, leading to a dominating first-order linear response and weak nonlinear effects. However, with the strong peak electric fields produced by short pulsing and focusing of the incoming high-intensity lasers, the higher order terms can contribute significantly to the induced polarization and detectable signals from these processes can be produced. Some of the common nonlinear optical spectroscopy processes are illustrated in Figure 1. In this work, SFG is of particular interest and is therefore discussed in more detail below in a separate section. However, brief overviews of the other processes will first be given.

Figure 1.

Diagrams of the photophysical processes for a variety of the most common nonlinear optical techniques for material characterization, including multiphoton excitation fluorescence (MPEF), second harmonic generation (SHG), coherent anti-Stokes Raman scattering (CARS), stimulated Raman scattering (SRS), and sum-frequency generation (SFG).

MPEF and SHG

MPEF relies on simultaneous absorption of multiple photons (most common is two-photon absorption) by the same molecule. It usually involves a virtual intermediate state as a path to the real excited state that is being probed. MPEF is often performed in the confocal scanning mode, where the short-pulsed excitation laser is focused down to one spot, from which the majority of the signal is produced due to the high photon flux in that spot. The quality of the image is given by the point spread function of the imaging system, for which the axial spread is much lower in MPEF compared to the corresponding linear fluorescence process.[47] This is because the signal has a multi-power dependence on the incoming laser intensity, leading to improved spatial resolution in the z-direction (depth-axis). As the excitation wavelength often can be in the IR or near-IR region, low absorption allows quite long penetration depths in biological samples and high excitation light intensities may be used without risks for photo-induced sample damage or bleaching - especially outside the focal plane where there is insufficient photon flux for significant absorption. Also, since the MPEF signal is at a wavelength shorter than the excitation wavelength, background and noise can be relatively low. These features, together with the excellent depth-resolution, make MPEF an increasingly popular nonlinear optical tool for imaging of biological samples.[47–52]

All the virtues of the two-photon version of MPEF (i.e. TPEF) outlined above are also true for SHG. However, the techniques differ in some very important ways.[53–56] First, SHG is a parametric process and does not rely on absorption of photons; however, resonant enhancement of the signal via resonant transitions can still occur. Second, electronic relaxation can happen to a variety of vibrational states in TPEF and leads to quite broad spectra, while the parametric SHG process simply yields a signal at the double frequency of the excitation laser light. Third, vibrational relaxation in the excited and ground states yields a Stokes shift in TPEF, which is not the case for SHG. Fourth, while SHG is a coherent process and exhibits a range of selection rules for the sample symmetry, the broad bandwidth and long lifetime of TPEF destroy the coherence and thereby relax those selection rules. While these four distinctions between SHG and TPEF are somewhat related, the fourth point is particularly important, as it is the origin of the interfacial specificity for coherent, even-ordered nonlinear optical processes. Figure 2 shows a schematic of SHG and TPEF with a simple multiphoton microscope setup. In accordance with Eq. 1, the intensity of the SHG signals can be described by

Figure 2.

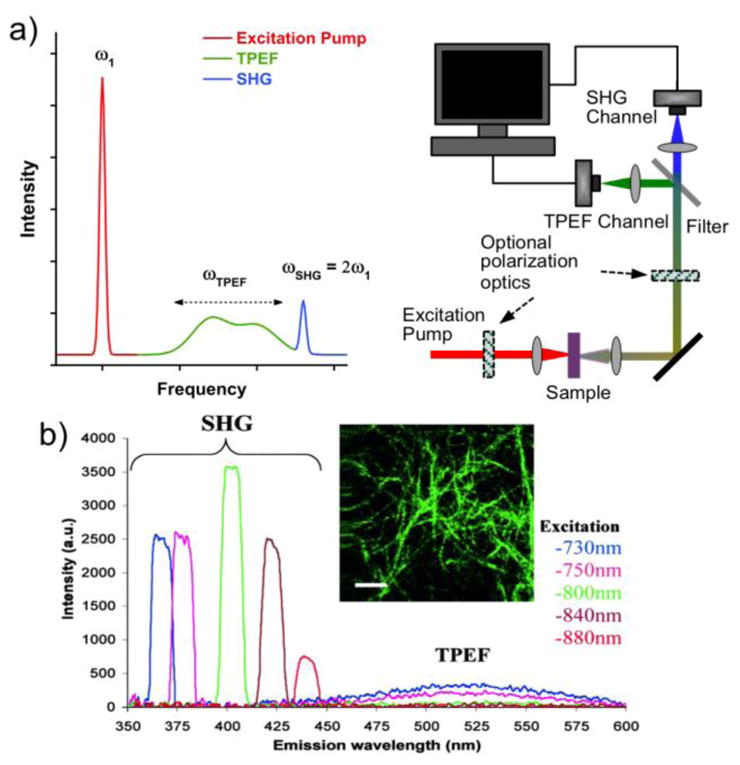
a) A short-pulsed excitation laser may produce SHG and TPEF signals, which can be detected in a multiphoton microscope. b) SHG signals, in this case from collagen fibers, always appear at the double-frequency of the excitation light, while the TPEF signals are broadened and Stokes-shifted to a characteristic peak with a longer wavelength. Figure 1b is reprinted with permission from ref [53], copyright 2002 National Academy of Sciences.

$$I_{\mathit{SHG}}\propto {\mid P_{\mathit{SHG}}\mid }^2={\left|{\epsilon }_0({\chi }_{\mathit{SHG}}^{(2)}{E}^2)\right|}^2$$ (2)

where E is the electric field of the incoming laser light and ${\chi }_{\mathit{SHG}}^{(2)}$ is the susceptibility tensor for the SHG process, which can be divided into 27 different tensor elements, ${\chi }_{\mathit{ijk}}^{(2)}$, where the ijk goes over all possible combinations of the lab coordinates x, y and z.[54,55] In this notation, i represents the electric field direction of the SHG signal, while j and k represent the electric field directions of the two incoming laser photons in the mixing process. If one inverts the sample that is probed, it is clear that one consequence is that all molecules would experience a flip in sign of all the electric field components, including the electric field of the SHG signal. In other words, a positive induced polarization should become negative under this operation, which requires ${\chi }_{\mathit{SHG}}^{(2)}$ to flip its sign according to eq. 2. However, if the sample is isotropic, the inversion should yield a situation that is macroscopically indistinguishable from the starting point. Since ${\chi }_{\mathit{SHG}}^{(2)}$ is a macroscopic sample property, it should therefore not change. The only way ${\chi }_{\mathit{SHG}}^{(2)}$ can flip in sign and simultaneously keep its value is if it is zero for isotropic samples. A more physical way of looking at this is that for each molecule with its dipole moment in a certain direction, there will always be another molecule within the coherence length that is positioned and/or orientated so that it cancels out the signal from the first in an isotropic sample. Such signal cancellation requires the process to be coherent, which connects the phenomenon to the fourth point made earlier with respect to the differences between TPEF and SHG. A more detailed discussion on the selection rules for sample symmetries is included in the section about vibrational SFG spectroscopy and is broadly applicable to SHG as well.

As samples with inversion symmetry do not yield SHG signals, it is an excellent method for label-free detection and/or imaging of non-centrosymmetric structures that exhibit long-range ordering (and that are thus non-isotropic). One example is collagen fiber networks in tissues, for which one example is shown in Figure 2. There are many publications that include high-contrast SHG images in the scientific literature.[53,57–64] Figure 3a shows an overlay of TPEF (green) and SHG (red) intensity images of a mouse ovary tissue sample, obtained with a multiphoton microscope having a 76 MHz repetition rate laser with a 200 fs pulse-length and a 790 nm excitation wavelength.[64] The ordered collagen fibers are the dominant features in the SHG channel. For collagen fibers with cylindrical symmetry, there are only three independent tensor elements that can be probed: ${\chi }_{z^{\prime }{z}^{\prime }{z}^{\prime }}^{(2)},{\chi }_{x^{\prime }{z}^{\prime }{x}^{\prime }}^{(2)}={\chi }_{x^{\prime }{x}^{\prime }{z}^{\prime }}^{(2)}={\chi }_{y^{\prime }{z}^{\prime }y}^{(2)}={\chi }_{y^{\prime }{y}^{\prime }{z}^{\prime }}^{(2)}$, and ${\chi }_{z^{\prime }{x}^{\prime }{x}^{\prime }}^{(2)}={\chi }_{z^{\prime }{y}^{\prime },y^{\prime }}^{(2)}$; where x′, y′, and z′ are the local coordinates for the fiber z′ with aligned with the fiber axis. When the excitation beams and the SHG signal are traveling in the y-direction, perpendicular to the x-z sample plane, the contributions of these tensor elements to the signal intensity are weighted differently depending on the polarization direction of the excitation light relative the fiber orientation, as described by,

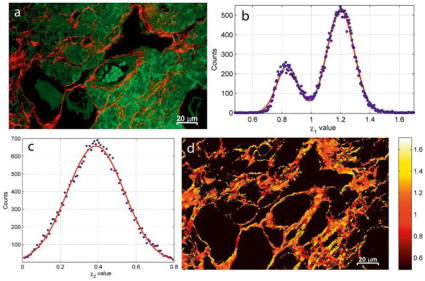
Figure 3.

a) The TPEF (green) identifies features in the mouse ovary tissue distinct from the SHG (red), which primarily shows the ordered collagen fiber regions. b) The ${\chi }_1={\chi }_{z^{\prime }{z}^{\prime }{z}^{\prime }}^{(2)}/{\chi }_{z^{\prime }{x}^{\prime }{x}^{\prime }}^{(2)}$ parameter shows two populations of collagen-related signals in the SHG channel, which are attributed to the presence of collagen type I (χ₁ = 1.2) and type III (χ₁ = 0.83). c) The ${\chi }_2={\chi }_{x^{\prime }{z}^{\prime }{x}^{\prime }}^{(2)}/{\chi }_{z^{\prime }{x}^{\prime }{x}^{\prime }}^{(2)}$, only includes one broad population that does not provide additional contrast for the collagen fibers in the χ-image of the tissue. d) A pseudo-colored image of χ₁. Reprinted with permission from ref [64], copyright 2015 John Wiley and Sons.

$$I_{\mathit{SHG}}=B({[{\mathit{sin}}^2\varphi +{\chi }_1{\mathit{cos}}^2\varphi ]}^2+{({\chi }_2)}^2{\mathit{sin}}^{2}2\varphi )$$ (3)

where B is a scaling factor and ϕ = ϕ_u − ϕ_v is the difference angle between the polarization direction of the excitation light (ϕ_u) and the collagen fiber axis (ϕ_v). If the collagen fiber polar angle, θ, is assumed to be zero for all pixels (i.e. the fiber axis is in the sample x-z plane, with the y′ axis aligned with the y-direction), the scaling factor may be defined as $B=b{\left|{\chi }_{z^{\prime }{x}^{\prime }{x}^{\prime }}^{(2)}\right|}^2$, which is just a modulation of the total intensity for each pixel. In this case, the equation has three unknown variables: the fiber orientation and the two tensor element ratios ( ${\chi }_1={\chi }_{z^{\prime }{z}^{\prime }{z}^{\prime }}^{(2)}/{\chi }_{z^{\prime }{x}^{\prime }{x}^{\prime }}^{(2)}$ and ${\chi }_2={\chi }_{x^{\prime }{z}^{\prime }{x}^{\prime }}^{(2)}/{\chi }_{z^{\prime }{x}^{\prime }{x}^{\prime }}^{(2)}$). By capturing multiple SHG signals with plane polarized excitation light in various directions, one can solve the equation for each pixel and thereby not only obtain the fiber orientation but also assign values to the two tensor element ratios. The first ratio has been shown to depend on the collagen type, with a value of about 0.83 for type III and 1.2 for the more common type I.[57] The second ratio only includes a single peak distribution and does not provide extra contrast in the SHG image. The polarization-dependent SHG imaging of tissues for identifying collagen fibers of various types is demonstrated in Figure 3b–d.[64] It should be mentioned that the polar angle is in general nonzero for the fibers. In such cases, the scaling factor becomes B′ = Bcos²θ and χ₁ has to be exchanged for Γ₁ = χ₁cos²θ + (2χ₂ + 1)sin²θ. The effects from this are a general signal reduction for pixels with high θ and that the polarization analysis will yield Γ₁ rather than χ₁. While this opens up for new interpretations of the origin of the bimodal distribution observed for this parameter, it is still possible to use it for distinguishing fibers from various types of collagen in a sample, assuming that the polar angle is independent from the χ₁ and χ₂.

In addition to imaging, SHG can be used in various label-free chemical sensors where only a recognition element is needed. For instance, ligand-receptor interactions at interfaces typically lead to a preferential orientation of the analyte that then can be directly detected with excellent sensitivity using nonresonant SHG.[65,66] For structures where the SHG susceptibility is not sufficient for distinguishing the analyte from other species in a complex sample, specific SHG-dyes have been developed and the search for new ones continues to be an active field of research.[67,68] Even when SHG labels are needed, the excellent contrast provided by the molecular ordering selection rule makes SHG competitive relative other methods based on fluorescence, for which background signals from nonspecific interactions can lead to false positive signals, poor contrast, as well as high limits of detection.

CARS and SRS

While SHG and MPEF can provide images with high structural contrast, they typically do not provide contrast with molecular specificity. However, CARS and SRS, two nonlinear vibrational spectroscopy methods, are commonly used for imaging with high sensitivity and can provide chemical information with high spatial resolution. CARS is a coherent parametric 3^rd-order process, in which one intense laser beam acts as pump and probe (called pump from here on), while a second tunable laser acts as a Stokes beam that guides the molecules to select Raman active vibrations.[69–72] The signal intensity is thus described by

$$I_{\mathit{CARS}}\propto {\mid P_{\mathit{CARS}}\mid }^2={\mid {\epsilon }_0({\chi }_{\mathit{CARS}}^{(3)}{E}_P^2{E}_S)\mid }^2$$ (4)

where ${\chi }_{\mathit{CARS}}^{(3)}$ is the nonlinear susceptibility factor for the CARS process, E_P is the electric field of the pump beam, and E_S is the electric field of the Stokes beam. Being an odd-ordered process, the flip in sign of the induced polarization for an inversed sample is realized already by the sign switch for E_P and E_S, allowing ${\chi }_{\mathit{CARS}}^{(3)}$ to be non-zero even for isotropic samples. Therefore, CARS is not surface or interface specific. A more physical way of looking at it is that the pump and Stokes beams ensure that the vibrational modes of the stimulated Raman resonances oscillate so that the emitted CARS photons have the same phase regardless of molecular orientation - analogous to how stimulated emission in a laser leads to a build-up of photons with the same phase. Therefore, no cancellation of signals will occur, even if the sample is isotropic. Ignoring possible contributions from resonant electronic transitions, the fitting function for the nonlinear susceptibility factor is given by

$${\chi }_{\mathit{CARS}}^{(3)}={\chi }_{NR}^{(3)}+{\sum }_q\frac{A_q}{{\omega }_q-(\mathrm{\Omega })-i{\mathit{\Gamma }}_q}$$ (5)

where ${\chi }_{NR}^{(3)}$ is a nonresonant contribution, A_q, Γ_q and ω_q are the amplitude, width and wavenumber of the q^th Raman active vibrational mode, while Ω = ω_P − ω_S is the difference frequency between the pump and Stokes beams. ${\chi }_{\mathit{CARS}}^{(3)}$ is a rank four tensor and the magnitude of A_q is dependent on the total contribution of the tensor elements (γ_abcd) of the molecular hyperpolarizabiliy (also a rank four tensor) to the nonlinear susceptibility tensor elements probed with the chosen polarization combination. When the difference frequency equals the frequency of a Raman transition, ω_q, a signal enhancement will occur at the CARS frequency,

$${\omega }_{\mathit{CARS}}=2{\omega }_P-{\omega }_S$$ (6)

The CARS photons add up coherently in the far field, which yields a quadratic dependency on the number of probed molecules. This, together with possible nonresonant contributions to ${\chi }_{\mathit{CARS}}^{(3)}$ and the imaginary component of the resonant parts yielding phase-relations, CARS line shapes typically differ from those in conventional Raman spectra. While this is not a problem in itself, the nonresonant contribution makes spectroscopic interpretation more difficult and limits the spectral contrast, in particular for the amide I and fingerprint regions. This is challenging to circumvent in a reliable and robust way. However, one method is to utilize the nonresonant background as a heterodyne amplification signal and post-process the data to retrieve the imaginary part of the CARS signal via a time-domain Kramers-Kronig transform.[73,74] A setup for this that includes a three-color excitation scheme with broad-band pump/Stokes beams and a narrowband probe beam was previously reported.[72] Despite the difficulties with nonresonant backgrounds, CARS microscopy is commonly used for imaging of specific chemical groups in biological samples and has provided much useful information. High-contrast imaging of myelin fibers in brain tissue[75] and the identification of lipids co-localized with amyloid plaques in Alzheimer’s diseased human brain tissue[76] are two examples.

Another 3^rd-order coherent Raman scattering process is SRS, where the frequency of the induced polarization matches either the pump frequency or the Stokes frequency (sometimes called probe frequency). In the far field, the produced SRS signal will interfere with and thereby modulate the intensity of the pump or Stokes beams in accordance with,

$$I_{\mathit{SRS}}={\mid E_1+E_{\mathit{SRS}}\mid }^2={\mid E_1\mid }^2+{\mid E_{\mathit{SRS}}\mid }^2+2{\mid E_1\mid }^2{\mid E_2\mid }^2[Re\{{\chi }_{\mathit{SRS}}^{(3)}\}\mathit{cos}(\mathrm{\Delta }\varphi )+Im\{{\chi }_{\mathit{SRS}}^{(3)}\}\mathit{sin}(\mathrm{\Delta }\varphi )]$$ (7)

where ${\chi }_{\mathit{SRS}}^{(3)}$ is the SRS susceptibility factor. For SRS signals with the same frequency as the pump beam, subscript 1 denotes the pump E-field (E_P), while subscript 2 denotes the Stokes beam E-field (E_S). In this case, the phase difference (Δ ϕ) between the interfering E-fields is −π/2, which leads to a signal loss at the pump frequency. This stimulated Raman loss (SRL) is described by,

$$I_{\mathit{SRL}}={\mid E_P+E_{\mathit{SRS}}\mid }^2={\mid E_P\mid }^2+{\mid E_{\mathit{SRS}}\mid }^2-2\mid E_P^2\mid \mid E_S^2\mid Im\{{\chi }_{\mathit{SRS}}^{(3)}\}$$ (8)

For SRS signals at the Stokes beam frequency, the representation of subscripts 1 and 2 in Eq. 6 is flipped. In this case, the phase difference (Δϕ) between the interfering E-fields is π/2, which leads to a signal gain. This stimulated Raman gain (SRG) at the Stokes frequency is then described by

$$I_{\mathit{SRG}}={\mid E_S+E_{\mathit{SRS}}\mid }^2={\mid E_S\mid }^2+{\mid E_{\mathit{SRS}}\mid }^2+2\mid E_S^2\mid \mid E_P^2\mid Im\{{\chi }_{\mathit{SRS}}^{(3)}\}$$ (9)

Normally, the pump and Stokes beams are much more intense than any nonresonant background signals, which eliminates potential problems with interference between ${\chi }_{NR}^{(3)}$ and the resonant components of ${\chi }_{\mathit{SRS}}^{(3)}$. However, one problem with detection at these frequencies is laser intensity noise. Such noise is mainly of low frequency, which means that a rapid modulation (>1 MHz) of the non-detected beam’s intensity (or frequency, phase, wavelength, and polarization) will yield a signal modulation of the other beam that can be identified and detected with a lock-in amplifier. Such a detection scheme (illustrated in Figure 4) can reduce the noise of the system down to the shot noise level of the detector. While the loss and gain signals have a quadratic dependence on both the incoming pump and Stokes E-fields (which can be normalized away), the dependence on the molecular concentration is linear. This together with the absence of nonresonant background signals mean that, in contrast to CARS, the SRS line shape will be identical to conventional spontaneous Raman spectra (Figure 4b). SRS data can thus be fitted with regular Lorentzian functions and one can easily show that the imaginary part of the resonant 3^rd-order susceptibility in Eq. 5 (which also applies to SRS) has a Lorentzian line shape. The doubly intensity dependence on the pump and probe beams ensures that the signal is only produced from the focus spots of the lasers, which allows for optical sectioning in 3D, just as in MPEF and SHG microscopy. The above virtues of the technique has resulted in the number of SRS publications focused on imaging biological samples increase rapidly, despite it being less than a decade since the first demonstration on such materials.[8,77,78] An important comment is that although the diagram of the SRS process in Figure 1 appears to be parametric, it is actually not since less energetic photons at the Stokes frequency are produced at the expense of the more energetic ones at the pump frequency, making the process dissipative.

Figure 4.

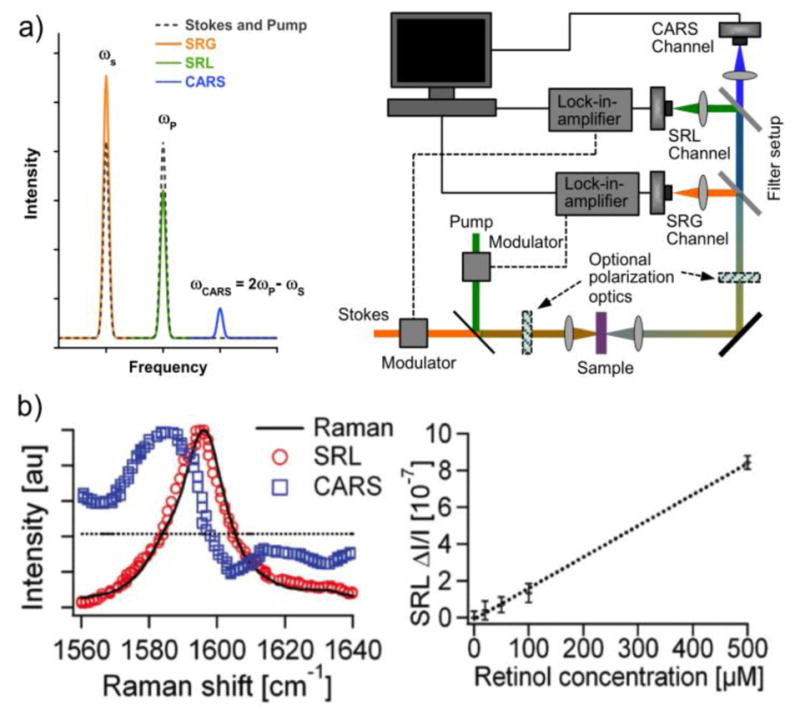
a) Short-pulsed excitation pump and Stokes lasers may produce SRS and CARS signals, which can be detected in nonlinear microscopes. By fast modulation of either the pump or the Stokes beam, coupled with a lock-in-amplifier, signals can be detected with low noise levels. b) Left: While interference with a nonresonant (dotted) background can shift the maximum signal from the vibrational peak in CARS (blue squares), the SRS signal (red circles) remains similar to the corresponding spontaneous Raman signal (solid line) from retinol. Right: The SRS signal intensity has a simple linear intensity dependence on the analyte concentration. Figure 4b is reprinted with permission from ref. [8], copyright 2008 American Association for the Advancement of Science.

Although local molecular ordering is not a requirement for CARS and SRS signal production, the angle between the induced molecular dipole moments and the mixing E-fields is still important for the ability of the molecules to produce a signal. Therefore, it is theoretically possible to extract the local average orientation for molecules with these techniques by using various polarization directions for plane-polarized pump and Stokes beams.[79,80] One problem with this approach is that the theoretical models needed to analyze the data rapidly grow in complexity. All tensor elements typically need to be taken into account for complex vibrational bonds.[81] However, by probing simple vibrations for which one may assume that one or just a few 3^rd-order molecular nonlinear susceptibility tensor elements contribute to the signal, the analysis can be simplified significantly by making sure all E-fields are all polarized within the sample plane. For methylene vibrations, reasonable results have been obtained by assuming that γ_{z′ z′ z′ z′} is the only contributing element, [82] which yielded the molecular orientation order for lipids in multilamellar vesicles (MLV) with polarized CARS and SRS microscopies.[79,83] The CH₂ stretch signal intensities for such a sample in the x-y plane can be described by,

$$\begin{gathered} I_{\mathit{CARS}}=I_X+I_Y\propto {\left|{\chi }_{\mathit{XXXX}}^{(3)}\langle {cos}^4\alpha \rangle +3{\chi }_{\mathit{XXXY}}^{(3)}\langle {cos}^3\alpha sin\alpha \rangle +3{\chi }_{\mathit{XYXY}}^{(3)}\langle {cos}^2\alpha {sin}^2\alpha \rangle +{\chi }_{\mathit{XYYY}}^{(3)}\langle cos\alpha {sin}^3\alpha \rangle \right|}^2 \\ +{\left|{\chi }_{\mathit{YXXX}}^{(3)}\langle {cos}^3\alpha sin\alpha \rangle +3{\chi }_{\mathit{YXXY}}^{(3)}\langle {cos}^2\alpha {sin}^2\alpha \rangle +3{\chi }_{\mathit{YYXY}}^{(3)}\langle cos\alpha {sin}^3\alpha \rangle +{\chi }_{\mathit{YYYY}}^{(3)}\langle {sin}^4\alpha \rangle \right|}^2 \end{gathered}$$ (10)

and

$$I_{\mathit{SRS}}\propto {\chi }_{\mathit{XXXX}}^{(3)}\langle {cos}^4\alpha \rangle +4{\chi }_{\mathit{XXXY}}^{(3)}\langle {cos}^3\alpha sin\alpha \rangle +6{\chi }_{\mathit{XYXY}}^{(3)}\langle {cos}^2\alpha {sin}^2\alpha \rangle +4{\chi }_{\mathit{XYYY}}^{(3)}\langle cos\alpha {sin}^3\alpha \rangle +{\chi }_{\mathit{YYYY}}^{(3)}\langle {sin}^4\alpha \rangle$$ (11)

where α is the angle between the polarization direction of the mixing beams and the x-axis. Each tensor element of the sample, ${\chi }_{\mathit{IJKL}}^{(3)}$, has a specific dependence on the orientation distribution of the nonlinearly induced dipoles and the x-axis. In a similar way as for the SHG microscopy example presented above, the average angles and the relative magnitudes of the even order parameters that go into ${\chi }_{\mathit{IJKL}}^{(3)}$ for the probed vibrations can be calculated if multiple spectra with different polarization angles are acquired for each pixel. The polarization dependence on the absolute values for CARS and SRS intensities of the CH₂ stretches from different regions of a MLV prepared from DPPC is presented in Figure 5, as well as the associated average orientations and 2^nd order parameter magnitudes.[79] As can be seen, the two techniques give similar qualitative results and show a perpendicular orientation for the CH₂ bonds relative the radial direction for the MLVs, as expected. However, they differ quantitatively on the magnitude of the 2^nd order parameter due to the CARS results being skewed by a nonresonant background that cannot easily be accounted for in a theoretical model.

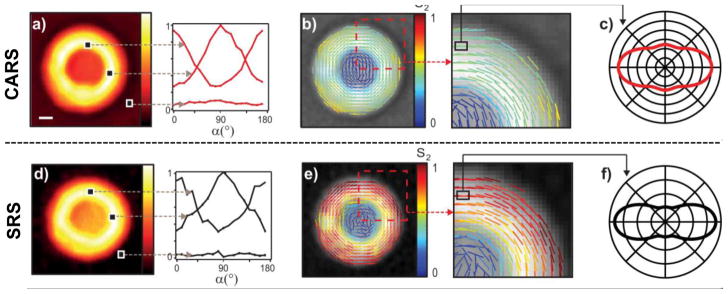
Figure 5.

A nonresonant contribution gives a non-zero background in CARS (a) that interferes with the vibrational signal from the MLV and causes an apparent broadening of the orientation distribution function as determined by the S₂ parameter in the theoretical model (b and c). However, the background is low in SRS (d) and the corresponding model and parameter give a more definite and narrow distribution function of the molecular orientation for the CH₂ groups in the MLV (e and f). The orientation of the lines denotes the average CH₂ orientation obtained, while the color indicates the magnitude of the S₂ parameter (b and e). Reprinted from ref. [79], copyright 2015 American Chemical Society.

Techniques based on CARS and SRS are growing increasingly popular for biomaterial characterization. In recent years, multiplex versions have been developed, combining a picosecond narrowband laser with a femtosecond broadband laser.[73,84,85] The narrowband laser ensures high spectral resolution, while the broadband gives the bandwidth for multiplex acquisition and this allows rapid detection of spectra enabling studies of dynamic processes in real time. Some technical difficulties with multiplex SRS, associated with the lock-in-amplifier detection, have prompted further developments. For instance, chirped femtosecond laser pulses where the well-controlled temporal delay between them determines the beat-frequency have successfully been used for rapid hyperspectral SRS imaging.[86]

Vibrational SFG Spectroscopy

The first reports of vibrational SFG spectroscopy were published in 1987.[1–3] It is a 2^nd-order process that exhibits similar selection rules as SHG, which means that isotropic samples typically do not yield a signal. As molecules tend to order themselves and thereby become nonisotropic at interfaces, SFG is considered interfacial sensitive. The technique utilizes one visible (or near IR) laser beam at a fixed narrowband frequency and one tunable or broadband IR laser beam. The pulsed and high-intensity beams need to be overlapped spatially and temporally on the sample, from which the produced SFG signal intensity then is given by

$$I_{\mathit{SFG}}\propto {\mid P_{\mathit{SFG}}\mid }^2={\left|{\epsilon }_0{\chi }_{\mathit{SFG}}^{(2)}{E}_{{\omega }_{\mathit{Vis}}}{E}_{{\omega }_{IR}}\right|}^2$$ (12)

where ${\chi }_{\mathit{SFG}}^{(2)}$ is the effective susceptibility factor for SFG, while E_ωVis and E_ωIR are the electric fields of the visible and IR laser beams respectively. Just as for SHG, ${\chi }_{\mathit{SFG}}^{(2)}$ is a tensor that can be divided into 27 tensor elements.[56] Vibrational SFG spectroscopy can be performed in both reflection mode and transmission mode, of which the former is the most common for surface studies.[87–90] For such experiments, the SFG-active vibrational modes can be probed at any interface accessible by the visible and IR beams; for example solid/liquid, solid/air and liquid/air interfaces in geometries illustrated in Figure 6.

Figure 6.

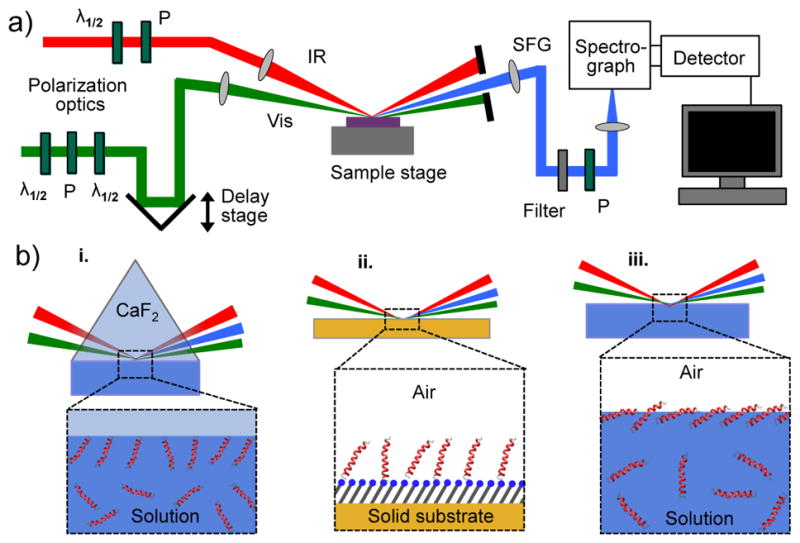
a) A schematic of a typical setup for vibrational SFG spectroscopy in reflection mode. b) Illustrations of solid/liquid (i), solid/air (ii), and liquid/air (iii) interfaces, which are commonly analyzed with SFG. The interactions at the interface typically induce a preferential orientation of the analyte that can then be characterized with SFG, while the isotropically distributed species in bulk do not contribute to the signal.

In SFG experiments, it is possible to control the polarization state of the SFG, visible, and IR beams, and thereby probe only a subset of the 27 possible ${\chi }_{\mathit{ijk}}^{(2)}$ tensor elements (where i is the direction of the SFG electric field, j is the direction of the visible electric field, and k is the direction of the IR electric field). Using the notation of p-polarization for electric fields oscillating in the x-z incidence plane, and s-polarization for electric fields oscillating in the perpendicular y-direction, there are eight possible settings with clean polarization states of the three mixing beams. The corresponding effective susceptibilities and the tensor elements they include are outlined in Table 1, as well as notes on the nonvanishing tensor elements for various interfacial symmetries with a symmetry plane aligned with the plane of incidence.

Table 1.

The effective susceptibility ( ${\chi }_{\mathit{eff}}^{(2)}$) for each polarization combination in SFG includes a unique subset of the probed susceptibility tensor elements ( ${\chi }_{\mathit{ijk}}^{(2)}$) of the sample, many of which vanish for common sample symmetries. The non-zero elements often have interdependencies, however, note that the evaluation of the achiral and chiral tensor elements in this table assumes that a symmetry plane is aligned with the plane of incidence.

${\chi }_{\mathit{eff}}^{(2)}$	ijk of probed ${\chi }_{\mathit{ijk}}^{(2)}$	ijk of the non-vanishing ${\chi }_{\mathit{ijk}}^{(2)}$ depending on the sample symmetry
		symmetry	achiral elements	chiral elements
${\chi }_{\mathit{ppp}}^{(2)}$	zzz, zxx, xzx, xxz xxx, xzz, zxz, zzx	C1	All tensor elements are nonvanishing and independent.
${\chi }_{\mathit{ssp}}^{(2)}$	yyz, yyx	C2	zzz, zxx, xzx, xxz, yyz, yzy, zyy	xzy, zxy, xyz, zyx, yxz, yzx
${\chi }_{\mathit{sps}}^{(2)}$	yzy, yxy	C2v	zzz, zxx xzx, xxz, yyz, yzy, zyy	–
${\chi }_{\mathit{pss}}^{(2)}$	zyy, xyy	C3	xxy = xyx = yxx = −yyy, xxz = yyz xyy = yxy = yyx = −xxx, xzx = yzy zxx = zyy, zzz	xzy = −yzx, zxy = −zyx, xyz = −yxz
${\chi }_{\mathit{sss}}^{(2)}$	yyy	C3v	xyy = yxy = yyx = −xxx, xxz = yyz xzx = yzy, zxx = zyy, zzz	–
${\chi }_{\mathit{pps}}^{(2)}$	xzy, zxy, zzy, xxy	C4; C6; C∞	zzz, zxx = zyy, xzx = yzy, xxz = yyz	xzy = −yzx, zxy = −zyx, xyz = −yxz
${\chi }_{\mathit{psp}}^{(2)}$	xyz, zyx, zyz, xyx	C4v; C6v; C∞v	zzz, zxx = zyy, xzx = yzy, xxz = yyz	–
${\chi }_{\mathit{spp}}^{(2)}$	yxz, yzx, yzz, yxx	D∞	–	xzy = −yzx, zxy = −zyx, xyz = −yxz

When molecules adsorb on an interface, they often do so with a preferred orientation relative the surface normal due to intermolecular forces, such as electrostatics, dipole-dipole interactions and hydrogen bonds. However, such interactions do not normally lead to long-range net directionality of the molecules within the x-y interfacial plane. In this case, the probed molecular groups in a sample would exhibit azimuthal isotropy with an average tilt angle, θ, at the interface. Such samples can be rotated by any angle around their z-axis (surface normal) without changing the value of the tensor elements. This is called C_∞ symmetry, for which it is easy to show that many of the ${\chi }_{\mathit{ijk}}^{(2)}$ tensor elements must be zero and the non-vanishing ones are the seven achiral elements ${\chi }_{\mathit{xxz}}^{(2)}={\chi }_{\mathit{yyz}}^{(2)},{\chi }_{\mathit{xzx}}^{(2)}={\chi }_{\mathit{yzy}}^{(2)},{\chi }_{\mathit{zxx}}^{(2)}={\chi }_{\mathit{zyy}}^{(2)},{\chi }_{\mathit{zzz}}^{(2)}$, and the six chiral elements ${\chi }_{\mathit{xyz}}^{(2)}=-{\chi }_{\mathit{yxz}}^{(2)},{\chi }_{\mathit{xzy}}^{(2)}=-{\chi }_{\mathit{yzx}}^{(2)},{\chi }_{\mathit{zxy}}^{(2)}=-{\chi }_{\mathit{zyx}}^{(2)}$. The six latter are the tensor elements with perpendicular directions for all the electric fields of the mixing beams, for which only samples with intrinsically chiral groups or chiral organizations of (coupled or uncoupled) achiral groups can have nonzero values.[91] A surface without such groups will have vertical mirror symmetry, C_∞v, in which case only the first seven achiral elements can be nonzero. However, biomolecules - such as proteins - often include chiral groups. The fact that it is possible to selectively probe the chiral vibrations with the psp, spp, or pps polarization combinations, may facilitate the assignment of detected spectral features and the structural analysis of such samples.[92–95] For instance, it has been shown that α-helices in several proteins and peptides exhibit achiral but not chiral signals in the amide I region, while β-sheets produce amide I signals in both the achiral and chiral polarization combinations.[92] If azimuthal isotropy (C_∞, C_∞v, or D_∞) is not part of the symmetry of the interface, or if the molecular groups have a preferred tilt angle at the interface, it can become possible for achiral molecular hyperpolarizabilities to contribute to the chiral macroscopic nonlinear susceptibility tensor elements. In such cases, macroscopic SFG chirality is not automatically synonymous to interfacial molecular chirality.

As mentioned above, the SFG susceptibility is a macroscopic sample property. However, there is a connection between ${\chi }_{\mathit{ijk}}^{(2)}$ and the microscopic hyperpolarizability, β_abc, of the vibrational modes of the individual molecules in the sample. β_abc is also a tensor with 27 tensor elements that scale with the change in polarizability and the transition dipole moment along the normal mode coordinate for the q^th vibrational mode.

$${\beta }_{\mathit{abc},q}\propto \frac{\partial {\alpha }_{ab}}{\partial Q_q}\frac{\partial {\overrightarrow{\mu }}_c}{\partial Q_q}$$ (13)

This means that a vibrational mode must be both Raman and IR active in order to have a nonzero β_abc,q and exhibit signal enhancement in a vibrational SFG spectrum. It also means that the relative strengths of the hyperpolarizability tensor elements of a vibrational transition can be estimated by quantum mechanical calculations of its change in polarizability and transition dipole moment.[96] This is often helpful for the interpretation of SFG spectra, [97–99] as the tensor elements of the nonlinear susceptibility probed in an SFG experiment can be described as a linear combination of β_abc,q according to eq. 14,

$${\chi }_{\mathit{ijk},q}^{(2)}=N{\sum }_{a,b,c}\langle R_{ia}{R}_{jb}{R}_{kc}\rangle {\beta }_{\mathit{abc},q}$$ (14)

where N is the number density of the probed molecules, while 〈 R_ia R_jb R_kc 〉 are elements from the average transformation matrices for rotating each β_abc,q element in the molecular coordinate system (x′, y′ and z′) onto the i, j, and k coordinates of the lab coordinate system (x, y, and z). As the probed effective susceptibility is a linear combination of the ${\chi }_{\mathit{ijk},q}^{(2)}$ elements, which in turn are a linear combination of β_abc,q, the line shape of a vibrational SFG spectrum is dictated by the line shape of the probed hyperpolarizabilities. When the SFG signal and the visible laser beam are far off-resonance from electronic transitions, the line shape of β_abc,q is a Lorentzian curve with a real and an imaginary component, plus a potential nonresonant background. The following function is then used in eq. 12 to fit the effective nonlinear susceptibility of an SFG spectrum,

$${\chi }_{\mathit{SFG}}^{(2)}={\chi }_{NR}^{(2)}+{\sum }_q\frac{A_q}{{\omega }_q-{\omega }_{IR}-i{\mathrm{\Gamma }}_q}$$ (15)

where ${\chi }_{NR}^{(2)}$ is the nonresonant contribution, A_q, Γ_q and ω_q are the amplitude, width and frequency of the q^th vibrational mode, and ω_IR is the frequency of the infrared beam. It can here be seen that the chemical specificity of vibrational SFG spectroscopy arises from a signal enhancement when the IR light matches a Raman and IR active vibrational mode that exhibits a net orientation at the interface.

$$\left(\begin{array}{ccc}{R}_{x{x}^{\prime }}& R_{x{y}^{\prime }}& R_{x{z}^{\prime }}\\ R_{y{x}^{\prime }}& R_{y{y}^{\prime }}& R_{y{z}^{\prime }}\\ R_{z{x}^{\prime }}& R_{z{y}^{\prime }}& R_{z{z}^{\prime }}\end{array}\right)=\left(\begin{array}{ccc}cos\psi & -sin\psi & 0\\ sin\psi & cos\psi & 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}cos\theta & 0& sin\theta \\ 0& 1& 0\\ -sin\theta & 0& cos\theta \end{array}\right)\left(\begin{array}{ccc}cos\varphi & -sin\varphi & 0\\ sin\varphi & cos\varphi & 0\\ 0& 0& 1\end{array}\right)$$ (16)

The matrices above include a rotation of ϕ (twist angle) around the molecular z′ axis, a rotation of θ (tilt angle) towards the lab z coordinate, and a rotation of ϕ (azimuthal angle) around the lab z coordinate. This represents the transformation from the molecular hyperpolarizability to the lab coordinate system mentioned above and the appropriate matrix elements that go into Eq. 14 are defined on the left-hand side. If we consider molecular groups with inherent C_2v symmetry, such as water or methylene groups, adsorbed at an interfaces with isotropic azimuthal and twist angles (i.e. C_∞v interfacial symmetry), the non-zero nonlinear susceptibility tensor elements for the sample will depend on the molecular tilt as described in eqs. 17–21.[56]

$${\chi }_{\mathit{zzz}}^{(2)}=N[\langle {cos}^3\theta \rangle {\beta }_{z^{\prime }{z}^{\prime }{z}^{\prime }}+{\beta }^{\prime }]$$ (17)

$${\chi }_{\mathit{xxz}}^{(2)}={\chi }_{\mathit{yyz}}^{(2)}=\frac{N}{2}\left[\langle {sin}^2\theta cos\theta \rangle {\beta }_{z^{\prime }{z}^{\prime }{z}^{\prime }}+\langle cos\theta \rangle ({\beta }_{x^{\prime }{x}^{\prime }{z}^{\prime }}+{\beta }_{y^{\prime }{y}^{\prime }{z}^{\prime }})-{\beta }^{\prime }\right]$$ (18)

$${\chi }_{\mathit{xzx}}^{(2)}={\chi }_{\mathit{yzy}}^{(2)}=\frac{N}{2}\left[\langle {sin}^2\theta cos\theta \rangle {\beta }_{z^{\prime }{z}^{\prime }{z}^{\prime }}+\langle cos\theta \rangle ({\beta }_{x^{\prime }{z}^{\prime }{x}^{\prime }}+{\beta }_{y^{\prime }{z}^{\prime }{y}^{\prime }})-{\beta }^{\prime }\right]$$ (19)

$${\chi }_{\mathit{zxx}}^{(2)}={\chi }_{\mathit{zyy}}^{(2)}=\frac{N}{2}\left[\langle {sin}^2\theta cos\theta \rangle {\beta }_{z^{\prime }{z}^{\prime }{z}^{\prime }}+\langle cos\theta \rangle ({\beta }_{z^{\prime }{x}^{\prime }{x}^{\prime }}+{\beta }_{z^{\prime }{y}^{\prime }{y}^{\prime }})-{\beta }^{\prime }\right]$$ (20)

$${\beta }^{\prime }=\frac{1}{2}\langle {sin}^2\theta cos\theta \rangle \left[{\beta }_{x^{\prime }{x}^{\prime }{z}^{\prime }}+{\beta }_{x^{\prime }{z}^{\prime }{x}^{\prime }}+{\beta }_{z^{\prime }{x}^{\prime }{x}^{\prime }}+{\beta }_{y^{\prime }{y}^{\prime }{z}^{\prime }}+{\beta }_{y^{\prime }{z}^{\prime }{y}^{\prime }}+{\beta }_{z^{\prime }{y}^{\prime }{y}^{\prime }}\right]$$ (21)

The uniform azimuthal and twist angles yield this limited set of equations; however, when such an assumption is invalid, the expressions have to be evaluated with the rotation matrices in Eq. 16 applied to Eq. 14. Depending on how many of the molecular hyperpolarizabilities are negligible and non-zero, respectively, Eqs. 17–21 can often be further simplified. For other molecules with C_3v symmetry, the number of independent tensor elements of the molecular hyperpolarizability is reduced to five or fewer. In the case of the asymmetric stretch of CH₃, there are only two non-vanishing independent elements: β_{z′z′ z′} and β_{x′ x′ z′} = β_{y′ y′ z′}. This has often been utilized to analyze the average orientation and organization of methyl groups in polymers, proteins, lipids and other small molecules.[100–104] The corresponding equations for the nonlinear susceptibility tensor elements in this case for molecules on an interface with C_∞v symmetry are

$${\chi }_{\mathit{zzz}}^{(2)}=N[\langle {cos}^3\theta \rangle ({\beta }_{z^{\prime }{z}^{\prime }{z}^{\prime }}+{\beta }_{x^{\prime }{x}^{\prime }{z}^{\prime }})+\langle cos\theta \rangle {\beta }_{x^{\prime }{x}^{\prime }{z}^{\prime }}]$$ (22)

$${\chi }_{\mathit{xxz}}^{(2)}={\chi }_{\mathit{yyz}}^{(2)}=\frac{N}{2}[\langle {cos}^3\theta \rangle ({\beta }_{x^{\prime }{x}^{\prime }{z}^{\prime }}-{\beta }_{z^{\prime }{z}^{\prime }{z}^{\prime }})+\langle cos\theta \rangle ({\beta }_{x^{\prime }{x}^{\prime }{z}^{\prime }}+{\beta }_{z^{\prime }{z}^{\prime }{z}^{\prime }})]$$ (23)

$${\chi }_{\mathit{xzx}}^{(2)}={\chi }_{\mathit{yzy}}^{(2)}={\chi }_{\mathit{zxx}}^{(2)}={\chi }_{\mathit{zyy}}^{(2)}=\frac{N}{2}[\langle {cos}^3\theta \rangle ({\beta }_{x^{\prime }{x}^{\prime }{z}^{\prime }}-{\beta }_{z^{\prime }{z}^{\prime }{z}^{\prime }})+\langle cos\theta \rangle {\beta }_{z^{\prime }{z}^{\prime }{z}^{\prime }}]$$ (24)

The effective susceptibilities probed by different polarization combinations include unique subsets of these tensor elements, as shown in Table 1. It is therefore possible to make ratios between signals acquired in different polarization combinations to remove the molecular number density (N) dependence and obtain an expression that only depends on θ and the tilt angle distribution.[104,105] For the case of the CH₃ vibrations shown above it is convenient to consider ${\chi }_{\mathit{SSP}}^{(2)}$ and ${\chi }_{\mathit{SPS}}^{(2)}$, for which the full expressions are

$${\chi }_{\mathit{SSP}}^{(2)}=L_{yy,\mathit{SFG}}{L}_{yy,\mathit{Vis}}{L}_{zz,IR}sin{\alpha }_{IR}{\chi }_{\mathit{yyz}}^{(2)}$$ (25)

$${\chi }_{\mathit{SPS}}^{(2)}=L_{yy,\mathit{SFG}}{L}_{zz,\mathit{Vis}}{L}_{yy,IR}sin{\alpha }_{\mathit{Vis}}{\chi }_{\mathit{yzy}}^{(2)}$$ (26)

where L_ii,j are the Fresnel factors for the respective beams and are α_j the incidence (or reflection) angles relative the surface normal, which is needed to get the z-components of the p-polarized IR and visible beams via sin α_j (cos α_j is needed for x-components). The calculated I_SSP/I_SPS ratios of the methyl group in acetonitrile for various tilt angles and angle distributions at a liquid/air interface was previously investigated with SFG.[100] The results showed that the sensitivity towards the molecular tilt angle is highly dependent on the width of the angle distribution. Therefore, without any knowledge of the approximate angle distribution, one may only be able to use the intensity ratio to determine maximum or minimum tilt angles. This means that one need to be careful when interpreting peak ratios from complex molecules, such as proteins, that may already in themselves have a rather wide distribution of the probed transition dipole moments. For instance, the χ_SSP/χ_SPS peak ratio of the asymmetric CH₃ stretch for lysozyme adsorbed onto polystyrene surfaces have been shown experimentally to not depend strongly on the bulk protein concentration (Figure 7).[101] One interpretation of this could be that the average methyl orientation for the protein on the surface does not significantly depend on protein concentration. Another interpretation that agrees with the data is that a wide angular distribution of the methyl groups in the protein yields a negligible tilt angle sensitivity. Therefore, it is good to use additional techniques that can complement the SFG analyses and help determine the orientation more accurately, which is discussed more below within the context of enzyme characterization at interfaces. Thereafter follows a section about phase-relations in SFG spectra, which also can be utilized for orientation analysis.

Figure 7.

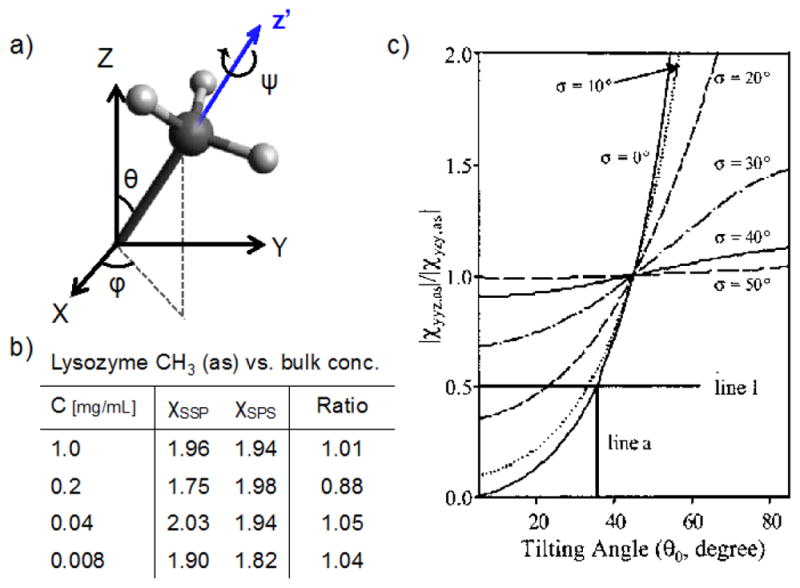
a) A model of a CH₃ group with the tilt (θ), azimuthal (φ) and twist (ψ) angles defined. b) Measured values of the asymmetric stretch vibration of CH₃ for lysozyme adsorbed at hydrophilic silica surfaces from different bulk concentrations. The error of the ratios is about 20 %. c) ${\chi }_{\mathit{yyz}}^{(2)}/{\chi }_{\mathit{yzy}}^{(2)}$ ratios for the CH₃ (as) vs. θ, assuming isotropic φ and ψ. If the gaussian distribution function for θ is broad, the tilt angle sensitivity is low, illustrating the difficulty to specifically identify one angle for complex macromolecules. The data are reprinted from ref [101], copyright 2003 American Chemical Society.

Enzymes immobilized on various substrates are used in a wide range of applications, such as biosensors, biofuel cells, and within the food industry. As unfavorable orientations of the enzyme and changes to its conformation can severely reduce its catalytic activity, much effort has been made to optimize the enzyme surface immobilization protocols to avoid these problems. However, analytical techniques with surface specificity that can confirm the enzyme conformation as well as its orientation are needed and SFG is an excellent technique for such investigations.[15,106–112] The ${\chi }_{\mathit{zzz}}^{(2)}/{\chi }_{\mathit{yyz}}^{(2)}$ ratio for the amide I peak has been used to calculate the approximate tilt and twist angles for enzymes on solid/liquid interfaces and the results for β-Gal are presented in Figure 8.[106] As can be seen, a unique tilt and twist angle that agree with the data cannot be identified, however, additional results from polarization sensitive attenuated total reflection-Fourier transform infra-red (ATR-FTIR) experiments narrow the range of possible angles significantly. It is worth noting that neither of these techniques is able to provide the twist and tilt angles with high precision by themselves, highlighting the advantage of using different techniques that can complement each other. The analysis takes into account the relative orientations of the various α-helices in the enzyme, based on the crystal structure, so the distribution of tilt and twist angles are somewhat accounted for. However, it may also be expected that the enzymes as complete units have a distribution of orientations at the interface and the tertiary conformation should be dynamic compared to the rigid crystal structure. This would likely broaden the tilt and twist angle distributions of the α-helices at the interface and thereby potentially skew the results. Nevertheless, the tilt and twist angles are in agreement with the expected outcome for the chosen approach used to immobilize the enzyme. A final comment is that the SFG experiment was performed at near total internal reflection, for which ${\chi }_{\mathit{zzz}}^{(2)}$ is the dominant tensor element of the protein amide I vibrations contributing to ${\chi }_{\mathit{PPP}}^{(2)}$, which is crucial to get the sensitivity needed for reliable conclusions.

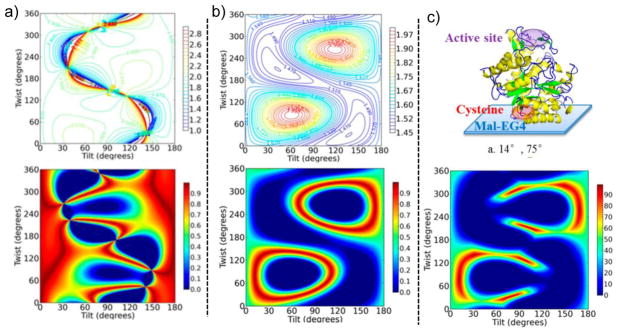
Figure 8.

a) Top: A color map of the ${\chi }_{\mathit{zzz}}^{(2)}/{\chi }_{\mathit{yyz}}^{(2)}$ ratio depending on the tilt and twist angles for an azimuthally isotropic distribution of the β-Gal enzyme with a V152C mutation. Bottom: Based on the measured ${\chi }_{\mathit{zzz}}^{(2)}/{\chi }_{\mathit{yyz}}^{(2)}$ ratio of 1.9, the orientation map has been color-coded 0 to 1 from worst to perfect fit with the top color map. b) The corresponding color maps for the ratio of s- and p-polarized ATR-FTIR measurements of the same interface. c) When combined, only a limited range of orientations give values that agree with both the SFG and ATR-FTIR data. The protein illustration shows one of the predicted orientations, given the data and the V152C mutation. Reprinted with permission from ref. [106], copyright 2013 American Chemical Society.

As the resonant contributions to the effective susceptibility are complex, they are all associated with an absolute, frequency-dependent, phase. The absolute value and subsequent squaring in Eq. 12 gives rise to cross-terms between the peaks in a spectrum, and the relative phases of vibrational modes close in frequency can thereby lead to quite complicated and unexpected line shapes. However, if the spectrum can be unambiguously fitted, these phase-relations can be very informative as they are dependent on the relative orientations for the various vibrational modes probed. Such fits may be done for spectra with low noise and high spectral resolution. However, the analysis can sometimes be challenging if the sample has off-resonance peaks and/or a nonresonant background, ${\chi }_{NR}^{(2)}$, which is often the case, in particular for samples with certain metal substrates. The difficulty is that the phase of these contributions relative the resonant vibrations is generally not known a priori and has only been determined for a limited range of samples. One example is C-H stretch vibrations on a gold surface. It has been shown that when the C-H transition dipole moments point along the positive direction of the lab z-coordinate the SFG amplitude is negative, which results in destructive interference with a nonresonant gold signal. Constructive interference occurs instead when they point in the negative z direction.[113–115] In this particular case, a strong ${\chi }_{NR}^{(2)}$ from a gold substrate can be useful for sorting out the approximate orientation of C-H species identified in spectra.

The square of the absolute value of χ⁽²⁾ in Eq. 12 also means that the orientations and phase information gained by fits and ratios of the effective susceptibilities exhibit an uncertainty of 180° and π, respectively. However, the absolute orientation can be accessible in certain cases. As mentioned above, the relation between a strong nonresonant background and the resonant modes can be sufficient to determine absolute orientations of molecules. Likewise, phase sensitive SFG spectroscopy (PS-SFG, also called heterodyne SFG) can be employed to determine the phase and absolute orientation of SFG active modes.[115–121] PS-SFG, furthermore, gives access to the imaginary and real parts of the SFG signal. In PS-SFG, the SFG signal of the sample is delayed and overlapped with a strong nonresonant SFG signal of a local oscillator (LO, often a gold mirror, a quartz crystal or a GaAs plate). Interference between the LO signal (E_LO) and the resonant SFG signal (E_R) is described by

$$I_{\mathit{SFG}}={\mid E_{LO}+E_R\mid }^2={\mid E_{LO}\mid }^2+{\mid E_R\mid }^2+E_R{E}_{LO}^{\ast }+E_R^{\ast }{E}_{LO}$$ (27)

$$E_R{E}_{LO}^{\ast }+E_R^{\ast }{E}_{LO}\propto {\chi }_{\mathit{SFG}}{A}_{LO}{e}^{i(\phi +\omega \tau )}+{\chi }_{\mathit{SFG}}^{\ast }{A}_{LO}{e}^{-i(\phi +\omega \tau )}$$ (28)

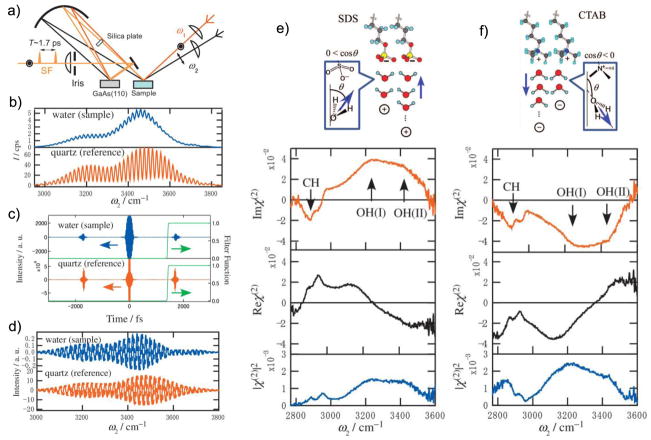
where A_LO is the amplitude of the LO field (E_LO), φ is the phase difference between the resonant SFG field (E_R) and E_LO at zero delay, while ωτ represents an additional phase for E_LO due to a delay of τ between the two signals. The cross terms on the right hand side of Eq. 27 represent the PS-SFG signal, which is enhanced by a strong LO signal. Inverse Fourier transformation of the SFG signal from the frequency domain into the time domain separates the cross terms by +τ and −τ, respectively, which allows selective filtering to isolate just one of the cross terms. After Fourier transforming the chosen cross term back to the frequency domain, the complex ${\chi }_{\mathit{SFG}}^{(2)}$ can be retrieved by division through the corresponding signal of a purely nonresonant spectrum (e.g. gold, quartz or GaAs), since it can be considered a constant that just contains the information of E_LO. Especially the imaginary part of the complex ${\chi }_{\mathit{SFG}}^{(2)}$ is useful, for example, to determine molecular orientations, as its sign for each resonant peak is independent of the wavenumber. However, deducing absolute molecular orientations with precision using this technique still requires knowledge of the molecular hyperpolarizability tensor elements. Figure 9 shows an early example of PS-SFG applied to water/air interfaces including surfactant molecules with different head group charge.[115] The time delay (τ = 1.7 ps) between the SFG signal and the LO signal was achieved via a sequential setup between the sample and LO reference, which resolved issues with unstable phase relations between them. This allowed identifying a sign switch of the complex water resonance peaks relative the surfactant CH vibrations when switching from sodium dodecyl sulfate (SDS) to cetyltrimethylammonium bromide (CTAB). This is due to different orientations for the water molecules, induced by electrostatic interactions with the negatively and positively charged head groups, respectively.

Figure 9.

a) A setup for PS-SFG. A concave mirror ensures that the Vis, IR and SFG beams from the sample are refocused onto the LO and that the SFG signal and the LO signal are collinear. The silica plate induces a delay of 1.7 ps between SFG and LO signals. b and c) A frequency domain interferogram is obtained, which can be Fourier transformed into the time domain where one of the interference terms (in this case at +1.7 ps) can be selected by filtering. d) Transforming back to the frequency domain yields the real (solid) and imaginary (dashed) interferograms. Division of the sample signals by the nonresonant reference yields the clean spectra. e and f) The real and imaginary parts of the water vibrations flip in sign relative the CH_X stretches when switching from SDS to CTAB surfactants at liquid/air interfaces as the head-group charge induces different water orientations. Reprinted with permission from ref. [115], copyright 2009 American Institute of Physics Publishing.

Water is a molecule that has been extensively studied with vibrational methods for a long time, as it is one of the key molecules enabling life on earth. Since the development of the interface specific vibrational SFG spectroscopy, a deeper understanding of the behavior of water molecules at interfaces has been achieved. Consequently, water has been one of the main topics of SFG research. SFG spectroscopy revealed the presence of free OH bonds at the air/vapor interface. Dangling OH modes, located near 3700 cm⁻¹, lead to the conclusion that a free, unbound OH group must be pointing out of the water surface into the vapor.[122] In the following years, water interfaces – water/detergent, water/lipid, water/quartz and many more – have been explored and published. Phase Sensitive (heterodyne) SFG spectroscopy has been used to extract the imaginary part of the complex SFG signal to obtain more information about the orientation and structure of water molecules at interfaces.[120] In addition to PS-SFG, pump-probe SFG spectroscopy has been employed to understand water reorientation dynamics. 2D SFG spectroscopy has, furthermore, provided information on the couplings of vibrational modes for water molecules at interfaces. Recently, the phenomenon of a quasi-liquid layer at the ice surface, first described by Faraday in 1859, has been studied with SFG spectroscopy and experimental and theoretical evidence for bilayer-by-bilayer surface melting of crystalline ice have been presented.[123]

In summary, SFG has high interfacial specificity and sensitivity, and detailed information may be extracted from spectra due to the selection rules and phase-relations discussed above. It is an increasingly popular tool for analysis of biomolecules at interfaces. The technique has been used to probe the orientation and structure of proteins[124–133] as well as protein fiber formation at interfaces, [134–136] the phase transitions and vanishing asymmetries via flip-flopping in supported lipid bilayers, [137–139] the surface chemistry of functionalized nanoparticles, [140,141] the orientation and hybridization of DNA at interfaces, [142–145] the signatures of molecular substrates through living cells, [146–148] and many other systems of biological relevance.[13–15] SFG has also been used for imaging, [149–151] with similar virtues as in SHG imaging, but with contrast for specific chemistries. Recently, a collinear heterodyne setup capable of PS-SFG microscopy was reported, which can be used to characterize spatially heterogeneous surfaces and get local molecular orientations with relatively high resolution.[152] While SFG in reflection or transmission mode cannot readily probe interfaces in three-dimensional environments that are isotropic on long scales, which is the case for many types of biomaterials, signals may still be produced via scattering processes. This is the topic of the next and final section of this introduction into the theory and application of nonlinear optics for interfacial and structural analysis.

Nonlinear Scattering Mode

Both SHG and SFG can be performed in the scattering mode, [43,44] abbreviated SHS and SFS respectively, which allows spectroscopic investigation of ordered regions and interfaces of scattering structures in bulk environments. This can be done even for centrosymmetric structures that are isotropically arranged, such as spherical particles in suspension for which there are numerous examples in the scientific literature.[45,46,153–177] For instance molecular adsorption onto gold nanoparticles been monitored with SHS, [165,166] as well as the molecular transport across liposome bilayers.[157–159] An example for SFS is the orientation and state of water at hydrophobic interfaces.[172–174] There are two key principles that make this possible. The first is a phase-shift for the mixing beams across the scattering object due to a difference in path length at angles away from the phase-matched direction, which ensures that signals from molecular groups with opposite orientations on either side of the object will not completely cancel each other out in the far field. Figure 10 illustrates an example of this for spherical structures. The second principle is that the scattered signal is typically detected at an angle away from the phase-matched direction, which reduces the coherence length significantly. This means that a higher concentration of scatterers is allowed before they coherently start to cancel each other out due to an average spacing that is shorter than the coherence length between them. Signal production still requires local ordering of the probed vibrational modes that add up coherently, leading to a quadratic dependence on the number density of molecules per scattering object. However, there is a linear dependence on the scattering object concentration, up to the point where they get closer to each other than the coherence length. Qualitatively, the connection between SHG and SHS is similar to the connection between SFG and SFS. Therefore, only the latter case will be discussed below.

Figure 10.

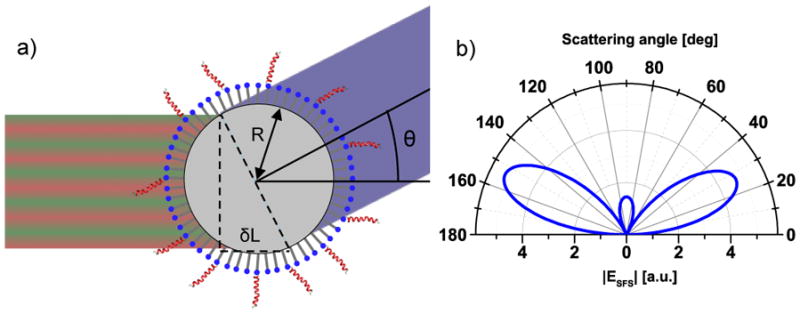
a) At a scattering angle away from the phase-matched direction, the travelling distances for the three mixing beams on either side of the spherical particle are slightly different, which yields a phase-shift across the particle diameter. The difference in traveling distance (δL) for the IR and visible beams is here illustrated for the two opposite sides perpendicular to the scattering angle; however, the integrated contributions from the particle surface has to be considered. b) The angular scattering pattern is dependent on factors such as particle size and shape, molecular orientation, and the angle between the excitation beams. A simulated pattern for achiral signals from spherical particles is shown, for which strong signals are precluded in the phase-matched direction (0°).

For the case where molecules on the interface of particles are probed, the tensor elements of the effective susceptibility for SFS (for which the symbol ${\mathrm{\Gamma }}_{\mathit{ijk}}^{(2)}$ is used) will be a linear combination of the effective susceptibilities for SFG on a corresponding planar interface with the molecules oriented similarly relative the surface normal.[46,167,168] In other words, it is possible to use equations similar to the ones for SFG to fit SFS spectra.

$$I_{\mathit{SFS}}\propto {\mid P_{\mathit{SFS}}\mid }^2={\left|{\epsilon }_0{\mathrm{\Gamma }}_{\mathit{SFS}}^{(2)}{E}_{{\omega }_{\mathit{Vis}}}{E}_{{\omega }_{IR}}\right|}^2$$ (29)

$${\mathrm{\Gamma }}_{\mathit{SFS}}^{(2)}={\mathrm{\Gamma }}_{NR}^{(2)}+{\sum }_q\frac{A_q}{{\omega }_q-{\omega }_{IR}-i{\gamma }_q}$$ (30)

A theoretical framework for calculating the expected SFS scattering patterns and relative signal strengths of various polarization combinations has been developed for arbitrarily shaped particles.[167] However, the common spherical case will be focused on here. For a particle with spherical symmetry, it is natural to define the tensor elements of its effective susceptibility in terms of components perpendicular and parallel to the particle surface. Different subsets of these tensor elements will be probed, depending on the polarization combination in the experiment. If the polarization states are defined as p for electric fields within the incidence plane of the visible and IR beams and s for electric fields perpendicular to this plane, the four non-zero achiral effective susceptibilities for spherical particles are ${\mathrm{\Gamma }}_{\mathit{ppp}}^{(2)},{\mathrm{\Gamma }}_{\mathit{ssp}}^{(2)},{\mathrm{\Gamma }}_{\mathit{sps}}^{(2)}$ and ${\mathrm{\Gamma }}_{\mathit{pss}}^{(2)}$. They can be expressed as, [168]

$${\mathrm{\Gamma }}_{\mathit{ppp}}^{(2)}=cos\left(\frac{\theta }{2}\right)cos\left(\frac{\theta }{2}-\alpha \right)cos(\frac{\theta }{2}-\alpha +\beta ){\mathrm{\Gamma }}_1+cos(\theta -\alpha +\beta )cos\left(\frac{\theta }{2}-\alpha \right){\mathrm{\Gamma }}_2+cos(\theta -a)cos\left(\frac{\theta }{2}-\alpha +\beta \right){\mathrm{\Gamma }}_3+cos(\beta )cos\left(\frac{\theta }{2}\right){\mathrm{\Gamma }}_4$$ (31)

$${\mathrm{\Gamma }}_{\mathit{ssp}}^{(2)}=cos\left(\frac{\theta }{2}-\alpha \right){\mathrm{\Gamma }}_2$$ (32)

$${\mathrm{\Gamma }}_{\mathit{sps}}^{(2)}=cos\left(\frac{\theta }{2}-\alpha +\beta \right){\mathrm{\Gamma }}_3$$ (33)

$${\mathrm{\Gamma }}_{\mathit{pss}}^{(2)}=cos\left(\frac{\theta }{2}\right){\mathrm{\Gamma }}_4$$ (34)

where θ and α are the angles for the detected SFS signal and the incidence IR laser beam relative the phase-matched direction, while β is the angle between the IR and visible laser beams. Various combinations of the effective susceptibility tensor elements are included in the gamma-factors, which are defined as ${\mathrm{\Gamma }}_1={\mathrm{\Gamma }}_{\perp \perp \perp }^{(2)}-{\mathrm{\Gamma }}_{\Vert \Vert \perp }^{(2)}-{\mathrm{\Gamma }}_{\Vert \perp \Vert }^{(2)}-{\mathrm{\Gamma }}_{\perp \Vert \Vert }^{(2)},{\mathrm{\Gamma }}_2={\mathrm{\Gamma }}_{\Vert \Vert \perp }^{(2)},{\mathrm{\Gamma }}_3={\mathrm{\Gamma }}_{\Vert \perp \Vert }^{(2)}$, and ${\mathrm{\Gamma }}_4={\mathrm{\Gamma }}_{\perp \Vert \Vert }^{(2)}$. These gamma-factors can conveniently be connected to the ${\chi }_{\mathit{ijk}}^{(2)}$ elements for a flat surface geometry using the following matrix representation:[168]

$$\left(\begin{array}{c}{\mathrm{\Gamma }}_1\\ {\mathrm{\Gamma }}_2\\ {\mathrm{\Gamma }}_3\\ {\mathrm{\Gamma }}_4\end{array}\right)=\left(\begin{array}{cccc}2F_1-5F_2& 0& 0& 0\\ F_2& 2F_1& 0& 0\\ F_2& 0& 2F_1& 0\\ F_2& 0& 0& 2F_1\end{array}\right)\left(\begin{array}{c}{\mathrm{\chi }}_1\\ {\mathrm{\chi }}_2\\ {\mathrm{\chi }}_3\\ {\mathrm{\chi }}_4\end{array}\right)$$ (35)

where ${\mathrm{\chi }}_1={\mathrm{\chi }}_{\perp \perp \perp }^{(2)}-{\mathrm{\chi }}_{\Vert \Vert \perp }^{(2)}-{\mathrm{\chi }}_{\Vert \perp \Vert }^{(2)}-{\mathrm{\chi }}_{\perp \Vert \Vert }^{(2)},{\mathrm{\chi }}_2={\mathrm{\chi }}_{\Vert \Vert \perp }^{(2)},{\mathrm{\chi }}_3={\mathrm{\chi }}_{\Vert \perp \Vert }^{(2)}$, and ${\mathrm{\chi }}_4={\mathrm{\chi }}_{\perp \Vert \Vert }^{(2)}$. The factors inside the square matrix are form factor functions that connect the planar geometry to the spherical geometry via the scattering vector norm, q, and the radius, R, of the particle, [168]

$$F_1=2\pi i\left(\frac{sin(qR)}{{(qR)}^2}-\frac{cos(qR)}{qR}\right)$$ (36)

$$F_2=4\pi i\left(3\frac{sin(qR)}{{(qR)}^4}-3\frac{cos(qR)}{{(qR)}^3}-\frac{sin(qR)}{{(qR)}^2}\right)$$ (37)

$$q=\Vert \overrightarrow{q}\Vert =2\Vert {\overrightarrow{k}}_0\Vert sin\left(\frac{\theta }{2}\right)$$ (38)

where k⃗₀ is the wave vector for a signal in the phase matched direction, while θ and q⃗ are the scattering angle and scattering vector away from this direction.

Eqs. 31–38 connect the effective susceptibilities probed in SFS experiments with the tensor elements for the corresponding situation on a planar interface. As discussed in the previous section about SFG, the χ_i elements in Eq. 35 can ultimately be described as linear combinations of the molecular hyperpolarizabilities, with factors that depend on the average molecular orientation relative the surface normal. For the case where achiral molecules exhibit rotational isotropy around their molecular axis as well as around the surface normal of the structure they are adsorbed to, the χ_i factors above depend on the molecular tilt θ as[168]

$$\left(\begin{array}{c}{\mathrm{\chi }}_1\\ {\mathrm{\chi }}_2\\ {\mathrm{\chi }}_3\\ {\mathrm{\chi }}_4\end{array}\right)=\frac{N\langle cos\theta \rangle }{2}\left(\begin{array}{cccc}5D-3& 0& 0& 0\\ 1-D& 2& 0& 0\\ 1-D& 0& 2& 0\\ 1-D& 0& 0& 2\end{array}\right)\left(\begin{array}{c}{\mathrm{\beta }}_1\\ {\mathrm{\beta }}_2\\ {\mathrm{\beta }}_3\\ {\mathrm{\beta }}_4\end{array}\right)$$ (39)

where N is the molecular number density and D is the ratio 〈 cosθ 〉³/〈 cosθ 〉. The beta-factors are defined as ${\beta }_1={\beta }_{\mathit{ccc}}^{(2)}-{\beta }_2-{\beta }_3-{\beta }_4,{\beta }_2=\left({\beta }_{\mathit{aac}}^{(2)}+{\beta }_{\mathit{bbc}}^{(2)}\right)/2,{\beta }_3=\left({\beta }_{\mathit{aca}}^{(2)}+{\beta }_{\mathit{bcb}}^{(2)}\right)/2$, and ${\beta }_4=\left({\beta }_{\mathit{caa}}^{(2)}+{\beta }_{\mathit{cbb}}^{(2)}\right)/2$. From this, it becomes clear that if the relative strengths of the hyperpolarizability tensor elements are known, SFS can be used to probe the average tilt of molecules at the interfaces of spherical structures by measuring the relative strengths of the effective susceptibilities in different polarization combinations. Figure 11 shows theoretical calculations of this for water molecules and CH₃ groups adsorbed on a particle with a 500 nm radius.[168]

Figure 11.

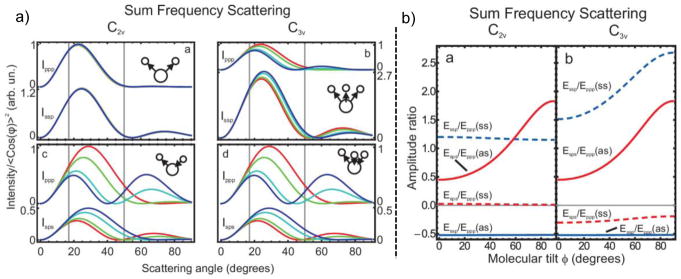
a) The scattering pattern for water (C_2v symmetry) and CH₃ (C_3v symmetry) depend on the specific vibration (symmetric vs. asymmetric stretch), the polarization combination, and the molecular orientation on the particle (R = 500 nm) surface. The tilt angles in the simulations are 0° (blue), 30° (cyan), 60° (green), and 90° (red). b) The ratio between signals in different polarization combinations can be used to identify the molecular tilt angle; however, certain combinations have poor sensitivity. Reprinted with permission from ref [168], copyright 2010 American Institute of Physics.

The model above only deals with achiral signals, but the effects of chiral vibrations have also been determined for spherical particles.[166] The details will be omitted here, but one key point to be mentioned is that chiral ${\chi }_{\mathit{ijk}}^{(2)}$ elements map onto chiral ${\mathrm{\Gamma }}_{\mathit{ijk}}^{(2)}$ elements. For geometries where the incidence IR and visible beams as well as the scattered SFS signal are all in one plane, one can therefore selectively probe the chiral components by selecting the appropriate polarization combinations, just as in regular SFG experiments. Also, the dependence on the incidence angles of the visible and IR beams is different for chiral and achiral vibrations. It has been shown theoretically that by increasing the angle between the incoming beams from 5° to 45°, the chiral/achiral ratio of the in-plane SFS signals can increase by an order of magnitude or more.

Recently, emulsions of water nanodroplets in hydrophobic solvents were studied with SFS.[174] It was shown that the D₂O spectra for the nanodroplets significantly differ from the corresponding spectra for planar surfaces (Figure 12). Specifically, the peak at 2370 cm⁻¹ that signifies more strongly H-bonded water is higher in SFS relative the peak at 2500 cm⁻¹, when compared to the SFG results for the planar geometry. In other words, the curvature of the droplets must be associated with a phenomenon that facilitates strong H-bonding for water. Additionally, the peak at 2745 cm⁻¹ observed with SFG for the planar geometry is not observable for the nanodroplets. This peak corresponds to free OD groups that are not H-bonded. The absence of this feature may be due to H-bonding with the surfactant used to stabilize the droplets; however, it was shown that this interaction cannot explain the increase in strongly H-bonded water at 2370 cm⁻¹.

Figure 12.

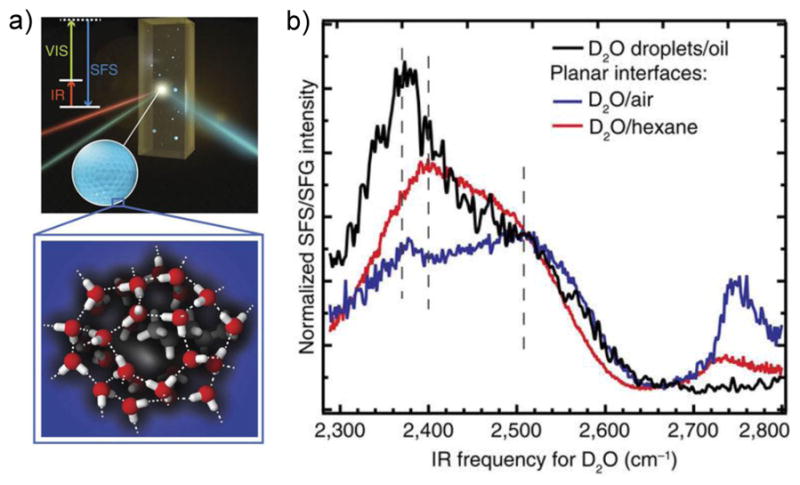
a) Schematic of a SFS experiment of water nanodroplets in oil. b) The spectral features for the D₂O stretch vibrations of water nanodroplets in hydrophobic environments (black) are distinct from the corresponding data of planar interfaces (blue and red). The nanodroplets have more of strongly H-bonded vibrations appearing at ~2370 cm⁻¹ and they lack the free OD groups at ~2745 cm⁻¹. Reprinted with permission from ref. [174], copyright 2017 Nature Publishing Group.

So far, few SFS studies on samples of biological relevance have been made. However, it has been shown that lipid monolayers on hydrophobic particles and liposomes with transmembrane asymmetry can produce SFS signals, [174–178] and that the inherent ordering of collagen fibers leads to very large SFS cross-sections.[178] This, together with the readily demonstrated capacity to probe the surface chemistry of colloidal interfaces, makes vibrational SFS an exciting potential tool for detailed investigation of biomaterial structures and interfaces in biological environments.

Summary

The range of NLO methods available today provide a powerful approach to obtaining detailed information about the molecular structure and surface chemistry of a wide range of biological materials. In this article the strengths and limitations of MPEF, SHG, CARS, SRS and SFG were discussed along with a description of the key theoretical principles and data analysis methods used to apply these methods in biological studies. Significant advances in methods to analyze NLO spectra and images that has occurred in recent years has allowed characterization of increasingly complex biological systems. Some key features to consider when selecting a particular NLO method to use for studying a biological system include spatial resolution, chemical/molecular specificity and interface/surface specificity of that method. For example, MPEF provides good depth resolution for confocal imaging of biological materials, but only has limited chemical/molecular specificity and no interface/surface specificity. CARS and SRS provide good imaging with chemical/molecular specificity, but no interface/surface specificity. SHG and SFG provide excellent interface/surface specificity and can be employed in different modes (e.g., reflection mode for characterizing planar surfaces and scattering mode for characterizing particles in solution). The vibrational spectroscopy aspect of SFG provides good chemical/molecular specificity to go along with the interface/surface specificity.