Correlation between small-volume spinal cord doses for spine stereotactic body radiotherapy (SBRT)

Abstract

Purpose

Doses to small spinal cord isodose volume (such as those ranging from Dmax 0.0 cc to 0.5 cc) as well as to large volumes (such as those ranging from 0.5 cc to 3.0 cc) are critical parameters to guide safe practice of spine SBRT. We here report a mathematical formula that links the most probable dose volume limits together for common spine SBRT cases.

Methods and materials: A dose ripple formula parameterized with equivalent dose radius (EDR) was derived to model spinal cord small-volume doses for a spine SBRT treatment. A cohort of spine SBRT cases (n=68), treated with either a robotic x-band linac or a conventional S-band linac, was selected to verify the model predictions. The mean prescription dose was 22± 4 Gy (range, 12-40 Gy) delivered in 2±1 fractions. The mean and median target volume was 39.4±42.5 cc and 30.3 cc (range, 0.24-264.2 cc), respectively. Direct correlations between the spinal cord Dmax and variable spinal cord doses of increasing isodose volumes (ranging from 0.0 cc to 3.0 cc) of different planning organ-at-risk volumes (PRVs) were investigated. The PRV structures for the study included the true cord, thecal sac and the true cord plus variable margins ranging from 1.0 mm to 3.0 mm.

Results

No direct linear correlation was observed amongst the small volume doses to the spinal cord PRVs. However, strong linear correlations (R² > 0.96) for all the studied PRVs were observed when correlating EDRs amongst isodose volumes ranging from 0.0 cc to 3.0 cc. In particular, EDR dependence was found to differ significantly for the thecal sac versus the spinal cord with or without 1-3 millimeter margins. With strong EDR correlation, the most probable relationship among the small-volume dose limits was derived for the spinal cord PRVs.

Conclusion

An analytical formula linked the most probable pin-point/small isodose volume doses with relatively large isodose volume doses of the spinal cord for spine SBRT. As a result, a small number of dose limits such as Dmax or D(0.35cc) are likely sufficient to surrogate the spinal cord dose tolerance for consistent treatment planning optimization and outcome analysis.

Introduction

Spine stereotactic body radiation therapy (SBRT) has been rapidly expanding in de novo and re-irradiation settings with respect to both metastatic and benign tumors [1-8]. One of the key challenges of spine SBRT is to maximally spare the spinal cord, which is often adjacent to the planning target volume (PTV). In most cases, a sharp dose fall-off is demanded from the target across the spinal cord in order to achieve optimal sparing [9-11]. This leads to a significantly inhomogeneous dose deposition within the spinal cord volume, which results in large variations between the point maximum dose (Dmax) and the doses encompassing finite hot-spot isodose volumes such as D(0.1 cc) to D(1.0 cc) [12]. Various approaches of limiting spinal cord dose have thus been reported for treatment planning optimization as well as outcome analysis[13].

Some multi-institutional studies have adopted the thecal sac as a surrogate for the planning-organ-at-risk volume (PRV) [5, 9, 11, 14, 15]. Other studies have adopted dose to small isodose volumes (for example, D(0.1 cc) or D(0.35 cc) of the true spinal cord with no PRV as the critical dose volume limits [16-18]. The question arises as to whether a single or a few number of dose-volume limits would be sufficient to surrogate the full spinal cord dose tolerance. In particular, a large volume of the spinal cord may receive a significant dose during treatment; there is uncertainty in how to specify other dose-volume limits such as doses to 0.35 cc, 1.0 cc, and 2.0 cc without causing conflictive and/or suboptimal treatments.

The fundamental question to these concerns is whether the most probable dose volume limits of small volume irradiation (such as Dmax or D(0.35 cc)) can be linked to relatively large volume irradiation (such as D(0.5 cc) or D(1.0 cc) etc.). The goal of this study is therefore to investigate whether such a relationship exists, and if so, its correlative power as well as its mathematical expression and implication on the PRV selections.

Materials and Methods

Modern spine SBRT treatments are predominantly administered with the robotic X-band linear accelerator (i.e., CyberKnife SBRT) or the conventional S-band linear accelerator (i.e. Linac-based SBRT)[7, 18, 19]. For the current study, a cohort of 68 patients treated with spine SBRT were randomly selected and analyzed (n = 42 for linac-based SBRT and n = 26 patients for CyberKnife SBRT). A mean dose of 22 ± 4 Gy (ranging 12-40 Gy) in 2±1 fractions (ranging from 1 to 5) was prescribed for the studied cases. The mean prescription isodose value was 87.7±9.7%. The prescription isodose volume (encompassed at least 95% of the target volume) was 51.2±50.8 cc (range 0.4 cc to 298.4 cc), and the planning target volume was 39.4±42.5 cc with contoured thecal sac volume of 18.8±43.3 cc (range 4.4 cc to 68.1 cc).

The spinal cords for all the cases were located in the vicinity of the PTV in the peripheral dose fall-off region. The thecal sac was investigated first as the volume of reference for the current study based on the previous publication [15]. Subsequently, true cord and variable margin-expanded (e.g. 1 mm, 2 mm and 3 mm margins) cord volumes were obtained and analyzed for comparisons.

Both robotic and linac-based SBRT treatment techniques of our institutions have been extensively reported in the literature[9, 16, 20, 21]. In short, robotic treatments used near real-time 2D stereoscopic imaging to guide treatment setups and the treatment utilized 100 to 300 non-isocentric beams to produce a conformal dose distribution surrounding a target volume. In contrast, linac-based spine SBRT treatments primarily apply 3D volumetric cone-beam CT imaging coupled with a rigid body fixation device for treatment setups. The delivery of linac-based SBRT used either fixed intensity modulated or rotational volume modulated arc beams.

To determine the most probable relationship among the small-volume PRV dose limits for a spine SBRT treatmentt, we introduced an Equivalent Dose Radius (EDR) to convert a non-uniform expanding isodose surfaces from a target to concentric expanding dose surfaces similar to a ripple radiation. The EDR is defined as follows,

(1).

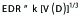
where V is a peripheral isodose volume surrounding an irradiated target volume for a given dose level D [22], and k is a constant dependent on the shape of the target. For example, k = (3/(4Π))^1/3 = 0.6 for a spherical volume and k = (1/(nΠ))^1/3 for a cylindrical volume, where n is a scaling factor given as the ratio of its length and base radius (Figure 1). Despite variable k values, if we normalize EDR with a reference EDR₀, then the dependence of k is eliminated.

Figure 1.

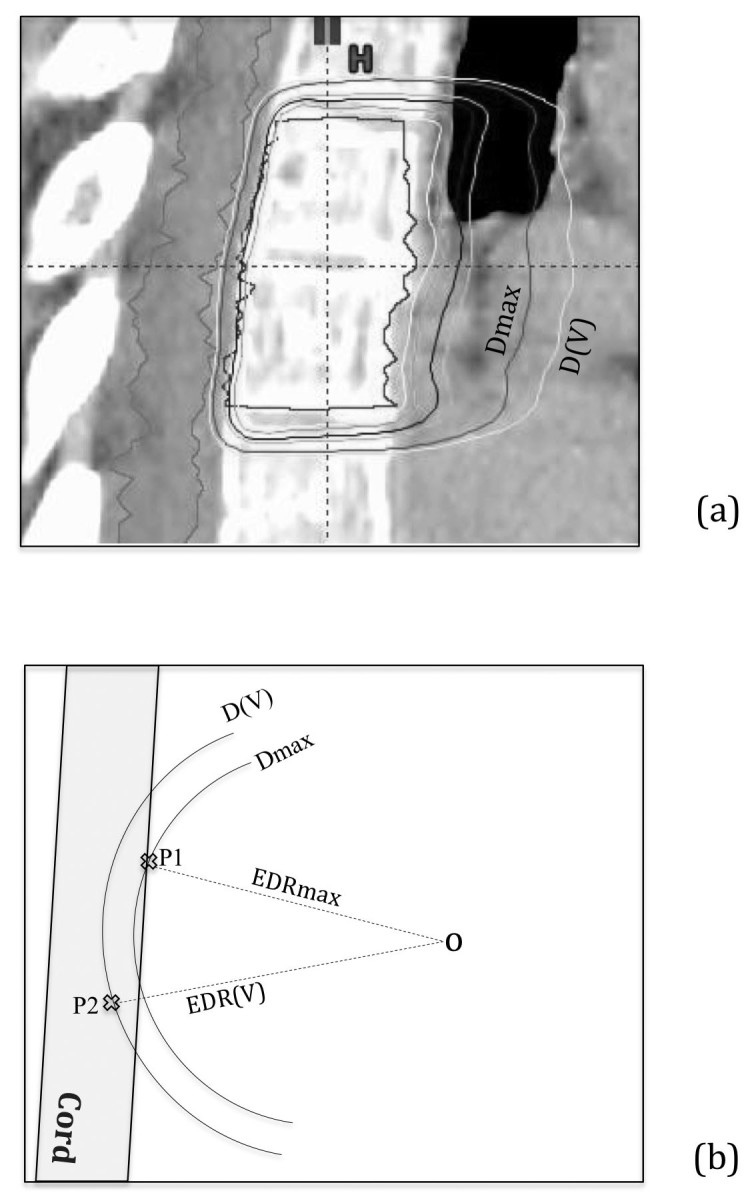
Schematic illustration of the EDR definition: (a) shows a clinical case with the peripheral isodose surface corresponds to the spinal cord Dmax value and another corresponds to small-volume D(V) such as D(0.3 cc) etc. and (b) illustrates the corresponding EDR parameters including Dmax of the spinal cord for the case.

Furthermore, if a reference EDR₀ is taken as the equivalent dose radius for isodose volume (V₀) at the dose of (D₀), then Equation (1) for the most probable EDR and D values can be rendered as

(2).

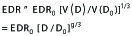
In the second step of Equation 2, general mean dose fall-off model of our previous publication[22] was applied, i.e., the peripheral isodose volume V(D) and its corresponding isodose level D is described as follows,

(3).

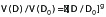
where γ≠ 0 is an empirical parameter. In the above derivations of Equation 2 and 3, it is assumed that the spinal cord is located in the peripheral dose fall-off region of the target without overlaps. For such cases, γ= -1.5 (i.e. λ = 2) following the inverse square law from the previous publication [22].

Furthermore, if we let the small-volume dose (D) inside the PRV correspond to the peripheral isodose surface of the same value (For example, if D_max = 14 Gy for the spinal cord PRV, then EDR_max would correspond to the 14-Gy isodose volume, and if D(0.1 cc) = 13 Gy, then EDR(0.1 cc) would correspond to the 13-Gy isodose volume, etc.) , and we can further substitute EDR₀=EDR_max and D₀=D_max and solving for EDR/EDR_max via Equation 2, then we have ,

(4).

where λ is a fixed parameter, i.e., λ = 3/γ. Note that if the most probable EDR/EDR_max value can be reliably estimated from the mean EDR/EDR_max value over the studied cases, then the most probable D versus D_max relationship would be also established.

For the current study, EDRs of variable isodose volumes (from EDRmax to EDR(3 cc) of the spinal cord PRVs (e.g., thecal sac, cord, cord plus 1 mm to 3 mm margin) were extracted and computed for each case. Dose and EDR values at finite volumes (ranging from 0.1 cc to 3.0 cc) for all structures were fitted via linear regression analysis. The goodness of the fit and confidence intervals on the fitting parameters were analyzed for thecal sac, cord and cord with expanded margins for 1 mm to 3 mm.

Results

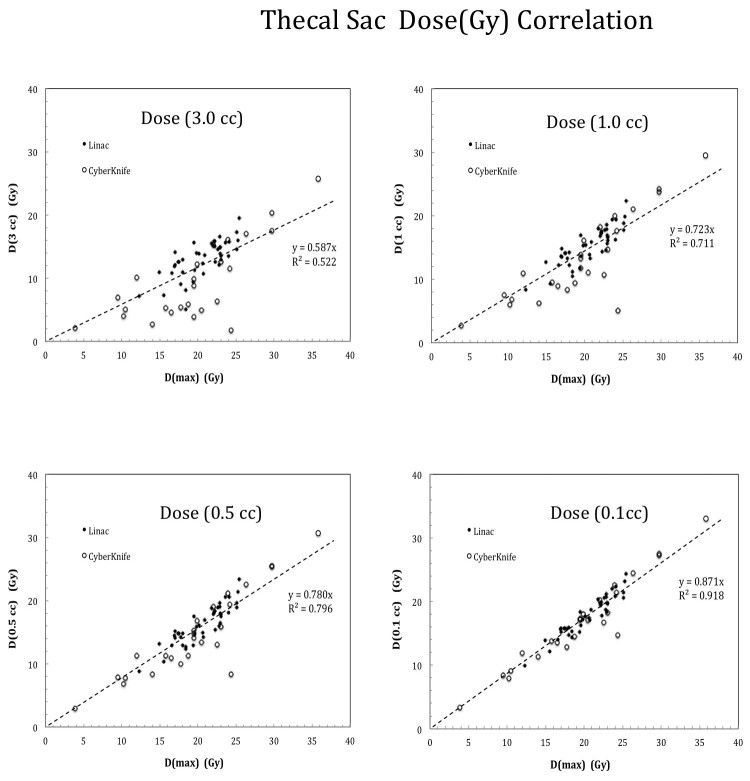
Figure 2 shows the direct correlation results for the thecal sac point Dmax versus doses at variable hot-spot isodose volumes. Note that Dmax = D(0 cc) by definition. As shown in Figure 2, D(0.1 cc) or smaller volume dose parameters correlated somewhat with the Dmax due to near neighborhood approximation. However, such an effect degraded rapidly with increasing isodose volumes. For example, R² = 0.918, 0.796, 0.711, 0.522 for D(0.1 cc), D (0.5 cc), D(1.0 cc) and D (3.0 cc) , respectively. Both Linac-based and Cyberknife cases (except some outliers) followed similar trend of dependence as shown in Figure 2. As a result, direct linear correlation could not be used to estimate the most probable small-volume dose limits from the studied cases.

Figure 2.

Dose correlation results for the thecal sac at variable isodose volumes from 0.1 cc to 3.0 cc. Relatively strong correlation (R²=0.918) was observed for small isodose volume such as 0.1 cc due to the near-neighborhood effect while significantly weaker correlation was seen for large isodose volumes such as R²=0.522 at 3.0 cc instead.

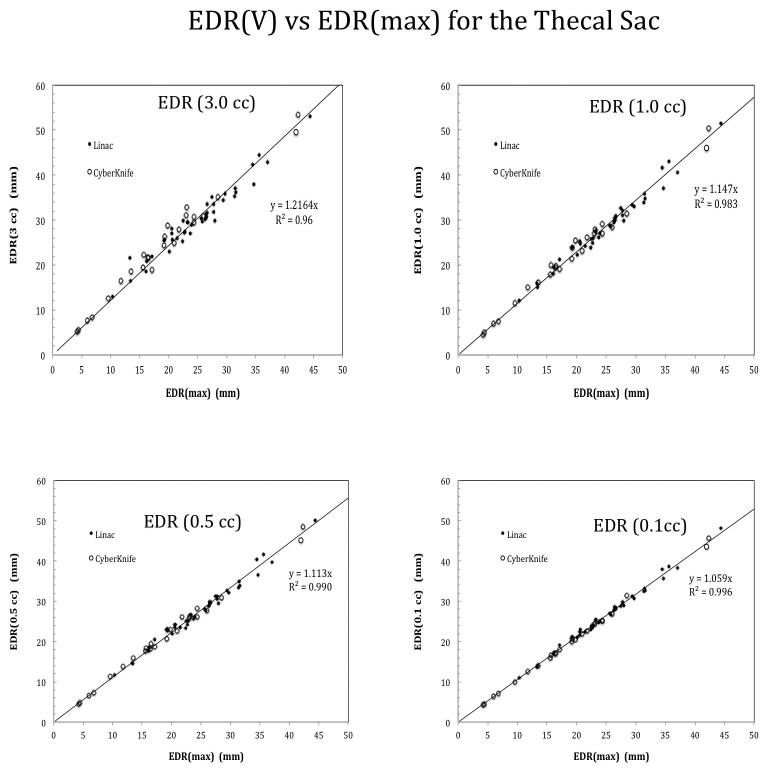
In contrast, strong EDR correlation (R²> 0.96) across the isodose volumes from EDR(0.0 cc) or EDRmax (the maximum dose point) up to EDR(3.0 cc) as shown in Figure 3. Furthermore, the slope (S) of the fitted line increases with increasing isodose volumes. Based on the mean S values, the most probable D_max versus D relationship was derived via Equation 4. No statistically significant difference in the slope values was detected via t-scores between the robotic Cyberknife and conventional linac treated cases for all the isodose volumes, e.g., p=0.20, 0.40, 0.45, 0.92 corresponding to EDR(0.1 cc), EDR(0.5 cc), EDR(1.0 cc) and EDR(3.0 cc) , respectively.

Figure 3.

EDR correlation results at variable isodose volumes ranging from 0.1 cc to 3.0 cc. Note that a strong correlation with R² > 0.98 was observed for isodose volumes up to 1.0 cc regardless Cyberknife or linac-based treatments.

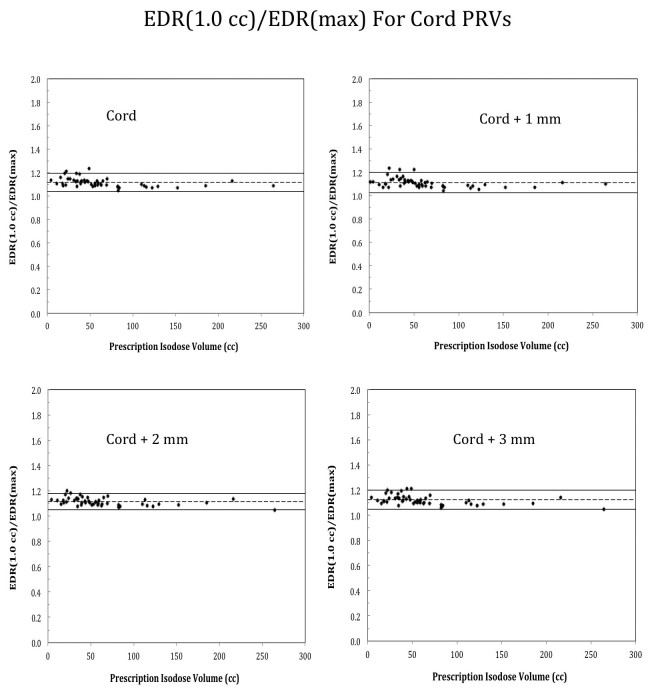
In addition, EDR correlations were similarly observed for the cord and PRVs consisting the cord plus 1 to 3 mm margins. This is illustrated in Figure 4, where EDR(1.0 cc)/EDRmax value is shown for the cord plus 1-3 mm margin respectively. Note that the mean EDR(1.0 cc)/EDRmax agreed excellently for variable margin sizes.

Figure 4.

Plots of EDR(1.0 cc)/EDR(max) ratio for the true cord and true cord plus 1 mm to 3 mm margin without assuming linear correlation of all the parameters.

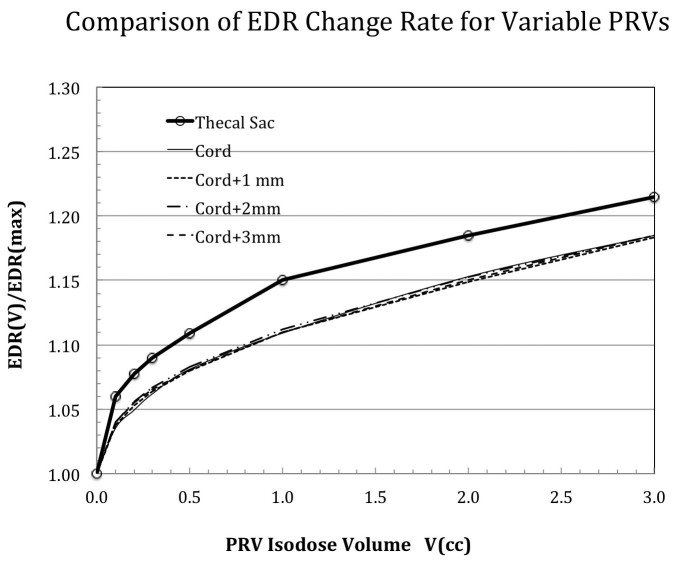
Figure 5 further summarizes the dependence of the EDR/EDRmax ratio for different PRV definitions. Note the large discrepancies between the thecal sac and the cord and cord-related PRVs in Figure 5. This suggests that thecal sac cannot be simply equated to the true cord plus a uniform margin for simple dose volume limits applications.

Figure 5.

Comparison of the fitted EDR slopes for the studied planning risk volumes (PRVs). Significant differences were noted in the trend of slope changes between the thecal sac and the true cord with and without 1-3 mm margins.

Discussion

A mathematical formula was found to strongly link the most probable adjacent spinal cord doses from the Dmax to variable volumetric parameters ranging from D(0.1cc) to D(3.0cc). The fitted model was found applicable to variable dose fractionation schemes and different treatment modalities, i.e., robotic CyberKnife SBRT and linac-based SBRT.

At the isodose level of up to 1.0 cc, a strong EDR correlation (R²> 0.98) was surprisingly observed for all the PRV values. Such a correlation enables a user to empirically convert the small-volume dose limits to different spinal cord PRVs via Equation 4 and Figure 5. For example, a dose of 10 Gy to 0.35 cc of the cord would correspond to a Dmax dose of 12 Gy. This can be calculated by first obtaining EDR(0.35cc)/EDRmax =1.075 from Figure 5, and then by applying Equation 4 such that Dmax=10*(1.075)^2.=12 Gy.

Our study has also shown that adopting consistent PRV definitions is critical when imposing the spinal cord dose volume limits or cross-comparing treatment outcome. For example, the thecal sac PRV does not approximate the true cord plus a PRV margin of 1 to 3 mm or vice versa.

It is also worth noting that the EDR relationship of our study is based on the assumption of single target irradiation with the spinal cord in the peripheral dose fall-off region of the target. However, in cases with multiple targets or hypothetical overlapping volumes between the planning target volume (PTV) and the spinal cord PRV producing focal dose hot spots inside the spinal cord PRV, the formula can deviate significantly from the actual dose limits of such cases so a user should exercise caution for these situations.

In conclusion, a mathematical relationship was found to empirically link the most probable spinal cord PRV dose volume limits across finite isodose volumes such as from Dmax to D(1.0 cc) for common spine SBRT treatments. Further studies are needed to determine general applicability and usefulness of the formula to other SBRT cases.