A mixed alchemical and equilibrium dynamics to simulate heterogeneous dense fluids: Illustrations for Lennard-Jones mixtures and phospholipid membranes

Abstract

An algorithm to efficiently simulate multi-component fluids is proposed and illustrated. The focus is on biological membranes that are heterogeneous and challenging to investigate quantitatively. To achieve rapid equilibration of spatially inhomogeneous fluids, we mix conventional molecular dynamics simulations with alchemical trajectories. The alchemical trajectory switches the positions of randomly selected pairs of molecules and plays the role of an efficient Monte Carlo move. It assists in accomplishing rapid spatial de-correlations. Examples of phase separation and mixing are given in two-dimensional binary Lennard-Jones fluid and a DOPC-POPC membrane. The performance of the algorithm is analyzed, and tools to maximize its efficiency are provided. It is concluded that the algorithm is vastly superior to conventional molecular dynamics for the equilibrium study of biological membranes.

I. INTRODUCTION

Computer simulations of condensed phases are powerful tools to investigate the thermodynamic properties of a wide range of molecular systems. Nevertheless, challenges remain. One of the challenges is the simulation of multi-component dense fluids (MCDFs). Their broad spectra of spatial and temporal scales prevent the effective use of Molecular Dynamics (MD) or Monte Carlo (MC) simulations in numerous cases.

Following experimental conditions, we frequently simulate systems that are translationally invariant on average (TIOA). If the system is of a single component, the simulated model is likely to be TIOA prior to production runs and relatively short trajectories are required to sample from the correct distribution. However, if the system is a dilute solution, averaging over the positions of the solute molecules can be expensive. The average length scale separating the solute molecules may be large, and the distribution of distances may be wide and poorly sampled in a single snapshot in time. In practice, it is exceptionally hard to converge MD simulations with only a few solutes in a simulation box. Molecular Dynamics (MD) simulations are therefore restricted to aqueous solutions with a high concentration of solutes. Low concentrations of solute molecules can have a profound impact on structures and dynamics. For example, minute concentrations of magnesium ions are necessary for RNA folding.¹

Another significant simulation challenge in multi-component systems is assembly and separation of phases. Let the initial condition of a simulation be a uniform, well-mixed fluid. Let the equilibrium state be separate phases in which each component aggregates to form a pure phase. To model this process, substantial large-scale rearrangements are required which are more expensive to compute than the calculations of thermodynamics of a single component (and a single phase) fluid for which the computational challenges are different.

Concrete examples of MCDF with significant computational complexity are biological membranes. The dynamics of molecular components of the membrane have received considerable experimental attention using sophisticated experimental methods such as fluorescence correlation spectroscopy² or NMR.³ Typically, one, two, or three component mixtures have been used to understand the dynamics and structures of membranes, though biological membranes can have thousands of components.⁴ This difference may impact important observables. For example, molecular diffusion in model membranes is up to 50 times faster than the diffusion of the same molecules in membranes of living cells.⁵

Local assemblies of specific lipids, proteins, and cholesterol molecules in biological membranes led to the “raft” hypothesis, which is more than 20 years old.^6,7 According to the raft hypothesis, rafts capture membrane proteins and hence serve biological functions. The concept is intuitive, appealing, and perhaps not surprising given the heterogeneity of biological membranes. Nevertheless, the notion of rafts in biological membranes remains debatable,^4,8–10 likely due to the broad range of observations reported as evidence for rafts. Rafts have been reported to exist with length scales of nanometers to micrometers^11–13 and lifetimes of microseconds and seconds.^14,15

Computer simulations of heterogeneous membranes may add useful information to the ongoing debate on biological membranes. Indeed, a large body of recent investigations has focused on model membranes with two or more components.^16–21 A study using a coarse-grained model of more than 60 different types of lipids represents to our knowledge the most diverse mixture studied with MD,²² and a recent simulation using the Anton ASIC machine illustrated the capacity of straightforward MD to sample the equilibrium of a small two-component system from a phase separated state to a mixed state.²³

Nevertheless, significant challenges in simulation of heterogeneous membranes remain. Slow two-dimensional diffusion of membrane constituents makes equilibration via conventional MD prohibitively expensive. Moreover, local aggregation and phase separation add to the complexity. Indeed, computer simulations of model membranes usually invoke only a few components to reduce complexity and even with this simplification, sampling in these systems is challenging. In vivo, one finds membranes with thousands of different types of lipids. An efficient algorithm to simulate such heterogeneous biological membranes is highly desired.

In computational approaches that use a local displacement to generate a new move, the diffusion constant, D, is a critical parameter to assess efficiency. Let Δx be the displacement of a particle after a time interval Δt, and let ⟨…⟩ be an equilibrium average over all indistinguishable particles and time origins. The relationship $4D\cdot \mathrm{\Delta }t\simeq ⟨{\left(\mathrm{\Delta }x\right)}^2⟩$ provides an estimate for the equilibration time as a function of system size. This relationship should be considered an upper bound, as the effective diffusion is expected to be slower for heterogeneous systems. An increase in the length of the system by a factor of 10 will require an increase of the equilibration time by a factor of 100 for the same diffusion constant. Recently, it was demonstrated that the length scales required to stabilize phase separation in heterogeneous membranes may be larger than what is typically used in simulations.²⁴

Enhanced sampling MD algorithms focused on increasing membrane mixing by replica exchange.^25,26 These simulation methods achieved significant enhancement of the dynamics of the lipids, upon increasing the observed diffusion constant by up to a factor of 10. However, one should keep in mind the poor scalability with membrane size and the need to keep the simulation box large enough to detect assemblies of the relevant sizes.²⁴

An alternative approach to MD simulations of equilibrium is the MC method.²⁷ In MC, a trial move is generated at random and the resulting structure is tested for acceptance or rejection using (for example) the Metropolis criterion. An interesting set of studies^28,29 exploited the integration of MD and MC to explore the phase diagram of lipid membrane mixtures. They consider a move in which the identity of a single phospholipid is modified. No large spatial displacement is required to obtain significant rearrangements, which is a significant advantage of MC compared to MD. The move alters the lipid composition in the system and generates configurations from the grand canonical ensemble. The choice of the type of the MC move remains, however, challenging, and the changes of the groups are limited to similar lipids that differ by a few atoms at their tails. In some cases the simulations with low acceptance probability were successful.

A particular realization of a random move, which is useful for equilibration of a multi-component system, is an exchange between two randomly chosen particles or groups of particles. For example, let a particle of type A be at coordinate r₁ and particle type B be at position r₂. The move exchanges the positions of the two particles. Hence particle type A after the exchange move is now at r₂, and particle type B is placed at r₁. This is a large spatial displacement of each of the particles that is not bound by the magnitude of the diffusion constant, as is the case in MD, reducing the dependency of the equilibration time on the system size. The same large displacement cannot be generated quickly using dynamics that follows time dependent physics with small steps. Large spatial correlation (or de-correlation) can be achieved with a relatively small number of MC moves. The exchange move also retains the chemical composition of the system and therefore generates configurations from the canonical ensemble. Such exchange moves are the focus of the present paper and are called throughout the manuscript “exchanges” or “exchange moves.”

The caveat of MC moves employing the metropolis criterion is the acceptance probability. If the energy of a proposed structure, U(x₁), is higher than the energy of the current structure, U(x₀), the acceptance probability, P_accept, is exponentially small with the energy difference ΔU = U(x₁) − U(x₀), where P_accept(ΔU > 0) = exp(−βΔU) and β = 1/k_BT. If ΔU ≤ 0, the trial move is accepted with probability of one. If the random move is chosen poorly, generating high energies for the trial steps, the moves are unlikely to be accepted making the MC approach inefficient.

If the molecules of the different components vary appreciably in size and interactions, the acceptance probabilities of the proposed exchange moves in MC are small or in MD the effective mixing is slow. This is perhaps the reason why atomically detailed simulations of heterogeneous biological membranes are rare and most simulations use only one or a few components.

Recently a class of algorithms was discussed for more rapid calculations of thermodynamic variables that are based on a mixture of equilibrium and non-equilibrium dynamics.³⁰ These non-equilibrium methods exploit the insight of Jarzynski into non-equilibrium systems.³¹ We consider an average over an ensemble of non-equilibrium trajectories with initial conditions sampled from equilibrium. Such an ensemble can be presented by a single equilibrium trajectory chopped into pieces. Each piece represents a trajectory sampled according to an equilibrium distribution as outlined in Ref. 30. The single trajectory formulation is more appropriate for the task discussed in this paper since it enables the generation of a Markov chain and an MC move with a high acceptance probability. The higher acceptance is obtained with greater computational cost to generate proposed moves.

The algorithm of this manuscript aims to simulate equilibrium in MCDF using a sequence of conventional MD trajectories and trajectories modeling Alchemical Steps (AS) of group exchanges. The alchemical steps are represented as non-equilibrium work along a mixing parameter λ. We therefore named this algorithm MDAS for Molecular Dynamics with Alchemical Steps. We describe the algorithm that is a concrete implementation of the general formulation of non-equilibrium candidate Monte Carlo move³⁰ for system mixing in Sec. II. Others have used an implementation of the same general formulation for molecular docking and a conformational search in a peptide.^32,33

II. METHODS

A. The MDAS algorithm

Consider a MCDF system with N molecules. The different components are molecules or molecular groups (for example, an amino acid or a phospholipid molecule) with coordinate vectors r_i, respectively. The task is to simulate an equilibrium distribution of this system using molecular dynamics. The mixing of the system components is slow to converge with conventional MD, and we wish to accelerate the convergence with MC-like moves. This combination of MD with MC means that the simulation will only provide information on the thermodynamics of the system. It has, however, the potential to greatly reduce the time of relaxation to equilibrium of the MCDF system as we illustrate in Secs. III A and III B.

We seed the MD trajectories (which we denote by D) with MC-like exchange moves between randomly selected pairs of molecules or molecular groups. The exchange moves (which we denote by M) are performed at uniformly spaced intervals in simulation time. The series of MD trajectories and MC-like moves leads to a sequence of events DMDMDMD… The D component is conducted with a fixed Hamiltonian and samples configurations from one of the well-known ensembles (NVE, NVT, or NPT).

Here the MC move is a non-equilibrium trajectory, M, with a known statistical weight that proposes an exchange move. The weight is used to accept or reject the trajectory M in a similar spirit to the Metropolis algorithm that proposes a change in a single step. If the M trajectory is accepted, a trajectory D continues from the final configuration of the M trajectory. Otherwise, the trajectory M is rejected and the system returns to the point from which the M trajectory was initiated. Another D segment is conducted, and this process is repeated until termination of the simulation.

Configurations are collected from D trajectories for sampling from the desired ensemble. Each of the M trajectories is considered as an MC trial move to exchange the chemical identity of two randomly selected molecules or molecular groups. The trial move returns at the end of the alchemical calculations to a system with the same composition but different coordinates.

We consider in more detail the exchange move, in which group i of type k changes position with group j of type l, l ≠ k. The potential energy has the general form $U\left(r_1,\dots ,r_i^k,\dots ,r_j^l,\dots ,r_N\right)$ and after the exchange it is $U\left(r_1,\dots ,r_i^l,\dots ,r_j^k,\dots ,r_N\right)$. The energy difference between the states before and after the trial move can be positive and high if the difference between groups k and l is large resulting in low acceptance probabilities.

We wish to construct a more “gentle” exchange move with a reasonably high acceptance probability. We therefore define an intermediate state using a parameter λ such that when λ = 0 the pair state is $\left\{r_i^k,r_i^l\right\}$, when λ = 1 it is $\left\{r_i^l,r_j^k\right\}$. The intermediate state is written as a linear interpolation of the potentials between the extreme cases

$$\begin{array}{ccc}\hfill U_{\lambda ,linear}& =\hfill & \left(1-\lambda \right)U\left(r_1,\dots ,r_i^k,\dots ,r_j^l,\dots ,r_N\right)\hfill \\ \hfill & \hfill & +\lambda U\left(r_1,\dots ,r_i^l,\dots ,r_j^k,\dots ,r_N\right).\hfill \end{array}$$ (1)

However, a linear interpolation between λ = 0 and λ = 1 may not be optimal. We seek a continuous path from λ = 0 to λ = 1 such that the distribution of the energy difference between morphed states ΔU_λ = U_λ+Δλ − U_λ will be as narrow as possible. A non-linear definition of the intermediate state may be desirable. For example, when a particle vanishes, the free energy contribution of the Lennard-Jones potential term is singular and difficult to compute with linear interpolation.³⁴

As written by Jarzynski,³¹ the work, w, done on the system is

$$w\left(\lambda =0\to \lambda =1\right)=\underset{0}{\overset{1}{\int }}\frac{\partial U_{\lambda }}{\partial \lambda }\frac{d\lambda }{dt}dt,$$ (2)

where the “time” t parameterizes the chosen λ path. The work is computed in an M trajectory by modifying λ from zero to one following a concrete time path (specifying dλ/dt). In the present manuscript, the M trajectory exchanges the chemical identities of two groups of particles at different positions. The end result looks like that the two groups swap positions. For computational convenience, we use a particular realization of the time path of Eq. (2) and consider a discrete representation of the integral (see also Fig. 2)

$$w\left(\lambda =0\to \lambda =1\right)=\sum _{i=1}^L{\omega }_{{\lambda }_i}\left({\delta }_i\right)+{\omega }_{{\lambda }_i\to {\lambda }_{i+1}}\left({\mu }_i\right).$$ (3)

The index i follows a sequence of trajectory segments (δ_i, μ_i) as we progress from λ = 0 to λ = 1, and L is the number of segments. The μ trajectory is the only trajectory segment in which the value of λ is modified. We denote by ω the partial work conducted at a δ or a μ trajectory segments. Note the important difference between δ and D trajectories. δ is a short MD run conducted during an M trajectory. It relaxes the system after each change in the parameter λ, and it follows equations of motion of a Hamiltonian with a fixed λ, where λ ∈ [0, 1]. The value of the D trajectory is conducted between M trajectories and is a conventional MD run with λ equals either zero or one.

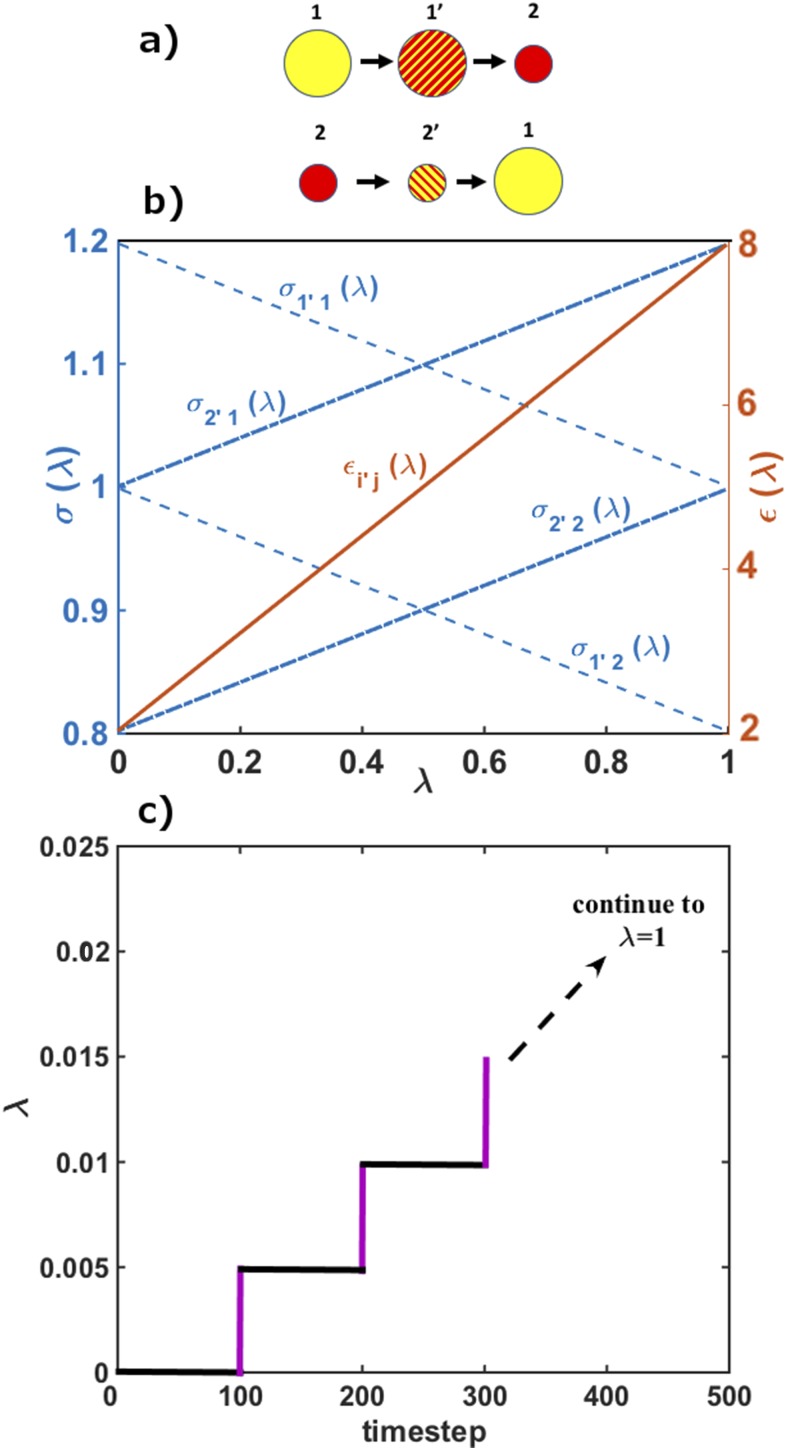
FIG. 2.

(a) Schematic representation of the alchemical step, exchanging the identities of particles 1 and 2: Particle type 1′ (or 2′) initially is a particle type 1 (or 2) and is modified to particle type 2 (or 1). (b) The change in LJ parameters for the type 1′ and 2′ particles. The ε_kl grows linearly for k ≠ l and decreases for k = l. (c) The evolution of the parameters during an M trajectory. Note that the work is different from zero only along the purple lines where the positions of the particles are fixed and the interaction parameters are modified. The acceptance or rejection of the MDAS move is based on the value of the work using a Metropolis criterion. The horizontal black lines correspond to δ trajectories.

During δ_i trajectories, the exchange parameter is fixed and the work is therefore zero. The expression for the work in Eq. (3) is reduced to

$$\begin{array}{ccc}\hfill w\left(\lambda =0\to \lambda =1\right)& =\hfill & \sum _i{\omega }_{{\lambda }_i\to {\lambda }_{i+1}}\left({\mu }_i\right)\hfill \\ \hfill & \cong \hfill & \sum _i\left[U_{{\lambda }_{i+1}}\left(x\left(t_i\right)\right)-U_{{\lambda }_i}\left(x\left(t_i\right)\right)\right],\hfill \end{array}$$ (4)

where x(t_i) is the configuration at the end of a δ_i trajectory. Equations (3) and (4) represent a particular choice of a λ(t) trajectory, which is convenient for the calculations of work.

A useful relationship of Eq. (2) with an algorithm to compute equilibrium averages is discussed below. Equation (4) has a connection to the algorithm of slow growth that computes free energy differences.³⁵ Slow growth determines the free energy difference with an M trajectory, at the limit of infinite time, $\mathrm{\Delta }F=\underset{t\to \infty }{lim}\underset{0}{\overset{t}{\int }}\left(\partial U/\partial \lambda \right)\dot{\lambda }d{t}^{\prime }\left(\lambda \left(0\right)=0,\lambda \left(t\right)=1\right)$. The free energy difference is the work conducted at an extremely slow rate.

At finite times, the work is a noisier function compared to the free energy. However, it is better than using a single MC move, which can be interpreted as an infinitely fast conduction of the work. The practical advantage of the work summation [Eq. (4)] compared to a direct and single MC move is that the changes of λ in a single μ step are small (typically 0.001-0.005) introducing minimal perturbation to the system. Moreover, the δ trajectories generate configurations with a smaller number of steric clashes and more accessible energies.

The Jarzynski equality³¹ provides a relationship between distribution of works conducted by an ensemble of trajectories and the free energy difference between the end states, $\exp \left(-\beta \mathrm{\Delta }F\right)=⟨\exp \left(-\beta w\right)⟩$. The average is over an ensemble of trajectories with initial conditions sampled from the canonical ensemble. The weight of a single trajectory is therefore exp(−βw). We use the weight in an acceptance-rejection criterion in a Metropolis-like algorithm of the complete λ trajectories

$$P_{accept}=min\left[1,\exp \left(-\beta w\right)\right].$$ (5)

The average of the Jarzynski equality can be conducted using a single long DMD…DMD trajectory in which we obtain a sequence of works, w-s, from the M trajectories. Following the ergodic hypothesis, the average from the time series of a system in equilibrium that undergoes sequential M transitions can replace phase space averages of different trajectories with initial conditions sampled from equilibrium.

The algorithm to efficiently mix a multi-component system is summarized in Table I.

TABLE I.

A sketch of the MDAS algorithm.

Algorithm step	Action
0	Initiate the structure and the MDAS algorithm
1	If the maximum number of steps of the DMD…DMD trajectory was achieved, then stop
2	Conduct a D trajectory (a conventional MD simulation)
3	Conduct an M trajectory (varying λ from 0 to 1 using a sequence of (δi, μi) steps) starting from the last configuration of step 2 to exchange the positions of two molecules or two groups of atoms
4	Reject or accept the move of step 3 using the trajectory weight w - min[1, exp(−βw)] If the trajectory is accepted, then return to step 1
	If the move is rejected, then change the current configuration to the last structure of the prior D trajectory and return to step 1

The specific task addressed in this manuscript of spatially equilibrating a multi-component system has a number of special features that we discuss below.

Consider an exchange move of two groups of particles using an infinitely long M trajectory interpolating between λ = 0 and λ = 1. As noted earlier the use of a long trajectory is equivalent to the algorithm of “slow growth” to compute free energy differences.³⁵ For a fluid in thermal equilibrium, the final state (λ = 1) is thermodynamically equivalent to the first state (λ = 0). The free energy difference is therefore zero and so is the work at the long time limit. From a practical viewpoint, we note that the longer the M trajectory, the closer the work to zero. Trajectories that are short may yield high values of work with low acceptance probability. A simple remedy is to make the trajectories longer with the anticipation that their work will be closer to zero. Of course, the longer trajectories are more expensive to compute and a compromise between trajectory lengths and acceptance probabilities must be made.

Second, the total work conducted in an M trajectory is a sum of partial works for a small Δλ step. The steps use structures generated at the end points of δ_i trajectories. If we assume that each δ_i trajectory is sufficiently long to de-correlate the initial and final structures, then the partial works are statistically independent. We invoke a central limit theorem argument and suggest that the distribution of $w=\sum _i{\omega }_{{\lambda }_i\to {\lambda }_{i+1}}\left({\mu }_i\right)$ can be modeled by a normal distribution with a known mean, m and variance σ² that can be determined computationally. That is, the probability density of w is

$$p\left(w\right)\cong \frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[-\frac{{\left(w-m\right)}^2}{2{\sigma }^2}\right].$$ (6)

Of course in the limit of a long M trajectory, we expect m = 0. However, for short trajectories, significant deviation from the asymptotic behavior can be obtained. The statistical model is useful since it helps us to predict the average acceptance probability and hence the efficiency of the algorithm

$$\begin{array}{ccc}\hfill ⟨P_{accept}⟩& =\hfill & ⟨min\left[1,\exp \left(-\beta w\right)\right]⟩\hfill \\ \hfill & =\hfill & \underset{-\infty }{\overset{0}{\int }}p\left(w\right)dw+\underset{0}{\overset{\infty }{\int }}p\left(w\right)\exp \left(-\beta w\right)dw\hfill \\ \hfill & =\hfill & \frac{1}{\sqrt{2\pi {\sigma }^2}}\left[\underset{-\infty }{\overset{0}{\int }}\exp \left[-\frac{{\left(w-m\right)}^2}{2{\sigma }^2}\right]dw\right.\hfill \\ \hfill & \hfill & \left.+\underset{0}{\overset{\infty }{\int }}\exp \left[-\frac{{\left(w-m\right)}^2}{2{\sigma }^2}\right]\exp \left(-\beta w\right)dw\right],\hfill \end{array}$$ (7)

where the last expression may be written as a sum of error functions (Fig. 1).

FIG. 1.

F(m, σ²) = N′, where N′ is the number of trial moves that maximizes $N\cdot ⟨P_{N,accept}⟩$. m and σ² are expressed in k_BT and (k_BT)², respectively. In this plot, N′ ranges from 1 to 12. For smaller values of m and larger values of σ², we can improve the sampling with multiple simultaneous trial moves. The dark blue region is where a single trial move is the most efficient choice.

Third, Eq. (7) makes it possible to evaluate the viability of many particle moves in which rather than an exchange of the position of two groups of particles we consider the simultaneous exchanges of several pairs. The efficiency of simultaneous MC moves was discussed in the past.³⁶ Using the same model of a normal distribution, this time for an attempt of simultaneous N exchanges, we have a new mean Nm and a new variance Nσ² and obtain the acceptance probability

$$\begin{array}{ccc}\hfill ⟨P_{N,accept}⟩& =\hfill & \frac{1}{\sqrt{2N\pi {\sigma }^2}}\left[\underset{-\infty }{\overset{0}{\int }}\exp \left(-\frac{{\left(w-Nm\right)}^2}{2N{\sigma }^2}\right)dw\right.\hfill \\ \hfill & \hfill & \left.+\underset{0}{\overset{\infty }{\int }}\exp \left(-\frac{{\left(w-Nm\right)}^2}{2N{\sigma }^2}\right)\exp \left(-\beta w\right)dw\right].\hfill \end{array}$$ (8)

The performance of the attempted N simultaneous pair exchanges versus a single pair exchange is not obvious. A single Monte Carlo test may lead to N simultaneous exchanges. However, the probability of acceptance of the N simultaneous exchanges is typically lower than the probability of acceptance of a single exchange move. The behavior of Eq. (8) will depend on the mean, variance of the work distribution, and the number of exchanges.

Figure 1 shows the numerical solution of F(m, σ²) = N′ in (m, σ²) space, where N′ is the number of simultaneous exchange moves that maximizes $N⟨P_{N,accept}⟩$. It can be seen that for a significant region of space, trials of multiple simultaneous moves lead to more acceptable exchanges. As the number of simultaneous trial exchange moves grows, the region of efficiency becomes smaller. For large m and small σ², single pair exchange attempts become a more efficient choice.

Even if p(w) is not an exact Gaussian, one may model the distribution using Eq. (7) and numerically solve for different trial moves to find the optimum value of N that maximizes $N⟨P_{N,accept}⟩$. In Sec. III C, we illustrate the application of multiple, simultaneous exchange moves on a heterogeneous membrane system and show that proposing 4 simultaneous moves improves the rate of approach to equilibrium. Finally, we comment that the discussion above is general and is applicable to exchange moves in any TIOA system.

B. Molecular dynamics protocols

We conducted two types of simulations to verify and assess the performance of the MDAS algorithm. In the first simulation, we investigated binary mixtures of two-dimensional Lennard-Jones fluids. Particles are initially placed on a hexagonal grid in the 30 × 30 box with periodic boundary conditions. The unit system is set for computational convenience. The temperature of the system and the mass of the particles are set to 1. The time step is 0.001 for both D and M trajectories, and the simulations were conducted with the Nose-Hoover thermostat.³⁷ The simulations have been conducted with LAMMPS.³⁸

The second simulation is for the lipid bilayer binary mixture. The system consists of 100 DOPC and 100 POPC molecules at each leaflet (400 phospholipids in total). The membrane is created for DOPC and POPC separately by CHARMM-GUI³⁹ and then merged into a single structure using Virtual Molecular Dynamics (VMD).⁴⁰ It is solvated with TIP3P water molecules and the ionic concentration is 150 mM (NaCl). The simulations were conducted with the NAMD program.⁴¹ Water molecules were kept rigid using the SETTLE algorithm.⁴² All bonds with hydrogen atoms are kept fixed with the SHAKE algorithm.⁴³ Particle Meshed Ewald⁴⁴ was used to sum electrostatic interactions with a grid space of 1 Å. The cutoff for Lennard-Jones interactions was 12 Å. The system is minimized first for 10 thousand steps with the conjugate gradient algorithm, and then equilibrated in the NPT ensemble using the Nose-Hoover Langevin piston pressure control^45,46 with a piston period and decay of 200 and 100 steps, respectively. The equilibration period was for 1 ns with a pressure of 1 atm and a temperature of 300 K. The production run was conducted in the NVT ensemble using Langevin dynamics⁴⁷ with a friction coefficient of 5 ps⁻¹ and temperature 300 K for additional 240 ns.

III. RESULTS AND DISCUSSIONS

A. Example 1: A two dimensional binary Lennard-Jones system

A phase diagram of binary Lennard-Jones systems has been studied extensively in the past.^48–50 In particular, finding byways to conventional MD and MC simulations enabled numerous advancements. The Gibbs ensemble method and the Gibbs-Duhem integration technique of Kofke were used to examine the solid-liquid phase diagram as a function of diameters σ_ij and the well depths ε_ij and serve as benchmarks for future investigations of crystallization.⁵⁰ The mixtures were also investigated by umbrella sampling⁵¹ and more recently by transition interface sampling⁵² and advanced Monte Carlo techniques.^53,54 Crystal growth and propagation have been topics of more recent investigations of Lennard-Jones systems.^55,56

The computational challenges of sampling equilibrium in TIOA systems can be addressed by tools that avoid conventional simulations and exploit enhanced sampling techniques. MDAS is quite close to conventional MD simulation combined with MC and is applicable to dense fluids with particles that differ appreciably in their parameters. Our goal in the following example is to illustrate MDAS on a well-investigated system that still poses significant numerical challenges. MDAS can be combined with the approaches referenced above (e.g., replica exchange). However, its simplicity is attractive and the generalization of this approach to other more complex fluids is straightforward which makes it useful as a standing-alone methodology.

The first example is a phase separation of two types of Lennard-Jones (LJ) particles initiated from a random mixture. There are 411 particles of each type in the system. The pair interaction potential is a 6-12 Lennard-Jones (LJ) energy term. For particles of types k and l and particle indices i and j, we have

$$u_{kl}\left(r_{ij}\right)={4\epsilon }_{kl}\left[\frac{{\sigma }_{kl}^{12}}{r_{ij}^{12}}-\frac{{\sigma }_{kl}^6}{r_{ij}^6}\right],$$ (9)

where r_ij $\left(r_{ij}=\left|{\mathbf{r}}_i-{\mathbf{r}}_j\right|\right)$ is the distance between particle i and particle j. The interaction between particles of the same type is chosen to be stronger than dissimilar ones: ε₁₁/k_B = ε₂₂/k_B = 8 > ε₁₂ = 2.

Additionally, particles have different LJ radii σ₁₁ = 1.2, σ₂₂ = 0.8, σ₁₂ = 1.0. The interaction range is 2.5σ₁₁. We use the largest particle radius to determine this range.

We estimate the density of the system as the fraction of the total area covered by the Lennard-Jones disks. The area covered by a single particle is estimated as $\pi {\sigma }_{ii}^2/4$. We therefore have ρ = 411 · π(0.8²/4 + 1.2²/4)/30² = 0.75.

Our choice is such that simply exchanging type 1 and type 2 particles (yellow and red in Figs. 2 and 3, respectively) in a Monte Carlo simulation of the fluid would result in a large difference in the potential energies and most moves will be rejected. Furthermore, the density of 0.75 is reasonably high and, therefore, a conventional MD simulation that follows the local diffusion of the particle would be too slow to exchange particles at large length scales. In MDAS, the particles change their identities gradually (Fig. 2) leading to a significantly higher acceptance ratio than a single MC exchange move.

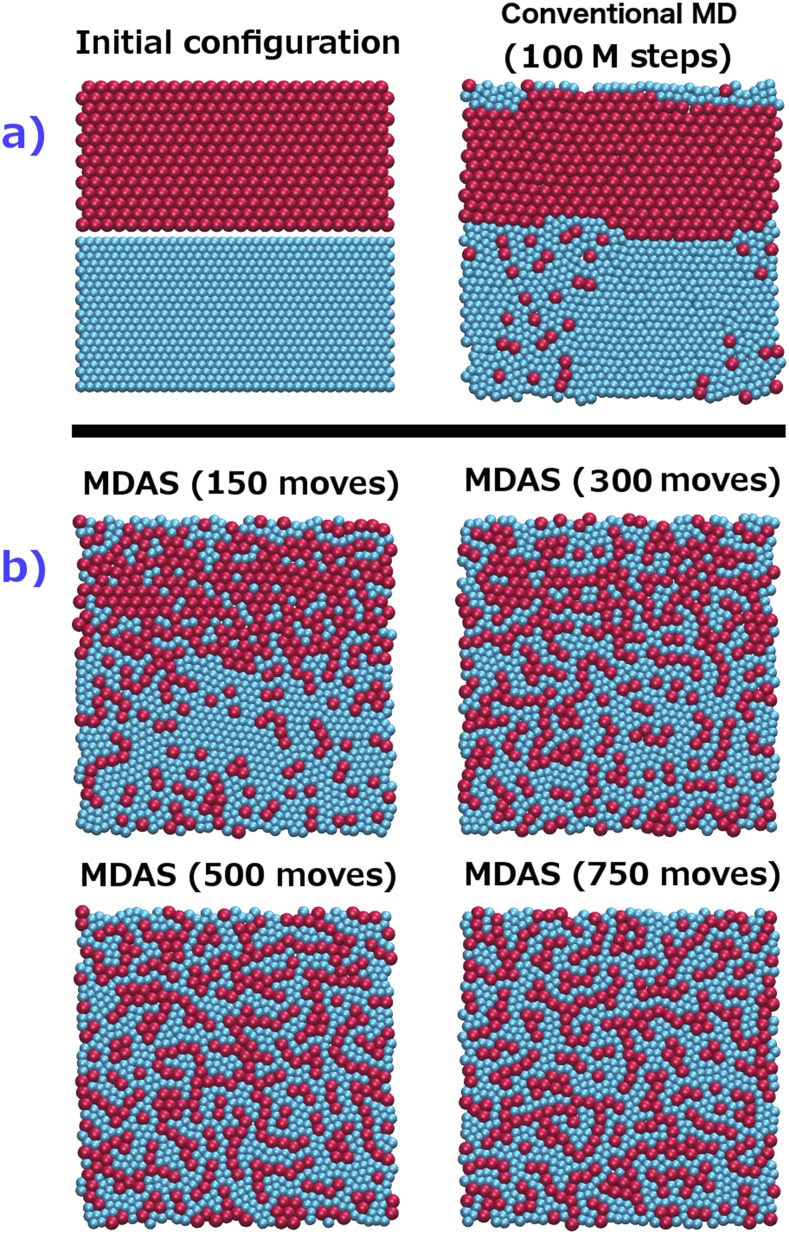
FIG. 3.

2D simulation of LJ fluid, first example. The interactions between similar particles (see Sec. III A) are chosen to be higher than dissimilar ones. One consequence of this choice may be a phase separation. The disks cover a fraction of 0.75 of the total area of the simulation square. (a) Left: Initial configurations of a 2D system of two types of LJ particles. Right: Final configuration of the system after 500 × 10⁶ steps of conventional MD. Significant aggregation does not occur at this time scale for this example. (b) Evolution of the system during 800 accepted MDAS moves.

1. The exchange

In Sec. II A we described the algorithm as an alternating sequence of a D and M trajectories. During the M trajectory, the exchange of the particles (the alchemical exchange) is conducted as follows.

We randomly pick two particles, each of them of a different type [called particles 1′ and 2′ in Fig. 2(a)]. Figure 2(b) shows how ε and σ of the selected pair of particles change. The gradual change is parameterized by λ that is modified in small discrete steps from 0 to 1. For this example, the gradual change is performed in 200 intervals with Δλ = 0.005. The M trajectory is conducted as follows: After 100 steps of conventional MD simulation with a Hamiltonian with a fixed value of λ (a δ trajectory), λ is modified to λ + Δλ in a single step (a μ trajectory) while keeping the coordinates fixed. The work done on the system at the corresponding interval, ω(λ → λ + Δλ), is $U_{\lambda +\mathrm{\Delta }\lambda }\left(x\left(t\right)\right)-U_{\lambda }\left(x\left(t\right)\right)$, where t is the end time of the δ trajectory (100 steps). Then an MD trajectory at the intermediate λ + Δλ (a δ trajectory) allows the system to equilibrate for 100 steps [Fig. 2(c)] and we repeat the small λ change. After 20 000 steps, we calculate the total work done on the system for the complete particle exchange [Eq. (4)]. With the work value at hand, we use the Metropolis criterion to test acceptance. If the exchange move is accepted, the two particles are switched and the system is simulated for another 1000 steps (a D trajectory) before performing the next alchemical step (an M trajectory).

2. The simulation

At the beginning of the calculation, when the binary mixture is distributed uniformly [Fig. 3(a)], the acceptance probability of an exchange move or an M trajectory is about 0.1. For a comparison, if a conventional MC step replaces the M trajectory, the acceptance probability is much lower. To test direct MC combination with MD, we conducted MD for 1000 steps and then attempted a single step MC exchange. We then repeated another 1000 MD steps before attempting MC exchange again. We repeated the MD and MC combination 100 000 times (the total number of MD steps is 100 × 10⁶), and not a single proposed exchange was accepted for the Lennard-Jones system.

As the simulation continues, the condition and the difficulties change. Our current algorithm chooses the pair randomly. Once aggregates are formed [Fig. 3(b)], it becomes exceedingly hard to propose an exchange that is acceptable. Pairs that can exchange are invariably at the interfaces of aggregates. An interface particle has at least one neighbor of a different type. An attempt to exchange particles embedded in the aggregate cores results in an exceptionally low acceptance probability. There are about 150 particles at the interface out of 411 particles of each type. The probability of finding an interface pair is about (150/411)² = 0.13, suggesting an acceptance probability of 0.13 × 0.1 = 0.013. The overall acceptance probability for this system in an M trajectory is estimated from the complete trajectories to be 0.03. The last acceptance probability is an intermediate value between 0.1 at the beginning of the calculations and 0.013 after aggregates were formed. Nevertheless, the acceptance probability of 0.03 is still small and it raises a question about the algorithm efficiency. Efficiency of MC simulations depends on the system and computed observables. For Monte Carlo simulations of hard spheres, it was argued that an acceptance probability between 0.2 and 0.5 is efficient.⁵⁷ One possible improvement for the future is to adjust the selection of the random pairs in a way that preferably proposes moves involving interfacial particles.

To gain further insight into the computational efficiency of MDAS, we compared it to conventional MD. We estimated the computational cost as the number of force evaluations during the trajectory. The number of force evaluations for 800 accepted MDAS moves (we counted also the force evaluations of the unaccepted moves) is similar to the number of force calculations in 500 × 10⁶ MD steps. Figure 3 compares a conventional MD simulation with an MDAS simulation. We start from a randomized system and we expect that the system will separate into different phases based on the designed potential. After MD simulation of 500 × 10⁶ steps, the particles in the system barely change their positions and only some small clusters of red (type 2) particles appear. However, after 800 accepted steps of MDAS, the particles show phase separation and red islands of smaller particles are formed inside the yellow matrix (particles of type 1).

The pair correlation function in the plane of particles of type 2 g₂₂(r) is shown in Fig. 4. It is computed from conformations sampled during the D trajectories as follows. Let the number of pairs of type 2 particles between r and r + Δr be N(r) then $g\left(r\right)=\frac{N\left(r\right)}{N_t}\frac{A}{2\pi r\mathrm{\Delta }r}$, where N_t is the total number of particles, Δr is a finite small change in the distance, r is the distance between the particles, and A is the area of the simulation square. When large clusters are formed, we expect a more significant first peak and the enhancement of long-range correlations as in Fig. 4. Significantly more relaxation to equilibrium is achieved with MDAS. However, it is not clear yet if the calculations are fully converged, as the peaks of the pair correlation functions are still changing their heights.

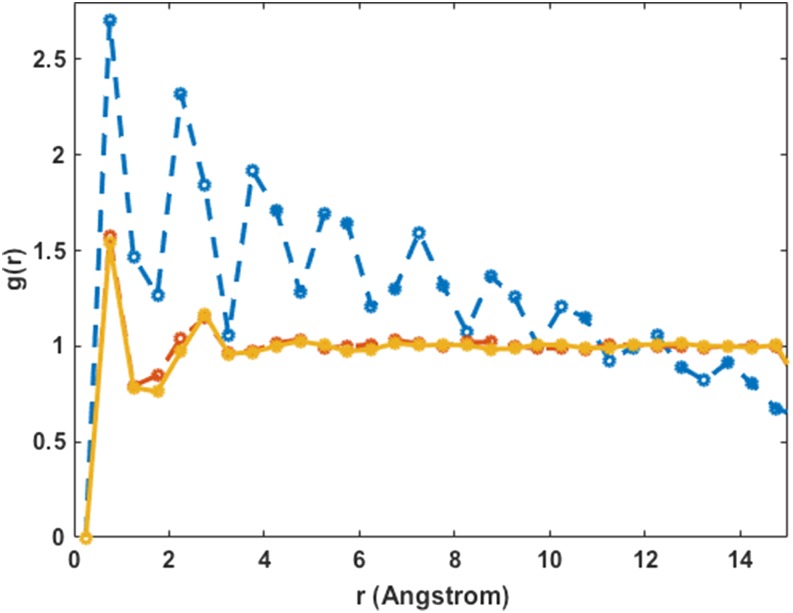
FIG. 4.

The pair correlation function for the red particles (particles of type 2) in the simulation of the two-component system with significant self-attraction. The blue dashed line corresponds to the initial configuration, the solid green line shows the results of a conventional MD run after 500 × 10⁶ steps, and dashed red and solid yellow lines are the MDAS results after 300 and 800 moves, respectively. Note the increase in the height of the first peak and in the long-range order as we expect from phase separation. The continued shift of the first peak height suggests that the simulation is not fully converged and more relaxation to order phases is expected. The MDAS simulations continuously approach equilibrium, while the straightforward MD simulations are “stuck” near the initial configuration. The inset shows the time evolution of the maximum of the pair correlation function versus the number of MDAS steps.

As a second example, the interaction between particles of types 1 and 2 (colored red and blue, respectively in Fig. 5) was made to be stronger with each other than with particles of the same type ε₁₁/k_B = ε₂₂/k_B = 1 < ε₁₂/k_B = 5.

FIG. 5.

(a) Left: Initial configuration of a 2D system of two types of LJ particles. The red particles are type 1, and the blue particles are type 2. The interaction between similar particles is smaller than dissimilar ones and leads to a mixture (see the text for more details). Right: Final configuration of the system after 100 × 10⁶ steps of conventional MD. The fully mixed state cannot be captured at this time scale. (b) Evolution of the system during 750 accepted MDAS moves.

The particles maintain the same size difference as in the previous example, where σ₁₁ = 1.2, σ₂₂ = 0.8, and σ₁₂ = 1.0. The purpose of this second example is to demonstrate the enhancement of the rate of mixing (rather than de-mixing) of the two types in a condensed phase system where the equilibrium state is a random mixture. The simulation starts from a phase separated state. Figure 5(a) shows the initial configuration where 354 red particles and 791 blue particles filled the upper and lower parts of the simulation box, respectively. The fraction of the total area that is covered by the LJ disks is 0.88, corresponding to high particle density. Conventional MD is unable to model the mixed conformation in 100 × 10⁶ steps [Fig. 5(a)]. We use the same protocol discussed in the first example to gradually change the position of two randomly selected particles. Figure 5(b) shows the evolution of the system during the MDAS procedure. Comparing the number of force evaluations, we note that 750 accepted MDAS steps are equivalent to 100 × 10⁶ steps of conventional MD. After 750 MDAS steps, the fully mixed and converged structure is observed.

To further illustrate the convergence of the MDAS simulations, we also show in Fig. 6 the progression of the pair correlation function of type 2 particles to a stationary value as the system is mixed. The average acceptance ratio of MDAS moves in this example is approximately 0.2.

FIG. 6.

The pair correlation function of only the blue (type 2) particles is shown as a function of the number of MDAS steps for the system described in Fig. 5. At the beginning, the system is ordered and the pair correlation function (the blue dashed line) shows a series of long range peaks. After about 350 accepted MDAS steps (the dashed red line), the system converges to a typical liquid-like distribution with one dominant peak and a shallower secondary distance peak. The distribution after 750 accepted MDAS steps remains essentially unchanged (the yellow line).

The pair correlation function of only the blue (type 2) particles is shown in Fig. 6. The blue line is a pair correlation function for the initial structure and illustrates significant order in the system having multiple peaks. The two other correlation functions are computed after 350 MDAS steps (red) and after 750 MDAS steps (yellow). The last two are liquid-like, showing significantly less order and are similar, suggesting convergence of the equilibration process at about 350 accepted MDAS steps.

To further explore the relaxation to equilibration, we also consider the time dependence of the entropy of mixing. The starting configuration is the ordered system [Fig. 5(a)], and we continue the simulation to equilibrium. To compute the mixing entropy, we divide the simulation box to N_box = 20 cells. Ten cells along the y axis and two cells along the x axis are used. Since the changes in the particle types are observed along the y axis, more boxes were used along it. The number of red (type 1) particles in each cell was counted as a function of time. The probability of a red particle to be in box i was estimated, and the entropy was approximated as $S=-\frac{1}{N_{box}}\sum _{i=1}^{N_{box}}{p}_i\log \left(p_i\right)$. The mean-field single-particle expression follows the discussion in Ref. 58. Similar approximate expressions were used in other studies.⁵⁹ The lines in Fig. 7 are the mixing entropies that approach a maximum at $p_i=0.5\forall i$. The red line in Fig. 7 is the mixing entropy from the conventional MD trajectory. The dark blue line follows the mixing entropy of the MDAS simulation as a function of time. The half-life for the mixing entropy was about 10 × 10⁶ force evaluations for the MDAS simulation. After 200 × 10⁶ force evaluations, the conventional MD simulation does not reach half of the asymptotic value.

FIG. 7.

The time dependent relaxation of the mixing entropy toward an equilibrium value. The red line is the mixing entropy as a function of the number of steps in a conventional MD trajectory. The small “bump” at around 120 × 10⁶ steps is the result of melting of the first solid layer. The dark blue line is the mixing entropy in MDAS trajectory. We also show in yellow “X” the change in the maximum of the pair correlation function for the blue (type 2) particles (Fig. 6). Note the different scales on the right and on the left sides. The light blue line that starts after 100 × 10⁶ steps is a conventional MD trajectory that is initiated from the last MDAS configuration to check that the system is in equilibrium. The x axis is set in such a way that the same computational effort (number of force evaluations, including moves that were rejected) in conventional MD and MDAS trajectories is the same for each time slice.

We also show in Fig. 7 the maximum of the pair correlation function as a function of time (yellow “X”) in the MDAS simulation. This maximum shows slower relaxation than the mixing entropy. This observation suggests that the rate of approach to equilibrium depends on the order parameter that we use to probe it. It is therefore important to carefully choose an order parameter, or order parameters, relevant to the equilibrium features we wish to examine. If we examine local order in the system, the pair correlation function tells more than the mixing entropy.

Note also that the mixing entropy for the MD simulation seems to be stable after 120 × 10⁶ steps. This observation may lead to the incorrect conclusion that the MD trajectory has equilibrated by that time. To further test that the system indeed reached equilibrium in the MDAS simulation, we used the final configuration of the MDAS run and continue it using conventional MD for another 100 × 10⁶ steps. No further changes in the mixing entropy were observed, supporting our suggestion that equilibrium was indeed attained.

B. Example 2: Lipid bilayer binary mixture

In nature, biological membranes are composed of many different lipid molecules and this heterogeneity is believed to be crucial for their function. Modeling a system containing multiple types of lipids requires a large system to include low-concentration components. Such a large system needs a significantly longer simulation time to reach equilibrium, far beyond the capabilities of conventional MD simulation. MDAS may improve equilibration and sampling of heterogeneous membranes. To illustrate this, we implemented MDAS for a binary membrane composed of DOPC and POPC phospholipids [Fig. 8(a)].

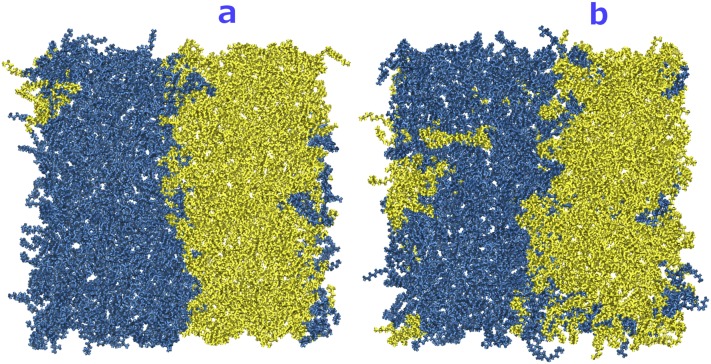
FIG. 8.

(a) Top view of the initial configuration of the DOPC/POPC system. POPC and DOPC molecules are shown in yellow and blue, respectively. (b) The system after 240 ns at a constant temperature of 300 K for comparison with MDAS results. After 240 ns, mixing of different lipids only starts at the boundaries between the lipid components. The images of the system were generated with VMD.⁴⁰

Initially each lipid type occupies half of the simulation box. Because of a highly similar melting temperature of the two phospholipids under considerations, they are known to be well mixed. In Fig. 8(b), we show that in conventional MD simulations of 240 ns the distribution of the phospholipid molecules hardly changes from the initial configuration.

To implement MDAS, we need to gradually convert a DOPC lipid to a POPC lipid and vice versa, as well as calculate the required work for the proposed alchemical exchange. A plausible alchemical path is to pick one lipid of each type randomly and gradually make them disappear, while at the same time a molecule of the other type gradually appears at the same position. This is the dual topology approach often used in alchemical evaluations of relative free energy changes computed by the free energy perturbation method.^35,60–63 However, we found in practice that this procedure has a low acceptance probability. The alchemical calculations require exchange of more than 100 atoms, which is costly and hard to complete without violation of hard-core overlaps. A more efficient approach to accomplish this task is to define a mixed topology^62,64 that includes a single copy of all the atoms that DOPC and POPC have in common plus the parts that are different in these molecules (Fig. 9). This mixed topology molecule has the ability to turn into either DOPC or POPC with the adjustment of only a few atoms. For example, according to Fig. 9(b), vanishing yellow particles and appearing green particles modify a DOPC to a POPC molecule.

FIG. 9.

(a) Schematic representation of the difference between DOPC and POPC molecules. Except for the 4 regions shown in green and yellow, the molecules are identical. MDAS proposes exchange of atom types of groups 1 and 3 with groups 2 and 4. Each time that a POPC turns into DOPC, 10 atoms vanish and 14 atoms appear and vice versa. (b) An example of a mixed topology molecule containing both the green and yellow regions shown in (a). (c) A schematic representation of MDAS on the DOPC/POPC mixture. Two randomly selected molecules turn to mixed topology and change their identity. An accepted MDAS move results in an exchange in the position of the selected molecules.

The algorithm is initiated by randomly picking a POPC and a DOPC molecule. Unless stated otherwise, we exchange molecules only in the upper leaflet of the membrane. The D trajectory is 100 ps long to allow for local equilibration and for sampling equilibrium configurations. The M trajectory (the alchemical step) is 40 ps long. At every 40 steps, the parameters of the non-bonded interactions are changed at a single step and the partial work, ω_i, is calculated. The partial charges are changed linearly by Δλ = 0.001 every 40 steps between the initial and final desired values, but for Van der Waals parameters a soft core potential is used to avoid the so-called end-point catastrophes⁶⁵

$$U_{soft}\left(r_{ij}\right)=4\epsilon \lambda \left[{\left(\frac{{\sigma }_{ij}}{r_{ij}^2+\eta \left(1-\lambda \right)}\right)}^6-{\left(\frac{{\sigma }_{ij}}{r_{ij}^2+\eta \left(1-\lambda \right)}\right)}^3\right],$$ (10)

where η = 5.0. Note that at λ = 1 the above expression turns into 6-12 Lennard-Jones and the interaction vanishes at λ = 0. After 40 000 steps with a time step of 1 fs, the selected DOPC and POPC molecules are exchanged. The total work performed on the system during this alchemical step can be calculated as $w={\Sigma }_{i=1}^{1000}{\omega }_i$. Then we apply the Metropolis criterion to reject or accept the M trajectory [Eq. (5)]. If the proposed move is accepted, a D trajectory is initiated from the last configuration of the M trajectory. If it is not, we return to the last configuration of the previous D trajectory. At this point, we may try a new M trajectory by selecting a different exchange pair, or if several M attempts fail, initiate a new D trajectory.

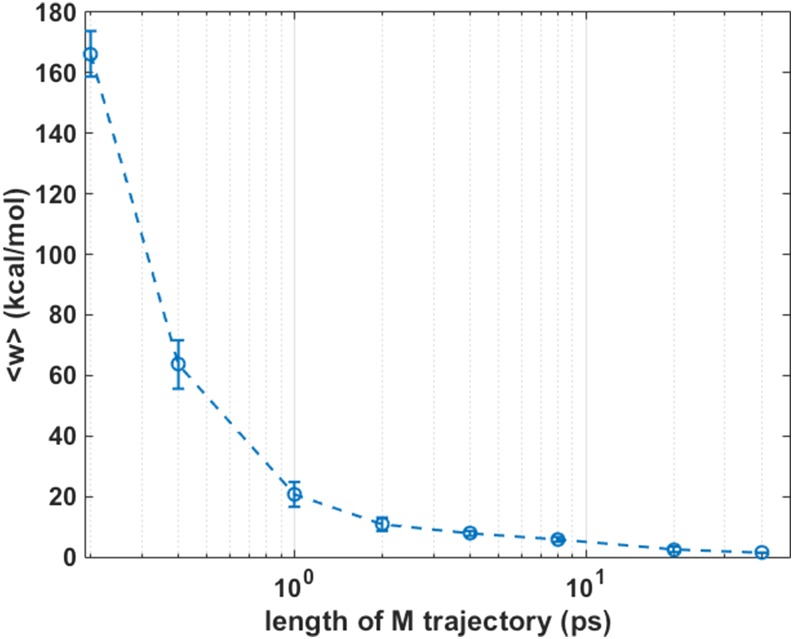
Figure 10 shows the average work, or the first moment “m,” of the work distribution P(w), which we modeled in Eqs. (6) and (7). The work is for a complete exchange of a pair of lipids conducted in an M trajectory. The average work, or the corresponding first moment m, is estimated from 100 M trajectories. At short length of M trajectories, the average work is large and positive resulting in very low acceptance ratios. This observation also illustrates why direct MC moves (M trajectories of one step) are inefficient for these systems. At longer times, the amount of work for making the exchange reduces as argued in Sec. II. At the limit of infinitely long time, the work to exchange a pair of molecules in a fluid system is zero. To appreciate the width of the work, distribution error bars are plotted in Fig. 10.

FIG. 10.

The average work in kcal/mol as a function of the length of the M trajectories. The data for averaging the work are obtained from 100 M trajectories at each length. This average corresponds to the first moment m of the work distribution that we modeled in Eqs. (6) and (7). The average work approaches zero when the trajectory length approaches infinite.

Figure 11 shows the evolution of the system after 500 accepted MDAS moves. The acceptance probability for this system is 0.33, and running MDAS to achieve 500 accepted moves is equivalent to ∼115 ns of conventional MD. Comparing to Fig. 8 of 240 ns of conventional MD, it is clear that MDAS reaches equilibrium much faster than conventional MD. In Fig. 12, the radial distribution function, g(r), of the distances between the choline nitrogen atoms of the head groups of the DOPC molecules is plotted. The pair correlation function is computed for the upper leaflet with the same expression we used for the LJ fluid. After 500 MDAS steps, the pair correlation function reaches equilibrium, yet conventional MD does not show any significant change from the initial distribution after 240 ns of simulation.

FIG. 11.

Top view of the DOPC/POPC system during 500 MDAS steps. POPC and DOPC molecules are shown in yellow and blue, respectively.

FIG. 12.

The MDAS evolution of the two-dimensional radial distribution function of DOPC head groups in the DOPC/POPC system. The dashed blue line corresponds to the initial distribution, and the solid green line shows the distance correlation function for conventional MD after 240 ns. The 350 MDAS moves and 500 MDAS moves are shown in dashed red and solid yellow, respectively. The g(r) for each step is averaged over configurations of the D trajectories. Configurations from the M trajectories are, of course, not included.

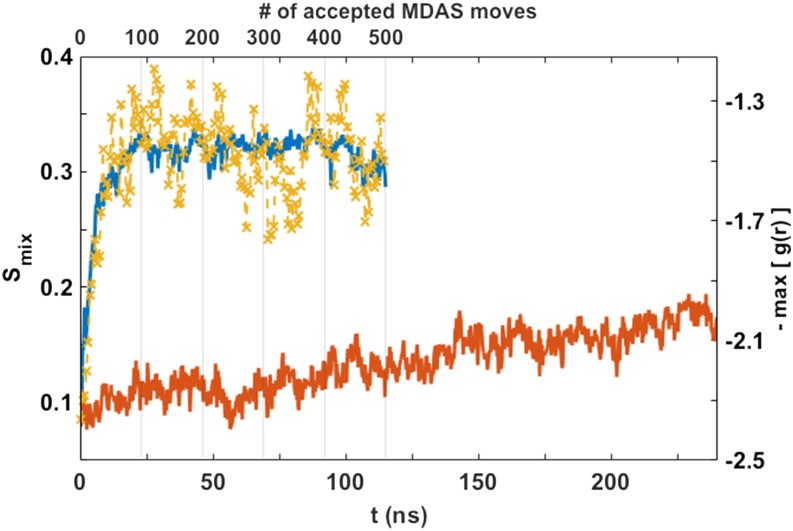
We also examined the mixing entropy in the MD and MDAS trajectories as a function of time (Fig. 13). The simulation box was divided into cells, and the probability of a particular type of a phospholipid to be in each cell was estimated. At the beginning, the DOPC lipids are separated from the POPC lipids along the x axis (Fig. 11). Large re-organization of the lipids is expected along the x axis during equilibration, and therefore more boxes are used along it. We use a finer grid of 10 cells along the x axis and only a grid of 2 cells along the y axis. After 40 ns, the MDAS simulation reached a plateau, while the MD simulation had not reached equilibrium after 240 ns. We also show the maximum value of the pair correlation function, max[g(r)], of the nitrogen atoms of the choline groups as a function of time (yellow X).

FIG. 13.

The entropy of mixing as a function of the simulation time for the DOPC/POPC system. The simulation with 500 MDAS moves is shown in blue. The unbiased MD is in red. The conventional MD hardly drifts toward equilibrium after 240 ns. The time evolution of the maximum of the pair correlation function of the DOPC head groups in the MDAS trajectory is shown in yellow “X,” and it overlays well with the mixing entropy. The time values are equivalent to the number of force evaluations, which for MDAS include moves that were not accepted.

C. Simultaneous and multiple exchange moves

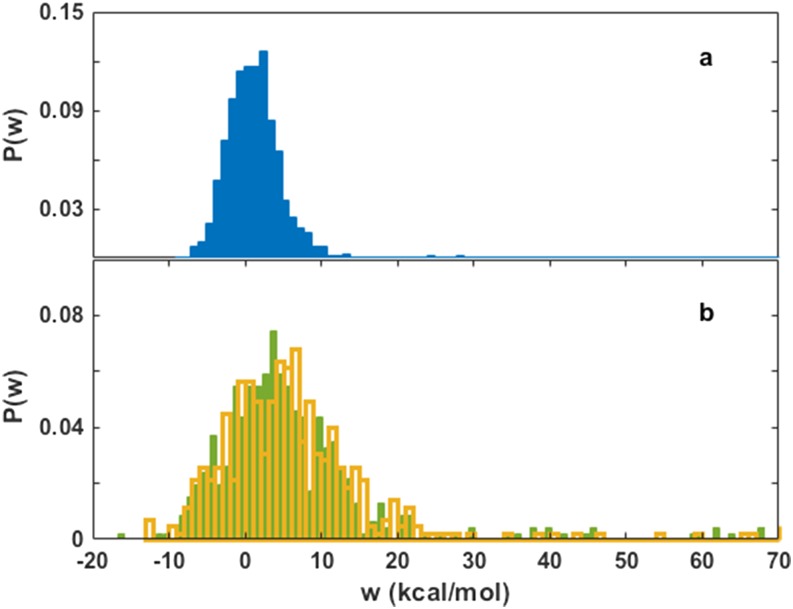
In Sec. II A we suggested that the use of multiple simultaneous trial moves can further improve the MDAS algorithm. Figure 1 illustrates domains of parameters for which such an improvement is expected. The efficiency of the algorithm is determined by the distribution of work, P(w). These distributions are shown for the DOPC/POPC system in Fig. 14 for one exchange per move, for four exchanges per single M trajectory in the upper leaflet, and for two exchanges per M trajectory in both the upper and lower leaflets. The distribution for a single exchange move has a mean value of 1.4 kcal/mol and a variance of 25.8 (kcal/mol)² and is approximately normal, thus multiple and simultaneously proposed moves are likely to benefit the acceptance and sampling of an MDAS simulation of the same M and D trajectory lengths.

FIG. 14.

The distributions of work obtained from 3 MDAS simulations for the DOPC/POPC system. (a) The distribution for a single proposed exchange move in the upper leaflet of the membrane. (b) The distributions of work for 4 proposed simultaneous exchange moves on the upper leaflet (yellow) and two exchange moves on each membrane leaflet (green). Note the similarity of the two distributions in (b) suggests that the simultaneous exchange moves are interacting weakly with each other. This is because the multiple sampled lipids are picked from different environments in the two cases. Note also that the size of the sample is insufficient to converge to a normal distribution.

We performed two simulations of multiple exchange moves. In the first, we apply 4 multiple exchanges per M trajectory of DOPC and POPC molecules on the upper leaflet. In the other simulation, we have 4 simultaneous exchanges per M trajectory too, but two simultaneous exchanges per M trajectory are proposed in each leaflet. Every time we choose 4 DOPC and 4 POPC lipid pairs at random, change their identity simultaneously, and calculate the work to examine the proposed move with the Metropolis criterion. If the move is rejected, we return to the initial state of the system before the M trajectory. If the move is accepted, we continue the simulation from the final coordinates of the M trajectory. The distribution of work obtained from these multiple moves is shown in Fig. 14. As expected, the distribution is wider than the one obtained from a single move and is skewed toward the positive values of work. The estimated acceptance probability of this move, composed of 4 exchanges, is 0.23. It is smaller than the acceptance probability of a single lipid exchange (∼0.33). However, since we exchange four pairs it is a significant enhancement of the rate of sampling.

To compare the three MDAS simulations, the maximum of the radial distribution function, max[g(r)], between the nitrogen atoms of the choline groups of DOPC is shown in Fig. 15 versus the computational cost for each of the simulations. The cost is estimated as the simulation time, which is equivalent to the number of force evaluations. Only the upper leaflet is considered. The thick lines are exponential fit to lines computed directly from the simulations. It can be seen that the simulations with multiple simultaneous proposed moves reach equilibrium faster that a single proposed move.

FIG. 15.

The evolution of the maximum of the pair correlation function, max[g(r)], of nitrogen atoms of the choline groups of the DOPC molecules as a function of the simulation time during the M and D trajectories. The solid lines are exponential fits to each curve. The reported time includes the rejected proposed moves.

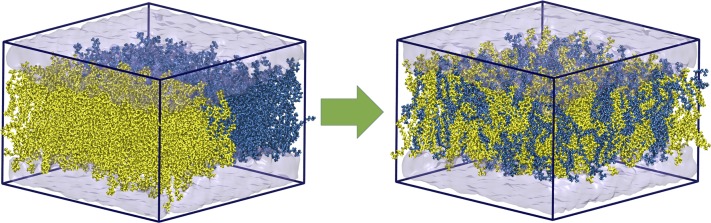
Figure 16 shows the equilibrated system for MDAS with 2 moves at each leaflet after 120 accepted moves. Counting the number of force evaluation (including accepted and rejected moves), we conclude that the MDAS simulation cost with 120 accepted moves is equivalent to 33 ns conventional MD.

FIG. 16.

The initial (left) and final (right) configurations of the DOPC/POPC system obtained from 2 simultaneous moves in each leaflet after 120 accepted MDAS moves, equivalent in cost to a 33 ns MD simulation.

IV. CONCLUSIONS

Simulations of membrane systems are challenging due to the large temporal and spatial scales that impact the system dynamics. Biological membranes are even more complex due to their heterogeneity. They consist of thousands of different types of phospholipids, which sometimes separate and aggregate to form rafts.^4,8–10,23 The heterogeneity and effective partitions between phases are not always known to begin with and require long simulations with large spatial rearrangements to converge. Important biological inserts to membranes, such as transmembrane proteins, add another layer of complexity.

In the present manuscript, we exploit non-equilibrium concepts proposed by Jarzynski³¹ and general algorithm development of a candidate Monte Carlo move^30,32 to propose an algorithm for efficient simulation of equilibrium in heterogeneous fluids. We illustrate that the algorithm performs well in heterogeneous systems and is therefore promising in further studies of membrane systems in biology. The mixture of equilibrium and non-equilibrium dynamics already showed promise in a number of other molecular systems such as simulation of docking sites.³² The generality of the combination of conventional MD and alchemical intermediates is likely to impact other fields as well.

In the field of simulations of biological membranes, more can be done to design moves for dissimilar molecules (e.g., cholesterol–phospholipid pairs and charged phospholipid–ion pairs) to increase acceptance and the rate of approach to equilibrium. The design of such moves to diverse materials is perhaps the greatest challenge to the proposed methodology.