Single-molecular and ensemble-level oscillations of cyanobacterial circadian clock

Abstract

When three cyanobacterial proteins, KaiA, KaiB, and KaiC, are incubated with ATP in vitro, the phosphorylation level of KaiC hexamers shows stable oscillation with approximately 24 h period. In order to understand this KaiABC clockwork, we need to analyze both the macroscopic synchronization of a large number of KaiC hexamers and the microscopic reactions and structural changes in individual KaiC molecules. In the present paper, we explain two coarse-grained theoretical models, the many-molecule (MM) model and the single-molecule (SM) model, to bridge the gap between macroscopic and microscopic understandings. In the simulation results with these models, ATP hydrolysis in the CI domain of KaiC hexamers drives oscillation of individual KaiC hexamers and the ATP hydrolysis is necessary for synchronizing oscillations of a large number of KaiC hexamers. Sensitive temperature dependence of the lifetime of the ADP bound state in the CI domain makes the oscillation period temperature insensitive. ATPase activity is correlated to the frequency of phosphorylation oscillation in the single molecule of KaiC hexamer, which should be the origin of the observed ensemble-level correlation between the ATPase activity and the frequency of phosphorylation oscillation. Thus, the simulation results with the MM and SM models suggest that ATP hydrolysis stochastically occurring in each CI domain of individual KaiC hexamers is a key process for oscillatory behaviors of the ensemble of many KaiC hexamers.

Significance.

Cyanobacterial proteins, KaiA, KaiB, and KaiC, can reconstitute a circadian clock when they are incubated with ATP in vitro. In order to understand this prototypical oscillator, we need to analyze both synchronization of a macroscopically large number of oscillating molecules and microscopic reactions in individual molecules. We introduced two theoretical models to unify macroscopic and microscopic viewpoints. Simulation results suggest that ATP hydrolysis is necessary for synchronization and temperature compensation and that ATPase activity is correlated to the oscillation frequency in individual molecules. Thus, ATP hydrolysis stochastically occurring in individual molecules should determine important features of the ensemble-level oscillation.

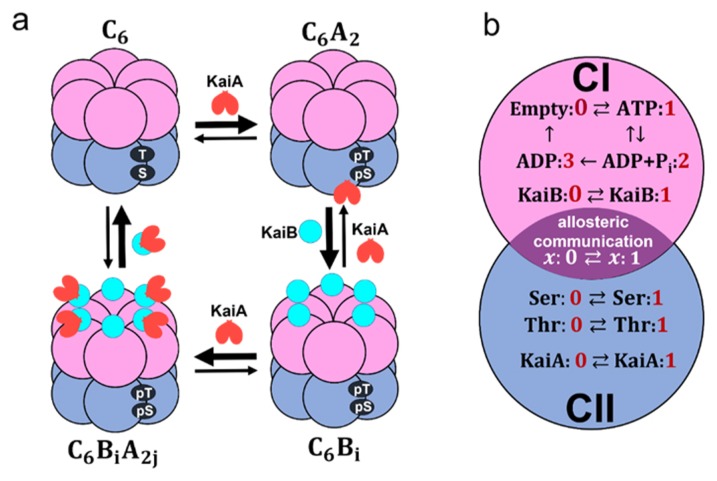
A cyanobacterial protein, KaiC, shows a stable oscillation in its phosphorylation level with approximately 24 h period when three proteins, KaiA, KaiB, and KaiC, are incubated with ATP in vitro [1]. Much attention has been focused on this prototypical oscillator and close investigations have been made on interactions among Kai proteins [2,3]. As shown in Figure 1, KaiC monomer consists of tandemly repeated N-terminal (CI) and C-terminal (CII) domains [4] and assembles into a hexamer [5,6] forming the CI–CII double rings [7]. We denote this KaiC hexamer as C₆. KaiA forms a dimer [8] and binds to the CII ring of C₆ to form a complex, C₆A₂ [9]. KaiB binds to the CI of each subunit of KaiC hexamer, and a KaiA dimer can further bind to each KaiB to form C₆B₆A_2j with 0 ≤ j ≤ 6 [10]. KaiC shows auto-phosphorylation (P) and auto-dephosphorylation (dP) at two specific sites, Ser431 and Thr432, of each CII domain, and the P reactions are promoted in the C₆A₂ complex [11–13]. In C₆B₆A_2j, binding of KaiA to the CII is suppressed, which promotes the dP reactions of KaiC [14,15]. Thus, the temporal appearance of different kinds of complexes, accompanied by the switching between P-phase and dP-phase, is the important feature of the oscillation in the KaiABC system.

Figure 1.

Coarse-grained models of the KaiABC system. a) Schematic of interactions among Kai proteins considered in the MM model. Two phosphorylation sites, Ser431 and Thr432, of each subunit in the CII domain (blue) are repeatedly phosphorylated (pS, pT) and dephosphorylated (S, T). KaiA dimer (red) binds to KaiC hexamer C₆ to form C₆A₂. The CI (pink) of each subunit binds to KaiB (cyan) to form C₆B_i with 1 ≤ i ≤ 6, which further binds to KaiA dimers to form C₆B_iA_2j with 1 ≤ j ≤ i. b) Reactions and states in a KaiC subunit in the SM model. ATP hydrolysis reactions and KaiB binding/dissociation reactions occur in the CI domain (pink). Phosphorylation (P)/dephosphorylation (dP) reactions and KaiA binding/dissociation reactions take place in the CII domain (blue). CI and CII domains are coupled through allosteric structural change.

In order to elucidate the mechanism of this KaiABC clockwork, we need to understand both the microscopic atomic-scale dynamics of reactions in individual molecules [16] and the macroscopic ensemble-level synchronization among many KaiC molecules; because the ensemble-level oscillation vanishes when individual molecules oscillate independently of each other, synchronization of a macroscopically large number of molecules is necessary for maintaining the coherent oscillation as observed in test tube. Therefore, it is important to understand mechanisms at both microscopic and macroscopic levels.

A key observation for solving the problem of the relationship between mechanisms at two levels is the slow ATPase reactions in KaiC. The CI domain of each KaiC subunit hydrolyzes approximately 10 ATP molecules and the CII domain of each subunit hydrolyzes several ATP molecules per one day [16,17]. In particular, by comparing KaiC molecules of various mutants, it was shown that the ATPase activity is correlated to the frequency of the ensemble-level P/dP rhythm [16,17], where the ATPase activity was measured by the frequency of ADP release in the condition in the absence of KaiA and KaiB, which is the non-oscillatory condition, and the frequency of the ensemble-level P/dP rhythm was measured in the oscillatory condition with appropriate concentrations of KaiA and KaiB. Furthermore, the ATPase activity of the truncated CI domain shows correlation to the frequency of the ensemble-level P/dP rhythm [16]. These observations suggested the intrinsic relationship between ATP hydrolysis occurring in the CI of individual molecules and the P/dP rhythm of the ensemble of many molecules [16–18].

Many theoretical models were developed by describing concentrations of various molecular species with continuous variables in kinetic differential equations to model the ensemble-level macroscopic dynamics of the oscillating system [11,19–24]. With these macroscopic models, various nonlinear mechanisms, including KaiA sequestration at various phases [11,19–23] and monomer shuffling [24], were proposed to explain how the oscillation is maintained. Other models described the system with the Monte Carlo methods by explicitly considering stochastic P/dP reactions in individual molecules and stochastic binding reactions among many molecules [23–27]. These Monte Carlo-type models should be useful for analyzing the relation between microscopic and macroscopic mechanisms. However, the ATP hydrolysis reactions and the activated intramolecular dynamics with ATP consumption were not considered in these models. The role of ATP consumption was analyzed by recent models [28,29], and the further comprehensive analyses are required for elucidating the relationship between ATP hydrolysis and the P/dP rhythm [29].

Here, in the present paper, we explain two “mesoscopic” models of oscillation for bridging the microscopic and macroscopic- level descriptions; the many-molecule (MM) model, and the single-molecule (SM) model. In both models, structure and reactions in individual KaiC molecules are represented by coarse-grained variables. For example, structure of the kth KaiC hexamer is represented by an order parameter, X_k (X in the SM model by dropping the suffix k); structural transition is described by the change between states with X_k ≈ 0 and X_k ≈ 1. In particular, the role of ATP hydrolysis is investigated with these models by considering the effects of ATPase reactions on the structural change; X_k is perturbed by the ATP hydrolysis in these models, and binding/dissociation reactions, P/dP reactions, and ATPase reactions are affected by X_k. With the MM model in the present paper, intermolecular interactions are analyzed to examine the necessary conditions for the stable ensemble-level oscillation. This model was introduced in our previous publication [29], and is used in the present paper to analyze the mechanism of synchronization and temperature compensation. In the SM model, more emphasis is placed on the intramolecular dynamics to analyze the origin of oscillation of individual molecules. In the present paper, we discuss the linkage between microscopic and macroscopic oscillations through the combined analyses with the MM and SM models.

Methods

The many-molecule (MM) model

In order to analyze the oscillation of ensemble of molecules, we use the many-molecule (MM) model introduced in our previous publication [29]. In the MM model, we describe structure and reactions of individual molecules in a coarse-grained manner and calculate the coupled dynamics of N = 1000 hexamers of KaiC by explicitly following the dynamics of individual hexamers. As represented in Figure 1a, we assume that a KaiA dimer binds to a KaiC hexamer to form C₆A₂. KaiB monomer binds to each subunit of KaiC to form C₆B_i with 1 ≤ i ≤ 6, and KaiA can further bind to C₆B_i to form C₆B_iA_2j with 1 ≤ j ≤ i [10]. We assume that the dimerization reaction 2A ⇌ A₂ is fast enough and equilibrated in the solution, and the concentration of A₂ is always proportional to the square of the concentration of A. Therefore, all the reactions involving A₂ are represented in terms of A for the convenience of model description. Then, the binding/unbinding reactions in the model are represented as

$$\begin{array}{l}2\text{A}+{\text{C}}_6\rightleftharpoons {\text{C}}_6{\text{A}}_2,\\ \text{B}+{\text{C}}_6{\text{B}}_i{\text{A}}_{2j}\rightleftharpoons {\text{C}}_6{\text{B}}_{i+1}{\text{A}}_{2j},\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{for\hspace{0.28em}}0\le i\le 5,0\le j\le i,\\ 2\text{A}+{\text{C}}_6{\text{B}}_i{\text{A}}_{2j}\rightleftharpoons {\text{C}}_6{\text{B}}_i{\text{A}}_{2j+2},\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{for\hspace{0.28em}}1\le i\le 6,0\le j\le i-1.\end{array}$$ (1)

We should note that C₆B₀A₀ in Eq. 1 is identical to C₆. We define P_C6A2(k, t) and P_C6BiA2j(k, t) as the probabilities of the kth KaiC hexamer C₆ to be bound in forms of C₆A₂ and C₆B_iA_2j, respectively, with 0 ≤ i ≤ 6 and 0 ≤ j ≤ i at time t and k = 1, …, N. Thus, the kinetic equation for P_C6A2 is given as

$$\frac{d}{dt}{P}_{C_6{A}_2}(k,t)=h_A{A}^2{P}_{C_6{B}_0{A}_0}(k,t)-f_A{P}_{C_6{A}_2}(k,t),$$ (2)

and the kinetic equation for P_C6BiA2j with 2 ≤ i ≤ 5 and 1 ≤ j ≤ i – 1 is

$$\begin{array}{l}\frac{d}{dt}{P}_{C_6{B}_i{A}_{2j}}(k,t)=(7-i)h_{B}B{P}_{C_6{B}_{i-1}{A}_{2j}}(k,t)-(i-j)f_B{P}_{C_6{B}_i{A}_{2j}}(k,t)\\ -(6-i)h_{B}B{P}_{C_6{B}_i{A}_{2j}}(k,t)+(i+1-j)f_B{P}_{C_6{B}_{i+1}{A}_{2j}}(k,t)\\ +(i-j+1)h_{BA}{A}^2{P}_{C_6{B}_i{A}_{2j-2}}(k,t)-j{f}_{BA}{P}_{C_6{B}_i{A}_{2j}}(k,t)\\ -(i-j)h_{BA}{A}^2{P}_{C_6{B}_i{A}_{2j}}(k,t)+(j+1)f_{BA}{P}_{C_6{B}_i{A}_{2j+2}}(k,t).\end{array}$$ (3)

See the Methods section of Ref. 29 for the equations in more general cases with 0 ≤ i ≤ 6 and 0 ≤ j ≤ i. Here, h_A, f_A, h_B, f_B, h_BA and f_BA are rate constants, and A and B are concentrations of unbound free KaiA and KaiB molecules, respectively. When we numerically solve Eqs. 2 and 3, we impose the following constraints;

$$\begin{array}{l}{P}_{C_6{A}_2}(k,t)+{\sum }_{i=0}^6{\sum }_{j=0}^i{P}_{C_6{B}_i{A}_{2j}}(k,t)=1,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{for\hspace{0.28em}}k=1,\dots ,N,\\ A_T=A+\frac{2}{V}{\sum }_{k=1}^N\left(P_{C_6{A}_2}(k,t)+{\sum }_{i=1}^6{\sum }_{j=1}^{i}j{P}_{C_6{B}_i{A}_{2j}}(k,t)\right),\\ B_T=B+\frac{1}{V}{\sum }_{k=1}^N{\sum }_{i=1}^6{\sum }_{j=1}^{i}i{P}_{C_6{B}_i{A}_{2j}}(k,t),\end{array}$$ (4)

where A_T and B_T are total concentrations of KaiA and KaiB, respectively, and V is the volume of the system. In this paper, we use units with V = 1.

Biochemical and structural observations [30–33] have suggested that the structure of KaiC hexamer at the phosphorylated state is different from the structure of KaiC hexamer at the unphosphorylated state. The structure at the unphosphorylated state is more stable than the structure at the phosphorylated state [33]. Assuming that a KaiC hexamer has a tight structure at the unphosphorylated state and a loose structure at the phosphorylated state, we can represent the allosteric transition between tight and loose structural states with a continuous variable X as X_k ≈ 1 when the structure of the kth KaiC hexamer is in the tight structural state, and X_k ≈ 0 when it is in the loose structural state. In Eqs. 2 and 3, we assume that the binding rate constants, h_A and h_B, and the dissociation rate constants, f_A and f_B, depend on the KaiC structure, X_k(t);

$$\begin{array}{l}{h}_A(k,t)=h_A^1{X}_k,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{f}_A(k,t)=f_A^0\hspace{0.17em}(1-X_k),\\ h_B(k,t)=h_B^0\hspace{0.17em}(1-X_k),\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{f}_B(k,t)=f_B^1{X}_k,\end{array}$$ (5)

where $h_A^1,h_B^0,f_A^0$, and $f_B^1$ are constants. With this assumption, the binding affinity of KaiA to KaiC increases when the kth KaiC is in the tight structural state. On the contrary, the loose structure of KaiC promotes KaiB binding to the KaiC hexamer. Because KaiA binds to KaiB in making C₆B_iA_2j, and does not bind directly to KaiC, we assume that the binding rate constant, h_BA, and the dissociation rate constant, f_BA, are independent of X_k(t).

In the MM model, the phosphorylation level of twelve sites (Ser431 and Thr432 in six subunits) of a single KaiC hexamer is represented by a continuous variable D as D_k(t) ≈ 1 when the 12 sites of the kth KaiC hexamer are fully phosphorylated, and D_k(t) ≈ 0 when the 12 sites are fully dephosphorylated. We describe the transition between D_k(t) ≈ 1 and D_k(t) ≈ 0 with the following kinetic equation,

$$\frac{d{D}_k}{dt}=k_p{P}_{C_6{A}_2}(k,t)-k_{dp}\left(1-P_{C_6{A}_2}(k,t)\right)-\frac{\partial }{\partial D_k}g(D_k).$$ (6)

Here, k_p and k_dp are rate constants of P and dP reactions, respectively, and ɡ(D) = aD(D – 1)(D – 1/2)² with a > 0. ɡ(D) is a double-well potential function, which has been used to describe two-state transition dynamics of spins or model neurons with kinetic differential equations [34], and here it was introduced to assume the bistability of the oscillating variable D. We also assume that the structural transition of KaiC between tight and loose states is much faster than other reactions in the system; therefore, the structure X_k can be represented as a quasi-equilibrium average. In this paper, this average is determined under the mean-field generated by D_k, the binding probability of KaiA and KaiB, and the effect of ATPase reaction as

$$X_k(t)=\frac{1}{2}\text{tanh\hspace{0.17em}}\left[\beta \left(c_0-c_1{D}_k(t)+c_2{p}_k^A\hspace{0.17em}(t)-c_3{p}_k^B\hspace{0.17em}(t)-q_k(t)\right)\right]+\frac{1}{2},$$ (7)

where β = 1/k_BT with k_B being the Boltzmann constant, and c₀, c₁, c₂, and c₃ are constants. $p_k^A\hspace{0.17em}(t)=P_{C_6{A}_2}(k,t)$ represents the level of KaiA binding to the kth KaiC hexamer, and the term $p_k^B\hspace{0.17em}(t)={\sum }_{i=1}^6\text{tanh\hspace{0.17em}}(i/n_B){\sum }_{j=0}^i{P}_{C_6{B}_i{A}_{2j}}(k,t)$ is the binding level of KaiB. We use n_B = 1 in this paper. The term q_k(t) represents the effect of ATPase reactions.

The term c₁D_k(t) with c₁ > 0 in Eq. 7 brings a negative feedback effect in the system. KaiC structure tends to stay in the loose structure with large D_k and small X_k, which reduces the binding affinity of KaiA in Eq. 5 and decreases P_C6A2(k, t) in Eq. 2. As a result, D_k is reduced in Eq. 6. The term $c_3{p}_k^B\hspace{0.17em}(t)$ with c₃ > 0 represents a positive feedback. Large $p_k^B\hspace{0.17em}(t)$ value, along with small X_k, brings KaiC structure to the loose state, which in turn increases the binding affinity of KaiB to KaiC through Eq. 5 and increases P_C6BiA2j (k, t) in Eq. 3. Competition among multiple feedback interactions leads the system to have multiple stationary states as described above. However, the system is easily shifted among the states when small perturbations are added to produce oscillation in the system. The term q_k(t), representing the effect of ATPase reactions, works as a perturbation.

The precise mechanism of ATPase reactions in KaiC has not been elucidated. In the other ATPases such as myosins [35], kinesins [36], and chaperonins [37], reactions proceed as (i) binding of ATP → (ii) hydrolysis of ATP → (iii) release of inorganic phosphate (P_i) → (iv) release of ADP. In F₁-ATPase, on the other hand, it has been claimed that the ADP release takes place prior to the P_i release [38], although this remains controversial [39]. Because KaiC has a P-loop motif, which is similar to the corresponding ATP-binding motifs of myosins, kinesins and chaperonins, we assume in the present paper that the P_i release is prior to the ADP release in KaiC. We assume that ATP is stochastically hydrolyzed with a frequency f₀ in each CI domain of subunits of each KaiC hexamer: q(i; k, t) = 0 when no nucleotide is bound or ATP is bound at time t in the ith subunit of the kth KaiC hexamer, and when ATP is hydrolyzed to be ADP and P_i, q(i; k, t) turns to nonzero as q(i; k, t) = q₀ ≠ 0. We consider that this switching from 0 to q₀ stochastically takes place with the frequency f₀ at each subunit. After q (i; k, t) turns to nonzero at time t = t₀, the ADP is kept bound for a time duration δ_k, which is represented by setting q(i; k, t) = q₀ for t₀ ≤ t ≤ t₀ + δ_k. Then, at t = t₀ + δ_k, the ADP is released and q(i; k, t) is set back to q(i; k, t) = 0. Because the observed ATPase activity is larger in the P-phase [17], we assume that the overall ATPase reaction rate is increased with a shorter ADP binding duration time δ_k when X_k is larger as

$${\delta }_k={\delta }_0(1-X_k).$$ (8)

The overall ATPase reaction rate decreases when δ_k is larger; with the parameterization in Ref. 29, δ_k was larger than in the present parameterization, which resulted in the smaller ATPase activity than in the present paper, but the qualitative behavior of the model was the same as the present work. Biochemical and NMR data suggested that the ATPase activity in the CI is necessary for the binding of KaiC to KaiB [31,33,40], which indicated that the ATP hydrolysis enhances the binding affinity of KaiC to KaiB. Therefore, we assume that the ATP hydrolysis changes the KaiC structure from tight to loose states. We represent this effect by imposing q₀ > 0 and writing the effects of ATP hydrolysis on the structure as $q_k(t)={\sum }_{i=1}^{6}q(i;k,t)$.

We should note that the following alternative assumption is also possible; q(i; k, t) = q₀ > 0 when P_i is released from the KaiC subunit but ADP is kept bound and q(i; k, t) = 0 when ATP is bound, ADP and P_i are bound or no nucleotide is bound on the CI [29]. There is no mathematical difference between this assumption and the assumption made in the last paragraph with the present simplified description of the ATPase reactions in the MM model. More precise modeling is necessary for distinguishing these different reaction schemes, but we do not go into these details in the present paper. We also note that the model feature remains unchanged even when the alternative mechanism of ATPase reactions with the ADP release prior to the P_i release is assumed; the mathematical structure of the model is not altered if we assume that q(i; k, t) = q₀ when P_i is kept bound.

Because ATP hydrolysis takes place predominantly in the CI domain and P/dP reactions occur in the CII domain, communication between CI and CII is needed to explain the observed effects of ATP hydrolysis on the P/dP reactions. In the present MM model, allosteric structural change represented by the change in X_k in Eqs. 5–8 enables such communication. The overall ATPase reaction rate is modulated by X_k through the change of the duration time of ADP bound state δ_k as in Eq. 8, but the timing of ATP hydrolysis is determined stochastically with the frequency f₀ in each subunit of each KaiC hexamer.

Eqs. 2–7 are numerically solved to follow the temporal change of D_k, X_k, P_C6A2(k, t), P_C6BiA2j(k, t), and $P_{CBA}(k,t)={\sum }_{i=1}^6{\sum }_{j=1}^i{P}_{C_6{B}_i{A}_{2j}}(k,t)$ by stochastically varying q(i; k, t) with the frequency f₀ and the lifetime δ_k with i = 1, …, 6 and k = 1, …, N. Oscillations in the ensemble level are monitored by calculating

$$\begin{array}{l}\overline{D}=\frac{1}{N}{\sum }_{k=1}^N{D}_k,\\ \overline{X}=\frac{1}{N}{\sum }_{k=1}^N{X}_k,\\ {\overline{P}}_{C_6{A}_2}=\frac{1}{N}{\sum }_{k=1}^N{P}_{C_6{A}_2}(k,t),\\ {\overline{P}}_{C_6{B}_i{A}_{2j}}=\frac{1}{N}{\sum }_{k=1}^N{P}_{C_6{B}_i{A}_{2j}}(k,t),\end{array}$$

and

$${\overline{P}}_{CBA}=\frac{1}{N}{\sum }_{k=1}^N{\overline{P}}_{CBA}(k,t).$$

Parameters in the MM model

We assume that the P/dP reactions are slow enough with the rates k_p~0.5–1 h⁻¹ and k_dp~0.5–1 h⁻¹ to realize the period ~24 hour of the P/dP rhythm as was suggested by Ref. [21]. The time scale of ATPase reactions, $f_0^{-1}$ and δ_k, should be also as slow as f₀~1–2 h⁻¹ and δ_k~0.5–1 hour; these slow rates of ATPase reactions are consistent with the structural observation [16]. We assume that the binding/dissociation rates of KaiA and KaiB defined as h_AA², h_BAA², h_BB, f_A, f_BA, and f_B should be h⁻¹–min⁻¹; such slow binding/dissociation of KaiB is consistent with the observed data [21,41]. With this rough estimation of parameter values, the ensemble oscillation in the MM model appears to be stable for the wide range of parameter values. We should note that the simulated period of oscillation depends on the parameter choice as discussed in the previous paper [29]. Because different values of period from 22 h to 26 h [1,42,43] were observed in different experimental conditions, we do not calibrate the parameters to reproduce a particular experimental report but use a typical set of parameters to grasp the important features of the oscillation. An example parameter set is summarized in Table 1. Unless otherwise mentioned, we discuss the results calculated with this parameter set in Results and Discussion section.

Table 1.

Parameters in the MM model

Rate constant of KaiA binding to KaiC	$h_A^1$	6.6 × 10−6 h−1
Rate constant of KaiB binding to KaiC	$h_B^0$	2 × 10−6 h−1
Rate constant of KaiA binding to KaiB	hBA	1.8 × 10−6 h−1
Rate constant of KaiA dissociation from KaiC	$f_A^0$	6 × 10−1 h−1
Rate constant of KaiB dissociation from KaiC	$f_{\text{B}}^1$	4 × 10−1 h−1
Rate constant of KaiA dissociation from KaiB	fBA	2 × 10−1 h−1
Constant for variable confinement	a	2.2 h−1
Rate constant of phosphorylation	kp	4.4 × 10−1 h−1
Rate constant of dephosphorylation	kdp	4.4 × 10−1 h−1
Frequency of ATP hydrolysis	f0	2.2 h−1
Max. lifetime of ADP binding after hydrolysis	δ0	2.6 h
Effect of ATP hydrolysis on structure	q0	kBT0*
Base-line temperature effect on structure	c0	10kBT0*
Effect of phosphorylation on structure	c1	8kBT0*
Effect of KaiA binding on structure	c2	0
Effect of KaiB binding on structure	c3	4kBT0*
Total copy number of KaiA monomers	AT	2N
Total copy number of KaiB monomers	BT	20N
Total copy number of KaiC hexamers	N	1000
System volume	V	1

^*T₀ = 30°C

In Table 1, the total concentrations of KaiA and KaiB, A_T and B_T, are set to 2N/V and 20N/V, respectively. In monomer basis, this corresponds to the concentration ratio of KaiA:KaiB:KaiC = 1:10:3. In many in vitro experimental measurements the ratio was set to KaiA:KaiB:KaiC = 1:3:3 [13,17,33], and the effects of varying these concentrations were tested by Nakajima et al. [43]. They showed that the oscillation amplitude and period were not changed when the KaiB concentration was varied between KaiA:KaiB:KaiC = 1:3:3 and 1:15:3 [43]. A_T and B_T used in Table 1 fall in this range. Values in Table 1 are shown with units of V = 1. Alternatively, by using units of V = 3 × 10⁻¹⁵ l, concentration of KaiC can be converted to 6N/V ≈ 3.3 μM with N = 1000, which is close to 3.5 μM, the KaiC concentration often used in in vitro experiment. A typical value of KaiB binding rate constant, which is $h_B^0=2\times {10}^{-6}\hspace{0.17em}{\text{h}}^{-1}$ with units of V = 1, can be converted to $h_B^0=(6.02\times {10}^{23})\times (3\times {10}^{-15})\hspace{0.17em}{\text{M}}^{-1}\times (2\times {10}^{-6}\hspace{0.17em}{\text{h}}^{-1})\approx 3.6\times {10}^3\hspace{0.17em}{\text{M}}^{-1}\hspace{0.17em}{\text{h}}^{-1}$ with units of V = 3 × 10⁻¹⁵ l. This value should be directly compared with the observed data when the experimental data of KaiB monomer kinetics becomes available.

The single-molecule (SM) model

In the MM model, the structure and reactions of individual molecules were described in a simplified manner to facilitate the calculation of an ensemble of a large number of molecules. In order to further analyze the role of ATPase reactions, we introduce a single-molecule model of KaiC hexamer by describing the more details of intra-molecular reactions and structural changes.

In the SM model, each subunit of a hexamer follows two conformational states; x_i = 0 when the ith subunit is in the loose structural state and x_i = 1 when it is in the tight structural state with i = 1, …, 6. Though both CI and CII domains have nucleotide binding sites, we focus on the CI domain because ATPase activity is predominant in the CI domain. The four nucleotide binding states in the CI of the ith subunit are represented as a_i = 0 when no nucleotide is bound, a_i = 1 when ATP is bound, a_i = 2 when ADP and P_i are bound, and a_i = 3 when P_i is released and ADP is kept bound. As shown in Figurer 1b, we define variables, Ser_i and Thr_i, as Ser_i = 1 (Thr_i = 1) when Ser431 (Thr432) of the ith subunit is phosphorylated and Ser_i = 0 (Thr_i = 0) when Ser431 (Thr432) of the ith subunit is dephosphorylated. We write KaiA = 1 when a KaiA dimer binds to the CII ring and KaiA = 0 when a KaiA dimer dissociates from the CII ring. We write KaiB_i = 1 when a KaiB monomer binds to the ith subunit and KaiB_i = 0 when a KaiB monomer dissociates from the ith subunit. Thus, as shown in Figure 1b, the state of KaiC subunits in the SM model is described by the variable KaiA and others;

$$\text{State\hspace{0.17em}of\hspace{0.17em}KaiC\hspace{0.17em}subunits}=KaiA,\hspace{0.17em}\{{KaiB}_i,a_i,{Ser}_i,{Thr}_i,x_i\}\hspace{0.17em}\text{with\hspace{0.17em}}i=1,\dots ,6.$$ (9)

Because the atomic structure is rapidly changing with the time scale of milliseconds or shorter but other variables should change more slowly in minutes or longer time scales, we describe the free energy G of the KaiC hexamer as a function of {x_i} as G = G (x₁, x₂, …, x₆);

$$G(x_1,x_2,\dots \dots ,x_6)={\displaystyle \sum _{i=1}^6}{x}_i[b_0+b_1^{Thr}{Thr}_i+b_1^{Ser}{Ser}_i-b_{2}KaiA+b_3{KaiB}_i-b_4\theta \hspace{0.17em}(a_i)]-J{\displaystyle \sum _{i=1}^6}\left(x_i-\frac{1}{2}\right)\left(x_{i+1}-\frac{1}{2}\right),$$ (10)

where b₀, $b_1^{Thr},b_1^{Ser}$, b₂, b₃, b₄, and J are constants. In the last term of Eq. 10, x₇ = x₁. If we regard the fast varying quantities {x_i} as “spin variables”, G of Eq. 10 should correspond to the “effective Hamiltonian” for spins, whereas the slow variables, Thr_i, Ser_i, KaiA, KaiB_i and θ(a_i) correspond to the magnetic fields acting on the spins. In other words, phosphorylation states, binding states, and ATPase states give biases for the structural change of each KaiC subunit. J represents coupling between two neighbor subunits; J > 0 implies that subunits change their structures in a cooperative way to give rise to two-state allosteric structure transition of the KaiC hexamer. The term x_ib₄θ(a_i) represents coupling between ATPase reactions and structure. Here, we assume that θ(a_i) = −1 when a_i = 2 or 3, θ(a_i) = 1 when a_i = 1, and θ(a_i) = 0 when a_i = 0. These assumptions imply that ATP binding increases the tendency of KaiC hexamer structure to be tight while the binding of ADP + Pi or ADP loosens the structure.

For the time scale of minutes, we can represent the structural state of each KaiC subunit with a quasi-equilibrium thermal average of x_i as 〈x_i〉= Tr x_i exp(−βG)/Z by approximately treating Thr_i, Ser_i, KaiA, KaiB_i, and θ(a_i) as stationary variables, where Tr represents a sum over all possible values of {x_i} and Z is a partition function, Z = Tr exp(−βG). Then, we represent the hexamer state by using the following variables;

$$\begin{array}{l}Ser=\frac{1}{6}{\displaystyle \sum _{i=1}^6}{Ser}_i,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }Thr=\frac{1}{6}{\displaystyle \sum _{i=1}^6}{Thr}_i,\\ X=\frac{1}{6}{\displaystyle \sum _{i=1}^6}\langle x_i\rangle ,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }D=\frac{1}{2}(Ser+Thr),\end{array}$$ (11)

where X and D correspond to X_k and D_k in the MM model.

By comparing Eqs. 7 and 10, we find that b₀, $b_1^{Thr}$ and $b_1^{Ser}$, b₂, b₃, and b₄ in the SM model correspond to c₀, c₁, c₂, c₃, and q₀ in the MM model, respectively. Thus, we find multiple feedback relations working through Eq.10 in the SM model. When b₂ > 0, binding of KaiA brings KaiC structure to the tight state as it decreases the energy G, which increases the binding affinity of KaiA to KaiC and enhances phosphorylation. When b₃ > 0, binding of KaiB brings the structure of KaiC into the loose state. This effect is consistent with the mass spectrometry observation [44] and enhances dephosphorylation, which further increases the binding affinity of KaiB. Therefore, b₂ > 0 and b₃ > 0 give positive feedback effects in the system. On the other hand, when $b_1^{Ser}>0$, phosphorylation of Ser431 stabilizes the loose structure of the KaiC subunit by lowering the energy G and this reduces the binding affinity of KaiA and stimulates dephosphorylation of Ser431. Hence, the $b_1^{Ser}>0$ term provides a negative feedback effect in the system. We assume $b_1^{Thr}<b_1^{Ser}$ so as to make the phosphorylation of Thr432 faster than the phosphorylation of Ser431 as observed in experiment [12,13]. In the present paper, we assume $b_1^{Thr}<0<b_1^{Ser}$. Therefore, the $b_1^{Thr}<0$ term gives a positive feedback effect. As a result of the coexistence of these multiple feedback relations, the system has multiple metastable states including the phosphorylated loose-structure state and the dephosphorylated tight-structure state. This is why the system tends to stay one of these multiple states and makes transitions among them. ATPase reactions add perturbation to the structure and stimulate the transition between them. The term x_ib₄θ(a_i) in Eq. 10 represents such perturbation through the ATPase reactions.

The binding/dissociation reactions of KaiA occur in the CII ring of KaiC hexamer. The reactions are defined as

$$KaiA=0\stackrel{h_a}{\to }KaiA=1,KaiA=1\stackrel{f_a}{\to }KaiA=0.$$ (12)

We consider that the binding affinity of KaiA is regulated by the allosteric structure change of KaiC hexamer; binding of KaiA is enhanced when the hexamer structure is tight whereas binding of KaiA is suppressed when the structure is loose. Therefore, we assume that the rates in Eq. 12 are regulated by X as

$$h_a=h_a^{1}X,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{f}_a=f_a^0\hspace{0.17em}(1-X).$$ (13)

A constant $h_a^1$ should depend on the concentration of free unbound KaiA molecules. Here in the present SM model, we use a simplified assumption that the free KaiA concentration is constant, so that $h_a^1$ is kept constant. This assumption represents the situation that the KaiA concentration is much larger than the KaiC concentration, so that the free KaiA concentration is not affected by the oscillation of individual KaiC molecules. In the MM model, as will be shown in Results and Discussion section, sequestration of KaiA to C₆B_iA_2j and the resultant temporal depletion of free KaiA concentration is the mechanism of synchronization among multiple KaiC hexamers; synchronization is lost when the free KaiA concentration is kept constant. Because synchronization is not discussed with the SM model, we here adopt a simple assumption that $h_a^1$ is kept constant.

The binding/dissociation reactions of KaiB in the CI domain of KaiC hexamer are described as

$${KaiB}_i=0\stackrel{h_{bi}}{\to }{KaiB}_i=1,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{KaiB}_i=1\stackrel{f_{bi}}{\to }{KaiB}_i=0.$$ (14)

We assume that the rates in Eq. 14 are regulated by the structure of subunits 〈x_i〉 in the following manner;

$$h_{b_i}=h_b^0\hspace{0.17em}(1-\langle x_i\rangle ),\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{f}_{b_i}=f_b^1\langle x_i\rangle .$$ (15)

In this way, the binding affinity of KaiB to the ith subunit of KaiC is decreased when the structure of the subunit is in the tight structure, and the KaiB binding affinity is large when the subunit is in the loose structure. Again, we use a simplified assumption that $h_b^0$ is kept constant through the simulation time course.

The P/dP reactions are described by

$$\begin{array}{l}{Ser}_i=0\stackrel{k_{i,0\to 1}^{Ser}}{\to }{Ser}_i=1,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{Ser}_i=1\stackrel{k_{i,1\to 0}^{Ser}}{\to }{Ser}_i=0,\\ {Thr}_i=0\stackrel{k_{i,0\to 1}^{Thr}}{\to }{Thr}_i=1,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{Thr}_i=1\stackrel{k_{i,1\to 0}^{Thr}}{\to }{Thr}_i=0.\end{array}$$ (16)

The rates in Eq. 16 are regulated by the binding status of KaiA as

$$\begin{array}{l}{k}_{i,0\to 1}^{Ser}=k_{0\to 1}^{Ser,1}\hspace{0.17em}KaiA+k_{0\to 1}^{Ser,0}\hspace{0.17em}(1-KaiA),\\ k_{i,1\to 0}^{Ser}=k_{1\to 0}^{Ser,1}\hspace{0.17em}KaiA+k_{1\to 0}^{Ser,0}\hspace{0.17em}(1-KaiA),\\ k_{i,0\to 1}^{Thr}=k_{0\to 1}^{Thr,1}\hspace{0.17em}KaiA+k_{0\to 1}^{Thr,0}\hspace{0.17em}(1-KaiA),\\ k_{i,1\to 0}^{Thr}=k_{1\to 0}^{Thr,1}\hspace{0.17em}KaiA+k_{1\to 0}^{Thr,0}\hspace{0.17em}(1-KaiA).\end{array}$$ (17)

Here, $k_{i,0\to 1}^{Ser},\hspace{0.17em}{k}_{i,1\to 0}^{Ser},\hspace{0.17em}{k}_{i,0\to 1}^{Thr}$, and $k_{i,1\to 0}^{Thr}$ are dynamical variables, while, $k_{0\to 1}^{Ser,1},\hspace{0.17em}{k}_{0\to 1}^{Ser,0},\hspace{0.17em}{k}_{1\to 0}^{Ser,1},\hspace{0.17em}{k}_{1\to 0}^{Ser,0},\hspace{0.17em}{k}_{0\to 1}^{Thr,1},\hspace{0.17em}{k}_{0\to 1}^{Thr,0},\hspace{0.17em}{k}_{1\to 0}^{Thr,1}$, and $k_{1\to 0}^{Thr,0}$ are constant parameters. We assume the following six equations for the change of nucleotide binding state;

$$\begin{array}{l}{a}_i=0\stackrel{k_{i,01}^a}{\to }{a}_i=1,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{ATP\hspace{0.17em}binding}\\ a_i=1\stackrel{k_{i,10}^a}{\to }{a}_i=0,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{ATP\hspace{0.17em}unbinding}\\ a_i=1\stackrel{k_{i,12}^a}{\to }{a}_i=2,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{hydrolysis\hspace{0.17em}reaction}\\ a_i=2\stackrel{k_{i,21}^a}{\to }{a}_i=1,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{backward\hspace{0.17em}reaction}\\ a_i=2\stackrel{k_{i,23}^a}{\to }{a}_i=3,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{\text{P}}_{\text{i}}\hspace{0.17em}\text{release}\\ a_i=3\stackrel{k_{i,30}^a}{\to }{a}_i=0.\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{ADP\hspace{0.17em}release}\end{array}$$ (18)

Here, both the forward and backward reactions are considered for binding/unbinding of ATP and ATP hydrolysis. Binding reaction of P_i or ADP is not considered by assuming that their concentrations are small. The rates in Eq. 18 are assumed to depend on the structure of each subunit 〈x_i〉 as in the following manner;

$$\begin{array}{l}{k}_{i,01}^a=k_{01}^{a,1}\hspace{0.17em}\langle x_i\rangle +k_{01}^{a,0}\hspace{0.17em}(1-\langle x_i\rangle ),\\ k_{i,10}^a=k_{10}^{a,1}\hspace{0.17em}\langle x_i\rangle +k_{10}^{a,0}\hspace{0.17em}(1-\langle x_i\rangle ),\\ k_{i,12}^a=k_{12}^{a,1}\hspace{0.17em}\langle x_i\rangle +k_{12}^{a,0}\hspace{0.17em}(1-\langle x_i\rangle ),\\ k_{i,21}^a=k_{21}^{a,1}\hspace{0.17em}\langle x_i\rangle +k_{21}^{a,0}\hspace{0.17em}(1-\langle x_i\rangle ),\\ k_{i,23}^a=k_{23}^{a,1}\hspace{0.17em}\langle x_i\rangle +k_{23}^{a,0}\hspace{0.17em}(1-\langle x_i\rangle ),\\ k_{i,30}^a=k_{30}^{a,1}\hspace{0.17em}\langle x_i\rangle +k_{30}^{a,0}\hspace{0.17em}(1-\langle x_i\rangle ).\end{array}$$ (19)

Here, $k_{i,01}^a,\hspace{0.17em}{k}_{i.10}^a,\hspace{0.17em}{k}_{i,12}^a,\hspace{0.17em}{k}_{i,21}^a,\hspace{0.17em}{k}_{i,23}^a$, and $k_{i,30}^a$ are dynamical variables, while $k_{01}^{a,1},\hspace{0.17em}{k}_{01}^{a,0},\hspace{0.17em}{k}_{10}^{a,1},\hspace{0.17em}{k}_{10}^{a,0},\hspace{0.17em}{k}_{12}^{a,1},\hspace{0.17em}{k}_{12}^{a,0},\hspace{0.17em}{k}_{21}^{a,1},\hspace{0.17em}{k}_{21}^{a,0},\hspace{0.17em}{k}_{23}^{a,1},\hspace{0.17em}{k}_{23}^{a,0},\hspace{0.17em}{k}_{30}^{a,1}$, and $k_{30}^{a,0}$ are constant parameters.

We perform numerical simulations of the stochastic dynamics with SM model: By using 〈x_i〉 and X calculated with Eq. 10, the rates of reactions are calculated with Eqs. 12–19. KaiA, KaiB_i, a_i, Ser_i, and Thr_i are updated with these rates by the Gillespie algorithm [45]. Then, by using thus updated KaiA, KaiB_i, a_i, Ser_i, and Thr_i, the structural variables 〈x_i〉 and X in the new time step is calculated with Eq. 10.

Parameters in the SM model

Parameters in the SM model were set to have the same order of magnitude as the corresponding parameters in the MM model. In the SM model, more detailed reaction schemes are considered, so that the larger number of parameters are defined than in the MM model. For example, the P/dP reactions are considered at two sites, Ser431 and Thr432, which are regulated by the KaiA binding status. Therefore, the rates of the P/dP reactions are defined by two sets of parameters, those in the KaiA bound state, $k_{0\to 1}^{Ser,1},\hspace{0.17em}{k}_{1\to 0}^{Ser,1},\hspace{0.17em}{k}_{0\to 1}^{Thr,1},\hspace{0.17em}{k}_{1\to 0}^{Thr,1}$, and those in the KaiA unbound state, $k_{0\to 1}^{Ser,0},\hspace{0.17em}{k}_{1\to 0}^{Ser,0},\hspace{0.17em}{k}_{0\to 1}^{Thr,0},\hspace{0.17em}{k}_{1\to 0}^{Thr,0}$. Here, superscripts 1 and 0 imply the rates in the KaiA bound and unbound states, respectively. We consider that the phosphorylation rates are larger in the KaiA bound state and the dephosphorylation rates are larger in the KaiA unbound state. Therefore, $k_{0\to 1}^{Ser,1},\hspace{0.17em}{k}_{0\to 1}^{Thr,1}>k_{0\to 1}^{Ser,0},\hspace{0.17em}{k}_{0\to 1}^{Thr,0}$ and $k_{1\to 0}^{Ser,1},\hspace{0.17em}{k}_{1\to 0}^{Thr,1}<k_{1\to 0}^{Ser,0},\hspace{0.17em}{k}_{1\to 0}^{Thr,0}$. Because the P/dP reactions at Thr432 precedes the P/dP reactions at Ser431, we consider $k_{0\to 1}^{Thr,1}>k_{0\to 1}^{Ser,1}>k_{1\to 0}^{Thr,1}>k_{1\to 0}^{Ser,1}$ and $k_{1\to 0}^{Thr,0}>k_{1\to 0}^{Ser,0}>k_{0\to 1}^{Thr,0}>k_{0\to 1}^{Ser,0}$. We assume ATP hydrolysis rates depend on the structure of each subunit; the reaction rates are larger when the structure is tight. Therefore, we assume $k_{01}^{a,1},\hspace{0.17em}{k}_{10}^{a,1},\hspace{0.17em}{k}_{12}^{a,1},\hspace{0.17em}{k}_{21}^{a,1},\hspace{0.17em}{k}_{23}^{a,1}$, and $k_{30}^{a,1}$ are larger than $k_{01}^{a,0},\hspace{0.17em}{k}_{10}^{a,0},\hspace{0.17em}{k}_{12}^{a,0},\hspace{0.17em}{k}_{21}^{a,0},\hspace{0.17em}{k}_{23}^{a,0}$, and $k_{30}^{a,0}$. Here, superscripts 1 and 0 indicate the rates in the tight and loose structures, respectively. An example set of parameters of rate constants and parameters in the free energy to determine the structure is summarized in Tables 2 and 3.

Table 2.

Rate constants in the SM model^*

ATP hydrolysis reactions in the tight structure	$k_{01}^{a,1}$	1.1
	$k_{10}^{a,1}$	1.0
	$k_{12}^{a,1}$	1.1
	$k_{21}^{a,1}$	1.0
	$k_{23}^{a,1}$	1.1
	$k_{30}^{a,1}$	1.1
ATP hydrolysis reactions in the loose structure	$k_{01}^{a,0}$	0.55
	$k_{10}^{a,0}$	0.5
	$k_{12}^{a,0}$	0.55
	$k_{21}^{a,0}$	0.5
	$k_{23}^{a,0}$	0.55
	$k_{30}^{a,0}$	0.55
P/dP reactions with KaiA unbound from KaiC	$k_{0\to 1}^{Thr,0}$	0.3
	$k_{1\to 0}^{Thr,0}$	3.9
	$k_{0\to 1}^{Ser,0}$	0.01
	$k_{1\to 0}^{Ser,0}$	0.5
P/dP reactions with KaiA bound to KaiC	$k_{0\to 1}^{Thr,0}$	4.8
	$k_{1\to 0}^{Thr,1}$	0.2
	$k_{0\to 1}^{Ser,1}$	0.6
	$k_{1\to 0}^{Ser,1}$	0.1
Binding and dissociation rates of KaiA	$h_a^1$	1.5
	$f_a^0$	0.1
Binding and dissociation rates of KaiB	$h_b^0$	1.5
	$f_b^1$	0.2

^*Values are in units of h⁻¹.

Table 3.

Free energy parameters in the SM model^*

Base-line temperature effect	b0	0.13
Effect of Thr432 phosphorylation	$b_1^{Thr}$	−1
Effect of Ser431 phosphorylation	$b_1^{Ser}$	6
Effect of KaiA binding	b2	1.5
Effect of KaiB binding	b3	1
Effect of ATP hydrolysis	b4	4
Coupling between subunits	J	4.5

^*Values are in units of k_BT₀ with T₀ = 30°C.

Results and Discussion

Oscillation and synchronization in the ensemble of KaiABC molecules

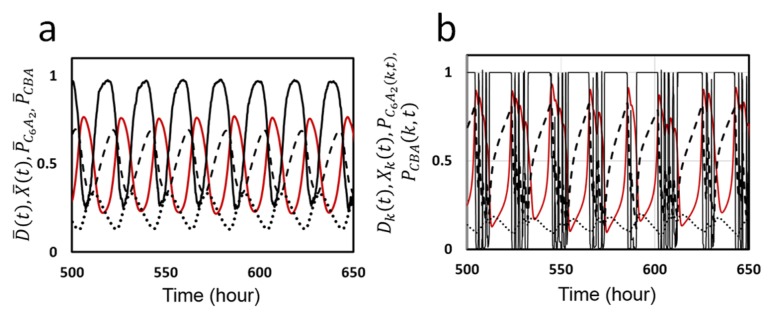
In Figure 2a, we show an example of the ensemble-level oscillation simulated with the MM model. Shown are the KaiC phosphorylation level, D̄ (t), structure of KaiC hexamers, X̄(t), probability of C₆ of forming the C₆A₂ complex, P̄ _C6A2, and probability of forming the C₆B_iA_2j complexes, P̄ _CBA(t), where overbars represent that averages were taken over the ensemble of N hexamers. Here, we find that P̄ _C6A2(t) and P̄ _CBA(t) show counter-phased oscillation. When P̄ _C6A2(t) dominates, binding of KaiA to KaiC hexamer enhances phosphorylation, which increases D̄ and decreases X̄. On the contrary, when P̄ _CBA(t) is large, KaiA is sequestered into C₆B_iA_2j, which depletes the free unbound KaiA. This depletion of free KaiA concentration enhances dephosphorylation, which then decreases D̄ and increases X̄. This sequestration of KaiA is the mechanism through which individual KaiC hexamers communicate with each other.

Figure 2.

Ensemble and single molecule oscillations in the KaiABC system simulated with the MM model. a) The ensemble oscillation of the phosphorylation level D̄ (t) (red line), structure of KaiC hexamer X̄(t) (black real line), probability to form complex C₆A₂, P̄ _C6A2 (dashed line), and probability to form complexes C₆B_iA_2j, P̄ _CBA (dotted line), are plotted as functions of time. Averaged over the ensemble of N = 1000 hexamers. b) The single molecule oscillation of phosphorylation level D_k(t) (red line), structure X_k(t) (black real line), P_C6A2(k, t) (dashed line), P_CBA(k, t) (dotted line) of a KaiC hexamer arbitrarily chosen from the ensemble are plotted as functions of time. Parameters in Table 1 were used.

Individual oscillation of single KaiC hexamer is shown in Figure 2b, where oscillation trajectories of D_k(t), X_k(t), P_C6A2(k, t) and P_CBA(k, t) of a KaiC hexamer arbitrarily chosen from the ensemble are plotted. When X_k(t) is large, the lifetime of bound ADP, δ_k, is short and ADP is frequently released from the CI. This short residence of ADP at CI does not affect X_k(t) much. However, when X_k(t) begins to be small, δ_k becomes longer and ATP hydrolysis provides larger influence to X_k(t). This gives rise to spike-like changes in X_k(t), which induces noisy fluctuating decrease of D_k(t). Synchronization of a large number of KaiC hexamers smooths out this fluctuation to give rise to a coherent oscillation of D̄ .

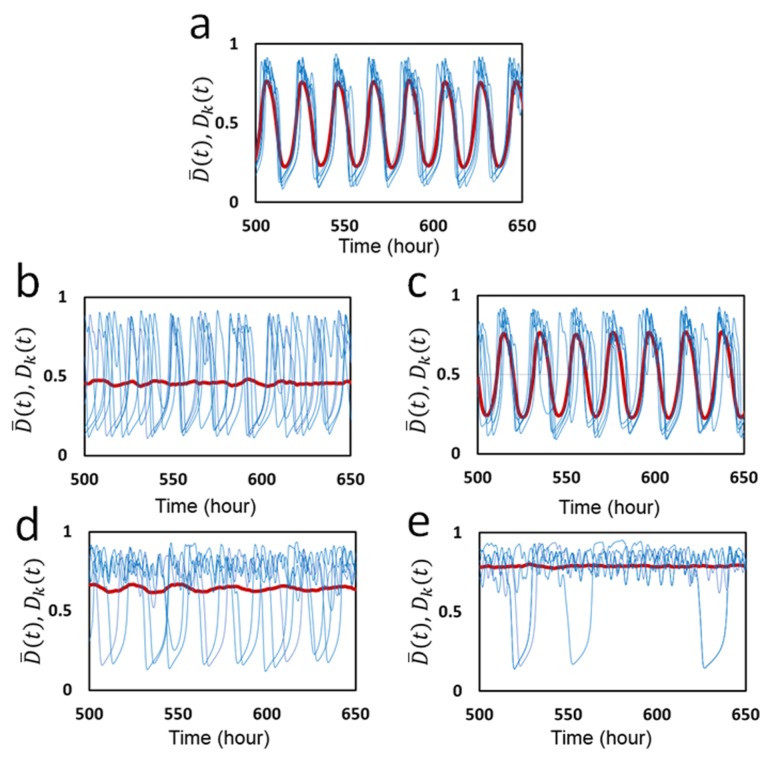
To analyze this synchronization furthermore, we plot individual oscillations D_k(t) of five KaiC hexamers arbitrarily chosen from N hexamers along with the ensemble-averaged oscillation D̄ (t). In Figure 3a, individual and ensemble oscillations calculated with the same parameter values as used in Figure 2 are shown. Fluctuating individual oscillations are synchronized and entrained into the ensemble oscillation, which gives rise to a stable coherent oscillation of the ensemble. The essential role of KaiA sequestration in this synchronization is clearly shown in Figure 3b, in which free KaiA concentration is fixed to be A = 0.2A_T. When the free KaiA concentration is fixed to be constant as in Figure 3b, the sequestration mechanism does not work and individual KaiC hexamers lose synchronization among them. Then, the ensemble-level oscillation vanishes though individual molecules remain oscillating with the large amplitude. Thus, the temporal change of the binding affinity of KaiA to KaiC due to the dynamical change of free KaiA concentration is essential for maintaining synchronization. In contrast, as shown in Figure 3c, synchronization and the ensemble oscillation are maintained when the free KaiB concentration is fixed to be B = 0.9B_T. This maintenance of synchronization shows that the temporal change in the concentration of free KaiB is not necessary for synchronization.

Figure 3.

Oscillations of individual molecules in the ensemble and the ensemble-averaged oscillation simulated with the MM model. The phosphorylation level D_k(t) (blue) of five individual KaiC hexamers arbitrarily chosen from the ensemble are superposed with the ensemble average D̄ (t) (red). a) Parameters in Table 1 were used with f₀ = 2.2 h⁻¹. b) Concentration of free KaiA molecules is fixed to be A = 0.2A_T, but concentration of free KaiB molecules remains dynamically changing. c) Concentration of free KaiA molecules remains dynamically changing, but concentration of free KaiB molecules is fixed to be B = 0.9B_T. Frequency of ATP hydrolysis was made small as d) f₀ = 0.8 h⁻¹ and e) f₀ = 0.5 h⁻¹.

Because ATP hydrolysis plays a significant role to generate individual oscillations as shown in Figure 2b, it is interesting to see how the ATP hydrolysis affects the synchronization. In Figure 3d, the frequency of ATP hydrolysis, f₀, was made smaller from f₀ = 2.2 h⁻¹ in Figure 3a to f₀ = 0.8 h⁻¹ in Figure 3d. We find synchronization is lost with this small frequency of ATP hydrolysis. Therefore, ATP hydrolysis with sufficient frequency is necessary for synchronization. ATP hydrolysis occurring with random timing in individual KaiC subunits should perturb each KaiC hexamer to adjust to the dynamical oscillation of free KaiA concentration; without this adjustment, individual KaiC hexamers stay oscillating with their own individual phases. As shown in Figure 3e, by further reducing the ATP hydrolysis frequency to f₀ = 0.5 h⁻¹ many KaiC hexamers stop oscillating and show small amplitude fluctuation. Therefore, when f₀ is decreased, KaiC oscillators first lose synchronization, and then lose individual oscillations.

Together, these results showed that in the MM model KaiA sequestration is a basis for synchronization of individual KaiC hexamers, and ATP hydrolysis helps individual KaiC hexamers to synchronize under the mechanism of KaiA sequestration.

Temperature compensation

An important feature of the KaiABC system is its insensitivity to temperature change, i.e., temperature compensation; the observed Q₁₀ defined by the relative change in the oscillation period upon 10°C temperature change was about 1.06 [1] to 1.01±0.02 [46]. However, the physical mechanism of such temperature insensitivity has been elusive. Here, we analyze this problem by using the MM model, particularly by investigating the role of ATP hydrolysis in determining temperature dependence of the oscillation period and amplitude.

The MM model has nine parameters for rate constants, $h_A^1,\hspace{0.17em}{h}_B^0$, h_BA, $f_A^0,\hspace{0.17em}{f}_B^1$, f_BA , a, k_p, and k_dp, and two parameters for the ATP hydrolysis reactions, f₀ and δ₀. We write their values at temperature T around T₀ = 30°C as

$$\begin{array}{l}{h}_A^1\hspace{0.17em}(T)=[h_A^1\hspace{0.17em}(T_0)\hspace{0.17em}\text{exp\hspace{0.17em}}(\mathrm{\Delta }{E}_{hA}/k_B{T}_0)]\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_{hA}/k_{B}T),\\ h_B^0\hspace{0.17em}(T)=[h_B^0\hspace{0.17em}(T_0)\hspace{0.17em}\text{exp\hspace{0.17em}}(\mathrm{\Delta }{E}_{hB}/k_B{T}_0)]\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_{hB}/k_{B}T),\\ h_{BA}(T)=[h_{BA}(T_0)\hspace{0.17em}\text{exp\hspace{0.17em}}(\mathrm{\Delta }{E}_{hBA}/k_B{T}_0)]\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_{hBA}/k_{B}T),\\ f_A^0\hspace{0.17em}(T)=[f_A^0\hspace{0.17em}(T_0)\hspace{0.17em}\text{exp\hspace{0.17em}}(\mathrm{\Delta }{E}_{fA}/k_B{T}_0)]\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_{fA}/k_{B}T),\\ f_B^1\hspace{0.17em}(T)=[f_B^1\hspace{0.17em}(T_0)\hspace{0.17em}\text{exp\hspace{0.17em}}(\mathrm{\Delta }{E}_{fB}/k_B{T}_0)]\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_{fB}/k_{B}T),\\ f_{BA}(T)=[f_{BA}(T_0)\hspace{0.17em}\text{exp\hspace{0.17em}}(\mathrm{\Delta }{E}_{fBA}/k_B{T}_0)]\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_{fBA}/k_{B}T),\\ a(T)=[a(T_0)\hspace{0.17em}\text{exp\hspace{0.17em}}(\mathrm{\Delta }{E}_a/k_B{T}_0)]\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_a/k_{B}T),\\ k_p(T)=[k_p(T_0)\hspace{0.17em}\text{exp\hspace{0.17em}}(\mathrm{\Delta }{E}_p/k_B{T}_0)]\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_p/k_{B}T),\\ k_{dp}(T)=[k_{dp}(T_0)\hspace{0.17em}\text{exp\hspace{0.17em}}(\mathrm{\Delta }{E}_{dp}/k_B{T}_0)]\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_{dp}/k_{B}T),\\ f_0(T)=[f_0(T_0)\hspace{0.17em}\text{exp\hspace{0.17em}}(\mathrm{\Delta }{E}_{f0}/k_B{T}_0)]\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_{f0}/k_{B}T),\\ {\delta }_0(T)=[{\delta }_0(T_0)\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_{\delta 0}/k_B{T}_0)]\hspace{0.17em}\text{exp\hspace{0.17em}}(-\mathrm{\Delta }{E}_{\delta 0}/k_{B}T).\end{array}$$ (20)

We compare various cases for the values of eleven activation energies, ΔE_hA, ΔE_hB, ΔE_hBA, ΔE_fA, ΔE_fB, ΔE_fBA, ΔE_a, ΔE_p, ΔE_dp, ΔE_{f 0}, and ΔE_δ0;

$$\begin{array}{l}(\text{I})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{\Delta }{E}_{hA}=\mathrm{\Delta }{E}_{hB}=\mathrm{\Delta }{E}_{hBA}=\mathrm{\Delta }{E}_{fA}=\mathrm{\Delta }{E}_{fB}=\mathrm{\Delta }{E}_{fBA}=\mathrm{\Delta }{E}_a=\mathrm{\Delta }{E}_p=\mathrm{\Delta }{E}_{dp}=\mathrm{\Delta }{E}_{f0}=\mathrm{\Delta }{E}_{\delta 0}=5k_B{T}_0,\\ (\text{II})\mathrm{\hspace{0.17em} }\mathrm{\Delta }{E}_{hBA}=15k_B{T}_0,\text{Other\hspace{0.17em}activation\hspace{0.17em}energies}=5k_B{T}_0,\\ (\text{III})\hspace{0.17em}\mathrm{\Delta }{E}_{hBA}=\mathrm{\Delta }{E}_{\delta 0}=15k_B{T}_0,\text{Other\hspace{0.17em}activation\hspace{0.17em}energies}=5k_B{T}_0,\\ (\text{IV})\hspace{0.17em}\mathrm{\Delta }{E}_{hBA}=\mathrm{\Delta }{E}_{\delta 0}=15k_B{T}_0\hspace{0.17em}\text{and\hspace{0.17em}}\mathrm{\Delta }{E}_{f0}=0,\text{Other\hspace{0.17em}activaiton\hspace{0.17em}energies}=5k_B{T}_0,\\ (\text{V})\mathrm{\hspace{0.17em} }\mathrm{\Delta }{E}_{f0}=0,\text{Other\hspace{0.17em}activation\hspace{0.17em}energies}=5k_B{T}_0,\\ (\text{VI})\hspace{0.17em}\mathrm{\Delta }{E}_{hBA}=15k_B{T}_0\hspace{0.17em}\text{and\hspace{0.17em}}\mathrm{\Delta }{E}_{f0}=0,\text{Other\hspace{0.17em}activation\hspace{0.17em}energies}=5k_B{T}_0.\end{array}$$ (21)

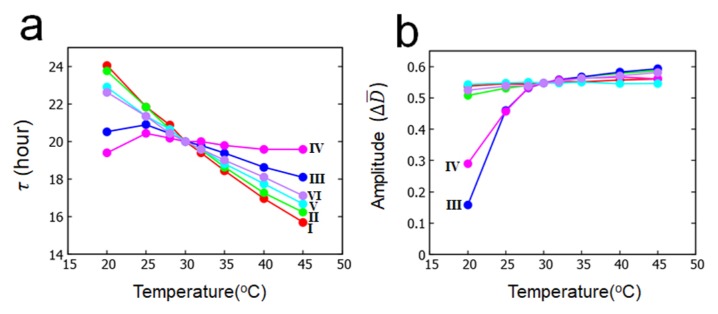
Here, case I is the simplest assumption to make all the relevant activation energies same. Case II is the assumption of the stronger temperature dependence of the binding affinity of KaiA to KaiB. Hatakeyama and Kaneko [20] discussed that enhancement of the KaiA sequestration at higher temperature reduces the phosphorylation rate, which should lead to the temperature compensation. In the present MM model, this enhancement of KaiA sequestration is represented by the larger ΔE_hBA than others. As shown in the previous paper [29], the important features of the MM model are the dependence of the oscillation period on the frequency of the ATP hydrolysis f₀ and on the lifetime of the ADP binding state δ₀. In case III, the stronger temperature dependence of δ₀ is assumed with the larger ΔE_δ0; as temperature increases, the rate of ADP release is enhanced and δ₀ becomes small with the larger temperature dependence than other reactions. The frequency of ATP hydrolysis was shown to be temperature insensitive [17]. A possible explanation for this temperature insensitivity is the regulation of the reaction rate by the diffusive non-activation type binding process of ATP to the CI, but the precise mechanism of this temperature insensitivity has not been known. Here, to represent this temperature insensitivity, we assume ΔE_{f 0} = 0 in case IV. Cases V and VI are calculated to test the effects of assuming ΔE_{f 0} = 0.

In Figures 4a and 4b, the calculated temperature dependences of period and amplitude of the ensemble-averaged oscillation D̄ (t) are shown for cases I–VI. As shown in Figure 4a, there are only small differences between case I and case II and between case V and case VI; therefore, the enhancement of KaiA sequestration at higher temperature contributes only slightly for temperature compensation in the present model. On the other hand, period calculated in cases III and IV is much more insensitive to temperature than period calculated in cases I and II, showing that the enhancement of shortening of the lifetime of the ADP-bound state at higher temperature gives a significant effect on temperature compensation. Temperature insensitivity of ATP hydrolysis frequency gives some effect to make period temperature insensitive as shown in the differences between case III and case IV and between II and VI in Figure 4a. Q₁₀ of the oscillation period calculated between 30°C and 40°C is Q₁₀ = 1.17 (case I), 1.16 (case II), 1.07 (case III), 1.02 (case IV), 1.13 (case V), and 1.10 (case VI).

Figure 4.

Temperature dependence of period and amplitude of the ensemble oscillation D̄ (t) simulated with the MM model. a) Period τ and b) amplitude ΔD̄ . Six cases defined in Eq. 21 are compared: case I (red), case II (green), case III (blue), case IV (magenta), case V (cyan), and case VI (purple). Parameters in Table 1 were used.

As shown in Figure 4b, amplitude of oscillation becomes only slightly small as temperature decreases in cases I , II, V, and VI, but the amplitude approaches rapidly to 0 as temperature is decreased in cases III and IV. In cases III and IV, the oscillation amplitude continuously decreases and vanishes at a certain threshold temperature; in other words, the oscillation disappears with the Hopf bifurcation mechanism in low temperature, which is the behavior consistent with the experimental observation [42].

Summarizing these results, we found that the accelerated release of ADP from the CI with increased temperature largely contributes to temperature compensation of oscillation period, and insensitivity of ATP hydrolysis frequency to temperature gives some help to temperature compensation. The prolonged release of ADP at low temperature is consistent with the observed disappearance [42] of oscillation through the Hopf bifurcation at low temperature. Meanwhile, enhancement of KaiA sequestration does not help much for temperature compensation.

Oscillation in individual KaiC hexamer

In the preceding subsections, roles of ATP hydrolysis in the KaiABC oscillation were analyzed with the MM model. Though ATPase reactions randomly occur in individual molecules, they have significant effects on the simulated ensemble-level oscillation. In the following subsections, we use the SM model for further investigating the roles of ATP hydrolysis.

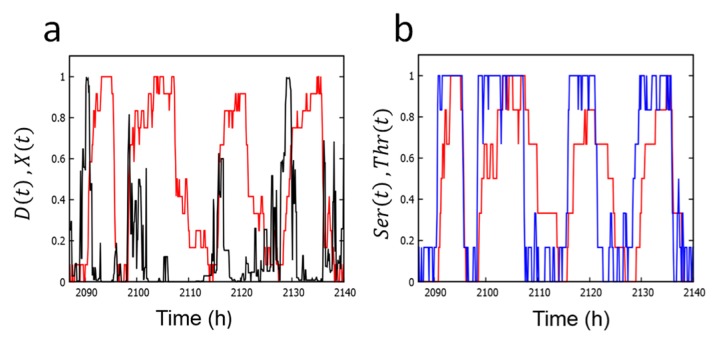
In Figure 5, we plot the simulated single-molecular phosphorylation levels, D, Ser, and Thr, and structure X; these quantities are defined in Eq. 11 in Method section. As shown in Figure 5a, the phosphorylation level and structure oscillate with opposite phases in a similar way to the oscillation in the MM model. From the simulated oscillation of Ser and Thr in Figure 5b, we find that the phase of Thr precedes the phase of Ser. In this way, the simulated single-molecular oscillation is noisy stochastic oscillation, but it captures the important features observed in the ensemble-level oscillation. Therefore, the physical origin of features of the ensemble-level oscillation exists at the single-molecular level.

Figure 5.

Oscillations of single KaiC hexamer simulated with the SM model. a) Simulated oscillation of the phosphorylation level D(t) (red) and structure X(t) (black). b) Simulated oscillation of phosphorylation at Ser432 (red) and Thr431 (blue). Parameters in Tables 2 and 3 were used.

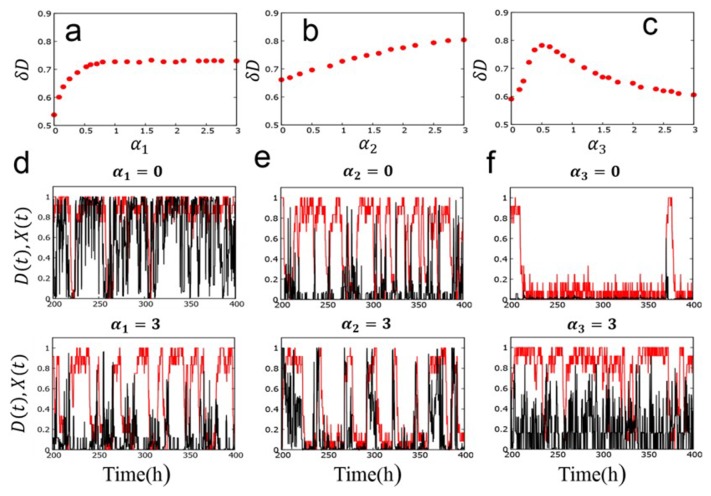
The mechanism of this single-molecular oscillation can be more closely analyzed by changing the parameters, $b_1^{Thr},\hspace{0.17em}{b}_1^{Ser}$, b₂, b₃, and b₄ in Eq. 10, which represent the strength of coupling between reactions and structural change. In Figure 6, we plot the oscillation amplitude, δD, by introducing scaling factors α₁, α₂, and α₃ to scale the parameters as $b_1^{Ser}\to {\alpha }_1{b}_1^{Ser}$ (Fig. 6a), $b_1^{Thr}$, b₂, $b_3\to {\alpha }_2{b}_1^{Thr}$, α₂b₂, α₂b₃ (Fig. 6b), and b₄ → α₃b₄ (Fig. 6c). Here, δD = 2 × (standard deviation of the distribution of D), where the values of D were sampled from the trajectory D (t) calculated over 2²⁴ steps. As discussed in Method section, α₁ modulates the strength of negative feedback interaction between P/dP reactions and structure, α₂ modulates the strength of positive feedback interactions between P/dP reactions and structure or between binding and structure, and α₃ modulates the effect of the ATPase reactions on structure. As shown in Figure 6a, δD drops to a small value when α₁ becomes small. This appreciable decrease of δD can be confirmed by examining the calculated trajectories as shown in Figure 6d. In Figure 6d, oscillations of D and X are masked by intense fluctuations when the negative feedback is lost with α₁ = 0, while the oscillations remain distinct when the negative feedback is strong enough with α₁ = 3. The oscillation features with α₁ = 3 are similar to those found in Figure 5a, which were calculated with α₁ = 1. This weakening of oscillation for the small α₁ explains the behavior of δD in Figure 6a. As shown in Figure 6b, δD mildly decreases when α₂ becomes small. Trajectories in Figure 6e show that the oscillations of D and X become somewhat noisy when the positive feedback is lost with α₂ = 0, while the oscillations turn to trains of pulses when the positive feedback is strong with α₂ = 3. As shown in Figure 6c, δD shows a peak at α₃ ≈ 0.5 and diminishes both at small and large α₃. As shown in Figure 6f, the system tends to stay long at the small X and small D state when α₃ = 0, which prevents oscillations, while the system tends to stay at large D with frequent noisy oscillation of X when large α₃ = 3. Therefore, there is a suitable range of the coupling strength between ATPase reactions and structure to keep the oscillation amplitude large. To summarize, we find that the large amplitude oscillation in individual KaiC hexamers is supported by negative and positive feedback interactions in structure change as well as the suitable strength of coupling between ATPase reactions and structure change.

Figure 6.

Effects of variation of the coupling strength between reactions and structure in the SM model. a) Oscillation amplitude δD is plotted as a function of the scaling factor α₁ of coupling between P/dP reactions at Ser431 and structure. α₂ = α₃ = 1. b) δD as a function of the scaling factor α₂ of coupling between P/dP reactions at Thr432 or Kai protein binding reactions and structure. α₁ = α₃ = 1. c) δD as a function of the scaling factor α₃ of coupling between ATPase reactions and structure. α₁ = α₂ = 1. Example trajectories of D (red) and X (black) calculated with d) α₁ = 0 (upper panel) and α₁ = 3 (lower panel) with α₂ = α₃ = 1, e) α₂ = 0 (upper panel) and α₂ = 3 (lower panel) with α₁ = α₃ = 1, and f) α₃ = 0 (upper panel) and α₃ = 3 (lower panel) with α₁ = α₂ = 1.

Correlation between ATPase activity and oscillation frequency

The observed correlation between the frequency of ATP hydrolysis, or the ATPase activity, and the frequency of KaiC oscillation [16,17] is important for analyzing the relationship between the ATPase reactions occurring in individual KaiC hexamer and the ensemble-level P/dP rhythm. As discussed in previous subsections, many features of the ensemble-level oscillation are already found in the single-molecular level. Therefore, it is meaningful to analyze the relation between the ATPase activity and the frequency of the single-molecular oscillation.

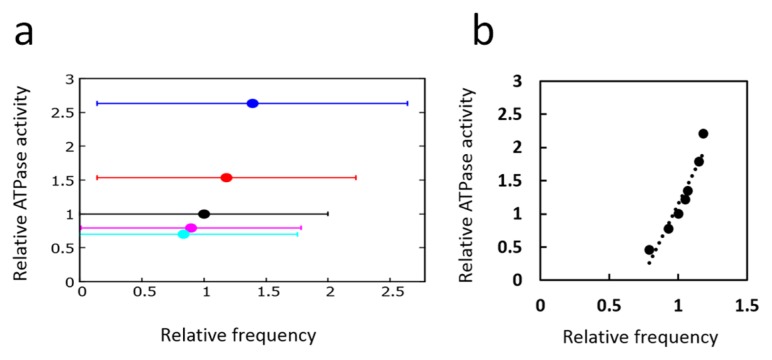
In Figure 7a, the single-molecular ATPase activity was calculated with the SM model by introducing a scaling factor ɛ; the rate constants of ATPase reactions defined in Eq. 19 were uniformly changed from the values of Table 2 as $k_{01}^{a,i}\to \varepsilon k_{01}^{a,i},\hspace{0.17em}{k}_{10}^{a,i}\to \varepsilon k_{10}^{a,i},\hspace{0.17em}{k}_{12}^{a,i}\to \varepsilon k_{12}^{a,i},\hspace{0.17em}{k}_{21}^{a,i}\to \varepsilon k_{21}^{a,i},\hspace{0.17em}{k}_{23}^{a,i}\to \varepsilon k_{23}^{a,i}$, and $k_{30}^{a,i}\to \varepsilon k_{30}^{a,i}$ with i = 1 and 0. With these scaled parameters with various values of ɛ, the number of released ADP molecules (i.e., the number of a_i = 3 → 0 transitions) was counted as a measure of the ATPase activity in the condition in the absence of KaiA and KaiB, which was represented in the model by imposing $h_a^1=h_b^0=0$. Also shown in Figure 7a is the averaged peak frequency of the power spectrum of the Fourier transform of the D oscillation calculated with nonzero $h_a^1$ and $h_b^0$ defined in Table 2 for the corresponding values of ɛ. Because oscillations bear intense stochasticity, the averaged peak frequency and its error bar were derived from extensive calculations: 50 power spectra were calculated from the Fourier transform of 50 trajectories of D(t), with each trajectory having 2¹⁸ data points. Then, the peak of the spectrum obtained by averaging 50 spectra was identified. This calculation was repeated 100 times by using different random numbers, and from the distribution of 100 peak frequencies, the averaged peak frequency was obtained and the error bar was calculated from the standard deviation. In spite of the intense stochasticity as seen from the large error bars in Figure 7a, we can see that the ATPase activity is correlated to the P/dP oscillation frequency in single KaiC hexamer.

Figure 7.

Correlation between ATPase activity and frequency of phosphorylation oscillation. a) Single-molecular correlation calculated with the SM model. Each point represents the ATPase activity calculated in the non-oscillatory condition and the average frequency calculated in the oscillatory condition for various scaling values ɛ of the ATPase reaction rates: ɛ = 4 (blue), ɛ = 2 (red), ɛ = 1 (black), ɛ = 0.6 (magenta), and ɛ = 0.4 (cyan). Error bars are the standard deviation of the distribution of the peak frequency of the Fourier transform spectra. b) Ensemble-level correlation calculated with the MM model. Each point represents the ATPase activity calculated in the non-oscillatory condition and the average frequency calculated in the oscillatory condition for various values of f₀. Each point is the average of 10 trajectories, each of which is 2 × 10³ h long.

In Figure 7b, the results of the ensemble calculation with the MM model were plotted. Here, the number of released ADP in the ensemble were calculated in the condition of A_T = B_T = 0 with various values of ATP hydrolysis frequency f₀, and the corresponding ensemble-level P/dP rhythm was calculated with the nonzero values of A_T and B_T as defined in Table 1. Figure 7b shows that there is a distinct correlation between ATPase activity and the P/dP rhythm in the ensemble.

Comparing the results of Figures 7a and 7b, we find that the important feature of the ensemble-level correlation between the ATPase activity and the P/dP rhythm already appears at the single-molecule level.

Conclusion

We constructed two models, the MM model, which explains oscillation dynamics of an ensemble of a large number of Kai molecules and the dynamics of constituent individual molecules, and the SM model, which explains oscillation dynamics of individual molecules in more details. In these two models, we have hypothesized that KaiC hexamers undergo allosteric transitions between tight and loose structural states. The binding affinity of KaiA and KaiB was assumed to depend on the structure of KaiC hexamer and the rates of P/dP reactions were defined to depend on the binding status of KaiA. The binding of KaiB to KaiC leads to the KaiABC complex formation, which sequesters KaiA to deplete the free KaiA concentration and affects the phosphorylation rate of the other KaiC molecules. ATPase activity of the CI domain of KaiC was assumed to be regulated by the structure of KaiC, and the ATP hydrolysis reactions were assumed to bring about the perturbation on the allosteric transition of the KaiC structure.

Simulations with the MM model showed that stochastic individual oscillations are synchronized through the communication among KaiC hexamers, which was realized by the sequestration of KaiA into the KaiABC complex, and the frequent ATPase reactions in the CI domain perturb individual KaiC hexamers to allow them to generate the ensemble-level oscillation. Thus, both KaiA sequestration and frequent ATPase reactions perform pivotal roles to maintain a coherent ensemble-level oscillation. Temperature dependence of the period and amplitude of the ensemble-level oscillation were examined with the MM model, and it was shown that the intense temperature dependence of the lifetime of the ADP bound state in the CI domain is important to realize the temperature compensation of the oscillation period, and such dependence is consistent with the observed disappearance of oscillation at low temperature [42]. It was also shown that temperature insensitivity of the frequency of ATP hydrolysis helps temperature compensation to some extent.

Simulations with the SM model showed that the many features of the ensemble-level oscillation shown with the MM model appear also in the single-molecular oscillation in the SM model though the single-molecular oscillation bears intense stochastic fluctuation. Results in the SM model showed that perturbation of the ATP hydrolysis reactions on the structure is necessary to maintain the large amplitude single-molecular oscillation and that ATPase activity and the P/dP oscillation frequency are correlated to each other at single-molecule level, which largely explains the correlation between ATPase activity and the P/dP oscillation frequency found in the ensemble level.

Thus, both MM and SM models suggest that ATP hydrolysis reactions stochastically occurring in individual KaiC hexamers play important roles in synchronization, temperature compensation, and frequency determination at the ensemble-level oscillation. In order to verify these suggestions, the present “mesoscopic” models should be further compared with the microscopic atomic-level observations of structure and reactions [16] and also with the macroscopic ensemble-level observations of phase shift, synchronization, and entrainment [46,47]. In this way, a comprehensive picture that unifies explanations of microscopic through macroscopic phenomena should open a new perspective of biomolecular systems working coherently in living cell systems.