Prediction equation for calculating residual kidney urea clearance using urine collections for different hemodialysis treatment frequencies and interdialytic intervals

Abstract

Background

The purpose of the study was to explore the precision of an equation designed to estimate residual kidney urea clearance (K_RU) from interdialytic urine collection data and pre-hemodialysis (HD) serum urea nitrogen (SUN) in different hemodialysis treatment schedules.

Methods

The generalizability of the proposed equation was tested in 32 731 HD treatments where urine was collected prior to a dialysis session, mostly for 24 h but sometimes longer, in patients being dialyzed 1–4 times/week.

Results

The residual kidney urea clearance estimating equation predicted a K_RU that matched the one computed by formal modeling within 5% in >98% of sessions analyzed. The errors in estimated versus modeled K_RU for interdialytic intervals (IDIs) of 2, 3, 4 and 7 days, were 1.6 ± 1.5%, −0.4 ± 1.6%, 0.9 ± 1.6%, and 1.5 ± 1.2%, respectively. Percent errors were similar for schedules of 1–4/week with the exception of urine collection during the 2-day interval of a 2:5-day twice-weekly schedule; here error averaged 5.0 ± 1.2%. Use of the average of the SUN values at the start and end of the collection period overestimated modeled K_RU by 11.3 ± 4.5%, whereas an equation suggested by others underestimated modeled K_RU by −9.9 ± 3.4%.

Conclusions

The equation tested predicts values for K_RU that are similar to those obtained from formal urea kinetic modeling, with percent errors that only rarely exceed 5%. It gives relatively precise results for a wide range of HD treatment schedules, IDIs and urine collection periods.

Keywords

chronic hemodialysis, clearance, guidelines, hemodialysis, predialysis

INTRODUCTION

There is increased interest in measuring, monitoring and preserving residual kidney function in maintenance hemodialysis (HD) therapy [1], as well as in the use of residual kidney urea clearance (K_RU) in predicting mortality risk [2] and guiding prescription of incremental HD [3]. K_RU commonly is measured by collecting urine for 24–68 h prior to a dialysis session, calculating the per-minute urinary urea nitrogen (UN) excretion rate, and then dividing this by the estimated time-averaged serum (theoretically, plasma) water urea concentration during the collection interval. The latter concentration is not easy to estimate in the absence of a computer program that generates a weekly interdialytic serum urea nitrogen (SUN) profile. Usually, the only serum sample used in the calculation is that taken at the end of the urine collection period, i.e. at the start of the subsequent dialysis session. For logistic reasons, a second SUN measurement at the beginning of the urine collection period is obtained only rarely. Use of a two-pool urea kinetic modeling program that generates a weekly SUN profile [4] allows calculation of the time-averaged SUN during any collection period during any interdialytic interval (IDI). Based on modeling of a small number of hypothetical patient data, a prediction equation was developed to estimate the time-averaged concentration (TAC) SUN during any predialysis urine collection period [5]. The prediction equation terms include predialysis SUN (of the dialysis session immediately following the collection period), the urea reduction ratio (URR, expressed as a percentage) from that session and the ratio of the duration of the collection period to the length of the IDI during which the collection was performed. Because dialysis schedules, IDIs, URRs and durations of the urine collection period can be highly variable, here we test the ability of the above equation to predict K_RU. Equation-predicted values were compared with those calculated by a urea kinetic modeling program.

MATERIALS AND METHODS

The parent study was approved by the Institutional Review Boards of the Los Angeles Biomedical Research Institute at Harbor-UCLA, University of California Irvine Medical Center and the University of Washington as exempt from informed consent. We extracted, refined and examined electronic data from all incident dialysis patients who were age ≥18 years and received conventional HD treatment in a total of 1737 facilities operated by a large dialysis organization in the USA from 1 January 2007 to 31 December 2011 [6]. Information on death, race/ethnicity, primary insurance, access type and ICD-9 codes were obtained from the electronic database of the dialysis provider. Blood samples were drawn using uniform techniques in all dialysis clinics and were transported to the central laboratory in Deland, Florida, typically within 24 h. All laboratory values were measured by automated and standardized methods.

Patient characteristics are expressed as means ± standard deviation, medians (interquartile range) or percentages, as appropriate. Analyses were conducted using STATA MP version 13.1 (StataCorp, College Station, TX, USA).

Subject selection for the derivation and validation datasets

In order to validate the new equation for estimating K_RU, we identified 104 078 urine collections between consecutive hemodialysis sessions with simultaneous measurements of urinary urea, predialysis SUN and postdialysis SUN, from 51 774 HD patients who did not receive dialysis treatments by other modalities (i.e. peritoneal dialysis, hemodiafiltration, home HD or nocturnal HD) and who were not hospitalized during the preceding week. We excluded 12 315 measurements with extreme values (see flow diagram in Supplementary data, Figure S1). We assumed that urine collection was completed 60 min before the start of HD treatment. In 393 observations, reported urine collection time exceeded the maximum expected time [i.e. more than 2880 minutes minus the HD session time minus 60 min for those with 2-day IDI] and was corrected to the maximum expected time. We also excluded 33 493 measurements when the maximum difference in dialysis session time exceeded >10 min compared to the session length during the preceding week of measurement because the Solute Solver assumes a steady state where treatment time is consistent over time.

We randomly selected one measurement per patient from 58 270 measurements among 33 391 patients. We then put those data on 13 variables (i.e. day of measurement, treatment schedule in the preceding week, predialysis SUN, pre-urine collection postdialysis SUN, post-urine collection postdialysis SUN, blood flow rate, dialysate flow rate, predialysis weight, postdialysis weight, dialyzer mass transfer area coefficient (K₀A), urinary UN concentration, urine volume, duration of urine collection) into the Solute Solver with an assumption that urine collection was completed 1 h before HD start on the day of measurement. Error was reported in 657 measurements, including a modeled anthropometric volume ratio <0.35 (suggesting inadvertent sampling of outlet dialyzer blood); we obtained 32 734 values of urea kinetics model-based K_RU (i.e. modeled K_RU). Pre-urine collection postdialysis SUN, which was measured at the last HD session before urine collection, was available in 1804 measurements.

Calculation of K_RU

Modeled K_RU values were obtained through use of a javascript-HTML Web form (available via www.ureakinetics.org), the Solute Solver [4], which models the entire weekly SUN profile. The urine volume, the urine UN concentration and the duration of the collection period is input into the program, as well as the time lag between the end of the urine collection period and the start of the following dialysis session, which was assumed to be 60 min in all cases.

K_RU was also calculated using an estimating equation described by Daugirdas [5]. The per-minute excretion of UN is computed from the urine collection during the collection period, and then this is divided by an estimate of the time-averaged serum water UN during the collection period. This TAC SUN value is estimated as the SUN measured at the end of the collection period (effectively, the predialysis SUN of the subsequent dialysis treatment), multiplied by the following ratio, R: R = 1.075 − (0.0038 × URR + 0.059) × UDUR/IDI, where URR is the urea reduction ratio (as percent) of the dialysis session following the urine collection, UDUR is the duration of the urine collection period and IDI is the duration of the interdialytic interval in which the urine collection is done.

As an example, if the urine is collected for a 24-h period, and 750 mL of urine is collected, the UN concentration of which is 500 mg/dL, then the per-minute UN excretion rate is 750 mL × 5 mg/mL = 3750 mg excreted over 1440 min or a UN excretion rate of 2.6 mg/min. Now, assume that the SUN at the end of the collection period (predialysis SUN of the subsequent treatment) is 40 mg/dL or 0.4 mg/mL. If the SUN during the collection period were 0.4 mg/mL, then K_RU during the collection period would be 2.6/0.4 = 6.5 mL/min. However, the predialysis SUN needs to be adjusted by R from the above estimating equation, where R is 1.075 − (0.0038 × URR + 0.059) × UDUR/IDI. Assume that the URR is 75% and that the IDI during the collection period was 2 days less the 4 h dialysis session length, = 2880−240 = 2640 min. R = 1.075 − (0.0038 × 75 + 0.059) × 1440/2640 = 1.075 − (0.344 × 0.545) = 1.075 −  0.187 = 0.888. So, the predialysis SUN must be multiplied by R to estimate the TAC SUN water concentration during the collection period, and 0.4 × 0.888 = 0.355 mg/mL. As a final step, to compute K_RU, one divides the per-minute UN excretion rate (2.6 mg/min) by the estimated TAC SUN during the collection period (0.355 mg/mL), and the K_RU during the collection period is 2.6/0.355 = 7.32 mL/min. Note that in the estimating equation for R, as UDUR approaches zero, R approaches 1.075. This 1.075 value is simply 1/0.93, and results from the need to correct the predialysis SUN concentration for plasma water.

We also studied variants of this equation, where the postdialysis SUN in the URR term was not the postdialysis SUN of the dialysis session following the collection period, but the postdialysis SUN of the dialysis preceding the urine collection. This ‘previous postdialysis SUN’ value was measured in 1804 instances, or alternatively, it was taken from the weekly SUN trace produced by the modeling program, or else estimated by the following empirically derived equation:

ΔIDI = (IDI in days prior to collection interval) − (IDI in days of the collection interval)

NDAYS = number of treatments per week

Estimated previous postdialysis SUN = 1.1 × postdialysis SUN × (0.07 × NDAYS × ΔIDI + 1.03)

K_RU values were also calculated by alternative ‘simple’ methods. The first was to divide the per-minute UN excretion rate by 0.9 × predialysis SUN. In a second method, when urine was collected over 90% of IDI and when pre-urine collection measured postdialysis SUN was available, we also calculated K_RU values by using the average of predialysis SUN and pre-urine collection postdialysis SUN as the denominator of the clearance equation. We further evaluated the equation recommended by Jindal and Goldstein [7].

RESULTS

The number of cases remaining after exclusions described in the Materials and Methods section (and in detail in Supplementary data, Figure S1) are shown in Table 1, organized by dialysis frequency, duration of the IDI in which the collection had taken place, and the duration of the collection period. Among 32 734 urine collections analyzed, the great majority were done in patients hemodialyzed 3/week during IDIs of 2 or 3 days. The great majority of urine collection periods were 24 h or less. Patient and dialysis treatment characteristics are shown in Table 2.

Table 1.

Number of cases by interdialytic urine collection characteristics

Frequency, IDI	Urine collection period (h)
	>6 to 24	>24 to 48
4/week
IDI = 2	352	0
IDI = 3	126	0
3/week
IDI = 2	14 003	338
IDI = 3	14 413	40
IDI = 4	79	0
2/week
IDI = 2	828	13
IDI = 3	1545	11
IDI = 4	408	0
IDI = 5	292	0
1/week
IDI = 7	287	0

IDI = interdialytic interval in days

Table 2.

Patient characteristics

	1/week	2/week	3/week	4/week
Number of cases	287	3097	28 872	478
Age (years)	62 ± 16	64 ± 15	62 ± 15	62 ± 15
Male (%)	53	58	63	59
Diabetes (%)	53	58	63	59
Race/ethnicity (%)
Non-Hispanic white (%)	56	63	54	59
Non-Hispanic black (%)	26	21	25	25
Hispanic (%)	10	10	12	10
Other races (%)	8	7	8	7
Weight (kg)	83 ± 24	82 ± 23	85 ± 23	87 ± 24
Modeled V2pl (L)	40 ± 14	39 ± 13	40 ± 14	42 ± 13
Urine vol/24 h (mL)	1000 (510–1440)	900 (500–1400)	650 (400–1100)	700 (400–1100)
Collection duration (min)
720 to <1440	0	0.4	0.5	0
1440	100	98.8	98.1	100
>1440 to 2 880	0	0.8	1.3	0
Modeled KRU (mL/min)	3.3 (1.7–5.8)	3.6 (2.0–5.5)	2.6 (1.4–4.3)	2.7 (1.5–4.7)
Pre-HD SUN (mg/dL)	58 (45–77)	51 (40–64)	50 (39–62)	45 (34–56)
Present post-HD SUN (mg/dL)	19 (13–27)	16 (11–21)	15 (11–20)	14 (11–20)
Last post-HD SUN (mg/dL)	NA	17 (12–24)	16 (12–21)	17 (10–22)
URR (%)	66 ± 10	68 ± 9	68 ± 8	67 ± 8
Qb (mL/min)	349 ± 73	374 ± 67	387 ± 67	375 ± 68
Qd (mL/min)	700 (600–800)	700 (600–800)	761 (600–800)	800 (600–800)
Td (min)	187 (180–216)	195 (180–215)	210 (184–227)	210 (185–230)
UF (L)	1.5 (0.8–2.4)	1.8 (1.0–2.8)	2.3 (1.4–3.2)	2.1 (1.2–3.0)
UF/estimated V2pl (%)	3.9 (2.2–6.3)	4.9 (2.6–7.5)	5.9 (3.6–8.3)	5.3 (3.0–7.5)
Kd (estimated, mL/min)	236 ± 33	246 ± 28	253 ± 29	249 ± 29
spKt/V	1.23 ± 0.34	1.35 ± 0.34	1.38 ± 0.30	1.32 ± 0.29
Dialysis stdKt/V	0.68 ± 0.11	1.45 ± 0.23	2.22 ± 0.30	2.88 ± 0.40
Full stdKt/V (100% KRU)	1.54 (1.15–2.21)	2.42 (1.98–2.99)	2.92 (2.58–3.38)	3.65 (3.22–4.11)
nPCR 2pl (g/kg/day)	0.69 ± 0.29	0.88 ± 0.27	0.96 ± 0.28	0.94 ± 0.27

Available in 467, 1322 and 24 patients on 2/week, 3/week and 4/week HD, respectively.

UF, ultrafiltration volume; V2pl, modeled 2-pool postdialysis urea distribution volume; Kd, dialyzer clearance, stdKt/V, standard Kt/V; nPCR 2pl, 2-pool normalized protein catabolic rate; NA, not available.

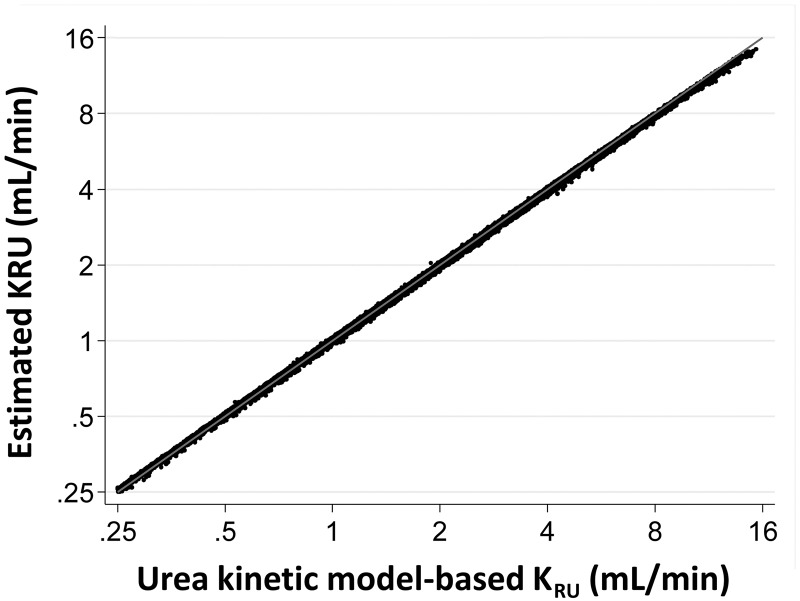
Figure 1 shows, on the horizontal axis, the K_RU values computed using the formal two-pool model [4], and on the vertical axis, the K_RU values calculated using the estimating equation [5]. The URR term in the estimating equation was computed from the laboratory-measured predialysis and postdialysis SUN values of the HD treatment that followed the collection period. Estimated K_RU showed a very high correlation with urea kinetic model-based K_RU.

FIGURE 1.

Comparison of K_RU from formal two-pool modeling, where the time-average plasma water SUN is computed on a minute-to-minute basis from the weekly concentration profile (horizontal axis), and K_RU from the estimating equation described in the text, using the pre- and postdialysis SUN values taken from the HD session immediately following the end of the collection period.

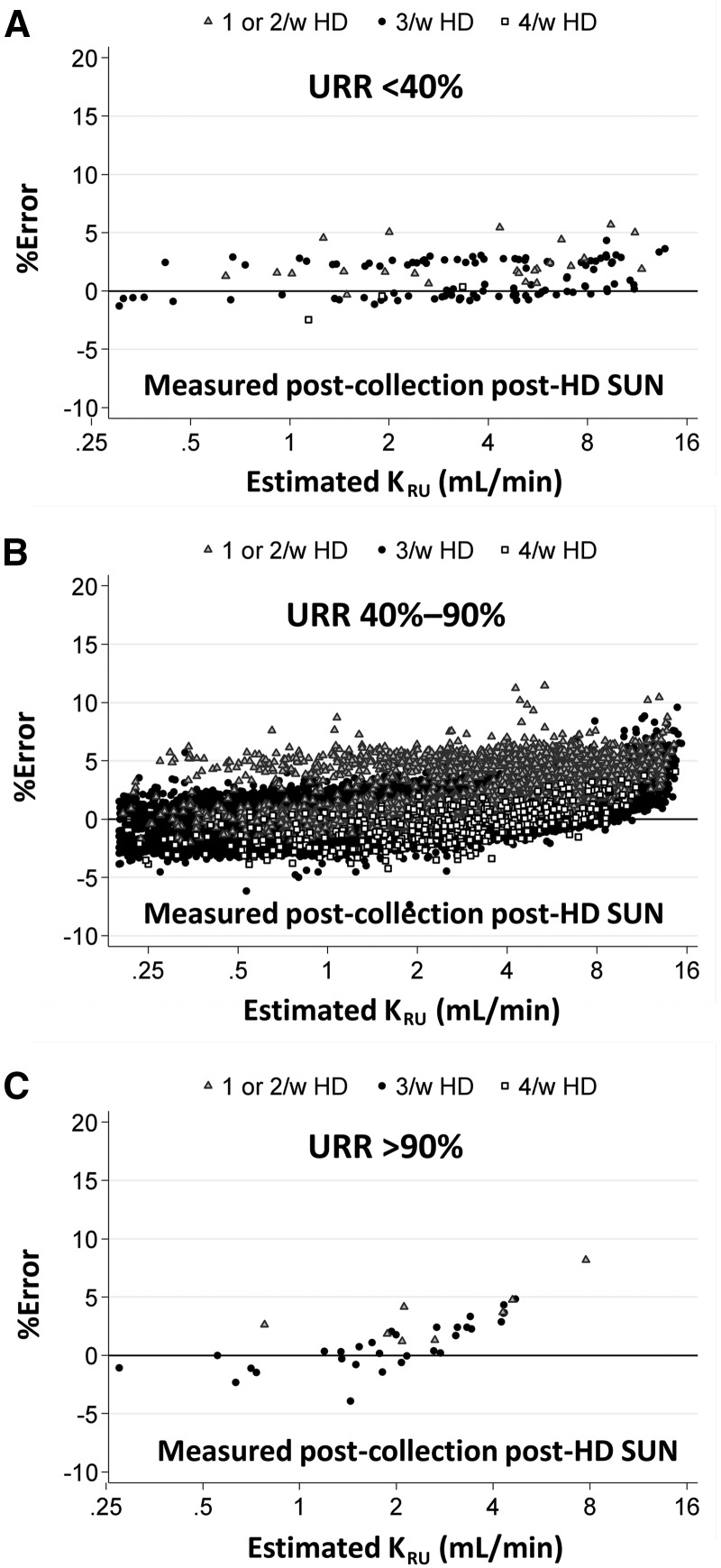
Figure 2 explores the percent error in the estimate of K_RU using the estimating equation. Again, the URR term was computed from the laboratory-measured SUN values around the dialysis session that followed the urine collection. Data are divided into three ranges of URR: <40% (n = 133), the ‘usual’ range of 40–90% (n = 32 561) and >90% (n = 40). In each graph, the data points are further subdivided according to dialysis schedule, marking 1 or 2/week, 3/week and 4/week schedules by differently shaped data points. Although there appeared a slight tendency toward overestimating K_RU at very high levels (i.e. >8 mL/min) or in patients with less frequent dialysis schedules (≤2/week), overall error using the equation was low 0.6 ± 1.9%. The overall percentage of estimated K_RU within 5% of urea kinetic model-based K_RU was 98.2%, and consistent across URR categories (i.e. 97.0%, 98.2% and 97.5% in <40%, 40–90% and >90%, respectively). All except for five urine collections were within 10% error.

FIGURE 2.

Percent error in K_RU, comparing the estimating equation (URR from measured predialysis SUN and postdialysis SUN of dialysis session following the collection period) versus the modeled K_RU, as a function of estimated K_RU for several ranges of URR.

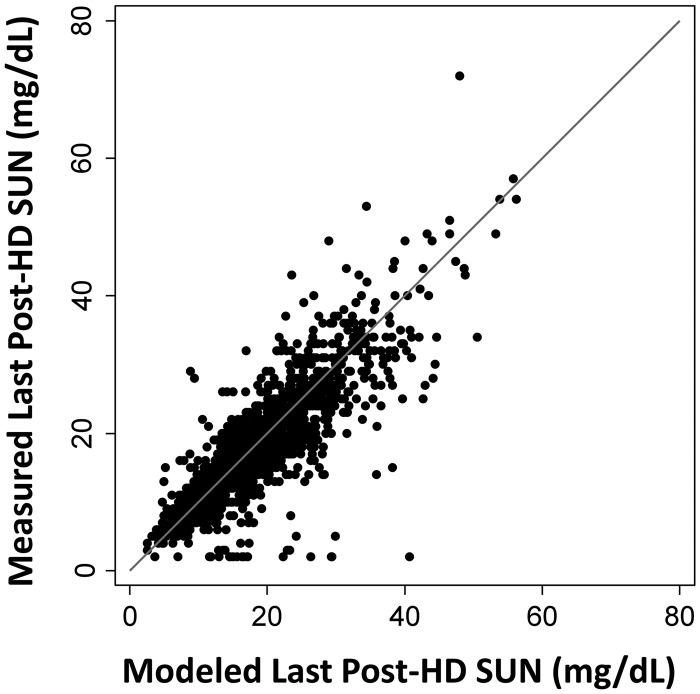
Theoretically, one of the main variables of interest in predicting the time-averaged serum water UN concentration during the urine collection should be the postdialysis SUN of the dialysis preceding the collection period, and not the postdialysis SUN of the dialysis following the collection. Accordingly, we explored use of a modified estimating equation in which the URR term used the postdialysis SUN of the dialysis session that preceded the urine collection period. This ‘last-postdialysis SUN’ was obtained in one of three ways: (i) from actual laboratory measurement (available in a subset of patients), (ii) as estimated from the 7-day SUN trace generated by the urea kinetic model and (iii) from a separate prediction equation that we devised to estimate the postdialysis SUN of the prior dialysis session from the postdialysis SUN value of the dialysis following the collection period and the ratio of the IDI preceding the urine collection to the IDI of the urine collection, with an adjustment term based on dialysis schedule (see Materials and Methods). The values predicted from the weekly SUN trace of the urea kinetic model were strongly correlated with the actual laboratory-measured preceding dialysis postdialysis SUN values (Figure 3).

FIGURE 3.

Postdialysis SUN of the dialysis session preceding the urine collection period. Modeled value on the horizontal axis versus measured value (in a subset of patients) on the vertical axis. The line of identity is shown.

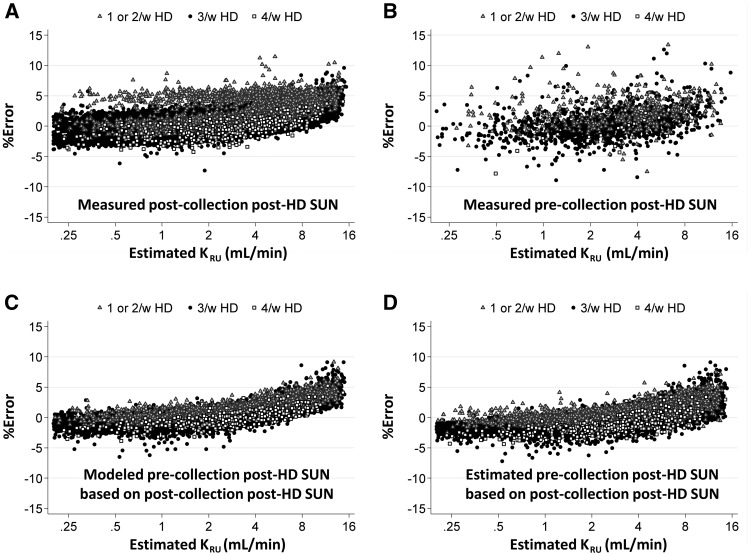
The results comparing percent error in K_RU calculated using the estimating equation with the various alternative ways of obtaining the postdialysis SUN of the prior dialysis session are shown in Figure 4. The K_RU estimating equation using the preceding dialysis postdialysis SUN (Figure 4B–D) obtained by any of the three methods described above, gave slightly lower errors than when the postdialysis SUN of the post-collection dialysis session (Figure 4A) was used.

FIGURE 4.

Percent error with the same estimating equation, but using postdialysis SUN values in the URR term that were derived in different ways. The predialysis SUN term in the URR value was always the measured value of the dialysis session following the collection period. In (A), the equation was computed in the usual fashion, with URR using the postdialysis SUN from the dialysis session following the urine collection. (B) A subset of patients in whom the postdialysis SUN term from the dialysis before the collection period was available, and in whom the URR term was computed from the prior postdialysis SUN and the predialysis SUN term from the dialysis after the collection period. In (C) and (D), the postdialysis SUN prior to the collection period was used in the URR, but this value was either the Solute Solver modeled value (C) or was estimated using a separate prediction equation described in Materials and Methods section.

Comparison with previously described methods of estimating K_RU

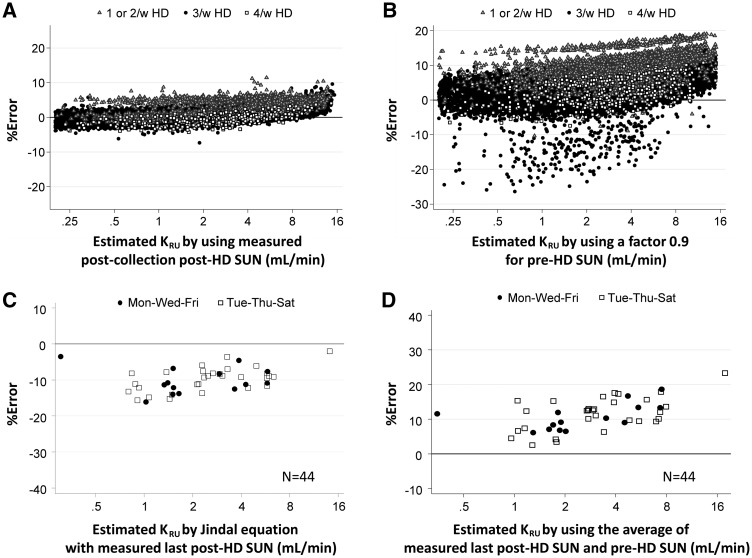
In Figure 5, we compared the precision of the new equation (Figure 5A) with that of three previously described methods: (i) the recommendation of dividing the per-minute UN excretion rate during the urine collection by 90% of the predialysis SUN (Figure 5B), (ii) an equation for 3/week schedule recommended by Jindal et al. [7] (Figure 5C) and (iii) the method dividing the per-minute excretion rate of UN by the average of the previous postdialysis SUN (the value at the start of the collection period) and the predialysis SUN (at the end of the collection period; Figure 5D). No serum water correction was made. In evaluation of the last two methods, cases analyzed were limited to 44 observations where the urine collection period encompassed an entire IDI, where the previous postdialysis SUN was measured, where dialysis frequency was 3/week and where the duration of the IDI was 2 days. Data from patients on ≤2/week, 3/week and 4/week HD schedule were shown as gray triangles, black circles and open squares, respectively. The new equation in Figure 5A showed the highest precision with the lowest variation; overall error in each equation was 0.6 ± 1.9%, 4.5 ± 4.0%, −9.9 ± 3.4% and 11.3 ± 4.5%, respectively. A tendency toward overestimating K_RU was noted again at very high levels or in patients with less frequent dialysis schedules, irrespective of models.

FIGURE 5.

Percent error in K_RU estimated based on (A) the new equation using the postdialysis SUN from the dialysis session following the urine collection, (B) the recommendation of dividing the per-minute UN excretion rate during the urine collection by 90% of the predialysis SUN, (C) Jindal’s equation [7] and (D) the recommendation of dividing the per-minute UN excretion rate during the urine collection by the average of the measured postdialysis SUN of the dialysis session prior to the collection period and the predialysis SUN of the dialysis session following the collection. No correction for serum water. Cases analyzed in Figures (C) and (D) were limited to instances where the urine collection period included the entire IDI and where the preceding postdialysis SUN was measured (n = 44). Gray triangles, black circles and open squares in (A) and (B) indicate data from patients on ≤2-times, 3-times and 4-times weekly HD, respectively. Black circles and open squares in (C) and (B) indicate data from 3-times weekly HD patients on Monday–Wednesday–Friday and Tuesday–Thursday–Saturday schedules, respectively.

Tables 3 and 4 tabulate the percent errors in K_RU calculated using all methods described above. Table 3 focuses on results organized by IDIs of 2, 3 and 4 days, whereas Table 4 focuses on results organized by frequencies of treatments per week. It can be seen that each of the three previous methods of estimating K_RU had less precision than the estimating equation. Dividing per-minute UN excretion rate by the average of the preceding postdialysis SUN and following predialysis SUN resulted in an average error of +11%, whereas the Jindal equation showed an error in the opposite direction of approximately the same magnitude (−10%). As shown in Table 4, the strategy of dividing the per-minute excretion rate of UN by 0.9 × predialysis SUN had a precision that was highly dependent on the frequency of dialysis and the duration of the urine collection interval. URR, weekly ultrafiltration, urine collection time, dialysis treatment time, post-HD SUN, modeled two-pool volume, post-HD weight and the ratio of modeled two-pool volume to Watson’s total body water showed no meaningful influence on the estimation error (Supplementary data, Figure S2). Stratification by treatment frequency and IDI revealed that K_RU was consistently overestimated by approximately 5.0% irrespective of K_RU levels when urine was collected during a 2-day interval from patients on a 2:5-day 2/week schedule (Supplementary data, Figure S3). Error was not increased in patients following a 1/week schedule (Supplementary data, Figure S4).

Table 3.

K_RU results by IDI and collection period (1–4 dialysis treatments per week)

	IDI
	2 days				3 days				4 days
	Urine collection time				Urine collection time				Urine collection time
	≤1440 min		>1440 min		≤1440 min		>1440 min		≤1440 min		>1440 min
	n	Percent error	n	Percent error	n	Percent error	n	Percent error	n	Percent error	n	Percent error
Measured post-collection post-HD SUN	15 183	1.6 ± 1.5	351	1.7 ± 2.6	16 084	−0.4 ± 1.6	51	−0.3 ± 2.9	486	0.9 ± 1.6	0	–
Modeled pre-collection post-HD SUN based on post-collection post-HD SUN	15 183	0.3 ± 1.2	351	−0.6 ± 2.0	16 084	0.3 ± 1.4	51	0.6 ± 2.3	486	1.4 ± 1.5	0	–
Estimated pre-collection post-HD SUN based on post-collection post-HD SUN	15 183	−0.8 ± 1.1	351	−2.4 ± 1.6	16 084	−0.2 ± 1.4	51	−0.2 ± 2.4	486	1.2 ± 1.5	0	–
Factor 0.9 for pre-HD SUN	15 183	2.0 ± 2.8	351	−10.3 ± 7.1	16 084	6.6 ± 2.1	51	−0.7 ± 7.1	486	11.3 ± 2.0	0	–
Measured pre-collection post-HD SUN	1377	0.9 ± 2.6	114	0.2 ± 3.9	219	0.7 ± 1.7	7	1.9 ± 2.9	58	1.4 ± 1.6	0	–
Average of measured post-collection post-HD SUN and pre-HD SUN	0	–	44	11.3 ± 4.5	0	–	0	–	0	–	0	–
Jindal equation	0	–	44	−9.9 ± 3.4	0	–	0	–	0	–	0	–

NA, not available.

Table 4.

K_RU results: effect of schedule

	Treatment frequency
	1/week				2/week				3/week				4/week
	Urine collection time				Urine collection time				Urine collection time				Urine collection time
	≤1440 min		>1440 min		≤1440 min		>1440 min		≤1440 min		>1440 min		≤1440 min		>1440 min
	n	Percent error	n	Percent error	n	Percent error	n	Percent error	n	Percent error	n	Percent error	n	Percent error	n	Percent error
Measured post-collection post-HD SUN	287	1.5 ± 1.2	0	–	3073	2.5 ± 2.0	24	5.8 ± 3.7	28 494	0.4 ± 1.7	378	1.1 ± 2.4	478	−0.5 ± 1.5	0	–
Modeled pre-collection post-HD SUN based on post-collection post-HD SUN	287	1.5 ± 1.2	0	–	3073	1.4 ± 1.3	24	2.1 ± 2.0	28 494	0.2 ± 1.2	378	−0.6 ± 2.0	478	−0.2 ± 1.3	0	–
Estimated pre-collection post-HD SUN based on post-collection post-HD SUN	287	1.2 ± 1.2	0	–	3073	0.8 ± 1.2	24	0.5 ± 1.6	28 494	−0.6 ± 1.2	378	−2.3 ± 1.7	478	−1.3 ± 1.5	0	–
Factor 0.9 for pre-HD SUN	287	16.1 ± 1.4	0	–	3073	8.8 ± 3.2	24	−1.2 ± 6.6	28 494	4.1 ± 3.2	378	−9.6 ± 7.6	478	–	0	–
Measured pre-collection post-HD SUN	0	–	0	–	456	2.2 ± 2.5	10	2.6 ± 5.3	1203	0.4 ± 2.2	111	0.1 ± 3.7	24	−1.0 ± 2.5	0	–
Average of measured post- collection post-HD SUN and pre-HD SUN	0	–	0	–	0	–	0	–	0	–	44	11.3 ± 4.5	0	–	0	–
Jindal's equation for 3/week	0	–	0	–	0	–	0	–	0	–	44	–9.9 ± 3.4	0	–	0	–

NA, not available.

DISCUSSION

Based on an examination of the pre-, post- and interdialytic urinary and serum data in one of the largest HD cohorts to date with comprehensive urine collection data, our results suggests that K_RU calculated using a prediction equation used to compute time-averaged serum water UN during the urine collection period [5] substantially agrees with K_RU calculated using a two-pool variable volume urea kinetic model [4]. The estimated K_RU values deviated from the formally modeled values by <5% in 98% of cases, and the percent error seemed to be only modestly affected by the duration of the urine collection interval, body size, modeled urea distribution volume V, the URR and the duration of the HD session (see figures in Supplementary data). The percent error was somewhat affected by the number of treatments given per week, with a slight positive error with 2/week compared with 3/week dialysis schedules (Table 4).

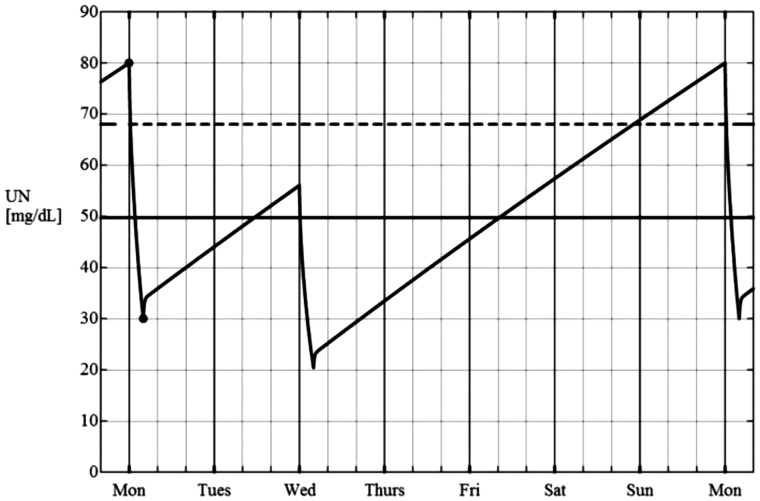
There was one circumstance where the K_RU estimating equation seemed to have slight positive bias. This set of points is visible as triangles in Figure 4, panel A. These triangles represent data from patients following a 2/week schedule where the IDIs were 2 and 5 days, and where the urine was being collected in the course of the 2-day IDI (see Supplementary data). To better understand the source for this error, we examined the predicted SUN trace during the week with this schedule (Figure 6). The postdialysis SUN prior to the collection period with this schedule is considerably higher than the postdialysis SUN of the dialysis session immediately following the collection period. In the K_RU estimating equation used, the URR of the session following the urine collection period is used to infer the bounds of the SUN during the IDI in which the collection takes place. Because the preceding postdialysis SUN is markedly underestimated in this particular case, the predicted TAC SUN during the collection period will be lower than that calculated from integrating the appropriate time segment of the weekly SUN profile. From the urea kinetic model 7-day SUN trace, we could easily extract the postdialysis SUN of the dialysis session preceding the urine collection period, and when this modeled ‘last postdialysis SUN’ value was used to compute the URR term of the estimating equation instead of the postdialysis SUN of the dialysis session following the collection, the +5% error with the 2/week 2:5-day schedule was substantially reduced (Figure 4C vs. 4A and Table 4).

FIGURE 6.

A weekly SUN curve modeled for a 2/week dialysis schedule with dialysis treatments given on Monday and Wednesday. If the urine is collected during the Monday–Wednesday IDI, the postdialysis SUN value of the Wednesday dialysis is considerably lower than that following the pre-collection Monday dialysis. This is due to the long IDI from Wednesday to Monday, resulting in a markedly higher predialysis SUN on Monday compared with Wednesday.

A potential overall bias in the K_RU estimating equation was a trend toward overestimation of K_RU as K_RU increased to relatively high values. When the K_RU was small (e.g. 1–3 mL/min), the percent error tended to be slightly negative. The error was close to null in the 3–5 mL/min range of K_RU (Figure 3) and then the error turned slightly positive as the K_RU exceeded values of 5 mL/min. Although the magnitude of this bias was not substantial, the possible cause needs to be understood. We believe that the bias can best be explained by considering two hypothetical patients modeled using the urea kinetic program (see Supplementary data, Figure S5). Both instances model a 3/week dialysis schedule with predialysis SUN of 80 and postdialysis SUN of 30 mg/dL, but in one trace the K_RU is set at 1.0 mL/min and in the other, K_RU is set at 7.0 mL/min (necessitating a somewhat unphysiological urea generation rate). As can be seen from a comparison of the traces, in the situation where K_RU is high, the interdialytic SUN curve has distinct convex-upwards curvature. This will result in a higher calculated TAC SUN during the collection period compared with the linear analysis used in the prediction equation. Because the TAC SUN during the collection period is slightly lower with the prediction equation at higher values of K_RU, the K_RU estimate will be slightly higher, explaining this positive bias.

How does this new method of estimating TAC SUN during the urine collection period differ from what is commonly practiced? Three approaches are in common use: the first is to simply divide the per-minute urine UN excretion rate obtained from the urine collection by 90% of the predialysis SUN value [8]. A second is to divide by the average of the postdialysis SUN value of the preceding dialysis session and the predialysis SUN of the session immediately following the urine collection. A third method is based on an adjusted average of the SUN values before and after the urine collection, also taking into account the relative duration of the collection period [7]. From Tables 3 and 4, one can see that the precision of the method of using 90% of the predialysis SUN depends on both the dialysis schedule and the duration of the urine collection period. Dividing renal UN excretion rate by 90% of the predialysis SUN value did work relatively well when the collection period is 24 h and IDI is 2 days. The method of averaging pre- and post-collection SUN values leads to an 11% overestimation of K_RU. The method recommended by Jindal and Goldstein [7] would substantially underestimate K_RU (by about 10%).

Our study has several potential limitations. Of the ∼32 000 treatments analyzed, a second SUN sample at the beginning of the IDI was obtained in only 1812 treatments, and in only 44 of these was urine collected during the entire (>90%) IDI. In the remaining 1770 cases, the initial SUN at the start of the urine collection period was obtained using modeling. Also, no interval SUN measurements were obtained during the urine collection period on any of the patients. However, there is no a priori reason to believe that there would be marked deviation from relative linearity of the increase in SUN, apart from the slight curvature noted in patients with quite high levels of K_RU. For the 1377 treatments where the postdialysis SUN was at the start of the IDI was actually measured, the values agreed quite well with those derived from the urea kinetic modeling program’s weekly SUN profile. Using modeling, we also explored the nonlinearity of the increase in SUN during the IDI as a function of estimated fluid gain during the IDI, and found that this resulted only a minor change in the accuracy of the prediction equations (data not shown). Nevertheless, whether or not urine was collected during 44 h or 24 h during those IDIs where SUN values at both the start and end of the IDI were available, important interval values for the SUN during the collection period were missing and had to be interpolated assuming a more or less linear increase in SUN during the IDI [after adjusting for postdialysis UN rebound and for dilution due to extracellular fluid (ECF) accumulation during the IDI]. It remains possible that the SUN increase during the IDI was nonlinear (even after adjusting for dilution). On an individual patient basis, there may have been spikes in UN generation during the IDI due to spikes in protein intake, and on a more general basis, the liver UN generation rate may have increased progressively during IDI due to enhanced liver blood flow as ECF volume reaccumulates. This is a question that would benefit from further investigation.

One problem with collecting urine during part of an IDI is that K_RU, be it inulin or urea, tends to increase over the course of an IDI [9]. This probably is due to accumulation of fluid and better renal perfusion as one leaves the previous dialysis session behind, but it also may be due to increasing osmotic load as urea and other solutes accumulate in the blood. The change in clearance can be substantial, and for this reason, some have recommended collecting urine over the entire IDI to best reflect the average weekly K_RU. However, due to practicality, the great majority of urine collections being done in the USA, as evidenced by our own data, are performed over a 24-h period prior to a dialysis session. Given the data of van Olden et al. [9], a K_RU estimate derived from a 24-h predialysis collection may be somewhat higher than the K_RU averaged over the entire week. Despite this theoretical limitation, Kjaergaard et al. [10] found that 24-h predialysis urine collection periods gave relatively reproducible results, and as long as one is consistent in terms of the time period during which urine is collected, this overestimation of weekly K_RU can be simply kept in mind, and perhaps adjusted downwards slightly if desired. One can apply somewhat complex mathematical corrections to a urine collection period to account for this change in K_RU in the course of an IDI (see [11], Supplementary data), but this is not routinely done.

Recently, one of us J.T.D.) used the data of van Olden to determine which urine collection periods during various dialysis schedule are optimal, in that K_RU or urine volume would be similar to the weekly average values [12]. This analysis (see Table 3 in [12]) suggests that, for a 3/week standard schedule a 24-h urine collection done during the second half of a 2-day IDI should yield values for both K_RU and urine volume that would be similar to average weekly values. For a 2/week schedule, with 3-day and 4-day IDIs, a 2-day collection during the 3-day IDI would be most similar to weekly average values, whereas for a 2/week 2-day and 5-day IDIs, the value for K_RU or urine volume calculated from a 1-day or 2-day collection would need to be adjusted downward or upwards, depending on whether the collection was done during the 2-day or 5-day IDI.

The availability of this new K_RU estimating equation does not diminish the overall advantages of using formal kinetic modeling to quantify HD. In addition to further minimizing the calculation error for K_RU, use of formal kinetic modeling allows for rejection of modeling sessions where results clearly show an error in blood sampling or recorded dialysis treatment parameters (e.g. when modeled volumes are far different from anthropometric estimates or from previously obtained modeled values), and formal modeling also allows for easy computation of continuous equivalent measures of dialysis dose such as the standard Kt/V and the equivalent urea clearance [13].

In conclusion, our data derived from a large nationally representative and contemporary cohort of HD patients suggest that K_RU estimated using an equation that includes urine collection data, the predialysis SUN and URR of the subsequent dialysis treatment and the ratio of the urine collection period to the IDI agrees well with the K_RU calculated using a formal kinetic modeling program. With the increased attention being given to monitoring residual kidney function as well as potential use of K_RU to guide prescription of incremental dialysis, this simple approach may help standardize K_RU estimates and facilitate comparison of results across different treatment schedules, urine collection periods and IDIs.

SUPPLEMENTARY DATA

Supplementary data are available online at http://ndt.oxfordjournals.org.