The respiration rate inside plant organs such as pear fruit is controlled both by diffusion limitation of oxygen and through additional regulatory processes in a temperature-dependent manner.
Keywords: Diffusion, down, regulation, hypoxia, modelling, Pyrus communis, respiration
Abstract
The respiration rate of plant tissues decreases when the amount of available O2 is reduced. There is, however, a debate on whether the respiration rate is controlled either by diffusion limitation of oxygen or through regulatory processes at the level of the transcriptome. We used experimental and modelling approaches to demonstrate that both diffusion limitation and metabolic regulation affect the response of respiration of bulky plant organs such as fruit to reduced O2 levels in the surrounding atmosphere. Diffusion limitation greatly affects fruit respiration at high temperature, but at low temperature respiration is reduced through a regulatory process, presumably a response to a signal generated by a plant oxygen sensor. The response of respiration to O2 is time dependent and is highly sensitive, particularly at low O2 levels in the surrounding atmosphere. Down-regulation of the respiration at low temperatures may save internal O2 and relieve hypoxic conditions in the fruit.
Introduction
Gas exchange in plant organs relies on diffusion, causing gas to move from a high to a low concentration according to Fick’s law. Limited gas diffusion inside bulky organs (roots, fruits and tubers) may affect metabolic processes such as respiration, and lead to metabolic changes (Denison, 1992; Drew, 1997; Geigenberger et al., 2000; Franck et al., 2007; Ho et al., 2010a; Armstrong and Beckett, 2011a; Verboven et al., 2012). In seeds, restriction of gas diffusion during development or germination may result in hypoxic conditions (Rolletschek et al., 2003; Borisjuk and Rolletschek, 2009; Verboven et al., 2013) locally affecting respiratory activity. In fruit, the high resistance to gas transport of cortex tissue and the high respiration rate associated with ripening induces local anoxia during controlled atmosphere (CA) storage (Lammertyn et al., 2003; Ho et al., 2010a, 2013). In such anoxic stress conditions, metabolism is likely to switch from the respiratory to the fermentation pathway, causing physiological disorders (Franck et al., 2007; Herremans et al., 2013; Ho et al., 2013).
Decreasing respiratory O2 consumption in response to a reduction in the available O2 has been described in different plant tissues, including seeds (van Dongen et al., 2004), fruit (Lammertyn et al., 2001, 2003; Ho et al., 2010b, 2011), and roots (Geigenberger et al., 2000; Gupta et al., 2009; Zabalza et al., 2009; Armstrong and Beckett, 2011a). While the respiratory metabolism is likely to be affected by local anoxia due to limited gas transport (Armstrong and Beckett, 2011a), active regulation of the respiratory metabolism may also play a role (Gupta et al., 2009; Zabalza et al., 2009). The arguments for both hypotheses have been reviewed (Gupta et al., 2009; Armstrong and Beckett, 2011b; Nikoloski and van Dongen, 2011). Changes in the respiratory metabolism might also be explained by a combination of both mechanisms (Gupta et al., 2009); however, this has not yet been investigated in detail.
As invasive measurement of gas concentrations in pear fruit is difficult without distorting and damaging the tissue, and thus affecting the gas exchange process itself, mathematical models provide a useful alternative. Such reaction–diffusion-type models have been commonly constructed by combining Michaelis–Menten respiration kinetics with Fick’s diffusion equation (Lammertyn et al., 2003; Ho et al., 2008, 2011, 2016; Armstrong and Beckett, 2011a). In earlier modelling works, diffusion coefficients and respiration parameters were explicitly and experimentally measured (Lammertyn et al., 2003; Ho et al., 2008). Armstrong and Beckett (2011a) did not experimentally determine diffusion coefficients and respiration rate, but estimated these from the data by means of the model describing O2 diffusion of roots using a multicylindrical geometry. As the experimental measurement of diffusion coefficients is prone to errors due to artefacts induced by cutting of the samples (flooding the intercellular spaces by leaking of the cell content), Ho et al. (2011, 2016) developed a method to compute these coefficients using microscale diffusion models and 3-D synchrotron X-ray tomography images of the tissue. For the respiration kinetics, the maximal rates were considered to vary with temperature while the Michaelis–Menten constants were shown to be relatively independent of temperature (Hertog et al., 1998). Lammertyn et al., (2001) estimated a value of 3 μM (0.14 kPa O2) for pear cell protoplasts. Armstrong and Beckett (2011a) used a value of 0.14 μM (0.011 kPa O2), averaged from values cited for isolated mitochondria from several plant species. Ho et al. (2013) estimated the of apple tissue to be within the range 0.13–0.17 kPa. The maximal rate coefficients in the Michaelis–Menten expression are typically obtained by fitting the model to respiration measurements (Hertog et al., 1998; Lammertyn et al., 2001; Armstrong and Beckett, 2011a; Ho et al., 2013). Simulations with these reaction–diffusion models consistently predicted the existence of considerable gas gradients in the fruit, and local O2 concentrations in the centre of the fruit approaching the Km of cytochrome c oxidase (COX), the rate-limiting enzyme in the oxidative respiration pathway. This suggests a passive regulation of the respiratory metabolism, but without excluding other regulatory mechanisms, for example at the transcriptome level as a consequence of a putative oxygen sensor. Such an oxygen sensor has been found recently in Arabidopsis thaliana (Licausi et al., 2011), but its existence has yet to be shown in pear fruit. Typically, diffusion limitation is more pronounced at higher temperatures when the respiration rate is high. If the temperature is reduced (i.e. from 20 °C to 0 °C), the respiratory activity decreases correspondingly (Ho et al., 2013). Any gradients of the O2 concentration in the fruit would then be reduced and the O2 concentration would become close to uniform throughout the fruit. This provides direct experimental control over internal O2 concentration of the uniform fruit by changing the fruit external atmosphere, thereby potentially exposing other regulatory mechanisms of the respiration pathway.
In this article, we aim to improve our understanding of the response of the oxidative respiratory metabolism of pear fruit to external O2 levels by challenging our previously developed gas exchange model (Ho et al., 2010a, 2011) with new experimental data on pear respiration. The objectives, therefore, were (i) to evaluate whether changes of the respiratory activity under hypoxic conditions are due to diffusion limitation and/or active down-regulation; and (ii) to update our modelling concepts regarding the response of respiration to O2 concentrations at low temperature accordingly. We consider pear as it has a dense tissue with a high diffusion resistance inducing large internal gas gradients. Also, pears are commercially stored under low oxygen conditions that aggravate hypoxic conditions inside the fruit.
Materials and methods
Fruit
Pear fruit (Pyrus communis L. cv. ‘Conference’) were picked from the experimental orchard of the Research Station of pcfruit (Velm, Belgium) on 9 September 2010 and 24 August 2014. In 2016 independent validations, fruit which were harvested on 12 September 2016 were purchased commercially from a local fruit co-operative. For the experiments in 2010, fruit were cooled and stored under ambient air at –1 °C. For the experiments in 2014, fruit were cooled and stored according to commercial protocols for a period of 21 d at –1 °C followed by CA conditions (2.5 kPa O2, 0.7 kPa CO2, –1 °C). For the experiment in 2016, fruit were stored for 2 months under regular air at –1 °C. Picking data and cooling procedures were according to optimal commercial practices used for long-term storage of fruit determined by the Flanders Centre of Postharvest Technology (VCBT, Belgium).
Respiration measurements
A first experiment (Experiment A) was used to determine the maximal O2 consumption rate and the maximal fermentative CO2 production rate of fruit at different temperatures (see Supplementary Table S1 at JXB online). Fruit were placed in 1.7 litre glass jars (two fruit per jar ~0.43 litres) and flushed for 24 h. The gas mixture contained 21 kPa O2, 0 kPa CO2, and 79 kPa N2 for measuring the maximal O2 consumption rate, and 0 kPa O2, 0 kPa CO2, and 100 kPa N2 for measuring the maximal fermentative CO2 production rate. The experiment was carried out at 20, 10, and 0 °C. Four repetitions were carried out following the methodology of Ho et al. (2010b). In brief, flushing was arrested after 24 h, jars were closed, and changes of the O2 and CO2 partial pressures were measured over time by a gas analyser (Checkmate II, PBI, Dansensor, Denmark). The gas partial pressures were converted to molar concentrations following the ideal gas law. The respiration rate was calculated from the difference in gas concentration and the time lag between two measurements, and expressed in μmol per unit fruit volume (m3) per time (s).
Experiments B and C were used to determine kinetic parameters relating the response of respiration to O2 level. In experiment B, we investigated the response of respiration to abruptly changing O2 levels at low temperature. Samples were taken from CA storage and stored under regular air at 0 °C for 1 d before starting the experiment. Fruit were placed in 1.7 litre glass jars (two fruit per jar) at 0 °C at O2 levels that were dynamically varied during a period of 18 d measuring the respiration rate daily. After each respiration measurement, the flushing was restarted. During the first 3 d, the O2 level was set to 20 kPa. Then the O2 level was reduced to 15 kPa O2 (experiment B1) and 5 kPa O2 (experiment B2), respectively. After 13 d, the O2 level was increased again to 20 kPa. The temperature and CO2 level were kept at 0 °C and 0 kPa, respectively. Three repetitions were carried out. In addition, an experiment (B3) was conducted to measure the respiration rate (two repetitions) under dynamically changing O2 levels from 20 kPa to 8, 4, 20, and 4 kPa after 2, 4, 6, and 14 d, respectively (Supplementary Table S1).
In experiment C, we investigated changes in respiration when the O2 was slowly decreasing. Samples were taken from fruit stored under CA conditions (2.5 kPa O2, 0.7 kPa CO2, –1°C). Fruit were placed in 1.7 litre glass jars (two fruit per jar) and flushed with a gas mixture of 7 kPa O2, 0 kPa CO2 at 0 °C for 24 h. Then, the jars were closed and the changing gas conditions were measured during 14 d from which the respiration rate was calculated. The air pressures in the closed jars were also monitored by a pressure sensor (DPI 142, GE Druck, Germany, accuracy ±0.01%). Three repetitions were carried out.
Experiment D was carried out to validate the model. Samples were taken from fruit stored under normal atmosphere conditions (21 kPa O2, 0 kPa CO2, –1°C). Fruit were placed in 1.7 litre glass jars (two fruit per jar) and flushed with a gas mixture for 24 h. The mixture contained 21 kPa O2, 0 kPa CO2, and 79 kPa N2 for the experiments at 20 °C (D3, D5) and 10 °C (D1, D4, D6), 11 kPa O2, 0 kPa CO2, and 89 kPa N2 for the experiments at 5 °C (D7), and 7 kPa O2, 0 kPa CO2, and 93 kPa N2 for the experiments at 0 °C (D2, D8). Then, the jars were closed and the changing gas conditions were measured during 6, 10, 14, and 15 d for the experiments at 20, 10, 5, and 0 °C, respectively. Four replicate measurements were carried out. We used available respiration data of pear harvested in 2010 (Ho et al., 2015) and data of pear harvested in 2014 and 2016 for validations.
In all cases, fruit were stored in the dark inside cold rooms during the incubation period for the various respiration measurements.
Reaction–diffusion model for intact fruit
A previously developed reaction–diffusion model (Ho et al., 2008, 2011; Verboven et al., 2012) was used to describe the overall gas exchange of intact fruit to the externally applied O2 level (Ho et al., 2008, 2011; Verboven et al., 2012):
| (1) |
with αi the gas capacity of component i (O2 and CO2) of the tissue (Ho et al., 2008, 2011; Verboven et al., 2012), Ci (µmol m−3) the concentration of component i, Di (m2 s−1) the apparent diffusion coefficient, Ri (mol m−3 s−1) the production term of gas component i related to O2 consumption or CO2 production, ∇ (m−1) the gradient operator, and t (s) time. Based on preliminary calculations, we found that permeation could be neglected. The gas capacity αi is defined as (Ho et al., 2008, 2011; Verboven et al., 2012):
| (2) |
where ε is the fractional porosity of tissue, and Ci (µmol m−3) and Ci,tissue (µmol m−3) are the concentration of gas component i in the gas phase and the tissue, respectively. The concentration of the compound in the liquid phase of fruit tissue normally follows Henry’s law represented by constant Hi (mol m−3 Pa−1). R (8.314 J mol−1 K−1) is the universal gas constant and T (K) the temperature.
At the fruit surface, the following boundary condition was assumed:
| (3) |
with n the outward normal to the surface; the index ∞ referring to the gas concentration of the ambient atmosphere; and hi the skin permeability for gas i (m s−1) (see Table 1).
Table 1.
Parameters of the respiration diffusion model
| Physical parameters | O2 | CO2 |
|---|---|---|
| Diffusivity of cortex tissue (m2 s−1) |
(1.32 ± 0.39)×10–8a | (2.12 ± 0.34)×10–8a |
| Skin permeability (m s−1) | 6.74 × 10–7b | 10.2 × 10–7b |
| Respiration parameters | ||
| (kPa) | 0.17c | |
| (kPa) | 2.4 × 10–2c | |
| (kPa) | 66.4d | |
| rq,ox | 0.77 ± 0.03e | |
| Maximal O2 consumption rate (µmol m−3 s−1) | See Table 2 | |
| Maximal CO2 fermentative production rate (µmol m−3 s−1) | See Table 2 | |
| Parameters of dynamic adaption of to O2 level at 0 °C | ||
| VR,1 (µmol m−3 s−1) | 0.34×VR,2f | |
| VR,2 (µmol m−3 s−1) | 14.9f | |
| ΔVR=VR,2–VR,1 (µmol m−3 s−1) | 0.66×VR,2f | |
| Kd (d−1) | 1.3f | |
| m | 2f | |
| KH (kPa−2) | 23.3f | |
| (µmol m−3 s−1) at 0 °C | 1.7.8 ± 1.7g |
a Ho et al. (2015).
b Value computed from simulated 3-D microscale of epidermis tissue.
e Value was calculated from the ratio of measured to in ambient air at 20 °C (experiment A).
fValue was estimated from the experimental data (experiment B and C) at 0 °C (see more details in Table 3).
g Value was calculated from the measurement (experiment A, see Table 2).
The gasses within the head space of a closed jar were assumed to be uniformly distributed given their fast diffusivities in air (typically five magnitudes higher than in fruit). Therefore, for an intact fruit placed in the closed jar, the O2 and CO2 concentration in the headspace of the jar changed in response to the respiration of the pear fruit and was modelled as follows:
| (4) |
where Vfruit (m3) and Vair (m3) and are the volume of the fruit and the free air volume of the jar, respectively. The term on the right-hand side expresses the respiration of the entire fruit. Equations 1–4 were numerically solved using the finite element method (Comsol 3.5, Comsol AB, Stockholm) on a 3-D pear geometry generated by means of the shape generator (Rogge et al., 2015).
Response of respiration to the external O2 level at low temperature
A non-competitive inhibition model (Hertog et al., 1998; Lammertyn et al., 2001; Ho et al., 2010b) was used to describe the consumption of O2 by respiration as formulated by Equation 5)
| (5) |
with (µmol m−3 s−1) the maximum oxygen consumption rate, [O2] (µmol m−3) the O2 concentration, [CO2] (µmol m−3) the CO2 concentration, (µmol m−3) the Michaelis–Menten constant for O2 consumption, (µmol m−3) the Michaelis–Menten constant for non-competitive CO2 inhibition, and (µmol m−3 s−1) the O2 consumption rate of the tissue.
The equation for the production rate of CO2 consists of an oxidative respiration part and a fermentative part (Peppelenbos and van’t Leven, 1996; Ho et al., 2010b).
| (6) |
with (µmol m−3 s−1) the maximum fermentative CO2 production rate, (µmol m−3) the Michaelis–Menten constant of O2 inhibition on fermentative CO2 production, rq,ox the respiration quotient at high O2 partial pressure, and (µmol m−3 s−1) the CO2 production rate of the sample.
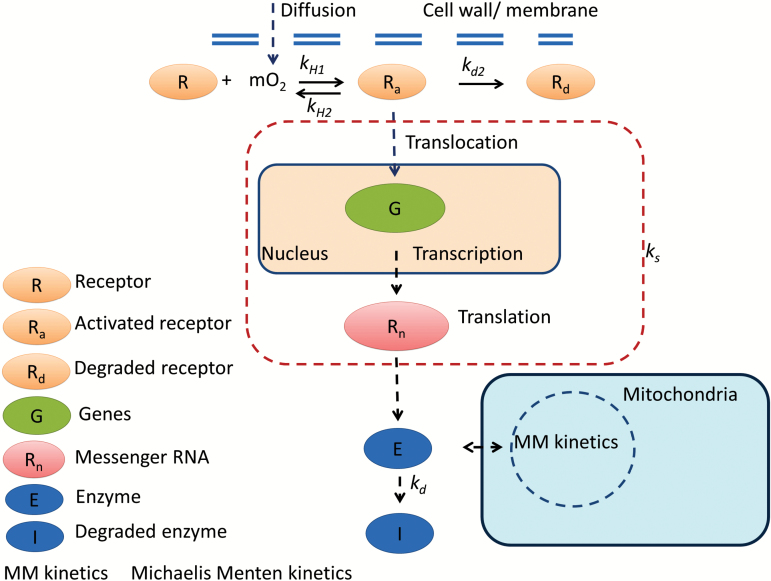
To account for a regulatory mechanism that would adapt the maximal respiration rate in response to changing O2 levels, we assumed that a sensor would be activated by O2, resulting in a signal transduction cascade that eventually would change the amount of enzymes involved in respiration (Fig. 1). A decrease of the O2 level would alter due to adjustment of the balance between enzyme synthesis and degradation according to Supplementary Protocol S1 and Supplementary Fig. S1
Fig. 1.
Proposed response of receptor, enzyme, and respiration to O2 level. The receptor in a pear cell was assumed to be activated by O2, and subsequently to trigger a biochemical chain involving transcription and translation steps, resulting in the final level of the enzyme E. A change in level of the enzyme E in response to the activated receptor was characterized by a lumped synthesis rate ks agglomerating multiple conversion steps in a signal transduction cascade. Solid arrows represent direct conversions, while the dashed arrows indicate more general pathway interactions containing multiple conversion steps. Reaction equations are derived and shown in Supplementary Protocol S1 and Supplementary Fig. S1.
| (7) |
| (8) |
where kd (d−1) is the rate of the response of to changing O2 levels; KH is the sensitivity of to O2; and m is the number of O2 molecules aggregating one signal molecule. VR,2 in Equation 8 is the maximal O2 consumption rate in the presence of O2, while VR,1 is a base affinity for O2; VR is the maximal O2 consumption rate at a steady O2 condition. ΔVR=VR,2–VR,1 is the amplitude of regulation of the maximal respiration rate by O2. Equations 7 and 8 imply that may vary depending on the O2 concentration in a hyperbolic way between VR,1 and VR,2, and that this change is not abrupt but according to an exponential (first-order) response. Equations 1–6 will further be called the ‘gas exchange model’ and Equations 1–8 the ‘adapted gas exchange model’.
The maximal O2 consumption rate and the maximal fermentative CO2 production rate are temperature dependent and were assumed to follow Arrhenius’s law (Hertog et al., 1998) (see Supplementary Protocol S2).
Model parameters
The apparent O2 and CO2 diffusivities of tissue were computed from microscale simulations in small cubical samples obtained from synchrotron radiation X-ray tomography images as described by Ho et al. (2015) (see Table 1). Diffusivities of the tissue depend not only on the porosity but also on the degree of connectivity of the pores since diffusion in the gas phase of a gas was mainly through the connected pores but not through the dead pores (unconnected pores). We did not need to differentiate between the cortex and the ovary ground tissue since the ovary ground tissue is located in the fruit core and its size is much smaller compared with the fruit size.
The Michaelis–Menten constant, which is a ratio of rate constants, would be expected to be relatively independent of temperature (Hertog et al., 1998). The values of and were therefore assumed to be independent of temperature and are taken from Ho et al. (2013) (Table 1).
was obtained from the CO2 production rate measured at 0 kPa O2 (data of experiment A). The maximal O2 consumption rate VR,2 was obtained from the O2 consumption rate measured at 21 kPa O2 (data of experiment A) in which the O2 consumption rate was assumed to be saturated. The parameters kd, KH, and VR,1 of the adapted gas exchange model were estimated by minimizing the squared difference between O2 the consumption rates predicted by Equations 1–8 and those measured from experiments B and C using a non-linear least squares estimation program written in Matlab (The Mathworks, Inc., USA) integrated with Comsol Multiphysics v. 3.5. In the estimation, a 2-D axisymmetrical model of the pear was implemented. Note that simulated results obtained from the 2-D axisymmetrical geometry were similar to those obtained from the 3-D geometry. However, the model with the 2-D axisymmetrical geometry had a low number of degree of freedoms, hence the computational time of the estimation was reduced considerably. The effect of temperature on the respiration parameters was not considered in the estimation since experiments B and C were carried out at constant temperature (0 °C).
The data of experiment D were used for validation purposes only.
Factors affecting fruit respiration
The validation experiment was carried out in a closed system. Response of respiration as a function of the O2 level was in fact affected by three main factors, namely accumulation of CO2 during respiration, regulation of the respiratory metabolism, and O2 diffusion limitation. A series of simulations was carried out to analyse the relative contribution of these factors to decreasing the fruit respiration rate.
The O2 level inside a closed jar with an entire fruit was simulated. From this, the actual O2 consumption rate was computed as a function of the (decreasing) O2 level where the rate of the response of to changing O2 levels follows Equations 7 and 8. Next, a reference O2 consumption rate was computed assuming no CO2 inhibition (in Equation 5). Another reference O2 consumption rate was computed as a function of time assuming a constant .
The relative effect of CO2 inhibition on the O2 consumption rate due to CO2 accumulation was then calculated from:
| (9) |
where is the maximum O2 consumption rate of the fruit during the entire simulation for normalization purposes.
The relative effect of down-regulation fDR was computed from:
| (10) |
The relative effect of the remaining diffusion limitation fDL on the O2 consumption rate was calculated from:
| (11) |
Results
Temperature dependency of respiration capacity
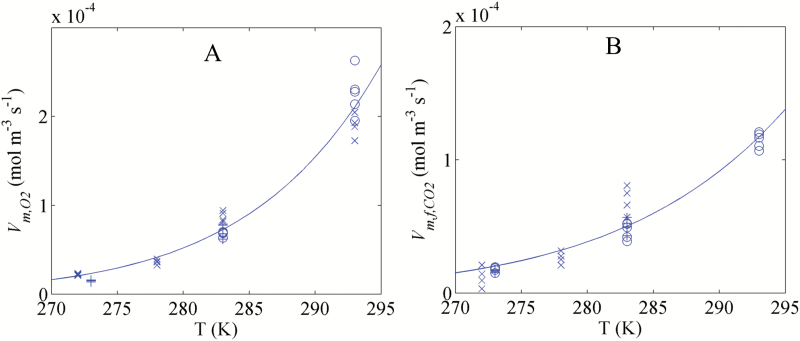
The maximal O2 consumption rate and the maximal fermentative CO2 production rate measured at different temperatures are shown in Table 2. Temperature had a significant effect on the pear respiration. Because of biological variability, and were found to vary from batch to batch, depending on fruit maturity and season. For example, a difference as great as 29 % was found for measured at 10 °C between season 2010 (87.8 ± 5.9 µmol m−3 s−1 and season 2016 (67.9±.3.0 µmol m−3 s−1). The temperature dependency of and was further modelled using Arrhenius’ equations (Supplementary Protocol S2). The results are shown in Fig. 2. The maximal respiration rates were significantly affected by the temperature since the estimated values of the activation rates and were equal to 73.4 ± 3.8 kJ mol−1 and 58.5 ± 3.3 kJ mol−1, respectively. and exponentially increased with increasing temperature. The predicted values at 0 °C and 5 °C were 16% and 66% larger than those measured at the same temperatures, respectively. In addition, some variability between the measured and in different seasons was observed. Therefore, in the model for a particular season, the input maximal rates were taken from the measured data in the same season to compensate for seasonal differences that otherwise would obscure the effects of changing O2 levels in relation to temperature that we were interested in.
Table 2.
Measured maximal O2 consumption and maximal CO2 production rates during different seasons
| Season | Temperature (°C) | (µmol m−3 s−1) | (µmol m−3 s−1) |
|---|---|---|---|
| 2010 | 20 | 230 ± 25 | 114 ± 6 |
| 10 | 67.9 ± 3.0 | 46.9 ± 6.1 | |
| 0 | – | 17.8 ± 1.7 | |
| 2014 | 10 | 71.4 ± 8.0 | 50.4 ± 5.8 |
| 0 | 14.9 ± 0.9 | 16.6 ± 10.2 | |
| 2016 | 20 | 190 ± 13 | – |
| 10 | 87.8 ± 5.9 | 69.6 ± 10.4 | |
| 5 | 36.2 ± 2.9 | 26.3 ± 4.5 | |
| -1 | 22.1 ± 1.0 | 12.0 ± 7.6 |
Fig. 2.
Temperature dependency of the maximal O2 consumption rate (A) and the maximal fermentative CO2 production rate (B). Symbols indicate the measurements, while lines present the Arrhenius model. Symbols (+), (open circles) and (×) indicate the measurements in 2010, 2014, and 2016, respectively.
Table 3.
Estimated parameters of response of respiration to external O2 level at low temperature
| Parameters | m=2 |
|---|---|
| K d | 1.30 ± 0.23 (d−1) |
| K H | 23.3 ± 5.3 (kPa−2) |
| V R,1 | (0.34 ± 0.06)×VR,2 (µmol m−3 s−1) |
| R 2 adj | 0.77 |
Diffusion limitation affects respiration of intact fruit at high temperature
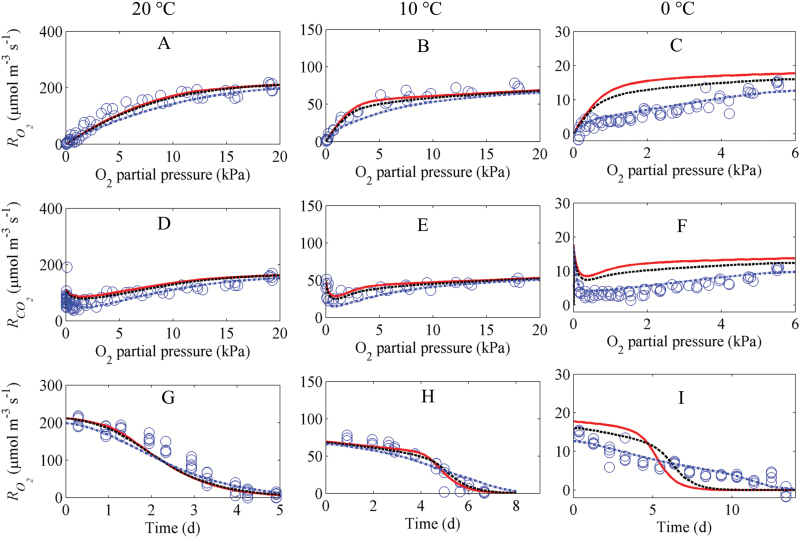
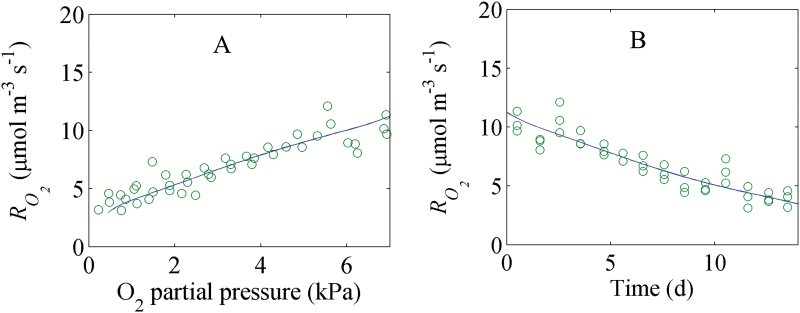
In the next step, the gas exchange model was used to evaluate whether respiration was diffusion limited by comparing simulated and measured values of respiration at 10 °C and 20 °C (Fig. 3) assuming a constant maximal O2 consumption rate (=VR,2 Initially the O2 concentration in the closed jar was 21 kPa, but, as O2 was consumed by respiration, the O2 concentration and thus the O2 consumption rate of the fruit decreased with time. The O2 gradient inside the pear changed from steep in the beginning to shallow at the end of the experiment (Fig. 4). There was good agreement between simulated and measured values of respiration rates.
Fig. 3.
Respiration rate of intact pear fruit as a function of the O2 concentration at 20 °C (A, D), 10 °C (B, E), and 0 °C (C, F), and as a function of time at the same temperatures (G– I). and are the O2 consumption rate and CO2 production rate, respectively. Open circles indicate measurements (experiment D). Solid lines (—), dashed lines ( – –), and dotted lines (⋅⋅⋅) correspond to simulations with an assumed ΔV/VR,2 of 0, 0.21, and 0.66, respectively. The ratio ΔV/VR,2 represents the amplitude of the regulation of maximal respiration rate by O2 (see Supplementary Protocols S1, S3 for its derivation). The maximal O2 consumption rate VR,2 at 20, 10, and 0 °C was measured at 21 kPa O2, 0 kPa CO2, and was equal to 230, 71.4, and 18.4 µmol m−3 s−1, respectively.
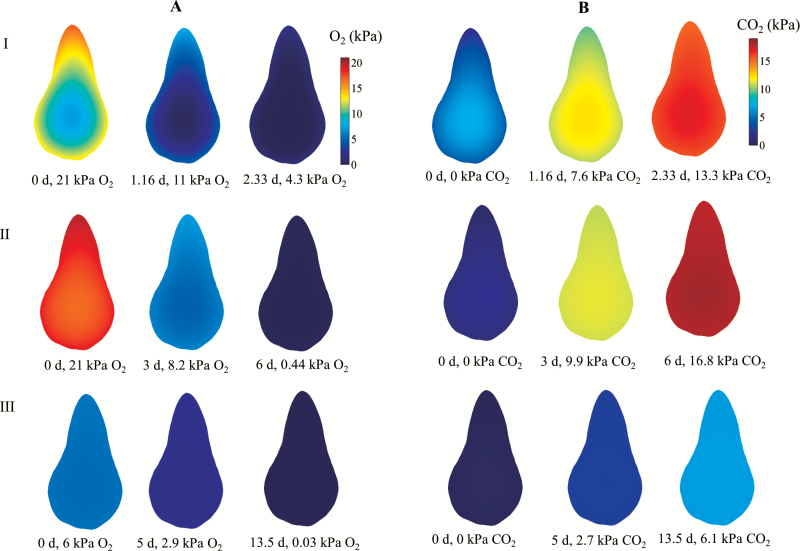
Fig. 4.
Simulated O2 (A) and CO2 (B) partial pressure inside pear fruit in a closed jar at 20 °C (I), 10 °C (II), and 0 °C (III) and different times. The initial atmosphere composition was 21 kPa O2, 0 kPa CO2, and 79 kPa N2 (I and II), and 6 kPa O2, 0 kPa CO2, and 94 kPa N2 (III). The contour graphs in (A) and (B) represent the O2 and CO2 partial pressures inside the pear, respectively. The ratio ΔV/VR,2 was set to 0.21, 0.21, and 0.66 at 20, 10, and 0 °C, respectively.
The simulation results suggest that at 20 °C the large respiration rate caused a rapid depletion of O2 towards the centre of the fruit. In combination with the diffusion resistance of the fruit cortex and skin tissue, this caused a steep O2 gradient inside the fruit. As a consequence, the limited O2 availability in the centre of the fruit reduced the local and thus also the overall respiration rate (Fig. 3A, D).
At 10 °C, the respiration rate was considerably smaller (Fig. 3B, E). Since the diffusivity of O2 and CO2 is only slightly affected by temperature, the relative rate of O2 transport compared with consumption was higher than at 20 °C, and the O2 (and CO2) gradient was more shallow (Fig. 4). The O2 concentration in the jar at which the O2 consumption rates decreased to half their maximal values was equal to 1.8 kPa and 4.9 kPa at 10 °C and 20 °C, respectively. The duration of the experiments at 20 °C and 10 °C was 5 d and 7 d, respectively (Fig. 3G, H).
To evaluate whether the maximal respiration rate varied during the experiment, respiration measurements were carried out at 21 kPa O2, 0 kPa CO2, and 10 °C on four consecutive days. The respiration rate after 3 d increased slightly by 3%, but was not significantly different from that at day 1 (Supplementary Fig. S2).
Down-regulation of respiration at low temperature
At 0 °C the respiration rate was very low (one order of magnitude lower than respiration at 20 °C), and it would take a considerable amount of time to deplete the O2 in the jar. We therefore started the experiment at an O2 concentration of 7 kPa. As the rate of O2 diffusion was now much larger than that of O2 consumption, the O2 concentration profile was now almost uniform and there were hardly any gradients (Fig. 4). The rate-limiting enzyme of respiration is believed to be COX (Armstrong and Beckett, 2011a), and we thus expected a Michaelis–Menten-like behaviour with a saturation O2 consumption rate at an O2 level larger than the Km of COX. Surprisingly, the measurements showed a clear linear decrease of both the O2 consumption rate and the CO2 production rate with decreasing O2 levels until 1 kPa. (Fig. 3C). The ratio of to was >1 at an O2 level lower than 0.5 kPa (Fig. 3F). By assuming a constant the gas exchange model predicted a Michaelis–Menten-like overall respiration rate that saturated at sufficiently large O2 concentrations, which was not consistent with the measurements (Fig. 3C, F). We thus modified our model to incorporate an adaption of to the O2 level in the jar.
Dynamic adaption of to O2 level at low temperature
In a next step we estimated the parameters kd, KH, and VR,1 of Equations 7 and 8 using the combined data of experiment B and C (Supplementary Table S1). At 0 °C, VR,2 in Equation 8 was set equal to the measured O2 consumption rate at 21 kPa O2, 0 kPa CO2, and 79 kPa N2. We observed that the O2 consumption rate at 21 kPa O2 and 0 kPa CO2 was not constant but decreased during long-term storage at –1 °C (Supplementary Fig. S3) but at a rather slow pace (–3.64 × 10–2 µmol m−3 s−1 d−1). Hence, VR,2 was set equal to the measured O2 consumption rate at the initial time of the experiment, assuming it to be constant for the duration of the simulated storage period of 15 d (Supplementary Fig. S3). A good agreement between the fitted respiration rates and corresponding measurements was observed (Figs 5, 6). The change of with an abrupt decrease of the O2 level from 20 kPa to 5 kPa O2 (Fig. 5A, D) was large; when O2 decreased from 20 kPa to 15 kPa O2, it was hardly visible (Fig. 5B, E). We found that the adapted respiration model with m equal to 2 gave a better fit to the observed data than that with m equal to 1 (Supplementary Figs S4, S5). R2, a criterion for the goodness of fit (see definition in Supplementary Protocol S4), was 0.677 and 0.753 for the adapted respiration model with m equal to 1 and 2, respectively. Therefore, only estimated parameters with m equal to 2 were considered. The estimated values of kd and KH were 1.30 ± 0.23 d−1 and 23.3 ± 5.3 kPa2, respectively (Table 2). The estimated value of KH implied that reduced to half of VR,2 at a constant O2 level of 4.8 kPa (Supplementary Fig. S6A). The estimated value of kd suggested that the time for–VR to decrease by 37% in response to a sudden drop in the O2 concentration was 0.77 d (Supplementary Fig. S6B). The estimated value of VR,1 was 0.34 ± 0.06×VR,2. All in all, these results indicate that even at O2 concentrations much larger than the Km of COX, the respiration rate of the fruit is reduced, presumably due to down-regulation of key enzymes of the respiration pathway.
Fig. 5.
Dynamic response of the O2 consumption rate to changing O2 levels and time at 0 °C (experiment B). (A–C) and (D–F) represent the and external O2 level as a function of time, respectively. Open circles and solid lines (—) indicate measurements and model predictions, respectively.
Fig. 6.
Response of the of intact pear fruit to O2 (A) and time (B) (experiment C). Open circles and solid lines (—) indicate measurements and model predictions, respectively.
We also tested the alternative hypothesis that varied at low temperature but remained constant. The estimated value of was 2.04 ± 0.01 kPa, which was much larger than that of pear cell protoplasts and isolated mitochondria. Since the R2 of this model (0.668) was lower than that of the adapted respiration model with m equal to 2 (0.753) and the fit was also worse than that of the adapted respiration model with m equal to 2 (Supplementary Figs S7, S8), we rejected this alternative hypothesis.
Adaption of respiration in response to O2 level at different temperatures
We further tested the hypothesis that while adaption of respiration with O2 levels was considerably high at low temperature, it was relatively insignificant at high temperature. As can be seen in our model analysis, ΔV at 0 °C was 66% of the total maximal respiration rate VR,2. We further simulated different responses of respiration to O2 level with ΔV/VR,2 of 0, 0.21, and 0.66, respectively. At 20 °C and 10 °C, the simulated results were comparable with the measured values when ΔV/VR,2 was low (0 or 0.21) (Fig. 3). In contrast, at 0 °C, the model fitted the measured data best for ΔV/VR,2 equal to 0.66. Replicate measurements of the respiration rate in response to different O2 levels were additionally carried out in 2016 at 5, 10, and 20 °C (Supplementary Fig. S9). Again the simulated O2 and CO2 consumption rates at 10 °C and 20 °C with ΔV/VR,2 equal to 0 or 0.21 fitted the data well (Supplementary Fig. S9A–D) while at 5 °C a ΔV/VR,2 of 0.66 gave the best fit (Supplementary Fig. S9E, F). Our simulation results confirmed that down-regulation was temperature dependent and significant at low temperature.
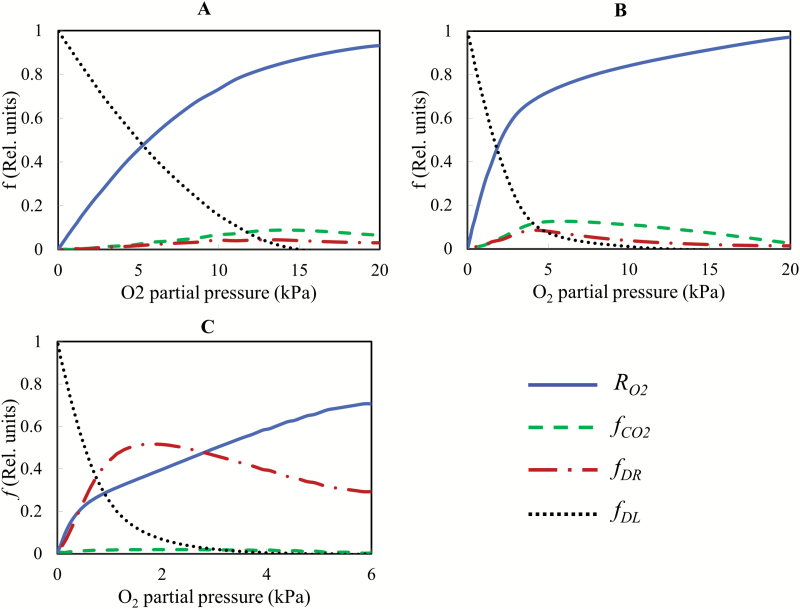
Factors affecting fruit respiration
The relative importance of the different factors affecting the respiration rate under decreasing O2 levels is shown in Fig. 7. At 20 °C, respiration was rapidly reduced by diffusion limitations at a high respiration rate when the O2 concentration decreased. The effect was found to increase predominantly when the O2 partial pressure decreased to <12 kPa (Fig. 7A). At 10 °C, respiration was slightly reduced by the accumulating CO2 concentration when the experiment evolved and the O2 concentration decreased. When the O2 partial pressure decreased below 4 kPa, diffusion limitations caused a progressively steep decline of the O2 consumption curve. Note that at this stage, although the accumulated CO2 level was high, CO2 inhibition of respiration was much smaller than that caused by diffusion limitation (Fig. 7B).
Fig. 7.
Factors affecting the O2 consumption rate as a function of the O2 level. (A–C) Temperatures of 20, 10, and 0 °C. is the O2 consumption rate, while fDR, and fDL are the relative effect of CO2 inhibition, down-regulation, and diffusion limitations on the O2 consumption rate, respectively. ΔV/VR,2 was set to 0.21, 0.21, and 0.66 at 20, 10, and 0 °C, respectively.
At 0 °C, the inhibition of respiration by CO2 as shown in Fig. 7C was less profound due to the limited accumulation of CO2. Also, the simulation results showed that diffusion limitations at O2 levels >2 kPa did not affect respiration much. A bi-linear decrease was found. The first decrease was the adaptive response of the respiration rate at the O2 level >2 kPa probably due to down-regulation. When the O2 level was <2 kPa, however, the rate of O2 diffusion through tissue became more predominantly limiting as the decline of the O2 consumption rate became sharper until it reached zero.
Discussion
Potential of gas exchange model in a systematic study of respiration response to O2 level
Armstrong and Beckett (2011a) have shown the effect of O2 diffusion on respiration of roots using a reaction–diffusion model on a multicylindrical geometry. These authors did not explicitly determine diffusion coefficients. To better understand the response of respiration to O2 level, we analysed the respiration behaviour by means of a reaction–diffusion model that incorporated more detailed Michaelis–Menten kinetics for O2 and CO2 consumption and production, respectively, and that accounted for CO2 inhibition effects. The corresponding diffusion coefficients were calculated by means of a microscale model following Ho et al. (2016). While earlier modelling work did show an obvious internal concentration gradient in pear at low temperature (Ho et al., 2008), this did not become visible in the current work. The gradients predicted before came from an underestimation of the experimentally measured diffusivities due to artefacts induced by cutting of the samples, inundating the intercellular spaces by leaking of the cell content (Ho et al., 2016). The current model predictions are more reliable as they are based on the improved diffusion properties determined from simulations at the microscale based on 3-D synchrotron microtomography images (Ho et al., 2016).
Simulations showed that at above 10 °C, the overall respiratory activity of the fruit was predicted well by a gas diffusion model incorporating Michaelis–Menten kinetics to describe respiration, suggesting that under these conditions respiration is mainly controlled by diffusion limitations. Similar results were reported by Armstrong and Beckett (2011a) for root pieces. While respiratory down-regulation was not clearly found in our measurement and simulation results at high temperature, such an effect could have been annihilated by an increase of by fruit ripening during the course of the experiment. However, this was not the case as the measurements showed that did not significantly change during the experimental period (Supplementary Fig. S2). The observed decrease of respiration was therefore mainly due to diffusion limitation and the inhibition effect of accumulated CO2 (Fig. 7A, B).
The value of rq was equal to 0.77, indicating that the measured CO2 production rate was lower than the measured O2 consumption rate. Note that rq for an ideal respiration with carbohydrate substrate is considered equal to 1, and CO2 solubilization might cause undercalculation of the CO2 production rate. Our simulations with the input parameter rq equal to 1 predicted much larger CO2 production rates compared with those of the measurements. The CO2 production rate profiles predicted with parameter rq equal to 0.77 were well comparable with the measured profiles (Fig. 3D–F). The simulations indicated that the CO2 production rate is likely to be unaffected by CO2 solubility.
Down-regulation may explain the response of respiration to O2 level at low temperature
The conventional Michaelis–Menten-like model for gas exchange assumes that the respiration rate of plant cells would already saturate at an O2 level as low as 1.5 kPa in the tissue. When we measured respiration rates at 0 °C (Fig. 3C, F) and 5 °C (Supplementary Fig. S9E, F) to minimize the effect of O2 diffusion, we found that the O2 consumption rate was considerably reduced in response to decreasing O2 levels well above 1.5 kPa (nine times the Km of tissue). In the experiments, the cooling capacity of our experimental cold rooms was sufficiently large to decrease the temperature from 20 °C to 0 or 5 °C within hours and keep the fruit at constant and almost uniform temperature (Supplementary Protocol S5; Supplementary Fig. S10). Note that Km represents the O2 concentration at which the respiration rate reaches half of its maximum value (Armstrong and Beckett, 2011a). Km might be temperature dependent, similar to the maximum respiration rate (Kruse et al., 2011). However, Hertog et al. (1998) proposed that Km, being a ratio of rate constants, was relatively independent of temperature when the activation energies of individual rate constants were similar. The value of Km is 0.17 kPa O2 for tissue (Ho et al., 2013), 0.14 kPa O2 for cell protoplasts (Lammertyn et al., 2001), and 0.10–1 µM (~4.5 × 10–3–4.5 × 10–2 kPa) for COX [0.10–0.12 µM (~4.5 × 10–3–5 × 10–3 kPa), Rawsthorne and Larue (1986); 1 µM (~4.5 × 10–2 kPa), Taiz and Zeiger (1993), and 0.14 μM (~6 × 10–3 kPa), Millar et al. (1994)]. Km described in the model was much larger than that obtained from isolated mitochondria since Km for tissue accounted for diffusion barriers through the cell wall, cell membrane, and within the cytosol. Simulations with a two-compartment model (core and cortex) and different combinations of O2 diffusivities and Vmax values were also carried out (Supplementary Fig. S11). Respiration was assumed to follow conventional Michaelis–Menten kinetics without a regulatory mechanism. While at 10 °C the model fitted the data well, this was not the case at 0 °C for any of the aforementioned parameter combinations. The experimental data contradicted simulation results obtained with the gas exchange model incorporating conventional Michaelis–Menten-based respiration kinetics, suggesting an additional reduction in respiration rate beyond the substrate effects already accounted for. When we modified the respiration kinetics to allow for to change as a function of the O2 level rather than keeping constant, the simulations fitted the measurements well (Fig. 3C, E, F; Supplementary Fig. S9E, F). This indicated that additional regulatory effects of the respiration pathways are likely to occur. The dynamics of regulatory and signalling pathways in the cell were modelled by reaction kinetics at the transcriptome level. We assumed that an O2 signal could modulate the biosynthesis of respiratory enzymes in the cell through activation of an O2 receptor. The response of the maximal respiration rate was proportional to the change of amount of enzymes involving in the respiration. We assumed that a decrease of the O2 level would alter the maximal respiration rate due to adjustment of the balance between enzyme synthesis and degradation (see Fig. 1; Supplementary Protocol S1; Supplementary Fig. S1). So, fundamentally, the model allows a bidirectional change in enzyme activity. We observed a relatively slow adaption to changing O2 levels with an estimated kd of 1.30 d−1. Our results showed that the response of to changing O2 levels was more sensitive at low O2 than at high O2 levels (see Figs 3, 4; Supplementary Figs S9, S12).
Zabalza et al. (2009) found that the respiratory demand in pea root was 300 nmol g−1 min−1 O2 (equivalent to 5 × 104 µmol m−3 s−1) for pea root at 25 °C. For barley root at 25 °C, the respiratory demand was observed to be 100 µmol g−1 h−1 O2 (equivalent to 2.7 × 105 µmol m−3 s−1) (Gupta et al., 2009). These values are considerably larger than that of pear fruit measured in this study (230 µmol m−3 s−1 at 20 °C). This difference is due to the fact that mature but pre-climacteric pear fruit are much less metabolically active as compared with roots that are actively involved in uptake processes. Respiratory down-regulation in plant tissues has been suggested by Gupta et al. (2009) and Zabalza et al. (2009). Zabalza et al. (2009) observed a slow but linear decrease of the respiratory rate of roots of pea and Arabidopsis with decreasing O2 levels until ~4 kPa, below which it steeply declined. However, the respiratory demand of roots of pea and Arabidopsis in the experiments performed by these authors was more than an order of magnitude larger than the pear respiration performed at 20 °C in this study, resulting in scavenging of oxygen from their system being completel in <2 h. Since down-regulation might require long exposure at specific O2 levels, a change of respiration to O2 levels has been alternatively suggested by substantial diffusion limitation on O2 supply when O2 respiratory demand was high (Armstrong and Beckett, 2011a). At low temperature due to low respiration demand, the adaptive response of the respiration rate to O2 levels was shown to be due to down-regulation rather than diffusion limitation on O2 supply (Figs 3C, E, F, 4; Supplementary Figs S13, S14). This has implications with respect to commercial storage of pear fruit under hypoxic conditions [‘controlled atmosphere (CA) storage’]. Abruptly and drastically changing the O2 level is known to cause browning and cavity formation in pear, probably because respiration may consume most O2 in the centre of the pear (Verlinden et al., 2002). This may create near anoxic conditions initiating a chain of events eventually causing the symptoms of the disorder. Adaption of the fruit to low O2 levels by reducing the respiration rate would eventually result in less severe O2 concentrations in the centre of the fruit and a reduction in the symptoms. This procedure is in fact applied in practice and may be further optimized. While the model was developed using ‘Conference’ pear data, it should be extended to other pear cultivars or to ‘Conference’ pears grown under different agronomic/climate conditions that may well affect both fruit respiration and microstructural properties. Note that the gas transport model that was used herein assumes that gas transport properties are uniform and isotropic, and that the respiration kinetics do not depend on position. Future research should incorporate more realistic features into the model and investigate their effect on gas transport.
AOX might play a role in regulation of respiration
The alternative oxidase (AOX) has been proposed to play a role in adaption of respiration to O2 level within mitochondria (Szal et al., 2003; McDonald and Vanlerberghe, 2006; Gupta et al., 2009). At a short-term temperature change from 17 °C to 36 °C, the ratio of alternative respiration to total respiration was reported to be relatively constant and ~0.21–0.30 for different leaves of Nigella sativa, Cucurbita pepo, and Vicia faba (Macfarlane et al., 2009). However, partitioning of electrons via the alternative respiration pathway has been shown to be increased after long-term cold acclimation in some species (Gonzalez-Meler, 1999; Fung et al., 2004; Sugie et al., 2006). Our simulation results showed that the magnitude of regulation of respiration in response to O2 level was relatively low at high temperature but significantly high at low temperature. Note that we did not explicitly model distinct AOX and COX pathways. If the AOX pathway is indeed responsible for the regulatory effects by O2, ΔV can be interpreted as its capacity, while the time and O2 responses are lumped in the parameters kd and KH. Assuming that at 10 °C and 20 °C the amplitude of the regulation of the respiration rate, ΔV, was 0.21 times the total maximal respiration rate VR,2, we found good agreement between simulation and measurements. This magnitude was similar to the partition of the AOX pathway to the total respiration at high temperature (0.21–0.30 from 17 °C to 36 °C, Macfarlane et al., 2009). At 0 °C, ΔV was found to be 0.66 times the total maximal respiration rate VR,2. Likewise, the ratio of the AOX pathway to the total respiration for maize leaves (Zea mays L. cv Penjalina) growing at 25 °C was reported to be 0.25 but increased to 0.6 after 5 d at 5 °C (chilled) (Ribas-Carbo et al., 2000). These results indicate that the regulation of AOX might be involved in the response of respiration to changing O2 levels at low temperature.
Supplementary data
Supplementary data are available at JXB online.
Protocol S1. Modelling the response of to O2 level.
Protocol S2. Temperature dependency of respiration capacity.
Protocol S3. Amplitude of regulation of maximal respiration rate by O2.
Protocol S4. Criterion for goodness of fit of the model.
Protocol S5. Heat conduction model.
Table S1. Description of data sets used in calibration and validation of model.
Fig. S1. Proposed reactions and modelled equations describing response of receptor, enzyme, and respiration to O2 level.
Fig. S2. O2 consumption rate of intact pear fruit as a function of time at 20 kPa O2, 0 kPa CO2 at 10 °C.
Fig. S3. O2 consumption rate of intact pear fruit as a function of time during storage of fruit at 20 kPa O2, 0 kPa CO2 at 0 °C.
Fig. S4. Dynamic response of O2 consumption rate to O2 level and time at 0 °C (experiment B).
Fig. S5. Response of of intact pear fruit to O2 (A) and time (B) (experiment C).
Fig. S6. (A) Steady-state modelled response of relative maximal O2 consumption rate to O2 level. (B) Change of maximal O2 consumption rate in response to a sudden drop of the O2 concentration.
Fig. S7. Comparison of fitting between the adapted respiration model (m=2) and the respiration model with assumption of variation of at 0 °C.
Fig. S8. Comparison of fitting between the adapted respiration model (m=2) and the respiration model with assumption of variation of at 0 °C.
Fig. S9. Respiration rate of intact pear fruit as a function of the O2 concentration at 20 °C (A, B), 10 °C (C, D), and 5 °C (E, F) harvested in season 2016.
Fig. S10. Predicted temperature of pear fruit during cooling.
Fig. S11. Simulations with a two-compartment model (core and cortex) and different combinations of diffusivities and Vmax values.
Fig. S12. Steady-state modelled response of relative maximal O2 consumption rate (/max) to O2 level.
Fig. S13. Simulated of pear fruit in the closed jar at 20 °C (I), 10 °C (II), and 0 °C (III) and different times.
Fig. S14. Simulated O2 and CO2 gas partial pressure profiles from the centre to the surface along the radial direction in the closed jar at 20 °C (I), 10 °C (II), and 0 °C (III) at different times.
Acknowledgements
The authors thank the Research Council of the KU Leuven (C16/16/002), the Flanders Fund for Scientific Research (project G060516N), and the Institute for the Promotion of Innovation by Science and Technology in Flanders (project IWT-050633, IWT scholarship SB/0991469) for financial support. This research was carried out in the context of the European COST Action FA1106 (‘QualityFruit’).
References
- Armstrong W, Beckett PM. 2011a Experimental and modelling data contradict the idea of respiratory down-regulation in plant tissues at an internal [O2] substantially above the critical oxygen pressure for cytochrome oxidase. New Phytologist 190, 431–441. [DOI] [PubMed] [Google Scholar]
- Armstrong W, Beckett PM. 2011b The respiratory down-regulation debate. New Phytologist 190, 276–278. [DOI] [PubMed] [Google Scholar]
- Borisjuk L, Rolletschek H. 2009. The oxygen status of the developing seed. New Phytologist 182, 17–30. [DOI] [PubMed] [Google Scholar]
- Denison RF. 1992. Mathematical modeling of oxygen diffusion and respiration in legume root nodules. Plant Physiology 98, 901–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drew MC. 1997. Oxygen deficiency and root metabolism: injury and acclimation under hypoxia and anoxia. Annual Review of Plant Physiology and Plant Molecular Biology 48, 223–250. [DOI] [PubMed] [Google Scholar]
- Franck C, Lammertyn J, Ho QT, Verboven P, Verlinden B, Nicolaï BM. 2007. Browning disorders in pear fruit. Postharvest Biology and Technology 43, 1–13. [Google Scholar]
- Fung RWM, Wang CY, Smith DL, Gross KC, Tian M. 2004. MeSA and MeJA increase steady-state transcript levels of alternative oxidase and resistance against chilling injury in sweet peppers (Capsicum annuum L.). Plant Science 166, 711–719. [Google Scholar]
- Geigenberger P, Fernie AR, Gibon Y, Christ M, Stitt M. 2000. Metabolic activity decreases as an adaptive response to low internal oxygen in growing potato tubers. Biological Chemistry 381, 723–740. [DOI] [PubMed] [Google Scholar]
- Gonzalez-Meler MA, Ribas-Carbo M, Giles L, Siedow JN. 1999. The effect of growth and measurement temperature on the activity of the alternative respiratory pathway. Plant Physiology 120, 765–772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta KJ, Zabalza A, van Dongen JT. 2009. Regulation of respiration when the oxygen availability changes. Physiologia Plantarum 137, 383–391. [DOI] [PubMed] [Google Scholar]
- Herremans E, Verboven P, Bongaers E, Estrade P, Verlinden BE, Wevers M, Hertog M, Nicolai B. 2013. Characterisation of ‘Braeburn’ browning disorder by means of X-ray micro-CT. Postharvest Biology and Technology 75, 114–124. [Google Scholar]
- Hertog MLATM, Peppelenbos HW, Evelo RG, Tijskens LMM. 1998. A dynamic and generic model of gas exchange of respiring produce: the effects of oxygen, carbon dioxide and temperature. Postharvest Biology and Technology 14, 335–349. [Google Scholar]
- Ho QT, Rogge S, Verboven P, Verlinden BE, Nicolaï BM. 2016. Stochastic modelling for virtual engineering of controlled atmosphere storage of fruit. Journal of Food Engineering 176, 77–87. [Google Scholar]
- Ho QT, Verboven P, Verlinden BE, Herremans E, Wevers M, Carmeliet J, Nicolaï BM. 2011. A three-dimensional multiscale model for gas exchange in fruit. Plant Physiology 155, 1158–1168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho QT, Verboven P, Verlinden BE, Lammertyn J, Vandewalle S, Nicolaï BM. 2008. A continuum model for metabolic gas exchange in pear fruit. PLoS Computational Biology 4, e1000023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho QT, Verboven P, Verlinden BE, Nicolaï BM. 2010a A model for gas transport in pear fruit at multiple scales. Journal of Experimental Botany 61, 2071–2081. [DOI] [PubMed] [Google Scholar]
- Ho QT, Verboven P, Verlinden BE, Schenk A, Delele MA, Rolletschek H, Vercammen J, Nicolaï BM. 2010b Genotype effects on internal gas gradients in apple fruit. Journal of Experimental Botany 61, 2745–2755. [DOI] [PubMed] [Google Scholar]
- Ho QT, Verboven P, Verlinden BE, Schenk A, Nicolaï BM. 2013. Controlled atmosphere storage may lead to local ATP deficiency in apple. Postharvest Biology and Technology 78, 103–112. [Google Scholar]
- Kruse J, Rennenberg H, Adams MA. 2011. Steps towards a mechanistic understanding of respiratory temperature responses. New Phytologist 189, 659–677. [DOI] [PubMed] [Google Scholar]
- Lammertyn J, Franck C, Verlinden BE, Nicolai BM. 2001. Comparative study of the O2, CO2, and temperature effect on respiration between ‘Conference’ pear cell protoplasts in suspension and intact pears. Journal of Experimental Botany 52, 1769–1777. [DOI] [PubMed] [Google Scholar]
- Lammertyn J, Scheerlinck N, Jancsók P, Verlinden B, Nicolaï B. 2003. A respiration–diffusion model for ‘Conference’ pears I: model development and validation. Postharvest Biology and Technology 30, 29–42. [Google Scholar]
- Licausi F, Kosmacz M, Weits DA, Giuntoli B, Giorgi FM, Voesenek LA, Perata P, van Dongen JT. 2011. Oxygen sensing in plants is mediated by an N-end rule pathway for protein destabilization. Nature 479, 419–422. [DOI] [PubMed] [Google Scholar]
- Macfarlane C, Hansen LD, Florez-Sarasa I, Ribas-Carbo M. 2009. Plant mitochondria electron partitioning is independent of short-term temperature changes. Plant, Cell and Environment 32, 585–591. [DOI] [PubMed] [Google Scholar]
- McDonald AE, Vanlerberghe GC. 2006. Origins, evolutionary history, and taxonomic distribution of alternative oxidase and plastoquinol terminal oxidase. Comparative Biochemistry and Physiology Part D, Genomics and Proteomics 1, 357–364. [DOI] [PubMed] [Google Scholar]
- Millar AH, Bergersen FJ, Day DA. 1994. Oxygen affinity of terminal oxidases in soybean mitochondria. Plant Physiology and Biochemistry 32, 847–852. [Google Scholar]
- Nikoloski Z, van Dongen JT. 2011. Modeling alternatives for interpreting the change in oxygen-consumption rates during hypoxic conditions. New Phytologist 190, 273–276. [DOI] [PubMed] [Google Scholar]
- Peppelenbos HW, van’t Leven J. 1996. Evaluation of four types of inhibition for modelling the influence of carbon dioxide on oxygen consumption of fruits and vegetables. Postharvest Biology and Technology 7, 27–40. [Google Scholar]
- Rawsthorne S, Larue TA. 1986. Metabolism under microaerobic conditions of mitochondria from cowpea nodules. Plant Physiology 81, 1097–1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribas-Carbo M, Aroca R, Gonzàlez-Meler MA, Irigoyen JJ, Sánchez-Díaz M. 2000. The electron partitioning between the cytochrome and alternative respiratory pathways during chilling recovery in two cultivars of maize differing in chilling sensitivity. Plant Physiology 122, 199–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogge S, Defraeye T, Herremans E, Verboven P, Nicolaï BM. 2015. A 3D contour based geometrical model generator for complex-shaped horticultural products. Journal of Food Engineering 157, 24–32. [Google Scholar]
- Rolletschek H, Weber H, Borisjuk L. 2003. Energy status and its control on embryogenesis of legumes. Embryo photosynthesis contributes to oxygen supply and is coupled to biosynthetic fluxes. Plant Physiology 132, 1196–1206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugie A, Naydenov N, Mizuno N, Nakamura C, Takumi S. 2006. Overexpression of wheat alternative oxidase gene Waox1a alters respiration capacity and response to reactive oxygen species under low temperature in transgenic Arabidopsis. Genes and Genetic Systems 81, 349–354. [DOI] [PubMed] [Google Scholar]
- Szal B, Jolivet Y, Hasenfratz-Sauder M-P, Dizengremel P, Rychter AM. 2003. Oxygen concentration regulates alternative oxidase expression in barley roots during hypoxia and post-hypoxia. Physiologia Plantarum 119, 494–502. [Google Scholar]
- Taiz L, Zeiger E. 1993. Plant physiology. California: The Benjamin/Cummings Publishing Company Inc. [Google Scholar]
- van Dongen JT, Roeb GW, Dautzenberg M, Froehlich A, Vigeolas H, Minchin PE, Geigenberger P. 2004. Phloem import and storage metabolism are highly coordinated by the low oxygen concentrations within developing wheat seeds. Plant Physiology 135, 1809–1821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verboven P, Herremans E, Borisjuk L, Helfen L, Ho QT, Tschiersch H, Fuchs J, Nicolaï BM, Rolletschek H. 2013. Void space inside the developing seed of Brassica napus and the modelling of its function. New Phytologist 199, 936–947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verboven P, Pedersen O, Herremans E, Ho QT, Nicolaï BM, Colmer TD, Teakle N. 2012. Root aeration via aerenchymatous phellem: three-dimensional micro-imaging and radial O2 profiles in Melilotus siculus. New Phytologist 193, 420–431. [DOI] [PubMed] [Google Scholar]
- Verlinden BE, de Jager A, Lammertyn J, Schotsmans W, Nicolai BM. 2002. Effect of harvest and delaying controlled atmosphere storage conditions on core breakdown incidence in ‘conference’ pears. Biosystems Engineering 83, 339–347. [Google Scholar]
- Zabalza A, van Dongen JT, Froehlich A et al. 2009. Regulation of respiration and fermentation to control the plant internal oxygen concentration. Plant Physiology 149, 1087–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.