Automatic structure prediction of oligomeric assemblies using Robetta in CASP12

Abstract

Many naturally occurring protein systems function primarily as symmetric assemblies. Prediction of the quaternary structure of these assemblies is an important biological problem. This manuscript describes automated tools we have developed for predicting the structure of symmetric protein assemblies in the Robetta structure prediction server. We assess the performance of this pipeline on a set of targets from the recent CASP12/CAPRI blind quaternary structure prediction experiment. Our approach successfully predicted five of seven symmetric assemblies in this challenge, and was assessed as the best participating server group, and one of only two groups (human or server) with two predictions judged as high quality by the assessors. We also assess the method on a broader set of 22 natively symmetric CASP12 targets, where we show that oligomeric modeling can improve the accuracy of monomeric structure determination, particularly in highly intertwined oligomers.

Introduction

Oligomeric protein assemblies are important and ubiquitous in nature. Many proteins function as higher order symmetric assemblies, and understanding the nature of these higher order assemblies is key in understanding their function; disruption of these symmetric assemblies may be useful in developing drugs to inhibit function. These proteins only adopt a functional conformation when in their native oligomeric state, and therefore structure prediction methods that do not consider oligomeric state will be unable to determine the functional state. Despite this importance, however, there has been limited effort in performing structure prediction and oligomeric state assignment simultaneously; many efforts subdivide the problem into two tasks [1]: structure prediction [2–5], which consider determination of the constituent monomers, and protein docking [6–9], which considers predicting the structure of assemblies from largely-rigid monomers.

In this manuscript, we describe the fully automated multimeric structure prediction pipeline we have developed as part of the Robetta server [10]. When predicting the oligomeric assembly of a protein, our methods combine information on the oligomeric state of evolutionarily related proteins with Rosetta’s physically realistic force field to assess the energetics of oligomer formation. The force field, fully described elsewhere [11,12], combines several energy terms assessing particular physical interactions, and parameters are fit to a combination of experimental thermodynamic data and structure prediction goodness. We assess the performance of these methods on 22 natively symmetric targets from the recent CASP12 experiment, as compared to other structure prediction methods. We also compare to protein docking methods on a subset of seven targets chosen as part of a CASP/CAPRI combined challenge. We use this experiment to test whether or not a method combining oligomeric state prediction and structure prediction could perform better than either method alone. That is, we wanted to assess whether explicit consideration of the oligomeric state would lead to improved prediction of monomeric structure compared to other structure prediction approaches, and whether it would lead to improved prediction of interface structure compared to other protein/protein docking methods.

Materials and Methods

Our symmetry detection, modeling, and determination pipeline broadly consists of three stages. The approach is based on the homology modeling of RosettaCM [13], with two additional steps aimed at determining the correct symmetry of the target complex. An overview of our approach is indicated in Figure 1. In RosettaCM – as well as in this pipeline – modeling begins by using three sequence alignment methods (Raptor [4], Sparks [5], and HHpred [14]) to identify related template structures over a wide range of sequence identities. From these templates (up to ten from each of the three methods), two quantities are computed that control the behavior of the protocol: target_difficulty and P_correct. The first, target_difficulty, estimates the GDT-TS of the template-based model for given target by comparing the average pairwise TM-score of the top-ranking templates identified by three methods. “Difficult targets” in Rosetta have target_difficulty < 0.5. The latter measure, P_correct, is a value that gets computed for each identified template, and measures the probability a particular ranked model is correct, given the target difficulty.

Figure 1.

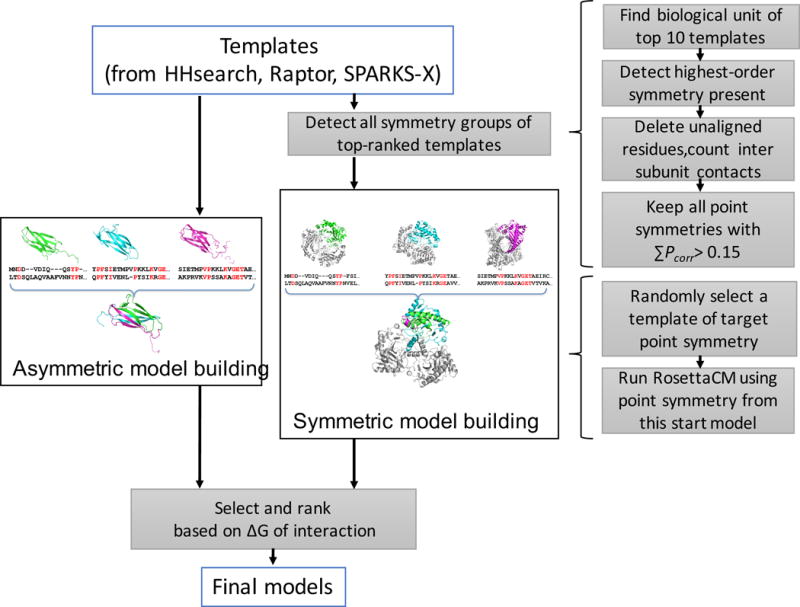
A graphical overview of the symmetry determination and refinement pipeline. Starting with sequence alignments from Raptor, SPARKS, and hhpred, we identify templates that are natively symmetric, ensure that aligned residues form the symmetric interfaces, and then model symmetrically in RosettaCM. Simultaneously, models are built and refined asymmetrically; model selection considers the predicted ΔG of oligomerization when choosing symmetric versus asymmetric predicted models.

We have added to this pipeline an additional step where we detect the native symmetry of templates, using author-assigned biological assembly records to determine template oligomerization. Templates that are symmetric are checked to ensure that residues making the symmetric interface exist in the current alignment, that is, that a residue deletion has not removed the entire interface. For targets that our pipeline predicts as difficult (target_difficulty < 0.5) [13], or that our pipeline predicts should be modeled as multi-domain targets [10,15], the symmetry detection and modeling step is omitted. Only the top three templates from each sequence alignment method are considered in symmetry generation, and the sum of P_correct values from a particular point symmetry group must exceed 0.15 for that particular point group to get modeled.

In the second stage of the approach, we perform structure modeling and refinement in the context of the symmetric assembly. All symmetric configurations from the first stage are considered separately, and homology modeling is carried out with RosettaCM. All stages of RosettaCM, including template combination, rebuilding of insertions and deletions, and all-atom refinement, take into account the energetics of the entire symmetric assembly. Each detected symmetry group is considered separately, and RosettaCM is always carried out asymmetrically in parallel (left path in Figure 1). All detected symmetry groups are then considered in the final step, where we use the results of the RosettaCM calculations with different symmetry configurations, and make a final decision on the overall symmetry of the system based on the predicted binding affinity of the oligomer. For each symmetry configuration, the best five clusters are selected using a previously described Boltzmann-weighted clustering [13]. For each cluster, we calculate the average ΔG of oligomer formation per subunit. If the ΔG is less than −10 kcal/mol, the system is treated symmetrically; if multiple different symmetric conformations exceed this threshold, then the one with the best ΔG is accepted.

Symmetry Detection

Homology modeling in Robetta begins by using three sequence alignment methods – SPARKS [5], Raptor [4], and HHsearch [14] – to identify up to thirty putative templates, ten from each method [13]. For symmetry modeling, we further consider the top three models only from each of these methods. For these nine templates, we identify the biological assembly annotated in the PDB file. For all cases that contain only one chain identity, the script make_symmdef_file.pl [16] is used to assess the closest point symmetry to each. The script works by arbitrarily choosing a single chain as the asymmetric unit, and calculating the superposition between this chain and all others. Only chains with RMSD < 3Å to the chosen chain are considered, and for each, a rotation and translation (R_i,T_i) are calculated. Then for each (R_i,T_i), we compute a symmetrized version: we identify the number of applications N (potential number of symmetric units) of this transformation that bring the rotation closest to unity, and measure the net deviation N applications of rotation and translation from identity and 0, respectively. The script eliminates subunits where the net translational error > 5Å or the net rotational error > 3 degrees. Finally, for each template, only the highest-order symmetry detected is considered in subsequent steps.

The next step filters out detected symmetries where most of the interface is comprised of unaligned residues. All symmetric templates are trimmed to only contain residues that are present in the alignment (whether or not their identity has changed). Then, the number of inter-subunit interactions are counted, using only these aligned residues. If this value is less than a predefined cutoff, nres^1/2 contacts per subunit, with nres residues in the target, then the template symmetry is not used. This avoids inferring symmetry in cases where the residues responsible for oligomerization have significantly changed, or (say) an oligomerization domain has been deleted.

For all point symmetries determined to this point, the P_correct [13] weight for all templates of each unique point symmetry is summed (e.g., all C2-symmetric templates are summed, all C3-symmetric, etc.). For each symmetry with a summed P_correct > 0.15, we consider modeling with that symmetry in the next step. As a rough rule of thumb, this value is exceeded if a single top-ranked template is detected as symmetric, or 3+ non-top-ranked symmetric templates are detected. Symmetry operators (the origin and all axes) are calculated for each accepted symmetric template, and saved as a “symmetry definition file” to be used by Rosetta modeling.

Symmetric modeling in RosettaCM

Symmetric modeling in RosettaCM is carried out as described previously [16]. For each point symmetry, we run multiple (general 100s-1000s) RosettaCM trajectories where all models are generated in a particular point symmetry group; all templates with that particular symmetry are used in model building. Running RosettaCM with symmetry is largely the same as the asymmetric variant with several minor modifications as following. Only templates with the target symmetry are considered as starting models (all models are considered in the recombination stage, however). When a model is chosen as the starting model, the symmetry operations from that starting model are also used, and all conformational sampling is carried out in that symmetric coordinate frame. Asymmetric modeling is always run, even if all templates had detected symmetry. Finally, for all templates, only the highest-order detected symmetry is used in modeling: if we have (say) a D₄ symmetric template, even though there are C₄ and C₂ symmetries present, we only consider this template as D₄ symmetric. This same situation arises with high-order cyclic symmetries, e.g. C₆ and C₃.

Final symmetry group assignment

The final step of the protocol makes a decision on the point symmetry from among all the symmetries modeled. This step builds upon Robetta’s model-selection tool [13], where a Boltzmann-weighted neighbor count is used to find up to 5 low-energy clusters of structures. For each putative point symmetry group, we calculate these five low-energy clusters, and the most central representative from each cluster. For the top-ranked cluster, we calculate the average ΔG of oligomerization per subunit. If ΔG is less than −10 kcal/mol per subunit, we decide the symmetric conformation is correct; if it is greater than this, the asymmetric model is correct. If there are multiple different symmetric conformations that exceed this threshold, then the one with the best ΔG is selected. In many cases where multiple symmetries are modeled, one is a subset of the other (e.g., a system is modeled as both C4 and D4, where the D4 system is a dimer of the C4 system); in these cases, our selection criteria will typically (but not always) favor the higher symmetry (e.g. D4 over C4), as it has more opportunity to make energetically favorable interactions.

Limitations

There are several limitations with the symmetry operations inferable on Robetta. Only C (cyclic) and D (dihedral) symmetries are automatically detected; polyhedral and lattice symmetries are not recognized currently. Robetta also considers only the highest-order symmetry in detection, and will not consider modeling subsymmetries (e.g., a detected D4 will only be modeled as D4, not necessarily as C4). Finally, if the biological assembly contains multiple chain identities, it is not used, even if it contains a single chain with a fully connected point symmetry group.

Parameter tuning and benchmark sets

The algorithm was initially developed for use in CASP11. However, its performance was significantly hampered by software bugs related to symmetric modeling and refinement, which ultimately necessitated that the pipeline be disabled for most of CASP11. The training set used for method development consisted of a set of 46 symmetric complexes from the CASP9 competition [13]. These structures included complexes with C2, C3, C4, and D2 symmetries. Of those 46 complexes, 42 had at least one template with the correct symmetry group (though in some cases the symmetric configuration was quite different than native).

This benchmark was used to develop the initial algorithm, and – more importantly – to tune several parameters of symmetry detection and final determination, in particular, what cutoffs on target_difficulty and P_correct the symmetry detection should use to identify as many correct (native) symmetries as possible while generating as few false positives as possible. Supplemental Tables 1 and 2 show the results of that experiment: for all targets, naively considering all possible template symmetries leads to 42 correct symmetry groups and 52 false positives; applying filtering on target_difficulty and P_correct leads to 28 correct symmetry groups with only 25 false positives.

From these experiments, and subsequent tuning in CAMEO [17], it was found that: a) considering the top three templates from each template detection and sequence alignment method, b) skipping symmetry detection in cases with target_difficulty<0.5, c) ensuring that at least (nres^1/2) residue pairs are in contact (Cβ−Cβ distance less than 6Å) at each symmetric interface, d) ensuring that the sum of P_correct values of all symmetric templates needed to be above 0.15, and e) ensuring the per-subunit ΔG of binding was less than −10 kcal/mol (according to Rosetta), led to the most correctly predicted assemblies and the fewest falsely predicted assemblies. Ultimately, this lead to all 28 targets being correctly detected as symmetric, with only 6 false positives (that is, nonsymmetric natives detected as symmetric). Furthermore, these incorrect predictions (all homodimeric) did not lead to a worsening in the prediction accuracy of the monomeric structure, with a GDT-TS difference of less than 1 in all cases.

Results

Our approach for automatic oligomeric structure determination was tested in CASP12. While this pipeline was present in CASP10 and CASP11, several bugs in symmetric refinement led to poor performance overall; these bugs were identified and fixed prior to the CASP12 experiment. In addition, in CASP12, a new force field was used [11] that showed significant improvements in energetics of protein/protein interfaces; this should further improve both our ability to refine symmetric structures, as well as improve our ability to predict the correct symmetric state of each target. For CASP12, this pipeline was used by the Robetta server for structure prediction of all targets. The assessor-provided oligomerization state was not used, rather, the oligomerization state of each target was predicted using the symmetry pipeline of Figure 1. This allowed us to determine the correct oligomerization for several targets that were initially misannotated.

Table 1 summarizes the results of the automatic symmetry detection and modeling, listing all targets in which either the native structure was symmetric, or the Robetta pipeline predicted a symmetric structure. In total, 72 targets were run using Robetta during the CASP12 experiment (not including cancelled targets). Of those 72 targets, 35 were considered too difficult to perform symmetry assignment (including 8 natively symmetric targets, T0859, T0863, T0864, T0865, T0866, T0880, T0886, and T0888) according to target_difficulty metric, and of the remaining 37 targets, 1 (T0896) was eliminated as it was parsed into domains (neither domain was natively symmetric). Of the remaining 36 targets, 23 had either: a) no identified symmetric templates (20), all of which turned out to be natively monomers, or b) identified symmetric templates that were not highly ranked (3). Two of these three cases were in fact natively symmetric targets (T0875 and T0913). For these final 13 targets symmetric predictions were made, and in all 13 cases, the resulting ΔG was better than the threshold required (for none of the 13 cases were more than one symmetric configuration considered). Table 1 lists these 13 structures plus 11 natively symmetric complexes Robetta modeled asymmetrically.

Table 1.

Robetta accurately predicts about half of the symmetric assemblies in the CASP12 experiment.

target	CASP/CAPRI target	native symmetry	predicted symmetry	reason for failure
T0859/T0929		C2	—	target difficulty below threshold (0.10)
T0860	x	C3	C3
T0861		C2	C2
T0863/T0930		C2	—	target difficulty below threshold (0.14)
T0864/T0932		C2	—	target difficulty below threshold (0.22)
T0865		C3	—	target difficulty below threshold (0.44)
T0866		C6	—	target difficulty below threshold (0.20)
T0867	x	C3	C3
T0873		C2*	C2
T0875	x	C2	—	symmetric templates were too poorly ranked
T0880		C3*	—	target difficulty below threshold (0.07)
T0881	x	C3	C3
T0886/T0933		D6	—	target difficulty below threshold (0.05)
T0887/T0931		C2	C2
T0888		C3*	—	target difficulty below threshold (0.06)
T0889		D2	D2
T0893	x	C2	C2	template symmetric interface different than target
T0896/T0934		C2	—	domains parsed and reassembled
T0906	x	D4	D4
T0909		C3	C3
T0912		—	C2	misidentification of symmetric template
T0913		C6/D3*	—	symmetric templates were too poorly ranked
T0917	x	C2	C2
T0945		—	C2	misidentification of symmetric template

^*Native structure not yet publically available

Of these 13 symmetric predictions made by Robetta, there were two incorrect predictions (T0912 and T0945; we predicted as symmetric while the native was asymmetric), one “partially correct” prediction (T0873; we correctly predicted one of the two symmetric interfaces, modeling the natively D2 complex as a C2 complex), and 10 correct predictions (T0860, T0861, T0867, T0881, T0887, T0889, T0893, T0906, T0909, and T0917). In both incorrect cases, a false homodimer interface was discovered that was not present in the crystal structure. The remainder of this section walks through several specific cases where Robetta’s oligomeric modeling was successful and where it performed poorly. We consider both the accuracy of monomeric structure prediction as well as the CAPRI-assessed interface accuracy, as – using Robetta’s energy-guided conformational sampling – we would only expect an energy signal for the native structure when the oligomeric state is considered [18].

Oligomeric modeling improves monomeric structure quality

There were several cases where, for oligomeric predictions, Robetta’s predicted structure of the monomer was the most (or among the most) accurate of all submitted models. These include targets: a) T0860, a trimer where Robetta had a more accurate prediction than any other server, exceeding the next best GDT-TS by 2 (82 versus 80); b) T0867, a relatively easy trimer comparative modeling case where 6 servers including Robetta had the top model with GDT-TS 98; c) T0873, a tetramer, where the Robetta model was more accurate than the next best server model by a GDT-TS of 4 (84 versus 80); d) T0881, a trimer where Rosetta was within 1 GDT-TS unit of the top server group (69 versus 68) and third-best overall; e) T0906, an octamer where the Robetta model was the second best overall and within 0.3 GDT-TS units of the best submitted model; and f) T0917, a dimer where the top Robetta was more accurate than any other server, with a GDT-TS nearly 5 units higher than the next-best server.

The cases where Rosetta improvements were largest tended to be cases where sequence alignments were straightforward, and the subunits were in some way intertwined. These include T0860 (Figure 2), where a long beta hairpin (residues 34-47) interacts extensively with an adjacent subunit, and its conformation is energetically dominated by inter-subunit interactions. A sequence insertion in this region compared to the best template, makes modeling without considering this symmetry relatively difficult. Similarly, T0873 and T0917 (Figure 3) also feature some degree of intertwining: in T0873, a C-terminal helix (residues 489-501) is completely stabilized by inter-subunit interactions, and connected by a loop making significant inter-subunit hydrogen bonds (Figure 3c); in T0917, while not intertwined, individual subunits make extensive beta strand pairings across the symmetric interface (Figure 3f), with the N-terminus (residues 8-14) mostly stabilized by these inter-subunit strand-pair interactions. These cases are likely successful cases of monomeric structure prediction since these intertwined residues and cross-subunit beta strands are difficult to refine in the absence of the symmetric partner. Since few servers consider this symmetry, the Robetta predictions tend to be more accurate, and to obtain high-accuracy structure predictions, any energy-based refinement method needs to model these interactions.

Figure 2.

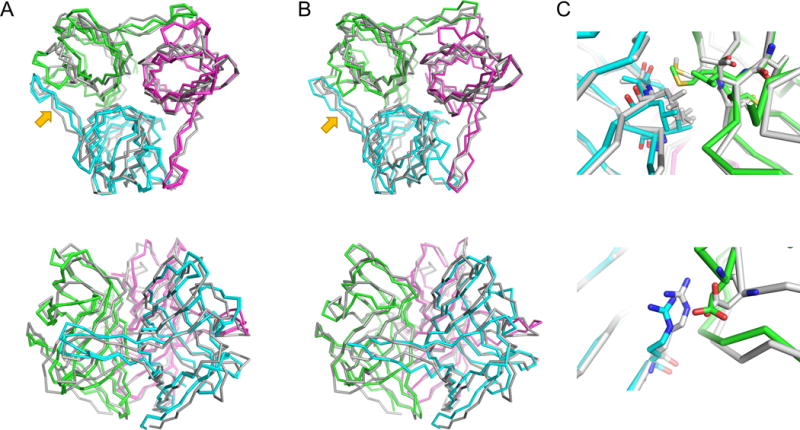
Symmetric modeling of T0860 enables accurate modeling of both monomeric and multimeric configuration. (a) The symmetric templates used determination of oligomeric state, shown overlaid on the native state in grey. (b) The Robetta model, also shown overlaid on the native in grey. An insertion in the beta hairpin (arrow) extended between subunits makes this case difficult to model if symmetry is not considered. (c) Both nonpolar and polar interactions between subunits are correctly predicted when symmetry is used in modeling.

Figure 3.

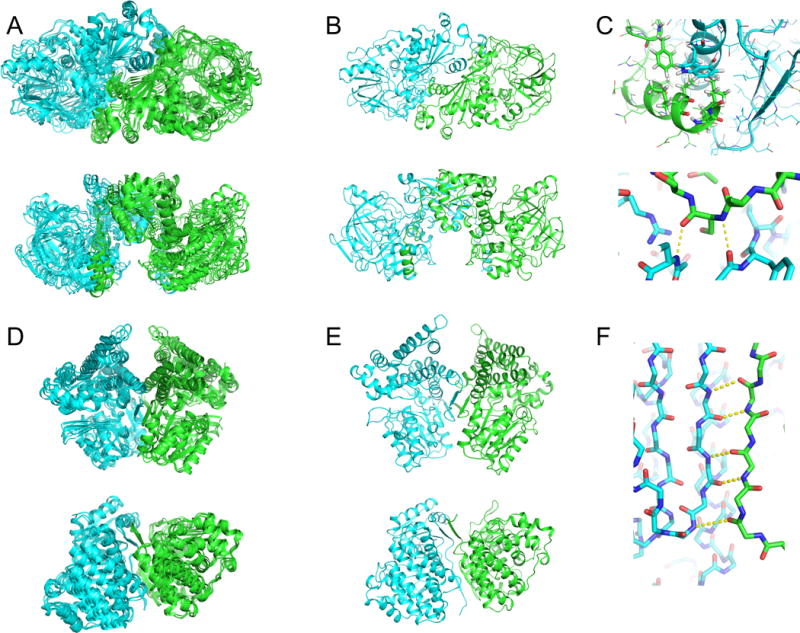
Symmetric modeling of T0873 and T0917 lead to improved monomeric structure accuracy. (a-c) The templates for T0873 show a mostly conserved dimeric configuration with some small deviations (a), which is recapitulated in the Robetta multimeric prediction (b). Oligomeric modeling improves the accuracy of the model within the monomer by maintaining physically favorable interactions across the dimeric interface, including hydrophobic packing (c, upper) and backbone hydrogen bonding (c, lower). (d-f) Templates for T0917 show a very tightly converged dimeric arrangement (d), which is maintained in the Robetta multimer prediction. Maintaining an extensive network of strand-pair interactions across the dimeric interface in the Robetta model leads to improved monomeric structure accuracy.

Finally, there were several cases where Robetta was able to correctly identify the oligomeric state, but the resulting models were still significantly less accurate than the best predictors. These were due to poor template detection or incorrect sequence alignment; that is, cases where other groups identified an accurate template that Robetta missed, or better sequence alignment to the same template(s). This is most notable for T0909, a beta repeat protein, where the GDT-TS of the best Robetta model was about 13 GDT-TS units worse than the best overall prediction (62 versus 49). This loss in accuracy of the Robetta model was due to a combination of: a) alignment errors in the C-terminal repeats that other server groups get correct, and b) errors in modeling the conformation of several large insertions, all of which are far from the symmetric interface.

Oligomeric modeling accurately recapitulates native protein interfaces

Even in cases where modeling structure symmetrically does not help the overall accuracy of monomeric structure prediction, there are many applications where it may be important to model the symmetric interface correctly. Indeed, for a wide range of symmetries, Robetta was able to very accurately recapitulate the symmetric interface (Figure 4). It is most informative here to consider the subset of oligomers posed as CASP12/CAPRI targets, where both structure modeling and protein/protein docking methods attempted to predict the conformation of symmetric assemblies, and both CASP12 and CAPRI metrics were used to evaluate both structure and interface prediction accuracy. In this subsection, we focus on analysis of these structures, particularly the seven homomeric complexes (see targets marked as “x” on the second column of Table 1) considered as part of this challenge (three other hetromeric systems were considered as well, which were not modeled by Robetta).

Figure 4.

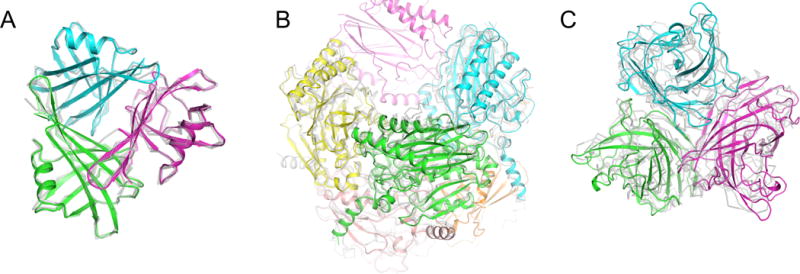
Robetta was able to predict acceptable or better predictions for five of the six CASP/CAPRI targets for which it made predictions, representing a range of different symmetries. Such predictions include the high-quality predictions of trimeric T0867 (a) and octameric T0906 (b), as well as the acceptable quality prediction of the trimeric T0881. In all figures, the refined models are shown colored by chain, while – for a subset of chains – all symmetric templates used in prediction are overlaid in a pale grey.

Of the seven homomeric complexes in the CASP/CAPRI challenge, six were modeled in the correct symmetry group by Robetta (all except T0875), with five (T0860, T0867, T0881, T0906, and T0917) deemed “acceptable” or better quality using the CAPRI assessment criteria (two were “high quality” and two were “medium quality”). Only T0875 was not modeled symmetrically by Rosetta (symmetric templates were detected but failed the P_correct filter). The target T0893 was modeled by Robetta but deemed of unacceptable quality, as the template we used had a significantly different oligomeric configuration than the target (no other good templates were available). The two cases where Robetta produced high-quality interfaces were the trimeric target T0867, and the octameric target T0906 (Figure 4a-b), while the medium quality interfaces include the trimeric target T0860 (Figure 1) and the dimeric target T0917 (Figure 2). Finally, for trimeric target T0881, Robetta produced an acceptable quality interface model (Figure 4c).

Compared to other servers, the best Robetta interface predictions were largely in line with other groups’ approaches, as most groups largely inferred symmetry from the oligomeric state of the same template structures. During modeling, Robetta only modifies the symmetry operators in two ways: by sampling the (typically only slightly different) symmetry operations implied by the template structures (see the left column of Figures 3), and through minimization of the symmetric degrees of freedom of the system. Thus, it is difficult for Robetta to significantly modify the symmetric interface in the course of refinement except for regions unaligned to any template, generally leading to performance in-line to other approaches. In two cases – T0860 (Figure 2) and T0917 (Figure 3d-f) – we do see a notable improvement compared to other CAPRI and CASP groups: using the F1 measure to combine precision and recall of predicted interface contacts, we see an improvement over the next-best group by 4 and 3 units, respectively. As both targets featured very well-conserved templates, and the monomeric structure was modeled very well, it is likely this is due to subtle backbone rearrangements near the interface and modeling variable or absent regions in templates rather than large-scale refinement of symmetric operators.

What went wrong?

Aside from the one template-alignment error and the three cases where template symmetry was incorrect, the largest failures in the symmetric pipeline were problems of omission. Of the 22 natively symmetric targets, there were only 11 where Robetta was able to predict the correct symmetry group; in 10 of these cases it was at least acceptably correct. So Rosetta was largely able to identify and model symmetry from templates. However, there were 11 additional cases where no symmetric templates were identified. For a few of these cases, T0865 and T0913, there are symmetric templates available that are suitable for modeling, however, the target_difficulty cutoff prevented them from being considered. Revisiting this target difficulty cutoff may help detection in these cases. Finally, for the other 9 cases, there are no detectable symmetric templates. In these cases, were they to be detected, our modelling protocol would need to be augmented with moves that sample the rigid body orientation of subunits. Such work is a promising area for future research efforts.

Discussion

As pointed out in the results section, there is significant room for improvement in this relatively naïve approach. While protein conformations in RosettaCM explore large regions of conformational space using long Monte Carlo trajectories, we only sample variations of quaternary structure through local minimization. Knowledge-based sampling of rigid body orientations during conformational sampling (as in previous work [19]) could enable more robust refinement of symmetry operations that are close, but not within the local minimization well (as with T0893). This strategy might also allow for de novo determination of oligomeric state: by randomizing the initial symmetry operations and refining, the Rosetta energy function might allow for the correct oligomerization assignment, without needing to draw symmetry operations from homologous structures.

Finally, while the results presented in this manuscript are very promising, the small sample size (with only 11 predicted symmetric structures) makes broad conclusions difficult to make. We have taken a retrospective look at recent blind predictions of oligomeric state in CAMEO [17], to assess whether or not oligomeric modeling helps in improving the accuracy of monomeric structure prediction. For these predictions, the same pipeline was used as that used in CASP, and we compared the results of both monomeric and multimeric RosettaCM calculations. The results are presented in Figure 5. Unfortunately, the signal here is ambiguous: while there are several cases where the monomeric accuracy improves, there are others where it worsens. However, the results in this manuscript show that oligomeric structure may be accurately predicted, and there is at least a possibility that such predictions may lead to overall more accurate structures.

Figure 5.

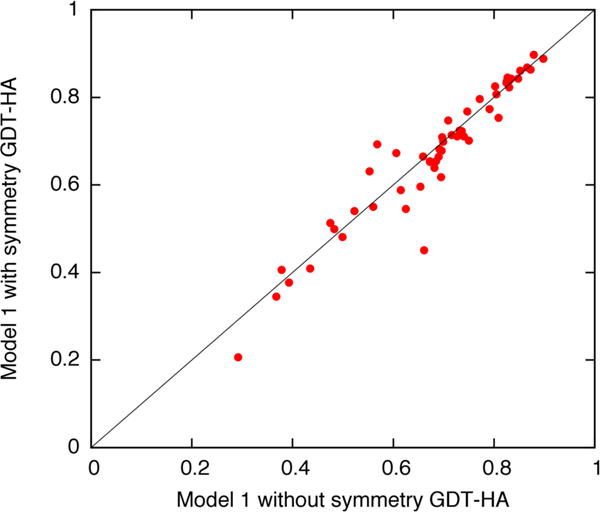
On a set of recent CAMEO [17] oligomeric structure prediction targets, we compare the monomeric structure accuracy for all predicted oligomeric structures, to the same structures refined monomerically. Each point on the scatterplot indicates a single prediction, with the y-axis showing the GDT-HA of the monomeric prediction and the y-axis showing GDT-HA of the multimeric prediction. While there are several targets for which accuracy improves when considering multimeric configuration, most cases show roughly the same accuracy, and one case shows a distinct worsening.

Conclusion

In this manuscript, we present a pipeline that enables automated prediction of oligomeric assemblies. We showed that for protein targets where template identification is straightforward, oligomeric state and configuration could be predicted with reasonable accuracy. We also showed that model rebuilding and refinement can be carried out in the native oligomeric state of a molecule, and in do so can lead to accurate prediction of both monomeric state and multimeric state of the protein. Further development and improvement of this framework will prove important in understanding the biology behind large symmetric systems, and their accurate prediction will enable a better understand of the biology, opening the door to design of (for example) small molecule inhibitors of oligomerization.