Abstract
Rewards have important influences on the motor planning of primates and the firing of neurons coding visual information and action. When eye movements to a target are differentially rewarded across locations, primates execute saccades towards the possible target location with the highest expected value, a product of sensory evidence and potentially earned reward (saccade to maximum expected value model, sMEV). Yet, in the natural world eye movements are not directly rewarded. Their role is to gather information to support subsequent rewarded search decisions and actions. Less is known about the effects of decision rewards on saccades. We show that when varying the decision rewards across cued locations following visual search, humans can plan their eye movements to increase decision rewards. Critically, we report a scenario for which five of seven tested humans do not preferentially deploy saccades to the possible target location with the highest reward, a strategy which is optimal when rewarding eye movements. Instead, these humans make saccades towards lower value but clustered locations when this strategy optimizes decision rewards consistent with the preferences of an ideal Bayesian reward searcher that takes into account the visibility of the target across eccentricities. The ideal reward searcher can be approximated with a sMEV model with pooling of rewards from spatially clustered locations. We also find observers with systematic departures from the optimal strategy and inter-observer variability of eye movement plans. These deviations often reflect multiplicity of fixation strategies that lead to near optimal decision rewards but, for some observers, it relates to suboptimal choices in eye movement planning.
Keywords: visual search, rewards, eye movements, decisions, ideal searcher, Bayesian, optimal
1. Introduction
The varying quality of visual processing across the visual field prompts many animals (Land & Nilsson, 2002) to move their eyes to explore the visual environment to make decisions about the presence, location and identity of sought objects (targets). For example, for humans the visual periphery is limited by reduced spatial resolution (Rovamo, Leinonen, Laurinen, & Virsu, 1984), increased crowding effects (Pelli, 2008) and position uncertainty (Michel & Geisler, 2011). Thus, scrutinizing the scene with eye movements can improve decision accuracy during search. The primate brain has evolved a variety of coding schemes and strategies to succeed at search. The human brain utilizes knowledge about target and distractor physical properties (Eckstein, Beutter, Pham, Shimozaki, & Stone, 2007; Findlay, 1997; Malcolm & Henderson, 2009; Peelen & Kastner, 2011; Tavassoli, Linde, Bovik, & Cormack, 2009), contextual information and cues predictive of the target locations in the environment (Brockmole, Castelhano, & Henderson, 2006; Castelhano & Heaven, 2010, 2011; Chun & Jiang, 1998; Droll, Abbey, & Eckstein, 2009; Eckstein, Drescher, & Shimozaki, 2006; Hayhoe & Ballard, 2005; Jovancevic-Misic & Hayhoe, 2009; Mack & Eckstein, 2011; Neider & Zelinsky, 2006; M. S. Peterson & Kramer, 2001; Preston, Guo, Das, Giesbrecht, & Eckstein, 2013; Torralba, Oliva, Castelhano, & Henderson, 2006), and oculomotor plans (Chen & Zelinsky, 2006; He & Kowler, 1989; Kowler, 2011; Najemnik & Geisler, 2005; Zelinsky, 1996) to optimize the probability of finding the searched targets.
Rewards have potent effects on the behavior (Chelazzi et al., 2014; Stritzke, Trommershäuser, & Gegenfurtner, 2009; Sullivan, Johnson, Rothkopf, Ballard, & Hayhoe, 2012; Theeuwes & Belopolsky, 2012; Trommershäuser, Glimcher, & Gegenfurtner, 2009) and firing of neurons of animals (Gold & Shadlen, 2002; Platt & Glimcher, 1999; Sugrue, Corrado, & Newsome, 2004; Trommershäuser et al., 2009). When two perceptual tasks have differential implicit rewards, humans adapt their gaze to the reward structure (Sullivan et al., 2012). When the environment during visual search presents a complex distribution of rewards associated with directing the gaze at various locations or targets, humans tailor their oculomotor planning (Liston & Stone, 2008; Navalpakkam, Koch, Rangel, & Perona, 2010) to try to maximize the total amount of rewards gathered by biasing their saccades towards the location/object with higher reward. If the reward is earned when the observer fixates a target that is hard to detect or discriminate, then humans and animals use an optimal Bayesian strategy. On each trial the optimal Bayesian strategy is to use the product of the reward of each location (Liston & Stone, 2008; Navalpakkam et al., 2010), the prior probability that each location contain the target, and the sensory evidence that the target be present at the location to make a fixation to the possible target location with the maximum product (saccade to maximum expected value; sMEV; Figure 1a). Indeed, this is optimal if the reward to the organism requires correct fixation of the target location such as in many laboratory tasks (Liston & Stone, 2008; Stritzke et al., 2009). However, in the real world, an eye movement to an object (e.g., a fruit) is seldom followed by an immediate reward. It is a post-eye movement correct decision to localize the object and to approach it that can result in obtaining the reward. The goal of eye movements is not to fixate an object but to gather visual information to support follow-up decisions or actions (Najemnik & Geisler, 2005). An ideal reward searcher (IS, Figure 1a) considers foveating all possible locations and calculates the expected reward of a decision following the fixation. The ideal reward searcher takes into consideration not only target locations, reward structure, and sensory evidence for target presence but also includes knowledge of the display configuration and the varying target detectability across retinal eccentricities (visibility map; Figure 1b; (Najemnik & Geisler, 2005) and see Legge, Klitz, & Tjan, 1997; Legge, Hooven, Klitz, Stephen Mansfield, & Tjan, 2002; Peterson & Eckstein, 2012; Renninger, Coughlan, Verghese, & Malik, 2005 for related models). In many circumstances, the IS will make eye movements to the possible target location with highest expected value like the sMEV model (Najemnik & Geisler, 2009; Zhang & Eckstein, 2010), yet for other scenarios the models’ predictions will diverge.
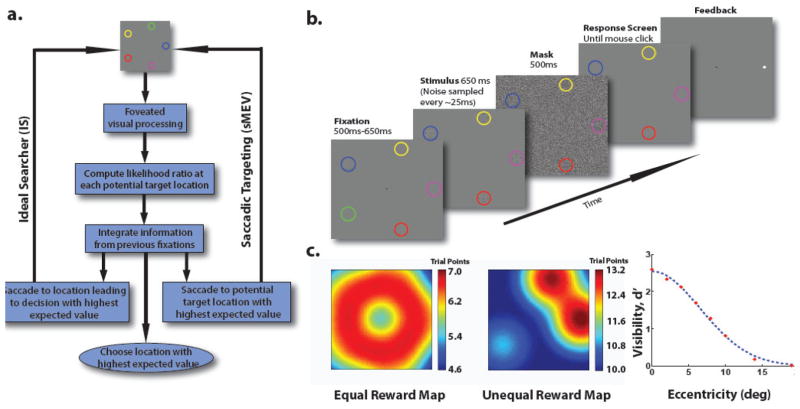
Figure 1.
a. Flow chart for two different models of human eye-movement search for rewards: Ideal Bayesian Reward Searcher (IS) and the saccade to maximum expected value (sMEV). b. Timeline of a trial for the search of a bright Gabor among dimmer Gabors. c. Reward Maps for Ideal Reward Searcher for equal reward condition (left), unequal reward condition (center). Right: Visibility map quantifying detectability of the target as a function of retinal eccentricity measured separately for each observer. Sample data for one observer.
There have been few studies investigating how rewarding decisions influences human eye movements plans (but see, Ackermann & Landy, 2010, 2013; Eckstein, Schoonveld, & Zhang, 2010), how the fixation changes impact the total rewards gathered, and how human behavior compares to that of an ideal reward searcher that takes into account the distribution of rewards and the foveated nature of the human visual system. Ackerman and Landy (2013) have shown that inhomogeneous rewards can influence human eye movements, but that their strategies are suboptimal relative to an ideal reward searcher. The study did not dissociate an eye movement strategy consistent with an ideal reward searcher (IS) from a saccade to maximum expected value model (sMEV).
In this paper, we first evaluate whether humans modify their eye movement strategies to increase rewards when only the follow-up perceptual decision is rewarded (experiment 1). We compare human fixations and decisions to an ideal reward searcher and a model that makes eye movements to the location with highest expected value (sMEV). In experiment 2, we designed a search display configuration with four clustered low reward target locations, which dissociates eye movements of the two models, and assess whether human eye movement plans are consistent with saccades to the highest expected value (sMEV) or to locations that maximize decision rewards (IS). In experiment 3, we vary the reward assignments but maintain the spatial configuration of experiment 2 so that the ideal reward searcher frequently fixates the high reward locations. Experiment 3 serves to verify that human eye movements towards the clustered cues (experiment 2) are not a fixed strategy irrespective of the optimality of such oculomotor plans. Finally, we evaluate models with a variety of eye movement strategies in experiment 2 and 3 and suggest that for some displays different fixation distributions can lead to near-optimal decision rewards and thus might explain why humans adopt variable strategies for such displays.
2. Search task
We used an m-alternative forced choice localization task in which a target (high contrast vertical Gabor) appeared in one of m (m =5 for experiment 1 and m=6 for experiment 2 and 3) locations with equal probability. The remaining m-1 locations contained lower contrast vertical Gabor elements. During the brief presentation for the display, the observer searched (with no eye movement restrictions) for the higher contrast Gabor target and after the presentation of a mask, the observer chose a location for their final perceptual decision. Feedback is provided about the correct target location after the trial ends. The associated gained reward points for that trial and the entire experiment are displayed. The contrasts of the Gabor elements were independently perturbed with Gaussian contrast noise every 25 ms (see methods for theoretical justification). Circular pre-cues (of different colors or the same color) around the possible target locations indicated the reward points associated with finding the target at that location (see methods for more details). The spatial configuration of the cues around a circle remained constant but rotated randomly from trial to trial. We informed observers that their average points per trial relative to other participants would determine a percentage of total lottery tickets assigned to them for a lottery of a $ 100 prize.
3. Theory
In this section we outline the two main models of eye movements evaluated: the saccade to maximum expected value model and the ideal searcher. For each trial, the two models generated eye movements, temporally integrating visual information up to 75 ms before saccade generation, which is consistent with the information driving saccade planning in humans (Caspi, Beutter, & Eckstein, 2004; Ludwig, 2009).
Saccade to maximum expected value (sMEV)
The sMEV model is a natural extension of the saccadic targeting model (or maximum a posteriori probability, MAP, Eckstein, Beutter, & Stone, 2001; Najemnik & Geisler, 2008; Rao, Zelinsky, Hayhoe, & Ballard, 2002) which directs its eye movement to the possible target location with highest sensory evidence for the presence of the target. The sMEV model extends the MAP model by taking into account the value of rewards, which is integrated with sensory evidence, and like the MAP model only fixates possible target locations. The sMEV model directs its saccades on each trial towards the location (among the M possible target locations) with the highest product of the reward of each location, υi (Liston & Stone, 2008; Navalpakkam et al., 2010), the prior probability that each location contain the target, πi, and the sensory evidence that the target be present at the location (likelihood ratio LR; (Beutter, Eckstein, & Stone, 2003; Green & Swets, 1989; Navalpakkam et al., 2010). The next eye movement, T+1, is to the target location, k*, with the maximum product (Figure 1a):
| (1) |
where Pk(T),i is the posterior probability of the target being at the ith location given the current fixation at k(T) and is the product of the likelihood ratio, LRk(t),i, and the prior probability (πi). For each fixation, the likelihood ratio for each ith location is given by:
| (2) |
where pi(xi| n) and pi(xi|s) are the probability density functions (pdf) modeling the likelihoods of the responses (xi) given the noise only (n) and the target (s). For the images in the current paper, the targets and distractors were Gabor elements with contrast perturbed by Gaussian random variables. Thus, all probability density functions can be described by Gaussian functions (N(μ, σ)) where the target’s pdf has a larger mean:
The index of detectability, d′k(t),i, is for the ith possible target location and for a retinal eccentricity given by fixation at k(t).
The term Π LRk(t),i, (Equation 1) for the ith location after T eye movements is the product of likelihood ratios from previous fixations and assumes statistical independence. For the case of a multiple forced choice localization task, where the stimuli have Gaussian contrast noise, taking the logarithm of the posterior probability, Equation 1 becomes (see Appendix for derivation, also Green & Swets, 1989)
| (3) |
The saccade endpoint for the T+1 saccade is chosen from the possible target locations (arg max across i) by summing the log-likelihood ratios (sensory evidence) across previous fixations and the logarithm of the product of the ith location’s prior probability (πi) and the reward associated with that location (υi). The term labeled sensory evidence (log-likelihood ratio) for each ith location consists of two terms. The first term is calculated by taking the product of the internal response of the model to the stimulus (rk(t),i, which is the result of a linear template operation on the Gabor stimulus for a given retinal eccentricity determined by the, k(t), fixation) for a given ith location and the expected mean response elicited by the target (d′k(t),i) at an eccentricity given by k(t) fixation). The second term subtracts half the squared target detectability (1/2 d′k(t),i; see Appendix A for derivation).
3.1. Ideal Reward Searcher
An ideal reward searcher (Figure 1a) considers foveating all possible locations in the display and calculates the expected decision rewards based on the possible target locations, reward structure, the sensory evidence for target presence and varying target detectability across retinal eccentricities (visibility map; Figure 1b; Najemnik & Geisler, 2005 and see Legge, Klitz, & Tjan, 1997; Legge, Hooven, Klitz, Stephen Mansfield, & Tjan, 2002; Peterson & Eckstein, 2012; Renninger, Coughlan, Verghese, & Malik, 2005 for related models). An ideal reward searcher chooses as the next fixation the location (k*IS(T+1)) which maximizes the accrued decision reward (see Appendix A for derivation)1 taking into consideration the display configuration, the visibility of the target across retinal eccentricities, the sensory evidence supporting the presence of the target, and the rewards associated with finding the target at each location:
| (4) |
where, Pk(T),i is the posterior probability at location i for fixation k(T) (see Equation1) and RMk(T+1),i, is an element in a reward map (Figure 1c) describing the expected value of decision rewards given that the next fixation is k(T + 1) and that the target location is i, and considering the sensory evidence collected. The summation is over all possible m target locations. RMk(T+1),i, is given by the probability that the product of reward (υi ) and posterior probability for the ith location exceed that of the other locations given the hypothesis that the target is at location i (Hi), multiplied by the associated reward to that location (υi):
| (5) |
For the case of statistically independent Gaussian contrast noise, the reward map in Equation 5 can be written as:
| (6) |
where ϕ is the normal probability density function and Φ is the normal cumulative density function. Also, the variables yk(t),i and yk(t),j are the logarithm of the likelihood ratios computed at the ith location (see Appendix A for detailed expressions).
3.2. Modeling alternative eye movement strategies
Aside from the sMEV and IS models we also evaluated the decision rewards of eye movement strategies associated with different relative frequencies of fixations to different reward cues. To manipulate the frequency of fixations to various cues, we varied the rewards (νi) used by the sMEV model to plan saccades (Equation 1). For example, a ν1 = 1 and νi = 0 for all i≠ 1 would result in the model making all eye movements to a single reward cue. Whereas a ν1 = 0.5 and ν2 = 0.5, and νi = 0 for all i≠ 1,2 would result in the model making half the eye movements to one cue and the other half to another reward cue. Note that the decision rewards assigned for correct target localizations for these simulations are specified by the task rewards and only the models’ internal reward values ruling sMEV’s saccade planning are manipulated. These simulations allow us to evaluate how alternative eye movement strategies diminish decision rewards below those achieved by optimal eye movement planning.
3.3. Perceptual Decisions
For all models, the final perceptual decision about the target location was obtained by combining the prior probability πi, the reward value vi, and the likelihood ratios LRk(t)i, for each possible target location across all fixations and choosing the location with the highest expected reward (or equivalently sum of logarithms):
| (7) |
All eye movement models integrate information ideally across fixations by multiplying statistically independent samples (external noise refreshed every 25 ms) of the likelihood ratio across fixations.2 Although the computation to make perceptual decisions is the same for the IS and the saccadic targeting model (sMEV), the actual values of the decision variables are different across models because their different fixation strategies lead to different gathered responses and likelihood ratios. Average reward of the perceptual decision in localizing the target was calculated for each model by tallying the outcome reward of the model’s perceptual decisions over a finite set of trials (20,000).
3.5 Parameters of the eye movement models
All models require as inputs a function that describes the detectability of the target as a function of eccentricity (visibility map). Here, we measured the ability to detect the contrast increment of the Gabor as a function of eccentricity in separate psychophysical studies (see methods). A Gaussian function was used to fit the d′ vs eccentricity function for each individual subject. The model predictions were specific to each observer, using their observer’s visibility map. We only obtained a 1-D d′ vs eccentricity function although studies have shown that anisotropies are present in human visibility maps (Abrams, Nizam, & Carrasco, 2012; Carrasco, Evert, Chang, & Katz, 1995; Najemnik & Geisler, 2005). However, given that our reward assignments varied across trials in their location, we simplified the model by assuming a single 1-D visibility map. There were
4. Psychophysical Studies
4.1. Experiment 1: Strategizing eye movements to increase search decision rewards
The first study manipulates the rewards awarded to the observer for correctly localizing the target at different locations (Figure 2, top left). In one condition, all locations had associated values of 17.4 for correct localization for each possible target spatial location. In the second condition, the reward values were 1, 10, 1, 25, and 50 points. In the first study, three observers searched in a briefly presented display (650 ms) for a high contrast luminance Gabor target among dimmer Gabor distractors in one of five locations (equal probability; forced choice paradigm; Figure 1c). A brief presentation was used to ensure that the eye movement strategies had an important impact on gathered rewards. Highly visible circular pre-cues indicated the reward obtained if a target was correctly localized in that cue-position (Figure 1c). A response screen was presented after a mask and observers chose a target location using the mouse. Critically, in one condition, correct target localization at each black circle cue was associated with the equal reward (17.5 points; Figure 2a) while in a second condition the rewards were unequal across different color cue locations (1 through 50 points; Figure 2a). In the unequal reward condition the configuration of colored cues was kept constant across trials but chosen from eight random rotations.
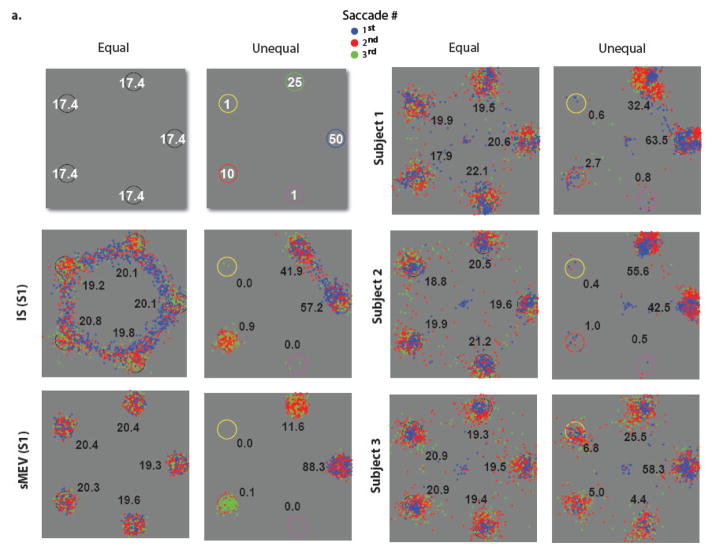
Figure 2.
Endpoints of 1st, 2nd and 3rd fixations for models (IS, sMEV) and human subjects for equal and unequal reward search for a bright Gabor target among dimmer Gabor distractors. For reference, top left graph shows the points earned for correctly finding the target at each location for the equal and unequal reward point conditions. For the unequal reward condition, the cue circular configuration was randomly rotated from trial to trial but maintained their spatial relationship of color cues to one another Numbers in all other images indicate the percentage of 1st fixations directed to each location defined using a minimum distance criterion (largest standard errors equal reward = 1.8 %; unequal reward = 4.5 % for the highest value location, S1).
4.1.1. Methods
Participants
Three naive observers participated in each search task. All observers were between the ages of 18 and 27. Observers had normal or corrected vision.
Apparatus
Stimuli were viewed binocularly on a color Dell CRT monitor at a resolution of 1024×768 pixels with a refresh rate of 85Hz. The luminance vs. gray level relationship was linearized (OptiCal software by ColorVision, Inc.) with a maximum luminance of 50.0 cd/m2.
Eye Movement Recording
An infrared video-based eye tracker sampling at 250 Hz (Eyelink I, SMI/SR Research Ltd., Osgoode, ON, Canada) was used to measure gaze position of the left eye. At the beginning of each session, calibration and validation were performed by using nine black dots that were arranged in a 16° by 16° grid. A head camera compensated for small head movements. In addition, observers were positioned on a chin rest and instructed to hold their head steady. Saccades were detected when both eye velocity and acceleration exceeded a threshold (velocity greater than 35°/s; acceleration greater than 9,500°/s2). The saccade terminations were detected when either the velocity or acceleration dropped below the thresholds.
Stimuli
The target and the distractors were Gabor patches with a full width at half maximum of 0.632° and a spatial frequency of 9 cycles/degree. Their luminance contrast amplitudes were randomly changed every 25 ms by sampling from separate normal distributions for the target and the distractors. The independent contrast noise was used to make the statistical independence assumption in the modeling (see modeling) more likely to be valid. Both target and distractor distributions had a standard deviation of 2.94 cd/m2 (root mean square contrast: RMS = 0.118). The target’s mean peak amplitude was 38.7 cd/m2 (RMS = 0.548) and that of the distractors was 35.8 cd/m2 (RMS = 0. 432). Possible target locations were evenly spaced (separated by angles of 72°) along an imaginary circle with an eccentricity of 9.3°. Each target location was enclosed by a circle with a diameter of 2.5° and a thickness of 0.12°. For equal reward trials, all circles were black and the reward was 17.4 points. For unequal reward trials, each circle was a different color (red, green, blue, yellow and magenta). The circle configuration was randomly rotated from trial to trial but maintained their spatial relationship to one another (clockwise reward values were 1, 10, 1, 25, and 50 points). The assignments of colors to reward values were randomized across participants but the spatial arrangement of rewards was kept constant.
Procedure
Observers were instructed that the goal of this task was to earn as many points as possible and that they would only receive points whenever they correctly localized the high contrast target Gabor. They were also informed that their average points per trial relative to other participants would determine a percentage of total lottery tickets assigned to them for a lottery of a 100 $ prize. Observers participated in 6 blocks of 100 trials as practice. Following, observers performed twenty 100 trial blocks, alternating blocks between equal and unequal reward conditions. At the beginning of each block, the running total of points for all observers was displayed. At the beginning of each trial, the observer fixated a small circle in the center of the screen and pressed the space bar to initiate the trial. A fixation cross and empty circles (pre-cues at each possible target location) were displayed for a random time ranging from 1 and 1.3 seconds. During the initial fixation, the trial was aborted if the observer moved their eyes more than 1.1° from the fixation cross. The fixation cross then disappeared and the four distractor Gabors and one target Gabor appeared within the empty circles. Target and distractors remained present for 650 ms. Observers were free to move their eyes during the search task. The display was then replaced with a white noise mask for 1 second followed by a response screen that consisted of the five empty circles. Observers selected a choice for target location by placing the mouse at a possible target location and clicking. Following the response, a small white dot was presented to indicate the correct target location while another screen indicated the points received on that trial and the total accrued points in the block of trials. This and all studies in the paper were approved by the UC Santa Barbara Human Subjects Committee and conducted in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki).
Measurement of human visibility maps
Procedure
After the eye movements study, observers performed a 2 interval forced choice (IFC) discrimination task designed to measure their ability to discriminate the target Gabor from the distractor Gabor at various retinal eccentricities. They performed eight sessions of 240 trials. Each session consisted of eight blocks of 30 trials at each of the eight possible retinal eccentricities (0°, 2°, 4°, 8°, 10°, 14°, 19°) for the Gabor elements. The order of eccentricity blocks within a session was randomized. The contrast amplitudes were also sampled independently every 25 ms as in the search experiments to ensure that the visibility maps measured were valid for the search experiment.
At the beginning of each trial observers fixated a small central circle and pressed the space bar to initiate the trial. A fixation cross then appeared on the screen and observers were instructed to move their eyes to the cross. Observers were allowed 280ms to move their eyes to the fixation cross or the trial would be aborted. The trial was also aborted if they moved their eyes more than 1.1° away from the fixation cross at any point during the trial. The fixation cross appeared at different random positions along the semi-circumference of an invisible circle centered on the Gabor patch with a different radius matching the desired retinal eccentricity. Half the measurements were made in the right visual field and the remaining half in the left visual field. Given that the search display configuration rotated, we assumed, for simplification, an isotropic visibility map and averaged all measurements across positions for each retinal eccentricity. Gabor patches were displayed for 125ms. After a 500ms inter-stimulus interval a second Gabor was displayed for another 125ms. The presentation time was chosen to approximately match the visual information processing time preceding a saccade (median latency of 200 ms minus 75 ms.). One of the intervals contained the bright Gabor while the other presented a dimmer distractor Gabor. Observers indicated the interval containing the brighter Gabor. Feedback was provided about the correctness of each trial’s decision. For the foveal (eccentricity = 0°) condition we used an empty circle as a fixation point to minimize masking effects. The 2-IFC proportion correct responses were transformed to an index of detectability using the classic signal detection transformation (Green & Swets, 1989) assuming equal variance and unbiased selection of each of the alternatives: where g(x−d′) is the probability density function for a Gaussian distribution and G(x) is the Gaussian cumulative probabilities. This is the general MAFC formulation that for the special case of 2-IFC can be reduced to: . For each observer the d′ vs. retinal eccentricity curve was fit with a Gaussian function (see Figure 1) centered at zero eccentricity and with the standard deviation and the peak amplitude as fitting parameters.
Statistical analysis of frequency distributions of fixations
Model and human eye movements can be compared using various methods. For example, one can compare the actual spatial distribution of fixations. Although this in principle might seem the most adequate comparison, human saccades typically undershoot their goal (hypometric saccades) and are also subject to motor noise. Here, we concentrate on comparing the frequency of fixations towards various locations (Droll et al., 2009; Navalpakkam et al., 2010) and how these frequencies are influenced by reward configurations. We calculated the distance from each fixation to the center of all possible target locations and assigned the fixation to the location with the minimum distance (Eckstein et al., 2001; Findlay, 1997). Fixations within 2 degrees of initial central fixation were discarded from the analysis and amounted to less than 1 % of all fixations. Frequency distributions for human observers were compared to that of the computational search models using a χ2 test and the associated p-values. Statistical comparisons of single frequencies across reward conditions were done using simple parametric t-tests.
4.1.2. Results
Eye movement analysis
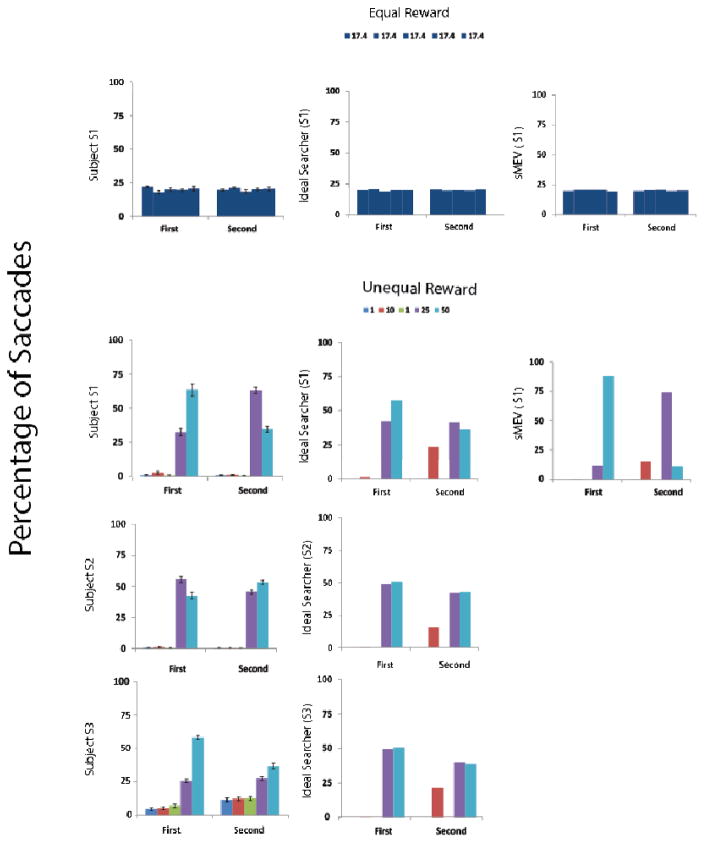
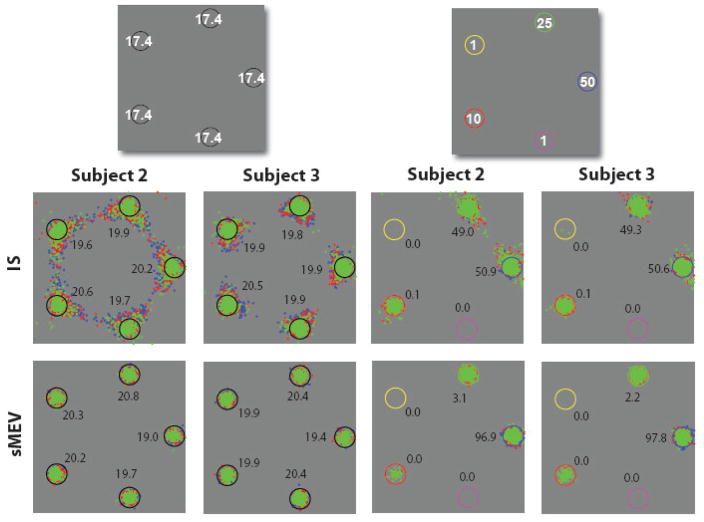
Model predictions for the sMEV model (equation 1) and the IS (equation 4) were generated for each observer using the separate two interval forced choice psychophysical measurements of how the detectability of the target degraded with retinal eccentricity (visibility map) and no fitting parameters. Figure 2 shows the distribution of saccades across locations for both models based on subject 1’s (S1) visibility map for the equal and unequal reward conditions (see Figure A.1. in the Appendix B for S2 and S3 model predictions which are very similar to those for S1). The numbers next to each location in Figure 2 correspond to the percent of 1st saccades directed to each reward cue.3 Figure 3 shows the percent of saccades for each reward cue for first and second saccades of models and human observers. Figures 2 and 3 show that, for the equal reward condition, the frequency of 1st saccades towards each possible target location did not differ across locations for both models and humans (χ2 –test for frequencies; S1: p = 0.48; S2: p = 0.051; S3: p =0.58; Figures 2 and 3). A similar pattern was observed for the 2nd saccades (Figure 3). For the unequal reward condition and the associated visibility maps, both models resulted in an increased number of saccades being directed towards the high-reward locations (50 and 25 points) for the 1st and 2nd saccades. However, the frequency of first saccades towards the highest reward cue was more pronounced for the sMEV model (see Figure 2 and 3; percentage of saccades were 88.3, 96.9 and 97.8 % for model predictions specific to each observer) while the frequencies were more evenly distributed between the two highest reward locations for the ideal reward searcher and human observers (Figure 2 and 3).
Figure 3.
The y-axis of each graph corresponds to percentage of saccades (first and second eye movements) directed to each of the locations for equal and unequal reward locations. Equal reward results are shown for Subject 1 (additional subjects are shown in the Appendix). Unequal reward results are shown for each subject, for the ideal reward searcher (IS) using the visibility map of each observer and the sMEV model for subject 1 (sMEV model predictions for the other two observers are similar to those of observer 1 and are included in the Appendix B). Error bars for human observers are standard errors of the mean across sessions. Legends provide the reward for each location indicated by black cues (equal reward cues) or color cues (unequal reward condition).
All subjects also showed biasing of 1st and 2nd saccades towards high-reward locations (frequency towards the two highest reward locations vs. each of the low reward locations: p < 0.001 for S1, S2, S3).4 However, the 3rd observer (S3) showed a greater percentage of saccades directed to the three lower reward locations (S3 = 16.2 % vs. S1 = 4.1%; S2 = 1.9 %; Figure 2 and 3) than the models and other human observers. A comparison between 1st saccade frequencies for the human observers and the IS model for the unequal reward condition resulted in significant differences for S3 (p < 0.001), but did not reach significance for S2 (p = 0.058) nor S1 (p=0.148). For all three observers the frequency distributions of 1st saccades were different from those of the sMEV model (χ2 – test for frequencies: p < 0.001).
Comparison of earned points per trial
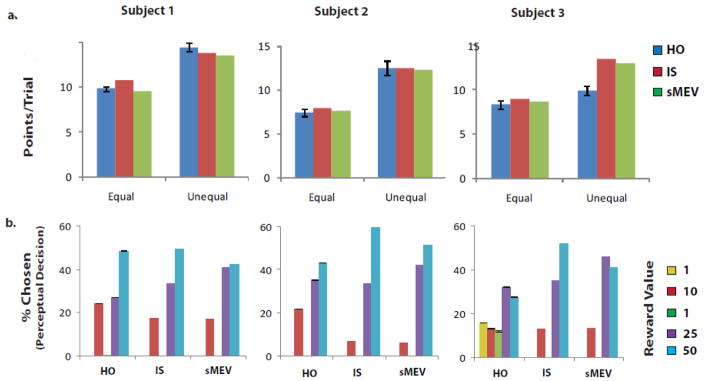
Figure 4a compares the average points per trial gathered by the observers in the experiment to that collected by the models. If observers disregarded the reward distribution structure in their decision making process, then the total points gathered per trial should remain constant across both equal and unequal reward conditions. However, all human observers collected significantly more points per trial for the unequal reward condition (S1: p < 0.001; S2: p =0.006; S3: p= 0.031). Figure 4a also shows the points/trial for the sMEV and IS model using the visibility map of each individual and no fitting parameters. Perceptual decisions for both models were obtained by choosing the location with the highest product of posterior probability and value and ideally integrating all information across time and saccades (see Theory and Appendix A). Both models benefit greatly in the number of points per trial garnered in the unequal reward condition. Furthermore the points per trial gathered by the model using independently estimated visibility maps and no fitting parameters, were comparable to those collected for S1 and S2 (Figure 4a; only a comparison between S1’s equal reward condition points/trial and the IS model reached significance; p = 0.002). In addition, for the current display configuration and visibility maps, the earned rewards for both models of eye movements are similar. Although S3’s points per trial increased in the unequal reward condition relative to the equal reward, the increase was small. S3’s points per trial for the unequal reward condition are significantly below the models’ predictions (p < 0.001), consistent with S3’s eye movement strategy departing from optimal.
Figure 4.
a. Points/trial for the equal and unequal reward search conditions for each human observer and for the models using visibility maps measured separately for each human observer. b. Distribution of perceptual decision choices across locations after search for models (IS and sMEV) and human observers (HO). Standard errors for humans that are not visible are smaller than symbols.
Distribution of decision choices across reward cues
In addition to the eye movements, we compared the influence of rewards on the perceptual decision strategies of humans to those of the models. We analyzed the frequency of decision selections for each cue-reward. For the uniform reward condition, human and models’ decision choices were uniformly distributed across locations (Figure 3). For the unequal reward condition, human observers and both IS and sMEV models’ rank order of frequency of choices corresponded closely to the rank order of reward values: high reward locations were chosen more often than low reward locations (Figure 4b; p < 0.001 for all observer). In addition, the percentage of trials selecting the lowest two reward locations (ν=1) was lower than 1% for the models, S1 and S2. However, S3 showed highly suboptimal selection of locations in the final perceptual decision (Figure 4b), often choosing the low reward (ν=1) locations. Comparisons of the distributions of decision selections in the unequal rewards condition between humans and the models resulted in statistically significantly differences with the exception of S1 and the IS model selections (p = 0.23; see Figure 4b).
Summary
The results from experiment 1 demonstrate that even when observers’ perceptual decisions following visual search (rather than the actual eye movements) are rewarded, human observers can adjust their eye movement strategy to optimize the accrued rewards. Although the optimality of the frequency of fixation and decision selections of cues vary across observers, all subjects showed some degree of change in their eye movements, decision selections, and an improvement in accrued rewards.
An additional possible inference from the results is that, at least for S1 and S2, the frequency distribution of saccades is more consistent with the IS than the sMEV model. However, such a conclusion relies on the assumption that observers’ internal utility values for each cue are a linear function of the experimental reward points. An adoption of a different utility function in the sMEV model, such as a non-linear function of the experimental rewards (Louie, Grattan, & Glimcher, 2011), might make the observed human frequencies consistent with the sMEV model (Ackermann & Landy, 2014). In addition, the theoretical simulations show that observers could adopt either strategy (sMEV and/or IS) and attain similar decision rewards.
4.2. Experiment 2: Saccades to maximum expected value location vs. saccades to maximize decision rewards
To clearly dissociate a strategy of executing saccades to the possible target location with maximum expected reward (sMEV) from an ideal reward searcher, we designed a 2nd study with the same contrast discrimination task but a different arrangement of elements: a 6 alternative forced choice task with four clustered locations with low reward values (3 points) and two spatially more isolated locations with higher reward values (6 and 12 points; Figure 5a). The spatial configuration of rewards was chosen so that: 1) The eye movements of the IS were to the clustered low value cues and thus distinct from the sMEV models; 2) Eye movements following a sMEV strategy would lead to significantly lower decision rewards than an ideal searcher. The presentation time for this display was purposely shortened (375 ms) to allow for only one saccade (observers executed 2nd saccades in less than 9 % of the trials) and force observers to strategically plan their single saccade.
Figure 5.
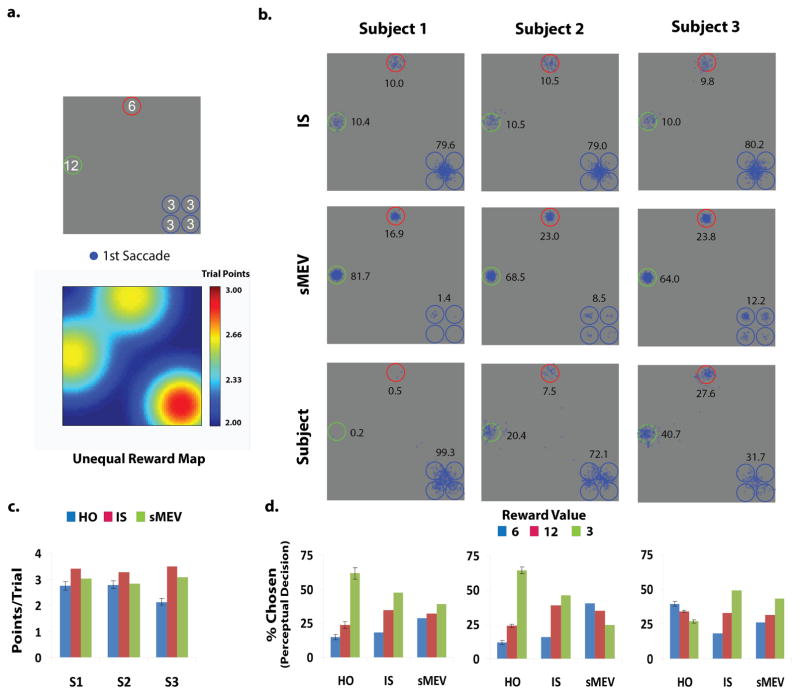
a. Top: Configuration of locations containing the target and distractors and assigned reward points for correctly finding the target at each location. Display varied randomly across four rotations. Below: Reward map for the Ideal Reward Searcher for the configuration shown above. b. First saccade endpoints (blue) for each observer and his/her associated model (IS and sMEV) predictions. Numbers correspond to percentages of 1st saccades to each location (frequency for the four clustered locations were combined into a single number). Standard errors for these percentages ranged from 2.0 % to 4.0 % for the two high reward locations and from 0.65 to 6.0 % for the four clustered locations with low rewards. c. Points/trial for observers and models (IS and sMEV). d. Percentage of trials in which a location was selected in the perceptual decision (% chosen) for human observers and models.
4.2.1. Methods
Stimuli
The target and the distractors were Gabor patches with a full width at half maximum of 0.632° and a spatial frequency of 9 cycles/deg. Contrast amplitudes were randomly changed every 23.5 ms (42.5 Hz) by sampling from separate normal distributions for the target and the distractors (standard deviation 0.98 cd/m2, RMS= 0.038). The target’s peak amplitude was 34.8 cd/m2 (target peak RMS= 0.392) and that of the distractors was 30.88 cd/m2. (RMS = 0.235). Target and distractor contrast were adjusted to achieve foveal human performance that would lead to dissociation across the theoretical models. The spatial layout of the locations is shown in Figure 5 with four locations clustered together and two further apart. Locations were 9.04° from central fixation. For the four clustered locations 9.04° represented the distance from central fixation to the center of the four locations. Each target location was enclosed by a circle with a diameter of 2.5° and a line thickness of 0.12°. Each circle had a different color and associated reward. The display was randomly rotated from trial to trial by 0°, 90°, 180°, or 270°. Assignment of colors and rewards was randomized across participants but spatial arrangement of rewards was kept constant.
Procedure
Procedures were very similar to experiment 1 with a few exceptions. The test-image remained present for 375ms to motivate observers to strategize their eye movements. Observers performed 5 blocks of 100 trial blocks. Similar to experiment 1 observers were informed that their average points per trial relative to other participants would determine a percentage of total lottery tickets assigned to them for a lottery of a $ 100 prize. The lottery for experiment 2 was separate than that for experiment 1.
4.2.2. Results
For this display and our subjects’ visibility maps, the sMEV model predicted that most 1st saccades should be directed towards the highest reward location (Figure 5b; 81.7 %, 68.5 %, 64.0 % for the sMEV model predictions for S1, S2, and S3 respectively). The sMEV model also predicts the fewest percentages of saccades towards the cluster of low reward locations: 1.4 %, 8.5 % and 12.2 % for the visibility maps of S1, S2 and S3 respectively. In contrast, the IS predicted saccades towards the cluster of low reward (υ = 3) locations (Figure 5b). Saccades toward the low reward locations allow the IS model to process four of the six locations with high foveal sensitivity. If the target is present at one of the four clustered locations then the IS model can choose the target location. On trials in which the target is not at one of the clustered locations, the IS can often reject the four locations and narrow the possible target location to the remaining two high reward locations. Of the three observers tested, two observers showed a strategy that strongly favored the clustered four locations with lower rewards (p < 0.001) and thus more closely corresponded to the ideal searcher while the third observer saccade endpoints are split between the cluster of low reward locations and the highest reward location consistent with a strategy that lies in between both models. The two observers (S1 and S2) with more optimal eye movement patterns achieved the highest garnered points (Figure 5c), but were still outperformed by IS points predictions (with no fitting parameters) by 10%.
We also examined the frequency of choices for the human and model perceptual decision choices. The IS model often executes saccades towards the cluster of four low value locations and most of its decision choices correspond to the four low reward locations which will contain the target 2/3 of the trials and are often foveated. S1 and S2 also showed this bias towards the low value locations but their bias is more pronounced. S3 who gathered the least points showed a suboptimal decision choice selecting the high-reward locations in most of the trials.
4.3. Experiment 3: Ideal reward searcher vs. eye movements to high density locations
Although experiment 2 suggests that humans can be more consistent with the IS eye movement strategy, there is a possibility that the strategy adopted by humans simply reflects eye movements to the regions of the image that contain a higher density of possible target locations. If observers are adopting a fixed strategy of executing saccades towards high density possible target locations, then we should expect that such a strategy should be unaltered by the rewards assigned to the cluster of low reward locations in experiment 2. To dissociate the IS from a fixed strategy of directing eye movements to clustered locations, we conducted a supplementary experiment which retained the same spatial configuration of possible target locations of experiment 2 but modified the reward structure by drastically lowering the rewards associated with the four clustered locations so that an ideal reward searcher rarely executed its saccade towards them. If observers modified their eye movement strategy with the new reward structure and stopped directing the majority of their fixations to the highly clustered locations, it would further suggest that humans are optimizing their eye movements following an IS strategy. The new set of observers also repeated the experiment in study 2 to provide within-subject comparisons across both reward conditions.
4.3.1. Methods
Participants
Observers were four new naïve participants (two male) between the ages of 18 and 23. All observers had normal or corrected to normal vision. The observers were different than those participating in experiments 1 and 2.
Stimuli
The stimuli for the four new participants were identical to those used for Experiment 2 with the exception of a small increase in the peak signal amplitude (from 34.8 to 36.7 cd/m2) to approximately match the performance of the original participants.
Procedure
The timing and trial structure for experiment 3 were identical to those of experiment 2. Each observer first performed ten 100 trial sessions of the reward condition of experiment 2 (6, 12, 3, 3, 3, 3, Figure 6). They then participated in ten 100 trial sessions of the new reward condition (9.9, 19.7, 0.1, 0.1, 0.1; see Figure 6) with the exception of Subject 4, who due to time constraints was only able to perform five sessions of the 2nd reward condition. We did not collect visibility maps for the four new observers in experiment 3 and thus all model predictions were based on the visibility maps of the observers that participated in experiment 2. Model predictions did not vary greatly with the visibility map of the different observers in experiment 2 and in the results section we show model predictions using the visibility map of S1.
Figure 6.
Top: Configuration of locations containing the target and distractors and assigned reward points for correctly finding the target at each location for the two conditions in experiment 3. Cues were randomly rotated across four rotations. First saccade endpoints (blue) for each subject and the IS model predictions. Numbers correspond to percentages of 1st saccades to each location (frequency for the four clustered locations were combined into a single number). Standard errors for these percentages ranged from 0.4 % to 2.9 % for the two high reward locations and from 1.2 to 3.8 % for the four clustered locations with low rewards.
4.3.2. Results
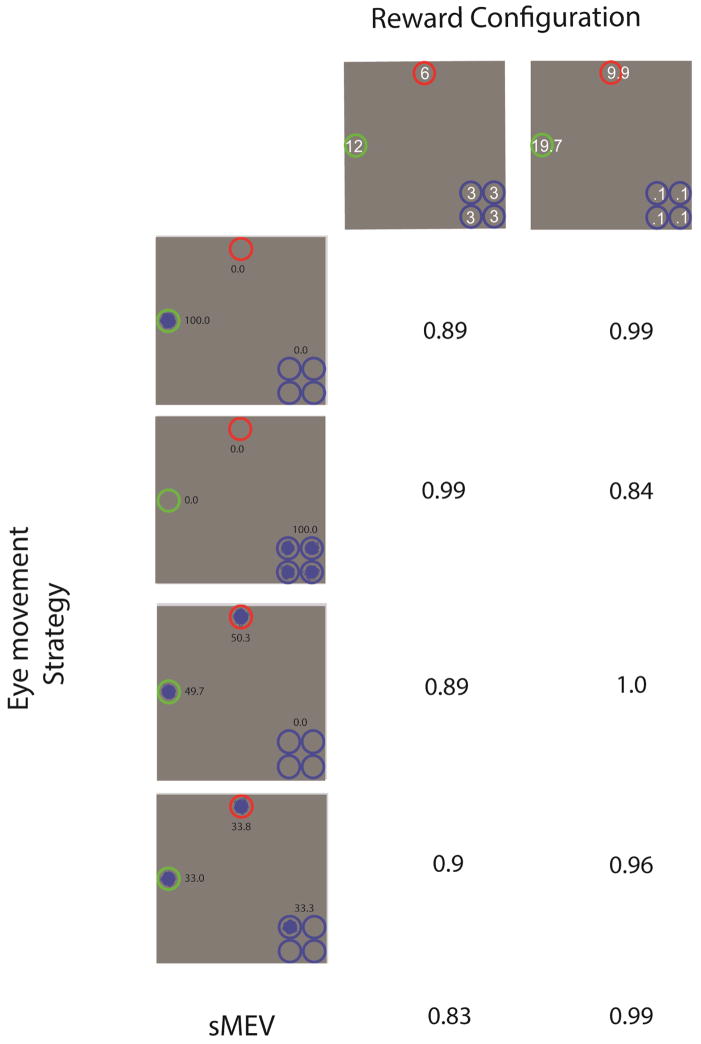
Figure 6 shows the predictions of the distribution of 1st saccade locations for the IS model with the visibility map of S1 in experiment 2 (see methods). The results show that lowering the rewards for each of the locations clustered together to 0.1 has a dramatic effect on the optimal eye movement strategy. The IS model modifies its 1st eye movements which are directed to the higher reward locations rather than the four clustered locations. Figure 6 also shows the distribution of 1st saccade locations for the four subjects for the two reward conditions. The human results for the 6, 12, 3, 3, 3, 3 points replicate the results from experiment 2 with three of the four observers showing a pattern of eye movements significantly biased towards the four clustered locations as the IS model (p < 0.01 for S1, S2, S4). Subject 3 fixation distribution departed significantly from the IS model and did not show a significant bias of fixations towards the clustered low reward locations (p =0.12).5 Incidentally, Subject 3 also achieved the lower reward points per trial across all four observers in experiment 3 (mean ± standard error; S1: 2.42 ± 0.105; S2: 2.86 ± 0.111; S3: 1.24 ± 0.125; S4: 2.36 ± 0.114). Figure 6 also shows the frequency of 1st saccade endpoints for the condition in which the rewards at the four clustered locations were reduced to 0.1 and those of the high rewards were increased to 19.7 and 9.9. Three of the four subjects showed a significant reduction in the percentage of eye movements towards the four clustered locations (p < 0.01) when compared to the 6, 12, 3, 3, 3, 3 reward distribution. Subject 3 again did not show any statistically significant change in the frequency of saccades directed to the low reward locations (p = 0.14) and also showed the lowest points per trials for the 2nd reward condition (but not statistically lower than S2; mean ± standard error; S1: 4.67 ± 0.25; S2: 2.45 ± 0.2; S3: 2.1 ± 0.25; S4: 4.36 ± 0.229). The overall results of experiment 3 suggest that observers do not have a fixed strategy of fixating clustered locations irrespective of the reward associated to those target locations. Instead, the observers seem to modify the frequency of saccades based on the rewards assigned to the cue-locations and these biases are similar to those predicted by the IS. However, even though there is a tendency of observers to adjust their eye movements away from the four clustered locations, there is large variability across observers in the adopted strategy and departures from the optimal strategy in all but one subject (S1) who showed fixation distributions close to IS (p =0.04). Is there an explanation for the large variability and departure from the ideal fixation strategy in this reward configuration of experiment 3? We assessed the decision rewards of models that included the strategies observed in humans (Figure 6) in experiment 3 (rewards: 9.9, 19.7, 0.1, 0.1, 0.1). These strategies are: 1) Fixate on the highest reward location 100 % of the trials (S4); 2) Split the fixations between the two highest reward locations (S3); 3) Fixate 1/3 of the trials on highest reward, 1/3 on the 2nd highest reward, and 1/3 on the cluster low value locations (S2); 4) Fixate all trial on the clustered locations. Note that these models’ fixations are still driven by sensory evidence but their internal reward values guiding the saccades (within the sMEV model framework) were manipulated to match the fixation frequencies listed above (see Theory for more detail).
Figure 7 shows the ratio of points per trial of the different eye movement strategies (followed by optimal decisions) and that of an ideal reward searcher. A ratio of 1 indicates that the eye movement strategy achieves the same points per trial as an ideal searcher. Our results show that for the [9.9, 19.7, 0.1, 0.1, 0.1] reward configuration there are a variety of eye movement strategies that result in near optimal decision rewards. In particular, fixating 100 % on the highest reward (S4) does not lead to any decision rewards cost relative to the ideal searcher. This can be understood if one considers that for this reward configuration an optimal decision involves mostly deciding between the two high reward locations given that the four clustered locations have insignificant rewards (0.1). Thus, fixating one or the other high reward location has little effect on the final decision reward: if the model fixates one location and there is little sensory evidence for the presence of the target, the model chooses the non-fixated location for its perceptual decision. If the display consisted of a third location with high reward then the precise location of the 1st fixation among the high reward locations would have a larger influence on the search decision reward.
Figure 7.
Decision rewards obtained by a specific eye movement strategy relative (ratio) to that obtained by an ideal reward searcher. Top: Reward Configuration for the two conditions in experiment 3. Left column images show frequency distribution of fixations for alternative eye movement strategies.
5. Discussion
5.1. Decision rewards influence eye movements
Studies have shown how assigning different rewards to eye movements to various locations and element features can influence human saccades in a manner akin to that of an optimal Bayesian observer which maximizes the probability of an eye movement towards the location with the highest product of sensory evidence and expected reward (Liston & Stone, 2008; Navalpakkam et al., 2010). However, less is known about the effect of differential decision rewards across locations on eye movement strategies, a manipulation that is relevant to the real world. Experiment 1 suggests that when rewards vary across locations of a searched target, humans change their eye movements and decision selections to increase the decision rewards (Ackermann & Landy, 2010, 2013; Eckstein et al., 2010). In general, the results are consistent with the saccade choice preferences of an ideal reward searcher that executes eye movements to high reward locations to maximize the total subsequent decision rewards. Our results are not inconsistent with Ackermann & Landy (2013) who also found some similarities, although to a lesser degree, in the influences of reward configurations on humans and ideal reward searches. However, they also found significant statistical differences when comparing the actual spatial distribution of fixations. Here, we compared human and model frequencies of fixations to the various reward cues rather than the precise spatial distribution of fixations. A comparison of human vs. model spatial distribution of actual fixations for our data would likely reveal statistically significant differences (e.g., see Figure 1 IS for S1 vs. S1), consistent with Ackermann and Landy (2013). Our approach here was to concentrate on assessing how the different reward configurations influence the frequency of saccades towards the various cues. At this level of analysis we found a better agreement between the human and ideal reward searcher than a previous study (Ackermann & Landy, 2010, 2013). A possible explanation for the difference in optimality of eye movements across studies might be related to the intermixed (Ackermann & Landy, 2010, 2013) vs. blocked (present study) presentation of the uniform and non-uniform reward configurations. Observers might have more difficulty in strategizing their eye movements when the reward configuration varies across trials.
Importantly, the increased frequency of eye movements towards high reward locations in experiment 1 is consistent with an ideal reward searcher but also a model that executes eye movements to the target location with highest expected value (sMEV model). Experiment 2 was designed to dissociate these two models. The sMEV model predicts high frequency of fixations to the high reward cues while the IS predicts saccades towards the clustered low value cues. Consistent with the IS model, we found a tendency to increasingly saccade towards the clustered low value cues present in five of the seven tested observers, although there are varying deviations from optimality across observers. To verify that the human eye movements did not reflect a fixed eye movement strategy to clustered locations (irrespective of the optimality of the eye movements), we conducted a control experiment (experiment 3) which drastically reduced the rewards (0.1) of the clustered locations so that an ideal reward searcher fixated the high reward locations. We found that the three observers that were previously fixating the clustered low value cues modified their eye movement plans to increase the fixations to the high reward locations. This third control experiment also resulted in a great variability of human eye movement strategies which is discussed in detail in the next section.
In terms of model and human accrued points per trial, results show that the IS model (with no fitting parameters and utilizing each observer’s visibility map) can predict the accrued human rewards within 10 % for four of the six observers (reward configuration 1 and 2). The differences between model and human accrued rewards for these four observers might be explained by a departure from the optimal choice selection in the final human perceptual decisions (Figure 3d) for which humans over-select the low reward locations. Alternatively, there is the possibility that the visibility of the target measured in isolation (visibility map experiment) is not fully representative of the detectability of the target in the presence of the other elements in the search array. A recent study has shown that in some circumstances visibility maps for targets in isolation are not equivalent to those measured when surrounded by search array elements (Verghese, 2012). In addition, the three different observers (S3 for reward configuration 1 and S3 and S6 for reward configuration 2) which accrued significantly fewer points than that predicted by the IS model, had both decision selections and eye movements that departed the most from the optimal.
5.2. Variability in eye movement strategies of humans
Studies assessing the optimality of eye movements during search have resulted in a variety of outcomes. Although there are some studies that show how human eye movements statistics approximate optimality (Najemnik & Geisler, 2005, 2008), there are numerous conditions for which human eye movement plans depart to different degrees from an optimal strategy (Ackermann & Landy, 2010, 2013; Morvan & Maloney, 2012; W. A. Schoonveld & Eckstein, 2006; Verghese, 2012). In the present study, for fourteen eye movement data sets, we found three data sets that seem to reveal suboptimal fixation choices (S3 for reward configuration 1; S3 & S66 for reward configuration 2) and three data sets (S2, S3, S4 for reward configuration 3) for which observers choose alternative eye movement strategies that theoretically lead to near optimal decision rewards.
Together these results contribute to a better understanding of departures from optimal eye movement planning. First, if adopting an optimal eye movement strategy will result in little performance or reward benefits over other default strategies, then humans simply maintain their suboptimal yet over-practiced default strategy, such as fixating at possible target locations, at little cost (Schoonveld & Eckstein, 2007; Shimozaki, Schoonveld, & Eckstein, 2012). Second, if a task and display/reward configurations leads to a multiplicity of eye movement strategies attaining near optimal decision rewards (e.g., Third, eye movements might be directed to objects that are associated with shorter saccades to allow for cost-savings in saccade generation (Araujo, Kowler, & Pavel, 2001; Kowler, 2011). In the current study we tried to minimize these effects by having the initial fixation to be close to equidistant from potential target locations.
Fourth, some fast eye movements seem to be directed towards salient features even if they are associated with a lower reward (Stritzke et al., 2009) suggesting a dynamic weighting of a saliency and a value-based computations (Schütz, Trommershäuser, & Gegenfurtner, 2012) in which saliency is weighted more heavily earlier on. In our current study, saccade latencies were short (171 ms mean latency in experiment 1 and 186 ms for experiment 2) but observers might have still been able to strategize their eye movements due to the presentation of the color cues 500–650 ms prior to the display of the test image (see also, Ghahghaei & Verghese, 2014). In addition, recent studies have also shown that humans can execute a suboptimal strategy when searching for multiple targets during search (Verghese, 2012 but see, Janssen & Verghese, 2013), fail to switch from a saccadic targeting strategy (Beutter et al., 2003; Findlay, 1997) to a center of mass (ideal searcher) strategy when varying the separation between two possible target locations (Morvan & Maloney, 2012), and also depart from optimality when presented with faces with uncommon optimal points of fixations (e.g., mouth, Peterson & Eckstein, 2013b).
In general, laboratory tasks which probe eye movement strategies that are commonly used by humans in perceptual tasks in the real world will more likely reveal human eye movement plans close to optimal strategies. These include the distribution of saccades reflecting the anisotropy in the visibility map of humans (Najemnik & Geisler, 2005, 2008) and the destination of saccades when performing specific tasks with faces (Peterson & Eckstein, 2012, 2013a) and reading (Legge et al., 1997; Legge et al., 2002). In contrast, more artificial laboratory tasks, such as the task in the current paper and previous studies (Ackermann & Landy, 2013; Morvan & Maloney, 2012; Shimozaki, Schoonveld, & Eckstein, 2012; Verghese, 2012) will likely reveal more inter-observer variability and larger degrees of suboptimality in eye movement strategies.
5.3. High reward locations do not always automatically lead to oculomotor capture
The present results also serve as a counterpoint to recent studies suggesting that the association of a spatial cue with a high reward will automatically lead to oculomotor capture (Anderson, Laurent, & Yantis, 2011; Anderson & Yantis, 2012). Experiment 2 and 3 illustrate a scenario where the majority observers did not execute eye movements toward the highest reward cue but instead moved their eyes to lower value cues in order to maximize decision rewards. A tendency of human observers to favor high reward cues and locations is expected because such bias typically agrees with that of an optimal eye movement strategy for a majority of display configurations. However, our results demonstrate that when the task requires a different strategy to maximize rewards, observers can refrain from looking at high reward locations. Although we did not obtain verbal reports from observers, it is likely that observers adopted an explicit cognitive strategy to fixate the four clustered target location and rule out as many locations as possible with a single fixation.
5.4. Implications for the relationship between perception and action
Our results show the important effects of decision rewards on oculomotor planning. Theories supporting the concept that perception and action are two distinct and independent pathways (Goodale & Milner, 1992) might predict that rewarding a perceptual decision would not optimize eye movement strategies. In contrast, our results are consistent with theories suggesting interactions across both pathways (Eckstein et al., 2007; Gegenfurtner, Xing, Scott, & Hawken, 2003; Krauzlis, 2005; Krauzlis & Stone, 1999) which would predict that eye movements would indeed be optimized even though it is a subsequent perceptual decision that is rewarded. The theory would also be consistent with the idea that pathways for perception and oculomotor control largely overlap, leading to significant sharing of visual information (Dassonville & Bala, 2004; Gegenfurtner et al., 2003; Krauzlis & Stone, 1999).
5.5. Implications for computations in monkey LIP and biologically plausible approximations to IS
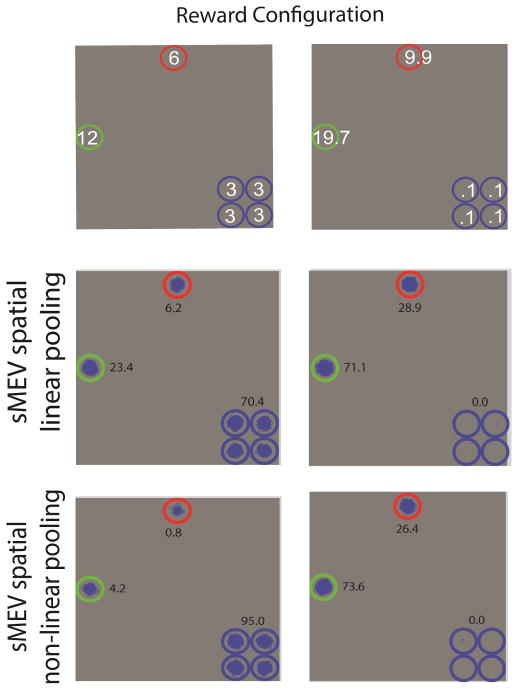
Our findings might have some implications for neuro-scientific theories of visual processing. Current theories suggest that the lateral intra-parietal area is involved in biologically representing a priority map (Bisley & Goldberg, 2010; Bisley, Mirpour, Arcizet, & Ong, 2011) in which an increasing firing rate to objects represents increasing behavioral priority. This priority map has been computationally described as a decision variable measuring sensory evidence akin to a likelihood (Gold & Shadlen, 2002) (Equation 2) which correlates with behavioral decision confidence and that it is modulated by rewards in a similar manner to the sMEV model. Thus, current models of LIP responses would predict that for our 2nd experiment (Figure 3b) an LIP neuron would maximally fire (on average) when the highest reward stimulus was located within its receptive field. Yet, our psychophysical results suggest an alternative prediction that the maximal firing would result when the four clustered low rewards (r= 3) were located within the neuron’s receptive field. In principle, this could potentially be achieved by larger receptive field LIP cells that performed an excitatory spatial pooling of rewards across locations followed by a saccade to the location with maximum expected value. We refer to this model as a sMEV with spatial pooling of rewards (sMEV). We modfied the sMEV model to either linearly sum the rewards of the four clustered locations or to combine them non-linearly (see Appendix A for mathematical details on the model). The pooled reward is assigned to each of the four clustered location and is used for the sMEV’s saccade planning but not its final perceptual decision which utilizes the original rewards. Figure 8 shows the distribution of fixations for the sMEV model with spatial pooling and the total number of decision points/trial accrued for the model relative to the ideal searcher. The results show that a simple linear summation of rewards can reproduce optimal eye movement behavior and a non-linear accelerating function can mimic the distribution of saccades of the human observers with the highest fixation frequencies (0.99) towards the clustered locations. Thus, the sMEV model with spatial pooling might be a biologically plausible implementation of the ideal searcher in areas LIP and other areas which have been shown to code value and probability of anticipated rewards in sensory motor tasks (Hikosaka & Watanabe, 2000; Leon & Shadlen, 1999; Watanabe, 1996).
Figure 8.
Distribution of first fixations for two reward configurations for two variations of the sMEV model which eye movements (but not decisions) are based on spatial pooling of rewards at the clustered locations. Reward values at clustered locations are pooled linearly or non-linearly and assigned to each of the clustered locations. The sMEV model with spatial pooling of rewards can mimic the ideal reward searcher and also predict the range of eye movement behaviors in humans.
Reward layouts can lead an ideal reward searcher to fixate clustered low value cues.
Humans can implement search eye movements to low value cues to increase decision rewards.
Multiplicity of near optimal saccade plans related to fixation variability across observers.
Suboptimal eye movements likely more common for non-ecologically valid lab tasks.
Acknowledgments
This research was supported by National Institute of Health grants EY023097 and EY015925, and the Institute for Collaborative Biotechnologies through grant W911NF-09-0001 to MPE. The content of the information does not necessarily reflect the position or the policy of the Government, and no official endorsement should be inferred. We thank the UCSB Grid Computing for access to their systems. We also thank Mike Landy and an anonymous reviewer for useful suggestions to improve the presented work.
Appendix A
Here, we describe the mathematical details for the ideal reward searcher (IS) and the saccade to maximum expected value model (sMEV). The supplementary materials are organized in the following sections: 1) Linear template theory and decision variables; 2) Modeling the visibility maps for a foveated visual system; 3) Computational models of multiple fixation visual search. The perceptual decision making after multiple fixations is discussed in the main text theory section.
1 Linear templates and decision variables
Both multiple fixation models (sMEV and IS) start with a linear operation based on statistical decision theory for forced choice localization tasks in noise [1–4]. Let the vectorg denote the grey values of the pixels in a 2-D image patch. In an m alternative forced choice (mAFC) task, we refer to a signal-present patch (target present) of the image as and to a target-absent patch as , j = 1, 2, ···m −1. In a forced choice trial, a signal, s, is added to the image background, b0, in one of m possible locations chosen at random: . For target-absent locations, the image patch consists of background only or a distractor: . For the task at hand the signal/target is a Gabor with a contrast increment. Note that s is a deterministic vector, and image backgrounds are considered to be random with some statistical properties.
The linear model observer forms a response variable, r, as an inner product between g and a vector of weights w: r = wTg+ε. The set of weights applied to the image is referred as the template. The value, ε, is sample of internal noise drawn from a normal distribution with standard deviation proportional to the external noise: ε ~ N(0,kσrext) where σrext is the standard deviation of the response variable, r, due to the external noise and k is a constant. When presented with and , the observer forms one response variable and m −1 response variables, . Given these template responses, a calculation that will be useful when determining the models’ next fixation and making perceptual decisions is the likelihood ratio at each possible ith location (LRi; [1–4]):
| (A1) |
where fb(●) and fs(●) are the probability density functions (pdf) modeling the likelihoods of the responses given the background only and the target, respectively. To avoid underflow, the log likelihood ratio may be used instead of LR. For the images in the current paper, the targets and distractors were Gabors with contrast perturbed by Gaussian random variables. Thus, all pdfs can be described by Gaussian functions.
2 Modeling the Visibility Map for a foveated visual system
The detrimental effect of retinal eccentricity on the detectability of the target was implemented by modeling detectability, d′, as a function of eccentricity (e):
| (A2) |
where the magnitude μ and standard deviation σ are fit to measured d′ as a function of eccentricity for each individual human observer, and the eccentricity e is the distance between the fixation k and the template response location, i. We assume a simplified model in which the target detectability is dependent in eccentricity but rotationally invariant. This is likely not right but given that the display was rotated across different angles, we use a simpler model that uses the dependence on eccentricity averaged across different angles.
The template responses can be modeled as random variables sampled from Gaussian distributions as:
| (A3a) |
| (A3b) |
(A3b)
Thus, the likelihood ratio becomes
| (A4) |
In the following sections, we shall describe how to use LRi to determine the next fixation and make perceptual decisions for the IS and sMEV models.
3 Computational models of multiple fixation visual search
3.1 Fundamentals of computational models
Determining the next fixation for both models (IS and sMEV) requires calculating the posterior probability that the target is at that location given the template responses at all m locations. Suppose Hi is the ith hypothesis which refers to the target being at the ith location. The posterior probability P(Hi|r1,..., rm) at the ith location is related to the likelihood and the prior probability by Bayes’ rule:
| (A5) |
where P(r1,..., rm|Hi) is the likelihood of the template responses at all M locations (r1,..., rm) given the ith hypothesis; P(Hi) = πi is the prior probability of the target being at the ith location. Assuming hypotheses are mutually exclusive, statistical independence across locations, one can equivalently replace the likelihood function P(r1,..., rm|Hi) with the likelihood ratio (LR) of the response ri given target presence or absence at the ith location weighted by ith location’s prior probability of containing the target (πi):
| (A6) |
which is obtained by dividing the LRi by .
The external noise is independently sampled through time (every 25 ms) and we assume that the dominating internal noise is proportional to the external noise standard deviation (ε ~ N(0,kσrext)) and is temporally independent, as the external noise. We assume that the proportional external noise dominates the constant additive internal noise (Burgess & Colborne, 1988)7. Assuming statistical independence across fixations (given the statistical independence across time), we define the dynamic posterior after the Tth eye movement as:
| (A7) |
where rk(t),i is the template response at potential location i for fixation k(t).
Accordingly, the posterior probability after multiple fixations is proportional to the weighted product of likelihood ratios:
| (A8) |
where is the likelihood ratio at potential location i for fixation k(t).
3.2. Inclusion of rewards into decisions
When each hypothesis is associated with a different reward (vi),the optimal decision variable for non-foveated models is to weight the posterior probability of each location by the reward:
| (A9) |
Equation A9 considers, consistent with instructions to observers, that there is no penalty for incorrect answers, otherwise such penalties need to be considered.
3.3. Saccade targeting (sMEV) model
Given the template response rk(t),i, across eye movements k(t), and reward vi across different locations, i, the sMEV model selects as the next fixation the possible target location with the highest expected value (product of likelihood ratios, priors and reward for each location):
| (A10) |
Using the Gaussian probability density functions for the likelihood ratio in Equation (A4) and using the logarithm, the sMEV model determines the next fixation by summing template responses weighted by the target detectability at each location’s eccentricity and an additive logarithm of the reward and prior:
| (A11) |
3.4. Ideal Reward Searcher (IS) model
The ideal searcher (Najemnik & Geisler, 2005), unlike the saccadic targeting (sMEV) model, selects as a next fixation the location that will maximize the expected reward in the perceptual decision. It first calculates for each possible subsequent fixation location, k(T+1), the expected reward of an ideal observer given that the target location is i. The expected rewards across all possible fixation locations define a reward map, RMk(T+1),i. The IS model selects the next fixation by computing a weighted sum of reward maps across possible target locations (i), where the weights correspond to the posterior probabilities that the target is present at the ith location:
| (A12) |
A difference between the IS and sMEV model (Equation A11 vs. Equation A12) is that the fixations of the IS model are not limited to the potential target locations.
The reward map, RMk(T+1),i, given that the target is at the ith location is equal to the product of that ith location’s reward and the probability that the ideal observer makes the correct choice (i.e., that the product of reward and posterior probability at the target location, i, take a greater value than that at any other location):
| (A13) |
To compute the reward map analytically we use Equation (A8):
| (A14) |
Assuming conditional independence, Equation (A13) can be rewritten as the product of probabilities.
| (A15) |
for any t > 0, using the logarithm of Equation S4:
| (A16a) |
| (A16b) |
Note that when 1≤t≤T, yk(t),i and yk(t),j, the log-likelihood ratios are deterministic scalar values based on detectabilities and acquired template responses only (previous sensory evidence), but yk(T+t),i, and yk(T+t),j, are random variables describing loglikelihoods assuming a future fixation. 8 Considering the probability density function describing the internal response as a function of eccentricity (Equations A3a and A3b) and assuming the target is at the ith location
| (A17a) |
| (A17b) |
Thus the log-likelihood ratios, yk(T+t),i, and yk(T+t),j, are also Gaussian
| (A18a) |
| (A18b) |
where is the detectability at target location i, given fixation at location k(T + 1). The reward map in Equation (A15) can be rewritten as
| (A19) |
where ϕ is the normal probability density function in Equation (A18a) and Φ is the normal cumulative density function (cdf) in Equation (A18b).
3.5 Saccade targeting (sMEV) model with spatial pooling of reward values
This is a variation of the sMEV model in which reward values of spatially clustered locations are pooled together. The equations selecting which possible target location will be the next fixation remains the same as the sMEV model except that the assigned rewards at the clustered locations are spatially pooled. The pooled reward value (vp) at the four clustered locations (vi for i=3, 4, 5, 6) is given by:
We considered two pooling methods. A simple linear summation of rewards at the clustered locations when c=0 and b =1 and a non-linear pooling when c = 0.25 and b = 1.5. Following the pooling operation for the four clustered locations, the location of the saccade is determined using the same equation as for the standard sMEV model (Equation A.11) with the pooled reward assigned to each of the four clustered locations. The perceptual decision for the model is also the same as with the standard sMEV model (Equation 7). Note that the model does not pool the rewards for the perceptual decision.
Appendix B
Figure B.1.
Predictions of the IS and sMEV models for S2 and S3 using their individual visibility maps for equal (left) and unequal reward conditions (right)
Footnotes
As with Najemnik and Geisler (2005), the model looks at one fixation at a time and does not evaluate all combinations of saccades.
We temporally refreshed the external noise to make our model assumption of statistical independence across fixation more likely to be valid. We also assume that the dominating eccentricity dependent internal noise is proportional to the external noise (Burgess & Colborne, 1988) and follows the same temporal statistics as the external noise. no fitting parameters for the models that were adjusted to the multiple eye movement search data (Experiments 1 and 2).
We analyzed the accuracy and frequencies based on target spatial location (upper right vs. lower left) rather than cues and did not find any systematic differences and thus for the remaining of the paper we present results averaged across spatial locations of the target.
Third saccades were executed less frequently: 8 % of the trials for the unequal reward condition and 19 % of the trials for the equal reward condition.
Note that we do not make statistical comparisons to the IS predictions as reported for experiment 2 because we did not collect visibility maps for the observers in experiment 3 and thus not allowing us to make IS predictions specific to the observer in experiment 3.
The sixth data set for reward configuration 2 is labeled S3 in Figure 6. reward configuration 3 in the current paper), then it is likely that human observers might adopt variable eye movement strategies which depart from the optimal fixation plans.
Note that the assumption of independence is typically adopted even in displays that do not refresh the external noise (Najemnik & Geisler, 2005)
The derivation is similar to Najemnik & Geisler (2005) but uses the log-likelihood ratio as the decision variable rather than the posteriors. The log-likelihoods are Gaussian distributed and allow us to express the log-posteriors from previous fixations as an additive term in Equation (A19).
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abrams J, Nizam A, Carrasco M. Isoeccentric locations are not equivalent: The extent of the vertical meridian asymmetry. Vision Research. 2012;52(1):70–78. doi: 10.1016/j.visres.2011.10.016. http://doi.org/10.1016/j.visres.2011.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ackermann JF, Landy MS. Suboptimal Choice of Saccade Endpoint in Search with Unequal Payoffs. Journal of Vision. 2010;10(7):530–530. http://doi.org/10.1167/10.7.530. [Google Scholar]
- Ackermann JF, Landy MS. Choice of saccade endpoint under risk. Journal of Vision. 2013;13(3) doi: 10.1167/13.3.27. http://doi.org/10.1167/13.3.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ackermann JF, Landy MS. Suboptimal decision criteria are predicted by subjectively weighted probabilities and rewards. Attention, Perception & Psychophysics. 2014 doi: 10.3758/s13414-014-0779-z. http://doi.org/10.3758/s13414-014-0779-z. [DOI] [PMC free article] [PubMed]
- Anderson BA, Laurent PA, Yantis S. Value-driven attentional capture. Proceedings of the National Academy of Sciences. 2011 doi: 10.1073/pnas.1104047108. http://doi.org/10.1073/pnas.1104047108. [DOI] [PMC free article] [PubMed]
- Anderson BA, Yantis S. Value-driven attentional and oculomotor capture during goal-directed, unconstrained viewing. Attention, Perception & Psychophysics. 2012;74(8):1644–1653. doi: 10.3758/s13414-012-0348-2. http://doi.org/10.3758/s13414-012-0348-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Araujo C, Kowler E, Pavel M. Eye movements during visual search: the costs of choosing the optimal path. Vision Research. 2001;41(25–26):3613–3625. doi: 10.1016/s0042-6989(01)00196-1. [DOI] [PubMed] [Google Scholar]
- Beutter BR, Eckstein MP, Stone LS. Saccadic and perceptual performance in visual search tasks. I. Contrast detection and discrimination. Journal of the Optical Society of America. A, Optics, Image Science, and Vision. 2003;20(7):1341–1355. doi: 10.1364/josaa.20.001341. [DOI] [PubMed] [Google Scholar]
- Bisley JW, Goldberg ME. Attention, intention, and priority in the parietal lobe. Annual Review of Neuroscience. 2010;33:1–21. doi: 10.1146/annurev-neuro-060909-152823. http://doi.org/10.1146/annurevneuro-060909-152823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bisley JW, Mirpour K, Arcizet F, Ong WS. The role of the lateral intraparietal area in orienting attention and its implications for visual search. The European Journal of Neuroscience. 2011;33(11):1982–1990. doi: 10.1111/j.1460-9568.2011.07700.x. http://doi.org/10.1111/j.1460-9568.2011.07700.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brockmole JR, Castelhano MS, Henderson JM. Contextual Cueing in Naturalistic Scenes: Global and Local Contexts. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2006;32(4):699–706. doi: 10.1037/0278-7393.32.4.699. http://doi.org/10.1037/0278-7393.32.4.699. [DOI] [PubMed] [Google Scholar]
- Burgess AE, Colborne B. Visual signal detection. IV. Observer inconsistency. Journal of the Optical Society of America. A, Optics and Image Science. 1988;5(4):617–627. doi: 10.1364/josaa.5.000617. [DOI] [PubMed] [Google Scholar]
- Carrasco M, Evert DL, Chang I, Katz SM. The eccentricity effect: Target eccentricity affects performance on conjunction searches. Perception & Psychophysics. 1995;57:1241–1261. doi: 10.3758/bf03208380. http://doi.org/10.3758/BF03208380. [DOI] [PubMed] [Google Scholar]
- Caspi A, Beutter BR, Eckstein MP. The time course of visual information accrual guiding eye movement decisions. Proceedings of the National Academy of Sciences of the United States of America. 2004;101(35):13086–13090. doi: 10.1073/pnas.0305329101. http://doi.org/10.1073/pnas.0305329101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castelhano MS, Heaven C. The relative contribution of scene context and target features to visual search in scenes. Attention, Perception & Psychophysics. 2010;72(5):1283–1297. doi: 10.3758/APP.72.5.1283. http://doi.org/10.3758/APP.72.5.1283. [DOI] [PubMed] [Google Scholar]
- Castelhano MS, Heaven C. Scene context influences without scene gist: Eye movements guided by spatial associations in visual search. Psychonomic Bulletin & Review. 2011 doi: 10.3758/s13423-011-0107-8. http://doi.org/10.3758/s13423-011-0107-8. [DOI] [PubMed]
- Chelazzi L, Eštočinová J, Calletti R, Gerfo EL, Sani I, Libera CD, Santandrea E. Altering Spatial Priority Maps via Reward-Based Learning. The Journal of Neuroscience. 2014;34(25):8594–8604. doi: 10.1523/JNEUROSCI.0277-14.2014. http://doi.org/10.1523/JNEUROSCI.0277-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Zelinsky GJ. Real-world visual search is dominated by top-down guidance. Vision Research. 2006;46(24):4118–4133. doi: 10.1016/j.visres.2006.08.008. http://doi.org/10.1016/j.visres.2006.08.008. [DOI] [PubMed] [Google Scholar]
- Chun MM, Jiang Y. Contextual cueing: implicit learning and memory of visual context guides spatial attention. Cognitive Psychology. 1998;36(1):28–71. doi: 10.1006/cogp.1998.0681. http://doi.org/10.1006/cogp.1998.0681. [DOI] [PubMed] [Google Scholar]
- Dassonville P, Bala JK. Perception, action, and Roelofs effect: a mere illusion of dissociation. PLoS Biology. 2004;2(11):e364. doi: 10.1371/journal.pbio.0020364. http://doi.org/10.1371/journal.pbio.0020364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Droll JA, Abbey CK, Eckstein MP. Learning cue validity through performance feedback. Journal of Vision. 2009;9(2):18.1–23. doi: 10.1167/9.2.18. http://doi.org/10.1167/9.2.18. [DOI] [PubMed] [Google Scholar]
- Eckstein MP, Beutter BR, Pham BT, Shimozaki SS, Stone LS. Similar neural representations of the target for saccades and perception during search. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2007;27(6):1266–1270. doi: 10.1523/JNEUROSCI.3975-06.2007. http://doi.org/10.1523/JNEUROSCI.3975-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckstein MP, Beutter BR, Stone LS. Quantifying the performance limits of human saccadic targeting during visual search. Perception. 2001;30(11):1389–1401. doi: 10.1068/p3128. [DOI] [PubMed] [Google Scholar]
- Eckstein MP, Drescher BA, Shimozaki SS. Attentional Cues in Real Scenes, Saccadic Targeting, and Bayesian Priors. Psychological Science. 2006;17(11):973–980. doi: 10.1111/j.1467-9280.2006.01815.x. http://doi.org/10.1111/j.1467-9280.2006.01815.x. [DOI] [PubMed] [Google Scholar]
- Eckstein MP, Schoonveld W, Zhang S. Optimizing eye movements in search for rewards. Journal of Vision. 2010;10(7):33. http://doi.org/10.1167/10.7.33. [Google Scholar]
- Findlay JM. Saccade Target Selection During Visual Search. Vision Research. 1997;37(5):617–631. doi: 10.1016/s0042-6989(96)00218-0. http://doi.org/10.1016/S0042-6989(96)00218-0. [DOI] [PubMed] [Google Scholar]
- Gegenfurtner KR, Xing D, Scott BH, Hawken MJ. A comparison of pursuit eye movement and perceptual performance in speed discrimination. Journal of Vision. 2003;3(11):865–876. doi: 10.1167/3.11.19. http://doi.org/10:1167/3.11.19. [DOI] [PubMed] [Google Scholar]
- Ghahghaei S, Verghese P. Efficient saccade planning requires time and clear choices. Journal of Vision. 2014;14(10):1197–1197. doi: 10.1016/j.visres.2015.05.006. http://doi.org/10.1167/14.10.1197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. Banburismus and the brain: decoding the relationship between sensory stimuli, decisions, and reward. Neuron. 2002;36(2):299–308. doi: 10.1016/s0896-6273(02)00971-6. [DOI] [PubMed] [Google Scholar]
- Goodale MA, Milner AD. Separate visual pathways for perception and action. Trends in Neurosciences. 1992;15(1):20–25. doi: 10.1016/0166-2236(92)90344-8. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal Detection Theory and Psychophysics. Peninsula Pub; 1989. [Google Scholar]
- Hayhoe M, Ballard D. Eye movements in natural behavior. Trends in Cognitive Sciences. 2005;9(4):188–194. doi: 10.1016/j.tics.2005.02.009. http://doi.org/16/j.tics.2005.02.009. [DOI] [PubMed] [Google Scholar]
- He PY, Kowler E. The role of location probability in the programming of saccades: implications for “center-of-gravity” tendencies. Vision Research. 1989;29(9):1165–1181. doi: 10.1016/0042-6989(89)90063-1. [DOI] [PubMed] [Google Scholar]
- Hikosaka K, Watanabe M. Delay Activity of Orbital and Lateral Prefrontal Neurons of the Monkey Varying with Different Rewards. Cerebral Cortex. 2000;10(3):263–271. doi: 10.1093/cercor/10.3.263. http://doi.org/10.1093/cercor/10.3.263. [DOI] [PubMed] [Google Scholar]
- Janssen CP, Verghese P. Towards a Better Understanding of Eye-Movement Strategies in Multiple Target Search. Journal of Vision. 2013;13(9):526–526. http://doi.org/10.1167/13.9.526. [Google Scholar]
- Jovancevic-Misic J, Hayhoe M. Adaptive Gaze Control in Natural Environments. The Journal of Neuroscience. 2009;29(19):6234–6238. doi: 10.1523/JNEUROSCI.5570-08.2009. http://doi.org/10.1523/JNEUROSCI.5570-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowler E. Eye movements: the past 25 years. Vision Research. 2011;51(13):1457–1483. doi: 10.1016/j.visres.2010.12.014. http://doi.org/10.1016/j.visres.2010.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krauzlis RJ. The control of voluntary eye movements: new perspectives. The Neuroscientist: A Review Journal Bringing Neurobiology, Neurology and Psychiatry. 2005;11(2):124–137. doi: 10.1177/1073858404271196. http://doi.org/10.1177/1073858404271196. [DOI] [PubMed] [Google Scholar]
- Krauzlis RJ, Stone LS. Tracking with the mind’s eye. Trends in Neurosciences. 1999;22(12):544–550. doi: 10.1016/s0166-2236(99)01464-2. [DOI] [PubMed] [Google Scholar]
- Land MF, Nilsson D-E. Animal Eyes. Oxford University Press; USA: 2002. [Google Scholar]
- Legge GE, Hooven TA, Klitz TS, Stephen Mansfield JS, Tjan BS. Mr. Chips 2002: new insights from an ideal-observer model of reading. Vision Research. 2002;42(18):2219–2234. doi: 10.1016/s0042-6989(02)00131-1. [DOI] [PubMed] [Google Scholar]
- Legge GE, Klitz TS, Tjan BS. Mr. Chips: an ideal-observer model of reading. Psychological Review. 1997;104(3):524–553. doi: 10.1037/0033-295x.104.3.524. [DOI] [PubMed] [Google Scholar]
- Leon MI, Shadlen MN. Effect of Expected Reward Magnitude on the Response of Neurons in the Dorsolateral Prefrontal Cortex of the Macaque. Neuron. 1999;24(2):415–425. doi: 10.1016/s0896-6273(00)80854-5. http://doi.org/10.1016/S0896-6273(00)80854-5. [DOI] [PubMed] [Google Scholar]
- Liston DB, Stone LS. Effects of prior information and reward on oculomotor and perceptual choices. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2008;28(51):13866–13875. doi: 10.1523/JNEUROSCI.3120-08.2008. http://doi.org/10.1523/JNEUROSCI.3120-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louie K, Grattan LE, Glimcher PW. Reward value-based gain control: divisive normalization in parietal cortex. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2011;31(29):10627–10639. doi: 10.1523/JNEUROSCI.1237-11.2011. http://doi.org/10.1523/JNEUROSCI.1237-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludwig CJH. Temporal integration of sensory evidence for saccade target selection. Vision Research. 2009;49(23):2764–2773. doi: 10.1016/j.visres.2009.08.012. http://doi.org/10.1016/j.visres.2009.08.012. [DOI] [PubMed] [Google Scholar]
- Mack SC, Eckstein MP. Object co-occurrence serves as a contextual cue to guide and facilitate visual search in a natural viewing environment. Journal of Vision. 2011;11(9) doi: 10.1167/11.9.9. http://doi.org/10.1167/11.9.9. [DOI] [PubMed] [Google Scholar]
- Malcolm GL, Henderson JM. The effects of target template specificity on visual search in real-world scenes: evidence from eye movements. Journal of Vision. 2009;9(11):8.1–13. doi: 10.1167/9.11.8. http://doi.org/10.1167/9.11.8. [DOI] [PubMed] [Google Scholar]
- Michel M, Geisler WS. Intrinsic position uncertainty explains detection and localization performance in peripheral vision. Journal of Vision. 2011;11(1):18. doi: 10.1167/11.1.18. http://doi.org/10.1167/11.1.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morvan C, Maloney LT. Human Visual Search Does Not Maximize the Post-Saccadic Probability of Identifying Targets. PLoS Comput Biol. 2012;8(2):e1002342. doi: 10.1371/journal.pcbi.1002342. http://doi.org/10.1371/journal.pcbi.1002342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Najemnik J, Geisler WS. Optimal eye movement strategies in visual search. Nature. 2005;434(7031):387–391. doi: 10.1038/nature03390. http://doi.org/10.1038/nature03390. [DOI] [PubMed] [Google Scholar]
- Najemnik J, Geisler WS. Eye movement statistics in humans are consistent with an optimal search strategy. Journal of Vision. 2008;8(3) doi: 10.1167/8.3.4. http://doi.org/10.1167/8.3.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Najemnik J, Geisler WS. Simple summation rule for optimal fixation selection in visual search. Vision Research. 2009;49(10):1286–1294. doi: 10.1016/j.visres.2008.12.005. http://doi.org/10.1016/j.visres.2008.12.005. [DOI] [PubMed] [Google Scholar]
- Navalpakkam V, Koch C, Rangel A, Perona P. Optimal reward harvesting in complex perceptual environments. Proceedings of the National Academy of Sciences of the United States of America. 2010;107(11):5232–5237. doi: 10.1073/pnas.0911972107. http://doi.org/10.1073/pnas.0911972107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neider MB, Zelinsky GJ. Scene context guides eye movements during visual search. Vision Research. 2006;46(5):614–621. doi: 10.1016/j.visres.2005.08.025. http://doi.org/10.1016/j.visres.2005.08.025. [DOI] [PubMed] [Google Scholar]
- Peelen MV, Kastner S. A neural basis for real-world visual search in human occipitotemporal cortex. Proceedings of the National Academy of Sciences of the United States of America. 2011;108(29):12125–12130. doi: 10.1073/pnas.1101042108. http://doi.org/10.1073/pnas.1101042108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelli DG. Crowding: A cortical constraint on object recognition. Current Opinion in Neurobiology. 2008;18(4):445–451. doi: 10.1016/j.conb.2008.09.008. http://doi.org/10.1016/j.conb.2008.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson MF, Eckstein MP. Looking just below the eyes is optimal across face recognition tasks. Proceedings of the National Academy of Sciences. 2012;109(48):E3314–E3323. doi: 10.1073/pnas.1214269109. http://doi.org/10.1073/pnas.1214269109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson MF, Eckstein MP. Individual Differences in Eye Movements During Face Identification Reflect Observer-Specific Optimal Points of Fixation. Psychological Science. 2013a doi: 10.1177/0956797612471684. http://doi.org/10.1177/0956797612471684. [DOI] [PMC free article] [PubMed]
- Peterson MF, Eckstein MP. Learning optimal eye movements to unusual faces. Vision Research. 2013b doi: 10.1016/j.visres.2013.11.005. http://doi.org/10.1016/j.visres.2013.11.005. [DOI] [PMC free article] [PubMed]
- Peterson MS, Kramer AF. Attentional guidance of the eyes by contextual information and abrupt onsets. Perception & Psychophysics. 2001;63(7):1239–1249. doi: 10.3758/bf03194537. [DOI] [PubMed] [Google Scholar]
- Platt ML, Glimcher PW. Neural correlates of decision variables in parietal cortex. Nature. 1999;400(6741):233–238. doi: 10.1038/22268. http://doi.org/10.1038/22268. [DOI] [PubMed] [Google Scholar]
- Preston TJ, Guo F, Das K, Giesbrecht B, Eckstein MP. Neural representations of contextual guidance in visual search of real-world scenes. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2013;33(18):7846–7855. doi: 10.1523/JNEUROSCI.5840-12.2013. http://doi.org/10.1523/JNEUROSCI.5840-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao RPN, Zelinsky GJ, Hayhoe MM, Ballard DH. Eye movements in iconic visual search. Vision Research. 2002;42(11):1447–1463. doi: 10.1016/s0042-6989(02)00040-8. [DOI] [PubMed] [Google Scholar]
- Renninger LW, Coughlan J, Verghese P, Malik J. An information maximization model of eye movements. Advances in Neural Information Processing Systems. 2005;17:1121–1128. [PubMed] [Google Scholar]
- Rovamo J, Leinonen L, Laurinen P, Virsu V. Temporal integration and contrast sensitivity in foveal and peripheral vision. Perception. 1984;13(6):665– 674. doi: 10.1068/p130665. http://doi.org/10.1068/p130665. [DOI] [PubMed] [Google Scholar]
- Schoonveld WA, Eckstein MP. Models of eye movement strategies: Optimal searcher vs. optimal saccadic targeting. Journal of Vision. 2006;6(6):455–455. http://doi.org/10.1167/6.6.455. [Google Scholar]
- Schoonveld W, Eckstein M. Optimal searcher, saccadic targeting model, and human eye movements during search: Effects of target visibility maps. Journal of Vision. 2007;7(9):635–635. http://doi.org/10.1167/7.9.635. [Google Scholar]
- Schütz AC, Trommershäuser J, Gegenfurtner KR. Dynamic integration of information about salience and value for saccadic eye movements. Proceedings of the National Academy of Sciences of the United States of America. 2012;109(19):7547–7552. doi: 10.1073/pnas.1115638109. http://doi.org/10.1073/pnas.1115638109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimozaki SS, Schoonveld WA, Eckstein MP. A unified Bayesian observer analysis for set size and cueing effects on perceptual decisions and saccades. Journal of Vision. 2012;12(6) doi: 10.1167/12.6.27. http://doi.org/10.1167/12.6.27. [DOI] [PubMed] [Google Scholar]
- Stritzke M, Trommershäuser J, Gegenfurtner KR. Effects of salience and reward information during saccadic decisions under risk. Journal of the Optical Society of America. A, Optics, Image Science, and Vision. 2009;26(11):B1–13. doi: 10.1364/JOSAA.26.0000B1. [DOI] [PubMed] [Google Scholar]
- Sugrue LP, Corrado GS, Newsome WT. Matching behavior and the representation of value in the parietal cortex. Science (New York, NY) 2004;304(5678):1782–1787. doi: 10.1126/science.1094765. http://doi.org/10.1126/science.1094765. [DOI] [PubMed] [Google Scholar]
- Sullivan BT, Johnson L, Rothkopf CA, Ballard D, Hayhoe M. The role of uncertainty and reward on eye movements in a virtual driving task. Journal of Vision. 2012;12(13):19. doi: 10.1167/12.13.19. http://doi.org/10.1167/12.13.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavassoli A, van der Linde I, Bovik AC, Cormack LK. Eye movements selective for spatial frequency and orientation during active visual search. Vision Research. 2009;49(2):173–181. doi: 10.1016/j.visres.2008.10.005. http://doi.org/10.1016/j.visres.2008.10.005. [DOI] [PubMed] [Google Scholar]
- Theeuwes J, Belopolsky AV. Reward grabs the eye: oculomotor capture by rewarding stimuli. Vision Research. 2012;74:80–85. doi: 10.1016/j.visres.2012.07.024. http://doi.org/10.1016/j.visres.2012.07.024. [DOI] [PubMed] [Google Scholar]
- Torralba A, Oliva A, Castelhano MS, Henderson JM. Contextual guidance of eye movements and attention in real-world scenes: the role of global features in object search. Psychological Review. 2006;113(4):766–786. doi: 10.1037/0033-295X.113.4.766. http://doi.org/10.1037/0033-295X.113.4.766. [DOI] [PubMed] [Google Scholar]
- Trommershäuser J, Glimcher PW, Gegenfurtner KR. Visual processing, learning and feedback in the primate eye movement system. Trends in Neurosciences. 2009;32(11):583–590. doi: 10.1016/j.tins.2009.07.004. http://doi.org/10.1016/j.tins.2009.07.004. [DOI] [PubMed] [Google Scholar]
- Verghese P. Active search for multiple targets is inefficient. Vision Research. 2012 doi: 10.1016/j.visres.2012.08.008. http://doi.org/10.1016/j.visres.2012.08.008. [DOI] [PubMed]
- Watanabe M. Reward expectancy in primate prefrontal neurons. Nature. 1996;382(6592):629–632. doi: 10.1038/382629a0. http://doi.org/10.1038/382629a0. [DOI] [PubMed] [Google Scholar]
- Zelinsky GJ. Using eye saccades to assess the selectivity of search movements. Vision Research. 1996;36(14):2177–2187. doi: 10.1016/0042-6989(95)00300-2. [DOI] [PubMed] [Google Scholar]
- Zhang S, Eckstein MP. Evolution and optimality of similar neural mechanisms for perception and action during search. PLoS Computational Biology. 2010;6(9) doi: 10.1371/journal.pcbi.1000930. http://doi.org/10.1371/journal.pcbi.1000930. [DOI] [PMC free article] [PubMed] [Google Scholar]
Appendix References
- 1.Burgess AE, Wagner RF, Jennings RJ, Barlow HB. Efficiency of human visual signal discrimination. Science. 1981;214:93–94. doi: 10.1126/science.7280685. [DOI] [PubMed] [Google Scholar]
- 2.Barrett HH. Objective assessment of image quality: effects of quantum noise and object variability. Journal of the Optical Society of America A. 1990;7:1266–1278. doi: 10.1364/josaa.7.001266. [DOI] [PubMed] [Google Scholar]
- 3.Eckstein MP, Abbey CK, Bochud FO. A practical guide to model observers for visual detection in synthetic and natural noisy images. In: Beutel J, Kundel HL, Van Metter RL, editors. Handbook of Medical Imaging: Volume 1, Physics and Psychophysics. Bellingham: SPIE Press; 2000. pp. 593–628. [Google Scholar]
- 4.Murray RF, Bennett PJ, Sekuler AB. Classification images predict absolute efficiency. Journal of Vision. 2005;5:139–149. doi: 10.1167/5.2.5. [DOI] [PubMed] [Google Scholar]