Interactions between climatic changes and intervention effects on malaria spatio-temporal dynamics in Uganda

Abstract

Background

Although malaria burden in Uganda has declined since 2009 following the scale-up of interventions, the disease is still the leading cause of hospitalization and death. Transmission remains high and is driven by suitable weather conditions. There is a real concern that intervention gains may be reversed by climatic changes in the country. In this study, we investigate the effects of climate on the spatio-temporal trends of malaria incidence in Uganda during 2013–2017.

Methods

Bayesian spatio-temporal negative binomial models were fitted on district-aggregated monthly malaria cases, reported by two age groups, defined by a cut-off age of 5 years. Weather data was obtained from remote sensing sources including rainfall, day land surface temperature (LSTD) and night land surface temperature (LSTN), Normalized Difference Vegetation Index (NDVI), altitude, land cover, and distance to water bodies. Spatial and temporal correlations were taken into account by assuming a conditional autoregressive and a first-order autoregressive process on district and monthly specific random effects, respectively. Fourier trigonometric functions modeled seasonal fluctuations in malaria transmission. The effects of climatic changes on the malaria incidence changes between 2013 and 2017 were estimated by modeling the difference in time varying climatic conditions at the two time points and adjusting for the effects of intervention coverage, socio-economic status and health seeking behavior.

Results

Malaria incidence declined steadily from 2013 to 2015 and then increased in 2016. The decrease was by over 38% and 20% in children <5 years and individuals ≥5 years, respectively. Temporal trends depict a strong bi-annual seasonal pattern with two peaks during April–June and October–December. The annual average of rainfall, LSTD and LSTN increased by 3.7 mm, 2.2 °C and 1.0 °C, respectively, between 2013 and 2017, whereas NDVI decreased by 6.8%. On the one hand, the increase in LSTD and decrease in NDVI were associated with a reduction in the incidence decline. On the other hand, malaria interventions and treatment seeking behavior had reverse effects, that were stronger compared to the effects of climatic changes. Important interactions between interventions with NDVI and LSTD suggest a varying impact of interventions on malaria burden in different climatic conditions.

Conclusion

Climatic changes in Uganda during the last five years contributed to a favorable environment for malaria transmission, and had a detrimental effect on malaria reduction gains achieved through interventions scale-up efforts. The NMCP should create synergies with the National Meteorological Authority with an ultimate goal of developing a Malaria Early Warning System to mitigate adverse climatic change effects on malaria risk in the country.

1. Background

Malaria is the most common parasitic infection worldwide accounting for over 210 million clinical cases and almost half a million deaths annually (World Health Organisation, 2017). The global campaign rolled out by the World Health Organization in the aftermath of the collapse of the malaria eradication campaign has accelerated the scale-up of vector control interventions and case management with Artemisinin Combination Therapies (ACTs) leading to a significant decline in malaria morbidity and mortality in endemic countries during 2000–2015 (Bhatt et al., 2015).

Nonetheless, malaria burden remains high in the sub-Saharan Africa (SSA) region, where P. falciparum causes the most severe clinical form of the disease (World Health Organization, 2016). Almost half a million deaths occur annually mostly in children <5 years old (World Health Organization, 2016).

In Uganda, malaria transmission remains very high and the disease ranks as the number one cause for hospitalization and death in the country (Katureebe et al., 2016), despite the reduction in parasitaemia prevalence achieved during 2009 and 2014 (Ssempiira et al., 2017). On the one hand, this high transmission is enabled by a suitable climate that is characterized by ample rainfall, optimal temperature and humidity that enhances mosquito breeding and survival of the vector and parasite (National Malaria Control Program, 2016). A number of field and laboratory studies are adduced to this effect. Temperature co-determines the duration of parasite development within the vector, larval development time and vector survival (Tanser et al., 2003). Optimum temperature range between 28 °C and 32 °C (Christiansen-Jucht et al., 2015). Very low (<17 °C) or high (>35 °C) temperatures slow down the development of the vector or increase its mortality (Bayoh and Lindsay, 2003). On the other hand, rainfall contributes to the formation and continuation of mosquito breeding sites, thus to the increase of the vector population (Thomson et al., 2017). Immature stages of the vector, i.e., eggs, larvae and pupae are aquatic forms and require suitable aquatic environments in which they develop prior to the emergence of adults from the pupae. Adult mosquitoes are dependent on moisture, as they are predisposed to dehydration in dry conditions having a direct negative effect on their survival (Christiansen-Jucht et al., 2015).

Therefore, changes in temperature and rainfall are likely to affect the natural habitats of mosquitoes, alter the density of the vector while potentially exposing previously low endemic settings to malaria (Tanser et al., 2003). In Uganda, the occurrence of extreme weather conditions in the recent past such as long droughts and flooding has had an immediate impact on malaria transmission resulting in aberrations from the normal seasonal pattern in affected areas (Cox et al., 2007; Lindblade et al., 1999). Whether this short-term variability has had long-term ramifications in the country is not yet established. For effective and sustainable long-term malaria programming, it is important to investigate the potential effects of climate changes on malaria burden in consideration of the climate sensitivity of vector and parasite, and the ubiquitous human-induced global warming.

A number of studies employing either mechanistic or statistical modeling frameworks have investigated climatic change effects on the distribution and intensity of malaria risk in different settings, but have yielded dissimilar results. In some studies, a linkage was established between climatic change and the exacerbation of the risk (Alonso et al., 2011; Caminade et al., 2014; Endo et al., 2017; Ermert et al., 2013; Ngarakana-Gwasira et al., 2016a; Tompkins and Caporaso, 2016), while in others the climatic effect was not established and instead the increasing malaria burden was attributed to other factors such as drug resistance, failure of vector control operations and changes in land use (Hay et al., 2002). Interpretations of findings from studies that employed a statistical modeling framework are often limited by the absence of good quality data stemming from the weak and fragmented nature of national health information systems in malaria-endemic countries (Yeka et al., 2012).

The Uganda Health Management Information System (HMIS) was established in the early 1990s to facilitate reporting of routine health facility data to the Ministry of Health (MoH). The system was upgraded from a paper-based reporting and storage system to an electronic web-based system in 2011 giving way to the District Health Information Software System version 2 (DHIS2) (Kiberu et al., 2014). As a result of this development, health facility data completeness and timeliness increased from 36% and 22% to >85% and 77%, respectively (Kiberu et al., 2014). This routine data provide an opportunity to investigate inter and intra-annual variation of malaria risk in the country and provides a wealth of information for monitoring and evaluation of malaria programming activities to support evidence-based decision making. The country's adoption of ‘Test and Treat’ campaign is helping to increase the number of health facility malaria cases confirmed by the rapid diagnostic tests (RDTs) (National Malaria Control Program, 2016).

Our study investigates the effects of climatic factors on the spatio-temporal patterns of malaria incidence in Uganda during 2013–2017 and assesses the relationship between climatic changes and changes in malaria incidence between 2013 and 2017 taking into account the coverage of control interventions, socio-economic factors, and malaria treatment seeking behavior patterns. Bayesian spatio-temporal negative binomial conditional autoregressive (CAR) models were fitted on district-aggregated monthly malaria cases reported in the DHIS2. Our results provide important information to National Malaria Control Programme (NMCP) for evidence-based decision making in malaria control programming in view of changing climatic conditions to sustain achieved gains and achieve elimination.

2. Materials and methods

2.1. Settings

Uganda is located in East Africa on a large plateau in the Great Lakes region. Its altitude varies between 1300 and 1500 m above sea level, and the mean annual temperature ranges from 16 °C to 30 °C. It has a diverse vegetation, mainly comprising of tropical rain forests in the South, wooded savanna in Central, and semi-arid in the North and North East regions. There are two rainy seasons; the first during March–May and the second from August to November. The population is 37 million, of which 18% are children <5 years (Uganda Bureau of Statistics, 2016). The country is divided into 112 districts and covers an area of 241,039 km².

Malaria transmission rates are some of the highest in the world (President's Malaria Initiative, 2017). Transmission is stable in 95% of the country. Low and unstable transmission is mainly present in the highland areas (>2500 m) (Ministry of Health, 2014). Malaria is responsible for 33% of outpatient visits and 30% of hospitalized cases. Anopheles gambiae s.l. is the dominant vector species followed by Anopheles funestus which is commonly found in areas having permanent water bodies with emergent vegetation. These two vectors are strongly endophagic and endophilic that is, feeding indoors and resting on walls after feeding, which makes indoor vector control approaches effective. Health facilities in Uganda are classified and graded according to their service scope and size of population they serve in the following (descending) order; hospitals, Health Center (HC) IVs, HCIIIs and HCIIs. By December 2017, there were a total of 5418 health facilities; 160 hospitals, 197 HCIVs, 1289 HCIIIs and 3772 HCIIs (President's Malaria Initiative, 2017).

2.2. Data sources

2.2.1. Malaria cases

Monthly data on confirmed malaria cases by RDT was extracted from the DHIS2 covering the period of January 2013 to December 2017. The data were reported by two age groups: children <5 years and individuals ≥5 years. Malaria incidence in each age group was estimated by dividing the district aggregated malaria cases by the district age group-specific population. The population size for each month was based on data from the national housing and population census of 2014 adjusted for the annual population growth rate (Uganda Bureau of Statistics, 2016).

2.2.2. Environmental/climatic, interventions, socio-economic, and malaria treatment seeking behavior data

Environmental and climatic data were downloaded from remote sensing sources for the period October 2012–December 2017. Day Surface Temperature (LSTD) and night Land Surface Temperature (LSTN), Normalized Difference Vegetation Index (NDVI), and land cover were extracted from Moderate Resolution Imaging Spectroradiometer (MODIS) at a spatial resolution of 1 × 1 km² and a temporal resolution of 8 days, 16 days and annually, respectively. Dekadal rainfall data was obtained from the US early warning and environmental monitoring system at 8 × 8 km² resolution (Early Warning and Environmental Monitoring Program, 2016). Altitude was based on digital elevation model obtained from the Shuttle Radar Topographic Mission (SRTM). The ESRI's ArcGIS 10.2.1 software was used to estimate distances between major water bodies and district centroids (http://www.esri.com/).

Data on insecticide treated net (ITN) coverage and ACT use were obtained from the Malaria Indicator Survey (MIS) of 2014–15 (Uganda Bureau of Statistics and ICF International, 2015) and from the Uganda Demographic Health Survey (DHS) of 2016. Indoor residual spraying (IRS) was not included in the analysis because of its sparse distribution in the majority of the districts owing to the targeted implementation strategy used in its deployment (National Malaria Control Program, 2016). Due to lack of monitoring and evaluation data outside the survey periods, we assumed that intervention coverage of 2013–14 is the same as that of 2014–15 (reported in MIS 2014–15) and the coverage of 2017 as similar to that of 2016 (available in DHS 2016). Six ITN coverage indicators were defined from the MIS 2014–15 and DHS 2016, corresponding to three ownership and three use indicators defined by Roll Back Malaria (RBM) namely; proportion of households with at least one ITN, proportion of households with at least one ITN for every two people, proportion of population with access to an ITN in their household, proportion of the population that slept under an ITN the previous night, proportion of children under five years old who slept under an ITN the previous night, proportion of existing ITNs used the previous night. Also, the wealth score computed from household possessions captured in the MIS 2014–15 and DHS 2016 questionnaires was used as a socio-economic proxy. A wealth index of five quintiles was generated from the score following the DHS methodology (Vyas and Kumaranayake, 2006).

We also considered that malaria cases seen at formal health facilities in Uganda are a fraction of the total cases due to low health seeking behavior (Ndyomugyenyi et al., 2007). We obtained the proportion of malaria treatment seeking behavior reported in the most recent MIS survey (Uganda Bureau of Statistics and ICF International, 2015). Model formulation details are given in the appendix.

2.2.3. Statistical analysis

Time series plots were employed to describe inter and intra-annual variation of malaria incidence and temporal variation of environmental and climatic factors during the study period.

Biological considerations of the malaria transmission cycle suggest that there is elapsing lag period between weather suitable for malaria transmission and occurrence of cases which is related to effects on the duration of the sporogony cycle i.e. the development of the parasite within the mosquito (Teklehaimanot et al., 2004). We took this into account by creating lagged variables for the time varying predictors (i.e. rainfall, NDVI, day LST and night LST). In particular, three analysis variables were constructed for each climatic factor by averaging its values over the following periods: the current and the previous month (lag1), the current and the two previous months (lag2) and the current and the three previous months (lag3). Categorical variables were generated based on tertiles of the variables' distributions since the relationship between malaria and environmental predictors is not always linear (Bayoh and Lindsay, 2003).

Bayesian spatio-temporal negative binomial models (Banerjee and Carlin, 2014) were fitted on the incidence data. Random effects at district level were used to model spatial correlation via CAR formulations (Banerjee and Fuentes, 2012). Temporal correlation was taken into account by monthly random effects modeled by autoregressive processes. Models were adjusted for seasonality by including Fourier terms as a mixture of two cycles with periods of six and 12 months, respectively (Rumisha et al., 2013). A yearly trend was fitted to estimate changes of the incidence rates over time. Bayesian variable selection implemented within the spatio-temporal model was applied to identify the most important ITN coverage indicator and lagged climatic factors with their functional form (i.e. linear or categorical). For ITN indicators, a categorical variable was introduced into the model taking values 1 to 7, (six values corresponding to the six indicators and the seventh defining the absence of all indicators from the model). The probabilities of the above values were treated as parameters and used to estimate the inclusion probabilities of the ITN indicator into the model, i.e. inclusion probability. Similarly, for each climatic factor, we introduced a categorical variable taking three values corresponding to its absence, or inclusion into the model in linear or categorical form. An ITN indicator or climatic factor was selected if its posterior inclusion probability was above 50%.

Intervention and wealth score data from the MIS and DHS, summarized at district level, may not provide reliable estimates of the coverage because the survey is designed to produce reliable estimates at country and regional levels (Banerjee and Fuentes, 2012). Therefore, we estimated coverage at district level by fitting Bayesian CAR binomial and Gaussian models for intervention and wealth score data, respectively. The details of the model formulation are given in the appendix.

The effects of climatic changes on the decline in malaria incidence between 2013 and 2017 were modeled as a function of the difference in climatic conditions between the respective years adjusted for the effects of intervention coverage, socio-economic status and health seeking behavior in 2017.

Models were implemented in OpenBUGS and parameters were estimated using Markov chain Monte Carlo (MCMC) simulation. We ran a two-chain algorithm for 200,000 iterations with an initial burn-in period of 5000 iterations. Convergence was assessed by visual inspection of trace and density plots and analytically by the Gelman and Rubin diagnostic (Raftery and Lewis, 1992). Parameters were summarized by their posterior medians and 95% Bayesian Credible Intervals (BCIs). Maps of estimated, smoothed incidence rates were produced in ESRI's ArcGIS 10.2.1 (http://www.esri.com/). Details on model formulations are provided in the appendix.

3. Results

3.1. Descriptive results

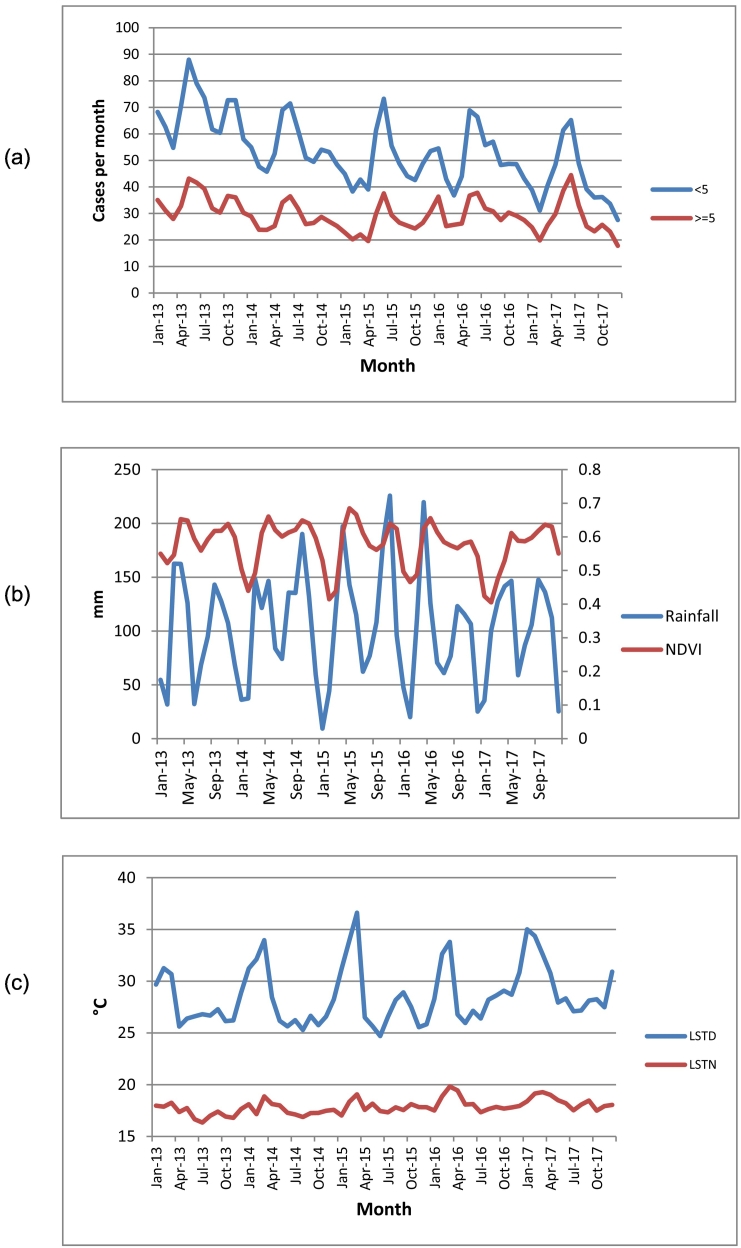
Overall, a total number of 71,664,624 malaria cases were reported from all health facilities during January 2013–December 2017. On annual basis, the number of reported cases declined from 16,364,773 in 2013 to 13,635,391 in 2014 and to 12,967,905 in 2015, but then increased in 2016 and 2017 to 15,016,031 and 13,680,523, respectively. This represents annual declines of 17%, 21%, 8% and 16% in 2014, 2015, 2016 and 2017, respectively compared to 2013. Throughout the years during the study period, malaria incidence in children <5 years was almost twice higher compared to individuals ≥5 years (Fig. 1a).

Fig. 1.

Monthly time series; (a) malaria incidence in children <5 years and individuals ≥5 years, (b) mean rainfall, (c) mean temperatures (LSTD and LSTN).

Temporal trends of incidence in both age groups depict a strong bi-annual seasonal pattern with two peaks during April–June and October–December (Fig. 1a). Similarly, climatic conditions are characterized by a bi-modal seasonality trend that is heavily influenced by the rainfall pattern marked by two rainfall seasons during March–May and August–November (Fig. 1b). The peaks of the rainfall seasons occur in the months of April and November for the first short and second longer season, respectively. Monthly rainfall increased from an average of 98.3 mm in 2013 to 115.3 mm in 2015, then decreased to 91.9 mm in 2016 and increased again to 102.1 mm in 2017. NDVI declined steadily from an average of 0.59 in 2013 to 0.55 in 2017, a reduction of 0.04 (6.8%).

Monthly LSTD and LSTN increased steadily from an average of 27.7 °C and 17.3 °C in 2013 to 29.8 °C and 18.3 °C in 2017 –an average increase of 2.1 °C and 1 °C, respectively (Fig. 1c).

The temporal variation of incidence of both age groups was closely related with that of climatic factors. Increases in land surface temperature initially favored high incidence in both age groups, but very high temperatures were followed by declines in incidence in both age groups. Also, increases and decreases in rainfall had a reciprocal though delayed influence on incidence in both age groups (Fig. 1a).

Correlation between monthly crude incidence rates and climatic averages differed in the two age groups in terms of magnitude and direction (Table 1). For example, malaria incidence is significantly positively correlated with rainfall of up to three months lags in children <5 years. For individuals ≥5 years, the correlation is positive, though only significant for lags of month one and month three. Correlation between incidence and NDVI for both age groups is significantly positive for the shorter lags (months 0–2), but significantly negative for longer lags.

Table 1.

Pearson correlation between mean monthly crude malaria incidence and climatic averages.

Climatic factor	<5 years				≥ 5 years
	Lag0	Lag1	Lag2	Lag3	Lag0	Lag1	Lag2	Lag3
Rainfall	0.05a	0.17a	0.18a	0.06a	0.01	0.14a	0.17	0.05a
LSTD	0.02	0.03a	0.14a	0.26a	−0.07a	−0.07a	0.04a	0.18a
LSTN	0.23a	0.27a	0.31a	0.33a	0.02	0.06a	0.10a	0.12a
NDVI	0.05a	0.06a	−0.01	−0.10a	0.13a	0.15a	0.08a	−0.02

^aStatistically significant.

3.2. Model-based analysis

3.2.1. Variable selection

Bayesian variable selection (Table 2) identified the same predictors for both age groups with the exception of the lag effects of rainfall. Regarding the climatic proxies with the lag effects, the highest inclusion probabilities were estimated for the categorical forms of LSTN (average of current and three previous months), LSTD (current and previous month), NDVI (current and two previous months) and rainfall (current and three previous months for children <5 yrs.; current and previous month for older individuals). Among ITN indicators, the proportion of households with at least one ITN was selected.

Table 2.

Posterior inclusion probabilities for climatic covariates and ITN coverage indicators.

Indicator	Probability of inclusion (%)
	<5 years	≥ 5 years
Climatic factors
Rainfall
Rain_01	0.0	0.0
Rain_01a	0.0	100.0
Rain_012	0.0	0.0
Rain_012a	0.0	0.0
Rain_0123	0.0	0.0
Rain_0123a	100.0	0.0
NDVI
NDVI_01	0.0	0.0
NDVI_01a	0.0	0.0
NDVI_012	0.0	0.0
NDVI_012a	100.0	100.0
NDVI_0123	0.0	0.0
NDVI_0123a	0.0	0.0
LSTD
LSTD_01	0.0	0.0
LSTD_01a	100.0	100.0
LSTD_012	0.0	0.0
LSTD_012a	0.0	0.0
LSTD_0123	0.0	0.0
LSTD_0123a	0.0	0.0
LSTN
LSTN_01	0.0	0.0
LSTN_01a	0.0	0.0
LSTN_012	0.0	0.0
LSTN_012a	0.0	0.0
LSTN_0123	0.0	0.0
LSTN_0123a	100.0	100.0
Altitude
Altitude	100.0	100.0
Altitudea	0.0	0.0
Distance to water bodies
Distance to water bodies	0.0	0.0
Distance to water bodiesa	100.0	100.0
Interventions
Proportion of households with at least one ITN	100.0	100.0
Proportion of households with at least one ITN for every two people	0.0	0.0
Proportion of population with access to an ITN in their household	0.0	0.0
Proportion of the population that slept under an ITN the previous night	0.0	0.0
Proportion of children under five years old who slept under an ITN the previous night	0.0	0.0
Proportion of existing ITNs used the previous night	0.0	0.0

In bold: variables with highest inclusion probability that included in the final Bayesian spatio-temporal model.

^aCategorical.

3.2.2. Effects of climatic factors on spatio-temporal changes in malaria incidence

Table 3 presents spatio-temporal model-based estimates of the effects of climatic factors on spatio-temporal changes in malaria incidence adjusted for interventions, socio-economic and health seeking confounders. The results were similar in both age groups. Increases in rainfall, NDVI, and LSTD were associated with an increase in malaria incidence. However, very high LSTD (above 29 °C) was related with an incidence decrease. Altitude and distance to water bodies were negatively related to malaria incidence. More so, malaria burden was higher in crop cultivated areas compared to other forms of land cover.

Table 3.

Effects of climatic factors and interventions on the spatio-temporal patterns of malaria incidence estimated from Bayesian negative binomial models adjusted for interventions, socio-economic and health seeking behavior proxies.

Predictor	Children <5 years	Individuals 5 years and above
	IRR (95%BCI)	IRR (95%BCI)
Rainfall (mm) (≤77.0)	1	1
77.1–126.0	1.09 (1.07, 1.13)a	1.08 (1.05, 1.10)a
126.1–354	1.13 (1.11, 1.17)a	1.09 (1.06, 1.13)a
NDVI (≤0.55)	1	1
0.56–0.66	1.13 (1.10, 1.16)a	1.18 (1.14, 1.23)a
0.67–0.81	1.19 (1.14, 1.24)a	1.28 (1.21, 1.32)a
LSTD (°C) (≤26.5)	1	1
26.6–29.3	1.06 (1.03, 1.09)a	1.04 (1.01, 1.06)a
29.4–44.6	0.94 (0.88, 0.98)a	0.94 (0.92, 0.97)a
LSTN (°C) (≤17.1)	1	1
17.2–18.9	1.00 (0.93, 1.11)	1.00 (0.97, 1.04)
19.0–23.3	1.00 (0.94, 1.10)	1.00 (0.95, 1.05)
Altitude	0.78 (0.72, 0.79)a	0.90 (0.86, 0.94)a
Land cover (Others)	1	1
Crops	1.07 (1.04, 1.10)a	1.10 (1.05, 1.17)a
Distance to water bodies (km)(≤16.9)	1	1
17.0–45.8	1.01 (0.93, 1.06)	0.87 (0.83, 0.90)a
46.0–152.6	0.86 (0.83, 0.90)	0.89 (0.80, 0.91)a
Interventionsc
ITNs	0.27 (0.21, 0.38)a	1.19 (1.00, 1.20)
ACTs	0.70 (0.62, 0.78)a	0.54 (0.42, 0.63)a
Interactions
Rainfall(mm) (≤77.0) ∗ ITNs	1	1
(77.1–126.0) ∗ ITNs	1.04 (0.67, 1.60)	1.19 (0.78, 1.79)
(126.1–354) ∗ ITNs	0.79 (0.50, 1.26)	0.82 (0.52, 1.28)
NDVI (≤0.55) ∗ ITNs	1	1
(0.56–0.66) ∗ ITNs	1.60 (1.03, 2.46)a	1.84 (1.21, 2.80)a
(0.67–0.81) ∗ ITNs	3.20 (1.88, 5.43)a	3.08 (1.85, 5.13)a
LSTD (°C) (≤26.5) ∗ ITNs	1	1
(26.6-29.3) ∗ ITNs	1.47 (1.05, 2.31)a	1.82 (1.18, 2.82)a
(29.4–44.6) ∗ ITNs	1.70 (1.03, 2.80)a	2.46 (1.52, 3.97)a
Rainfall(mm) (≤77.0) ∗ ACTs	1	1
(77.1–126.0) ∗ ACTs	1.00 (0.76, 1.30)	1.10 (0.85, 1.42)a
(126.1–354) ∗ ACTs	1.11 (0.82, 1.49)	1.26 (0.95, 1.67)a
NDVI (≤0.55) ∗ ACTs	1	1
(0.56–0.66) ∗ ACTs	1.12 (1.07, 1.48)a	1.05 (1.01, 1.37)a
(0.67–0.81) ∗ ACTs	1.26 (1.13, 1.72)a	1.18 (1.06, 1.59)a
LSTD (°C) (≤26.5) ∗ ACTs	1	1
(26.6–29.3) ∗ ACTs	1.18 (1.05, 1.55)a	1.37 (1.06, 1.77)a
(29.4–44.6) ∗ ACTs	0.91 (0.68, 0.97)a	1.24 (0.92, 1.66)
Wealth index (Poorest)	1	1
Poorer	0.82 (0.77, 0.88)a	1.09 (0.99, 1.14)
Middle	0.71 (0.67, 0.74)a	0.86 (0.83, 0.90)a
Richer	0.70 (0.68, 0.76)a	0.83 (0.78, 0.87)a
Richest	0.78 (0.73, 0.86)a	0.91 (0.79, 0.95)a
Malaria treatment seeking behavior	0.47 (0.40, 0.53)a	0.54 (0.45, 0.60)a

Temporal trendb	Median (95%BCI)	Median (95%BCI)
2014	−0.02 (−0.03, −0.01)	−0.18 (−0.21, −0.16)
2015	−0.04 (−0.06, −0.04)	−0.39 (−0.42, −0.37)
2016	−0.03 (−0.05, −0.02)	−0.15 (−0.20, −0.10)
2017	−0.09 (−0.12, −0.07)	−0.33 (−0.40, −0.29)
Seasonal parameters
Amplitude
Annual	0.11 (0.04, 0.17)	0.31 (0.19, 0.36)
Semi-annual	0.14 (0.07, 0.18)	0.08 (0.03, 0.11)
Phase (months)
Annual	2.57 (1.76, 5.90)	2.40 (1.90, 5.63)
Semi-annual	2.83 (1.19, 5.81)	1.76 (0.73, 4.64)
Spatio-temporal parameters
Spatial variance	1.42 (1.06, 1.81)	1.27 (0.97, 1.66)
Temporal variance	18.15 (12.21, 26.06)	18.61 (12.44, 27.06)
Temporal correlation	0.94 (0.90, 0.98)	0.98 (0.95, 0.99)
Dispersion	6.84 (6.61, 7.09)	7.95 (7.68, 8.24)

^aStatistically important effect.

^bVersus 2013.

^cCoverage was modeled on the scale of 0 to 1, therefore one unit increase in coverage corresponds to a 100% increase which implies a shift of the current by 100%.

A 100% increase in the proportion of households having at least one ITN was associated with a decline in malaria incidence in children <5 years by 73% (95%BCI: 62–79%). The effect of ITN coverage was also protective in older individuals but not statistically important. A 100% increase in the proportion of fevers treated with ACTs was related with a reduction in incidence by 30% (95%BCI: 22–38%) in children <5 years and by 46% (95%BCI: 37–58%) in older individuals. Socio-economic status was an important predictor of malaria incidence in both age groups, but the effect was much stronger in the younger group. The incidence is lower in those from higher socio-economic levels. A higher proportion of malaria treatment seeking behavior was related with a reduction in spatio-temporal trends of incidence in both age groups.

Results also suggested important interactions between interventions with land surface temperature and NDVI.

Temporal variation in incidence was much higher than the spatial variability. The amplitude values indicate that malaria incidence variation was almost twice as high in children <5 years compared to older individuals. The seasonality phase suggests that the peak of the malaria incidence occurs during February to May, in both age groups.

3.2.3. Space-time patterns of malaria incidence

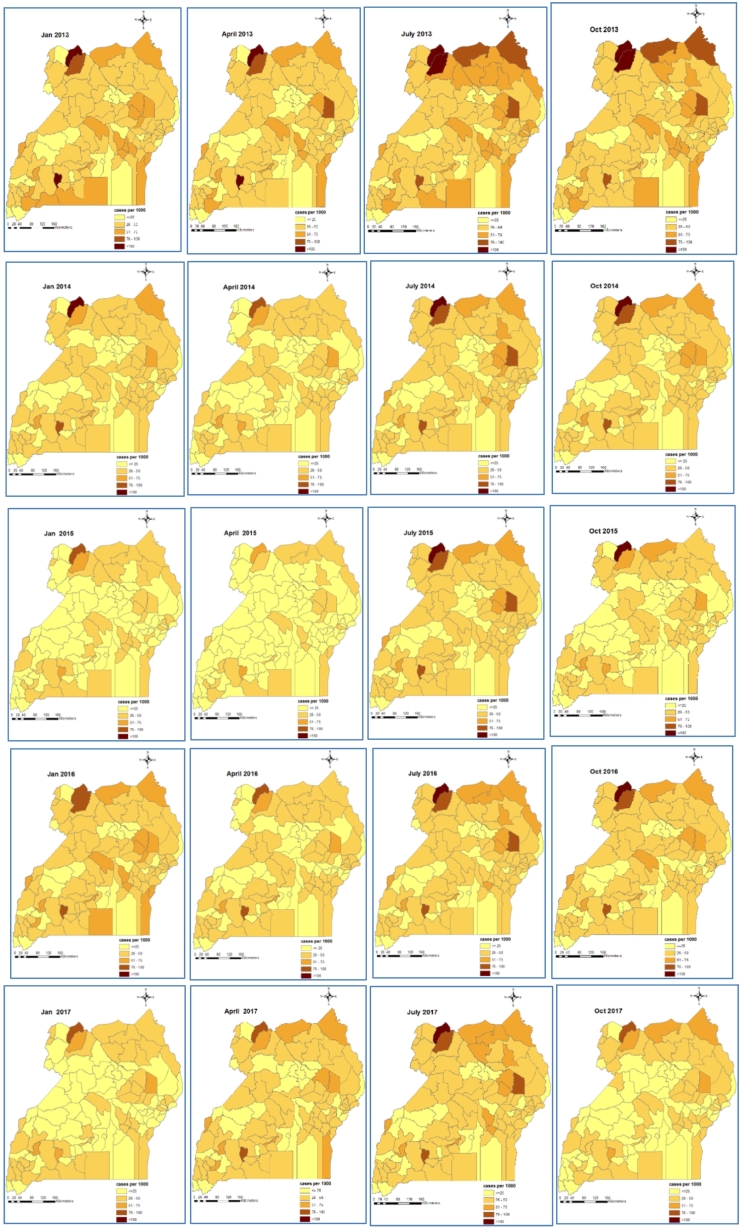
Maps of smoothed malaria incidence estimated from the Bayesian models are presented in Fig. 2, Fig. 3 for the first month of each quarter and study year (i.e. January, April, July and October). The high malaria burden districts throughout the study period were located in the northern and eastern Uganda. In children <5 years, the burden of malaria was very high in 2013 with most districts having a monthly burden of >75 cases per 1000 persons. In 2014, a reduction in malaria burden is visible across the country with the exception of the northern districts during the third quarter. In 2015, incidence further declined across all districts, reaching an overall district average of <55 cases per 1000 persons, and for the first time, most of the high burdened districts in the northern region experienced a burden of <100 cases per 1000 persons. However, in 2016 a resurgence was observed, especially in the North East region. The highest reduction occurred in 2017, with the majority of the districts carrying a burden of 25–50 cases per 1000 persons.

Fig. 2.

Bayesian model-based space-time patterns of malaria incidence in children <5 years.

Fig. 3.

Bayesian model-based space-time patterns of malaria incidence in individuals ≥5 years.

Individuals ≥5 years had a much lower and a more homogeneous distributed malaria burden throughout the country with minor differences among districts. In 2013, incidence rates in individuals ≥5 years varied between 25 and 50 cases per 1000 persons per month across all districts. A decline was observed through 2014 and 2015. However, incidence rates in this age group also increased in 2016 but declined in 2017 as was the case for children <5 years.

3.2.4. Effects of climatic changes on malaria incidence decline

Table 4 presents estimates of the effects of climatic changes on the decline in malaria incidence between 2013 and 2017. Malaria incidence decreased by over 38% and over 20% in children <5 years and individuals ≥5 years, respectively. In the same period, rainfall, LSTD, LSTN increased by an average of 3.7 mm, 2.2 °C and 1.0 °C, respectively, while NDVI decreased by 6.8%. The increase in LSTD and decrease in NDVI during the study period were associated with a decrease in the reduction of malaria incidence rates in both age groups.

Table 4.

Posterior estimates for the adjusted effect of climatic changes on malaria incidence rates decline obtained from the Bayesian spatio-temporal negative binomial model.

Covariate	<5 years	≥ 5 years
	IRR (95%BCI)	IRR (95%BCI)
Climatic changes
Difference in rainfall	1.01 (0.98, 1.04)	1.00 (0.97, 1.03)
Difference in LSTD	0.96 (0.92, 0.98)a	0.93 (0.90, 0.96)a
Difference in LSTN	0.98 (0.96, 1.02)	0.99 (0.97, 1.02)
Difference in NDVI	0.95 (0.92, 0.98)a	0.94 (0.91, 0.98)a
Interventions
ITN	1.20 (1.06, 1.48)a	1.79 (1.53, 1.99)a
ACTs	1.35 (1.13, 1.60)a	1.24 (1.06, 1.45)a
Proportion of malaria treatment seeking behavior	1.32 (1.12, 1.54)a	1.60 (1.39, 1.84)a
Wealth score	1.05 (1.02, 1.08)a	1.11 (1.08, 1.14)a
Other parameters
Spatial variance	1.15 (0.86, 1.52)	1.35 (1.00, 1.81)
Temporal variation	5.27 (2.12, 10.51)	5.73 (2.54, 11.06)
Dispersion	4.91 (4.54, 5.27)	6.01 (5.58, 6.50)

^aStatistically important effect.

However, the effect of rainfall increase between 2013 and 2017 was associated with an increase in malaria incidence rates reduction, although not statistically important. The coverage of malaria interventions and the socio-economic status in 2016 (year with the most recent data) were included in the model to adjust for the effects of climatic changes. ITNs and ACTs were associated with an increase in the reduction of incidence rates of 19% (95%BCI: 18%–29%) and 78% (95%BCI: 67%–84%), respectively in children≤5 years, and 34% (95%BCI: 28%–66%) and 34% (95%BCI: 28%–66%) in older individuals, respectively.

More so, higher socio-economic status and proportion of malaria treatment seeking behavior were related to a statistically important increase in the decline of malaria incidence rates across all ages.

4. Discussion

We analyzed health facility malaria case data, reported through the DHIS2 in Uganda, to determine the effects of climatic factors on the spatio-temporal patterns of the disease and to assess the effects of climate changes on the changes in malaria incidence during 2013–2017, taking into account the effects of disease interventions.

Our findings have indicated that incidence initially declined steadily during 2013–2015 followed by resurgence in 2016. In the same period, there was a steady increase in rainfall, day and night land surface temperature, and a steady decrease in NDVI, suggesting a more favorable environment for disease transmission. The temporal trends in incidence observed in Uganda are in line in with global malaria trends (World Health Organisation, 2017). The initial decline has been attributed to the effect of the scaled-up malaria interventions (Bhatt et al., 2015), whereas the resurgence has been explained by insecticide resistance (Talisuna et al., 2015), migration of non-immune populations such as refugees (Coldiron et al., 2017), and by the increasing role of climate change on malaria transmission (Ngarakana-Gwasira et al., 2016b).

Increases in land surface temperatures are in line with warming experienced in the past years at global and regional levels (Root et al., 2003). This increase in temperatures is consistent with observations that indicate a changing in the geographical distribution of endemic malaria in the country beyond previously endemic zone boundaries to epidemic-prone zones due to warmer temperatures providing suitable conditions for transmission (Lindblade et al., 1999). However, a likely implication of this finding is the possible development of a stronger immunity by populations living in these areas in response to an increased malaria exposure which will result in reduction of fatal outcomes in previously epidemic-prone areas (Färnert et al., 2015).

The positive association observed between malaria incidence and day land surface temperature, rainfall and NDVI is in line with other studies that have demonstrated the influence of the environment on malaria transmission (Siraj et al., 2014) and the increase of malaria transmission with temperature (Gullan, 2014) and rainfall (Githeko and Ndegwa, 2001; Kynast-Wolf et al., 2006). Temperature influences the survival of the mosquito vector and the duration of the development of the vector and the parasite (Gullan and Cranston, 2009). Rainfall contributes to the creation of breeding sites for mosquitoes and to an increase in humidity which favors vector development (Thomson et al., 2006). However, the relationship of malaria with rainfall is non-linear. Excess of rainfall is associated with a reduction in malaria (Lindsay et al., 2000) as it may flush out mosquito larvae (Paaijmans et al., 2007) and reduce temperature (Teklehaimanot et al., 2004).

The decline in malaria incidence is associated with extreme day land surface temperature which reduces mosquito survival (>35 °C) (Christiansen-Jucht et al., 2015; Bayoh and Lindsay, 2003; Teklehaimanot et al., 2004). The negative effect of altitude on malaria incidence is also expected since higher altitudes experience lower temperatures which make the malaria transmission slower as mosquito development cycle and the sporogony phase take much longer (Bødker et al., 2003). The inverse relationship between malaria incidence and distance to water bodies is in line with other studies that indicate a higher risk closer to breeding sites (Dlamini et al., 2015). The higher incidence of malaria in majorly cropping areas compared to forested areas may be explained by land transformation and poor agricultural practices in the former which may lead to creation of shallow ditches and trenches that collect water when it rains and become suitable breeding sites for mosquitoes (Kweka et al., 2016). These results are in agreement with findings from other studies that employed spatio-temporal analyses of routine health facility malaria data in Zimbabwe (Mabaso et al., 2006) and in Yunan Province, China (Clements et al., 2009), but differ with results reported from a study in northern Malawi (Kazembe, 2007) that reported a positive effect of altitude. Also, NDVI is influenced by rainfall, which explains its positive relationship with malaria incidence. A similar relationship has been described elsewhere (Liu and Chen, 2006; Midekisa et al., 2012; Thomson et al., 1999). Results of the spatio-temporal model regarding the relation between the climatic factors and malaria incidence are confirmed by the spatial model which directly quantifies the effects of climatic changes on the decline in malaria incidence between 2013 and 2017. Other studies have also reported evidence of malaria sensitivity to climate and indicated important associations between climatic changes and malaria burden changes; in Ghana (Klutse et al., 2014), Nigeria (Weli and Efe, 2015) and Kenya (Alonso et al., 2011). Indeed, in Uganda, prolonged periods of unusually high rainfall, and warmer temperatures experienced from longer drought seasons have been shown to alter the intensity, distribution and duration of malaria transmission (Kilian et al., 1999). At the global level, our findings agree with those of several studies that reported a linkage between climatic change and exacerbation of malaria risk (Caminade et al., 2014; Endo et al., 2017; Ermert et al., 2013; Alonso et al., 2010), and a World Bank report indicating an increase in susceptibility to malaria as temperatures increase (International Bank for Reconstruction and Development and World Bank, Washington, DC, 2012). The implication of these finding is that malaria distribution may increase both in space and time as a result of climate change spreading to areas that previously were malaria free (Tanser et al., 2003).

The interactions of intervention effects with land surface temperature and NDVI on the spatio-temporal patterns of malaria incidence suggest a varying impact of interventions on malaria burden in different climatic conditions. This finding will inevitably call for changes in malaria programming in Uganda in view of the evidence of the changing climate.

Notably, interventions had a much stronger positive effect on the decline of malaria incidence in both age groups compared to climatic changes further underlining the importance of interventions in malaria control and their potential to mitigate adverse effects of climate change on malaria. The effectiveness of interventions in influencing malaria reduction in Uganda is further enhanced by government policies of interventions scale-up through mass distribution of ITNs to achieve universal coverage and the formulation of guidelines supporting their smooth deployment such as one that recommends the use of ACTs for malaria treatment and prohibits the use of other antimalarial drugs in public health facilities (National Malaria Control Program, 2016). Our findings are consistent with results reported from other studies that reported a strong effect of interventions on malaria risk reduction (Bhattarai et al., 2007; Müller et al., 2006; O'Meara et al., 2010; Snow and Marsh, 2010).

More so, socio-economic status and proportion of health seeking behavior were all associated with an increase in odds of reduction in malaria incidence. The improving socioeconomic conditions and a high rate of urbanization, particularly in the central and southwestern regions, coupled with an increase in health facility coverage, probably explain the decline in malaria incidence and their mitigation effect on the influence of climatic change on malaria incidence during 2013–2017. The importance of socioeconomic factors on malaria burden cannot be overstated as has been shown in several studies (Feachem and Sabot, 2008; Greenwood et al., 2008; Protopopoff et al., 2009). Indeed the adverse effects of climatic factors on spatio-temporal trends of malaria incidence are highest in the northern and eastern based districts where poverty is very high, urbanization is low and other socio-economic indicators poor (Yeka, 2012). Similarly, the disparities in malaria distribution in the most-at-risk group of children <5 years neither reflects that of environmental factors nor malaria interventions, but they mirror socioeconomic and health access inequalities between the north/east and south/central regions of the country (Ssempiira et al., 2017).

A limitation in our study is the non-availability of monthly malaria interventions data and of intervention data during the years 2013 and 2017. Due to lack of monitoring and evaluation data outside the survey periods, we assumed that intervention coverage of 2013–14 is the same as that of 2014–15 (reported in MIS 2014–15) and the coverage of 2017 as similar to that of 2016 (available in DHS 2016). Although, this assumption holds for ITNs since they have an average lifespan of three years (Ngonghala et al., 2016), it may necessarily not be true for ACTs. Furthermore, malaria transmission in Uganda is perennial, therefore we assumed that the coverage estimated from the survey data at the district level reflects the coverage for that district throughout the year. These assumptions may affect the conclusions from our findings.

5. Conclusion

Our study has elucidated inter and intra-annual relationships between climatic factors and malaria incidence, estimated the space-time burden of estimates, and demonstrated the effects of climatic changes on the decline of malaria incidence across all ages during 2013–2017. Malaria incidence has declined during 2013–2017, despite a major resurgence in 2016. Results have attested to a significant interplay between climatic and intervention effects and indicated that climatic factors have had a detrimental effect on malaria reduction gains achieved through accelerated interventions scale-up. To mitigate adverse climatic effects on malaria, NMCP should create synergies with the National Meteorological Authority (NMA) and harmonize interventions deployments after taking into account forecasts produced by the latter of the short-term weather and long-term climatic conditions. This should lead to the development of a malaria early warning system (MEWS) to forecast malaria outbreaks in the event of adverse climatic events. Additional funding will be required for incorporating climatic mitigation plans in malaria programs, designing and operationalizing MEWS to achieve effective and sustainable malaria control in Uganda.

Appendix A. Statistical model formulation

A.1. Modeling the effects of climatic factors on spatio-temporal trends of incidence

Let Y_ijt be the number of malaria cases reported in calendar month t = 1, …,12, year j = 1, …,5 and district i = 1, …, 112. Y_ijt is assumed to follow a negative binomial distribution, Y_ijt~NB(p_ijt, r) where p_ijt = r/(r + μ_ijt) where r is the dispersion parameter and μ_ijt is the average number of monthly malaria cases in the district. The model with a log link function is described below:

log(μ_ijt) = log (N_ijt) + α + X^Tβ + f_T(Z_j) + f_s(t) + ϵ_{(j−1)∗12+t} + ω_i, where N_ijt is the offset district-month specific population, α is the intercept, β is a vector of regression coefficients associated with the vector of predictors X_it (interventions, environmental, socio-economic status). ϵ_{(j−1)∗12+t} are monthly random effects modeled by a first order autoregressive process with temporal variance σ_t². f_T(Z_j) and f_s(t) are parameters modeling the time trend and seasonality, f_T(Z_j) describes an annual trend with the year Z treated as categorical covariate, ω_i is the spatial random effect for district i. The seasonal pattern f_s(t) was captured by a mixture of two harmonic cycles with periods T₁=6 and T₁ = 12 months, respectively, that is, $f_s\left(t\right)=\sum _{j=1}^2{A}_j\mathit{cos}\left(\frac{2\pi }{T_j}t-{\phi }_j\right)=\sum _{j=1}^2\left\{a_j\ast \mathit{cos}\left(\frac{2\pi }{T_j}t\right)+b_j\ast \mathit{sin}\left(\frac{2\pi }{T_j}t\right)\right\}$, where t is time in months. A_j is the amplitude of the jth cycle and estimates the incidence peak by the expression A_j = √ (a_j² + b_j²). φ_jis the phase which is the point where the peak occurs estimated as φ_j = arctan (a_j/b_j), a_j and b_j are model parameters. ω_i, i = 1, …,112, are modeled via a conditional autoregressive (CAR) process - each ω_i conditional on the neighbor ω_j follows a normal distribution with mean equal to the average of neighboring districts ω_j and variance inversely proportional to the number of neighbor districts n_i, that is; ${\omega }_i\mid {\omega }_j~N\left(\mathrm{\gamma }\sum _{l\in {\delta }_i}{\omega }_j,\frac{{\sigma }_{\omega }^2}{n_i}\right)$, where γ quantifies the amount of spatial correlation present in the data, σ_ω² measures the spatial variance. ω_i and ω_j are adjacent districts in the set of all adjacent districts δ_i of district i, and n_i are the number of adjacent districts.

Following Bayesian model formulation, prior distributions were specified for all model parameters. For the regression coefficients a non-informative normal prior distribution was assumed, a Gamma distribution with mean 1 and variance 100 was adopted for the parameter, r. ϵ_t = 2, …, 59 are error terms considered to be temporally correlated and modeled via an autoregressive process of first order i.e., ϵ_t~AR(1), assuming that ${ϵ}_1~N\left(0,\frac{{\sigma }^2}{1-{\rho }^2}\right)$ and ϵ_t~N(ρϵ_t−1, σ²), t = 2, …, 59, where ρ is the autocorrelation parameter that quantifies the degree of dependence between successive months. We assumed a Uniform prior distribution for ρ, i.e. ρ~U[−1, 1]. Since the above specification conditions on the first observation, we assigned it a student t prior distribution with one degree of freedom. An inverse gamma prior distribution with mean 10 and variance 100 was considered for σ_ω² and σ_t², i.e. σ_ω⁻², σ_t⁻²~Ga(0.1, 0.001).

A.2. Modeling the effects of climatic changes on the changes in malaria incidence

The change in malaria incidence between 2013 and 2017 was modeled on the log scale as a function of the difference in climatic conditions between the two time points, the effects of intervention coverage, socioeconomic status, and the proportion of malaria treatment seeking behavior in 2017, that is,

log(IR)_it′=log(IR_it)+β(X_it′ − X_it)^T + αΨ_it′ + ϵ_t + ω_i, where IR_it and IR′_it are the malaria incidence rate in 2013 and 2017, respectively, log(IR_it) = log (μ_it)-log(N_it), μ_it is the average number of monthly malaria cases in district i, and month t. X_it and X′_it, are climatic covariates in 2013 and 2017 respectively and Ψ_it′ are the non climatic covariates in 2017. The coefficients β and α represent the magnitude of the effect associated with an increase in the rates of decline in malaria incidence from 2013 to 2017, ϵ_t are monthly random effects modeled by a first order autoregressive process with temporal variance σ_t² and ω_i are spatial random effects as described in the section above.

A.3. Estimating district-level interventions coverage, socioeconomic status, and health seeking behavior

Data for intervention coverage, wealth index and health seeking behavior were only available at regional level from the MIS 2014–15 and DHS 2016 surveys. This is because the population based surveys are designed to give precise estimates only at regional and country levels. A Conditional Autoregressive (CAR) model was developed to estimate district level estimates of formulated with a binomial distribution for intervention coverage and health seeking behavior indicators, and a Gaussian distribution for the wealth score, a measure of socioeconomic status. Slightly fewer than all the 112 districts had clusters selected in the original sample, therefore to fit the CAR models the districts with missing data were assigned a median value of the districts located within a specific region. The models were formulated as follows;

Let Y_i be the number of households that possessed at least one ITN in district i = 1, …, 112, and N_i, the total number of households sampled and interviewed in district i. We assume that Y_i follows a Binomial distribution, that is, Y_i ∣ N_i, π(i)~Bin(N_i, π(i)) ∀i = 1, …, 112, where π(i) is the proportion of households with at least one ITN in district i. A Bayesian CAR model to estimate district-level ITN coverage was formulated as follows;

logit(π(i)) = β₀ + ω_i, where β₀ is a constant, and ω_i, i = 1,…,112, are modeled via a CAR process. Each ω_i conditional on the neighbor ω_j follows a normal distribution with mean equal to the average of neighboring districts ω_j and variance inversely proportional to the number of neighbor districtsn_i, that is; ${\omega }_i\mid {\omega }_j~N\left(\mathrm{\gamma }\sum _{l\in {\delta }_i}{\omega }_j,\frac{{\sigma }_{\omega }^2}{n_i}\right)$, where γ quantifies the amount of spatial correlation present in the data, σ_ω² measures the spatial variance. ω_i and ω_j are adjacent districts in the set of all adjacent districts δ_i of district i, and n_i are the number of adjacent districts. Following standard formulation of Bayesian regression models, we assumed vague priors; A non-informative Gaussian distributions with mean 0 and variance 10² for β₀, that is, β₀~N(0, 10²). An inverse gamma prior distribution with mean 10 and variance 100 was considered for σ_ω², i.e. σ_ω⁻²~Ga(0.1, 0.001).

Similar formulations were applied for ACTs, malaria treatment seeking behavior, and household asset index, however the latter was modeled by a first stage Gaussian distribution.

A.4. Bayesian variable selection

To choose the most important ITN coverage indicator that explains the maximum variation in malaria incidence, Bayesian variable selection using stochastic search (Chammartin et al., 2013) was implemented separately for ITN indicators, and environmental and climatic factors. For ITN indicators, a categorical variable  X_p was introduced into the model and assigned values 1 to 7 representing exclusion of the variable from the model (I_p = 1), and inclusion of the six indicators as follows; proportion of existing ITNs used the previous night (I_p = 2), proportion of children under five years old who slept under an ITN the previous night (I_p = 3), proportion of the population that slept under an ITN the previous night (I_p = 4), proportion of households with at least one ITN for every two people (I_p = 5), proportion of households with at least one ITN (I_p = 6), and proportion of population with access to an ITN in their household (I_p = 7). Also, for lagged climatic predictors, a categorical variable  Y_p was created with values 1 to 7 introduced into the model to represent exclusion of the variable from the model (I_p = 1), and inclusion of different variables as follows; lag1 (continuous) (I_p = 2), lag1 (categorical) (I_p = 3), lag2 (continuous) (I_p = 4), lag2 (categorical) (I_p = 5), lag3 (continuous) (I_p = 6) and lag3 (categorical) (I_p = 7) For non-lagged climatic factors that is, altitude and distance to water bodies, a categorical variable  Z_p with three values was defined representing exclusion from model (I_p = 0), inclusion of continuous form (I_p = 1), and inclusion of categorical form (I_p = 2). In the latter scenario, I_p has a probability mass function ∏_j=1²π_j^δ_j(I_p), where π_j denotes the inclusion probabilities of functional form j (j = 1,2,3) so that $\sum _{\mathrm{j}=1}^3{\mathrm{\pi }}_{\mathrm{j}}=1$ and δ_j(.) is the Dirac function, ${\mathrm{\delta }}_{\mathrm{j}}\left({\mathrm{I}}_{\mathrm{p}}\right)=\left\{\begin{array}{c}1,\text{if}{\mathrm{I}}_{\mathrm{p}}=\mathrm{j}\\ 0,\text{if}{\mathrm{I}}_{\mathrm{p}}\ne \mathrm{j}\end{array}\right).$A spike and slab prior distribution was assumed for the regression coefficients. In particular for the coefficient β_p of the corresponding variable X_p, we assumed β_p~δ₁(I_p)N(0, τ_p²) + (1 − δ₁(I_p))N(0, ϑ₀τ_p²), that is a non-informative prior for β_p if X_p is included in the model (slab) and an informative normal prior shrinking β_p to zero (spike) if X_p is excluded from the model, setting ϑ₀ to be a large number, e.g., 10⁵. Similarly, β_{p, l}~δ₂(I_p)N(0, τ_{p, l}²) + (1 − δ₂)N(0, ϑ₀τ_{p, l}²) was assumed for the scenario of selecting one out of six indicators/variables or exclusion of the variable. The coefficients {β_{p, l}}_{l=1, . . , 7} corresponding to inclusion of X_p, p = 1, …,7 in the model. For inclusion probabilities, a non-informative Dirichlet distribution was adopted with hyper parameter α = (1, 1, 1, 1, 1, 1, 1)^T, that is, π = (π₁, π₂, π₃, π₄, π₅, π₆, π₇)^T~Dirichlet(7, α). We also assumed inverse Gamma priors for the precision hyper parameters τ_p² and τ_{p, l}², l = 1, …, 7.

Appendix B. Supplementary data

Supplementary material