Pattern separation and completion of distinct axonal inputs transmitted via micro-tunnels between co-cultured hippocampal dentate, CA3, CA1 and entorhinal cortex networks

Abstract

Objective

Functions ascribed to the hippocampal sub-regions for encoding episodic memories include the separation of activity patterns propagated from the entorhinal cortex (EC) into the dentate gyrus (DG) and pattern completion in CA3 region. Since a direct assessment of these functions is lacking at the level of specific axonal inputs, our goal is to directly measure the separation and completion of distinct axonal inputs in engineered pairs of hippocampal sub-regional circuits.

Approach

We co-cultured EC-DG, DG-CA3, CA3-CA1 or CA1-EC neurons in a two-chamber PDMS device over a micro-electrode array (MEA60), inter-connected via distinct axons that grow through the micro-tunnels between the compartments. Taking advantage of the axonal accessibility, we quantified pattern separation and completion of the evoked activity transmitted through the tunnels from source into target well. Since pattern separation can be inferred when inputs are more correlated than outputs, we first compared the correlations among axonal inputs with those of target somata outputs. We then compared, in an analog approach, the distributions of correlation distances between rate patterns of the axonal inputs inside the tunnels with those of the somata outputs evoked in the target well. Finally, in a digital approach, we measured the spatial population distances between binary patterns of the same axonal inputs and somata outputs.

Main Results

We found the strongest separation of the propagated axonal inputs when EC was axonally connected to DG, with a decline in separation to CA3 and to CA1 for both rate and digital approaches. Furthermore, the digital approach showed stronger pattern completion in CA3, then CA1 and EC.

Significance

To the best of our knowledge, these are the first direct measures of pattern separation and completion for axonal transmission to the somata target outputs at the rate and digital population levels in each of four stages of the EC-DG-CA3-CA1 circuit.

Introduction

Three main sub-regions of the mammalian hippocampus, the dentate gyrus (DG), CA3 and CA1, are used to encode episodic memories (Rolls 1996). Separate functions are postulated for each of these subregions. A function of pattern separation is proposed to allocate memorable features of environmental stimuli for downstream identification of familiarity or novelty in memory. A function of pattern completion is thought to occur by recognition of prior similar experience. In particular, the dentate gyrus (DG) is postulated to specifically function in pattern separation (Marr 1971, Rolls 1989a, Rolls 1989b, Treves and Rolls 1994) and the CA3 in pattern completion (Gold and Kesner 2005, Leutgeb S and Leutgeb J K 2007, Rolls 2013). The main levels of evidence for these concepts come from the anatomy, behavioral paradigms with in vivo recordings in individual sub-regions in the rat, human EEG and fMRI and computational modeling. Anatomically, the larger number of DG neurons than the primary inputs from layer II of the entorhinal cortex (EC) suggests a fan-out of information needed for pattern separation (Andersen et al 2006). Conversely, the recurrent collateral anatomy of the CA3 suggests a coding mechanism involved in pattern completion (Lebovitz et al 1971). Carefully designed in vivo shifts in visual inputs or changes to the rat physical environment (Leutgeb S and Leutgeb J K 2007, Leutgeb et al 2004, Leutgeb et al 2005, Neunuebel and Knierim 2014), and small changes in visual inputs in macroscopic human EEG or fMRI studies (Bakker et al 2010, Kirwan and Stark 2007, Yassa and Stark 2011, Santoro 2013) further support pattern separation in DG and completion in CA3. Finally, computational models also suggest a role for these hippocampal sub-regions in pattern separation and completion (Marr 1971, Treves and Rolls 1994, Myers and Scharfman 2009, 2011, Renno-Costa 2014, Faghihi and Moustafa 2015, Chavlis 2017). However, little in vivo or in vitro evidence exists for the computational properties among small neural populations needed in EC and DG to perform these processes. Moreover, because of the sub-micrometer caliber of axons (Bartlett and Banker 1984), no evidence exists for the nature of information transmitted by the axons between these hippocampal subregions. Santoro (2013) urged a reassessment of pattern separation in the dentate gyrus as a computational digital-spatial ensemble code in contrast to analog rate coding, because no study has directly confirmed the existence of this mechanism at the cell population level in the EC-DG-CA3-CA1 circuit. Furthermore, most in vivo studies use behavioral conditions as categorical inputs (behavioral discrimination), which are of uncertain scaling since their changes are usually qualitative.

Therefore, to monitor samples of the actual inputs as scaled measures of the communicating axons between co-cultured hippocampal networks and to specifically describe functions of pattern separation and completion, we were inspired by Richard Feynman’s 1988 advice “What I cannot create, I do not understand”. We isolated rat neurons from each hippocampal sub-region and cultured them in pairs in a two-chamber device over a multi-electrode array (MEA) with interconnected micro-fluidic tunnels for axon transmission (Taylor et al 2005, Dworak and Wheeler 2009, Pan et al 2011, Brewer et al 2013). This system was designed to complement in vivo models, providing useful new strategies for elucidating complex biological systems, with more precise inputs, multiple stimulation sites and better access to individual axons than in vivo recordings (Brewer et al 2013, Poli et al 2015). Furthermore, the micro-tunnels allowed robust axonal connection between chambers because of a strong dependence of the network functional strength of connectivity on the number of tunnels inputs (Pan et al 2015, DeMarse et al 2016). We applied paired-pulse stimulation at 22 electrode sites in this model system to promote native feed-forward information transmission, facilitating evoked network responses that correlated between the source and the axons in the tunnels, as well as between the transmitted axonal activity and target subregion (Poli et al 2017a). Pattern separation can be inferred when inputs are more similar than outputs. In pattern completion, the outputs are more similar than the inputs. In order to investigate these phenomena, we employed Pearson coefficients and Jaccard coefficients in either an analog or binary approach, respectively. Specifically, we determined how well pattern separation could be quantified by these two widely used similarity measures as follows: 1) The analog approach compared the distributions of correlation distances between rate patterns among axonal inputs (i.e., spike rates in the tunnels) versus those among somata outputs (i.e., spike rates in the target well). This comparison was based on Pearson coefficients because of their robustness for continuous variables such as spike rates. 2) Conversely, the second approach, termed binary or digital, measured the spatial population distances between binary patterns distinguishing active (1) and silent electrodes (0) in the tunnels and target well. Since the Jaccard coefficient is a better measure of similarity with binary data (Chavlis et al 2017), 1-Jaccard coefficient was used to assess dissimilarity.

After statistical evaluation, both rate and binary approaches showed the strongest separation of the propagated axonal inputs for the case when EC axons connected to DG, with a decline in separation to CA3 and to CA1. Furthermore, using the binary metric, there was strong evidence of pattern completion for DG projecting to CA3, then to CA1 and EC. Finally, the methods and metrics used in this paper showed broad agreement with published results regarding pattern completion and separation for these brain subregions.

To the best of our knowledge, these are the first direct measures of pattern separation and completion of distinct axonal inputs transmitted through micro-tunnels into somata target outputs at the rate and digital population levels in an engineered EC-DG-CA3-CA1 circuit.

Methods

Dissection of hippocampal sub-regions for in vitro neuronal cultures

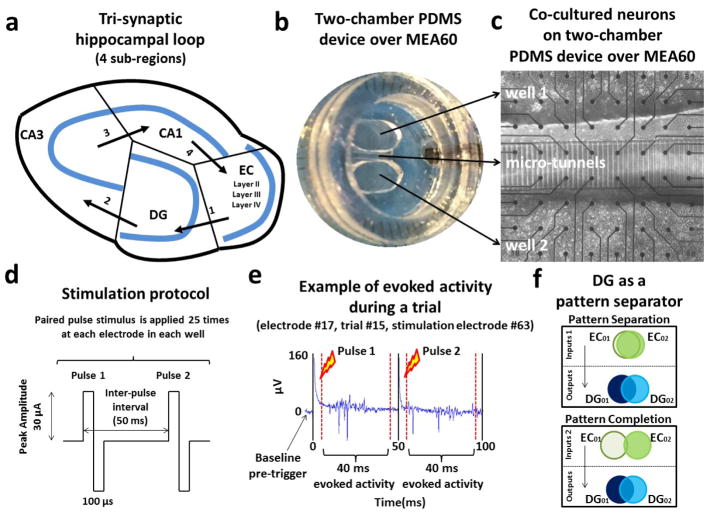
All experimental procedures and animal care have been approved by the Institutional Animal Care and Use Committee of the University of California Irvine in accordance with relevant guidelines and regulations. A detailed description of the dissection procedure of rat hippocampal sub-regions is described in our earlier work (Brewer et al 2013) and others (Mattson and Kater 1989, Baranes et al 1996, Zhao et al 2001, Lein et al 2004). Briefly, the intact hippocampus was extracted from the overlying neo-cortex of each hemisphere of postnatal day 3 rats. The entorhinal cortex (EC), dentate gyrus (DG), CA3 and CA1 neurons (figure 1(a)) were isolated under the dissecting microscope (Olympus CKX41), plated at different densities on a two-well polydimethylsilxane (PDMS) device over a micro-electrode array (MEA60, figure 1(b)) and inter-connected via micro-tunnels (figure 1(c)). Specifically, we used 1000 cells/mm² for DG, 330 cells/mm² for CA3, 410 cells/mm² for CA1 and 330 cells/mm² for EC within one specific chamber in order to mimic the regional density ratios of neurons in vivo (Braitenberg 1981), i.e. EC-DG 1:3, DG-CA3 3:1, CA3-CA1 1:1.25 and CA1-EC 1.25:1. To increase spontaneous spike rates and greater synapse density, the cells were maintained in culture in NbActiv4 medium in a humidified incubator with 5% CO₂ and 9% O₂ at 37°C (BrainBits, Springfield, IL, USA) (Brewer et al 2008, Bhattacharya et al 2016). The MEA60 amplifier recorded electrophysiological activity at constant temperature of 37°C and in a humidified atmosphere of 5% CO₂ and 9% O₂ (custom gas mixture, balance N₂; Airgas, Santa Ana, CA). Our previous works with two chambers (Brewer et al 2013; Poli et al 2017a) demonstrated not only excellent neuron survival equivalent to the original cell plating densities, but also strong axonal polarity consistent with the hippocampal anatomy. Polarity was determined from delay times as an axonal spike traveled from one electrode to the next in a micro-tunnel. These delay times showed more than 60% of spikes spontaneously travel in the “natural” direction (Brewer et al 2013). Structural specificity from stimulation of our co-cultures compared to the homogeneous pairings (e.g., DG-DG) showed spontaneous propagation in the native direction of over 80% of the activity (Bhattacharya et al 2016).

Figure 1.

Hippocampal neurons harvested from 4 sub-regions shown in (a) were co-cultured in pairs in a two-well PDMS device (b) over a micro-electrode array. (c) Micro-fluidic tunnels (3 x 10 x 400 um) exclude cell bodies from one well to the other, and permit axonal growth and propagation of axonal spikes. From the 51 communicating micro-tunnels, 7 of these tunnels overlaid 2 electrodes (one of the remaining tunnels had only a single electrode as the second was coupled to a the internal reference electrode). For each pair of tunnel electrodes we used the recording site reporting higher spike rate, under the assumption that the axon coupled more accurately to the more active electrode. (d) A paired-pulse stimulation protocol was applied at 22 different sites in each well and repeated 25 times to evoke activity between the co-cultures through the micro-tunnels. (e) Evoked responses during one stimulation trial at electrode 17 (column 1, row 7). (f) Illustration of pattern separation and completion (adapted from Yassa and Stark 2011).

Experimental set-up

We placed a PDMS device (Pan et al 2011, Poli et al 2017a) over 59 TiN₃ micro-electrodes (MEA60, Multichannel System, Reutlingen, Germany), creating two different wells in which we co-cultured hippocampal neurons in pairs (figure 1(b)). The chambers were separated by 51 micro-channels, 3 μm tall, 10 μm wide, 400 μm long, and spaced 40 μm apart (center-to-center). Micro-electrodes (30 μm in diameter on 200 μm spacing) were positioned so that 15 underlie the tunnels and 22 lie within each of the two chambers (figure 1(c)). The micro-tunnels allowed passage of axons but not somata, structural connectivity and information transmission between both chambers (Pan et al 2015, Bhattacharya et al 2016). Furthermore, 7 of 8 monitored micro-tunnels overlaid 2 electrodes. For each pair of these tunnel electrodes we choose one with the higher spike rates due to better axon to electrode coupling. A more detailed description of the fabrication of this device can be found in Pan et al (2011).

Spike detection

During the third week in vitro, we recorded the electrophysiological activity of our co-cultured hippocampal networks at 25 kHz sampling frequency, with 1100x amplification. To detect spikes, we used the peak-to-peak algorithm described in Maccione et al (2009), based on a differential threshold set at 8 times the standard deviation of the estimated baseline per channel noise levels. Peaks were detected within a 2 ms window with a subsequent 1 ms dead-time between peaks.

Stimulation Protocol

We used a paired-pulse stimulation protocol described in detail in Bouteiller et al (2010) and in Poli et al (2017a, 2017b) to increase the efficacy of stimulation and promote native feed-forward information transmission (e.g., from EC to DG) between our co-cultures through micro-tunnels (Bhattacharya et al 2016). Preliminary studies with single stimuli at 1 Hz or less confirmed their depressive effect compared to the paired pulse stimulation that was characterized by pulses biphasic with 30 μA amplitude, 100 μs duration beginning positive and 50 ms between stimuli (figure 1(d)) (Ide et al 2010). We applied this paired-pulse stimulus at one site in one well followed by another site in the opposite chamber to induce more efficient information transmission over the multi-synaptic network (Poli et al 2017a; 2017b). This alternation was repeated 25 times for all electrodes in both chambers. A wait period of 5 s was inserted between the pairs to minimize the plasticity effects of the electrical stimulation. We avoided electrical artifacts produced by saturation of the amplifiers during stimulation by using a blanking period of 5 ms after each stimulus (Wagenaar and Potter 2002, Wagenaar et al 2004). Furthermore, stimulation generally evoked action potentials whose rate returned to baseline levels after 40–45 ms (Ide et al 2010). Hence, we focused on the activity that began at 5 ms and ended at 45 ms post each stimulus (Poli et al 2017a). Examples of this evoked activity during a specific stimulation trial are shown in figure 1(e). Stimulation at some source electrodes may directly evoke axonal activity, but this activity would be propagated to the tunnels in less than a millisecond, a time not accessible because of the stimulus artifact. Therefore, we could not evaluate occasions when the source stimulus directly activated tunnel axons. Furthermore this protocol is classically known to facilitate pre-synaptic transmitter release and increase the efficacy of stimulation. However, if the pre-synaptic terminal is inhibitory or synapses onto an inhibitory neuron, the effect could be a reduction in spike counts. Therefore, pathways could change with repetition of a stimulus from excitatory to inhibitory.

Baseline was assessed by the activity in a 3 min. recording immediately prior to the stimulation protocol and also by the number of spikes recorded during the pre-trigger period (5 ms before each paired-pulse stimulus). In both cases the regional baseline rates were 4–5 times lower than the evoked firing rates (Poli et al 2017a). This baseline set at 22% of the evoked rate was similar to the 20% spontaneous threshold used by Chiappalone et al (2008) to discriminate the evoked responses from the spontaneous fluctuations of cortical activity level. However, the relevance of this discrimination may decrease due to the power law distribution of inter-spike intervals (ISI = 1/spike rate), where an average may not accurately summarize the distribution (Poli et al 2017a). Furthermore, if the stimulation protocol activates inhibitory neurons, a single-sided evaluation above baseline would exclude some sites with less evoked spikes.

Pattern separation by comparing the distributions of the correlation distances between analog input and output rate patterns

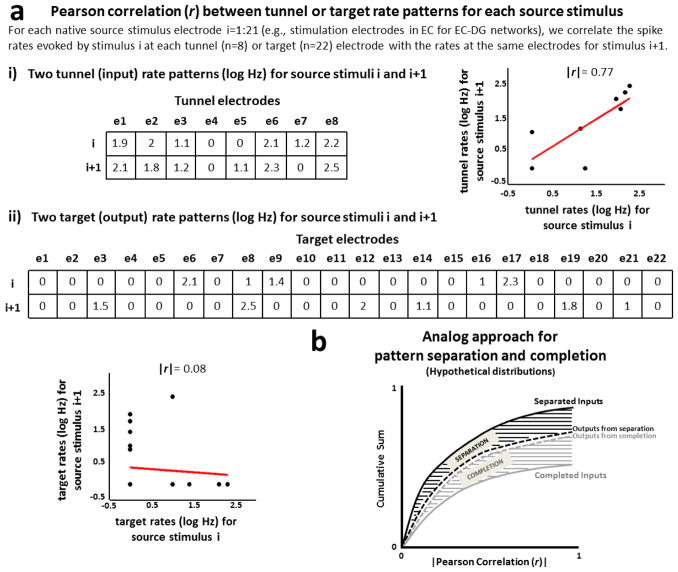
We hypothesized that if neural cultures derived from dentate gyrus act as a pattern separator of inputs from the entorhinal cortex (Yassa and Stark 2011, Santoro 2013), then similar axonal inputs transmitted via micro-tunnels from EC into DG would produce dissimilar DG outputs (figure 1(f)). As an experimentally accessible rate measure, we expected correlations among evoked firing rates from the distinct EC axons grown through the tunnels (the axonal inputs to the DG) would be greater than the correlations among the DG somata target outputs recorded in the chamber. To test this hypothesis, we first evaluated the spike rates > 12.5 Hz, i.e. the responses evoked in the tunnels and target well by paired-pulse stimulation with more than one spike in 80 ms (40 ms x 2 pulses). This protocol was applied 25 times at each of 22 sites in the EC chamber to promote the feed-forward native information transmission from source to target through the tunnels (i.e., from EC to DG in EC-DG networks) (Poli et al 2017b). We then estimated the correlation (Pearson) between rate patterns quantified as vectors containing spike rates evoked at each recording site by all possible combinations of trials and stimulus locations (i.e., (22 stimulus sites x 25 trials)² = 302,500 correlation values). These rate patterns represented 1) the axonal inputs when described by the log spike rates evoked at each of 8 axonal recording sites, 2) the target somata outputs when described by the log spike rates evoked at each of 22 sites in the target well. Log spike rates were used to accommodate the large dynamic range of activity. Figure 2 shows examples of two scatter plots depicting possible correlations between these rate patterns, one for the axonal inputs (figure 2(a.i)) and another one for the target somata outputs (figure 2(a.ii)), both evoked by the same combination of trial and stimulus location. Finally, we compared the distributions of the correlations between transmitted axonal inputs with those of the target somata outputs. To facilitate the comparison between these distributions, to smooth the effects of low frequency noise (Newman 2005) and to account for the sparseness of the responses, we aggregated any non-zero correlations of inputs in one cumulative curve and output correlations in another (figure 2(b)) with asymptotes below 1 for both. We used the area between these two curves to quantify the degree of pattern separation on those occasions where the aggregated correlations among inputs were greater than the correlations among outputs; otherwise, we quantified pattern completion as the area of excess output over input correlations in the graph of correlation density.

Figure 2.

Analog pattern separation or completion from distributions of correlation distances of input and output rate patterns. (a) Pearson correlation between rate patterns, computationally described by log spike rates evoked at each tunnel (input) or target (output) electrode. Examples of strong Pearson correlation between two rate input patterns (r=0.77, a.i) and weak Pearson correlation between two rate output patterns (r=0.08, a.ii) are shown in the figure. (b) Hypothetical distributions of correlation distances of input and output rate patterns. In our method we aggregate the non-zero input correlation distances in one cumulative curve and the non-zero output correlation distances in another. Therefore, both hypothetical curves show cumulative totals less than 1 because instances of zero correlations are not included in the cumulative sum. The area between these two curves would quantify pattern separation if the inputs correlated more frequently than the outputs (black area); otherwise, if the outputs correlated more frequently than the inputs, this area quantified pattern completion (gray area).

Pattern separation based on spatial population distances between digitized input and output patterns

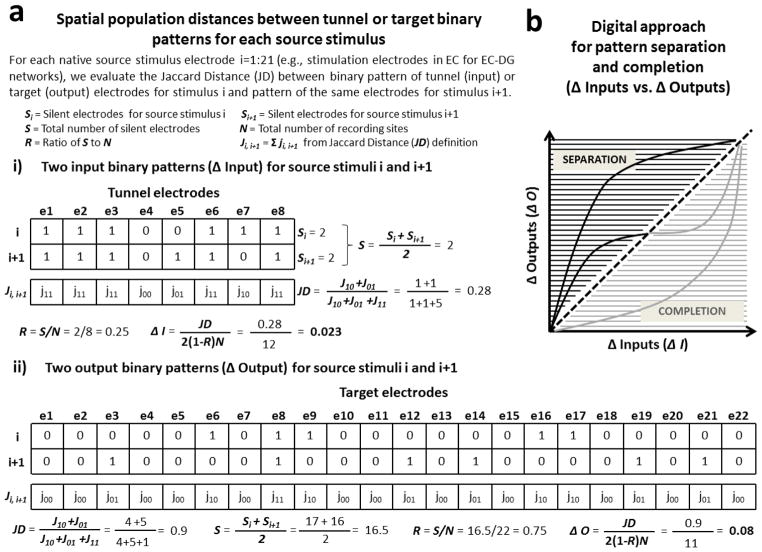
In order to quantify the separation and completion of the distinct axonal inputs transmitted through the tunnels into the target well, we also used an approach based on the spatial population distances among different binary patterns or cell assemblies (Chavlis et al 2017). The active responses in each subregion to each stimulation electrode were transformed from a spatial distribution of electrodes into a one-dimensional vector with active elements coded as 1’s and inactive elements as 0’s. The difference between different spatial population responses was calculated from these vectors, adjusted for sparseness and normalized according to established methods for calculation as Jaccard distances (Jaccard 1912, Chavlis et al 2017). Specifically, these binary patterns were described as binary vectors where each element corresponded to one of the 8 tunnel or 22 chamber recording sites spatially distributed in the tunnels or in the target well, respectively. We considered recording sites as “active” (1 in the binary vector) when at least one spike was evoked during 25 trials of one specific paired pulse stimulus location (1 spike in 40 ms x 2 pulses x 25 trials=1 spike/2 sec), or “silent” otherwise (0 in the binary vector) (Myers and Scharfman 2009). We evaluated the Jaccard Distances (JD) adjusted for sparseness (Jaccard 1912, Chavlis et al 2017) to quantify the input variations (Δ Inputs) between the spatial binary patterns evoked in the tunnels by all possible combinations of the stimulation sites in the source chamber. In the same way, we defined the output variations (Δ Outputs) among the spatial binary patterns evoked in the target well. Figure 3 shows an example of this approach applied to two binary input or output patterns evoked by two specific stimulation sites. Formally, X was the spatial binary pattern evoked by the stimulation site i and Y was the spatial binary pattern evoked by the stimulation site i+1. We first defined JD as:

$$JD=\frac{J_{01}+J_{10}}{J_{01}+J_{10}+J_{11}}$$ (1)

where J₀₁ is the total number of times in which X is equal to 0 when Y is equal to 1, J₁₀ when X is equal to 1 and Y equal to 0, J₁₁ when X and Y both have value of 1. Then we adjusted this distance for sparseness between these two spatial binary patterns (Chavlis et al 2017), defining Δ Inputs and Δ Outputs as follows:

$$\mathrm{\Delta }\mathit{Inputs}or\mathrm{\Delta }\mathit{Outputs}=\frac{JD}{2(1-R_{in,\mathit{out}})N_{in,\mathit{out}}}$$ (2)

where the in and out denote the axonal inputs transmitted through the tunnels and the target somata outputs, respectively. The factor of 2 limits the metric to zero, N denotes the number of all recording sites (8 in the tunnels, 22 in the target well) and R the ratio of the total number of silent electrodes (S) to N. Since one electrode could be silent during only one of the two stimuli i and i+1, we defined S as follows:

$$S=\frac{S_i+S_{i+1}}{2}$$ (3)

where S_i and S_i+1 are the total number of silent electrodes during the comparison of these stimuli i and i+1, respectively. Finally, we evaluated all Δ Inputs and Δ Outputs values from all possible combinations of the stimulation sites in the source chamber. Since a network performs separation of the inputs when the similarity among them is greater than outputs, the condition for pattern separation was Δ Outputs > Δ Inputs, the reverse for pattern completion (Δ Outputs < Δ Inputs) (figure 3(b)). We also allocated the Δinput values into constant bins of 0.005. We did this to facilitate the comparison among different hippocampal pairs showing different distance values.

Figure 3.

Digital pattern separation or completion from spatial population distances between binary input and output patterns. (a) Examples of spatial population distance based on Jaccard distance adjusted for sparseness between two binary input patterns (Δ Input, a.i) and between two binary output patterns (Δ Output, a.ii) are shown in the figure. (b) Model adapted from Yassa and Stark (2011) for pattern separation and completion based on spatial population distances of binary input and output patterns (Δ Inputs vs. Δ Outputs). The black portion describes situations in which outputs are more dissimilar than inputs (i.e. separation: Δ Outputs > Δ Inputs). The gray portion describes the reverse situation in which outputs are more similar than inputs (i.e. completion: Δ Outputs < Δ Inputs).

Statistical Analyses

We performed one and two-tailed t-tests or one-way ANOVA whenever the data were normally distributed (confirmed by the Kolmogorov-Smirnov test for normality). When the normality assumption failed, we applied non-parametric tests (Wilcoxon Rank Sum test). These statistical analyses were applied to all metrics (rate and spatial population distances) extracted from 4 EC-DG, 5 DG-CA3, 5 CA3-CA1 and 5 CA1-EC co-cultured networks (total number of co-cultures=19) and controls (5 DG-DG, CA3-CA3, CA1-CA1 and EC-EC, total n=20). Error bars represent s.e.m. when not specified and p values less than 0.05 are considered significant. Data analyzed during the current study are available from the corresponding authors by on reasonable request.

Results

Site-specific stimulation in EC strongly evoked axonal transmission in connecting micro-fluidic tunnels correlated to activity in DG target cells

In this study we created in vitro neural populations from distinct hippocampal regions in order to improve our understanding of the multi-step processing occurring in regions of the hippocampus. We reconstituted pair wise components of the rat hippocampus and their entorhinal cortical (EC) inputs, around the loop returning to the EC as output (figure 1(a)) in a uniform co-culture system (figure 1(b)) over multi-electrode arrays (figure 1(c)). In addition to application of specific stimuli at different electrodes with access to neuronal activity in each of two chambers, these engineered networks allowed electrical monitoring of the activity of individual axons that grew through the tunnels between two compartments (Bhattacharya et al 2016, Narula et al 2017, Poli et al 2017a). To test for functional axonal transmission, we correlated axonal activity to that of the source and the target well by averaging the evoked responses over 25 stimulation trials applied at each of 22 EC electrodes. A correlation less than r=1 was likely due to the need for a coding transformation to occur (Hopfield 1982).

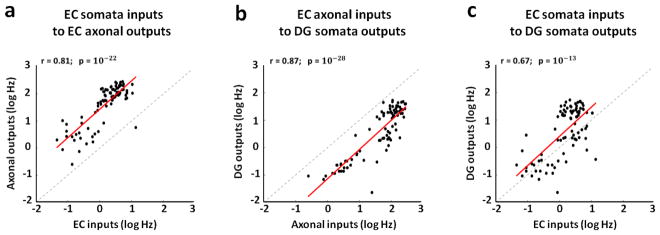
We found strong axonal activity propagated through the tunnels from EC into DG and significant correlations of the activity between these two hippocampal sub-regions (figure 4). Firing rates evoked in the stimulated EC source network were positively correlated with axonal responses in the tunnels (figure 4(a), r=0.81; 4 arrays), indicating a strong positive input-output relationship. The shift above the diagonal was indicative of axonal spike rates that were inherently higher than those evoked in the source chamber. Similarly, the axonal firing rates in the tunnels were positively and strongly correlated with DG target rates (figure 4(b), r=0.87), again with the axonal rates higher than those of somata in the target well. Furthermore, these correlations between EC axonal inputs propagated through the tunnels into DG and DG somata outputs measured in the apposing chamber were much higher than the direct correlation between the somata responses in EC and in DG (figure 4(c), r=0.67). For this reason we considered the axonal transmission between EC and DG via micro-tunnels as a more informative and perhaps a more direct method for decoding network input-output functions than activity of the somata in the separate compartments of EC and DG.

Figure 4.

The activity measured among axons correlates with the source and target evoked responses better than the separate EC somata with DG somata. We use a log scale to cover the large dynamic rage of the spike rates. (a) Strong positive correlation between EC inputs and axonal outputs in micro-tunnels (r=0.81, p=10⁻²², slope=1.05). (b) Stronger positive correlation between axonal inputs in the tunnels and DG somata outputs (r=0.87, p=10⁻²⁸, slope=1.07). (c) High proportionality between EC inputs and DG outputs, consistent with feed-forward propagation of the information flow (r=0.67, p=10⁻¹³, slope=1.07). All points show the averaged log spike rate evoked at the tunnel and chamber electrodes in 80 ms (i.e., 40 ms x 2 pulses) over 25 trials from multiple arrays. Therefore, all scatter plots show 4 arrays x 22 stimulation sites = 88 points.

Supplementary figure S1 shows the log spike rates of these EC axons propagated through the tunnels (panel (a)) and DG target neurons (panel (b)) in one array example at each of the 8 tunnel and 22 target recording electrodes. These firing patterns were evoked by paired-pulse stimuli applied at each of the 22 electrodes in the EC source well (rows in both panels) and repeated 25 times (columns in both panels). Since pattern separation can be inferred when inputs are more correlated than outputs, based on this axonal activity transmitted through the tunnels from source into target well, we first compared the correlations among axonal inputs with those of target somata outputs. We then compared, in an analog approach, the distributions of correlation distances between rate patterns of the axonal inputs inside the tunnels with those of the somata outputs evoked in the target well. Finally, in a digital approach, we measured the spatial population distances between binary patterns of the same axonal inputs and somata outputs (Chavlis et al 2017).

Correlations among axonal inputs propagated from EC into DG through micro-tunnels were greater than correlations among the DG somata outputs

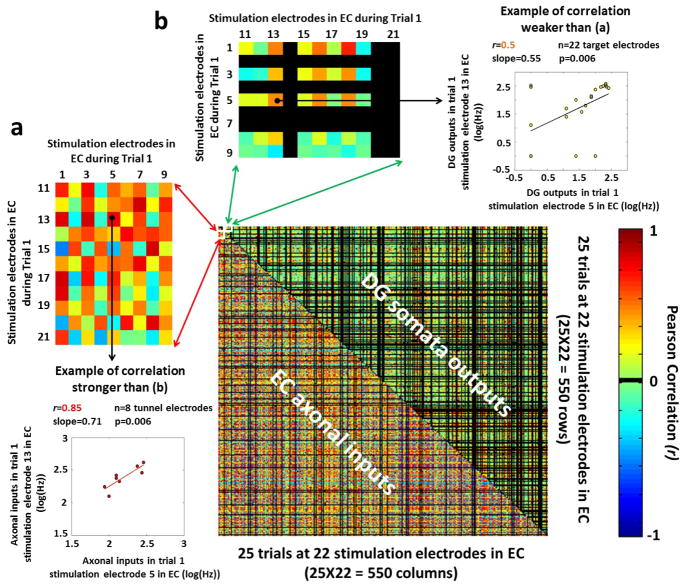
In order to evaluate DG target as a pattern separator of its transmitted axonal inputs from EC cells, we first analyzed the reproducibility of the correlations between the responses evoked in the tunnels and DG target well by 25 repeated paired-pulse stimulation trials applied at each of 22 sites in the EC well (supplementary figure S2). Contrary to our expectation that correlations would be reproducible across trials, we found weak reproducibility of the correlations not only between EC somata inputs and transmitted axonal outputs (supplementary figure S2(a), r=0.18), but also between the separate EC and DG somata (Supplementary figure S2(c), r=0.12). Better reproducibility of the correlations during the stimulation trials was found between the propagated axonal inputs from EC to DG and DG target somata outputs (supplementary figure S2(b), r=0.4). Furthermore, the correlated axonal inputs transmitted from EC into DG through the tunnels and the correlated DG target outputs did not consistently distribute around a fixed Pearson coefficient (supplementary figure S3(a) and S3(b), respectively), indicating a weak reproducibility of the correlations during the trials not only among the axonal inputs but also among the somata outputs. Supplementary figure S3(c) supports this result analyzing 4 arrays and showing high variability of the coefficients of variation (CV) of the Pearson correlations for the evoked responses in the tunnels and DG target well. Because of this weak reproducibility of the correlation values, we first considered the spiking activity evoked by each of the 25 paired-pulse stimulation trial applied at each of 22 sites in the EC well. We then evaluated the Pearson correlations between the rate patterns evoked by all possible combinations of trials and stimulus locations (i.e., (22 source stimulation sites x 25 trials)² = 302,500 correlation values) for the axonal inputs and the target somata outputs. The rationale of this analysis was to test the separation of the axonal inputs propagated via micro-tunnels into DG target outputs, demonstrating inputs more correlated than outputs. To facilitate the comparison of these symmetric Pearson correlations, we assembled in a matrix the correlations extracted from the non-repeated combinations trials/stimuli ((302,500 /2)-275=150,975 non-repeated combinations). The process of assembling the matrix is shown in panel 5(a) (for correlation among axonal inputs) and 5(b) (for correlation among somata outputs). The larger matrix in figure 5 shows correlations among axonal inputs (below diagonal) and those among somata outputs (above diagonal) for one array example and for the same set of stimuli and trials in EC. Information transmission in this EC-DG couple provided evidence of pattern separation as Pearson correlations among the axonal inputs (more red below diagonal; zoom in 5(a)) were greater than those obtained among the DG somata outputs (more green above diagonal; zoom in 5(b)). Specifically, the averages of non-zero absolute values of the correlation coefficients (r) among these axonal inputs were two-fold higher (0.5±0.0007) than the correlations among DG target outputs (0.26±0.0008) (p<10⁻⁶ by two-tailed t-test). We also provided a further qualitative evidence of pattern separation observing that 55% (82,710/150,975) of these Pearson coefficients in DG target well were equal to zero (uncorrelated outputs), 2.6x times more than the 21% (32,147/150,975) in the tunnels (uncorrelated inputs).

Figure 5.

Correlations extracted from the non-repeated combinations trials/stimuli in EC and assembled in one single matrix showing axonal spike rates evoked in the tunnels (below diagonal) more correlated than the DG target outputs (above diagonal). Note the larger fraction of r=0 (black) correlations among somata outputs than axonal inputs. (a) Examples of correlations among axonal inputs evoked by specific stimulation electrodes in EC during the first stimulation trial. Scatter plot (below) between two of these aforementioned axonal inputs: axonal inputs during trial 1, stimulation electrode 13 in EC vs. axonal inputs during trial 1, stimulation electrode 5 in EC). (b) Examples of correlations among somata outputs evoked by specific stimulation electrodes in EC during the first stimulation trial. Scatter plot (right) between two of these somata outputs: somata outputs during trial 1, stimulation electrode 13 in EC vs. somata outputs during trial 1, stimulation electrode 5 in EC.

Analog approach based on correlation distances between input and output rate patterns showed strong pattern separation in dentate gyrus and CA3, but evidence for pattern completion in CA1 and EC

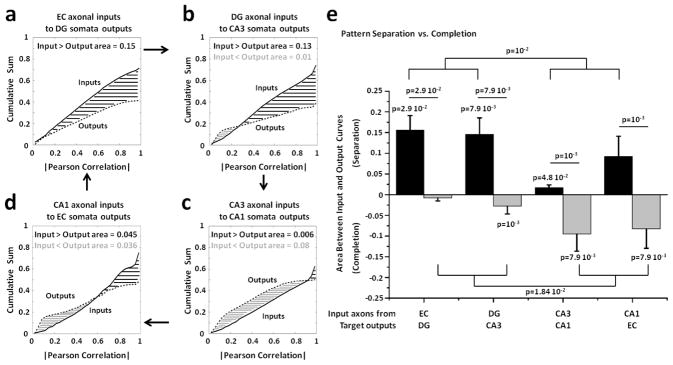
To further quantify the relative amounts of pattern separation and pattern completion we compared the distributions of the correlation distances between the transmitted axonal inputs and target somata outputs. For this comparison, we aggregated these correlations into a cumulative sum, obtaining one curve for the inputs and one for the outputs. We then quantified any separation and completion of the transmitted axonal inputs as differences between these input and output cumulative distributions of correlation values (see Methods). Figure 6 shows the input (solid line) and output (dashed line) cumulative distributions from multiple arrays. Evidence for pattern separation was inferred when the cumulative distribution of the correlations among axonal inputs was greater than the cumulative distribution of the correlations among somata outputs. Therefore, the magnitude of the area difference between these two distributions indicated the correlation distance between inputs and outputs. We found strong pattern separation not only for the EC axonal inputs propagated through the tunnels into DG (figure 6(a); area of 0.15, n=4 arrays) but also for the DG axonal inputs transmitted into CA3 (figure 6(b); area of 0.13, n=5 arrays), suggesting two successive stages of pattern separation. CA3 axonal inputs propagated into CA1 target well showed evidence of pattern completion (figure 6(c); area of 0.08, n=5 arrays), while a balance between pattern separation and completion was found for CA1 axonal inputs transmitted into EC target well (figure 6(d); n=5 arrays). Statistics of these results are shown in figure 6(e) where we compared pattern separation and completion degree in each set of sub-regions. We found pattern separation significantly greater than completion in EC-DG and DG-CA3 networks, confirming the separation of the axonal inputs in these co-cultures and, therefore, the successive stages of pattern separation shown in panel (a) and (b). We also confirmed a preference for pattern completion in CA3 to CA1 link, as well as the pattern completion at low correlation values and pattern separation at high correlations in the CA1 to EC link.

Figure 6.

Comparison of the distributions of the correlation distances between input and output rate patterns show strong pattern separation in dentate gyrus and CA3, but evidence for pattern completion in CA1 and EC. The first four panels show the cumulative distribution of the correlations among axonal inputs in micro-tunnels (solid line; Pearson correlations in absolute value) vs. the cumulative distribution of the correlations among target outputs (dashed lines). The area between curves, evaluated for each hippocampal pair, quantifies pattern separation (black; Outputs < Inputs) and pattern completion (gray; Outputs > Inputs). (a) Distribution of correlation distances from 4 EC-DG arrays between rate patterns evoked by all non-repeated combinations of 22 stimulation sites and 25 trials (n = 4 x 150,975 = 603,900 comparisons). Asymptotes are below 1 as only non-zero correlation values are used. (b) DG-CA3 networks (n=754,875 from 5 arrays). (c) CA3-CA1 networks (n=754,875 from 5 arrays). (d) CA1-EC co-cultures (n=754,875 from 5 arrays). (e) Black bar heights are the average integrated areas for pattern separation (inputs greater than outputs) from multiple arrays of the same configuration of hippocampal sub-regions (n=4 for EC-DG networks, n=5 for the other co-cultures). S.E.M. is a function of the variance for each of these 4 or 5 replicate configurations. Similarly, gray bar heights represent the average integrated areas for pattern completion (inputs less than outputs). Note that some configurations contain evidence for both pattern separation and pattern completion. Since the normality assumption fails by the Kolmogorov-Smirnov test, we perform the non-parametric Wilcoxon Rank Sum test. Pattern separation in EC-DG and DG-CA3 is significantly greater than zero (p=0.03 and p=0.008, respectively). In the same hippocampal sub-networks, pattern separation is significantly greater than the pattern completion (p=0.03 and p=0.008 for EC-DG and DG-CA3, respectively) and different from the pattern separation observed in the other sub-regions (p=0.01). CA3-CA1 co-cultures show a significant bias toward pattern separation (p=0.048) and completion (p=0.008). Furthermore, pattern separation is significantly greater than the pattern completion (p=0.001). CA1-EC networks also show significantly difference between pattern separation and completion (p=0.001) and a significant bias toward pattern completion (p=0.008). Finally, pattern completion in the co-cultures with CA1 involvement is significantly different from the co-cultures with DG neurons (p=0.02).

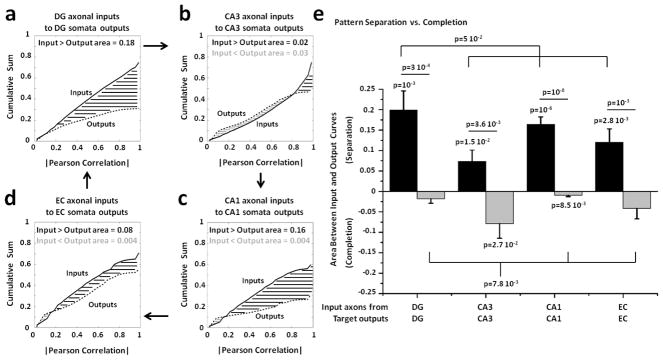
We also created homologous controls consisting of DG-DG, CA3-CA3, CA1-CA1 and EC-EC to evaluate and compare the specificity of pattern separation and completion with co-cultures of the same region alone. DG axonal inputs transmitted through the tunnels into DG target outputs provided the strongest evidence for pattern separation (figure 7(a); area between curves for separation equal to 0.18), compared to the other configurations (area between curves=0.02 for CA3-CA3 in panel (b), 0.16 for CA1-CA1 in panel (c) and 0.08 for EC-EC in panel (d)). Figure 7(e) shows the statistics from multiple arrays indicating pattern separation in DG-DG networks greater than zero and statistically different not only from the pattern completion in the same networks but also from the degree of separation of the other regions. This strong pattern separation with DG-DG networks, similar to that of EC-DG and DG-CA3 in figure 6, may relate to the high levels of inhibitory neurons in DG networks and in the hilus in vivo compared to CA3 networks (Brewer et al 2013). It suggests that DG pattern separation is more inherent in the DG networks than from the fan-out of axons into a more numerous DG target. Without DG or CA1 paired to CA3, CA3-CA3 co-cultures showed evidence of both pattern separation and completion, consistent with CA3 as an auto-association network (Rolls 2015). We also found evidence of pattern separation in CA1-CA1 and EC-EC networks.

Figure 7.

Control networks show distributions of correlation distances of axonal input and somata output rates indicative of pattern separation in DG, CA1 and EC. (a) Cumulative distributions of non-zero correlation distances of input and output rate patterns evoked by all non-repeated combinations of 22 stimulation sites and 25 trials from 5 DG-DG arrays stimulated in both chambers (n=5 arrays x 150,975 correlations x 2 stimulated chambers =1,509,750 correlation values). (b) Five CA3-CA3 networks (n=1,509,750). (c) Five CA1-CA1 networks (n=1,509,750). (d) Five EC-EC co-cultures (n=1,509,750). (e) Pattern separation in DG-DG networks is significantly greater than zero (p=0.001) and statistically different not only from the pattern completion in the same networks (p=0.0003) but also from the separation degree of the other regions (p=0.05). CA3-CA3 co-cultures show evidence of pattern separation and completion greater than zero (p=0.015 and p=0.027, respectively). CA1-CA1 networks show significant pattern separation (p=10⁻⁶) and completion (p=0.0085). Furthermore, pattern separation is statistically different from pattern completion (p=10⁻⁸). Pattern separation in EC-EC networks is significantly greater than zero (p=0.0028) and statistically different from pattern completion (p=0.001). Statistically significant differences have been assessed by one and two-tailed t-tests.

Finally in this analog rate approach, we compared the above measured spike rates evoked by both pulses in 80 ms (40 ms x 2 pulses) with the ratio of the relative rates evoked by the second pulse to those evoked by the first pulse (i.e., potentiation ratio). We first found both facilitation and substantial depression with lower spike rates after the second pulse (supplementary figure S4). Then, contrarily to the separation of EC somata inputs into DG somata outputs, we observed that this facilitation or depression did not influence the separation of the EC axonal rate patterns transmitted through the tunnels into DG (supplementary figure S5).

Digital approach based on spatial population distances between binary input and output patterns showed the contribution of the dentate gyrus as separator of its EC axonal inputs

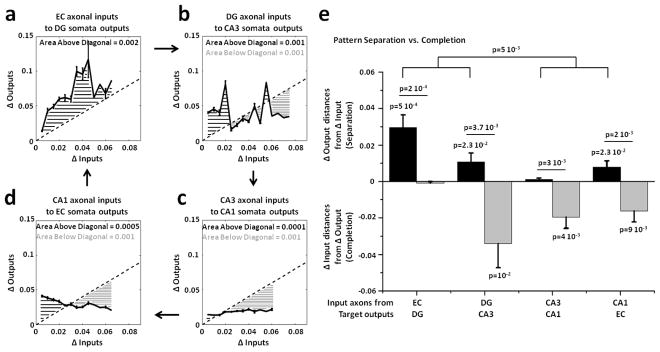
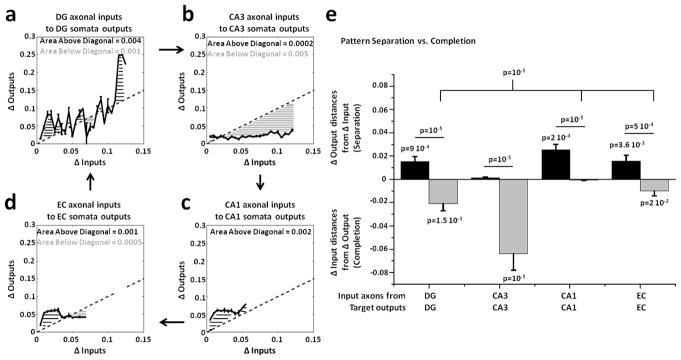
Since we applied an analog approach based on the correlation distances between input and output rate patterns, we also sought additional support from an alternative digital approach based on spatial population distances between binary input and output patterns using the Jaccard distance (JD, see Methods). This approach evaluated the differences among the binary inputs evoked in the tunnels by all stimulation sites (Δ Inputs) and compared them to the differences among all somata outputs evoked in the target well (Δ Outputs). JD measured the variations between two binary vectors distinguishing active (1) and silent electrodes (0). These distances were normalized over the number of active units to control the sparseness of the responses (Chavlis et al 2017). The property of pattern separation requires that similar inputs produce more dissimilar outputs. Hence we expected the change in somata target outputs (Δ Outputs) to be greater than the change in axonal inputs (Δ Inputs) during pattern separation and the reverse for pattern completion (Δ Outputs < Δ Inputs). Figure 8 compares these input and output variations of the input and output spatial binary patterns evoked by all possible non repeated combinations of 22 stimuli applied in EC in EC-DG (a), in DG in DG-CA3 (b), in CA3 in CA3-CA1 (c) and in CA1 in CA1-EC (d) networks. We found not only strong evidence of DG as a separator of its EC axonal inputs transmitted through the tunnels ((a); black area above diagonal equal to 0.002) but also evidence for pattern completion (gray area below diagonal equal to 0.001) in CA3 (b), CA1 (c) and EC (d) target regions. The average of the excess distances represented in the previous panels of Δ Outputs > ΔInputs above the diagonal (black bars) and the average of the excess distances of ΔOutputs < ΔInputs below the diagonal (gray bars) are shown in figure 8(e). Pattern separation of the axonal inputs propagated through the tunnels into target well was statistically significant in EC-DG, DG-CA3 and CA1-EC, but not in CA3-CA1. Pattern completion, measured by using the distances from the diagonal of the Δ Outputs lower than Δ Inputs, was significant for DG-CA3, CA3-CA1 and CA1-EC, but not for EC-DG. Furthermore, pattern separation and completion were significantly different in EC-DG, DG-CA3, CA3-CA1 and CA1-EC. Also, pattern separation in EC-DG and DG-CA3 (i.e., when DG is involved) was significantly different from CA3-CA1 and CA1-EC. Pattern completion was significantly greater than zero in DG-CA3, CA3-CA1 and CA1-EC networks. Finally, we found a significant decrease in pattern separation starting from EC to DG to CA3 and to CA1 (one-way ANOVA, p=0.0009), and evidence for completion from the other target regions (one-way ANOVA, p=0.026) (statistics not shown in the figure).

Figure 8.

Spatial population distances adjusted for sparseness between binary input (Δ Inputs) and output (Δ Outputs) patterns show pattern separation EC axonal inputs transmitted into DG and completion of DG axonal inputs propagated into CA3. Δ Inputs vs. Δ Outputs describe pattern separation (Δ Outputs > Δ Inputs) and completion (Δ Outputs < Δ Inputs). The first four panels depict the area above (black) and below (gray) the diagonal (Δ Outputs=Δ Inputs). The curves shown in these panels are obtained by evaluating the mean and S.E.M of Δoutputs (y axis) in constant bins of 0.005 allocated to the Δinput values of each pair. Since the maximum value of the spatial population distance could change from one pair to another, by using the same bin size we can have different numbers of bins involved. (a) Δ Outputs vs. Δ Inputs extracted from the spatial population distances between all non-repeated couples of binary patterns evoked in the tunnels and in DG by 22 stimuli in EC for 4 arrays (n = 4 x 231 = 924 comparisons; 0.005 bin size x 13 bins). (b) DG-CA3 (n=1,155 from 5 arrays in 15 bins). (c) CA3-CA1 (n=1,155 from 5 arrays in 12 bins). (d) CA1-EC (n=1,155 from 5 arrays in 13 bins). (e) Separation is measured by the sum of the excess distances of Δ Outputs > Δ Inputs above the diagonal (Δ Outputs=Δ Inputs), divided by the number of bins (black bars). Separation is significant for EC-DG (p=0.0005), DG-CA3 (p=0.023) and CA1-EC (p=0.023), not for CA3-CA1. Completion, similarly measured by the average of the excess distances of Δ Outputs < Δ Inputs (gray bars) below the diagonal, is significant for DG-CA3 (p=0.01), CA3-CA1 (p=0.004) and CA1-EC (p=0.009), not for EC-DG. Separation is also different from completion for EC-DG (p=10⁻⁵), DG-CA3 (p=0.0037), CA3-CA1 (p=0.003) and CA1-EC (p=0.002). Separation in EC-DG and DG-CA3 (i.e., when DG is involved) is further different from CA3-CA1 and CA1-EC (p=0.005). Statistical analyses have been assessed by one and two-tailed t-tests.

The subregion-specific events were controlled by evaluation of networks with homologous subregions in each compartment, as above. Figure 9 shows the input and output variations between all possible non-repeated couples of binary input or output spatial patterns evoked by 44 stimuli (22 stimulation sites in each well) in DG-DG, CA3-CA3, CA1-CA1 and EC-EC networks. Statistics and comparisons are shown in panel (e) where pattern separation was significant in DG-DG, CA1-CA1 and EC-EC. Pattern completion was strongest in CA3-CA3, but also seen in DG-DG and EC-EC. Notably, pattern separation decreased by 50% in DG-DG compared to levels in EC-DG (figure 9(e) vs. 8(e)), suggesting the importance for this digital approach of the “kind of inputs” and not just the number of neurons. The strong pattern completion in CA3-CA3 was consistent with the role of recurrent collaterals in CA3. Finally, evidence for pattern completion was nearly absent in CA1-CA1 and EC-EC compared to the heterologous networks.

Figure 9.

Spatial population distances adjusted for sparseness show a separation of DG axonal inputs in DG-DG control networks that is weaker than EC-DG co-cultures, while CA3 patterns appear to self-complete. (a) Δ Outputs vs. Δ Inputs extracted from the spatial population distances between all non-repeated couples of binary input or output patterns evoked by 44 stimuli (22 stimulation sites in each well) in 5 DG-DG arrays (n = 5 x 2 x 231= 2,310 comparisons; 0.005 bin size x 25 bins). (b) CA3-CA3 (n = 5 x 2 x 231= 2,310 from 5 arrays in 23 bins). (c) CA1-CA1 (n = 5 x 2 x 231 = 2,310 from 5 arrays in 11 bins). (d) EC-EC (n = 5 x 2 x 231= 2,310 from 5 arrays in 14 bins). (e) Pattern separation, measured by the sum of the excess distances of Δ Outputs > Δ Inputs above the diagonal, divided by the number of bins (black bars), is significant for DG-DG (p=0.0009), as well as CA1-CA1 (p=0.0002) and EC-EC (p=0.0036). Pattern completion, similarly measured by the average of the excess distances of the Δ Outputs < Δ Inputs (gray bars) below the diagonal, is significant for DG-DG (p=0.0015), CA3-CA3 (p=10⁻⁵) and EC-EC (p=0.02). Pattern completion is significantly different from separation for DG-DG (p=10⁻⁵), CA3-CA3 (p=10⁻⁵), CA1-CA1 (p=10⁻⁵) and EC-EC (p=0.0005). Pattern completion in CA3-CA3 is also significantly different from the other regions (p=10⁻⁵). Statistical significance was assessed by one and two-tailed t-tests.

Discussion

A clear distinction in the hippocampus of the separation or completion mechanism both in rate coding changes and binary engagement is lacking at neuronal population levels in vivo. Modeling results favor a population mechanism, while in vivo data has been largely analyzed for rate codes with less consideration of populations (Santoro 2013). Here we discuss the historical underpinnings of these mechanisms and how our approaches provide the first direct measures at the scale of small neural populations.

Historically, the property of pattern separation was pioneered in the visual system (Kulikowski 1978). The hippocampal studies have been largely in vivo with behavioral inputs and recording from one hippocampal sub-region, at the macro level by using fMRI and EEG measures, or in silica, all inspired by hippocampal anatomy. The sub-regional anatomy of the hippocampus provides a basis for differential coding schemes. For example, the number of DG neurons in the rat (1.2 million) exceeds by 11-fold those in the primary inputs from layer II of the EC (Amaral et al 2007). Human numbers are a much larger at 18 million DG neurons, a 27-fold increase from those in the human layer II of the EC. This anatomy alone suggests a fan-out flow of information needed for pattern separation, but does not establish the functional relationship. Carefully designed in vivo shifts in visual inputs or changes to the rat physical environment evoke pattern separation as de-correlations in coincidence patterns in the dentate gyrus and recruitment of distinct cell assemblies in the rat CA3 (Leutgeb S and Leutgeb J K 2007, Leutgeb et al 2004, Leutgeb et al 2005, Neunuebel and Knierim 2014). However, the nature of activity in the EC producing effects in DG as well as the axonal transmission after EC processing remain unknown by this approach. Macroscopic human EEG or fMRI studies also indicate a role for the DG in behavioral discrimination of small changes in visual inputs (Bakker et al 2010, Kirwan and Stark 2007, Yassa and Stark 2011, Santoro 2013), but again without knowledge of the specific input patterns or the axonal transmission involved. Early computational modeling (Marr 1971) proposed a role for the hippocampus in pattern separation that was better specified by more recent modeling, including feedback from hilar inhibitory neurons (Myers and Scharfman 2009), feedback from CA3 to DG (Myers and Scharfman 2011, Faghihi and Moustafa 2015) and dendritic branching (Chavlis et al 2017). Our live model will enable monitoring the development of these proposed inhibitory neurons and the need for back propagation in this EC-DG-CA3 function of pattern separation.

The recurrent collateral anatomy of the CA3 (Lebovitz et al 1971) suggests a coding mechanism involved in pattern completion (Leutgeb et al 2005). Evidence for pattern completion is clear even within slices of the rat hippocampus (Jackson 2013). Pattern completion dependent on recurrent collaterals has been modeled based on recurrent excitation to mediate auto-association (Treves and Rolls 1994) with attractor dynamics (Renno-Costa et al 2014), but again without knowledge of the distinct input patterns or the axonal transmission involved.

To better understand the computation transmitted between sub-regions, in this study, we focused on the measurement of axonal communication that occurred through micro-tunnels between hippocampal sub-regions. Our engineered networks uniquely allowed electrical monitoring of the activity of individual axons that pass through the tunnels and connect each neural population, in addition to equal access to neuronal activity at 22 electrodes in each of two wells (Brewer et al 2013, Poli et al 2015, Bhattacharya et al 2016, Poli et al 2017a). This improved access to multiple sites has also facilitated identification of spatial-temporal motifs for transmission (Bhattacharya et al 2016), dependence of transmission fidelity on tunnel density (DeMarse et al 2016), sparse coding (Poli et al 2017a) and stimulation at different locations. Transitions from potentiation to inhibition indicated frequent inhibition resulting in reduced output transmission in axons and in the target. This inhibition could be due to alternative routing (Jimbo et al 1999, Ide et al 2010, Poli et al 2016) or related to stimulation applied during off states of the network (Lee and Dan 2012).

Taking advantage of the axonal accessibility, we tested the hypothesis that DG co-cultured neurons separated patterns of the distinct EC axonal inputs transmitted through axons in the tunnels better than the other subregions at a continuous analog and/or discrete digital level. Based on an analog rate approach, the strong axonal spike rates evoked in the tunnels by different EC stimulation sites correlated more strongly than the DG somata outputs, consistent with pattern separation. Moreover, target outputs showed more dissimilar responses than their axonal inputs not only in EC-DG but also in DG-CA3 networks i.e., when DG neurons were involved. For this analog approach, we found pattern completion in CA3 surprisingly weaker than in the CA1 as target.

The sparsity of CA3 encoding (Poli et al 2017a) led us to consider possible digital encoding of the pattern separation and completion compared to the analog rate approach. This digital encoding of the pattern separation was equally robust in EC to DG, while pattern completion appeared more robustly encoded by the digital discrimination of spatial changes in inputs from DG into CA3 that continued with CA3 into CA1 and CA1 into EC. Thus, by considering the axonal inputs transmitted through the tunnels as digital information of the stimulus locations, changes in the spatial distribution of output may better describe pattern completion than their firing rates.

In conclusion, this study provides the first direct measures of pattern separation and completion at the rate and digital population levels, focusing on axonal transmission to the somata target outputs in live neuronal networks representing each of four stages of the EC-DG-CA3-CA1 circuit. This result translates the largely cognitive concepts of pattern separation and completion from the realm of behavioral decoding down to the level of intrinsic wiring and digital decoding properties of self-wired neurons in specific regions of the hippocampus. The reductionist approach down to a two-dimensional network with access to every neuron should enable functional mapping of the connections to establish coding mechanisms. However, our reductionist two-dimensional cultures have limitations for application to the in vivo 3D lamellar hippocampus. Some of these limitations have mitigating advantages, like the wealth of information obtained with hippocampal slices. While limitations of our system include a lack of behavioral inputs, advantages include greater control of inputs via stimulation electrodes in ways not possible with behavioral stimulation. Our system has reduced levels of astroglia, microglia and inputs from other modulating systems such as cholinergic and dopaminergic systems. As we have done previously, we could specifically determine the network effects of added astroglia (Chang et al 2006, Boehler et al 2007) or with added microglia (Viel et al 2001). Furthermore, our engineered network devices could possibly benefit from the higher resolution available in MOSFET arrays of 4096 electrodes (Ullo et al 2014).

Conclusion

Our studies have begun to fill the meso-scale gap of cell assemblies between molecular-synaptic and macroscopic EEG or fMRI measures, assigning distinct functions of pattern separation to the DG and pattern completion to the CA3 neuronal assemblies without knowledge of individual synaptic weights or circuit changes from excitation to inhibition. By controlling the axonal growth inside the micro-tunnels, we were able to discriminate single axon signals as scaled inputs that were more specific than the categorical behavioral inputs of uncertain scaling (behavioral discrimination) used in several in vivo studies. Therefore, to the best of our knowledge, this work could be the first report of pattern separation and completion directly measured at the level of axons to sub-networks in the EC-DG-CA3-CA1 circuit. The significance of these findings is heightened by impaired pattern separation in aging (Paleja and Spaniol 2013), Alzheimer’s disease (Ally et al 2013) and in schizophrenia (Das et al 2014).

In the future we will use this in vitro electrode array technology and engineered devices to realize a four-chamber system in which all four different hippocampal sub-networks develop on the same array, interconnected via micro-tunnels for axonal communication in a reconstituted hippocampal loop.