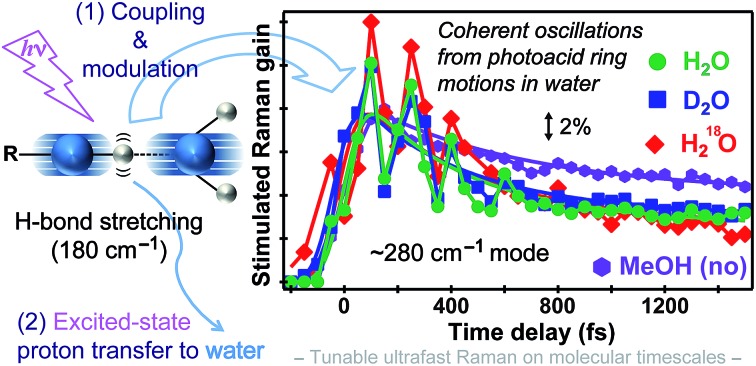
 Primary events that power ultrafast excited state proton transfer in water are revealed to involve coupled intermolecular and intramolecular motions.
Primary events that power ultrafast excited state proton transfer in water are revealed to involve coupled intermolecular and intramolecular motions.
Abstract
Photochemistry powers numerous processes from luminescence and human vision, to light harvesting. However, the elucidation of multidimensional photochemical reaction coordinates on molecular timescales remains challenging. We developed wavelength-tunable femtosecond stimulated Raman spectroscopy to simultaneously achieve pre-resonance enhancement for transient reactant and product species of the widely used photoacid pyranine undergoing excited-state proton transfer (ESPT) reaction in solution. In the low-frequency region, the 280 cm–1 ring deformation mode following 400 nm photoexcitation exhibits pronounced intensity oscillations on the sub-picosecond timescale due to anharmonic vibrational coupling to the 180 cm–1 hydrogen-bond stretching mode only in ESPT-capable solvents, indicating a primary event of functional relevance. This leads to the contact ion pair formation on the 3 ps timescale before diffusion-controlled separation. The intermolecular 180 cm–1 mode also reveals vibrational cooling time constants, ∼500 fs and 45 ps in both H2O and D2O, which differ from ESPT time constants of ∼3/8 and 90/250 ps in H2O/D2O, respectively. Spectral results using H218O further substantiate the functional role of the intermolecular 180 cm–1 mode in modulating the distance between proton donor and acceptor and forming the transient ion pair. The direct observation of molecular structural evolution across a wide spectral region during photochemical reactions enriches our fundamental understanding of potential energy surface and holds the key to advancing energy and biological sciences with exceptional atomic and temporal precision.
Introduction
Photochemical reactions lie at the heart of biological and energy processes and their primary molecular events occur on femtosecond to picosecond timescales. Elucidating reaction mechanisms of photosensitive functional chromophores is therefore crucial. In recent years, low-frequency atomic motions have been widely uncovered in the choreography of chromophores in heme proteins,1,2 rhodopsin,3 photosynthetic proteins,4,5 and green fluorescent protein (GFP).6 Such skeletal motions may dominate the primary molecular events and project strongly along the reaction coordinate to facilitate highly efficient reactions such as isomerisation or proton transfer.3,7–9 Therefore, the real-time dynamics, coupling, and interplay of these low-frequency motions among themselves or to other motions on the excited state potential energy surface (PES) are of pivotal importance to understand, engineer, and optimize chemical reaction pathways.
Despite the wealth of information obtained in the transient electronic domain, the broad detection range and sufficiently high spectral and temporal resolutions afforded by vibrational spectroscopy provide critical means to observe photoinduced changes in molecular structure. The addition of a precisely controlled time dimension means that nuclear motions in a multidimensional PES can be mapped in the electronic excited state starting from the Franck–Condon region. Previous useful experiments such as time-resolved resonance Raman (TR3) spectroscopy offer wide spectral coverage and sufficient frequency resolution (<15 cm–1), but typically for studying picosecond (ps) or longer processes due to the narrowband pulses used.10,11 Though time-resolved impulsive Raman achieves desirable high time resolution, it requires long data collection with fine steps in the time domain and resolves features mostly in the low-frequency region.12 Moreover, femtosecond mid-infrared spectroscopy can provide transient vibrational spectra with reasonable time resolution, but is commonly limited to high-frequency region (>1000 cm–1).8,13 In recent years, femtosecond stimulated Raman spectroscopy (FSRS) has provided a very powerful alternative by offering simultaneously high temporal and spectral resolutions to directly track molecular structural evolution across a broad frequency range (ca. 50–3500 cm–1) from the electronic ground to excited state.14–17 Tunable laser pulses can further enhance FSRS signals and improve signal-to-noise ratio (SNR) because the Raman pump can be tuned closer to resonance with an electronic transition during chemical reactions.
In this work, we exploit wavelength-tunable FSRS and investigate excited state proton transfer (ESPT) of the widely used photoacid pyranine (8-hydroxypyrene-1,3,6-trisulfonic acid, HPTS), a paradigm for proton motions in water.7,8,18–21 Previous results showed multi-stage proton transfer processes involving the formation and separation of the charge-separated contact ion pair on the ps timescale.19,20,22–25 In contrast to direct proton transfer from HPTS to carboxylate ions which can occur within ∼200 femtoseconds (fs) at high base concentrations,8,23,26 pure water provides a general environment with moderate H-bonding strength that can elucidate aqueous proton transfer pathways with different number of intervening water molecules,19,21,27 revealing characteristic time constants of ∼3 and 90 ps in the commonly reported kinetic scheme for ESPT. Based on femtosecond transient absorption results, we select a strategic Raman pump wavelength at 580 nm that pre-resonantly enhances both the photoexcited protonated and deprotonated chromophore through the entire time window, directly tracking molecular structural evolution of the photoacid along multiple atomic motion trajectories. Notably, no tapered Fourier filters are needed to retrieve underlying vibrational coherences from an electronic response signal28 because we directly observe time-resolved vibrational modes across a wide spectral window starting from time zero of photoexcitation. The onset of ESPT in water is delineated to involve anharmonic coupling between functionally relevant low-frequency (i.e., <350 cm–1) vibrational modes in the first electronic excited state (S1). Our findings highlight the integral role of anharmonic interaction between intramolecular and intermolecular vibrations on the intrinsic molecular timescales. This “functional” interaction optimizes local conformational space surrounding the photoexcited chromophore not limited to the proton dissociation site, effectively lowers the photochemical reaction barrier, and facilitates proton transfer in a rapidly relaxing environment with extensive hydrogen (H)-bonds around the photoacid.
Results and discussion
Ground-state FSRS characterization of the photoacid in solution
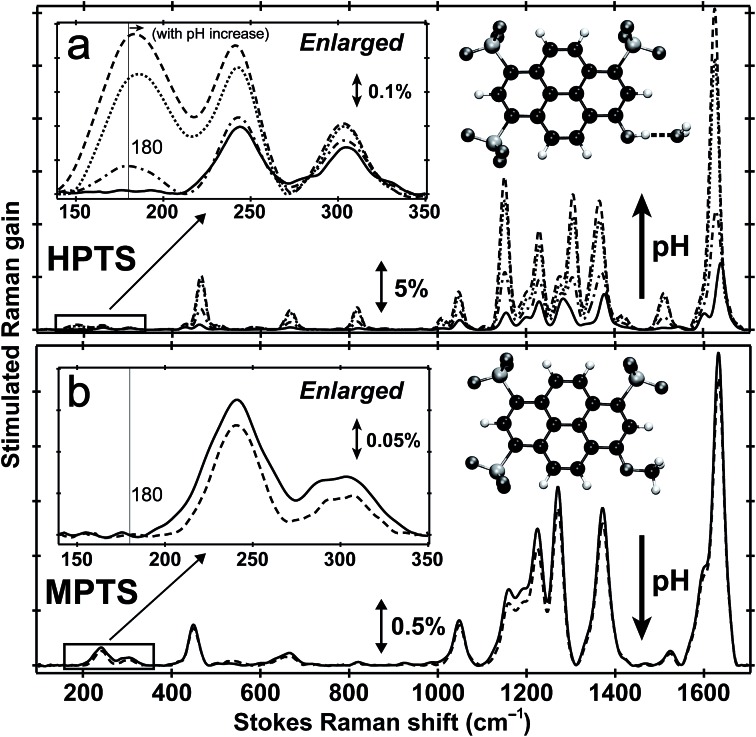
Fig. 1 shows the pH-dependent ground-state FSRS spectra of HPTS and its methylated derivative, MPTS. The localized ring-H bending and bond stretching modes are typically above 1000 cm–1, whereas lower-frequency modes mainly consist of skeletal motions and intermolecular vibrations.21 Notably, in basic solution the Raman modes of the largely deprotonated chromophore (photobase form, or PB) are enhanced because the PB absorption is closer to resonance with the 580 nm Raman pump compared to the photoacid (PA) form of the chromophore (see Fig. S1 in the ESI†). In the low-frequency region, the ∼240 and 305 cm–1 modes arise from ring in-plane and out-of-plane (OOP) deformation. The ∼180 cm–1 mode converts to ∼186 cm–1 for HPTS in H2O/D2O at pH/pD = 12 (see Fig. 1a inset and Fig. S2† inset, and mode depiction in Fig. S3a in ESI†), representing the change from PA to PB H-bonding mode. Notably, the solvent subtraction enables us to observe this mode free from bulk water so the spectral change as a function of pH/pD reflects the specific interaction between the chromophore and the solvent molecule(s). In systems without H-bonding at potential proton donating site, e.g., MPTS in H2O, this 180 cm–1 mode is largely absent across a wide pH range (Fig. 1b) so it is presumably an OH···OH2 mode. These spectral data suggest a strong connection of this particular low-frequency mode to H-bond interaction in solution.
Fig. 1. Ground-state FSRS of 40 mM HPTS and 20 mM MPTS in H2O. (a) HPTS in H2O at pH = 4.5 (solid), 7 (dash-dotted), 9 (dotted), and 12 (dashed line) from ∼100–1700 cm–1. The enlarged low-frequency region between 140 and 350 cm–1 is shown in the insert (left). (b) MPTS in H2O at pH = 4.5 (solid) and 12 (dashed line). The enlarged low-frequency region is shown. Molecular structures of HPTS (H-bonded to one nearby water molecule) and MPTS are depicted in the inset (right). Carbon, oxygen, and hydrogen atoms are depicted in black, dark gray, and white spheres, respectively. The Raman gain magnitude is indicated by the double-arrowed line. The largely featureless aqueous solvent blank spectrum has been subtracted. Notably, we only use this high sample concentration to enhance ground-state vibrational peaks particularly in the low-frequency region.
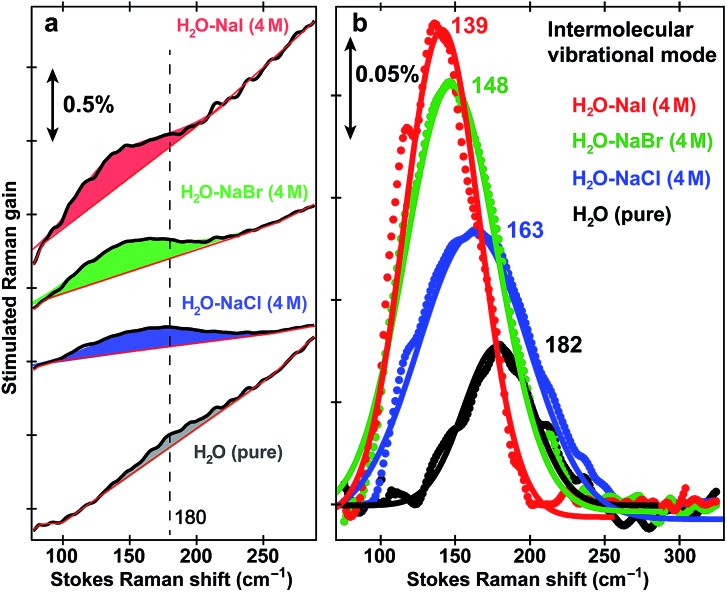
To further substantiate the mode assignment, FSRS was performed on water with various halide ions focusing on the low-frequency region (see Experimental). Fig. 2 shows that the ∼182 cm–1 mode appears in the ground-state FSRS spectrum of pure water, and redshifts by ∼19, 34, and 43 cm–1 upon adding 4 M Cl–, Br–, and I–, respectively.29 The Raman intensity rise in Fig. 2b indicates that the electric polarisability of the O–H···X– (X = Cl, Br, I) bond stretching mode increases as the halide ion becomes larger and heavier while interacting with water in the H-bonding complex. Therefore, we can unambiguously assign the observed ∼180 cm–1 mode of HPTS to its intermolecular H-bond stretching (O–H/D···O) in water,29–31 also corroborated by DFT calculations (see Fig. S3 in ESI†).32 In comparison with low pH conditions where the 180 cm–1 mode is largely absent (i.e., similar to bulk water so after spectral subtraction, it is within the SNR in Fig. 1a inset), the observed Raman mode intensity increase and frequency blueshift in high pH solution can be ascribed to stronger H-bonding interaction and reduced RO–···H/D–OH/D distance between water and a deprotonated chromophore (ROH is the photoacid form), respectively. It also shows that FSRS is capable of directly probing low-frequency modes below ∼200 cm–1 with high sensitivity that distinguishes specific H-bonds from the bulk water H-bonding network.
Fig. 2. Intermolecular H-bond stretching mode in H2O and aqueous salt solutions. Ground-state FSRS spectra of pure water (black) and aqueous solutions with 4 M halide salts: NaCl (blue), NaBr (green), and NaI (red) raw data are shown with the baselines in (a), and after pure water peak subtraction (except for water itself) and baseline removal in (b), respectively. The 580 nm Raman pump power is set at 4 mW (see the ESI†). Careful steps were taken to reduce scattering in the low-frequency region (<350 cm–1, see Experimental). The stimulated Raman gain magnitude is indicated by the double-arrowed vertical line.
Transient absorption guides Raman pump wavelength selection for excited-state FSRS
The pKa of HPTS drops from ∼7 to 0 following UV to near-UV electronic excitation and the phenolic proton transfers to surrounding solvent on ultrafast timescales.8,20–23,27 To track transient atomic motions using FSRS, we may encounter weak signal intensity due to intrinsically small Raman cross-sections.26,33 We studied ESPT reaction mechanisms of HPTS in different solvents using a conventional FSRS setup with 400 nm actinic pump and 800 nm Raman pump.21,26,34 Those reports provided useful but limited excited-state information for the photoacid (PA*) and photobase (PB*) because the 800 nm Raman pump is far from electronic resonance of HPTS in S1 (see Fig. S4 in the ESI†). This shortcoming can be overcome by tuning the Raman pump wavelength. In excited-state FSRS, when the Raman pump is electronically resonant with a transition gap, depletion of excited-state population by the Raman pump strongly competes with FSRS signal generation.33 Meanwhile, a transient absorption (TA) background generated by the Raman-pump-induced excited-state population change can distort the spectral baseline. Therefore, the Raman pump wavelength and power must be carefully selected to acquire FSRS data with high SNR and minimal TA background (see Experimental below).
In fs TA (Fig. S4a–c and e in the ESI†) following 400 nm photoexcitation of HPTS in solution, excited-state absorption (ESA) and stimulated emission (SE) of transient PA* and PB* species are clearly observed from ca. 460–660 nm on the fs-ps timescale.18–20,35 The dominant PA* ESA (SPA1 → SPAn) and PB* SE (SPB1 → SPB0) of HPTS in H2O (pH = 4.5) are spectrally adjacent (Fig. S4a in the ESI†), and as time progresses, TA shows a broad ESA band centred near 530 nm at 500 fs that evolves into to an SE band near 520 nm by 600 ps. In basic aqueous solution (pH = 12), HPTS is predominately deprotonated, and an ∼520 nm SE band from PB* dominates the TA spectrum (Fig. S4b in ESI†). In another control of HPTS in methanol with ESPT effectively blocked,20,34 the TA spectrum exhibits pure PA* ESA feature at ∼550 nm that persists longer than 600 ps (Fig. S4c and e in the ESI†). This result is consistent with the PA* fluorescence decay on the hundreds of ps to nanosecond (ns) timescale.34,36
Time-resolved excited-state FSRS of the photoacid in solution
Tuning the Raman pump to the red side of 550 nm, we observe dramatic pre-resonance enhancement of both PA* and PB* Raman features with less influence from the TA background. The enhancement effect arises because the Raman pump wavelength simultaneously matches (but is not on resonance with) the transition gap of PA* ESA as well as PB* SE37,38 which is a fortuitous property of HPTS. The 580 nm Raman pump we use is to the red side of the electronic transition features of PA* and PB* in all solvents, so the excited-state Raman peaks associated with both the protonated and deprotonated HPTS chromophore are pre-resonantly enhanced as ESPT proceeds from the reactant to product. We thus glean previously unavailable information about molecular structural dynamics along the multidimensional photochemical reaction coordinate in real time, largely free from ground state contributions.39
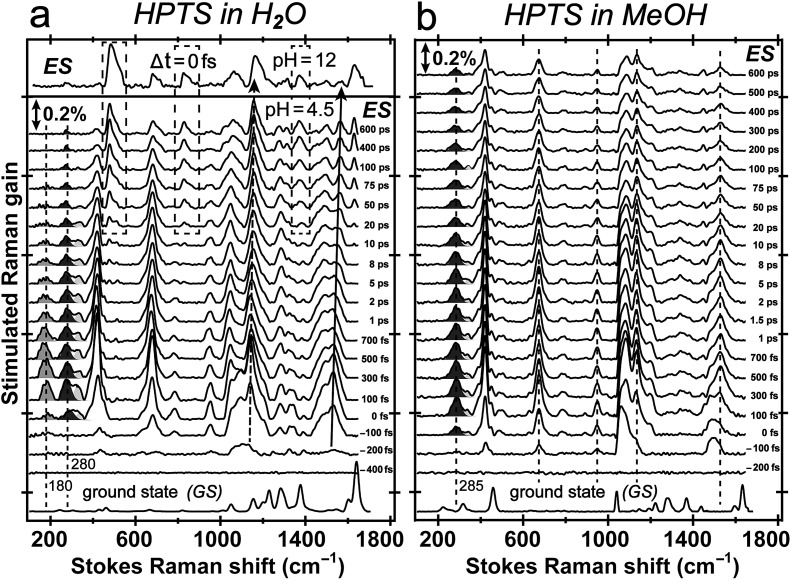
Fig. 3 reveals distinct structural evolution of HPTS from excited-state Raman intensity and frequency dynamics. Upon 400 nm photoexcitation, PA* modes emerge within ∼140 fs in both water and methanol but decay with very different time constants. Since HPTS cannot undergo ESPT in methanol,7,34 only PA* decay is observed in Fig. 3b. In contrast, HPTS in H2O exhibits PA* decay with concomitant PB* rise (Fig. 3a). By 600 ps, the modes in water have predominantly deprotonated character, confirmed by their similarity to the photoexcited chromophore spectrum at pH = 12 (Fig. 3a, and the top trace). Notably, the HPTS Raman signal strength in S1 is at least two orders of magnitude higher than previous data collected with the 800 nm Raman pump21,26,34 while the photoacid sample concentration is now at 1.5 mM versus the previously used 11 mM. In addition, the ∼180 cm–1 intermolecular PA* H-bonding mode is only observed in water that supports ESPT (see Fig. 3a in H2O, Fig. S5a in D2O in the ESI†) but not in solvents where ESPT is inhibited (Fig. 3b in methanol)34 or system without ESPT capabilities (Fig. S5b in ESI† for MPTS in H2O). Notably, HPTS H-bonds to methanol but largely in the protonated form (see Fig. S4d in ESI† for UV/Visible spectrum) so the H-bonding mode is weak. It is thus largely absent in methanol (see Fig. 3b bottom trace) as its difference from bulk methanol H-bonding mode is within the SNR of ground-state FSRS measurement. We will explore excited-state 180 cm–1 mode dynamics when a weak base is added to methanol in a future publication. These results highlight the unique sensitivity of this low-frequency, collective skeletal H-bonding mode to the deprotonation state of HPTS, and more generally, electronic and structural events near the phenolic hydroxyl end of the solvated chromophore.
Fig. 3. Time-resolved excited-state FSRS spectra between ca. 100–1700 cm–1 of 1.5 mM HPTS in water and methanol following 400 nm photoexcitation up to 600 ps. (a) HPTS in H2O at pH = 4.5. The S1 FSRS data (Δt = 0 fs) at pH = 12 is shown above. Dashed boxes highlight the emerging modes at later time of the chemical reaction. The blueshift of the ∼1140 and 1530 cm–1 modes is denoted by dashed and solid curved arrow, respectively. (b) HPTS in methanol. The dashed lines indicate largely unchanged Raman peak position in S1 as molecular structure responds to photoexcitation. The solvent-subtracted ground-state spectra are plotted at the bottom for comparison with the ground-state-subtracted excited-state spectra as a function of time delay (noted on the right to each trace) between the femtosecond actinic pump and Raman probe pulses.
Excited-state vibrational mode evolution tracks ESPT progress
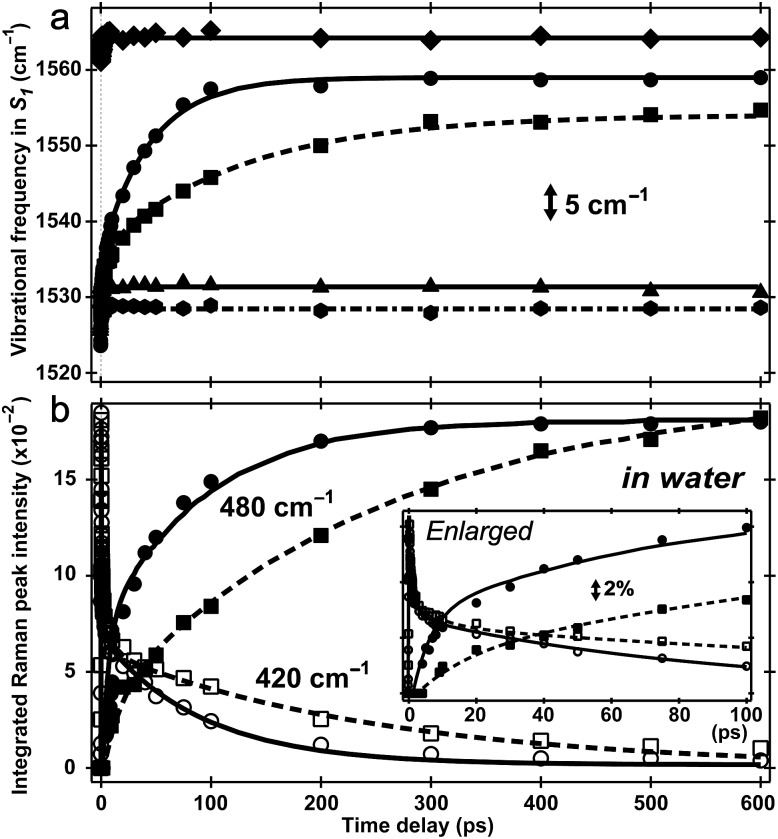
Two intense vibrational marker bands of PA*, the ring-H rocking with phenolic COH rocking at ∼1140 cm–1 and ring C C stretching with strong phenolic COH rocking at ∼1530 cm–1 of the photoexcited HPTS,21,26,34 exhibit a ∼20 and 30 cm–1 blueshift in water as ESPT proceeds (see Fig. 4a), directly correlating with the photoinduced PA* → PB* transition (see Fig. 3a and S5a in the ESI†). For HPTS in methanol (Fig. 3b) and MPTS in water (Fig. S5b in the ESI†) where ESPT is inhibited or absent, these marker band frequencies remain constant. In a control experiment, the 1564 cm–1 PB* mode in H2O at pH = 12 shows no frequency shift (Fig. 4a), bolstering the attribution of 1530 cm–1 mode blueshift to the chromophore deprotonation event as a result of ESPT.
Fig. 4. Excited-state vibrational frequency and intensity dynamics for marker bands of 1.5 mM HPTS and MPTS in various solvents up to 600 ps. (a) The high-frequency mode frequency shift of HPTS in aqueous basic solution (pH = 12, diamond), H2O (pH = 4.5, circle), D2O (pD = 4.5, square), methanol (hexagon), and MPTS in H2O (triangle). The double-exponential fits are shown for HPTS in H2O (solid) and D2O (dashed) with pronounced mode blueshift. Straight lines indicate unchanged frequencies at ∼1530 cm–1 for HPTS in methanol (dash-dotted) and MPTS in H2O (solid), and at ∼1564 cm–1 for HPTS in basic solution (solid line). (b) Intensity dynamics of the 420/480 cm–1 S1 Raman modes for HPTS in H2O (hollow circle/solid circle) and D2O (hollow square/solid square). Kinetic isotope effect of ∼3 is apparent (see ESI†). The enlarged plot within 100 ps is shown in the insert with the stimulated Raman gain magnitude depicted by the double-arrowed vertical line.
The time constants for both HPTS PA* and PB* mode evolution in H2O and D2O (Fig. 3a and 4, Table 1, and Fig. S5a in the ESI†) yield similar H/D kinetic isotope effect (KIE) values of 2.5–3.2, consistent with the reported KIE (≈3).19,21 Notably, the second time constant (45/130 ps in H2O/D2O, see ESI†) for the 1530 cm–1 mode blueshift is faster than previously reported timescale for diffusion-controlled proton transfer event (ca. 90/250 ps in H2O/D2O)8,19,21,26 that was commonly attributed to the nearly thermoneutral separation of contact ion pairs involving HPTS and nearby solvent molecules. These results indicate that besides dominant ESPT tracking PA* → PB* conversion, additional energy relaxation pathways such as vibrational cooling40–42 via H-bonding chains (i.e., still involving proton motions to some extent) may contribute and affect the overall observed high-frequency mode frequency dynamics.
Table 1. Characteristic time constants and structural origin of the chromophore undergoing excited-state proton transfer in water.
| Time constant | Structural origin | Experimental evidence/support |
| ∼500 fs | Intramolecular vibrational cooling/relaxation and solvent rearrangement in the vicinity of the HPTS phenolic hydroxyl group | PA* 180 cm–1 mode intensity decay a and frequency redshift; PA* 280, 420 cm–1 mode intensity decay b |
| ∼3/8 ps c | Transient contact ion pair formation mostly within the first solvation shell of the chromophore | PA* 280, 420 cm–1 mode intensity decay; PB* 480 cm–1 mode intensity rise d |
| ∼45 ps | Intermolecular vibrational cooling and heat transfer via diffusion-assisted processes from HPTS to water | PA* 180 cm–1 mode intensity decay |
| ∼90/250 ps c | Separation of contact ion pairs and rotational diffusion of chromophore and solvent molecules | PA* 280, 420 cm–1 mode intensity decay; PB* 480 cm–1 mode intensity rise d |
aThe 180 cm–1 mode is assigned to the intermolecular H-bond stretching motion in water. Its integrated intensity in the electronic excited state with high signal-to-noise ratio (see Fig. 5a) shows bi-exponential decay with ∼500 fs (85% amplitude weight) and ∼45 ps (15% amplitude weight) time constants.
bThe 280 and 420 cm–1 modes are assigned to HPTS ring deformation that are delocalized (see Fig. S3 in the ESI). Their excited-state vibrational intensities show similar ∼500 fs decay (60% weight) and typical ESPT time constants of ∼3/8 ps (15% weight) and 90/250 ps (25% weight) in H2O/D2O, respectively.
cThe difference in time constant upon solvent deuteration reports on the kinetic isotope effect (KIE) of ∼3 for photoacid ESPT reaction in aqueous solution.
dThe 480 cm–1 mode mainly consists of the deprotonated chromophore ring out-of-plane deformation with sidechain motions (see Fig. S3d in the ESI). Its intensity rises with two time constants of ∼6 ps (40%) and 95 ps (60% weight) in H2O, and ∼18 ps (20%) and 265 ps (80% weight) in D2O. The short time constant on the few ps timescale is affected by the dwell for PB* accumulation but the KIE is consistent with the PA* decay result.
Low-frequency vibrational dynamics provide ESPT mechanistic insights
The direct observation of low-frequency skeletal modes together with high-frequency localized modes provides deeper insights into elementary events of ESPT, particularly involving directed and deterministic atomic motions on initial coherent timescales. For HPTS in water, the PA* 420 cm–1 mode (in-plane ring deformation, see Fig. S3c in the ESI†) decays and the PB* 480 cm–1 mode (ring OOP deformation with sidechain motions, Fig. S3d in the ESI†) rises (see Fig. 4b and S6 in the ESI†), with the matching components reporting on typical ESPT time constants of ∼3/8 and 90/250 ps in H2O/D2O, respectively (Table 1, see ESI† for more details). In contrast, the ∼180 cm–1 PA* intermolecular stretching mode intensity shows bi-exponential decay with ∼500 fs (85% amplitude weight) and ∼45 ps time constants from least-squares fitting, insensitive to isotope effect of H/D or 16O/18O (Fig. 5a). Furthermore, the corresponding ground-state PA mode (while the PB mode, stronger and at higher frequency, dominates at higher pH, see Fig. 1a inset) blueshifts to ∼193 cm–1 upon photoexcitation to PA* as a result of electronic redistribution in response to HPTS photoacidity and increase of the H-bond interaction.35,43 The mode then redshifts to ∼175 cm–1 in water (Fig. 5b), owing to its strong vibronic coupling to the 400 nm electronic excitation and high sensitivity to the Franck–Condon wavepacket motions along a steep slope.6,30 This slope witnesses primary molecular events leading to ESPT, thus can be considered as part of the multidimensional photochemical reaction coordinate. Meanwhile, the excess energy from photoexcitation could rapidly dissipate via sub-ps intramolecular vibrational relaxation pathways and ps vibrational cooling that involve intermolecular solute–solvent interactions (e.g., H-bonding).40–42 The excited-state frequency downshift of the 180 cm–1 mode occurs with a ∼500 fs single-exponential time constant (Table 1) that is attributed to solvent rearrangement around the vicinity of the HPTS phenolic hydroxyl group, likely induced by the H-bond stretch coupled with other vibrational motions. Notably at time zero after photoexcitation (t = 0 fs), the H218O mode is downshifted by ∼12 cm–1 relative to H216O/D216O (Fig. 5b) because the increased mass of the oxygen atom is expected to decrease the intermolecular H-bond stretching frequency.
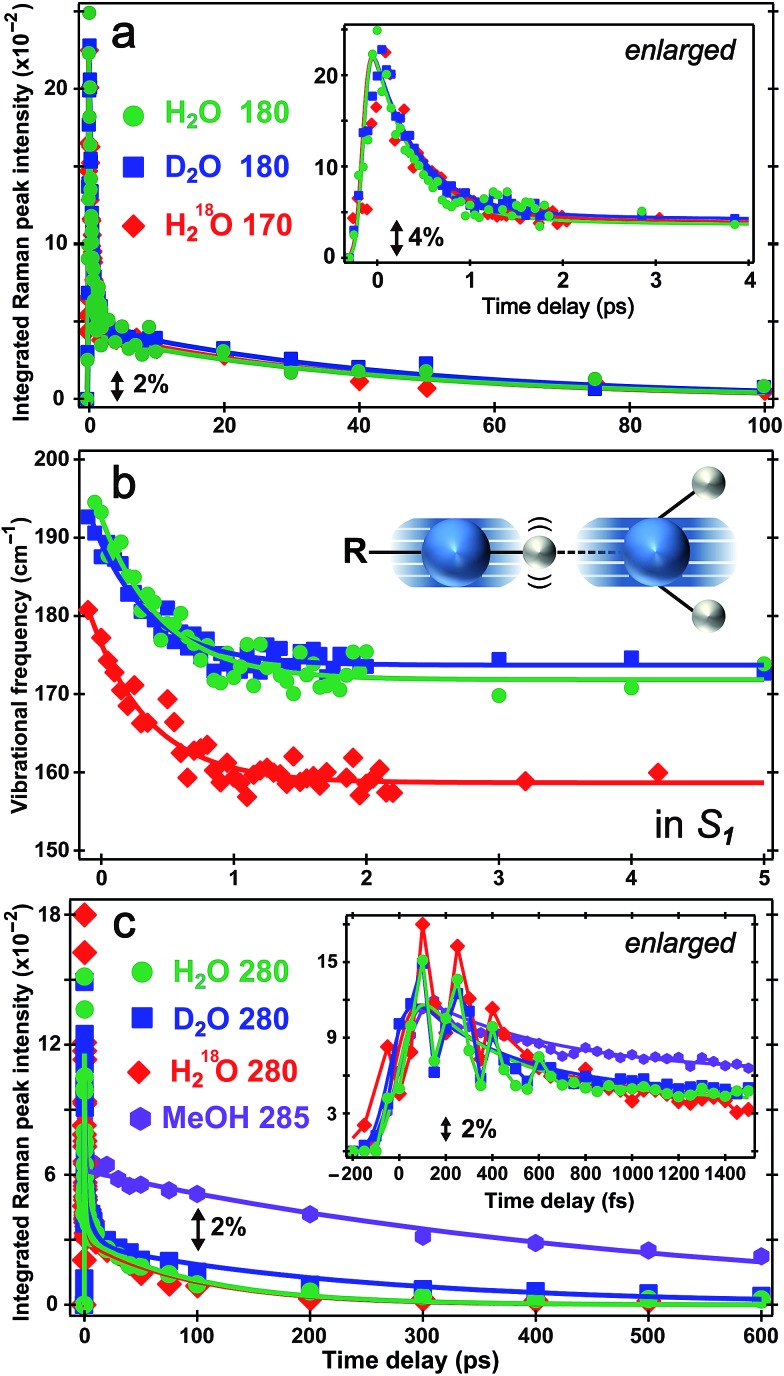
Fig. 5. Excited-state intensity and frequency evolution of ∼180 and 280 cm–1 modes of 1.5 mM HPTS in various solvents following fs 400 nm photoexcitation. Time-resolved (a) integrated intensity dynamics and (b) frequency shift of the 180 cm–1 S1 mode in H2O (pH = 4.5, green circle) and D2O (pD = 4.5, blue square), and 170 cm–1 mode in H218O (pH = 4.5, red diamond) are overlaid with multi-exponential fits (solid traces), respectively. The enlarged plot up to 4 ps is shown in (a) insert. The intermolecular O–H···O stretching motion is illustrated in (b) insert. The oxygen/hydrogen atom is shown as blue/white sphere, respectively, with the shadows and wiggles mapping their vibrational trajectories. (c) Intensity dynamics of the 280 cm–1 mode in H2O (green circle), D2O (blue square) and H218O (red diamond), and 285 cm–1 mode in MeOH (magenta hexagon) up to 600 ps. The enlarged plot with coherent spectral oscillations (except for MeOH) superimposed on the ∼280 cm–1 mode integrated intensity decay up to 1.5 ps is shown in the inset.
Our unique solvent choice of H218O substantiates the vibrational assignment for low-frequency modes, particularly the ∼180 cm–1 intermolecular H-bond stretch (Fig. 5b inset and Fig. S3a in the ESI†) which significantly modulates the O···O distance between the proton donor and acceptor and may play an important role in the formation of the PB*···H+(H2O) contact ion pair (see below, and text in ESI† for more details on fate of the 180 cm–1 mode), followed by water-mediated far removal of the proton (i.e., the ∼90 ps component of ESPT process) in the electronic excited state.20–22 At pH = 12, the 180 cm–1 mode is absent in S1 (see Fig. 3a top), indicating that the PB* form does not require further proton motion from ground-state configuration of the PB–water complex (i.e., RO–···OH2 with a deprotonated HPTS chromophore), hence the intermolecular O–···H–O stretching motion becomes largely insensitive to the 400 nm photoexcitation and does not exhibit noticeable excited-state dynamics after ground-state subtraction. This observation is consistent with the functional relevance of the H-bond stretching motion for ESPT reaction onset in S1.
The conserved redshift time constant (∼500 fs) of the 180 cm–1 skeletal mode matches its dominant intensity decay in all water solvents, likely due to local fluctuations of the O–H/D···O distance and angle induced by solvent rearrangement in close proximity to the chromophore since the simulated vibrational frequency correlation decay time constant is ∼600 fs in water.44 Because photoexcitation typically results in excited species with excess vibrational energy, the initial relaxation involves some thermal equilibration and collective motions of solute molecules being damped by surrounding solvent molecules (without proton transfer). The pertaining timescale for such vibrational cooling can be ultrafast,36,44,45 consistent with the observed sub-ps constant of the water-coupled mode as the photoexcited wavepacket moves out of the Franck–Condon region. Intramolecular vibrational relaxation or energy redistribution (IVR) on the sub-ps timescale may also contribute and can be inferred from anharmonic vibrational coupling matrix.13,39 The much longer ∼45 ps component contains further vibrational cooling pathways for the chromophore through diffusion-assisted processes in water, which typically involve low-frequency motions and heat transfer from vibrationally hot chromophore to the nearby solvent.40,46 In our present case the existence of a small ESPT barrier during the photochemical reaction slows heat transfer to solvent in comparison with pure vibrational cooling that typically occurs on the ∼10 ps timescale for a conjugated molecular ring system in solution.15,40,46
Notably, the lack of H/D or 16O/18O KIE for the 180 cm–1 mode dynamics (intensity in Fig. 5a and frequency in Fig. 5b) on the fs–ps timescale indicates the functional role of this mode (atomic motions mainly pertaining to intermolecular O···O stretching depicted in Fig. 5b inset and Fig. S3a in the ESI†) in setting up the stage for ESPT at early time but not actually tracking the ESPT progress (i.e., involving significant proton movement in solution). In other words, the intervening H/D (or 16O/18O on one side) will not cause significant difference in cooling rate via multiple heavy atom motions involving the chromophore sidechain and nearby solvent molecules. As a result, this skeletal mode acts as an effective vibrational probe to reveal the essential “local” H-bonding dynamics47 close to the HPTS hydroxyl end and largely within the first solvation shell. It is conceivable that the 180 cm–1 mode of the proton-(partially)-transferred complex remains dynamically stable on the tens of ps timescale (see Fig. 5a for its intensity decay dynamics) so it can continue to facilitate the aforementioned intermolecular heat transfer from the chromophore (during ESPT reaction) to the surrounding solvent (i.e., solvation shells with increasing radii).
The PA* 280 and 420 cm–1 ring deformation mode intensity of HPTS displays a similar ∼500 fs decay (62% weight) in water (Fig. 5c). For HPTS in methanol with weak intermolecular H-bonding, the decay constant becomes ∼650 fs (50% weight). In contrast, the prominent 480 cm–1 mode (Fig. 3a and S3d in ESI†) associated with the deprotonated HPTS in H2O (pH = 12) shows ∼260 fs decay (70% weight) with stronger H-bonding interaction. The variation of ultrafast vibrational cooling of HPTS in solvents reveals that the intermolecular H-bond strength determines the initial vibrational energy dissipation rate,41 which closely reflects the O···O distance between the proton donor and acceptor. This indicates that IVR, if present, plays a minor role in the observed mode intensity dynamics on the fs to ps timescale for HPTS in water. For instance, Fig. 1a insert shows that the 180 cm–1 mode blueshifts and strengthens for HPTS in H2O with pH increase (4.5 → 12), consistent with tighter H-bonding interaction between PB and nearby water molecules. The low-frequency skeletal motions effectively act as both action and reporter modes for the vibrational cooling pathway through the H-bonding chain,40,46 which leads to energy relaxation and change of the resonance Raman condition on the PES hence the observed vibrational mode intensity dynamics (e.g., Fig. 5a) in the electronic excited state. On the much longer timescale (e.g., 600 ps in Fig. 3a) when PB* forms H-bonds with surrounding water molecules, the absence of ∼180 cm–1 mode can be understood by considering the much smaller concentration and decreased Raman polarizability of nascent PB* H-bond species in a more relaxed state (versus the highly energetic, vibrationally hot PA* species before ∼1 ps, see ESI† text for additional discussion).
There has been much discussion about the functionality of low-frequency modes during ESPT,6,31,36,45 and the present comparison between their activities in solvents with different ESPT capabilities should offer some convincing evidence. The mismatch between our observed second decay constant of the 180 cm–1 mode intensity (i.e., ∼45 ps in both H2O and D2O) and the reported long-range ESPT time constants of ∼90/250 ps for HPTS in H2O/D2O8,19,21 strongly argues against the 180 cm–1 mode being just a spectator mode for the ESPT reaction. Remarkably, Fig. 5c insert shows strong intensity oscillations of the 280 cm–1 mode in S1 with a period of ∼190 fs in water, which yields the ∼180 cm–1 mode by Fourier transform analysis. This coherent modulation survives ensemble average and solvent collision meaning it projects strongly onto the initial photochemical reaction coordinate. In sharp contrast, the 280 cm–1 mode intensity of HPTS in methanol exhibits a largely smooth decay within 1.5 ps (see Fig. 5c insert for enlarged plot), which is consistent with the absence of the 180 cm–1 intermolecular PA* mode in Fig. 3b (i.e., no significant proton transfer motion following electronic excitation because HPTS does not dissociate in methanol in S0 or S1).7,34
This newly revealed coupling between two low-frequency vibrational modes in the excited state non-adiabatic regime strategically involves an intermolecular H-bond motion (180 cm–1) bridging the proton donor and acceptor,6,31,48 or more generally the solute and solvent molecules, which strongly indicates mode functionality. This mode differs from other intramolecular vibrational modes in that it does not report on ESPT time constants but instead, tracks vibrational cooling dynamics more as it interacts with other vibrational motions in a non-equilibrium environment in S1 (see Fig. 3 and 5). Based on major atomic motions that contribute to these observed low-frequency modes (see Fig. S3 in the ESI†), the anharmonic vibrational coupling could be mainly attributed to through–bond interactions that can mix σ bond (e.g., H-bond stretch between oxygen atoms of proton donor and acceptor) into the π bonds (e.g., conjugated ring deformation surrounded by solvent molecules).13,49 By developing time-resolved tunable excited-state FSRS, we directly observe key nuclear motions that rearrange and/or optimize the first solvation shell44,47 around HPTS through anharmonic coupling between the O–H···O intermolecular stretch and the HPTS four-ring deformation (280 cm–1) in water. These particular modes, which are strongly displaced and vibronically coupled to electronic excitation, contain the relevant atomic motions6,36 to concertedly optimize local geometry of the phenolic hydroxyl and the first solvation shell (i.e., involving three charged sulfonate groups, see ESI† text) of the photoexcited chromophore, particularly via cooperative low-frequency skeletal motions on the sub-ps to few ps timescale. The pertaining conformational change toward the ESPT transition state, which is commonly considered a charge-separated contact ion pair,8,19–21,50 is corroborated by the observed frequency redshift of the 180 cm–1 mode with ∼500 fs time constant (Fig. 5b) which does not match simple prediction of a mode frequency blueshift due to vibrational cooling. The intermediate contact ion pair that forms on the ∼3 ps timescale19–21 typically consists of no more than ∼30% of the excited-state HPTS population (e.g., matching the fitted 1530 cm–1 mode frequency blueshift time constant of ∼3 ps with a relative amplitude weight of ∼30%, see Fig. 4a and text in the ESI†) because the proton may shuttle back and forth between the photoacid and water molecules within the first solvation shell.8,21,22,26,34 The transient ion pair subsequently undergoes diffusion-assisted separation to free ions (likely involving rotational diffusion of both proton donor and acceptor) which can further transfer the proton away from HPTS on the ∼100 ps timescale in water, before ultimately reaching the fluorescent state of PB*.
The conceptual significance, fundamental importance and broad applicability of this line of inquiry have been recently highlighted by Miller and co-workers who reported local vibrational coherences that drive the primary photochemistry of vision.28 The optimization of the initial phase-space trajectory out of the Franck–Condon region therein is largely driven by local couplings and anharmonicities that redirect and redistribute energy and reaction trajectory, “thereby also playing a role in determining the yield and timescale of photoproduct appearance”.51 Moreover, it should be possible to manipulate certain skeletal motion(s) through optical coherent control techniques52 to further evaluate the dependence of intermolecular ESPT rates and efficiency on transient low-frequency mode coupling/interplay in water.
Experimental
Materials
The photoacid pyranine/HPTS (8-hydroxypyrene-1,3,6-trisulfonic acid trisodium salt) was purchased from TCI America (>85% purity), and the methoxy derivative (MPTS, 8-methoxypyrene-1,3,6-trisulfonic acid trisodium salt) was purchased from AnaSpec Inc. and used as received. We have confirmed from UV/Visible electronic spectroscopy and FSRS vibrational spectroscopy that no noticeable difference exists between spectral data and characteristic time constants obtained using this HPTS sample versus the >97% purity HPTS sample from Aldrich.21,26,34 The pH-dependent HPTS and MPTS solutions in H2O were prepared by adding sodium hydroxide (NaOH) to consecutively change pH values from 4.5 to 12. The pD variation of HPTS in D2O was achieved through mixing different concentrations of sodium carbonate (Na2CO3) (pD = 9, 12). We assume that the additional ions at this level do not significantly alter the H-bonding network. D2O at 99.9% deuteration grade and H218O at 97% 18O purity were purchased from Cambridge Isotope Laboratories, Inc. All experiments were performed at room temperature (22 °C) and ambient pressure (1 atm) on an air-float active-levelling RS4000 optical TableTop system (Newport, Inc.).
It is notable that the sample concentration for time-resolved excited-state FSRS measurements in this work is 1.5 mM (see Fig. 3–5, S5 and S6 in the ESI†), much lower than our previously used concentration of ∼10 mM with 800 nm Raman pump,21,26,34 but yielding high-quality spectral data due to pre-resonance enhancement from the strategic usage of 580 nm Raman pump. Without this resonance Raman effect, high concentration of HPTS in the tens of mM concentration range could lead to intrinsically high ionic strength (e.g., the triple negative charge of sulfonate sidechain groups in conjunction with nearby counter ions) in sample solution that may change the proton dissociation rate from HPTS to water. This could affect both the short and long time kinetics of HPTS especially concerning the interaction between the generated ion pair53,54 as inert salt ions have been reported to affect the solvent network and its fluctuations on various timescales.
Tunable femtosecond stimulated Raman method
A full description of methods is given in Methods in the ESI.† Briefly, for photoexcitation, the 400 nm actinic pump from double frequency generation of the 800 nm fundamental pulse was set at ∼0.5 μJ and ∼40 fs pulse duration after prism pair compression. The 580 nm Raman pump of ∼2 ps pulse duration at 4 mW was generated by a home-built tunable optical setup consisting of a second harmonic bandwidth compressor (SHBC, for ps 400 nm pump), fs noncollinear optical parametric amplifier (NOPA, with spectral filter for ps tunable seed), and a two-stage ps NOPA system (for successive amplification).17,55 The fs Raman probe from super-continuum white light generation is compressed and selected from ca. 585–650 nm that corresponds to ca. 100–1800 cm–1 Stokes Raman shift with the 580 nm Raman pump being used. All three incident laser pulses are focused by a parabolic reflective mirror onto the 1 mm-thick sample flow cell to ensure that a fresh sample spot is being irradiated each time. After the solution sample, only the Raman probe that carries the stimulated Raman signal is collimated and focused into the spectrograph (Acton SpectraPro SP-2356, Princeton Instruments), dispersed by a 1200 grooves per mm grating at 500 nm blaze and imaged on a 1340 × 100 CCD array camera (PIXIS:100F, Princeton Instruments). The instrument control and data collection are performed by a home-developed LabView program suite.
Resolving low-frequency Raman modes
A stable and broadband Raman probe is required to collect excited-state FSRS signals across a wide spectral window (ca. 100–1800 cm–1).16,21 Notably, scattering light from the much stronger Raman pump into the Raman probe beampath causes interference in the low-frequency region (ca. 100–500 cm–1) of the FSRS spectra with fluctuating baselines. To capture convincing low-frequency modes with high temporal resolution, the following steps are implemented to minimize Raman pump scattering: (i) all solution samples are filtered through a 0.2 μm filter to diminish scattering by larger particle impurities; (ii) the crossing angle between Raman pump and probe beams is increased to ∼7° with three additional irises in the probe beampath after the sample to further eliminate scattered Raman pump; and (iii) the 580 nm Raman pump power is set at 4 mW that is below the saturation regime to achieve enough SNR with less pump beam scattering and baseline distortion (see the power-dependence study on this sample system in Methods in the ESI†).33
Vibrational normal mode calculations
To obtain quantum mechanical predictions of the chromophore normal-mode frequencies in solution, we performed density-functional theory (DFT) calculations in Gaussian32 on HPTS (protonated and deprotonated) surrounded by five water molecules in proximity to the phenolic hydroxyl end: one in the four-ring chromophore plane, two above, and two below (see Fig. S3 in the ESI†). This configuration is intended to capture the essence of H-bonding network that is most relevant for primary events of ESPT reaction from the photoacid to solvent molecules.21,26 All calculations in the electronic ground state (S0) were performed at the DFT-RB3LYP 6-31G(d, p) level for both the protonated (–3 charge) and deprotonated (–4 charge) HPTS chromophore as well as five adjacent H2O molecules. Time-dependent DFT (TDDFT) calculations at the same level were also performed in the singlet excited state (S1) to compare with S0 results and aid in vibrational normal mode assignment (i.e., based on the experimental FSRS data from electronic ground to excited state, mainly the Raman peak frequency shift trend and magnitude upon electron redistribution). The rest of solvent effect was modelled by integral equation formalism polarisable continuum model (IEFPCM)-H2O in Gaussian.
Conclusions
Our work has developed versatile wavelength-tunable femtosecond Raman methodology to unravel photochemistry in aqueous molecular systems. The multidimensional reaction coordinate of the photoexcited pyranine molecules in H2O, D2O, and H218O starting from time zero of the ESPT reaction is revealed. The photoacid in methanol was also studied as a control sample wherein ESPT is inhibited. By strategically tuning the Raman pump to 580 nm and Raman probe to its lower energy side, we achieved simultaneous pre-resonance enhancement of transient reactant (i.e., protonated chromophore in S1) and product species (i.e., deprotonated chromophore in S1) as the non-stationary vibronic wavepacket moves out of the Franck–Condon region. This process is followed by ESPT reaction barrier crossing that is intimately related to solvent rearrangement within the first solvation shell. On the sub-ps timescale, the 280 cm–1 Raman mode intensity attributed to chromophore ring deformation only exhibits strong oscillatory behaviour in ESPT-capable environments (e.g., H2O, D2O). Meanwhile, the modulating 180 cm–1 intermolecular chromophore-solvent H-bond stretching mode is prominent in S1 and decays with characteristic time constants of ∼500 fs and 45 ps. The newly captured 180 cm–1 mode intensity decay reflects vibrational cooling via H-bonds and heat transfer to the solvent but it is the observed coupling between 180 and 280 cm–1 modes that reveals functional relevance of these low-frequency vibrational motions. Because an array of vibrational modes with higher frequencies exhibit characteristic time constants that closely report on the ESPT reaction in solution on tens of picoseconds, likely involving significant proton motions over larger distances, we assign the main functional role of the coupled 180 and 280 cm–1 modes in optimizing the local environment of photoexcited pyranine for proton transfer, i.e., the formation of a contact ion pair, but not actually transferring the proton. The nature of HPTS being a “weak” photoacid31 with pK*a ≈ 0 and τPT ≈ 100 ps may be the fundamental reason that we observe prominent coherent low-frequency motions modulating relevant skeletal motions (sub-ps to ps timescale) to effectively form the transient contact ion pair in water on the few ps timescale, thereby facilitating the ESPT reaction from photoacid to photobase form.
Through this work aided by transient absorption and DFT calculations, the tunable FSRS methodology demonstrates its unique power in tracking multiple atomic motions across a spectral window over 1600 cm–1 (particularly covering the low-frequency region below 500 cm–1) in the electronic excited state. Furthermore, it can monitor key anharmonic coupling in the vibrational domain via impulsively excited coherent nuclear motions, thereby elucidating primary molecular events of a photochemical reaction powering proton transfer. This represents a challenging yet promising field to make direct comparison to theoretical modelling and calculations on intrinsic molecular timescales, hence capable of synergistically elevating experimental and computational chemistry to new heights. Remarkably, we uncover the previously hidden multidimensional reaction coordinate and dominant anharmonic coupling terms by directly tracking spectrally resolved transient vibrational modes without the complication of retrieving such signals from broad electronic responses. The fundamental structural dynamics insights into photochemical reactions and processes in condensed phase can potentially enable the rational design from the bottom up of molecular complexes with improved and desired functionalities.
Supplementary Material
Acknowledgments
This work was supported in part by a U.S. NSF CAREER grant (CHE-1455353) and Oregon State University (OSU) Research Equipment Reserve Fund (to C. F.). Y. W. and L. T. are grateful to the Dorothy and Ramon Barnes Graduate Fellowship at OSU Chemistry for summer research support in 2014 and 2015.
Footnotes
†Electronic supplementary information (ESI) available: Fig. S1–S6 followed by additional discussions on electronic spectroscopy of HPTS and MPTS in water at different pH, ground-state FSRS data of HPTS in D2O at various pD conditions, major vibrational mode assignment of HPTS in water aided by density functional theory (DFT) calculations, time-resolved transient absorption spectra of HPTS in water and methanol, excited-state FSRS data of MPTS in H2O and HPTS in D2O, ultrafast dynamics of vibrational marker bands of photoexcited HPTS in H216O and H218O, and the fate of the excited-state 180 cm–1 mode, and references. See DOI: 10.1039/c6sc00672h
References
- Zhu L., Sage J. T., Champion P. M. Science. 1994;266:629–632. doi: 10.1126/science.7939716. [DOI] [PubMed] [Google Scholar]
- Liebl U., Lipowski G., Négrerie M., Lambry J.-C., Martin J.-L., Vos M. H. Nature. 1999;401:181–184. doi: 10.1038/43699. [DOI] [PubMed] [Google Scholar]
- Kukura P., McCamant D. W., Yoon S., Wandschneider D. B., Mathies R. A. Science. 2005;310:1006–1009. doi: 10.1126/science.1118379. [DOI] [PubMed] [Google Scholar]
- Vos M. H., Rappaport F., Lambry J.-C., Breton J., Martin J.-L. Nature. 1993;363:320–325. [Google Scholar]
- Kumble R., Palese S., Visschers R. W., Leslie Dutton P., Hochstrasser R. M. Chem. Phys. Lett. 1996;261:396–404. [Google Scholar]
- Fang C., Frontiera R. R., Tran R., Mathies R. A. Nature. 2009;462:200–204. doi: 10.1038/nature08527. [DOI] [PubMed] [Google Scholar]
- Agmon N., Huppert D., Masad A., Pines E. J. Phys. Chem. 1991;95:10407–10413. [Google Scholar]
- Rini M., Magnes B.-Z., Pines E., Nibbering E. T. J. Science. 2003;301:349–352. doi: 10.1126/science.1085762. [DOI] [PubMed] [Google Scholar]
- Hassanali A., Giberti F., Cuny J., Kühne T. D., Parrinello M. Proc. Natl. Acad. Sci. U. S. A. 2013;110:13723–13728. doi: 10.1073/pnas.1306642110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizutani Y., Kitagawa T. Science. 1997;278:443–446. doi: 10.1126/science.278.5337.443. [DOI] [PubMed] [Google Scholar]
- Kim J. E., Mathies R. A. J. Phys. Chem. A. 2002;106:8508–8515. doi: 10.1021/jp021069r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takeuchi S., Ruhman S., Tsuneda T., Chiba M., Taketsugu T., Tahara T. Science. 2008;322:1073–1077. doi: 10.1126/science.1160902. [DOI] [PubMed] [Google Scholar]
- Hochstrasser R. M. Proc. Natl. Acad. Sci. U. S. A. 2007;104:14190–14196. doi: 10.1073/pnas.0704079104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCamant D. W., Kukura P., Yoon S., Mathies R. A. Rev. Sci. Instrum. 2004;75:4971–4980. doi: 10.1063/1.1807566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weigel A., Ernsting N. P. J. Phys. Chem. B. 2010;114:7879–7893. doi: 10.1021/jp100181z. [DOI] [PubMed] [Google Scholar]
- Wang W., Liu W., Chang I.-Y., Wills L. A., Zakharov L. N., Boettcher S. W., Cheong P. H.-Y., Fang C., Keszler D. A. Proc. Natl. Acad. Sci. U. S. A. 2013;110:18397–18401. doi: 10.1073/pnas.1315396110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu L., Liu W., Fang C. Appl. Phys. Lett. 2014;105:041106. [Google Scholar]
- Tran-Thi T.-H., Gustavsson T., Prayer C., Pommeret S., Hynes J. T. Chem. Phys. Lett. 2000;329:421–430. [Google Scholar]
- Leiderman P., Genosar L., Huppert D. J. Phys. Chem. A. 2005;109:5965–5977. doi: 10.1021/jp050037b. [DOI] [PubMed] [Google Scholar]
- Spry D. B., Goun A., Fayer M. D. J. Phys. Chem. A. 2007;111:230–237. doi: 10.1021/jp066041k. [DOI] [PubMed] [Google Scholar]
- Han F., Liu W., Fang C. Chem. Phys. 2013;422:204–219. [Google Scholar]
- Gepshtein R., Leiderman P., Genosar L., Huppert D. J. Phys. Chem. A. 2005;109:9674–9684. doi: 10.1021/jp053479w. [DOI] [PubMed] [Google Scholar]
- Mohammed O. F., Pines D., Dreyer J., Pines E., Nibbering E. T. J. Science. 2005;310:83–86. doi: 10.1126/science.1117756. [DOI] [PubMed] [Google Scholar]
- Iftimie R., Tremblay M.-H., Thomas V., Hétu S., de Lasalle F., Rivard U. J. Phys. Chem. A. 2013;117:13976–13987. doi: 10.1021/jp410858d. [DOI] [PubMed] [Google Scholar]
- Simkovitch R., Akulov K., Shomer S., Roth M. E., Shabat D., Schwartz T., Huppert D. J. Phys. Chem. A. 2014;118:4425–4443. doi: 10.1021/jp5002435. [DOI] [PubMed] [Google Scholar]
- Liu W., Han F., Smith C., Fang C. J. Phys. Chem. B. 2012;116:10535–10550. doi: 10.1021/jp3020707. [DOI] [PubMed] [Google Scholar]
- Siwick B. J., Bakker H. J. J. Am. Chem. Soc. 2007;129:13412–13420. doi: 10.1021/ja069265p. [DOI] [PubMed] [Google Scholar]
- Johnson P. J. M., Halpin A., Morizumi T., Prokhorenko V. I., Ernst O. P., Miller R. J. D. Nat. Chem. 2015;7:980–986. doi: 10.1038/nchem.2398. [DOI] [PubMed] [Google Scholar]
- Heisler I. A., Meech S. R. Science. 2010;327:857–860. doi: 10.1126/science.1183799. [DOI] [PubMed] [Google Scholar]
- Heyne K., Huse N., Nibbering E. T. J., Elsaesser T. Chem. Phys. Lett. 2003;369:591–596. [Google Scholar]
- Simkovitch R., Shomer S., Gepshtein R., Huppert D. J. Phys. Chem. B. 2015;119:2253–2262. doi: 10.1021/jp506011e. [DOI] [PubMed] [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A., Nakatsuji H., Caricato M., Li X., Hratchian H. P., Izmaylov A. F., Bloino J., Zheng G., Sonnenberg J. L., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Montgomery J. J. A., Peralta J. E., Ogliaro F., Bearpark M., Heyd J. J., Brothers E., Kudin K. N., Staroverov V. N., Kobayashi R., Normand J., Raghavachari K., Rendell A., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Rega N., Millam J. M., Klene M., Knox J. E., Cross J. B., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R. E., Yazyev O., Austin A. J., Cammi R., Pomelli C., Ochterski J. W., Martin R. L., Morokuma K., Zakrzewski V. G., Voth G. A., Salvador P., Dannenberg J. J., Dapprich S., Daniels A. D., Farkas Ö., Foresman J. B., Ortiz J. V., Cioslowski J. and Fox D. J., Gaussian 09, Revision B.1, Gaussian, Inc., Wallingford, CT, 2009.
- Lee J., Challa J. R., McCamant D. W. J. Raman Spectrosc. 2013;44:1263–1272. [Google Scholar]
- Wang Y., Liu W., Tang L., Oscar B. G., Han F., Fang C. J. Phys. Chem. A. 2013;117:6024–6042. doi: 10.1021/jp312351r. [DOI] [PubMed] [Google Scholar]
- Pines E., Pines D., Ma Y.-Z., Fleming G. R. ChemPhysChem. 2004;5:1315–1327. doi: 10.1002/cphc.200301004. [DOI] [PubMed] [Google Scholar]
- Oscar B. G., Liu W., Zhao Y., Tang L., Wang Y., Campbell R. E., Fang C. Proc. Natl. Acad. Sci. U. S. A. 2014;111:10191–10196. doi: 10.1073/pnas.1403712111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kukura P., McCamant D. W., Mathies R. A. Annu. Rev. Phys. Chem. 2007;58:461–488. doi: 10.1146/annurev.physchem.58.032806.104456. [DOI] [PubMed] [Google Scholar]
- Niu K., Zhao B., Sun Z., Lee S.-Y. J. Chem. Phys. 2010;132:084510. doi: 10.1063/1.3330818. [DOI] [PubMed] [Google Scholar]
- Frontiera R. R., Fang C., Dasgupta J., Mathies R. A. Phys. Chem. Chem. Phys. 2012;14:405–414. doi: 10.1039/c1cp22767j. [DOI] [PubMed] [Google Scholar]
- Lian T., Locke B., Kholodenko Y., Hochstrasser R. M. J. Phys. Chem. 1994;98:11648–11656. [Google Scholar]
- Kovalenko S. A., Schanz R., Hennig H., Ernsting N. P. J. Chem. Phys. 2001;115:3256–3273. [Google Scholar]
- McCamant D. W., Kukura P., Mathies R. A. J. Phys. Chem. A. 2003;107:8208–8214. doi: 10.1021/jp030147n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohammed O. F., Dreyer J., Magnes B.-Z., Pines E., Nibbering E. T. J. ChemPhysChem. 2005;6:625–636. doi: 10.1002/cphc.200400510. [DOI] [PubMed] [Google Scholar]
- Fecko C. J., Eaves J. D., Loparo J. J., Tokmakoff A., Geissler P. L. Science. 2003;301:1698–1702. doi: 10.1126/science.1087251. [DOI] [PubMed] [Google Scholar]
- Leitner D. M. Chem. Phys. Lett. 2012;530:102–106. [Google Scholar]
- Nguyen S. C., Lomont J. P., Caplins B. W., Harris C. B. J. Phys. Chem. Lett. 2014;5:2974–2978. doi: 10.1021/jz501400t. [DOI] [PubMed] [Google Scholar]
- Genosar L., Leiderman P., Koifman N., Huppert D. J. Phys. Chem. A. 2004;108:1779–1789. [Google Scholar]
- Staib A., Borgis D., Hynes J. T. J. Chem. Phys. 1995;102:2487–2505. [Google Scholar]
- McHale J. L., Molecular Spectroscopy, Prentice-Hall, Upper Saddle River, NJ, 1999. [Google Scholar]
- Kulig W., Agmon N. Nat. Chem. 2013;5:29–35. doi: 10.1038/nchem.1503. [DOI] [PubMed] [Google Scholar]
- Mathies R. A. Nat. Chem. 2015;7:945–947. doi: 10.1038/nchem.2406. [DOI] [PubMed] [Google Scholar]
- Prokhorenko V. I., Nagy A. M., Waschuk S. A., Brown L. S., Birge R. R., Miller R. J. D. Science. 2006;313:1257–1261. doi: 10.1126/science.1130747. [DOI] [PubMed] [Google Scholar]
- Leiderman P., Gepshtein R., Uritski A., Genosar L., Huppert D. J. Phys. Chem. A. 2006;110:5573–5584. doi: 10.1021/jp060170j. [DOI] [PubMed] [Google Scholar]
- Cox M. J., Siwick B. J., Bakker H. J. ChemPhysChem. 2009;10:236–244. doi: 10.1002/cphc.200800406. [DOI] [PubMed] [Google Scholar]
- Zhu L., Liu W., Wang Y., Fang C. Appl. Sci. 2015;5:48–61. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.