Role of the Ocean’s AMOC in setting the Uptake Efficiency of Transient Tracers

Abstract

The central role played by the ocean’s Atlantic Meridional Overturning Circulation (AMOC) in the uptake and sequestration of transient tracers is studied in a series of experiments with the GISS and MIT ocean circulation models. Forced by observed atmospheric timeseries of CFC-11, both models exhibit realistic distributions in the ocean, with similar surface biases but different response over time.

To better understand what controls uptake, we ran idealized forcing experiments in which the AMOC strength varied over a wide range, bracketing the observations. We found that differences in the strength and vertical scale of the AMOC largely accounted for the different rates of CFC-11 uptake and vertical distribution thereof. A 2-box model enables us to quantify, and relate uptake efficiency of passive tracers to AMOC strength and how uptake efficiency decreases in time. We also discuss the relationship between passive tracer and heat uptake efficiency, of which the latter controls the transient climate response to anthropogenic forcing in the North Atlantic. We find that heat uptake efficiency is substantially less (by about a factor of five) than that for a passive tracer.

1. Introduction

Anthropogenic, biologically inactive, inert tracers with known histories of atmospheric concentration have been extensively used to study ocean ventilation and mixing and, by comparing against observations, assessing the skill of models in representing these processes [Waugh, 2014; Shao et al., 2013; Long et al., 2013; Trossman et al., 2012; Lebel et al., 2008; Gao and Drange, 2004; England and Maier-Reimer, 2001; Dixon et al., 1996]. This provides the context for the present study which has two main goals. First, we use CFC-11 and CFC-like tracers to quantify the role of the ocean’s Atlantic Meridional Overturning Circulation (AMOC) in vertical tracer transport and sequestration in the Atlantic sector. CFCs are much simpler than tracers such as temperature, for example, because they are passive and so do not affect ocean currents. Moreover, they can be referenced to the observational record more easily than temperature anomaly due to anthropogenic climate change. The second motivation of our study is the context of transient climate change: how can we connect the uptake of passive tracers to the efficiency with which the ocean takes up anthropogenic temperature, the latter being the focus of Gregory and Mitchell [1997] and Raper et al. [2001].

Our paper is set out as follows. In Section 2 we contrast the uptake of CFCs in historical simulations comparing two models against observations of the CFC inventory. In Section 3, by making use of CFC step functions, we argue that the difference between the two simulations is largely explained by the different ways in which they represent the AMOC. In Section 4, a two-box model of tracer uptake is used to quantify the link between tracer uptake and AMOC and make connections to heat uptake efficiency. Particular emphasis is placed on how uptake efficiency decreases with time. We conclude in Section 5 with a discussion of the implications of our work.

2. Historical CFC-11 uptake: model configurations and evaluation

The MITgcm (general circulation model) [Marshall et al., 1997a, b] and the GISS ocean model [Schmidt et al., 2014] were spun up at 1° resolution with realistic topography and driven by forcing fields from the Coordinated Ocean-Ice Reference Experiment phase I (CORE-I) framework [Griffies et al., 2009]. More complete details of the model configurations can be found in Marshall et al. [2017]. Both models used a ‘KPP’ representation of vertical mixing [Large et al., 1994] and a mesoscale eddy parameterization in the spirit of Gent and McWilliams [1990]. Other than the similar surface forcing and these aforementioned parameterizations, the two models represent unique computer codes with different numerics and parameterizations. By using two models in this way we believe that our results are not special to a particular model and have wider relevance.

The two models were spun up for 300 years to near-equilibrium at the surface and subsequently forced by the historical perturbations of CFC-11 atmospheric concentrations, in order to assess model uptake of passive tracers. We followed the Ocean Carbon-cycle Model Intercomparison Project (OCMIP) phase 2 protocol [Dutay et al., 2002], with piston velocity parameterized as in Wanninkhof [1992]. The atmospheric CFC-11 pressure, P_CFC, is assumed to be uniform in each hemisphere poleward of 10° latitude and is linearly interpolated between 10° N and 10° S. In our historical runs, the temporal variation of the atmospheric CFC-11 fraction was obtained from the observed histories of CFC-11 in the atmosphere [Bullister, 2014].

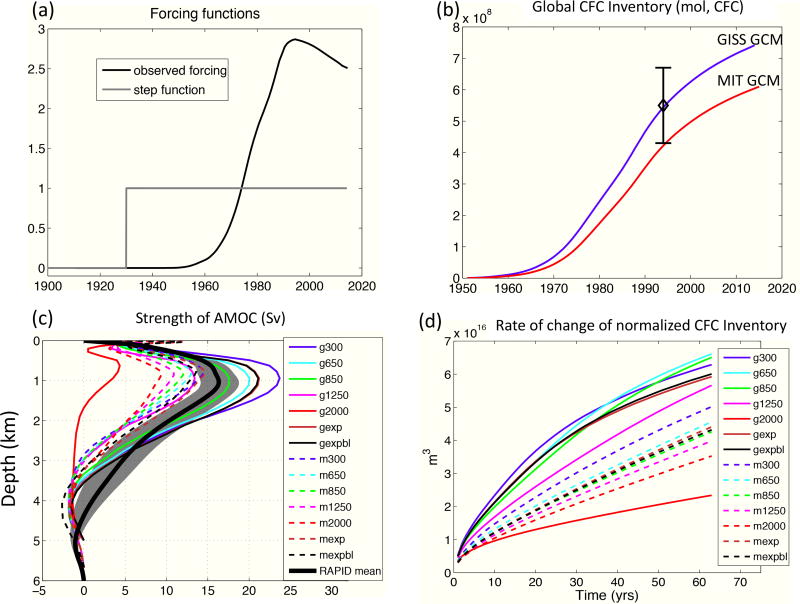
Modeled CFC-11 distributions using historical atmospheric forcing are compared against a CFC-11 climatology provided by the Global Ocean Data Analysis Project (GLODAP, Key et al. [2004]) which represents an annual-mean climatological CFC distribution in the surface and subsurface ocean of the 1990s. Comparisons of GLODAP data with model spatial distributions (averaged over the 1990 — 1999 period) in experiments forced with observed CFC concentrations (black line in Fig. 1a) are shown in the Supplemental-Fig. 1.

Figure 1.

(a) Boundary conditions for the different CFC uptake experiments: historical atmospheric forcing (black line), normalized relative to the mean observed over the period 1900–2014 [Bullister, 2014], and idealized step-function forcing (gray line). (b) GISS (blue) and MIT (red) global ocean CFC inventories timeseries for the realistic forcing runs. The observed global inventory estimate and uncertainty for year 1994 from Willey et al. [2004] are also denoted. (c) Vertical profile of the Atlantic meridional overturning streamfunction across model solutions compared to the 2005–2013 mean observed from the RAPID array. Shaded area denotes observed interannual variability around the RAPID mean. Colorcode refers to GISS(g) and MIT(m) ocean model experiments and the numeric label to the value of the mesoscale diffusivity K (e.g. “g300” is GISSmodel run with K=300 m²s⁻¹, “mexpbl” is the MIT model run with the exponential+Bryan-Lewis bottom boundary layer mixing etc). (d) Evolution of normalized ocean CFC inventory, $\frac{\mathit{\text{Inv}}}{C_1(20\mathit{\text{yrs}})}$, in the step-forcing experiment. The slope of the each line has units of m³s⁻¹ and at t = 20y yields q, Eq. 7.

Over time, the vertically-integrated CFC inventory in the two models differs substantially, with the GISS model taking up more CFC than the MITgcm (Fig. 1b). There are few observations on which to base estimates of the global CFC inventory, but the GISS model is in generally better agreement with those that we do have (Willey et al. [2004], for the year 1994), as plotted in Fig. 1b. To explore the cause of differences in CFC uptake between the two models, we go on to study uptake in a more controlled setting.

3. CFC step functions and their dependence on AMOC strength

To understand and quantify the sensitivity of CFC uptake on ocean circulation state, we perform a suite of idealized experiments in which the atmospheric CFC is held at a constant value (Fig. 1a) while the ocean circulation beneath varies with model simulation. In this study, we refer to this as a CFC-step tracer (which shares the same properties as CFC-11 except for its atmospheric history) and will quantify how its uptake depends on the ocean circulation.

Seven experiments were carried out with each of the GISS and MIT gcms, in which only the magnitude of the mesoscale diffusion coefficient K was varied, all other parameters being kept constant. In five of these experiments, K is constant in time and space with a value of 300, 650, 850, 1250 and 2000 m²s⁻¹, in two experiments K is prescribed an exponential profile which decays from a surface value (of 850 m²s⁻¹) to 300 m²s⁻¹ at depth and with and without enhancement of bottom boundary layer diapycnal mixing [Bryan and Lewis, 1979]. As we now describe, large changes in AMOC occur across our models as these parameters are varied. While other changes in ocean parameterizations or surface forcings can lead to AMOC changes (e.g. diapycnal diffusivity changes, or changes in evaporation minus precipitation) in this study we opted to only vary K, building on the understanding of model results described in Marshall et al. [2017].

3.1. AMOC variations across model simulations

As discussed in detail in Marshall et al. [2017], as K increases the AMOC decreases in a similar manner in both models (see profiles in Fig. 1c, contours in Fig. 2 and Table 1 of Supplementary Material). The model runs with the lowest mesoscale diffusivity (K=300 m²s⁻¹ and the two exponential profiles) have the strongest overturning streamfunction (ψ_AMOC = 27 Sv for the GISS model and 13.6 Sv for the MIT model). Conversely, the model runs with the highest mesoscale diffusivity (K=2000 m²s⁻¹) have the weakest overturning streamfunction (ψ_AMOC = 4.2 Sv for the GISS model and 8.6 Sv for the MIT model). We also note that the vertical extent of the AMOC (defined as the mean depth of the 5–10 Sv isopleths north of 35° S and below a depth of 1000 m), varies in a systematic way with AMOC strength and decreases with increasing K (see Fig. 2 and discussion in Marshall et al. [2017]).

Figure 2.

AMOC (contours) and tracer distribution (shaded) at 60 years in the idealized, step-forcing experiments plotted as a function of latitude (20° S to 60° N) and depth (in km). Color shading: Zonally averaged (between 18.5° W and 80.5° W in the Atlantic ocean) tracer distributions in the GISS (left column) and the MIT model (right column) across different experiments. Color transitions occur every 5 μmolm⁻³. Contours: AMOC streamfunction in Sv. Experiment number in the bottom right corner represents the magnitude of mesoscale diffusivity used, as in Marshall et al. [2017].

To assess the range of modelled AMOCs against observations we compare them to climatological observations obtained from the RAPID Climate Change Program array along 26.5° N (2004–present). As seen in Fig. 1c, modeled profiles capture the shape of the observed AMOC rather well. The profile corresponding to the GISS model with K=850 m²s⁻¹ best captures the magnitude and extent of the observed AMOC and is the only profile that falls within the observed variability over the top 3000 m. This was the value of K used in the historical simulations shown in Fig. 1b.

3.2. Calculation of CFC step functions

To compute CFC step functions, we instantaneously step-up atmospheric CFC concentrations to P_CFC = 1μatm everywhere and hold it constant in time. The CFC-step tracer has the same solubility as CFC-11. The CFC uptake, expressed as the rate of change of the tracer inventory in the North Atlantic normalized by the concentration C₁ at 20years (the significance of which will become apparent in the following section), is shown in Fig. 1d for all experiments. All GISS model runs, except the case with K = 2000m²s⁻¹ (for which the AMOC is near collapse), show a stronger tracer uptake than found in the MIT model. The set of curves from each model lie in order of increasing mesoscale diffusivity K which, as discussed in Marshall et al. [2017], leads to a decrease in AMOC strength. Zonally-averaged vertical sections of the CFC-like tracer in the North Atlantic, with superimposed AMOC, are shown in Fig. 2 for each of the model runs. As the mesoscale diffusivity K is increased and the strength of the AMOC decreases, less tracer is taken up by the ocean, less is sequestered to depth and less is transported southward out of the Atlantic sector. This behavior is seen in both ocean models but, just as in our historical runs, the GISS model typically takes up more tracer than the MITgcm because it has a stronger AMOC.

4. Quantitative interpretation of tracer uptake

4.1. Two-box model of tracer uptake

In this section we use an idealized two-box model of tracer uptake to interpret the increase in tracer inventory across our ocean GCMs. The two boxes are imagined to represent the mixed layer in the North Atlantic region (denoted 1) and the interior ocean down to depth of order 3 km below (denoted 2), with tracer concentrations C₁ and C₂ respectively. Similar models have been used to study, for example, the uptake of anthropogenic heat by ocean circulation in a warming climate — see, e.g. Gregory [2000]; Held et al. [2010]; Geoffroy et al. [2013]; Kostov et al. [2014].

We assume that C₁ is always close to equilibrium with the atmosphere above. Thus when atmospheric concentrations are instantaneously stepped-up to a constant value and thereafter held constant, C₁ is assumed to take on a constant value which does not vary in time. The area-averaged (30° S–90° N) tracer concentration as a function of depth over the North Atlantic from the K=850 m²s⁻¹ integration of the GISS model is shown in Fig. 3a as a function of time. After 10 years or so the surface concentration has ceased to change in time. The interior C evolves, however, as tracer is drawn down into the interior ocean. By year 20 or so onwards, the expression of the lower limb of the AMOC grows and is very pronounced by year 60.

Figure 3.

(a) North Atlantic area-averaged concentration as a function of depth and time in the GISS ocean model for K=850 m²s⁻¹. (b) Inferred overturning strength q (in Sv) from the 2-box model (Eq. 7) plotted against the strength of the AMOC in Sv (M_AMOC). (c) The evolution with time of implied uptake efficiency (κ in Wm⁻²K⁻¹) for each experiment, colorcoded as in Fig. 1d. Also shown are the inferred uptake efficiencies for heat (red, 0.3 Wm⁻²K⁻¹) and passive tracer (blue, 1.3 Wm⁻²K⁻¹) after 60 years of integration. (d) Ocean heat content (OHC) anomalies in the North Atlantic (in Joules, blue curves) and SST anomalies (degrees K, red curves) from the MITgcm in response to a uniform 4 W/m² heating applied at the ocean surface, starting at time year=0. Results from experiments in which temperature behaves like an active (passive) tracer are shown in dashed (solid) curves.

We assume that C₂ evolves according to:

$$𝒜h_2\frac{\partial C_2}{\partial t}-q(C_1-C_2)=0$$ (1)

where 𝒜 is the surface area, h₂ the thickness of the lower layer, q (C₁ − C₂) is the rate of tracer exchange and q is the volume flux between the upper and the lower layer with units of m³s⁻¹, i.e. Sv. The tracer inventory (Inv) is

$$\mathit{\text{Inv}}=𝒜(h_1{C}_1+h_2{C}_2)$$ (2)

whose time-evolution is controlled by C₂ (since C₁ is constant) and hence, in view of Eq.(1), by q. By adjusting q to mimic the time-evolution of tracer inventory in our GCMs, we seek a relationship between the fitted q and AMOC strength.

If C₁ is constant, then as t → ∞, C₂ → C₁, which corresponds to the whole body of ocean being saturated by tracer at concentration C₁. However, in the initial stages of interior uptake when we may assume that C₂ << C₁, the solution to Eq.(1) is:

$$C_2(t\prime )=C_1(1-e^{-\tau t\prime }),$$ (3)

where t′ = t −t_init, and t_init is the time after which C₁ may be assumed constant and the e-folding inverse timescale is:

$$\tau =\frac{q}{𝒜h_2}.$$ (4)

For times short enough that τt′ << 1, Eq.(3) reduces to:

$$C_2=C_1\tau t\prime .$$ (5)

This suggests that for t′ > 0, the inventory of tracer in the ocean, Eq.(2), should grow linearly with time at a rate set by q, thus:

$$\mathit{\text{Inv}}=\mathit{\text{Inv}}(0)+C_1\mathit{\text{qt}}\prime$$ (6)

In this limit the rate of exchange of tracer between the surface and the interior only depends on C₁q because the vertical gradient in Eq.(1) has no contribution from C₂. These simple relations will now be used to help interpret the rate of uptake of transient tracer in the GISS and MIT model solutions shown earlier and their dependence on AMOC.

Inventory

The time evolution of the tracer inventory normalized by C₁, Inv/C₁, is shown in Fig. 1d. For each model, the time-evolving tracer inventory was normalized by the surface concentration (C₁) at 20 years. After an initial adjustment, Inv increases linearly with time, as suggested by Eq.(6). From the slope of the line at 20yrs we can infer the value of q thus:

$$q=\frac{d}{\mathit{\text{dt}}}\left(\frac{\mathit{\text{Inv}}}{C_1}\right)$$ (7)

Note that Eq.(7) explains the ordering of the curves in Fig. 1d. The rate of increase of the inventory is the greatest for those simulations with the strongest overturning cells. Indeed the ordering of the curves is exactly that which would be expected based on the strength of AMOC (M_AMOC). This result is summarized in Fig. 3b: points cluster on a straight line illustrating the linear relationship between q and M_AMOC, clearly allowing us to associate q with the strength of the AMOC.

Note that our estimate of q in Fig. 3b (10 – 35 Sv) is considerably larger than the range of M_AMOC (5–25 Sv). This should not be of concern since the former is sensitive to our choice of 𝒜, the area of integration to obtain Inv, while the latter is sensitive to our choice of the latitude at which the overturning streamfunction is evaluated. The important point is that when one is plotted against the other we obtain a straight line.

4.2. Connections with ‘heat uptake efficiency’

We now seek to relate q to the heat uptake efficiency as discussed in Gregory and Mitchell [1997]; Raper et al. [2001]; Gregory and Forster [2008]; Gregory et al. [2015] and elsewhere. Gregory et al. [2015] use a two-layer model to express the uptake of heat into the lower layer as $\rho {\mathit{\text{ch}}}_2\frac{{\mathit{\text{dT}}}_2}{\mathit{\text{dt}}}=\kappa (T_1-T_2)$, where c is the specific heat capacity of water and κ is the ‘uptake efficiency’ for heat with units of Wm⁻²K⁻¹, the same as the climate feedback parameter. Clearly Eq.(1) has the same form as the one above and suggests that κ can be related to q thus:

$$\kappa =\frac{\rho c}{𝒜}q=\frac{\rho c}{C_1}\frac{d}{\mathit{\text{dt}}}(h_1{C}_1+h_2{C}_2)$$ (8)

using Eq. (7). For the reference GISS calculation case (K=850m²s⁻¹), we obtain a North Atlantic value for κ =3.8 Wm⁻²K⁻¹ at 20 years (see Table 1 in the Supplemental material for uptake efficiencies in all model runs). This is considerably higher than the global estimates of κ from climate models. In early climate models of the 1990s (CMIP2), values ranged from 0.6 to 0.9 Wm⁻²K⁻¹ [Raper et al., 2001]. CMIP3 models exhibited values ranging from 0.4–0.8 Wm⁻²K⁻¹ [Dufresne and Bony, 2008; Gregory and Forster, 2008] and CMIP5 models from 0.39–0.94 Wm⁻²K⁻¹. Such a difference between passive (CFC) and active (T) tracers could be explained as follows.

1. As Giorgetta and co authors [2013] and Gregory et al. [2015] point out, κ should decrease with time as the ocean takes up more heat. Our CFC-based estimate above is for the first few decades after imposing the step forcing. Fig. 1d clearly shows that the rate of increase of tracer inventory decreases in time, indicating that the efficiency of tracer uptake decreases. This is because over time C₂ increases becoming comparable to C₁ (see Fig. 3a) diminishing the difference C₁−C₂ and hence the vertical tracer flux. We plot the time-dependence of our CFC-based κ in Fig. 3c where Eq. (7) is evaluated as a function of time. We see that κ rapidly diminishes in amplitude to values closer to 2 Wm⁻²K⁻¹ after 60 yrs or so.

2. One might expect the Atlantic to be rather effective at drawing down heat into its interior relative to the global ocean, because of the presence of the AMOC, and so its κ ought to be correspondingly higher. Others [Armour et al., 2013; Exarchou et al., 2015] have discussed how regionality of climate feedbacks implies a time dependency in the climate sensitivity (and hence ocean uptake).

3. Temperature is an active tracer resulting in a weakening of the AMOC as the ocean warms. Thus passive tracer uptake may not be a good analogue for heat uptake [Banks and Gregory, 2006; Jackett et al., 2000; Russell, 2006].

To further explore the connection between active (anthropogenic T) and passive (CFC) tracers, we diagnose a climate change experiment carried out in the context of an ocean-only system, described in Marshall et al. [2015]. There, we used the MIT ocean model, spun up to equilibrium with K=850 m²s⁻¹ (exactly the same as the ‘control’ calculation described above) and perturbed it in a manner which mimics anthropogenic climate change. A spatially-uniform downwelling flux of F=4 Wm⁻² was imposed on the surface of the ocean simultaneously with a linear damping of SST at a rate of λ=1 Wm⁻²K⁻¹. As shown in Fig. 3d, SST and ocean heat content (OHC) in the Atlantic sector rise on multi-decadal timescales approaching equilibrium values. The induced T anomalies, however, are not passive and we observe that the AMOC weakens over the course of the experiment by 20% or so. The effect of this weakening on the heat uptake efficiency can be assessed by comparing with the evolution of a passive temperature-like tracer which is treated in every aspect the same as T but which does not affect the dynamics and hence the AMOC. As can be seen in Fig. 3d, the passive T-like tracer inventory increases more rapidly than that of the actual T, as one might expect.

To make our comparison quatitative, in Fig. 3c, we plot (as indicated by the additional points) the inferred κ for active and passive T-like tracers after 60 years. We choose 60 years because by this time the SST anomaly is approaching its equilibrium value, enabling exactly the same framework to be used as in our analysis of CFC uptake. Two things are worthy of note. First, we see that κ of a passive tracer (1.3 Wm⁻²K⁻¹) is approximately 5 times larger than κ of an active tracer (0.3 Wm⁻²K⁻¹), thus quantifying the non-passivity of T. Secondly, κ of a passive, T-like tracer has a rather similar value to κ of our CFC, thus reinforcing the connection between anthropogenic T and CFC that has been tacitly assumed to motivate our study.

5. Concluding remarks

We have explored uptake of CFC in two models across a large range of AMOC strengths, from considerably lower to considerably higher than the observed AMOC. To aid understanding and simplify analysis the uptake of an idealized tracer in response to a step CFC forcing was explored. Through application of a 2-box model we showed that the rate of tracer uptake in the Atlantic sector can be related to the strength of the AMOC and the vertical difference in CFC across it. We find that the implied uptake efficiency of the passive tracer κ is a strong function of time (see Fig. 3c), falling rapidly in the first decade or so to O(1 Wm⁻²K⁻¹) after 60 years. This can be attributed to the reduction in vertical CFC gradient as CFC accumulates in the interior ocean. This κ is larger than the global heat uptake efficiency estimated from coupled climate models [Gregory et al., 2015]. Comparison of the uptake efficiency of active and passive temperature tracer shows that in the North Atlantic, κ for the former is considerably smaller than for the latter. This can be attributed to the diminution of the strength of the AMOC in the active temperature case. This, together with the vertical gradient effect, leads to a κ for active temperature of only 0.3 Wm⁻²K⁻¹, after 60 years.

Gregory et al. [2015] point out that the spread of κ in CMIP5 models is predominantly caused “by the spread in the strength of the thermal coupling between the upper and deep oceans” while others attribute it to vertical diffusion differences [Long and Collins, 2013; Sokolov et al., 2003; Huntingford and Cox, 2000]. The large variation of κ in models suggests that the mechanisms responsible for it are model dependent. In previous modeling studies (Exarchou et al. [2015] and references therein) convection, mixed layers, thermocline/gyre ventilation, and eddy related processes were found responsible for changes in κ, particularly in the extratropics. Here we have shown that in the Atlantic sector the AMOC brings these processes together to set the magnitude of κ. This supports the perspective of Winton et al. [2014] who argued that the representation of AMOC was critical to understanding temperature bias and ocean heat uptake in climate change models. It is clear that processes that affect AMOC and how AMOC is represented in models will crucially determine how each model represents ocean heat uptake efficiency. Improving the representation of AMOC in models can clearly help reduce uncertainty in ocean heat uptake as the Earth warms.

Our work has important implications for the determination of the distribution and temporal evolution of anthropogenic CO₂ in the ocean. Presently, the best observationally-based estimates (e.g. Khatiwala et al. [2009]) assume steady state ocean circulation and thus neglect changes in AMOC strength, due to anthropogenic heat uptake or naturally-forced decadal variations. Unlike CFCs, CO₂ cannot be considered an entirely passive tracer because of its role in radiative forcing and anthropogenic temperature change. Anthropogenic warming slows the AMOC thus diminishing CO₂ uptake, an effect not captured in studies like Khatiwala et al. [2009].

Future work should further explore anthropogenic heat and passive tracer uptake efficiencies. Moreover, because of the ocean’s dual control on climate, through both heat and carbon uptake, carbon and heat uptake efficiency should be studied in tandem and be related to large scale ocean circulation properties.

Keypoints.

• The AMOC controls the depth and the strength of the ocean uptake of transient, passive tracers.

• Quantitatively, the rate and vertical extent of tracer sequestration scale linearly with the AMOC.

• Uptake efficiency for temperature is substantially less than that for a passive tracer.