Positional effects revealed in Illumina methylation array and the impact on analysis

Abstract

Aim:

We aimed to prove the existence of positional effects in the Illumina methylation beadchip data and to find an optimal correction method.

Materials & methods:

Three HumanMethylation450, three HumanMethylation27 datasets and two EPIC datasets were analyzed. ComBat, linear regression, functional normalization and single-sample Noob were used for minimizing positional effects. The corrected results were evaluated by four methods.

Results:

We detected 52,988 CpG loci significantly associated with sample positions, 112 remained after ComBat correction in the primary dataset. The pre- and postcorrection comparisons indicate the positional effects could alter the measured methylation values and downstream analysis results.

Conclusion:

Positional effects exist in the Illumina methylation array and may bias the analyses. Using ComBat to correct positional effects is recommended.

DNA methylation is an important epigenetic modification that regulates gene expression [1], chromatin structure and stability [2], and genomic imprinting [3]. DNA methylation has been implicated in the development of cancer [4–6] and other diseases [7–9]. Furthermore, several studies indicated that the DNA methylation levels could vary by age [10], sex [11], disease affected status [4–9], circadian rhythms [12], tissues types [13] and other factors.

Microarray-based technologies such as Illumina Infinium HumanMethylation27 BeadChip^® Array (Methyl27) [14], Illumina Infinium HumanMethylation450 BeadChip Array (Methyl450) [15,16] and Illumina Infinium MethylationEPIC BeadChip microarray (EPIC) [17], have been widely used for methylome profiling since the first chip came to market in 2006 [18]. This technology has the advantages of low cost, modest DNA requirement and throughput [19].

Methyl450 was one of the most popular and cost-effective tools available, allowing researchers to interrogate more than 485,000 methylation loci per sample at single-nucleotide resolution [20]. It has 12 sample sections in one array arranged in a six by two format (Supplementary Figure 1). Recently, the EPIC, measuring eight samples in one array with more than 860,000 probes, was released. While Methyl27 measures the methylation status of over 27,000 CpG sites in the genome using the Type I assay with 12 sample locations arranged by 12 rows (Supplementary Figure 1), Methyl450 and EPIC increased its capacities upon Methyl27 by adding the Type II assay. Different chemistries and populations of the two types make the probe groups different measurement distributions [21,22]. However, these platforms suffer from errors introduced by probe cross-hybridization [16,23], the probe type bias [15], polymorphic CpG targets [16,21] and so on. Filtering out probes with potential errors and adjusting experimental bias have been necessary data preprocessing steps.

Batch effects as defined by Leek et al. “… are subgroups of measurements that have qualitatively different behavior across conditions and are unrelated to the biological or scientific variables in a study” [24]. They proposed ComBat adjusts for known batches using empirical Bayesian method even in small sample sizes. ComBat is now considered to be the most efficient method of batch effect correction [24–29]. Other algorithms were also proposed, such as RUVm and BEclear. RUVm [30] can only be used on the premise of differential methylation analysis [31]. BEclear was developed to adjust the methylation levels of batch-associated genes [31]. However, even the best algorithms may not completely remove the effects [32]. The study design, random placement of samples is essential to the results.

There are also positional effects, the effects where the same sample in different physical positions on the array could be measured as different methylation levels [16,33–35]. The earliest mention of the positional effects in the Illumina gene expression microarray analysis did not provide a method for correction except an advisement to randomly set the samples in the array [33]. A few papers mentioned the possible existence of positional effects by other names such as the ‘Sentrix position effect’, ‘beadchip effect’, ‘slide effects’ or ‘beadchip position on plate effects’. But these papers did not show proof of the effects, the consequences, nor a convincingly effective method to correct the effect [16,33–35]. Conventional approaches to correct confounders such as the polygenic regression model [36] have been attempted, but the scientific rationality of the regression model in the randomly distributed effects is problematic [33]. One unsupervised method named functional normalization (FN) claimed to be able to correct the effect [37].

Controlling batch effects [24,26–29] has been a critical practice in data analysis. In contrast, the positional effects have not attracted as much attention as batch effects. The positional effects have rarely been controlled for in conventional data analysis [16,33–35]. Illumina HumanMethylation BeadChip platforms have already been implemented in epigenetic studies of cancer and many other diseases with about close to 1000 papers published so far (NCBI GEO database [38]). Few studies have properly addressed the positional effects, which could lead to potential bias, particularly when samples were not placed randomly [33].

In this study, we closely examined the important technical artefact, positional effects in the Illumina HumanMethylation BeadChip using multiple datasets of Methyl27, Methyl450 and EPIC. We proved the existence of the positional effect and discussed its origin, and the bias it brings to the research results. We also evaluated four methods to adjust this confounder: ComBat, linear regression model, FN and single-sample Noob (ssNoob). Specifically, four methodologies were utilized to evaluate the effects, including identification of CpG sites that are significantly associated with sample position, the relative contribution to overall variation in measured methylation levels, variation between technical replicates and significant differential methylation signals between cases and controls. We further tested several methods to control positional effects along with batch effects to ensure that both artifacts can be managed. After the evaluation, we recommend a ComBat-based procedure for the preprocessing of Illumina methylation data, and implemented an R package to automate the optimal procedures.

Materials & methods

We have collected eight datasets to test for positional effects. The datasets include three Methyl450 datasets, three Methyl27 datasets and two EPIC datasets. Description of datasets is listed in Table 1. All data presented in this article can be retrieved from the public repositories.

Table 1. . Information of datasets we used in this study.

Datasets (n samples)	Methyl450 datasets			Methyl27 datasets			EPIC datasets
	ROSMAP (743)†	GSE58885 (179)‡	GSE74193 (673)§	GSE38873 (153)¶	BrainCloud (106)#	GSE26133 (160)††	GSE93373 (16)	GSE86831 (15)‡‡
Number of batches	2	16§§	5	14§§	4	10§§	2§§	4§§
Number of positions	12	12	12	12	12	12	8	8
Tissue	FC	FC	DLPC (BA46/9)	CRBLM	CRBLM	LCLs	BCs, LCLs	T
Age, year	88.01 ± 6.66	-0.25 ± 0.07	36.13 ± 22.92	44.27 ± 9.84	35.86 ± 23.62	NA	NA	NA
Number of females	468	79	244	57	51	90	12	NA
Race	725 white, 14 AA, 1 N-A, 3 Asian	NA	317 white, 356 AA	White	42 white, 64 AA	Yoruba 160	16 Asian	NA
Affection status	236 C, 507 AD	C	224 C, 449 SZ	47 C, 45 SZ, 15 Dep, 46 BP	C	C	16 EBV	2 C
Results
ANOVA	Table 2	Table 2	Table 2	Table 2	Table 2	Table 2	Table 2	Table 2
Mean	Figure 2	Supplementary Figure 5	Supplementary Figure 3	Supplementary Figure 5	Supplementary Figure 5	Supplementary Figure 4	–	–
PVCA	Figure 3	Supplementary Figure 6	Supplementary Figure 6	Supplementary Figure 8	Supplementary Figure 8	Supplementary Figure 8	–	Supplementary Figure 7
TRPs	–	–	Figure 4	–	–	Figure 4	–	–
DMPs	Figure 5	–	–	–	–	–	–	–

We used three methyl450, three methyl27 and two epic datasets from public databases and our own data to study the effects. Rosmap is the primary dataset we studied. The others are verified datasets. The ‘–’ means the datasets are not suitable for the special analyses.

^†Data taken from [39,40]

^‡Data taken from [11]

^§Data taken from [41]

^¶Data taken from [42]

^#Data taken from [43]

^††Data taken from [44]

^‡‡Data taken from [45]

^§§The batch is represented by batches information and sentrix_id, seperately.

AA: African–American; AD: Alzheimer’s disease; ANOVA: Analysis of variance analysis; BA: Brodmann area; BC: B cell; BP: Bipolar; C: Control; CRBLM: Cerebellum; Dep: Depression; DLPC: Dorsolateral prefrontal cortex; DMP: Differentially methylated probe; EBV: Epstein–Barr virus; FC: Frontal cortex; LCL: Lymphoblastoid cell line; N-A: Native American; NA: Not available; NP: Not published; PVCA: Principal variance component analysis; SZ: Schizophrenia; T: A transformed prostate cancer cell line, primary cell culture of prostate epithelial cell, patient-matched cancer associated fibroblast, nonmalignant tissue associated fibroblast and infant blood from archival guthrie card; TRP: Technical replicate pairs.

Methyl450 datasets

The primary data used in this study were brain DNA collection obtained from Rush Alzheimer’s Disease Center in healthy controls and patients with dementia [39,40]. The samples included 236 healthy controls and 507 dementia samples from two longitudinal cohort studies at Rush University Medical Center – the Religious Orders Study and the Rush Memory and Aging Project (ROSMAP data). The detailed sample information and the analysis pipeline were described by De Jager et al. and Bennett et al. The ROSMAP data were generated using the Methyl450 dataset and a sample of dorsolateral prefrontal cortex obtained from each sample.

We used two other Methyl450 datasets to verify the results: 179 frontal cortex samples from human fetal brains [11] (GEO: GSE58885; GenomeStudio followed by wateRmelon in R. Normalized β-values generated via the Dasen method of the wateRmelon package, version 1.20.3); and 675 brain dorsolateral prefrontal cortex samples from Hernandez-Vargas’s study [41] (GEO: GSE74193), which included 191 schizophrenia patients and 335 controls, with 140 technical replicate pairs or triplets. The ROSMAP and GSE74193 datasets have the .idat file, a binary format containing the raw red and green channel intensities.

Methyl27 datasets

Three Methyl27 datasets were used to confirm the findings. The datasets included the following: 153 cerebellum samples from GSE38873 [42]; 106 brain prefrontal cortex samples from BrainCloud (downloaded from [46]) [43]; and 160 samples from GSE26133 with 83 technical replicates pairs, triplets or clusters included [44].

EPIC datasets

Two EPIC datasets were analyzed, including 15 samples from GSE86831 [45] and 16 samples from GSE93373.

Data quality control & preprocessing

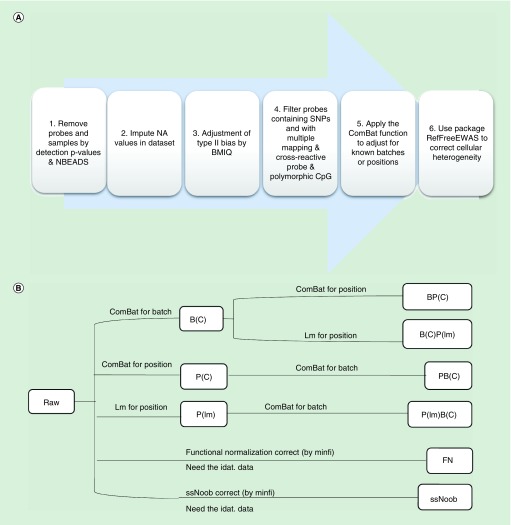
We processed and analyzed the data by R statistical language (release: 3.3.2) [47,48]. The main processing pipeline is shown in Figure 1A. The β values of these studies were used directly to assess slide batch and positional effects. We removed probes and samples by detection p-values obtained from GenomeStudio (Illumina, Inc., CA, USA). Samples were removed for those with more than 1% probes not detected (detection p-value >0.01). We removed the probes with a bead count less than three in at least 5% of samples and probes with a detection p-value above 0.01 in more than one sample (Figure 1A).

Figure 1. . The basic pipeline.

(A) The basic pipeline used to process ROSMAP dataset. (B) Datasets in different workflows correcting batch and positional effects. The Figure 1B is the detailed procedure of step 5 in Figure 1A. There are ten datasets in different workflows in Figure 1B, including: raw (data after primary QC and filtering); B(C): data corrected for batch effect; P(C): data corrected the positional effect by ComBat function; BP(C): data corrected the batch and positional effect sequentially by ComBat in order; PB(C): data corrected the positional and batch effect sequentially by ComBat in order: P(lm): data corrected the positional effect by lm; B(C)P(lm): data corrected the batch by ComBat and positional effect by lm sequentially; P(lm)B(C): data corrected for positional effect by lm and batch effect by ComBat sequentially; FN: data corrected by FN by using the preprocessFunnorm function in the minfi package; and ssNoob: data corrected by ssNoob by using the preprocessNoob function in the minfi package.

BMIQ: Beta Mixture Quantile dilation; FN: Functional normalization; NA: Not available; NBEADS: Number of the beads; QC: Quality control; SNP: Single nucleotide polymorphism; ssNoob: Single-sample Noob.

We then replaced the β values of 0 with 0.000001. Missing β value was imputed using a k-nearest neighbor algorithm by R impute.knn function in the impute package (version 1.50.1) [49]. To address the differences between the two types of probes, we used beta mixture quantile dilation (BMIQ) function in wateRmelon package (version: 1.20.3) [22] to adjust the β values of type II probes into a statistical distribution characteristic of type I probes, which has previously been shown to best minimize the variability between replicates [15,22].

The single nucleotide polymorphisms (SNPs) based on the 1000 Genomes database [50], small insertions and deletions (INDELs), repetitive DNA and regions with reduced genomic complexity may affect the probe hybridization by a subject’s genotype (Supplementary Table 1) [21]. The filter lists were based on the Naeem et al. They comprehensively assessed the effects of single nucleotide polymorphisms, INDELs, repeats and bisulfite induced reduced genomic complexity by comparing Methyl450 results with whole genome bisulfite sequencing. They determined which CpG probes provided accurate or noisy signals and derived a set of high-quality probes that provide unadulterated measurements of DNA methylation. The package RefFreeEWAS (version 2.1) was utilized to estimate cell proportion [51] for Methyl450; and linear regression model was used to correct the cell proportion for the cellular heterogeneity.

The Methyl27 datasets were processed by the same pipeline as with Methyl450 datasets except without the need to correct for the probe type bias and lack of effective methods to correct the cell types (Supplementary Figure 2). The filter list was obtained from Methyl450 [21] (Supplementary Table 2). As for the EPIC datasets, a looser filter list was used based on Pidsley et al. (Supplementary Table 3) [45].

As for the datasets without the idat. files (BrainCloud and GSE58885), we processed data based on data downloaded from GEO (Supplementary Figure 2).

Correction of the batch effects & positional effects

In our past studies, we found that the ComBat function [26] in the R package sva (version 3.24.4) [52] is effective in removing the batch effects [24,26–29]. ComBat uses an empirical Bayesian method to adjust for known batches. If the batch information was supplied, we used this information. If not, we used the Sentrix_ID as the batch.

As for the positional effects, we used four methods for correction: ComBat function; linear regression correction approach by using the lm function; the FN method by using the preprocessFunnorm function [37] in the minfi package (version 1.22.1) [53]; and ssNoob using the preprocessNoob function [54] in minfi package (version 1.22.1) (Figure 1B) [53]. In addition to evaluate the position correction effect, we assess the best order to correct the position and batch.

• ComBat function in sva: the positional effects are just like batch effects. Both refer to systematic bias on measurement associated with the position or experimental batch where the samples are tested. We treated the positions as the batch information and used the ComBat function applied to the high-dimensional data matrix, passing the full model matrix created without any known position variables. Position variables were passed as a separate argument to the function [52]. The output was a set of corrected measurements after positional effects were removed;

• Linear regression model: we used a linear regression model adjusting for positions and added the residuals to the mean values as the corrected results;

• FN: the FN method was evaluated to remove the positional effects [37]. It is an unsupervised method using control probes as surrogates for unwanted variation. It extends the idea of quantile normalization and regresses out surrogates captured by control probes. The method could be used to correct the positional effects and batch effects, as mentioned in the Fortin et al. It is worth noting that the FN method can only be used for the Methyl450 and EPIC data with .idat files [54], not applicable to Methyl27 data;

• ssNoob: ssNoob, a normalization procedure suitable for incremental preprocessing for individual methylation arrays is used when integrating data from multiple generations of Infinium methylation arrays. The ssNoob is a method adapted from the Noob [55] method without the need for a reference sample in the dye bias equalization procedure step. There was no difference between values returned by Noob or ssNoob on the β value scale [54]. The ssNoob can only be used with .idat files [54].

Ten datasets were generated through the processing. Except for the FN and ssNoob, we abbreviated the position to ‘P’, batch to ‘B’ and added the algorithm inside the ‘()’. Their processed datasets are B(C): data corrected for batch effect by ComBat only; P(C): data corrected the positional effects by ComBat; BP(C): data corrected the batch and positional effects sequentially by ComBat in order; PB(C): data corrected the positional and batch effects sequentially by ComBat in order; P(lm): data corrected the positional effects by lm; B(C)P(lm): data corrected the batch by ComBatand positional effects by lm sequentially and P(lm)B(C): data corrected for positional effects by lm and batch effect by ComBat sequentially (Figure 1). We attempted to modify the technique of calibrating variants like batch effects and positional effects (Figure 1B). We built an R package to remove the positional effects and batch effects based on the ComBat function, named ‘posibatch’, which can correct these two confounders together with an appropriate order. When we process the data, we normally correct the technical confounders first and then the biological confounders. Specific to the technical confounders, the correction orders are also important. In our opinion, we should leave the largest effects last if we cannot correct them together. In this package, we add a comparison of the positional effects and batch effects and correct the largest last. The package can be downloaded through [56].

Positional effects assessment

We used several metrics to evaluate positional effects for each dataset.

• The number of CpG loci significantly associated with positions: we used analysis of variance analysis (ANOVA) to calculate the p-values of correlation between methylation levels and position or batch. False discovery rate (FDR) q-value was computed for each nominal p-value by controlling the FDR at 0.05 using the R function 'qvalue' [57]. We then obtained the number of CpGs significantly associated with positions and batches. A good process should reduce the number of loci associated with both batches and positions;

• A principal variance component analysis (PVCA) plot measured the attribution of impact factors to the methylation levels: PVCA leverages the strengths of two statistic methods: principal components analysis and variance components analysis. Principal components analysis is one of the most essential and popular techniques for reducing the dimensionality of a large dataset, increasing interpretability and minimizing information loss. Variance components analysis fits a linear mixed model to match the random effects to the factors of interest for estimating and partitioning the total variations. We estimated the effects of each known factor by the lme4 package [58] (version 1.1–13) in R, then the residual effect that known factors could not explain would be calculated [58]. After that, the PVCA results can be used to assess the most efficacious processes to correct positional effects;

• The root-mean-square-error (RMSE) of technical replicated pairs: the RMSE was used to determine the adequacy of the ten processed datasets (including raw, B[C], P[C], BP[C], PB[C], P[lm], B[C]P[lm], P[lm]B[C], FN and ssNoob) separately. A good process should minimize the RMSE of technical replicate pairs;

• Differential methylation CpG loci analysis: to assess the impact of positional effects on analytical results, we discovered differentially methylated probes associated with schizophrenia in GSE74193 data (covariates: age, race and sex) and Alzheimer’s disease-associated probes in ROSMAP data (covariates: the two cell types; age at cycle – baseline (age_bl), which can be the cognitive date, interview date, or clinical evaluation; age at death (age_death); the education level; race; Spanish ancestry (Spanish); and sex using the limma package (version 3.32.2) [59] in R [59].

The GSE74193 dataset was divided into discovery and validation subgroups, with 30 schizophrenia patients and 46 controls in each subgroup. The limma package was used to identify the differentially methylated loci and obtain the fold change (FC) between cases and controls. The result is quantified using the area under a receiver operating characteristic curve (AUC of ROC), a commonly used measure of the accuracy. The curve was created by plotting the true positive rate and the false positive rate at various threshold settings. We identified AUC for the prediction of high and low FCs. The cut-off was a p-value lower than 0.05 and the log(FC) greater than 0.02. The AUC of ROC was used to measure the internal consistency in each normalization method. The DeLong’s test was used to compare the AUC of ROC curves [60].

These analyses test whether removing positional effects improve reproducibility of signals detected from case–control comparisons.

Results

ANOVA results of methylation levels & physical positions

We analyzed the ROSMAP data with 743 samples in 64 arrays. After quality control preprocessing and filtering, 161,862 probes were tested for the correlations between methylation levels and sample physical positions. A total of 52,988 of them were significantly associated with their sample positions by FDR q-value <0.05, while 152,977 loci were associated with batches. After removal of the batches (batches 0 and 1) using ComBat, the number of CpG loci associated with position increased to 61,725; and the batch-associated probes reduced to zero.

We corrected the positional effects only with ComBat, and still detected 112 CpG loci associated with positions but left 153,775 probes related to batches. Then the batch and positional effects were sequentially adjusted in two different orders. When corrected for the batch effects first, 94 loci associated with position were identified, and zero associated with the batch. However, when we corrected the positional effects first, 137 position-associated loci were detected, and none of the batch-associated signals were detected.

We also used the linear regression method [36,61,62], lm function in R, to correct the positional effects. Regardless of the correction orders of positional and batch effects, there were no CpG sites related to the physical positions. The FN and ssNoob were also used to normalize the data. In the ANOVA evaluated results, the FN method had a remainder of 108,296 position-associated CpGs and 134,263 batch-associated CpGs; the ssNoob method had a remainder of 85,114 position-associated CpGs and 153,621 batch-associated CpGs. We further analyzed another two Methyl450, three Methyl27 and two EPIC datasets (Materials & methods), and confirmed the existence of positional effects in those data (Table 2). Notably, we separately detected 10,438 and 7956 CpG loci significantly associated with the batches when we corrected for the batch effect first followed by positional effects in GSE26133 and the BrainCloud dataset (Table 2).

Table 2. . The number of CpG sites showed association with sample physical positions and batches in studies.^† .

Studies (n probes)	Methyl450 datasets						Methyl27 datasets						EPIC datasets
	ROSMAP (161,862)		GSE58885 (156,108)		GSE74193 (149,069)		GSE38873 (10,640)		GSE26133 (11,500)		BrainCloud (11,500)		GSE86831 (724,466)		GSE93373 (724,466)
Process	Position	Batch	Position	Batch	Position	Batch	Position	Batch	Position	Batch	Position	Batch	Position	Batch	Position	Batch
Raw	52,988	152,977	46,754	8,504	68,079	126,766	0	7471	1	10,301	1604	7848	269,705	128,435	0	0
B(C)	61,725	0	52,071	1	86,622	0	52	29	4182	0	3952	0	0	0	6	0
P(C)	112	153,775	0	11,850	5	127,739	0	7586	0	10,433	0	7934	325	0	0	8469
BP(C)	94	0	0	1	21	0	0	35	0	10,438‡	0	7956‡	0	0	0	14
PB(C)	137	0	0	2	45	0	0	14	0	0‡	6	0‡	0	0	0	4
P(lm)	0	153,245	0	12,982	0	126,546	0	7599	0	10,370	0	7909	0	0	0	0
B(C)P(lm)	0	0	0	1	0	0	0	36	0	0	0	0	0	0	0	0
P(lm)B(C)	0	0	0	1	11	0	0	21	0	0	0	0	0	0	0	0
FN	108,296	134,263	NA	NA	79,781	131,478	NA	NA	NA	NA	NA	NA	169,372	93,441	0	0
ssNoob	85,114	153,621	NA	NA	1656	124,890	NA	NA	3	8105	NA	NA	224,821	106,030	0	0

Methyl450 means Illumina Infinium HumanMethylation450 BeadChip Array and Methyl27 means Illumina Infinium HumanMethylation27 BeadChip Array. N probes mean the number of the probes after filtering and preprocessing. The result data means the number of loci correlated at methylation sites and position FDR q-value <0.05 in different datasets.

We used ANOVA analysis to calculate the p-values of correlation between methylation levels and position or batch. FDR q-value was computed for each nominal p-value by controlling the FDR at 0.05 using the R function 'qvalue'. We then obtained the number of CpGs significantly associated with positions and batches.

^†False discovery rate q-value <0.05.

^‡Table cells are notable due to the corrected order.

ANOVA: Analysis of variance; BP: Bipolar; FDR: False discovery rate; FN: Functional normalization; NA: Not available; ssNoob: Single-sample Noob.

In the preprocessing of these datasets, impute.knn was used to impute missing values using k-nearest neighbor averaging. For each CpG with missing values, an Euclidean metric was detected for confining the columns for which that CpG is not missing. That means the impute.knn was based on the methylation values among probes rather than samples. So, this step would not influence the evaluation results. Besides, only 0.05% (348 of 724,466 in GSE86831) were imputed, which accounted for only 0.04% (109 of 269,705) of position-associated CpGs. We used Fisher test to evaluate the significance of the enrichment; the p-value is 0.9909. The great majority of CpGs with positional effects are not imputed. So, the impute.knn step would not influence the results.

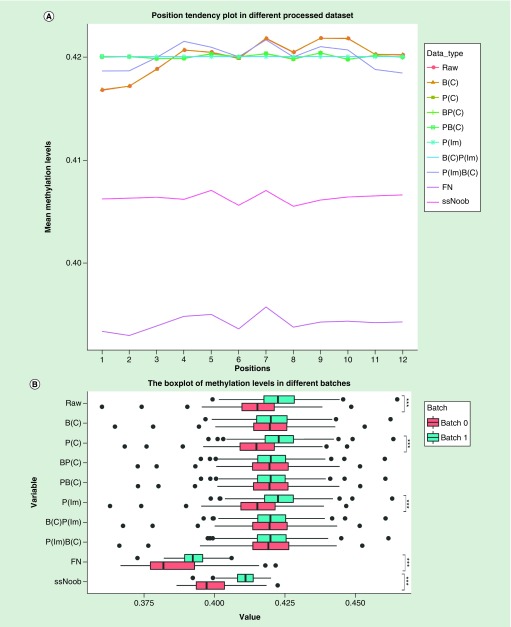
We further assessed the impact of the processes controlling batch and positional effects had on the data. We calculated the average methylation levels of ROSMAP data comparing pre- and postcorrection in 12 positions and two batches, respectively. After correcting the batch and positional effects by ComBat and Im, regardless of order, the methylation levels in the 12 physical positions became homogeneous (Figure 2A), and the differences of batch correction results remained statistically insignificant (Figure 2B). Alternatively, when we corrected positional effects by the FN and ssNoob method, the variation of methylation levels in different physical positions had no significant reduction (Figure 2A); same was seen for the batches (Figure 2B). The difference between sample locations was normalized after removing positional effects by ComBat and lm. Similar results of other replicated datasets were shown in the Supplemental Materials (Supplementary Figures 3 & 4).

Figure 2. . The average and variation of methylation levels of all probes in ROSMAP ten different processed datasets.

(A) Average methylation levels in different positions. (B) Methylation levels in different batches. When the linear regression model was used to correct the position effect, the correction result of each CpG was calculated by adding the average value of the CpG to the residual so that the data was within the normal range. The p-value was calculated using t-test.

***p-value statistically significant.

FN: Functional normalization; ssNoob: Single-sample Noob.

The variable effects measured by PVCA

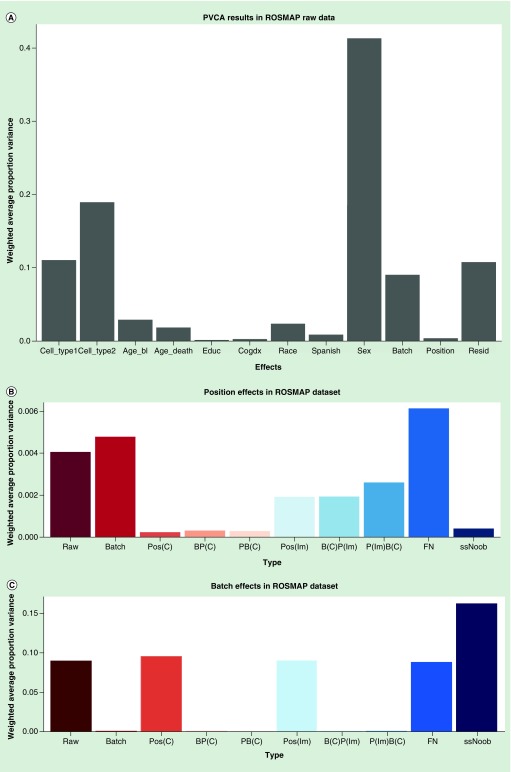
We made the PVCA plot to evaluate the relative weighted proportion variance (Figure 3). The PVCA plot describes the relative weights of corresponding eigenvectors related to the eigenvalues that can be explained by factors in the experimental design and other covariates [63,64]. Here we considered 11 possible sources of variations: the two cell types;  age_bl; age_death; education level; the cognitive diagnosis (cogdx); race; Spanish; sex; batch; positional effects (position); and the weight of residual effect (resid in the figure) caused by unexplainable factors.

Figure 3. . Principal variance component analysis results in ROSMAP dataset.

(A) PVCA results in ROSMAP raw data. PVCA estimated the contribution of each factor to the overall variation. We considered 11 possible sources of variation in the ROSMAP data: the two types of cell; and age at cycle – baseline (age_bl) which can be the cognitive date, interview date or clinical evaluation; age at death (age_death); the education level (educ); the cognitive diagnosis (cogdx); race (race); Spanish ancestry (Spanish); sex; batch; and positional effects (position). And we obtained the weight of residual effect (resid) that known factors could not explain. (B) Position effects in ROSMAP dataset detected by PVCA. (C) Batch effects in ROSMAP dataset detected by PVCA.

PVCA: Principal variance component analysis.

The effects of batch (Figure 3B) and position (Figure 3C) were the smallest in BP(C): 0.02% in position and 0.006% in batch and PB(C): 0.02% in position and 0.003% in batch compared with other processed data (P[lm]: 0.19% in position and 9% in batch; B[C]P[lm]: 0.19% in position and 0.0003% in batch; P(lm)B(C): 0.26% in position and 0.0004% in batch; FN: 0.6% in position and 9% in batch and ssNoob: 0.041% in position and 16% in batch). BP(C) and PB(C) performed equally well in the technical variants including batch effects and positional effects. The ComBat method outperformed lm in controlling the positional effects.

Other replicated datasets confirmed the observation of positional effects as shown in the Supplemental Materials (Supplementary Figures 6–8). For example, in GSE58885, the positional effects in BP(C) and PB(C) are 0.2 and 0.5% in B(C)P(lm), 0.4% in P(lm)B(C). These data indicate that the positional effects gave a relatively smaller contribution to the overall variation than other major factors like sex, age and race, but they are not negligible.

Analysis of the technical replicates

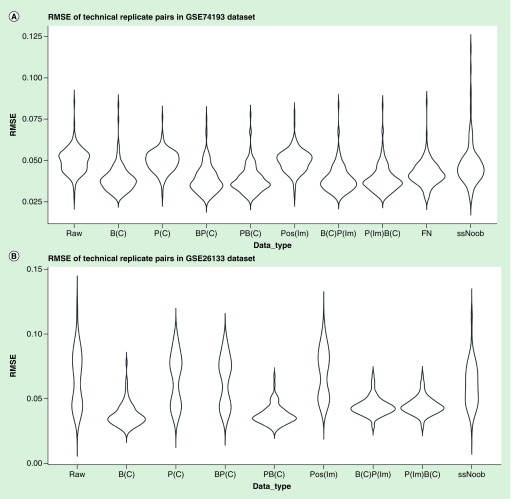
Technical replicates can be used to evaluate the consistency or precision of measurement. With this in mind, we tested whether removing positional effects can improve precision. The GSE74193 dataset had 140 pairs of technical replicates, and the GSE26133 dataset had 83 pairs. Subsequent to each correction step, the RMSE values of each pair were calculated. After removing the positional effects by ComBat, the RMSE decreased more than lm (Wilcoxon signed-rank one-tailed test, GSE26133: p = 4.627e^-11, GSE74193: p < 0.2483), FN (Wilcoxon signed-rank one-tailed test, GSE74193: p = 1.414e^-7) and ssNoob (Wilcoxon signed-rank one-tailed test, GSE26133: p < 2.2e^-16, GSE774193: p = 2.5e^-15) (Figure 4). Therefore, ComBat outperforms lm, FN and ssNoob in adjusting the positional effects and improving precision. The RMSE values in PB(C) is lower than BP(C): Wilcoxon signed-rank one-tailed test, GSE26133: p-value <2.2e^-16, GSE74193: p = 0.4329) (Figure 4); thus, correcting the positional effects first followed by batch effect improves precision. Correcting the positional effects and batch effects could reduce the RMSE of technical replicates pairs (Wilcoxon signed-rank one-tailed test, GSE74193 & GSE26133: p < 2.2e^-16) (Figure 4). However, there is no significant difference in comparing RMSE between data corrected for the positional effects before batch and data corrected for the batch only (Wilcoxon signed-rank one-tailed test, GSE74193: p = 0.2309, GSE26133: p = 0.7281) (Figure 4).

Figure 4. . The root-mean-square-error of technical replicate pairs.

(A) GSE74193. (B) GSE26133.

RMSE: Root-mean-square-error.

In summary, the best practice to correct the positional effect is to use the ComBat-based method.

Differential methylation CpG loci analysis

The impact of positional effects on the detection of differential methylation signals was assessed. Two datasets with disease information were analyzed.

An empirical Bayes test, limma in R, was used to identify differentially methylated CpGs between cases and controls of the processed GSE74193 dataset with 46 controls and 30 cases in two replicated groups; the number of CpGs associated with schizophrenia was noted (p-value <0.05 among all CpGs analyzed). A higher AUC was identified in the PB(C) and BP(C) compared with other processed datasets (DeLong’s test for two ROC curves, P(C) vs P(lm): p = 0.05; P(C) vs FN: p = 0.0005; P(C) vs ssNoob: p < 0.0001356; PB(C) vs P(C): p = 3.818e^-16; PB(C) vs BP(C): p = 0.9682).

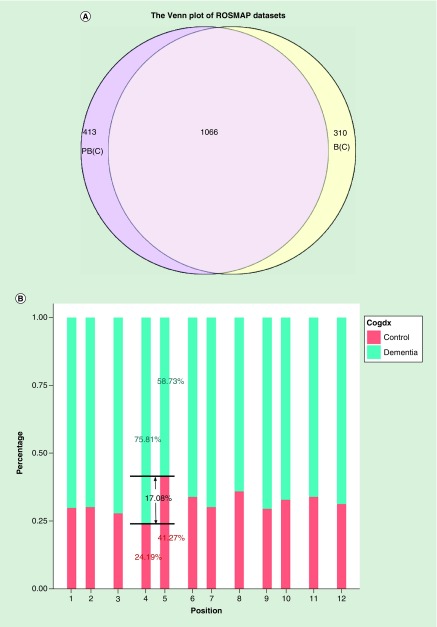
The ROSMAP dataset was also used to identify differentially methylated CpGs. A total of 161,862 probes have been tested for differential methylation after filtering. A total of 1376 of the CpG loci were differentially methylated in data corrected for the batch effects (p < 0.01). A total of 1479 CpG loci were significant in data corrected for positional effects followed by a batch correction (Figure 5A). A total of 310 CpG loci were detected in the B(C), but not in the PB(C), and 413 CpG loci were detected in the PB(C), but not the B(C). Therefore, the positional effects could have biased the methylation comparisons between case and control if the positional effects were not corrected during preprocessing, subsequently producing errors, including false negatives. When examining the sample plating, we noticed that the cases and controls had not been randomly placed in each position. Some positions have more cases than the others; positions four and five have the largest proportion differences (Figure 5B). Fortunately, the disease status has not confounded with positions (Supplementary Table 4), we can still correct the positions. No matter how optimal the data analysis is, without proper randomization of an experiment the data will produce bias in the analysis [33,55].

Figure 5. . Differential Methylation CpG loci analysis results in ROSMAP dataset.

(A) The Venn diagram plot of the differentially methylated CpG loci obtained from differently processed data. The datasets including B(C): data corrected for the batch effect), and PB(C): data corrected for the positional and batch effect sequentially by ComBat. (B) The sample distribution in cognitive diagnostic of ROSMAP data in 12 positions. The values showed in the figure are the control and dementia samples percentages in position four and five. Venn diagram showing the number of differentially methylated CpGs (false discovery rate <0.05) between each pair of datasets.

Discussion

Our analyses identified an important technical artifact of the Illumina Infinium HumanMethylation BeadChips in Methyl450, Methyl27 and EPIC, related to the position in the array called positional effects. When identifying the objectivity of this effect, the relevance of positions and other variables were evaluated for each dataset (Supplementary Table 4). None of the datasets except the GSE38873 were confounded with biological variables. The GSE38873 dataset was not used to detect the disease-associated probes, so the positional effects were determined to be objective. Because positional effects bias the measure and lead to possible false conclusions, particular attention needs to be paid in controlling this variable in data analysis. In the analysis, we noticed the effect of positional effects in Methyl450 is larger than in Methyl27. The Type II probes contribute 2.98-times more to the positional effects than the Type I probes in Methyl450 datasets. After we had corrected the bias by BMIQ, the proportion of position-associated probes in Type II and I was 1.11. Therefore, adjusting the Type II probes methylation levels into a statistical distribution characteristic of Type I probes could help to reduce the positional effects, to a degree. Considering that the probe type bias is related to the positional effects, the EPIC may also be influenced by the effects. However, we only got two EPIC datasets with very small sample size, which did not provide enough power to detect positional effects.

Although the technical replicate pairs could not prove the necessity of correcting the positional effects, the ANOVA results and differential CpGs analysis demonstrate that correction of the batch effect influences the positional effects and further bias measures at many CpG loci. Therefore, adjusting the positional effects is needed.

The best method to correct for these effects is ComBat according to our evaluation. Two primary reasons for choosing the ComBat to correct for the positional effects: the positional effects are randomly distributed in the same pattern as the batch effects [24,26–29]; and the RMSE of technical replicate pairs and PVCA illustrates that the ComBat function is better than lm, FN and ssNoob for correcting the positional effects.

As for the correction order of positional and batch effects, we suggest correcting the smaller effect first according to ANOVA, PVCA and technical replicate pairs evaluation results. We noticed that the batch effect is smaller than positional effect in the GSE58885 datasets from PVCA (Supplementary Figure 6), which is different from the others. After the position and batch effects correction, the BP(C) performed slightly better than PB(C). There may be some CpG loci influenced by both of these effects. So, if you try to correct multiple confounders by the same method, you should compare their effects in the real data and correct confounder with the larger effect last (Table 2, Figure 4B). The posibatch we built reflects such considerations. We added a comparison of the effects in position and batch, and corrected the largest last.

Conclusion

In summary, positional effects exist in the Illumina BeadChip data and can undoubtedly introduce bias into methylation level measures. Sample placement in each chip should be randomized [33,55], and most importantly, proper statistical methods should be used to remove the confounding artifacts. If the artifacts are not taken into consideration, false conclusions could be drawn. Given that hundreds of epigenetics studies have used these platforms without controlling for positional effects, the reported differential methylations may have been biased by the effects. Citing those findings and considering the effect may need some extra caution.

Summary points.

• We have collected eight datasets (including three Methyl450, three Methyl27 and two EPIC datasets) to evaluate the existence of positional effects and find a method to correct the effects by using four evaluation methods.

Major results

• A total of 52,988 CpG loci were significantly associated with their sample positions by false discovery rate q-value <0.05, 112 loci remained after correction of positional effects.

• The principal variance component analysis plot revealed that the BP(C) and PB(C) performed well.

• After removing the positional effects by ComBat, the technical replicates root-mean-square-error increased more than other methods.

• Positional effects could have biased the methylation comparisons between case and control if the positional effects were not corrected during preprocessing, subsequently producing errors, including false findings.

• A higher area under the curve was identified in the PB(C) and BP(C) compared with other processed datasets.

Conclusion

• The positional effects were found in the Illumina HumanMethylation BeadChip caused by physical positions where samples were placed.

• The positional effects could bring bias to the methylation analysis, and produce false findings.

• The recommended procedures for controlling both the positional effects and batch effects are to use ComBat to remove the positional effects first and then use ComBat again to remove the batch effects. We have implemented an R package to automate the procedures.