Finite element evaluation of the newest ISO testing standard for polyethylene TKR liners

Abstract

Current treatment for end-stage osteoarthritis is a total knee replacement. Given that the number of total knee replacement surgeries is expected to approach 3.48 million by 2030, understanding long term failure is important. One of the preclinical tests for total knee replacements is carried out using mechanical wear testing under generic walking conditions. Used for this purpose is the International Standards Organization’s generic walking profile. Recently this standard was updated by reversing the direction of anterior/posterior translation and internal/external rotation. The effects of this change have not been investigated and therefore it is unknown if comparisons between wear tests utilizing the old and new version of the standard are valid. In this study, we used a finite element model along with a frictional energy based wear model to compare the kinematic inputs, contact conditions, and wear from the older and newer versions of the ISO standard. Simulator tested components were used to validate the computational model. We found that there were no visible similarities in the contact conditions between the old and new versions of the standard. The new version of the standard had a lower wear rate, but covered a larger portion of the articular surface. Locations of wear also varied considerably. The results of the study suggest that major differences between the old and new standard exist and therefore historical wear results should be compared with caution to newly obtained results.

Introduction

Osteoarthritis of the knee is one of the leading causes of disability globally [1]. End-stage treatment for knee arthritis is a total knee replacement (TKR). The number of TKR surgeries is expected to approach 3.48 million by 2030 [2], making study of how and why these implants fail important. One of the leading causes of long term failure of TKRs is osteolysis caused by polyethylene wear particles [3–7]. This can lead to implant loosening, pain, and the eventual failure of the implant. Once an implant has failed, there is a need to perform revision surgery, which can be both costly and risky for the patient, and challenging for the surgeon [8]. To estimate how long TKRs will last before they are implanted, TKRs undergo preclinical wear testing. The gold standard for TKR preclinical wear testing is mechanical wear testing using generic standard walking profiles [9]. Currently used for this purpose is the ISO standard for TKR wear testing (ISO 14243-3) [10]. Wear testing using standardized protocols is necessary for FDA approval, and for comparing older designs to new ones.

Recently, there was a change in the ISO standard for knee testing (ISO 14243-3): the direction of motion in the anterior/posterior (AP) and internal/external (IE) rotation directions were reversed. The International Organization for Standardization does not provide any reasoning for the change. However, these modifications followed publications that compared motion analysis studies of TKR subjects during walking to the force and displacement control ISO standards [11, 12]. Studies had shown that contrary to ISO(2004), patients exhibited external rotation of the tibia during swing phase [11, 12]. A study examining how the natural knee responded to force control ISO standard at the time showed anterior tibial translation during swing phase [13]. These modifications may affect volumetric wear, wear area, and contact conditions, all of which may lead to different damage mechanisms. The effects of this change have not been investigated and therefore it is unknown if comparisons between wear tests utilizing the old and new standard are valid.

In the present study, we used a finite element analysis (FEA) model of a TKR, along with a novel frictional energy based wear model [14], to investigate differences between ISO 14243-3(2004)[15] and ISO 14243-3(2014)[10]. Kinematic inputs, contact conditions, and wear from the older and newer versions of the ISO standard were compared, and wear predicted by the FEA model was validated against simulator tested components.

Methods

Development of finite element wear model

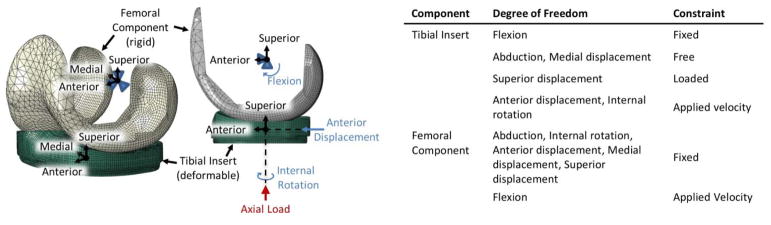
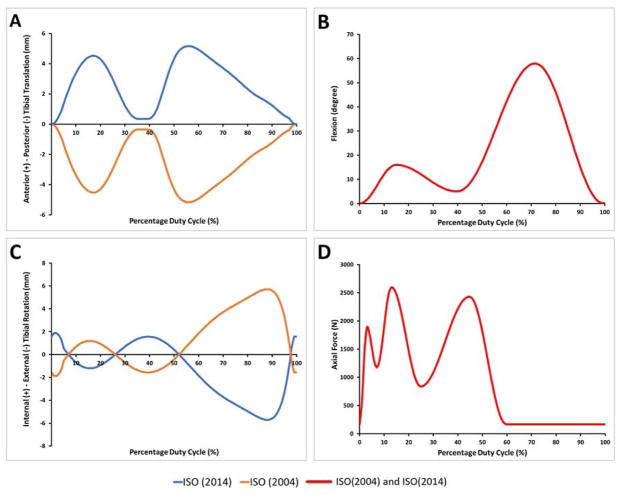
A FEA model was created from CAD models of a left sided NexGen Cruciate Retaining TKR (Zimmer, Warsaw, IN). 78,108 linear hexahedral elements (C3D8R) were used to model the ultra-high molecular weight polyethylene (UHMWPE) component. The cobalt chromium molybdenum femoral component was modeled as a rigid surface, utilizing a mix of 2^nd order quadrilaterals and tetrahedrons (4080 SFM3D8, 547 SFM3D6) (Figure 1). The UHMWPE component was modeled using the J-2 Plasticity model [16] with a density of 9.4E-7 kg/mm³ and an elastic modulus of 1,051 MPa. Parameters used in the J-2 Plasticity model can be found in Table 1. Contact between the UHMWPE insert and femoral component was modeled as penalty contact, with the friction coefficient set to 0.04 on the articular surface [17–19]. IE rotation, and AP translation were applied to the UHMWPE insert as velocity boundary conditions at a reference point located at the center of rotation as defined during simulator testing. Medial/lateral (ML) translation and abduction/adduction were left free, as was the case in our experimental testing. Flexion/extension was applied to the femoral component which was otherwise fixed. Axial force was applied through the UHMWPE reference point and offset 5 mm medially per ISO 14243-3. A summary of the boundary conditions applied to the model can be found in (Figure 1). FEA models were run using ABAQUS v2016/Standard (Dassault Systèmes, Waltham, MA). The loads and motions specified by simulator standard ISO 14243-3(2014) were compared to ISO 14243-3(2004) (Figure 2). Terms “ISO(2014)” and “ISO(2004)” will be used throughout to indicate ISO 14243-3(2014) and ISO 14243-3(2004), respectively.

Figure 1.

Summary of the model and associated boundary conditions.

Table 1.

Parameters for the J-2 Plasticity Model

Stress (MPa)	Strain
12.1	0.00
21.4	0.03
23.8	0.11
44.0	0.55
92.4	0.98
135.0	1.09
515.0	1.34

Figure 2.

Model inputs for ISO(2014) and ISO(2004). Blue is ISO(2014) and orange is ISO(2004). Red is inputs shared by both versions of the standard.

Wear was predicted following the concept of a previously published wear model based on energy loss due to friction [14] (Equation 1). Newly, the model was applied to the FEA mesh using the Fortran user subroutine UMESHMOTION available from within ABAQUS. The wear model utilizes a parameter, unit work, defined as the frictional energy required to remove a unit volume of material both parallel to and perpendicular to the primary fibril orientation. Values for unit work parameters (in J/mm³) were set as: δWork_x = 3.547E07, δWork_y = 3.855E08. All symbols defined in Equation 1 are listed in Table 2.

Table 2.

List of symbols for the wear model (Equations 1 and 2).

SD	Sliding Direction
V	Sliding Velocity
Ff	Tangential Force
θ	Primary Fiber Orientation
A	Area
t	Time
δWorkx	Unit work in X
δWorky	Unit work in Y

$${\mathit{WearDepth}}_{\mathit{cycle}}=\sum _{\mathit{Start}\mathit{time}}^{\mathit{End}\mathit{time}}\frac{F_f(t)\ast V(t)\ast {\mathit{cos}}^2(\left|\theta -SD\right|)}{\delta {\mathit{Work}}_x}+\frac{F_f(t)\ast V(t)\ast {\mathit{sin}}^2(\left|\theta -SD\right|)}{\delta {\mathit{Work}}_y}\ast \frac{\mathrm{\Delta }t}{\mathrm{\Delta }A}$$ 1)

As the wear model does not consider UHMWPE fibril mobility, we initialize each node as having an initial fibril direction. This means that UHMWPE modeled by a particular node is assumed to be aligned in a particular direction at the start of the wear simulation. We calculate this assumed direction by running the FEA model through an ISO cycle without modeling wear, and calculating the total frictional work at the UHMWPE contact surface in both the x and y directions. The initial direction is assigned as the angle between the total work done in each direction, or the resultant direction of total frictional work (Equation 2, symbols in Table 2).

$${\theta }_{\mathit{initial}}={tan}^{-1}\frac{\mathrm{\sum }{F}_{f,y}\ast V_y}{\mathrm{\sum }{F}_{f,x}\ast V_x}$$ 2)

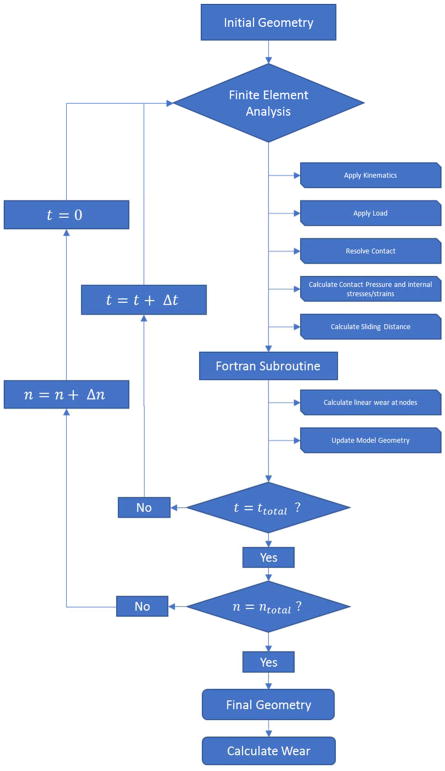
To simulate wear in the FEA model (Figure 3), first, for each contact node, ABAQUS outputs the nodal quantities for tangential contact forces (F_f) and sliding velocity (V). Angle (θ) is calculated as the difference between the tangential contact force direction, and the primary fibril direction defined in the model. Using an ABAQUS user subroutine, for every time increment, wear is calculated at each node using Equation 1. Wear is scaled by 500,000 cycles. The wear step is then repeated for a total of 1 million cycles. The number of mesh updates necessary was determined through a convergence study and is comparable to the values utilized in similar models [20].

Figure 3.

Process for wear prediction. t is the total time within a single gait cycle and n is the number of gait cycles simulated.

Mesh convergence was determined by comparing the contact pressure to the contact pressure error indicators available in ABAQUS/Standard. Local contact pressure error of an order of magnitude less than reported contact pressure was deemed acceptable as per guidelines by the developers [21].

Validation of wear model

Preliminary validation of the FEA model was carried out by comparing gravimetric wear from the simulator tested components to wear predicted by the FEA model for the ISO(2004) profile. A four-station knee wear simulator (Endolab, Rosenheim, Germany) was used to test tibial liners (NexGen CR, Zimmer, Inc., Warsaw, IN). In three stations, tibial liners were tested under ISO(2004) conditions in displacement control mode. In one station, the tibial liner acted as a loaded soak control and did not undergo displacement. The applied degrees of freedom were the same as described for the FEA model (Figure 1). In each of the four stations, the lubricant, tibial liner, tibial baseplate, and femoral component were contained in a sealed, temperature controlled (37° C) chamber. Lubricant consisted of bovine serum (Life Technologies Corporation, Carlsbad, California) diluted with saline to a protein content of 30 g/L and pH of 7.6. Ethylenediaminetetraacetic acid (EDTA) was added at 200 mg/L. Tests were conducted at 1.0 Hz for 4 million cycles. Testing was stopped every 0.5 million cycles for cleaning and weighing of the tibial liners. Before and after test completion, the articular surfaces of the tibial liners were digitized using a coordinate measuring machine (SmartScope, OGP, NY). A previously described autonomous mathematical reconstruction method [22] was used to construct wear contours on the surfaces of the tibial components from the pre- and post-test digitized surfaces for comparison to the FEA model. The simulator-produced gravimetric wear was compared to FEA wear by examining the change in volume of the entire mesh over the course of the FEA simulation and converted to gravimetric wear using the density for UHMWPE used in the model.

Results

Finite element predicted contact conditions and wear

There were no visible similarities between ISO(2004) and ISO(2014) contact pressure contours at most time points during the gait cycle. For example, at 15% and 50% of the gait cycle, the location of contact pressure contours for ISO(2004) are farther anterior than ISO(2014) on both the medial and lateral sides, and the lateral side contact pressure contours are more posterior than the medial side (Figure 4). The contact pressure contours for ISO(2014) during the two time points are on the posterior side of the tibial plateau, with both the medial and lateral compartment contact pressure contours parallel. At other points in the gait cycle, however, the contours are almost the same (for example 0%, 45%, and 100%). Overall, contact for ISO(2014) spends more time on the posterior side of the plateau, which would be expected from the input waveforms.

Figure 4.

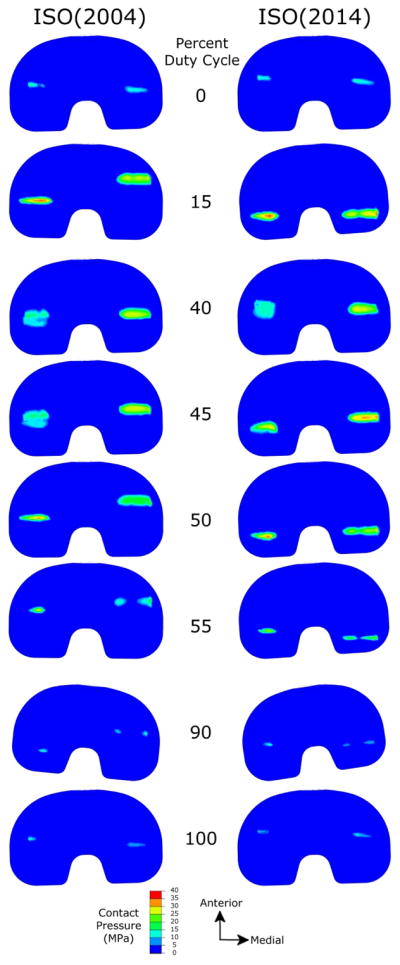
Contact pressure comparison between ISO(2004) and ISO(2014) at key points of the gait cycle. There were no obvious correlations between the old and new standard.

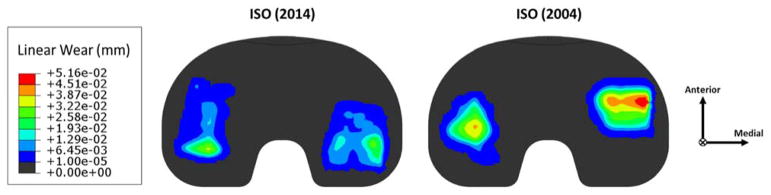
FEA predicted wear scars for ISO(2014) inputs covered a larger area of the articular surface and were longer than for ISO(2004) inputs (Figure 5, Table 3). Locations of higher wear predicted by the wear model varied considerably between ISO(2004) and ISO(2014), with high wear in the ISO(2004) predicted wear scar located more anterior on the tibial component, but more posterior for ISO(2014). The angle between the medial and lateral wear scar centroids (counter-clockwise is external rotation) was also different, with the ISO(2014) wear scars internally rotated compared to the ISO(2004) wear scars. FEA predicted wear rates showed the older standard having a higher wear rate (8.66 mg/million cycles) while the newer standard had a lower wear rate (4.45 mg/million cycles).

Figure 5.

Contact pressure comparison between ISO(2004) and ISO(2014) at key points of the gait cycle. There were no obvious correlations between the old and new standard.

Table 3.

Wear scar attributes for ISO(2004) and ISO(2014) from FEA. Coordinate system for centroids is located at the bottom edge centered medially/laterally. The angle between the centroids has counter clockwise as positive.

		Area (mm2)	ML Centroid (mm)	AP Centroid (mm)	Angle (°)	Perimeter (mm)	AP Length (mm)
ISO(2004)	Medial	344.8	22.91	9.99	NA	75.61	14.49
	Lateral	300.5	−23.56	3.45	NA	78.87	22.66
	Total	645.3			8.02
ISO(2014)	Medial	386.7	22.95	0.43	NA	84.63	22.64
	Lateral	356.3	−23.80	5.25	NA	91.11	26.18
	Total	742.9			−5.88
% Difference from ISO(2004)	Medial	12.13	0.17	−95.70	NA	11.93	56.25
	Lateral	18.59	1.02	52.17	NA	15.52	15.53
	Total	15.13			−173.3

Model validation

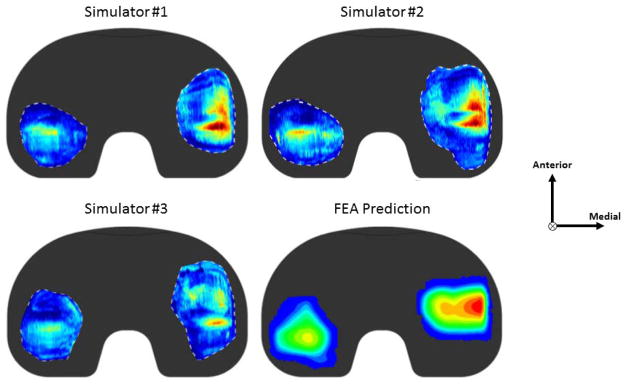
FEA wear scar predictions compared well with the simulator (Figure 6). There is a large variation present in the simulator tested components which the FEA wear scar predictions fall within. The location of highest wear in both the simulator tested components and the FEA tested components is on the medial side of the medial compartment, while the lateral compartment wear scar is smaller with less intense wear visible. Both simulator components and FEA simulations had medial wear scars located farther anterior than the lateral wear scars (externally rotated). Examining gravimetric wear, the wear of the simulator components was 5.14±2.18 mg/million cycles. FEA predicted wear for the 4 million cycle test was 8.66 mg/million cycles.

Figure 6.

Wear scar comparison of 3 simulator tested components to a FEA predicted wear scar after 4 million simulated cycles.

Discussion

The objective of this study was to compare the kinematic inputs, contact conditions, and wear from the ISO(2014) against ISO(2004). In ISO(2014), both the IE and AP inputs were reversed. This did not result in wear being mirrored medially/laterally or anteriorly/posteriorly as might be expected. Instead, there was no discernable relationship between wear scars or contact pressure generated using ISO(2004) or ISO(2014) inputs. ISO(2014) produced wear scars that were both longer and covered a larger area as compared ISO(2004). ISO(2004) inputs created wear scars with more localized wear and smaller wear scars. ISO(2014) had lower wear rates despite the larger wear scar. The wear rates produced during the simulator test for ISO(2004) were reasonably close to the wear rates for the ISO(2004) FEA predictions. Wear scars between the simulator tests and the FEA predictions were similar, with several features in common: (1) areas of high wear on the medial edge of the medial side were present on both the simulator components and the predictions; (2) the medial side wear scar was more anterior than the lateral side wear scar in both the FEA predictions and the simulator tests.

A limitation of the current study is that the volumetric wear calculation of the wear model has not been fully validated. While the model duplicated the distribution of wear (wear scars) seen in the simulator tested components well, the ISO(2004) wear rate was overpredicted. The range of errors in published computational models of wear of TKRs can be quite large, with the predictive power (R²) ranging from 0.12 (Archard) to 0.60 [23]. Another more recently published study [24] had errors as large as approximately 3.5 mm³/MC in both directions, very similar to the difference noted in our study. The error in the model can be accounted for by several factors. First, there is a large amount of variability in wear rates during mechanical testing. This can be seen in both the large standard deviation of the wear rate for our experimental test (±2.18mg/MC), and by examining the wear scars produced. Other factors could include differences in the lubricant, differences in the UHMWPE used to calibrate the model versus that used in the TKR samples (including the degree of crosslinking), the positioning of the components in the simulator, and the lack of UHMWPE chain mobility in the computational wear model. The original mechanical testing used to generate the unit work parameters [14] was also carried out at room temperature, while our simulator tests were run at 37° C. In addition, the comparison between ISO(2014) and ISO(2004) relies less on precise wear rates and more on the magnitude of the difference, as well as the distribution of wear. This study examined whether there were differences between the old and new versions of the ISO standard and our study predicted that there are indeed differences in wear volume and wear distribution. Attempts were made to find literature utilizing either version of the standard under displacement control and using NexGen components for comparison purposes however none were found. There are studies that utilize NexGen components under force control [9, 23, 25], and the wear rates in these studies vary from 5.12 mg/MC to 17.35 mg/MC. One study using a modified version of the ISO(2004) standard but with higher loading during swing phase showed a wear rate for NexGen tibial liners at 14.4 ± 2.8 mg/Mc [26, 27]. Another study using ISO-derived inputs reported wear rates of 22.0±5.8 mg/MC [28]. A study using a similar component under displacement ISO(2004) was shown to have a wear rate of 5.2 ± 1.9 mm³/MC [24]. The large variation in wear rates supports the decision to accept the results of the wear model. Another limitation of the study was that the tibial tray was excluded, and no attempt was made to consider backside wear. Given however that backside wear is a small portion of the total wear [20, 28], it was ignored for the sake of computational efficiency. Finally, while our model considers plastic deformation, viscoelastic effects are not included in our material model. Including viscoelasticity would increase CPU time and would likely only effect linear penetration, and not the comparison between the two versions of the standard. As such, we have not included values of linear penetration in our comparison of wear simulator test samples and our FEA predicted wear scars.

There has not been any attempt in the literature yet to compare the differences between the old and new versions of the standard. One study was found that compared the effect of reversing the polarity of the AP displacement, and similar to our results, they found that a switch to anterior translation of the tibia resulted in less wear (4.8 mm³/MC with anterior translation, 6.0 mm³/MC with posterior translation) [25]. The effect of this change was not investigated using the ISO Standard however, and only investigated changes in AP translation. The current direction of the field has shifted towards multi-activity and patient specific gait data [29], and while this is an important step, the standard should not be ignored as it is still relevant for regulatory approval, preclinical testing, and for comparison to other studies. The large differences between the old and new versions of the ISO standard indicate that care should be taken when comparing preclinical tests and wear studies that utilized different versions of the standard. It should be noted that wear scars seen in retrievals have been shown to cover a larger portion of the articular surface than was found in both the ISO(2014) and ISO(2004) predictions [30]. In future studies, we intend to investigate multi-activity and patient specific gait tests using our wear model and compare these to the ISO standard.

In conclusion, the results of the study suggest that major differences between ISO(2004) and ISO(2014) standard exist and therefore historical wear results should be compared with caution to newly obtained results. In addition, this study demonstrates the utility of FEA in wear analysis, though the wear model needs further work and validation before it can be used as a supplement to simulator testing.